Drosophila uses a tripod gait across all walking speeds, and the geometry of the tripod is important for speed control
- Department of Biology, Duke University, United States
- Department of Physics, Loyola University, United States
- Janelia Research Campus, Howard Medical Institute, United States
- School of Biomedical Engineering, Sciences and Health Systems, Drexel University, Duke Institute for Brain Sciences, Duke University, United States
Figures
Figure 1
A new mechanical model for a tripod gait.
(A) Schematic showing a simple model for the center of mass (CoM) movement during locomotion. In this model (spring-loaded inverted pendulum [SLIP]), the mass of the animal is concentrated into a point that is supported by a single massless spring. The arrow represents the direction of locomotion. This model can capture the basic features of the CoM movement during walking (in humans) and running (in both humans and cockroaches). (B) SLIP cannot describe the fly’s CoM movement, which has a mid-stance maxima in speed. (C) A fly walking on three legs can be described by a springy tripod. The sagittal plane mechanics is governed by the sagittal plane projection of the springy tripod (see rectangle). (D) A springy tripod will produce angular restorative forces. Any movement away from the mid-stance position will produce restorative forces (represented by thin arrows). The thick arrows represent forces from front and back legs; thickness of the arrow indicates the magnitude of the force. Top: before mid-stance, the front leg is stretched and the back leg is compressed, leading to larger forces from the back leg. Bottom: after mid-stance, the front leg is compressed and exerts larger tangential forces. Net result is restorative forces. (E) The sagittal projection of a springy tripod can be modeled as the angular and radial spring-loaded inverted pendulum (ARSLIP) model. The angular springs expand as the CoM moves away from the mid-stance position and thereby generate restorative forces. The restorative forces can produce the mid-stance maximum in speed observed in flies in addition to the CoM movement pattern in human walking and running.
Figure 2 with 2 supplements
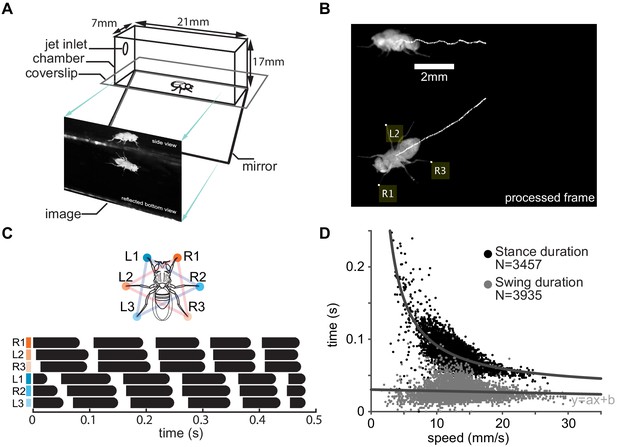
Experimental setup.
(A) Schematic of the arena. (B) A frame from a typical processed video of a fly walking in the chamber. The white traces track a point on the thorax and are a proxy for the center of mass. Yellow labels denote feet that are in stance, or the footholds. (C) Leg numbering and color coding (top), and gait maps (bottom) showing footfall patterns of individual legs in the R1–L2–R3 (orange) and L1–R2–L3 tripods (blue). Each row corresponds to a single leg. Black bars represent stance. (D) Stance and swing durations as functions of speed. The top dark gray line is the best fit of the reciprocal function to stance durations. The bottom lighter gray line is a best fit of linear regression to swing durations and shows a small decrease (a: −0.00018, p<0.00001, b = 0.03).
Figure 2—figure supplement 1
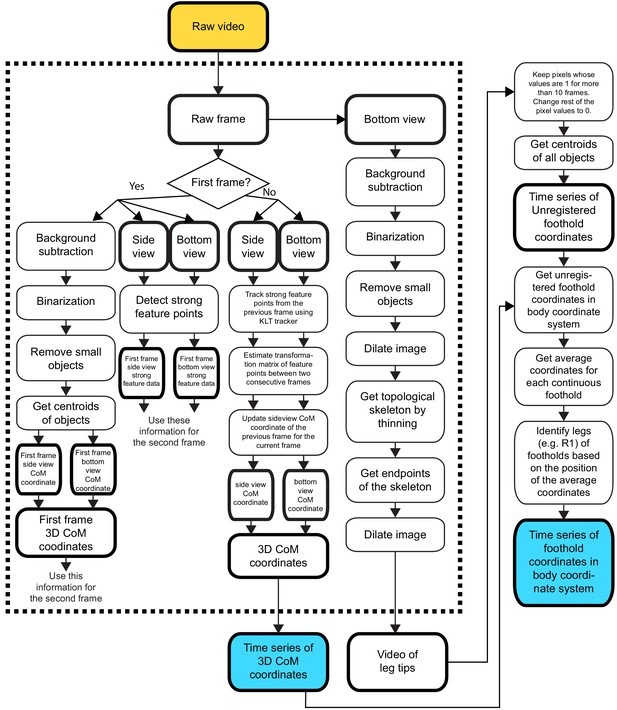
Image processing used to obtain the 3D coordinates of the center of mass (CoM) and the time series of footholds in the body coordinate system (referred to from 'Materials and methods').
Yellow box denotes input, and blue boxes denote output. Rectangular elements with thick edges denote processed output. Rectangular elements with thin edges denote processes.
Figure 2—figure supplement 2
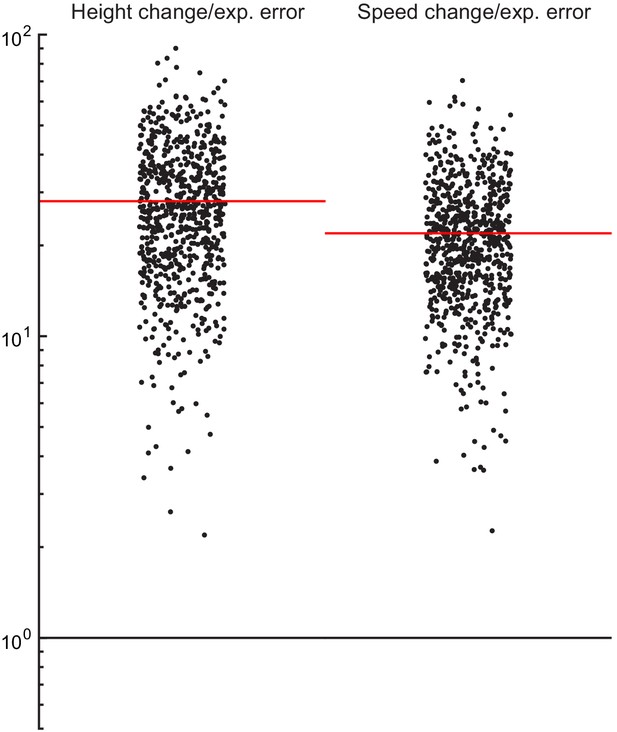
Size of experimental tracking error compared to height change and speed change values (referred to from 'Materials and methods').
Height change and speed change values were divided by root mean squared error of tracking. Height change and speed change values are similar but different to the metric defined in 'Materials and methods', 'Definition of M-tripod'. Here, after detrending a trajectory, we are subtracting minimum from maximum instead of summing. This quantity indicates the overall amplitude of fluctuation. Red lines are means of the ratios.
Figure 3
Interleg coordination pattern is consistent with a modified tripod (M-tripod) gait.
(A) Stance for all steps relative to R1 sorted by speed. (B) Normalized time delays of stance start times between legs within a tripod (R1 and L2, L2 and R3) and legs in the opposing tripod (R1 and L1). The time delays were normalized by cycle duration. R1–L2 and L2–R3 delays are small at low speeds and become even smaller as the walking speed increases (Wilcoxon sign-rank test). R1–L1 delays are unchanged. (C) The phase difference between legs is consistent with a single gait, which is a modified version of a tripod (M-tripod) in which the front leg of the tripod leads the middle leg that in turn leads the back leg. The delay between the legs has a small dependence on speed (v). (D) Definition of leg phase angles. Stances start and end at 0 and π, respectively; swings start and end at –π and 0, respectively. (E) The leg phases relative to R1 show that interleg coordinations at different speeds all consistent with M-tripod. The delays between tripod legs do become smaller with speed (Wilcoxon sign-rank test) while the delays between R1 and L1 leg remain unchanged. (F) The M-tripod based on phase lag (v=speed).
Figure 4 with 1 supplement
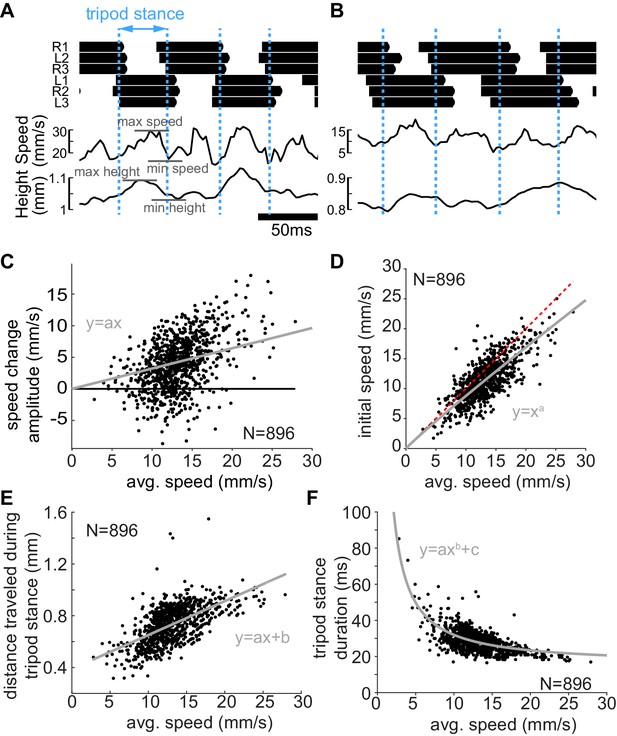
Mechanical changes associated with changes in speed.
(A) Example trace showing the changes in center of mass (CoM) speed and height. Dotted blue lines are the boundaries between consecutive tripod stance (see text). The CoM shows clear mid-stance maxima in height and speed. (B) A slower step is characterized by smaller initial speed, smaller speed changes, and lower height. (C) Within step speed changes increase with speed (p<0.0001). Line is the best fit of y=ax to the data. a = 0.32. (D) The initial speed increases as the fly walks faster, but this increased speed makes a smaller contribution at higher speed reflected by the increased deviation (gray line is the best fit) from the line of unity (dotted red line). a = 0.9438; 95% confidence bounds (0.9393, 0.9484). (E) Distance traveled during tripod stance increases with speed (p<0.0001). a = 0.026, b = 0.39. (F) Tripod stance duration decreases with speed. a = 187.8, b = −1.056, c = 15.45.
Figure 4—figure supplement 1
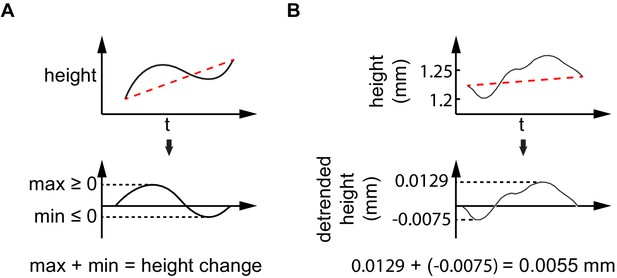
Calculation for height and speed change.
(A) Algorithm for height and speed change calculation. (B). Example calculation on the experimental data (referred to from 'Materials and methods').
Figure 5
The angular and radial spring-loaded inverted pendulum (ARSLIP) model is equivalent to the springy tripod model.
(A) The sagittal plane mechanics is governed by the sagittal plane projection of the springy tripod. The arrow denotes the direction of motion. The parameters that define the springy tripod model are shown. The overall stiffness of the springy tripod is determined by the spring constant of individual legs, k, the height of the tripod (rm), and the distance between the front and back legs (2L). See Table 1 as well. The behavior of the springy tripod is described by how the coordinates of the point mass – r and – change with time. (B) The sagittal plane projection of a springy tripod can be modeled as the ARSLIP model. The parameters that describe the ARSLP model are shown. Just like the springy tripod, ARSLIP is described by how the coordinates of the point mass – r and – change with time. The potential energy of the tripod can be derived as a sum of the elastic energies of the three legs. The ARSLIP potential energy can be derived by summing radial and angular potential energies. The equivalence of the two models is shown by finding parameter set for ARSLIP where the potential energies as a function of r and are similar when is small and changes in r are small (derived in 'Materials and methods').
Figure 6 with 1 supplement
Angular and radial spring-loaded inverted pendulum (ARSLIP) describes the kinematics of a fly’s center of mass (CoM).
(A) The best fit of SLIP (green) and (B) ARSLIP models – to the height (top) and horizontal position of the CoM (middle). Speed (bottom) was not used to fit but is plotted to simply show why SLIP fails. Gait maps are shown with CoM height. (C) ARSLIP is a significantly better model than SLIP (Wilcoxon rank-sum test; p<0.001 for both horizontal and vertical movement). Each dot is the root mean squared error (RMSE) for the best fit to a single tripod stance. The example step presented in (A) and (B) is marked as a black dot and was chosen close to the SLIP median RMSE. Black horizontal line is the median. (D) γs (left) and γa (right), which are nondimensionalized spring constants, increase with speed in most flies. Each line is a fit to the steps from a single fly. Black dots (n = 74) show values corresponding to individual steps for one fly and the fit corresponding to that fly. Solid lines are the regressions with p<0.05 from F-test, and dotted lines are p>0.05.
Figure 6—figure supplement 1
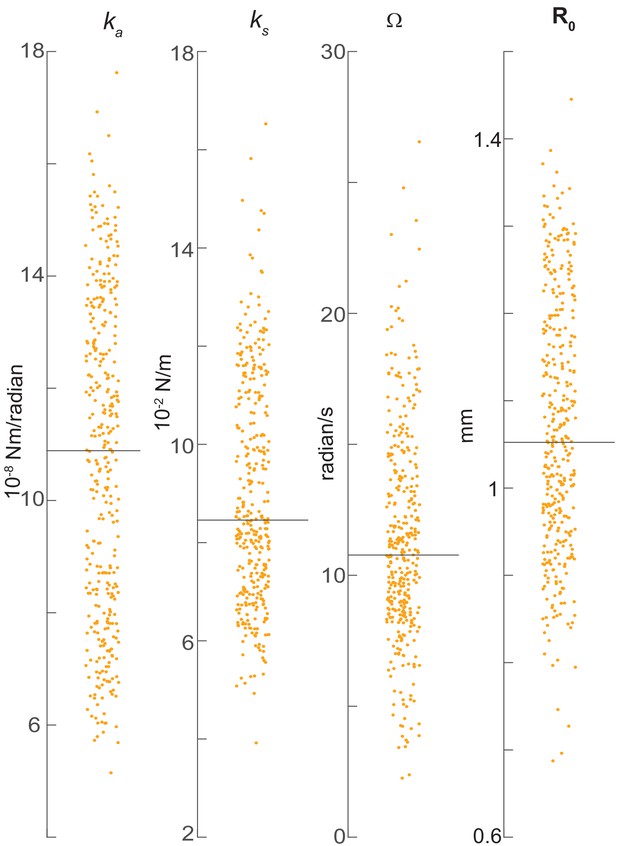
Fit parameters of the angular and radial spring-loaded inverted pendulum model.
Each dot is the the best fit parameter for a single tripod stance.
Figure 7
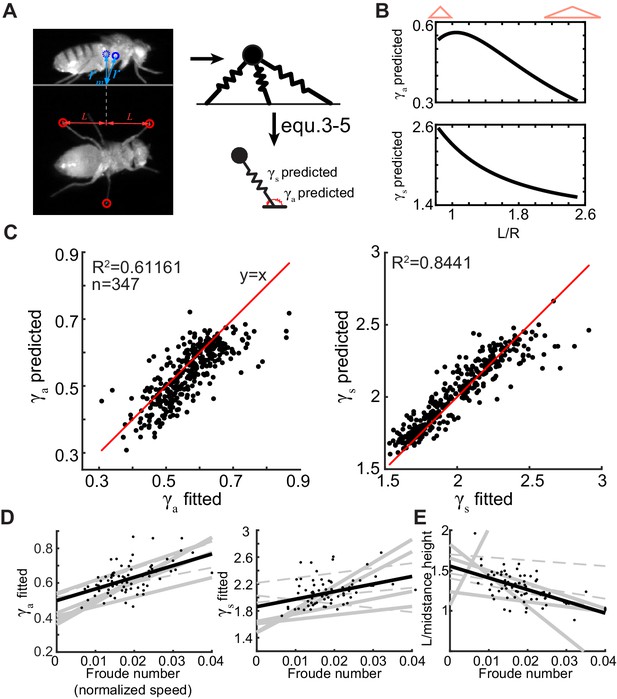
Flies increase their height and decrease the extent of their tripod as they increase their speed.
(A) We measure rm and L for each step which describe the tripod geometry during a step. The tripod geometry can be used to predict γa and γs using Equations 3–5. (B) γa (top) and γs (bottom) decrease as L/rm increases. Narrow and high tripods are stiffer (see red cartoons atop). (C) The spring constants predicted from geometry closely correlate to the optimal spring constants calculated in Figure 6 (γa: left and γs: right). The red line is the line of unity. (D) γa (left) and γs (right) replotted from Figure 6 show increase with speed. (E) Increases in Fr in most flies are concomitant with decrease in L/rm. Each line is a fit to a different fly. Solid lines are the regressions with p<0.05 from F-test, and dotted lines are p>0.05. Black dots (n = 74) show values corresponding to individual steps for one fly, and black line is a fit for that fly.
Figure 8
The large variation in tripod geometry can explain why insects that employ a tripod gait have varying speed and kinematics.
Two parameters that affect the stiffness of an animal walking on a tripod are the nondimensionalized stiffness of each leg (γ) and the geometry of the tripod defined by the ratio L/rm. (A) The curve divides the γ-L/rm plane into two regions with either fly-like or cockroach-like kinematics. The data points show the values from fits to the fly data. The alphabets represent approximate L/rm ratio for a few insects as noted below. Most insects have an L/rm ratio near the minimum of the curve, making it more likely that they can achieve an inverted fly-like kinematic profile. (B) Plot of leg spring constant as a function of L/rm ratio. Many insects have L/rm ratio such that changes in L/rm ratio can affect γs. Cockroaches have L/rm ratio where changes in geometry would have little effect on the spring constant.
a=Formica polyctena; b=Formica pratensis; c=Carausius morosus; d=Aretaon asperrimus; e=Medauroidea extradentata; f=Periplaneta americana; g=Blaberus discoidalis.
Videos
Video 1
Video of the fly showing the top and side views.
The center of mass is marked on both the top and side views. The rhythmic up and down movement of the center of mass can be seen on the top view. The stance legs are also marked.
Video 2
The output of each processing step is plotted.
Tables
Table 1
Notations used in the article.
| Symbol | Definition and units | Other explanation |
|---|---|---|
| r | Radial coordinate | Variable in ARSLIP and SLIP models |
| θ | Angular coordinate | Variable in ARSLIP and SLIP models |
| R | (AR)SLIP spring natural length | Optimized for each fly. Set to be within 10% of the measured mesothoracic leg |
| Rtri | Tripod spring natural length | Optimized for each fly |
| ks | Radial spring constant | Variable in ARSLIP and SLIP models |
| ka | Angular spring constant | Variable in ARSLIP and SLIP models |
| k | Spring constant for individual legs | Variable in springy tripod |
| rm | Mid-stance height | Experimentally determined for each step (see Figure 7A) |
| v | Speed or horizontal velocity | |
| V | ARSLIP potential energy | |
| ≡ r/ R | Nondimensional radial coordinate | |
| γs | Nondimensional radial spring constant | |
| γa | Nondimensional angular spring constant | |
| Nondimensional mid-stance height | rm / R | |
| Ω | Nondimensional mid-stance angular speed | |
| Fr | Froude number – nondimensionalized speed | v 2/(g*leg length) |
| L | Tripod spread | Experimentally determined for each step (see Figure 7A) |
| Vtri | Tripod potential energy | |
| g | Gravitational constant | |
| m | Mass of the fly | Mass was kept fixed; average mass of flies of a particular sex and genotype was measured |
| ARSLIP | Angular and radial spring-loaded inverted pendulum |
Table 2
Number of data points in the plots.
| Figures | ||||||||
|---|---|---|---|---|---|---|---|---|
| Figure 2D | Figure 3A | Figure 3B,E | Figure 4C–F | Figure 6C | Figures 6D, 7C,D | |||
| Fly | Genotype | Stance | Swing | |||||
| 1 | Berlin K | 8 | 9 | 1 | 0 | 2 | 2 | 0 |
| 2 | Berlin K | 4 | 9 | 0 | 0 | 0 | 0 | 0 |
| 3 | Berlin K | 152 | 194 | 20 | 15 | 42 | 14 | 6 |
| 4 | Berlin K | 284 | 330 | 40 | 46 | 82 | 78 | 78 |
| 5 | Berlin K | 72 | 90 | 10 | 12 | 21 | 18 | 18 |
| 6 | Berlin K | 108 | 114 | 16 | 17 | 31 | 28 | 28 |
| 7 | Berlin K | 367 | 458 | 43 | 53 | 97 | 74 | 74 |
| 8 | Berlin K | 388 | 454 | 47 | 59 | 102 | 44 | 44 |
| 9 | Berlin K | 50 | 63 | 5 | 7 | 9 | 0 | 0 |
| 10 | W1118 | 1496 | 1564 | 202 | 227 | 390 | 90 | 90 |
| 11 | Oregon RC | 45 | 53 | 5 | 6 | 5 | 0 | 0 |
| 12 | Tac 3 | 265 | 325 | 32 | 42 | 63 | 5 | 0 |
| 13 | Berlin K | 165 | 209 | 17 | 26 | 38 | 9 | 9 |
| 14 | Berlin K | 53 | 63 | 5 | 9 | 14 | 4 | 0 |
| Total | 3457 | 3935 | 443 | 519 | 896 | 366 | 347 | |
-
Data used for Figure 2D were stance and swing durations for each of the six legs. Data used for Figure 3A,B and E were derived from all complete gait cycles that include at least one frame of the last leg’s stance phase. Data for Figure 3A had an additional constraint that required a cycle data to have complete observation of the last leg’s stance phase from start to end. Data used for Figure 4 were derived from all tripod stance phase. Data used for Figure 6 and 7 were derived from tripod stance phases in which the single support phase constitutes at least 25% of stance. However, additional constraints were added to Figure 6D and 7: data with erroneous leg position tracks were eliminated, and then flies with less than six steps were eliminated.
Table 3
Measured parameter values for each species and gender.
| Fly number | Gender | Strain | (mm) | Mass (mg) |
|---|---|---|---|---|
| 1 | Female | Berlin K | 2.1032 | 1.0809 |
| 2 | Female | Berlin K | 2.184 | |
| 3 | Female | Berlin K | 2.1031 | |
| 4 | Female | Berlin K | 1.9988 | |
| 5 | Female | Berlin K | 1.9869 | |
| 6 | Male | Berlin K | 1.8888 | 0.6798 |
| 7 | Male | Berlin K | 1.9272 | |
| 8 | Male | Berlin K | 2.0646 | |
| 9 | Male | Berlin K | 2.0404 | |
| 10 | Female | W1118 | 2.042 | 1.123 |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Drosophila uses a tripod gait across all walking speeds, and the geometry of the tripod is important for speed control
eLife 10:e65878.
https://doi.org/10.7554/eLife.65878
