Evolving interpretable plasticity for spiking networks
Figures
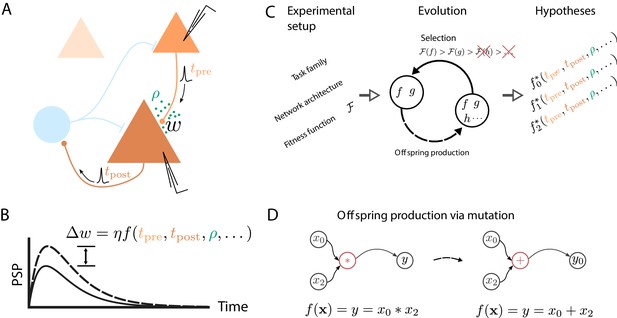
Artificial evolution of synaptic plasticity rules in spiking neuronal networks.
(A) Sketch of cortical microcircuits consisting of pyramidal cells (orange) and inhibitory interneurons (blue). Stimulation elicits action potentials in pre- and postsynaptic cells, which, in turn, influence synaptic plasticity. (B) Synaptic plasticity leads to a weight change () between the two cells, here measured by the change in the amplitude of post-synaptic potentials. The change in synaptic weight can be expressed by a function that in addition to spike timings () can take into account additional local quantities, such as the concentration of neuromodulators (ρ, green dots in A) or postsynaptic membrane potentials. (C) For a specific experimental setup, an evolutionary algorithm searches for individuals representing functions that maximize the corresponding fitness function . An offspring is generated by modifying the genome of a parent individual. Several runs of the evolutionary algorithm can discover phenomenologically different solutions () with comparable fitness. (D) An offspring is generated from a single parent via mutation. Mutations of the genome can, for example, exchange mathematical operators, resulting in a different function .
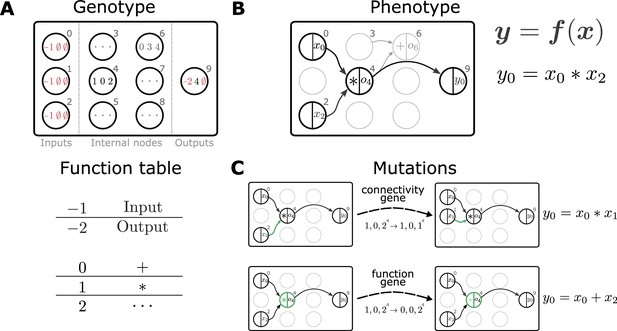
Representation and mutation of mathematical expressions in Cartesian genetic programming.
(A) The genotype of an individual is a two-dimensional Cartesian graph (top). In this example, the graph contains three input nodes (), six internal nodes () and a single output node (9). In each node, the genes of a specific genotype are shown, encoding the operator used to compute the node’s output and its inputs. Each operator gene maps to a specific mathematical function (bottom). Special values () represent input and output nodes. For example, node four uses the operator 1, the multiplication operation '*', and receives input from nodes 0 and 2. This node’s output is hence given by . The number of input genes per node is determined by the operator with the maximal arity (here two). Fixed genes that cannot be mutated are highlighted in red. ∅ denotes non-coding genes. (B) The computational graph (phenotype) generated by the genotype in A. Input nodes () represent the arguments of the function . Each output node selects one of the other nodes as a return value of the computational graph, thus defining a function from input to output . Here, the output node selects node four as a return value. Some nodes defined in the genotype are not used by a particular realization of the computational graph (in light gray, e.g., node 6). Mutations that affect such nodes have no effect on the phenotype and are therefore considered ‘silent’. (C) Mutations in the genome either lead to a change in graph connectivity (top, green arrow) or alter the operators used by an internal node (bottom, green node). Here, both mutations affect the phenotype and are hence not silent.
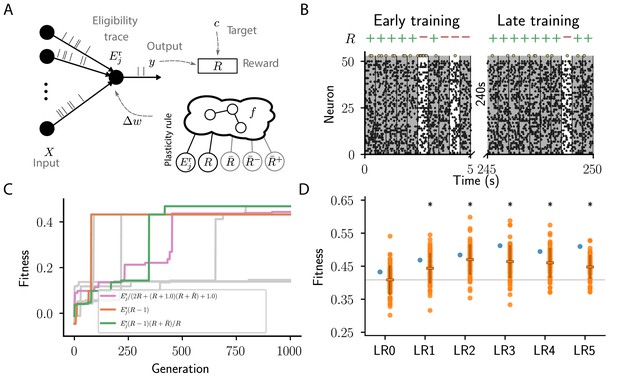
Cartesian genetic programming evolves various efficient reward-driven learning rules.
(A) Network sketch. Multiple input neurons with Poisson activity project to a single output unit. Pre- and postsynaptic activity generate an eligibility trace in each synapse. Comparison between the output activity and the target activity generates a reward signal. , and , represent the expected reward, the expected positive and the expected negative reward, respectively. Depending on the hyperparameter settings either the former or the latter two are provided to the plasticity rule. (B) Raster plot of the activity of input neurons (small black dots) and output neuron (large golden dots). Gray (white) background indicate patterns for which the output should be active (inactive). Top indicates correct classifications (+) and incorrect classifications (-). We show 10 trials at the beginning (left) and the end of training (right) using the evolved plasticity rule: . (C) Fitness of best individual per generation as a function of the generation index for multiple example runs of the evolutionary algorithm with different initial conditions but identical hyperparameters. Labels show the expression at the end of the respective run for three runs resulting in well-performing plasticity rules. Gray lines represent runs with functionally identical solutions or low final fitness. (D) Fitness of a selected subset of evolved learning rules on the 10 experiments used during the evolutionary search (blue) and additional 80 fitness evaluations, each on 10 new experiments consisting of sets of frozen noise patterns and associated class labels not used during the evolutionary search (orange). Horizontal boxes represent mean, error bars indicate one standard deviation over fitness values. Gray line indicates mean fitness of LR0 for visual reference. Black stars indicate significance () with respect to LR0 according to Welch’s T-tests (Welch, 1947). See main text for the full expressions for all learning rules.
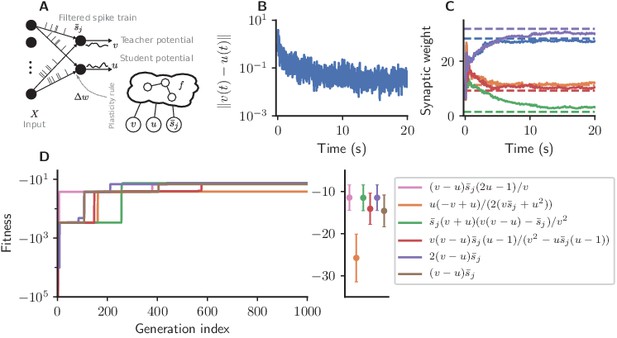
Cartesian genetic programming evolves efficient error-driven learning rules.
(A) Network sketch. Multiple input neurons with Poisson activity project to two neurons. One of the neurons (the teacher) generates a target for the other (the student). The membrane potentials of teacher and student as well as the filtered pre-synaptic spike trains are provided to the plasticity rule that determines the weight update. (B) Root mean squared error between the teacher and student membrane potential over the course of learning using the evolved plasticity rule: . (C) Synaptic weights over the course of learning corresponding to panel B. Horizontal dashed lines represent target weights, that is, the fixed synaptic weights onto the teacher. (D) Fitness of the best individual per generation as a function of the generation index for multiple runs of the evolutionary algorithm with different initial conditions. Labels represent the rule at the end of the respective run. Colored markers represent fitness of each plasticity rule averaged over 15 validation tasks not used during the evolutionary search; error bars indicate one standard deviation.
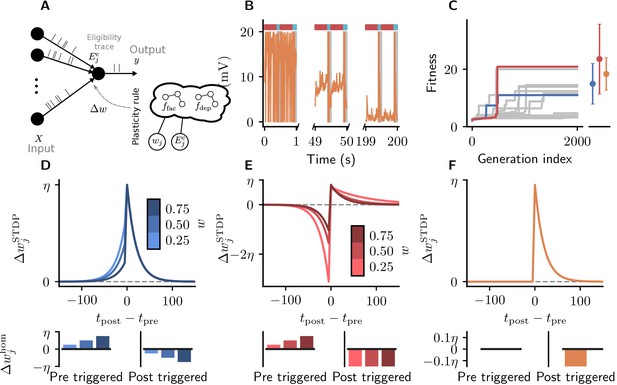
Cartesian genetic programming evolves diverse correlation-driven learning rules.
(A) Network sketch. Multiple inputs project to a single output neuron. The current synaptic weight wj and the eligibility trace are provided to the plasticity rule that determines the weight update. (B) Membrane potential of the output neuron over the course of learning using Equation 17. Gray boxes indicate presentation of the frozen-noise pattern. (C) Fitness (Equation 13) of the best individual per generation as a function of the generation index for multiple runs of the evolutionary algorithm with different initial conditions. Blue and red curves correspond to the two representative plasticity rules selected for detailed analysis. Blue and red markers represent fitness of the two representative rules and the orange marker the fitness of the homeostatic STDP rule (Equation 17; Masquelier, 2018), respectively, on 20 validation tasks not used during the evolutionary search. Error bars indicate one standard deviation over tasks. (D, E): Learning rules evolved by two runs of CGP (D: LR1, Equation 19; E: LR2, Equation 20). (F): Homeostatic STDP rule Equation 17 suggested by Masquelier, 2018. Top panels: STDP kernels as a function of spike timing differences for three different weights wj. Bottom panels: homeostatic mechanisms for those weights. The colors are specific to the respective learning rules (blue for LR1, red for LR2), with different shades representing the different weights wj. The learning rate is .
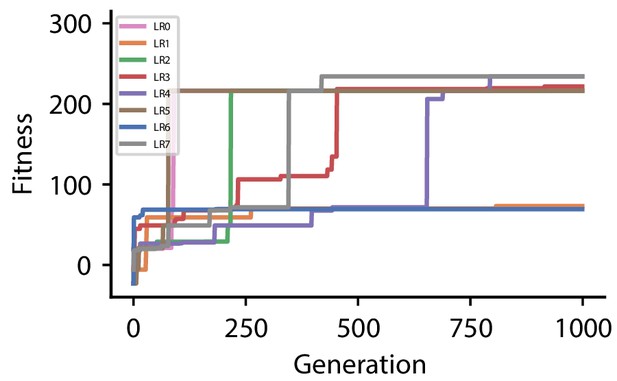
Fitness of best individual per generation as a function of the generation index for multiple runs of the evolutionary algorithm with different initial conditions for hyperparameter set 0.
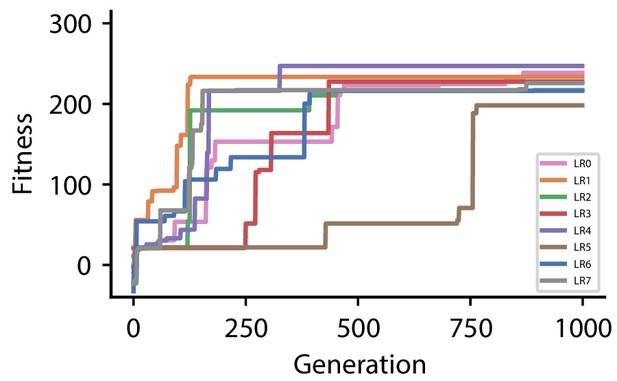
Fitness of best individual per generation as a function of the generation index for multiple runs of the evolutionary algorithm with different initial conditions for hyperparameter set 1.
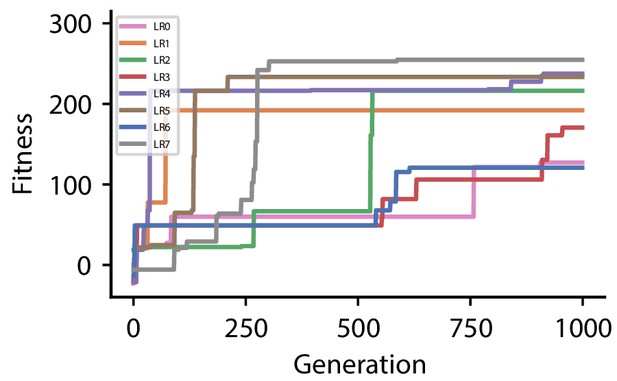
Fitness of best individual per generation as a function of the generation index for multiple runs of the evolutionary algorithm with different initial conditions for hyperparameter set 2.
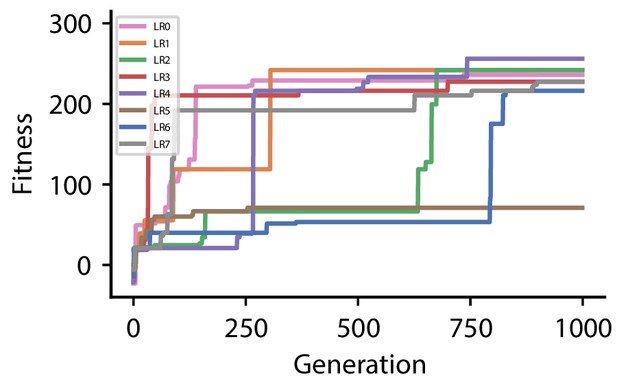
Fitness of best individual per generation as a function of the generation index for multiple runs of the evolutionary algorithm with different initial conditions for hyperparameter set 3.
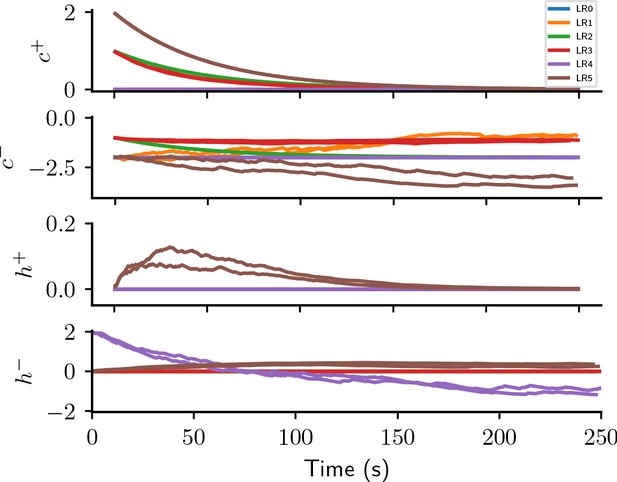
Causal and homeostatic terms of LR-LR6 over trials.
represent causal terms (prefactors of eligibility trace), represent homeostatic terms, for positive and negative rewards, respectively.
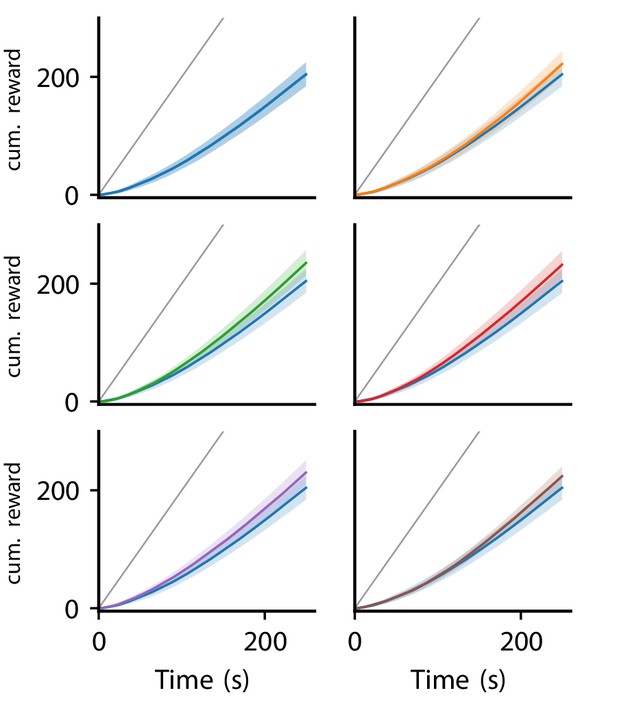
Cumulative reward of LR-LR5 over trials.
Solid line represent mean, shaded regions indicate plus/minus one standard deviation over 80 experiments. Cumulative reward of LR0 shown in all panels for comparison. Gray line indicates maximal performance (maximal reward received in each trial).
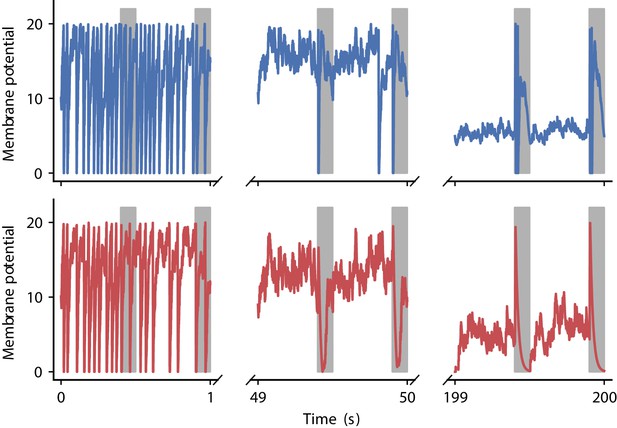
Evolution of membrane potential for two evolved learning rules.
Membrane potential of the output neuron over the course of learning using the two evolved learning rules LR1 (top row, Equation 19) and LR2 (bottom row, Equation 20) (compare Figure 5B). Gray boxes indicate presentation of the frozen-noise pattern.
Tables
Description of the network model used in the reward-driven learning task (4.5).
| A model summary | ||
| Populations | 2 | |
| Topology | — | |
| Connectivity | Feedforward with fixed connection probability | |
| Neuron model | Leaky integrate-and-fire (LIF) with exponential post-synaptic currents | |
| Plasticity | Reward-driven | |
| Measurements | Spikes | |
| B populations | ||
| Name | Elements | Size |
| Input | Spike generators with pre-defined spike trains (see 4.5) | |
| Output | LIF neuron | 1 |
| C connectivity | ||
| Source | Target | Pattern |
| Input | Output | Fixed pairwise connection probability ; synaptic delay ; random initial weights from |
| D neuron model | ||
| Type | LIF neuron with exponential post-synaptic currents | |
| Subthreshold dynamics | if not refractory | |
| else , : neuron index, : spike index | ||
| Spiking | Stochastic spike generation via inhomogeneous Poisson process with intensity ; reset of to after spike emission and refractory period of | |
| E synapse model | ||
| Plasticity | Reward-driven with episodic update (Equation 2, Equation 3) | |
| Other | Each synapse stores an eligibility trace (Equation 22) | |
| F simulation parameters | ||
| Populations | ||
| Connectivity | ||
| Neuron model | ||
| Synapse model | ||
| Input | ||
| Other | ||
| G CGP parameters | ||
| Population | ||
| Genome | ||
| Primitives | Add, Sub, Mul, Div, Const(1.0), Const(0.5) | |
| EA | ||
| Other | ||
Description of the network model used in the error-driven learning task (4.6).
| A model summary | ||
| Populations | 3 | |
| Topology | — | |
| Connectivity | Feedforward with all-to-all connections | |
| Neuron model | Leaky integrate-and-fire (LIF) with exponential post-synaptic currents | |
| Plasticity | Error-driven | |
| Measurements | Spikes, membrane potentials | |
| B populations | ||
| Name | Elements | Size |
| Input | Spike generators with pre-defined spike trains (see 4.6) | |
| Teacher | LIF neuron | 1 |
| Student | LIF neuron | 1 |
| C connectivity | ||
| Source | Target | Pattern |
| Input | Teacher | All-to-all; synaptic delay ; random weights ; weights randomly shifted by on each trial |
| Input | Student | All-to-all; synaptic delay ; fixed initial weights w0 |
| D neuron model | ||
| Type | LIF neuron with exponential post-synaptic currents | |
| Subthreshold dynamics | : neuron index, : spike index | |
| Spiking | Stochastic spike generation via inhomogeneous Poisson process with intensity ; no reset after spike emission | |
| E synapse model | ||
| Plasticity | Error-driven with continuous update (Equation 7, Equation 9) | |
| F simulation parameters | ||
| Populations | ||
| Connectivity | ||
| Neuron model | ||
| Synapse model | ||
| Input | ||
| Other | ||
| G CGP parameters | ||
| Population | ||
| Genome | ||
| Primitives | Add, Sub, Mul, Div, Const(1.0) | |
| EA | ||
| Other | ||
: Description of the network model used in the correlation-driven learning task (4.7).
| A model summary | ||
| Populations | 2 | |
| Topology | — | |
| Connectivity | Feedforward with fixed connection probability | |
| Neuron model | Leaky integrate-and-fire (LIF) with exponential post-synaptic currents | |
| Plasticity | Reward-driven | |
| Measurements | Spikes | |
| B populations | ||
| Name | Elements | Size |
| Input | Spike generators with pre-defined spike trains (see 4.5) | |
| Output | LIF neuron | 1 |
| C connectivity | ||
| Source | Target | Pattern |
| Input | Output | Fixed pairwise connection probability ; synaptic delay ; random initial weights from |
| D neuron model | ||
| Type | LIF neuron with exponential post-synaptic currents | |
| Subthreshold dynamics | if not refractory | |
| else , : neuron index, : spike index | ||
| Spiking | Stochastic spike generation via inhomogeneous Poisson process with intensity ; reset of to after spike emission and refractory period of | |
| E synapse model | ||
| Plasticity | Reward-driven with episodic update (Equation 2, Equation 3) | |
| Other | Each synapse stores an eligibility trace (Equation 22) | |
| F simulation parameters | ||
| Populations | ||
| Connectivity | ||
| Neuron model | ||
| Synapse model | ||
| Input | ||
| Other | ||
| G CGP parameters | ||
| Population | ||
| Genome | ||
| Primitives | Add, Sub, Mul, Div, Pow, Const(1.0) | |
| EA | ||
| Other | ||





