Ciliary chemosensitivity is enhanced by cilium geometry and motility
- Max Planck Institute for Dynamics and Self-Organization (MPIDS), Germany
- J. Stefan Institute, Slovenia
- Rudolf Peierls Centre for Theoretical Physics, University of Oxford, United Kingdom
Figures
Figure 1
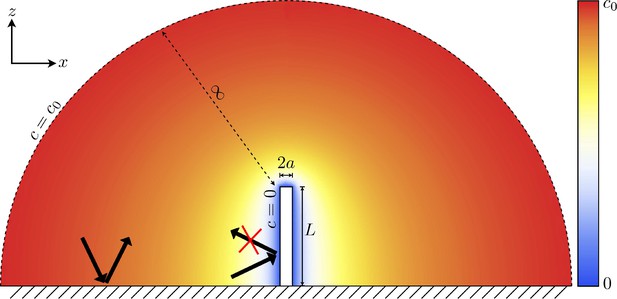
The concentration boundary conditions and general setup of the problem to be solved.
The cilium satisfies an absorbing boundary condition, and there is a constant concentration an infinite distance from the cilium. The coloured overlay shows the concentration field in the absence of any fluid flow.
Figure 2 with 1 supplement
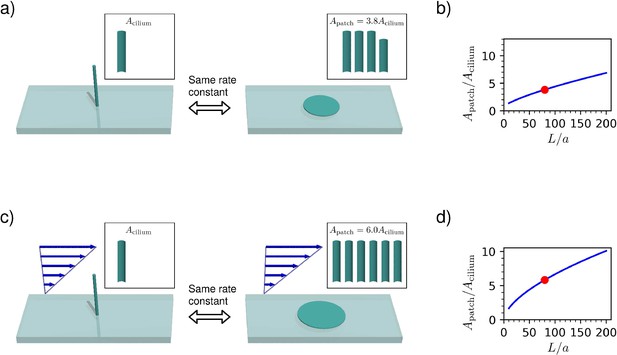
Comparison between capture rates of a non-motile cilium and a circular patch on the surface.
All diagrams use , indicated on the graphs by a red dot. (a) In a quiescent fluid, the cilium has the same capture rate as a surface patch with 3.8 times the surface area. (b) The area ratio as a function of the cilium aspect ratio in a quiescent fluid, given by Equation (6). (c) In a shear flow at a high Péclet number, the capture rate of the cilium reaches that of a surface patch with 6.0 times the surface area. (d) The area ratio as a function of the aspect ratio in the high Péclet number limit (Equation 14).
Figure 2—figure supplement 1
Capture rate as a function of the Péclet number for passive cilia in a shear flow, obtained from numerical simulations.
The lines show the capture rates for cilia that absorb particles only on a fraction of their length, starting from the tip. The schematics indicate the absorbing part of the cilium in blue and the non-absorbing part in black.
-
Figure 2—figure supplement 1—source data 1
Event counts and calculated rates as shown in Figure 2—figure supplement 1.
- https://cdn.elifesciences.org/articles/66322/elife-66322-fig2-figsupp1-data1-v2.zip
Figure 3 with 1 supplement
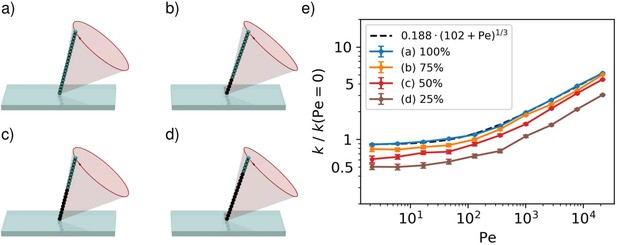
The capture rate of an active cilium for four types of motion.
(a) The cilium is undergoing reciprocal motion, which is not generating any net flow. (b) The cilium moves along a cone with its axis perpendicular to the surface, such that it produces a rotational flow, but no long-range fluid transport. (c) The cilium moves along a tilted cone, which generates a long-range volume flow. (d) The cilium follows a realistic trajectory, beginning with a recovery stroke along the no-slip surface in 1, then performing an overhead power-stroke from 2 to 3 before returning to one in another recovery stroke. (e) The capture rate constants of a beating cilium as a function of the Péclet number. The rates are determined using stochastic simulations. The error bars denote 95% confidence intervals and the dashed line shows a fit function that interpolates between the high and low-Péclet limits. All rates are normalised to the rate constant for a diffusion-limited capture with a cylindrical cilium with the same length and width.
-
Figure 3—source data 1
Event counts and calculated rates as shown in Figure 3e.
- https://cdn.elifesciences.org/articles/66322/elife-66322-fig3-data1-v2.zip
Figure 3—figure supplement 1
Capture rate of an actively beating cilium tracing out a tilted cone, plotted as a function of the Péclet number.
These results were obtained from numerical simulations. The lines show the capture rates for cilia that absorb particles only on a fraction of their length, starting from the tip. The schematics indicate the absorbing part of the cilium in blue and the non-absorbing part in black.
-
Figure 3—figure supplement 1—source data 1
Event counts and calculated rates as shown in Figure 3—figure supplement 1.
- https://cdn.elifesciences.org/articles/66322/elife-66322-fig3-figsupp1-data1-v2.zip
Figure 4
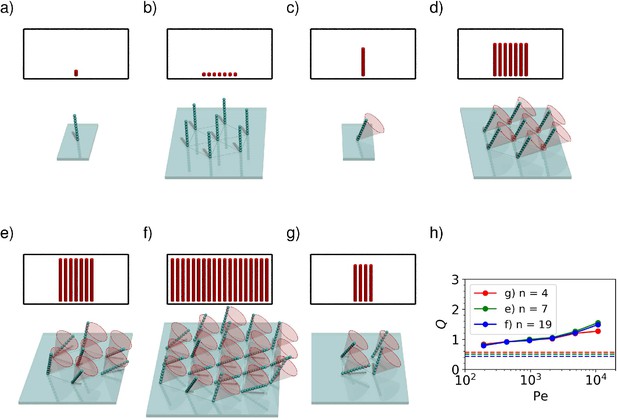
Comparison between the capture rate constant of a single cilium (a, c) and a bundle of cilia (b, d–g).
In the insets, the height of each red cylinder indicates the rate constant per cilium at , and the number of cylinders represents the number of cilia. For immotile cilia (a, b), a bundle has a lower per-cilium capture rate than an isolated cilium, although the the total rate constant of the bundle is higher. The reduced capture rate per cilium is caused by the depletion of ligands close to the bundle. For motile cilia (d–g), the situation is reversed and the capture rate per cilium in a bundle (d–g) can be significantly higher than for an isolated cilium (c). The increase can be explained by the collective flow generation, which helps the capture on all cilia. In (d) the cilia all beat with the same frequency corresponding to but with identical phases. In (e–g) all cilia beat with the same frequency corresponding to , but their phases are chosen randomly. It can be seen that the random phases give a higher rate constant than the uniform phases. (h) shows how the performance gain varies with the Péclet number for different configurations. The rates shown at each point are the average of 30 random phase configurations like the one shown in (e). The dashed line is the -value for for each configuration.
-
Figure 4—source data 1
Event counts and calculated rates as shown in Figure 4h.
- https://cdn.elifesciences.org/articles/66322/elife-66322-fig4-data1-v2.zip
Figure 5
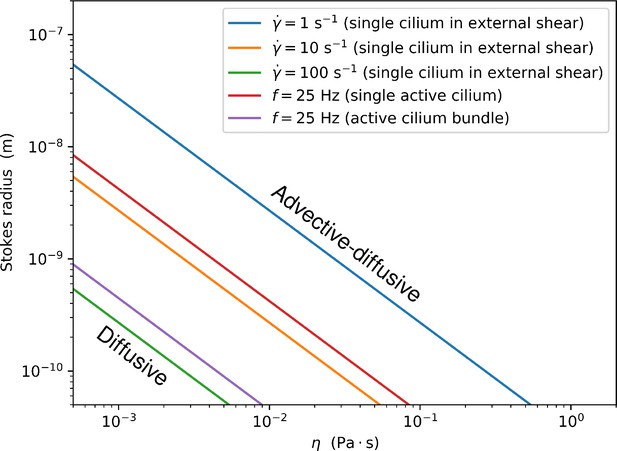
The demarcation between the regime where the rate constant is determined mostly by the diffusion limit and the regime in which it is enhanced by advection as a function of the fluid viscosity η and the particle Stokes radius.
Figure 6
The boundary conditions used for injection.
Since the fraction in incident particles absorbed by the cilium is small compared to the fraction absorbed by the outer surface, the concentration at the inner boundary is very close to c0. The coloured overlay shows the concentration as recorded in an example numerical simulation of a cilium in a shear flow with .
Appendix 2—figure 1
Streamlines (lines with a constant value of the stream function ψ) of the flow around a cylinder (black) and the concentration of emitted particles (red).
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Ciliary chemosensitivity is enhanced by cilium geometry and motility
eLife 10:e66322.
https://doi.org/10.7554/eLife.66322
