Figures and data in Quantitative theory for the diffusive dynamics of liquid condensates | eLife

Figures
Videos
Additional files

7 figures, 3 videos and 2 additional files

Figures

Figure 1

Download asset Open asset

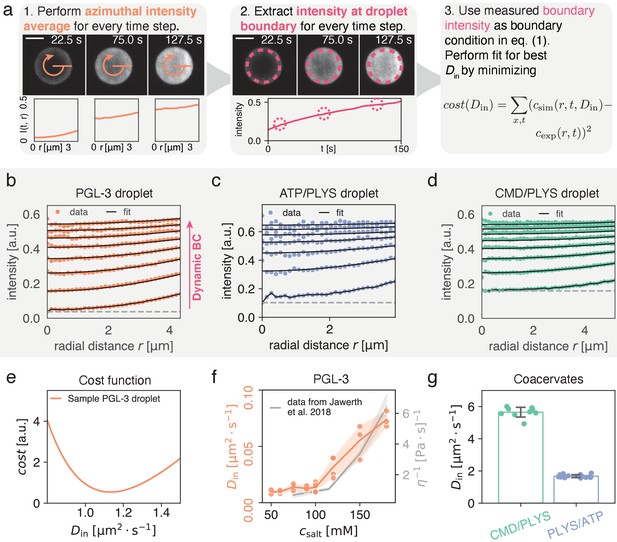
Quantitatively measuring $D_{i n}$ by extracting intensity at condensate interface.

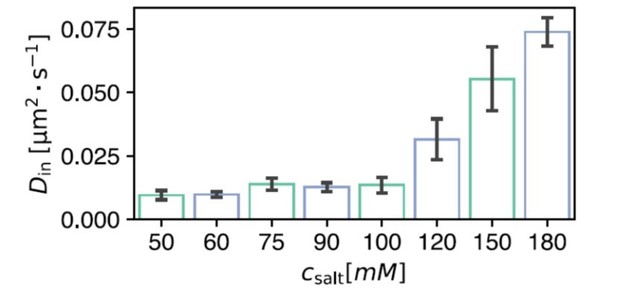
(a) (1) Spatial time course of FRAP recovery after full bleach for PLYS/ATP coacervate droplet. Azimuthal average (orange) is highlighted. (2) To obtain the boundary condition $c (r = R_{-}, t)$ , fluorescence intensity is extracted approximately $1.4 μ m$ away from the interface (see methods). Data closer to the droplet boundary can be subject to optical artefacts giving rise to an artificially broad interface. Lower panel shows azimuthal averages at different time points. (3) Cost function for fitting. For each fitting step, a numerical solution to Equation (1a) is calculated with a trial $D_{in}$ and the experimentally measured boundary condition from step (2). Subsequently simulation and experiment are compared according to the cost function, before choosing the next trial $D_{in}$ . Scale bar, $5 μ m$ . (b) Flurorescence recovery inside a PGL-3 condensate, along the radial direction (azimuthal averages, see (a)). $D_{in}$ is extracted by global fitting of Equation (1b) to the experimental profiles, using the experimentally extracted initial and boundary conditions (see panel (a) (1) and (2)). The gray line indicates an offset that comes about due to incomplete bleaching, and a small but visible, fast and uniform recovery with unknown cause (see Materials and methods). (c) Same as (b) but for ATP/PLYS coacervate droplet. (d) Same as (b) but for a CMD/PLYS coacervate droplet. (e) Cost function (see panel (a)) used to extract $D_{in}$ for a PGL-3 droplet. Due to the smoothness of the cost function, the minimum can be determined with high accuracy. (f) Comparison between $D_{in}$ and viscosity η for PGL-3 condensates at different salt concentrations. Viscosity data taken from Jawerth et al., 2018 for untagged PGL-3. Note, GFP-tagged PGL-3 has a higher viscosity than untagged PGL-3, which means the hydrodynamic radius of PGL-3:GFP cannot be directly computed from this panel (Jawerth et al., 2020). Replicates: salt concentration [mM]/#: 50/2, 60/3, 75/3, 90/3, 100/6, 120/4, 150/3, 180/3. (g) Diffusion coefficients for coacervate systems. Each data point represents $D_{in}$ for a single droplet time course. Note the low spread of the measured values. Replicates: CMD/PLYS: 9, PLYS/ATP:16.

Figure 2

Download asset Open asset

Ternary mixture accounts for the dynamics of bleached and unbleached molecules.

(a) Before bleaching, a droplet that is composed of fluorescently labeled molecules can be described by a binary mixture, namely unbleached molecules and solvent. After bleaching, the system is composed of three components, bleached molecules, unbleached molecules and solvent. If the system was at equilibrium prior to bleaching, the sum of bleached and unbleached molecules forms a stationary, non-uniform profile $ϕ_{tot} (r)$ (see panel b). (b) Snapshot of model dynamics at $t = 0.22 R^{2} / D_{in}$ . Initial conditions are $ϕ_{u} (r, t = 0) = ϕ_{out} \cdot Θ (r - R)$ , corresponding to a fully bleached droplet. Note that at any time we have $ϕ_{tot} = ϕ_{u} + ϕ_{b}$ . (c) Time course of spatial recovery. For long times, when nearly all bleached material has been exchanged, $ϕ_{u}$ approaches $ϕ_{tot}$ . Panels (c,d) use radial symmetry for illustration purposes, however, the theory is general (see Figure 3).

Figure 3

Download asset Open asset

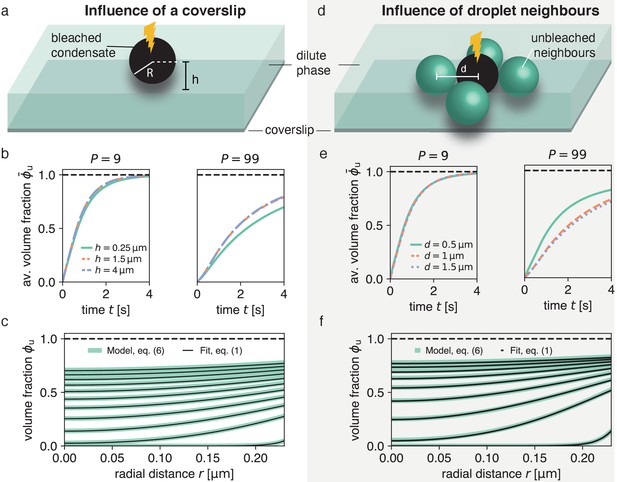
Impact of droplet environment on recovery dynamics.

(a) Sketch of a typical experimental set-up with a droplet above a passivated coverslip, where the droplet center has a distance $h > R$ to the coverslip. (b) Recovery of average unbleached volume fraction ${\bar{ϕ}}_{u} (t) = \int d^{3} r ϕ_{u} (r, t) \cdot 3 / (4 π R^{3})$ for different heights $h$ above the coverslip at different partition coefficients $P$ . Results were obtained by solving Equation (6) using the finite element method and considering the geometries depicted in (a). For even larger $h$ -values (e.g. no coverslip), results are approximately equal to the blue dashed line. (c) Using the method introduced in Figure 1 on the scenario with the largest influence of the coverslip (droplet sessile on coverslip) $h = 0.25 μ m$ in (a) results in an excellent fit and can reliably extract the input $D_{in}$ . (d) Sketch of neighboring droplets next to a bleached droplet. (e) Total recovery curves for finite element simulations of the geometry depicted in (d), for different distances between neighboring droplet centers, at different partition coefficients $P$ . Note the strong dependence on the distance of neighboring droplets. For even larger $d$ -values (e.g. no neighboring drops), results are approximately equal to the blue dashed line. (f) Same as (c) but for largest influence of neighboring droplets, that is $d = 0.5 μ m$ , where there is no distance between bleached droplet and neighboring droplets.

Figure 4

Download asset Open asset

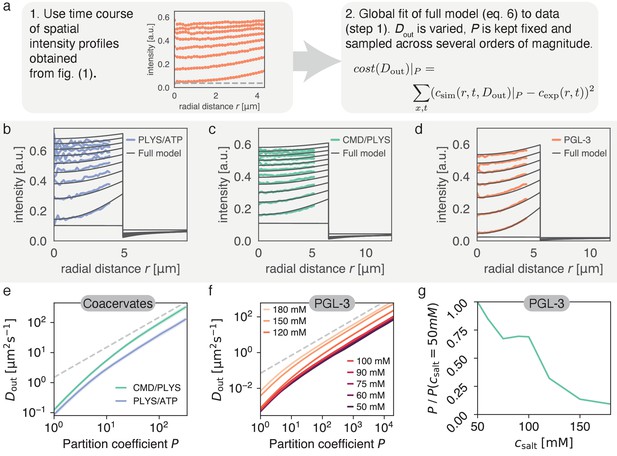
Varying partition coefficient $P$ and diffusivity outside $D_{out}$ simultaneously can lead to similar recovery kinetics.

(a) Schematics of the fitting approach used to extract the relationship between $P$ and $D_{out}$ . Although there is one specific pair ( $P$ , $D_{out}$ ) with the lowest cost (see Figure 5), there is a line in ( $P$ , $D_{out}$ ) space, which produces good fits for a range of values. (b) Spatial recovery of a single PLYS/ATP droplet (blue) with a fit to the full model (black). Note, data close to the droplet boundary cannot be fit, due to optical artefacts giving rise to an artificially broad interface (see Materials and methods and Figure 1a). (c) Same as (b) for a CMD/PLYS coacervate droplet. (d) Same as (b) for a PGL-3 droplet. (e) Given the partition coefficient $P$ , $D_{out}$ is found by fitting the coacervate data to the model. Note the convergence to a power law, $D_{out} \propto P^{n}$ with $n = 1$ for large partition coefficients (gray dashed line; for a discussion see Appendix 2). Shaded area around curves: standard deviation. Replicates: same as in Figure 1g. (f) Same as (e) but for PGL-3 with different salt concentrations. Note the order from top to bottom from highest to lowest salt concentration. (g) Based on (f), the change of partition coefficient $P (c_{salt})$ can be estimated for a given $D_{out}$ . Confidence intervals not shown for clarity. Similar to panel e. Replicates: same as in Figure 1f.

Figure 5

Download asset Open asset

Given the recovery dynamics inside a condensate, the key parameters $D_{𝐢𝐧}$ , $D_{𝐨𝐮𝐭}$ and $P$ can in theory be determined uniquely without measuring the outside dynamics, using Equation (6).

(a) Given the partition coefficient $P$ , $D_{out}$ is found by fitting the model to synthetically generated example data. As example systems, indicated by open circles, we consider in silico data, obtained by solving Equation (6) with known parameters $P$ and $D_{out}$ . To mimic the approach of initially determining $D_{in}$ (see Figure 1) we keep $D_{i n} = 0.01 μ m^{2} s^{- 1}$ for all in silico datasets. For each example system (open circles), the best fitting $D_{out}$ is found given a range of $P$ (solid lines). Parameters used were as follows: pink circle: $D_{o u t} = 0.1 μ m^{2} s^{- 1}$ , $P = 5$ , orange circle: $D_{o u t} = 1 μ m^{2} s^{- 1}$ , $P = 5$ , green circle: $D_{o u t} = 0.1 μ m^{2} s^{- 1}$ , $P = 150$ , blue circle: $D_{o u t} = 1 μ m^{2} s^{- 1}$ , $P = 150$ . (b) Cost function (colorbar, log-scale) as a function of $D_{out}$ and $P$ . We note that the global minimum coincides with the parameters used to generate the synthetic data (green circle). The valley in parameter space (dashed line) corresponds to the green line in (a). (c) Minimum of cost function for each $P$ , corresponding to curves shown in (a). This minimum corresponds to the valley indicated by the dashed line in (b). Note the minimum at the input parameter set, which indicates uniqueness of the outside dynamics for given values of $D_{out}$ and $P$ .

Appendix 2—figure 1

Download asset Open asset

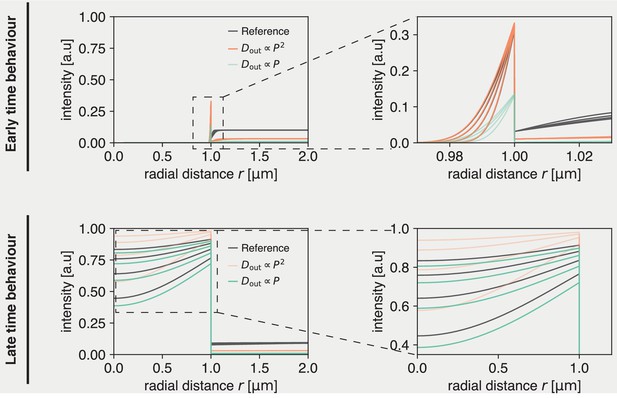
Solution to dynamics inside droplets is unique, but early and late time behavior can be approximated by different scaling regimes.

(Top) Early time behavior of numerical solutions. If a parameter set is chosen (’Reference’), at early times this can be approximately recovered by scaling $D_{out} \propto P^{2}$ (orange). A linear scaling does not recover the same inside dynamics at early times (green). (Bottom) Late time behavior of numerical solutions. At late times, the reference dynamics can be approximately recovered by scaling $D_{out} \propto P$ (green). Meanwhile, $D_{out} \propto P^{2}$ does not recover the reference inside dynamics (orange).

Author response image 1

Download asset Open asset

Videos

Video 1

Download asset

posterframe for video — FRAP dynamics in a PGL-3 droplet Left: Representative in vitro droplet after full bleach.

Time course starts after a small time lag due to a fast uniform recovery (see methods). Middle: Diffusion Equation (1) fit to azimuthally averaged droplet intensity with a global fit parameter $D_{in}$ . Right: Full model Equation (6) fit to azimuthally averaged droplet intensity.

Video 2

Download asset

posterframe for video — FRAP dynamics in a CMD/PLYS coacervate.

For description see Video 1.

Video 3

Download asset

posterframe for video — FRAP dynamics in a PLYS/ATP coacervate.

For description see Video 1.

Additional files

Source data 1 Quantification_Fig1_Fig4.: https://cdn.elifesciences.org/articles/68620/elife-68620-data1-v2.zip
Download elife-68620-data1-v2.zip
Transparent reporting form: https://cdn.elifesciences.org/articles/68620/elife-68620-transrepform-v2.docx
Download elife-68620-transrepform-v2.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Lars Hubatsch
Louise M Jawerth
Celina Love
Jonathan Bauermann
TY Dora Tang
Stefano Bo
Anthony A Hyman
Christoph A Weber

(2021)

Quantitative theory for the diffusive dynamics of liquid condensates

eLife 10:e68620.

https://doi.org/10.7554/eLife.68620

Sign up for email alerts

Privacy notice