Motor memories of object dynamics are categorically organized
- Mortimer B. Zuckerman Mind Brain Behavior Institute, Columbia University, United States
- Department of Neuroscience, Columbia University, United States
- Department of Psychology and Centre for Neuroscience Studies, Queen’s University, Canada
Figures
Figure 1
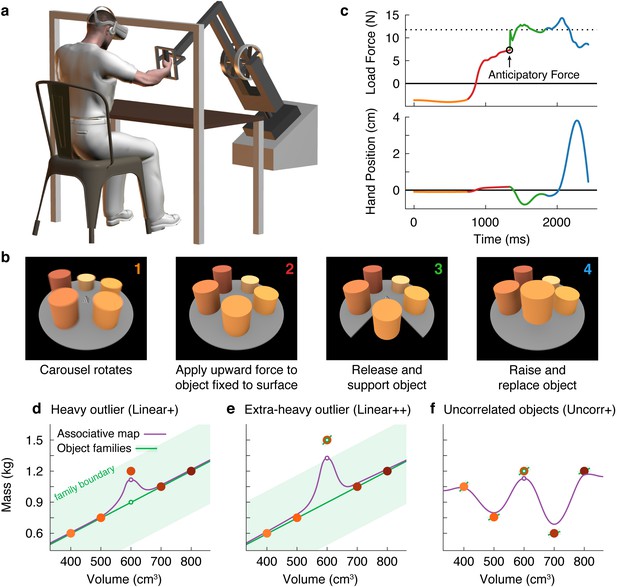
Object families and associative maps make different predictions for an outlier lifting task.
(a) Participants grasped the handle of a three-dimensional robotic interface (3BOT) with their right hand and viewed stereoscopic scenes (Oculus Rift). The 3BOT could track movement and simulate the haptic experience of manipulating objects. (b) Screenshots of the key stages of the lifting task. See text for details. (c) Load force and vertical position traces from an example trial, color-coded to match the numbers in (b). In this example, the anticipatory force was less than the weight of the object (dotted line), causing a downward movement of the hand and object. (d-f) Tasks used to examine family representations. In these tasks there were five visually similar objects of varying volume and mass. In the Linear+ condition (d), four of the objects had a linear relation between size and weight. A fifth object of intermediate size had a higher density (hence the + notation) and therefore was an outlier. Under the object families hypothesis, the four objects induce learning of the family structure (green line). Visually similar objects that fall within the category boundary for the family (shaded green region) are treated as family members. Because the outlier falls within the category boundary, its weight should be persistently misestimated based on the family structure (green circle). Under the associative map hypothesis, exposure to the outlier leads to partial learning of its actual weight (purple circle). In the Linear++ condition (e), the object families hypothesis predicts that when the outlier becomes sufficiently extreme, and crosses the family boundary, it will be categorized as an individual and its weight fully learned. The associative map hypothesis still predicts partial learning of this outlier. In the Uncorr+ condition (f), when size and weight are uncorrelated, the object families hypothesis predicts that the object weights will each be learned individually. Under the associative map hypothesis, there is no fundamental difference between this scenario and those depicted in (d, e), so the predictions for learning are similar to the object families hypothesis (i.e. all five objects will eventually be learned).
Figure 2
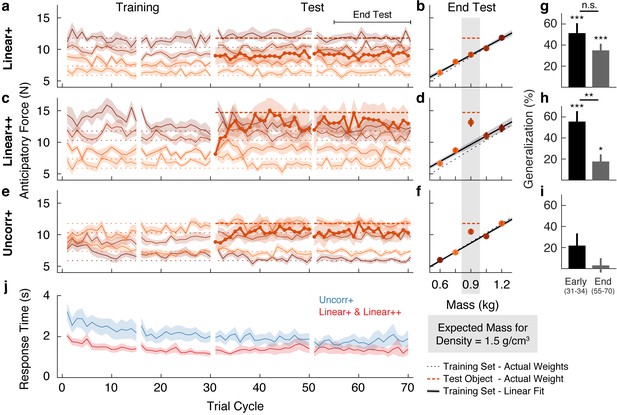
Objects are encoded according to the object families hypothesis.
(a) Trial-by-trial anticipatory forces for the five objects over the course of the Linear+ condition (mean ± SEM). The training objects (thin lines) are experienced from the first trial cycle and the test object (thick line) is introduced on trial cycle 31 as the first trial of each cycle. Traces are color-coded with darker shades indicating larger objects and the dashed lines indicate the associated actual object weights (thick dashed line shows outlier weight). Rest breaks are indicated by gaps in the traces. (b) Anticipatory forces at the end of the test phase for the Linear+ condition (mean ± SEM). The abscissa shows the weights of the training objects and, for the outlier, the expected weight based on the family density. The weights of the training objects lie on the dotted unity line. Dashed horizontal line shows the weight of the outlier. Regression line shows the average of the participants’ linear regressions ± SEM. (c, d) Same as (a, b) for the Linear++ condition. (e, f) Same as (a, b) for the Uncorr+ condition. Note that for each participant, the uncorrelated mapping of size and weight for the training objects was randomly selected; the shading in (e) and (f) depicts one mapping. In (f) the outlier is plotted at the expected weight based on the family density in the Linear conditions. (g) Single-trial generalization in the first four cycles (Early) and last sixteen cycles (End) of the test phase of the Linear+ condition (mean ± SEM, see Materials and methods for details). (h, i) Same as (g) for the Linear++ and Uncorr+ conditions. (j) Response times averaged over objects in each trial cycle (mean ± SEM). The Linear+ and Linear++ groups are combined in the red trace, as they did not differ on this measure. All SEM are across participants.
-
Figure 2—source data 1
Source data for Figure 2 (Linear+, Linear++, and Uncorr+ groups).
- https://cdn.elifesciences.org/articles/71627/elife-71627-fig2-data1-v3.txt
Figure 3
A memory of an individual is reorganized when an object family is introduced.
(a, c) Trial-by-trial anticipatory forces, as in Figure 2a and c, in a ‘reverse’ condition in which the outlier object was learned during the initial training phase, and the family objects were only introduced from trial cycle 31. Hence, we refer to these as +Linear and ++Linear. As the training phase trial cycles contained only one trial (the outlier), for clarity, the abscissa scale is compressed. After the test phase, in a ‘1:1’ phase the test object was presented four times in each trial cycle (rather than once as in the test phase), with each family member presented once (eight trials per cycle) such that the participant experienced the test object as often as a family member. For the 1:1 phase, we excluded trials from analysis in which the outlier object followed itself. (b, d) Average anticipatory forces at the end of the test phase, as in Figure 2b and d, but here plotted by volume.
-
Figure 3—source data 1
Source data for Figure 3 (+Linear and ++Linear groups).
- https://cdn.elifesciences.org/articles/71627/elife-71627-fig3-data1-v3.txt
Figure 4
Family boundary depends on history of sensorimotor experience.
(a) Trial-by-trial anticipatory forces (same format as Figure 2a) in an ‘increasing’ condition (Linear➚) in which the outlier starts at the weight of the Linear+ group on trial cycle 31 and increases gradually to the weight of the Linear++ condition. (b) Anticipatory forces at the end of the test phase (same format as Figure 2b). (c,d) Same as (a,b) for a ‘decreasing’ condition (Linear➘) in which the outlier starts at the weight of the Linear++ condition and decreases gradually to the weight of the Linear+ condition.
-
Figure 4—source data 1
Source data for Figure 4 (Linear➚ and Linear➘ groups).
- https://cdn.elifesciences.org/articles/71627/elife-71627-fig4-data1-v3.txt
Figure 5
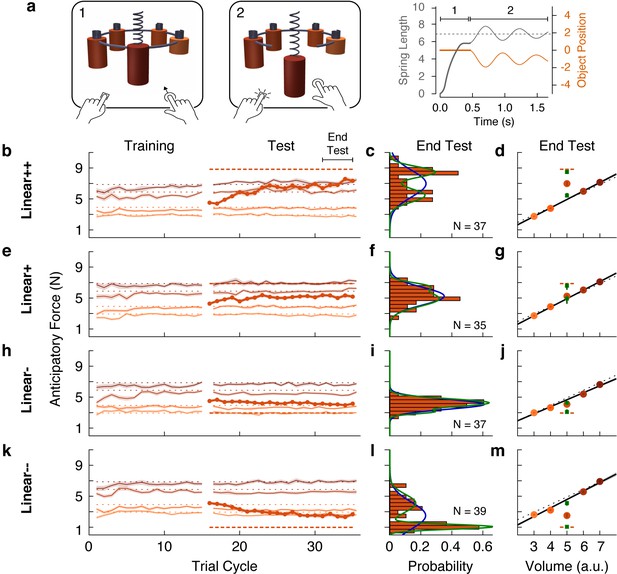
Individual differences show that outliers are either fully learned or not learned at all.
(a) Web-based lifting experiment. (1) Five visually similar objects were clamped onto a ring, which rotated to bring the target object to the front. Participants clicked and dragged upward using their mouse or trackpad to stretch a spring, thereby applying a lifting force to the object. (2) When ready, they pressed a key on the keyboard with their other hand to release the object from the ring. The object and spring were simulated as a mass-spring-damper providing visual feedback about performance, with greater errors giving rise to larger oscillations, which also took longer to decay. As in the laboratory experiments, the goal was to prevent the object from moving after the key press. Right column shows the spring length (i.e. lift force, gray) and object position (orange) traces for an example trial in which the anticipatory force was less than the object weight. (b, e, h, k) Trial-by-trial anticipatory forces (formatted as in Figure 2a) for four conditions: two with a heavy outlier (Linear+ and Linear++, as in Figure 2) and the others with a lighter (Linear-) or much lighter (Linear--) outlier. (c, f, i, l) Histograms show the distribution across participants of the average anticipatory force for the outlier object at the end of the test phase. Blue and green curves show the fits of a single-Gaussian and a two-Gaussian mixture model, respectively. (d, g, j, m) Anticipatory forces at the end of the test phase (as in Figure 2b). The mean of each Gaussian component of the two-Gaussian mixture model is plotted as a green square, with standard error estimated via parametric bootstrap.
-
Figure 5—source data 1
Source data for Figure 5 (web-based experiment).
- https://cdn.elifesciences.org/articles/71627/elife-71627-fig5-data1-v3.txt
Author response image 1
A MOSAIC model learns the weight of the Linear+ outlier in 200 trials.
Our model consists of five learning modules, each containing a responsibility predictor (a 1-10-1 feedforward neural network), an inverse model (with one scalar parameter as the motor output, i.e. the anticipatory force), and a forward model (with one scalar parameter as the predicted weight, subtracted from the final weighted motor output to predict the observed outcome, i.e. the force error). We first trained the model on the four training objects, which caused four of the five learning modules to learn each of the four different weights. The fifth module was extraneous and tended to learn to imitate one of the other modules. After the MOSAIC model learned to produce the correct forces for the four training objects, we introduced the outlier, randomly interspersed among the training objects for 200 trials (the same number of trials as the test phase in our first experiment). Here, in the same format as Figure 2b, we see that the model has learned the outlier, unlike our participants. The force output for the outlier is much greater than the force expected by interpolating within the family. Moreover, examining the internal states of the individual model components shows that they are fully consistent with the explanation above: the module responsible for lifting the heaviest object rapidly comes to dominate the motor response to the outlier as well.
Author response image 2
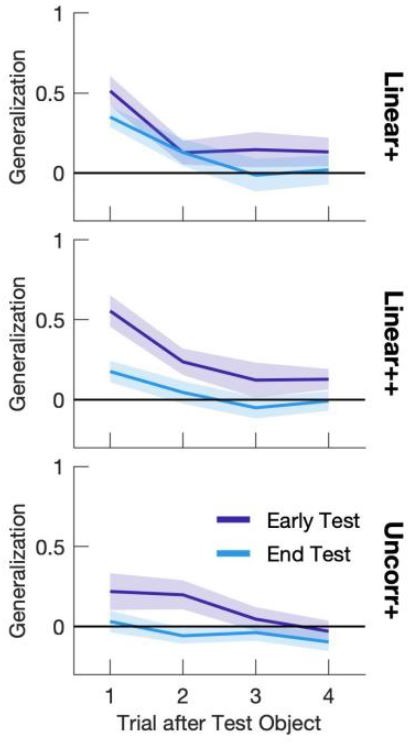
Generalization in each of the four trials after lifting the test object.
The depicted mean +/- SEM for Trial #1 is the same as shown in Figure 2g-i. This figure demonstrates how the generalization effect rapidly washes out in the second, third, and fourth lifts after the test object, and thus why it is not desirable to include these trials in the generalization analysis.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Motor memories of object dynamics are categorically organized
eLife 10:e71627.
https://doi.org/10.7554/eLife.71627
