Hybridization alters the shape of the genotypic fitness landscape, increasing access to novel fitness peaks during adaptive radiation
Figures

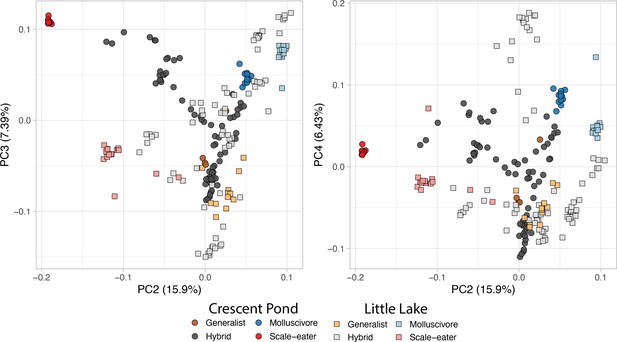
San Salvador Island pupfishes and their hybrids.
(a) From top to bottom: the generalist, Cyprinodon variegatus, the molluscivore Cyprinodon brontotheroides, and the scale-eater Cyprinodon desquamator. (b) Representative images of experimental field enclosures. (c) Principal component analysis of 1,129,771 linear discriminant (LD)-pruned single nucleotide polymorphisms (SNPs) genotyped in hybrids and the three parental species. (d) Unsupervised ADMIXTURE analyses for Crescent Pond (top) and Little Lake (bottom). G, M, and S indicate individual samples of generalists (G), molluscivores (M), and scale-eaters (S), respectively, followed by all resequenced hybrid individuals from field experiments. Colors indicate ancestry proportions in each population (K = 3).
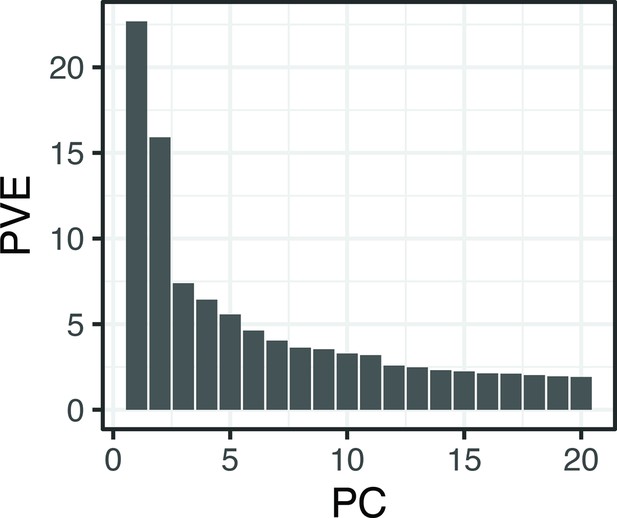
Proportion (%) genetic variance explained by the first 20 principal components obtained using all single nucleotide polymorphisms (SNPs) and individuals from Crescent Pond, Little Lake, and Osprey Lake, as well as experimental hybrids.
The first two principal component axes are plotted in Figure 1.
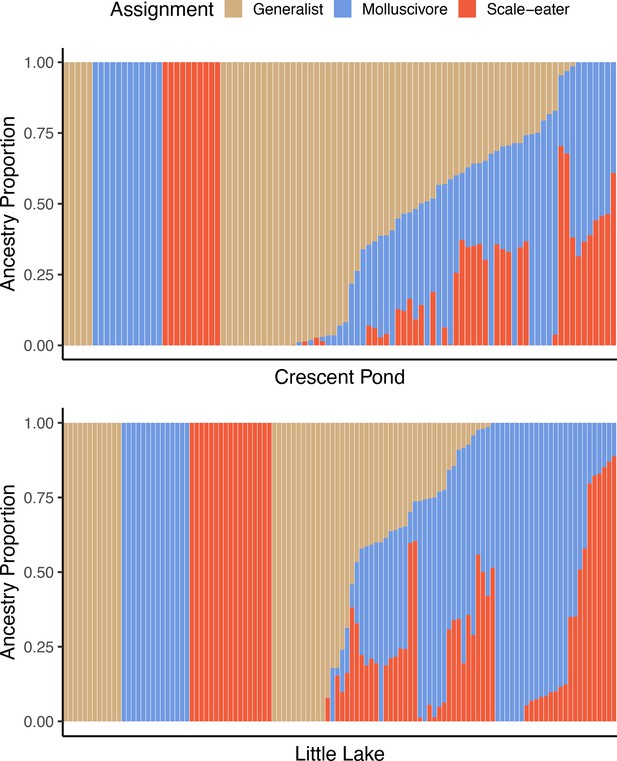
Supervised ADMIXTURE analyses for Crescent Pond (top) and Little Lake (bottom).
Sampled individuals of each species (leftmost) individuals were assigned to one of three populations, whereas ancestry proportions were estimated for all resequenced hybrid individuals from field experiments. Colors correspond to probability of assignment to one of three assumed populations/species (K = 3) in this analysis.
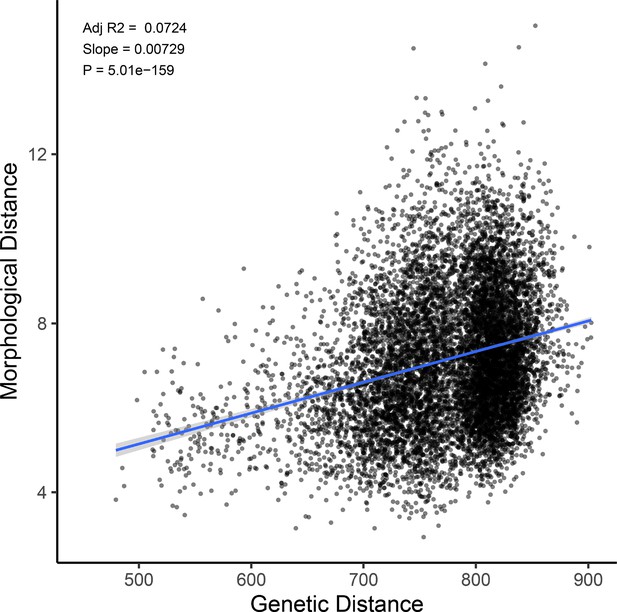
Genetic distance predicts morphological distance among sampled hybrids.

The proportion of generalist or specialist ancestry in hybrids did not predict fitness in experimental hybrids using either (a) composite fitness (tobit/zero-censored), (b) survival (binomial), or (c) growth (Gaussian).
Results of a generalized linear model in which survival (modeled as a binomial) is predicted by ancestry proportion, including lake and experiment as fixed effects. Points represent individual hybrids, with each individual represented by two points, one indicating their respective scale-eater (salmon and molluscivore blue) ancestry proportions. P-values correspond to the effect of each type of ancestry (scale-eater – red, molluscivore – blue) on survival probability. Lines are predicted values and are colored according to species.
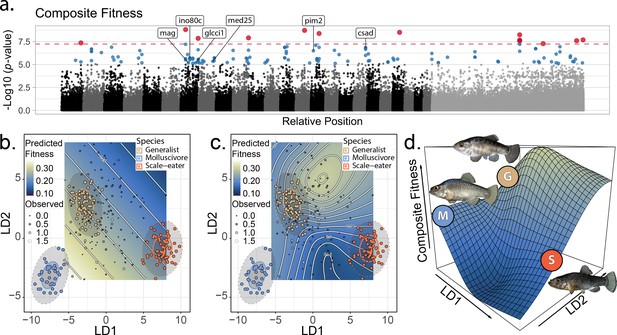
The genetic basis of fitness variation and improved inference of adaptive landscapes.
(a) Per-single nucleotide polymorphism (SNP) log10 p-values from a genome-wide association test with GEMMA for composite fitness (survival × growth). Lake and experiment were included as covariates in the linear mixed model. SNPs that were significant at false discovery rate (FDR) < 0.05 are indicated in blue; red SNPs above dashed red line cross the threshold for Bonferroni significance at α = 0.05. The first 24 scaffolds are sorted from largest to smallest and remaining scaffolds were pooled. The six genes associated with composite fitness which were both strongly differentiated (FST > 0.95) and differentially expressed between specialists (McGirr and Martin, 2020) are annotated. (b–c) Best-fit adaptive landscape for composite fitness using either morphology alone (b flat surface with only directional selection) or morphology in combination with fitness-associated SNPs (c highly nonlinear surface). Best-fit model in c was a generalized additive model (GAM) including a thin-plate spline for both linear discriminant (LD) axes, fixed effects of experiment and lake, and fixed effects of the seven (see Supplementary methods) SNPs most strongly associated with fitness shown in red in panel a. (d) Three-dimensional view of c with relative positions of the three parental phenotypes indicated.
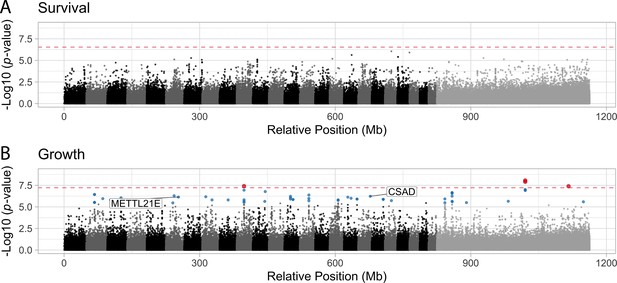
Manhattan plots illustrating the strength of association between individual single nucleotide polymorphisms (SNPs) and either survival (A) or growth (B) as inferred by GEMMA.
Significant associations are highlighted in blue (false discovery rate [FDR] < 0.05) or red (Bonferroni correction p < 0.05). The dashed red line indicates the threshold for significance following Bonferroni p-value adjustment. METTL21E and CSAD are both highly differentiated (FST > 0.95) among specialists, differentially expressed. METTL21E is also misexpressed in F1 hybrids, meaning it exhibits gene expression that is higher or lower than observed in both parental species (McGirr and Martin, 2020), indicating it is involved in intrinsic incompatibilies.
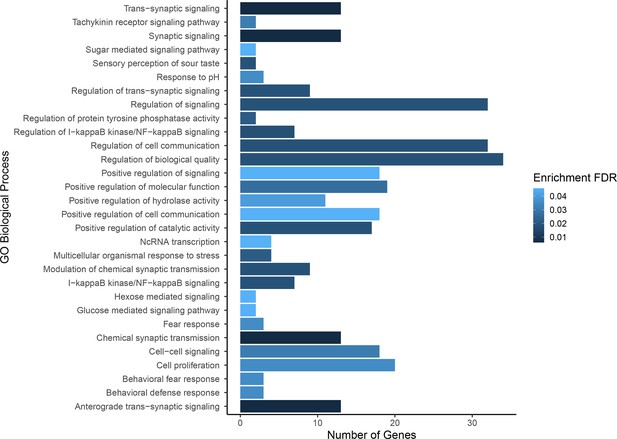
Gene ontology enrichment for single nucleotide polymorphisms (SNPs) found to be associated with composite fitness.
Darker colors indicate ontologies that are more significantly enriched following false discovery rate (FDR) correction. Length of bar is proportional to the number of genes assigned to an ontology.

Gene ontology enrichment for single nucleotide polymorphisms (SNPs) found to be associated with growth.
Darker colors indicate ontologies that are more significantly enriched following false discovery rate (FDR) correction. Length of bar is proportional to the number of genes assigned to an ontology.

The 29 landmarks used to digitally measure 30 linear traits plus standard length using DLTDV8a (Hedrick, 2008).
The corresponding traits are shown in Supplementary file 1–table 7.
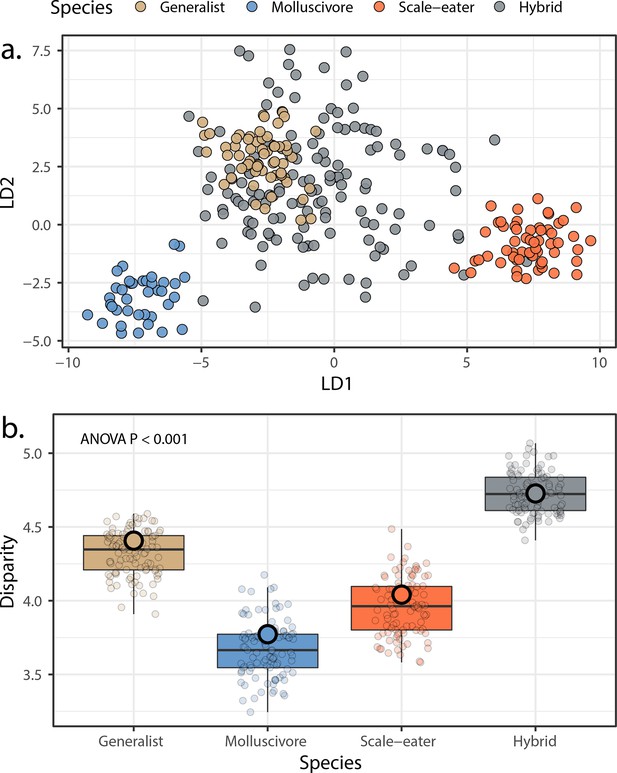
Morphological variation in the three San Salvador Island pupfish species and their experimentally produced hybrids.
(a) Linear discriminant (LD) morphospace. Parent species and hybrids are plotted using the two LD axes that together serve to distinguish species with 99.4% accuracy. (b) Within-group disparity calculated as the median distance between each individual and the groups centroid. Small, semi-transparent points are the result of 100 bootstrap replicates, and are summarized by box plots, which in turn show the median and interquartile ranges of these bootstrap replicates. Large, opaque points are the observed disparities using the full dataset per group. All pairwise comparisons using t-tests following correction for the false discovery rate were significant (p < 0.001).
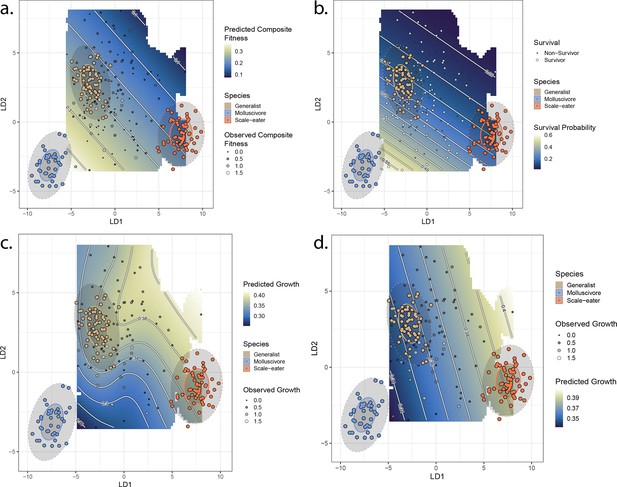
Best-fit fitness landscapes for composite fitness (a) survival (b), growth without associated single nucleotide polymorphisms (SNPs) (c), and growth including associated SNPs (d).
Colored points indicate locations of parent species in linear discriminant (LD) morphospace, and ellipses indicate their 50% (solid) and 95% (dotted) confidence intervals. Gray points indicate location of hybrid individuals, with size proportional to their fitness measure. Cooler colors on the adaptive landscape indicate lower predicted fitness.
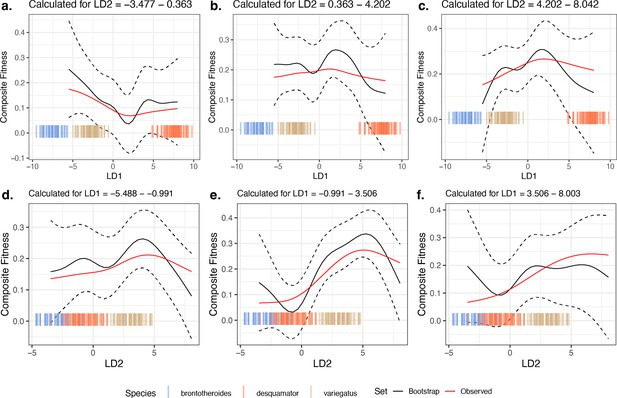
Comparison of 10,000 bootstrapped estimates of predicted mean composite fitness to estimations from observed data across slices of the fitness landscape.
The focal fitness landscape (Figure 3c–d) was estimated using composite fitness, linear discriminant (LD) axes obtained from all morphological traits, and the most-strongly fitness-associated single nucleotide polymorphisms (SNPs). The mean value of predicted fitness across all bootstrap replicates is plotted as a solid black line; the dashed black line indicates ±1 standard deviation. The observed predicted fitness is plotted as the solid red line. Observed parental morphological LD scores are plotted as colored vertical hashes: see legend at bottom. Subplots (a, b, and c) are estimates along LD1, as calculated from the bottom, middle, and top third of LD2 values, respectively. Subplots (d, e, and f) are estimates along LD2, as calculated from the bottom, middle, and top third of LD1 values, respectively.
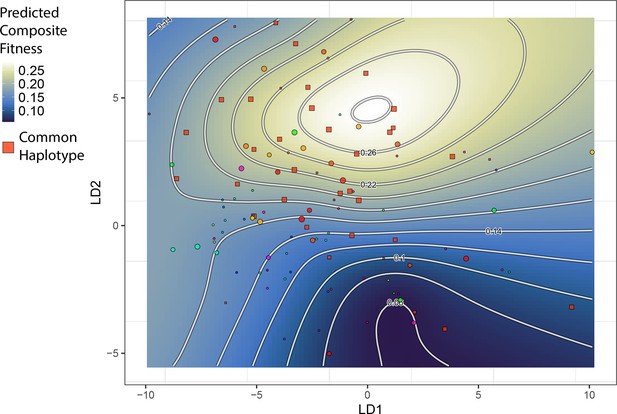
The topography of the composite fitness adaptive landscape is influenced by the distribution of a common single nucleotide polymorphism (SNP) haplotype.
Shown is the same landscape as in Figure 2, but the plotted points are unique SNP haplotypes for the 13 most strongly fitness-associated SNPs. One haplotype is particularly frequent among hybrids; individuals with this haplotype are closer in morphospace to generalists and appear to drive the emergence of a local fitness optimum for generalists. All other haplotypes (points) are plotted with a distinct color per haplotype.
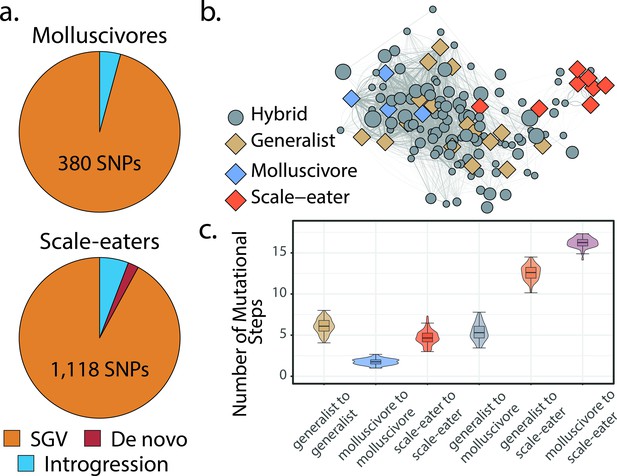
Scale-eaters are isolated on the fitness landscape.
(a) Most nearly fixed or fixed variants (FST ≥ 0.95) experiencing hard selective sweeps (hereafter ‘adaptive alleles’) originated as standing genetic variation (SGV: molluscivores = 96%, scale-eaters = 92%), followed by introgression (molluscivores = 4%, scale-eaters = 6%), and de novo mutation (scale-eaters = 2%)(Richards et al., 2021). Pie charts show adaptive alleles retained in our study for each species; networks are constructed from either set of adaptive alleles. (b) Genotypic network constructed from a random sample of 10 single nucleotide polymorphisms (SNPs), sampled from all SNPs shown in a. Each edge between nodes is up five mutational steps away; edge width is proportional to mutational distance: wider edges connect closer haplotypes; hybrid node size is proportional to fitness (larger nodes are of greater fitness value). (c) Median number of mutational steps within or between species (e.g. Figure 4a). All pairwise comparisons using Tukey’s HSD test (after false discovery rate [FDR] correction) were significant.
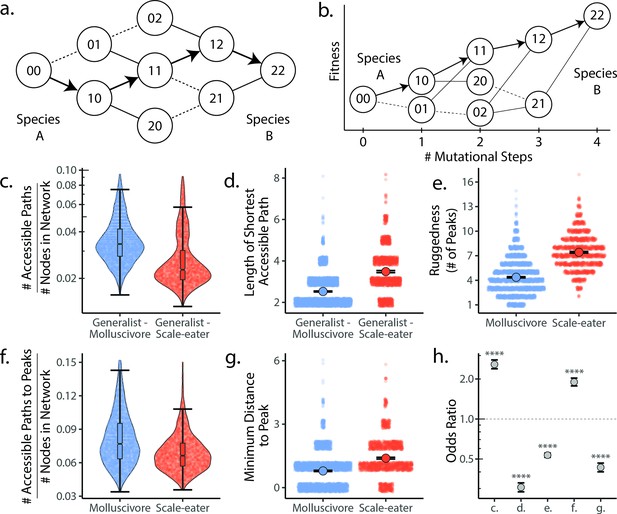
Molluscivore genotypes were more accessible to generalists on the genotypic fitness landscape than scale-eater genotypes.
(a) Diagram illustrating genotypic fitness networks and adaptive walks between species for a hypothetical two-single nucleotide polymorphism (SNP) genotypic fitness landscape. Species A and B are separated by four mutational steps. Dashed lines indicate inaccessible paths that decrease in fitness leaving a single possible accessible evolutionary trajectory between species A and B (indicated by bold arrows). Each node in our study is associated with an empirical measure of hybrid fitness from field experiments (Martin and Wainwright, 2013a; Martin and Gould, 2020). Edges are always drawn as directed from low to high fitness. (b) The same network as in (a), with fitness plotted on the y-axis and number of mutational steps from species A to B on the x-axis. The only accessible path between species A and B is indicated by solid arrows. (c) Number of accessible paths between generalists and either specialist, scaled by network size. (d) Length (# of nodes) of the shortest accessible paths. Means (large points) ± 2 standard errors are plotted. (e) Ruggedness, as measured by the number of peaks (genotypes with no fitter neighbors within a single mutational step; Ferretti et al., 2018). (f) Number of accessible paths to peaks, scaled by network size. (g) Length of the shortest accessible path to the nearest peak. (h) Odds ratios (OR: maximum likelihood estimate and 95% CI) for each measure of accessibility (x-axis corresponds to panel letters); molluscivore networks have significantly greater summary statistics when OR > 1. Molluscivore genotypes are more accessible to generalists than scale-eater genotypes due to a significantly greater number of accessible paths separating them (c) that are significantly shorter (d). Molluscivore genotypic networks were also less rugged, that is, they contained significantly fewer peaks (e), each of which were in turn more accessible from the generalist genotypes (f, g).
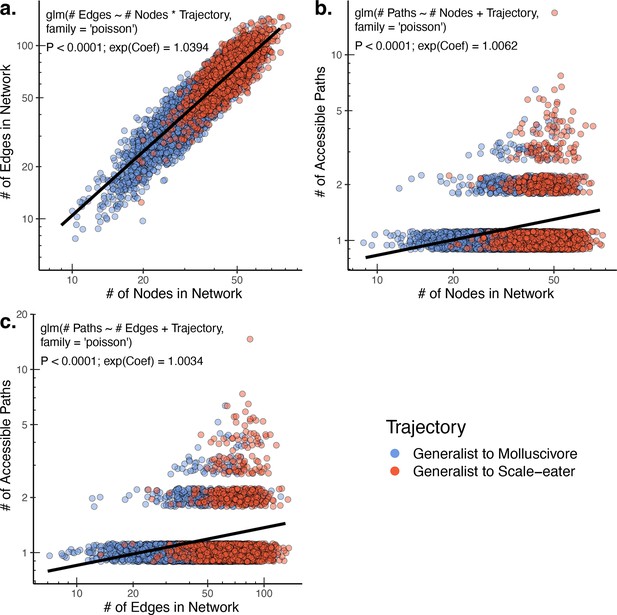
The raw number of accessible paths increases with network size.
The number of edges (and thus number of potential paths) is strongly positively correlated with the observed number of nodes (unique single nucleotide polymorphism [SNP] haplotypes) in a network (a). Correspondingly, both the number of nodes (b) and number of edges (c) positively correlate with the number of accessible paths between generalists and specialists in a given network. Only results for composite fitness are plotted; results are consistent across fitness measures. Models correspond to those in Supplementary file 1–table 13 Poisson regression was chosen as each response variable corresponds to count data. Because Poisson regression models are log-linear, we report the exponentiated coefficient which corresponds to the expected multiplicative increase in the mean of Y per unit value of X.
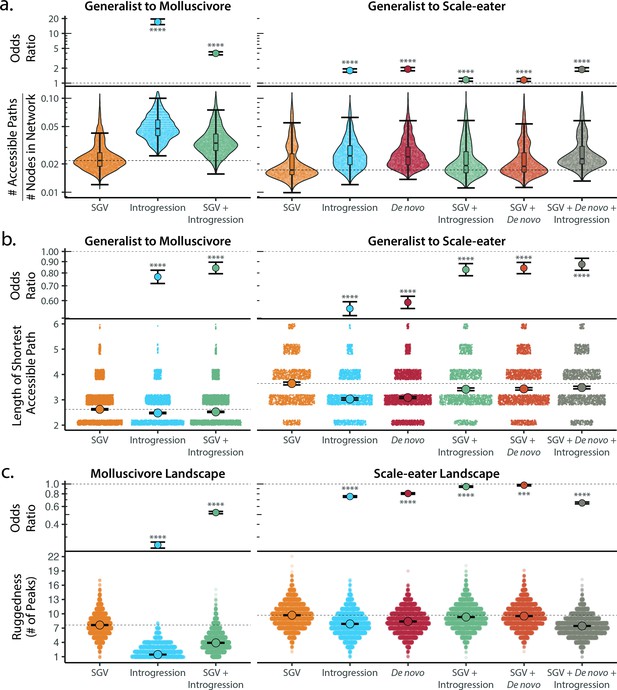
Adaptive introgression and de novo mutations increase access to specialist fitness peaks.
Odds ratios (maximum likelihood estimate and 95% CI) indicate the effect of each source of variation on accessibility compared to networks estimated from standing variation alone. Asterisks denote significance (p < 0.0001 = ****, < 0.001 = ***). (a) The number of accessible (i.e. monotonically increasing in fitness) paths per network, scaled by the size of the network (# of nodes in network). Significance was assessed using a likelihood ratio test, corrected for the false discovery rate (reported in Supplementary file 1–table 18). Dashed lines correspond to the median estimate for standing genetic variation to aid comparison to other sources of adaptive variation. (b) Number of mutational steps in the shortest accessible path. Means are plotted as large circles, with two standard errors shown; dashed horizontal lines correspond to the mean for standing genetic variation. (c) Ruggedness of molluscivore and scale-eater genotypic fitness networks constructed from each source of genetic variation measured by the number of peaks (genotypes with no fitter neighbors).
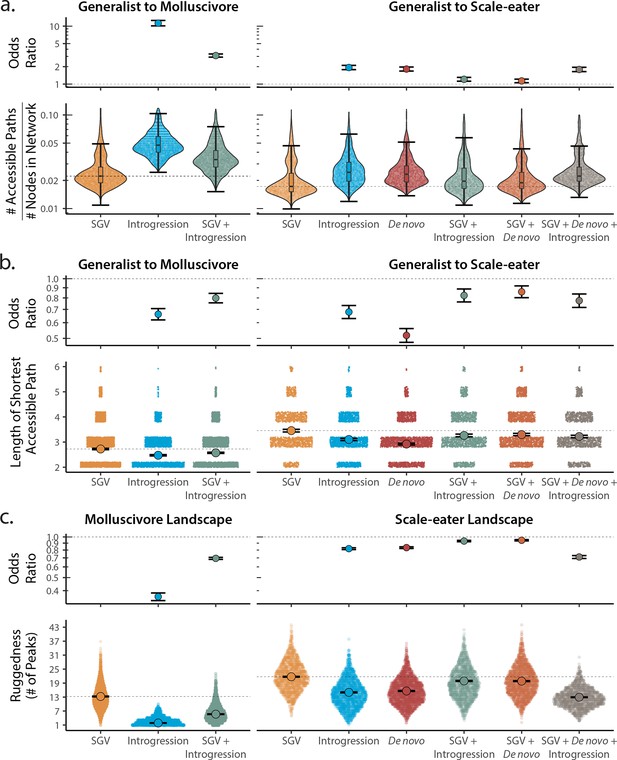
Adaptive loci sourced from introgression and de novo mutation reduce fitness landscape ruggedness and increase accessibility as compared to standing genetic variation (SGV) using survival as our proxy for fitness.
Odds ratios (maximum likelihood estimate and 95% CI) indicate the effect of each source of variation on accessibility as compared to networks estimated from standing variation alone. (a) The number of accessible (i.e. monotonically increasing in fitness) paths per network, scaled by the size of the network (# of nodes in network). Significance was assessed using a likelihood ratio test, corrected for the false discovery rate (reported in Supplementary file 1–table 13). Dashed lines correspond to the median estimate for standing genetic variation to aid comparison to other sources of adaptive variation. (b) Number of mutational steps in the shortest accessible path. Means are plotted as large circles, with two standard errors shown; dashed horizontal lines correspond to the mean for standing genetic variation. (c) Ruggedness of molluscivore and scale-eater fitness landscapes constructed from each source of genetic variation as measured by the number of peaks (genotypes with no fitter neighbors).
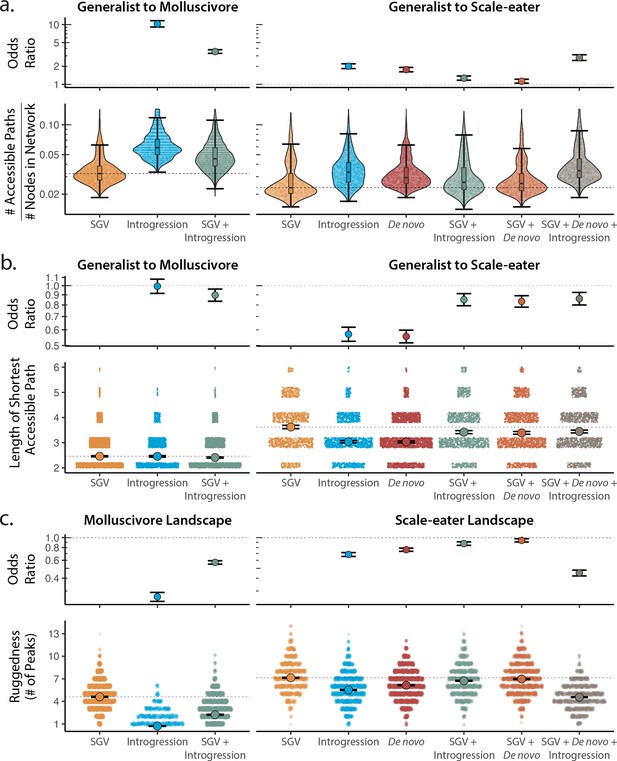
Adaptive loci sourced from introgression and de novo mutation reduce fitness landscape ruggedness and increase accessibility as compared to standing genetic variation (SGV) using growth as our proxy for fitness.
Odds ratios (maximum likelihood estimate and 95% CI) indicate the effect of each source of variation on accessibility as compared to networks estimated from standing variation alone. (a) The number of accessible (i.e. monotonically increasing in fitness) paths per network, scaled by the size of the network (# of nodes in network). Significance was assessed using a likelihood ratio test, corrected for the false discovery rate (reported in Supplementary file 1–table 13). Dashed lines correspond to the median estimate for standing genetic variation to aid comparison to other sources of adaptive variation. (b) Number of mutational steps in the shortest accessible path. Means are plotted as large circles, with two standard errors shown; dashed horizontal lines correspond to the mean for standing genetic variation. (c) Ruggedness of molluscivore and scale-eater fitness landscapes constructed from each source of genetic variation as measured by the number of peaks (genotypes with no fitter neighbors).
Additional files
-
Supplementary file 1
Supplementary tables.
(a)—Table 1. Samples of hybrids and parental studies used either in genomic or in morphological analyses, along with associated metadata. (b)—Table 2. Models tested to assess the extent to which specialist ancestry predicts measures of fitness and their respective fits using all samples and an unsupervised ADMIXTURE analysis. Best-fit models are bolded. (c)—Table 3. Models tested to assess the extent to which specialist ancestry predicts measures of fitness and their respective fits using all samples and a supervised ADMIXTURE analysis. Best-fit models are bolded. (d)—Table 4. Models tested to assess the extent to which specialist ancestry predicts measures of fitness and their respective fits using only samples from the second field experiment (Martin and Gould, 2020) and an unsupervised ADMIXTURE analysis. Best-fit models are bolded. (e)—Table 5. Models tested to assess the extent to which genome-wide variation (PC1/PC2) predicts measures of fitness and their respective fits using all samples and an unsupervised ADMIXTURE analysis. Best-fit models are bolded. (f)—Table 6. Single nucleotide polymorphisms (SNPs) found to be strongly associated with composite fitness using SnpEff (Cingolani et al., 2012). SNPs that were identified as being strongly associated with both growth and composite fitness are italicized, and those that remain significant after a Bonferroni correction are bolded. (g)—Table 7. Gene ontology term enrichment for genes associated with composite fitness. (h)—Table 8. SNPs found to be strongly associated with growth SnpEff (Cingolani et al., 2012). SNPs that were identified as being strongly associated with both growth and composite fitness are italicized, and those that remain significant after a Bonferroni correction are bolded, (i)—Table 9. Gene ontology term enrichment for genes associated with growth. (j)—Table 10. List of the 31 morphological traits measured for this study and standard length; corresponding landmark IDs match those shown in Figure 2—figure supplement 3. (k)—Table 11. Generalized additive models fitted to composite fitness. Model fit was assessed using AICc, and Akaike weights represent proportional model support. A thin-plate spline for the two linear discriminant axes s(LD1, LD2) is always included, as is a fixed effect of either experiment (i.e. Martin and Wainwright, 2013a; Martin and Gould, 2020) or lake (Crescent Pond/Little Lake) or an interaction between the two. In the last two models, experiment and lake are included as splines, modeled using a factor smooth (bs = ‘fs’). The best-fit model had five estimated degrees of freedom. (l)—Table 12. Generalized additive models fitted to growth. Model fit was assessed using AICc, and Akaike weights represent proportional model support. A thin-plate spline for the two linear discriminant axes s(LD1, LD2) is always included, as is a fixed effect of either experiment (i.e. Martin and Wainwright, 2013a; Martin and Gould, 2020) or lake (Crescent Pond/Little Lake) or an interaction between the two. In the last two models, experiment and lake are included as splines, modeled using a factor smooth (bs = ‘fs’). The best-fit model had 8.93 estimated degrees of freedom. (m)—Table 13. Generalized additive models fitted to survival. Model fit was assessed using AICc, and Akaike weights represent proportional model support. A thin-plate spline for the two linear discriminant axes s(LD1, LD2) is always included, as is a fixed effect of either experiment (i.e. Martin and Wainwright, 2013a; Martin and Gould, 2020) or lake (Crescent Pond/Little Lake) or an interaction between the two. In the last two models, experiment and lake are included as splines, modeled using a factor smooth (bs = ‘fs’). The best-fit model had five estimated degrees of freedom. (n)—Table 14. Generalized additive models fitted to growth including SNPs most strongly associated with composite fitness. Model fit was assessed using AICc, and Akaike weights represent proportional model support. The best-fit model for composite fitness using morphology alone (see Table 8) was used as the base model. The SNPs that were most strongly associated with composite fitness (following a Bonferroni correction) were included as fixed effects, modeled as splines using a factor smooth, treating genotype as an ordered factor. Note that three SNPs were excluded due to their close proximity to other SNPs that were more strongly associated. All SNPs were considered individually, as well as all SNPs together. We were unable to assess all possible combinations of SNPs due to the vast number of potential models given the number of SNPs under consideration; rather, we fit one final model that only included SNPs found to be significant in the full model. In turn this model led to a substantial improvement in AICc. The best-fit model had 20.29 estimated degrees of freedom. (o)—Table 15. Generalized additive models fitted to growth including SNPs most strongly associated with growth. Model fit was assessed using AICc, and Akaike weights represent proportional model support. The best-fit model for growth using morphology alone (see Table 9) was used as the base model. Each of the four SNPs that were most strongly associated with growth (following a Bonferroni correction) were included as fixed effects, modeled as splines using a factor smooth, treating genotype as an ordered factor. All SNPs were considered individually, as well as all possible combinations. This was only feasible due to the small number of SNPs assessed (four). The best-fit model had 7.97 estimated degrees of freedom. (p)—Table 16. General linear models fitted to examine the relationship between aspects of network size (i.e. number of nodes, number of edges linking neighboring nodes) and the number of accessible paths between generalists and specialists. Models were fitted using each of the three different fitness measures; bolded lines correspond to the best-fit model for each response variable, within each measure of fitness. Poisson regression was chosen as each response variable correspond to count-data. Because Poisson regression models are log-linear, we report both the estimated coefficient and its exponentiated value which corresponds to the expected multiplicative increase in the mean of Y per unit value of X. (q)—Table 17. Accessibility of specialists to generalists and the ruggedness of their respective fitness landscapes. Odds ratios were obtained by modeling the association between each summary statistic and the species from which adaptive loci were used to construct the fitness network. Scale-eaters were treated as the baseline of comparison in the comparison of odds ratios; thus, positive odds ratios imply that summary statistics for molluscivore fitness networks are greater than those constructed from scale-eater adaptive loci and vice versa. For generalist to specialist comparisons, accessible paths were identified between one randomly sampled generalist node and one randomly sampled specialist node. For comparison of the peaks in networks, these summary statistics were calculated from either molluscivore or scale-eater fitness networks, identifying the number of peaks (nodes with no fitter neighbors – see Materials and methods), and the scaled (total divided by number of nodes in the network) number of accessible paths separating all focal specialist nodes and all peaks in the network. (r)—Table 18. Influence of different sources of adaptive genetic variation on accessibility of fitness paths separating either generalists from molluscivores, or generalists and scale-eaters using all samples. Results for networks using all three measures of fitness (composite fitness, survival, and growth) are reported. Networks were constructed from random draws of five SNPs from either standing genetic variation (SGV), introgression, or de novo mutations, as well as their combinations. Odds ratios were obtained by modeling the association between each accessibility measure and the source of genetic variation used to construct the fitness network, relative to networks constructed from standing variation. Thus, positive odds ratios imply that networks from standing variation have measures of accessibility that are smaller as compared to the alternative (e.g. introgression, de novo mutations, etc.). (s)—Table 19. Influence of different sources of adaptive genetic variation on accessibility of fitness paths separating either generalists from molluscivores, or generalists and scale-eaters using only samples from the second field experiment (Martin and Gould, 2020). Results for networks using all three measures of fitness (composite fitness, survival, and growth) are reported. Networks were constructed from random draws of five SNPs from either standing genetic variation (SGV), introgression, or de novo mutations, as well as their combinations. Odds ratios were obtained by modeling the association between each accessibility measure and the source of genetic variation used to construct the fitness network, relative to networks constructed from standing variation. Thus, positive odds ratios imply that networks from standing variation have measures of accessibility that are smaller as compared to the alternative (e.g. introgression, de novo mutations, etc.).
- https://cdn.elifesciences.org/articles/72905/elife-72905-supp1-v1.docx
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/72905/elife-72905-transrepform1-v1.docx