Distinct representations of body and head motion are dynamically encoded by Purkinje cell populations in the macaque cerebellum
- Department of Biomedical Engineering, McGill University, Canada
- Department of Biomedical Engineering, Johns Hopkins University, United States
- Department of Otolaryngology-Head and Neck Surgery, Johns Hopkins University School of Medicine, United States
- Department of Neuroscience, Johns Hopkins University School of Medicine, United States
- Kavli Neuroscience Discovery Institute, Johns Hopkins University, United States
Figures
Figure 1 with 1 supplement
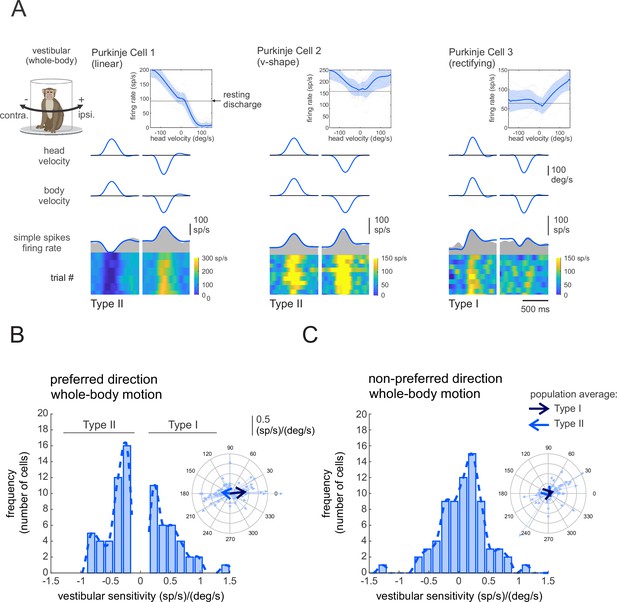
Purkinje cell simple spike’s responses to vestibular stimulation.
(A) Vestibular stimulation was generated by applying passive whole-body rotations about the vertical axis. The resulting neural responses are shown for three example Purkinje cells. The top two rows illustrate rotational head and body velocities. The bottom row shows the simple spike firing rate (gray shaded regions) with the linear estimation of the firing rate based on head motion superimposed (blue traces). The heat maps show the simple spike firing rate for individual trials. Insets: the relationship between simple spike firing rate (phase-corrected) and angular head-in-space velocity. (B,C) Distribution of vestibular sensitivities for motion in the preferred (B) direction (i.e., the direction resulting in the larger increase in simple spike firing rate) and non-preferred (C) direction. The dashed lines are fits on the distributions. Note, by convention positive and negative values in (B) represent cells with Type I versus II vestibular responses (i.e., preferred direction was ipsilateral versus contralateral, respectively). Insets: polar plots where the vector length and angle represent each neuron’s vestibular response sensitivity and phase, respectively. Filled and open arrows represent the population-averaged vectors for Type I and II cells, respectively.
Figure 1—figure supplement 1
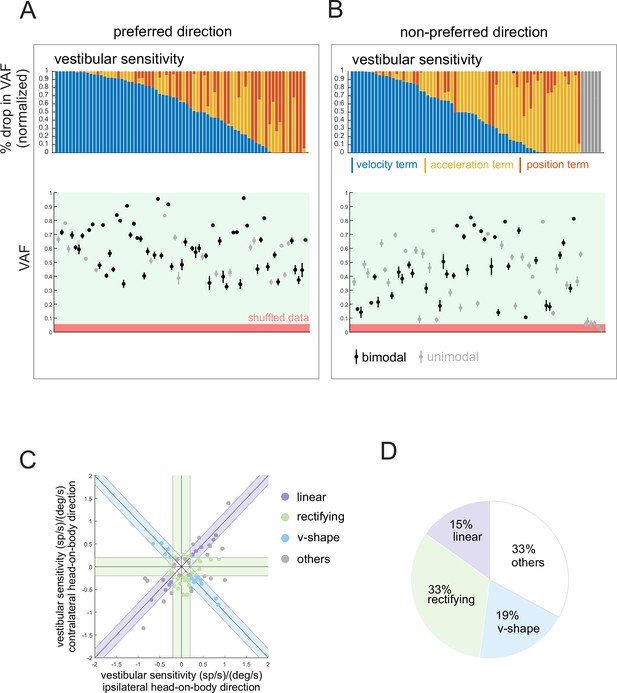
Purkinje cells show heterogeneity in their simple spike responses to vestibular stimulation.
(A) The contribution of each kinematic term (i.e., position, velocity, acceleration) in estimating the firing rate for the preferred (left) and non-preferred (right) direction of whole-body movement, computed as the % drop in total variance-accounted-for (VAF) when removed from the full model. Neurons that did not significantly respond to the non-preferred direction are shown as gray bars. Note, we sorted Purkinje cells based on the importance of the velocity term, since this is what is predominately encoded by their target neurons in the rostral fastigial nucleus (rFN) and vestibular nuclei. Interestingly, in the non-preferred direction, the acceleration term (yellow) contributes more to estimated firing rate (i.e., greater reduction VAF when removed) indicating that Purkinje cell’s responses generally led stimulation velocity. (B) The computed VAF (mean ± 95% CI) in estimating the firing rate for the preferred (left) and non-preferred (right) direction of whole-body movement. Black and gray bars represent bimodal and unimodal Purkinje cells, respectively. The red area corresponds to non-significant VAF values computed from the same stimulation and shuffled inter-spike intervals (ISI). (C) The response of the Purkinje cells grouped as (i) linear, which demonstrated increased and decreased firing rate in the preferred and non-preferred directions, respectively, (ii) v-shape, which demonstrated increased firing rate in both directions, (iii) rectifying, which demonstrated increased firing rate in the preferred direction and minimal modulation in the non-preferred direction, and (iv) others, which did not meet any of the mentioned criteria. (D) The pie chart illustrates the percentage of each category within the Purkinje cells.
Figure 2 with 3 supplements
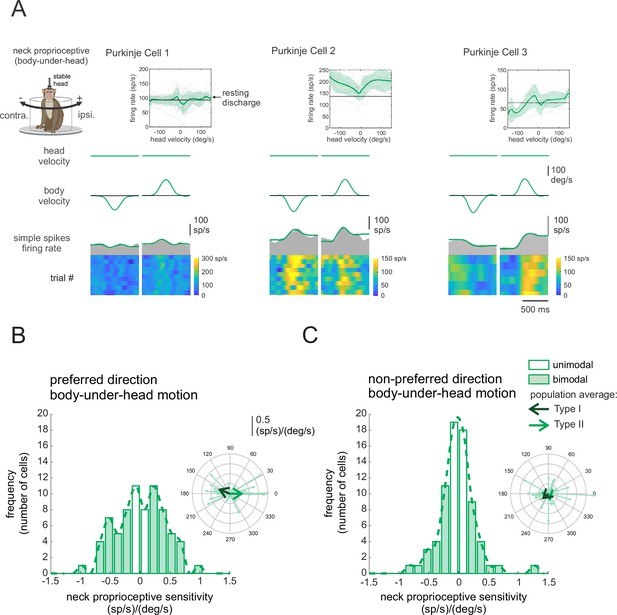
Purkinje cell simple spike’s responses to neck proprioceptive stimulation.
(A) Proprioceptive stimulation was generated by applying body-under-head rotation about the vertical axis while holding the head earth. The resulting neural responses are illustrated for the same three example Purkinje cells shown above in Figure 1. The top two rows illustrate rotational head and body velocities. The bottom row shows the resultant simple spike firing rate (gray shaded regions) with the linear estimation of the firing rate based on body motion superimposed (green traces). The heat maps show the simple spike firing rate for individual trials. Insets: the relationship between simple spike firing rate (phase-corrected) and angular body-in-space velocity. (B, C) Distribution of proprioceptive sensitivities for the preferred (B) and non-preferred (C) directions of body movement. Filled versus open bars represent neurons that were sensitive versus insensitive to neck proprioceptive stimulation (i.e., bimodal versus unimodal cells, respectively). The dashed lines are fits on the distributions. Insets: polar plots where the vector length and angle represent each neuron’s proprioceptive response sensitivity and phase, respectively. Filled versus open arrows represent the population-averaged vectors for neurons with Type I versus II vestibular responses (i.e., Figure 1), respectively.
Figure 2—figure supplement 1
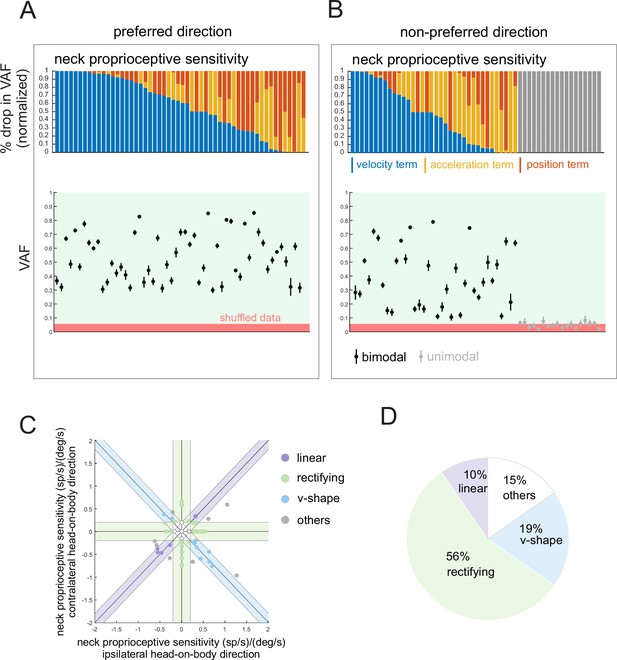
Purkinje cells show heterogeneity in their simple spike responses to proprioceptive stimulation.
(A) The contribution of each kinematic term (i.e., position, velocity, acceleration) in estimating the firing rate for the preferred (left) and non-preferred (right) direction of body movement (i.e., body-under-head) for bimodal Purkinje cells, computed as the % drop in total variance-accounted-for (VAF) when removed from the full model. Neurons that did not significantly respond to the non-preferred direction are shown as gray bars. Note, we sorted the Purkinje cells based on the importance of the velocity term, since this is what is predominately encoded by the target neurons in the rostral fastigial nucleus (rFN) and vestibular nuclei. (B) The computed VAF (mean ± 95% CI) in estimating the firing rate for preferred (left) and non-preferred (right) direction of whole-body movement. Black and gray bars represent bimodal and unimodal Purkinje cells, respectively. The red area corresponds to non-significant VAF values computed from the same stimulation and shuffled inter-spike intervals (ISI). (C) The response of the bimodal Purkinje cells, which are grouped as (i) linear, which demonstrated increased and decreased firing rate in the preferred and non-preferred directions, respectively, (ii) V-shape, which demonstrated increased firing rate in both directions, (iii) rectifying, which demonstrated increased firing rate in the preferred direction and minimal modulation in the non-preferred direction, and (iv) others, which did not meet any of the mentioned criteria. (D) The pie chart illustrates the percentage of each category within the Purkinje cells.
Figure 2—figure supplement 2
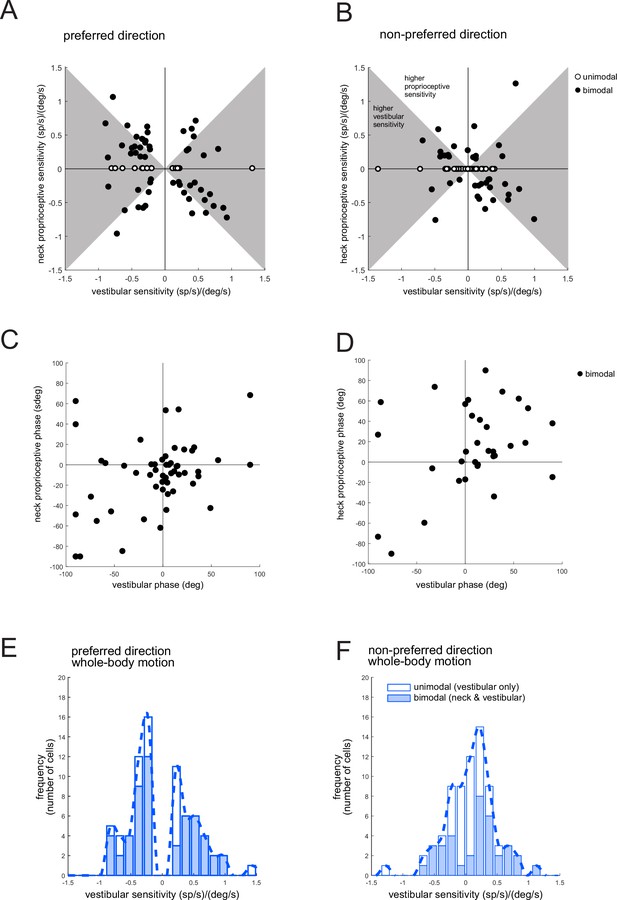
Purkinje cells show heterogeneity in their simple spike responses to vestibular versus proprioceptive stimulation.
(A, B) Scatter plots comparing the sensitivity to vestibular and neck proprioceptive stimulation for unimodal (white circles) and bimodal (black circles) Purkinje cells for preferred (A) and non-preferred (B) direction of movement. The gray shaded area corresponds to the Purkinje cells with larger sensitivity to vestibular compared to neck proprioceptive sensitivity. (C, D) Scatter plots comparing the phase of the responses to vestibular and neck proprioceptive stimulation for bimodal Purkinje cells for the preferred (C) and non-preferred (D) direction of movement. (E, F) The distribution of the neuronal sensitivity of the Purkinje cells simple spikes’ response to the vestibular stimulation for the preferred (E) and non-preferred (F) direction of movement. Open bars correspond to the cells that did not show a significant response to the neck proprioceptive stimulation (i.e., unimodal cells).
Figure 2—figure supplement 3
For most of the Purkinje cells, the responses to vestibular and neck proprioceptive stimulation were classified in different groups.
(A) Venn diagram showing the number of Purkinje cells that were grouped as linear, v-shape, rectifying, and other for vestibular and neck proprioceptive responses and their overlap (filled area). (B) The number of Purkinje cells that were classified in pairs of groups based on their response to vestibular (y-axis) and neck proprioceptive (x-axis) inputs.
Figure 3 with 2 supplements
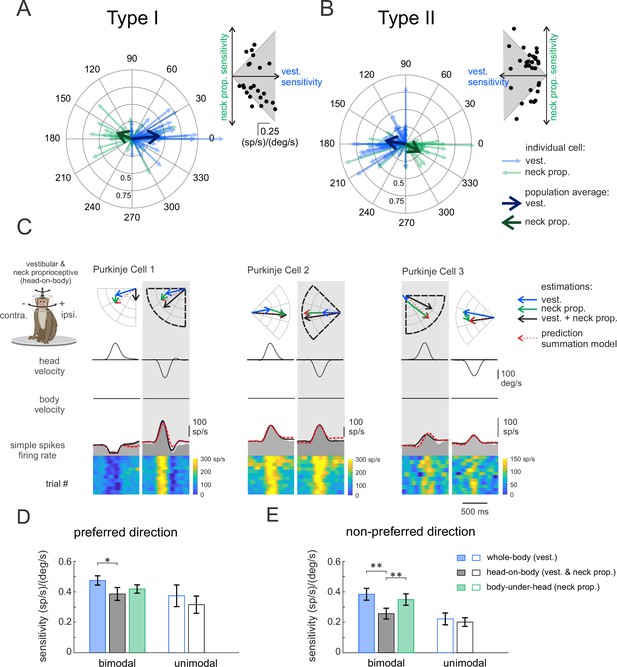
Purkinje cells simple spike’s responses to combined vestibular-proprioceptive stimulation.
(A, B) Polar plots illustrating the vestibular (blue) and neck proprioceptive (green) neuronal response sensitivities of Type I (A) and Type II (B) Purkinje cells for preferred direction of vestibular stimulation and complementary direction proprioceptive stimulation (i.e., body-under-head motion). Bold blue and green arrows represent the mean population vectors, respectively. Inset: scatter plots comparing the sensitivity of Type I (A) and Type II (B) Purkinje cells to vestibular and neck proprioceptive inputs. (C) Combined vestibular-proprioceptive stimulation was generated by applying passive head-on-body rotations about the vertical axis. The resulting neural responses are shown for the same three example Purkinje cells shown above in Figures 1 and 2. The top two rows illustrate rotational head and body velocity. The bottom row shows the resultant simple spike firing rate (gray shaded regions). The linear estimation of firing rate based on head motion (solid black traces) and the firing rate prediction based on the linear summation of neck proprioceptive and vestibular sensitivities (dashed red traces) are both superimposed. Each neuron’s preferred motion direction for vestibular stimulation is indicated by the gray column. Polar plots (top) represent the sensitivity and phase of each neuron’s response to vestibular, proprioceptive, and combined stimulation as well as the response predicted by the summation model. (D, E) Bar plots comparing the sensitivities of bimodal and unimodal Purkinje cells to vestibular, proprioceptive, and combined stimulation in the preferred (D) and non-preferred (E) motion directions, as defined by each neuron’s responses to vestibular stimulation. The response sensitivities of Type I and II neurons are reported as positive values relative to ipsilaterally and contralaterally directed head movements, respectively, to facilitate comparison across all Purkinje cells.
Figure 3—figure supplement 1
Purkinje cell’s responses to combined vestibular-neck proprioceptive stimulation in the non-preferred direction of vestibular stimulation.
(A, B) Polar plots illustrating the vestibular (blue) and neck proprioceptive (green) neuronal response sensitivities of Type I (A) and Type II (B) Purkinje cells for non-preferred direction of vestibular stimulation and complementary direction proprioceptive stimulation (i.e., body-under-head motion). Superimposed blue and green arrows represent the mean population vectors, respectively.
Figure 3—figure supplement 2
Polar representations of Purkinje cells simple spike’s response.
Polar plots representating each individual Purkinje cells’ response ordered by increasing discrepancy between the summed and combined responses in the preferred direction. Response vectors predicted by the summation model (red) are superimposed on those for vestibular (blue), proprioceptive (green), and combined stimulation (black).
Figure 4 with 1 supplement
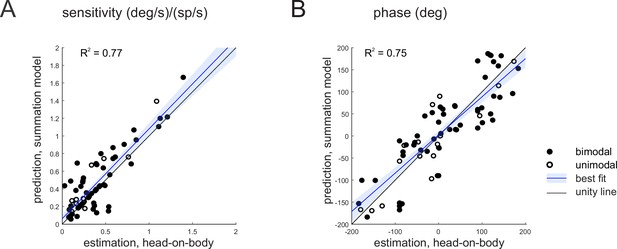
Purkinje cell simple spike’s responses to combined stimulation are well predicted by the linear summation of a given neuron’s responses to vestibular and proprioceptive stimulation when applied alone.
(A, B) Comparison of estimated and predicted sensitivities (A) and phases (B) of Purkinje cell’s responses to head-on-body rotations in the preferred movement direction. The linear summation of a given neuron’s vestibular and neck proprioceptive sensitivities well predicts both sensitivity and phase measures in the combined condition. Blue lines and shading denote the mean ± 95% CI of linear fit.
Figure 4—figure supplement 1
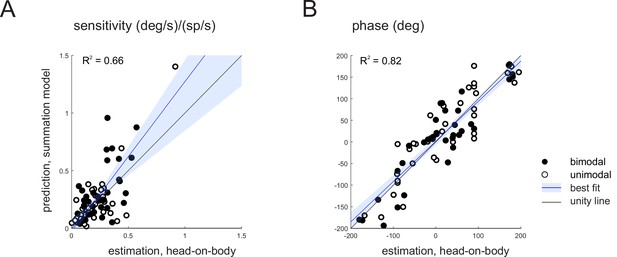
Purkinje cell simple spike’s responses to combined stimulation are well predicted by the linear summation of a given neuron’s responses to vestibular and proprioceptive stimulation when applied alone.
(A, B) Comparison of estimated and predicted sensitivities (A) and phases (B) of Purkinje cell’s responses to head-on-body rotations in the non-preferred movement direction. The linear summation of a given neuron’s vestibular and neck proprioceptive sensitivities well predicted both measures in the combined condition. Blue lines and shading denote the mean ± 95% CI of linear fit.
Figure 5 with 1 supplement
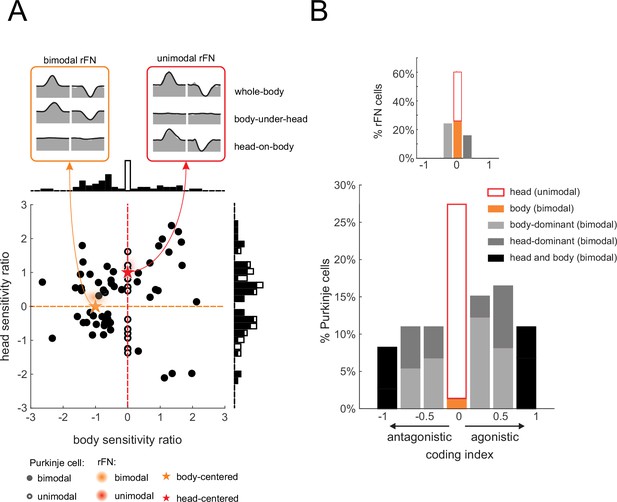
Heterogeneity in Purkinje cell simple spike encoding of head and body movement.
(A) Scatter plot of the relationship between the head sensitivity ratio (Svest.+prop./Svest.) and body sensitivity ratio (Sprop./Svest.) for the preferred direction. Histograms (top and right) illustrate the distributions of body and head sensitivity ratios, respectively. Orange versus red stars indicate ideal encoding of body versus head movement in space, respectively. For comparison, the red and orange shaded areas representing the distribution of values estimated for unimodal and bimodal rostral fastigial nucleus (rFN) neurons (Brooks and Cullen, 2009) are superimposed. Inset: examples of the responses of a bimodal (orange) and unimodal (red) rFN neurons during whole-body, body-under-head, and head-on-body movement are shown for comparison (Figure 5A has been adapted from Figure 1 from Brooks and Cullen, 2013). (B) Distribution of coding indexes (see Materials and methods). Positive and negative values correspond to agonistic and antagonistic responses to head versus body encoding, respectively. Inset: the distribution of coding indices estimated for rFN neurons (Brooks and Cullen, 2009) is shown for comparison.
Figure 5—figure supplement 1
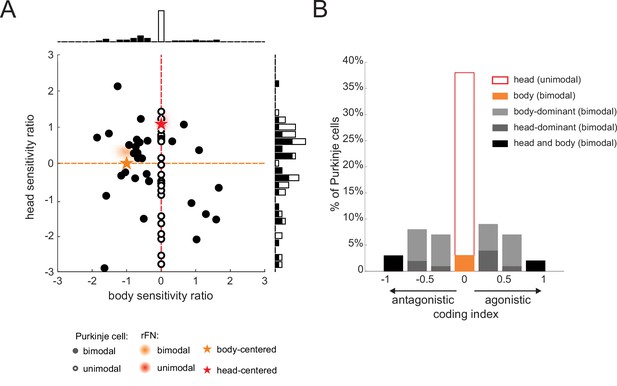
Heterogeneity in Purkinje cell simple spike encoding of head and body movement for the non-preferred direction.
(A) Scatter plot of the relationship between the head sensitivity ratio (Svest.+prop./Svest.) and body sensitivity ratio (Sprop./Svest.) for the non-preferred direction. Histograms (top and right) illustrate the distributions of body and head sensitivity ratios, respectively. Orange versus red stars indicate ideal encoding of body versus head movement in space, respectively. For comparison, the red and orange shaded areas representing the distribution of values estimated for unimodal and bimodal rostral fastigial nucleus (rFN) neurons (Brooks and Cullen, 2009) are superimposed. (B) Distribution of coding indexes (see Materials and methods). Positive and negative values correspond to agonistic and antagonistic responses to head versus body encoding, respectively.
Figure 6
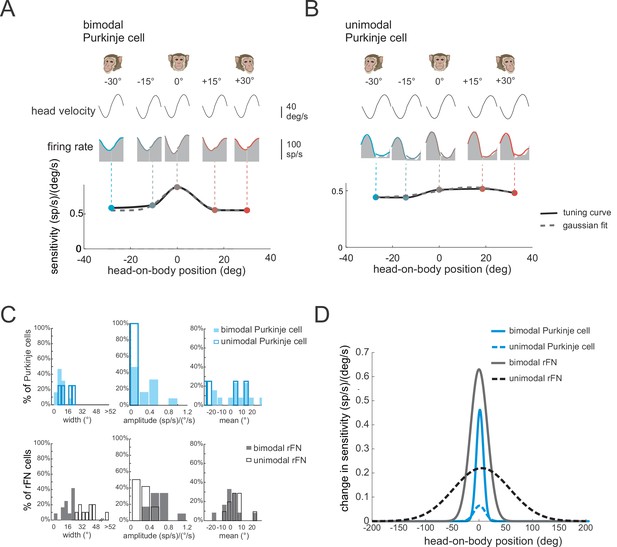
The vestibular responses of bimodal Purkinje cells show head-on-body position-dependent tuning.
(A, B) Tuning curves for the vestibular sensitivities of an example bimodal (A) and unimodal (B) Purkinje cell measured by applying whole-body rotation with the head oriented at different positions relative to the body. Note, bimodal neurons, but not unimodal neurons, show tuning as a function of head-on-body position. (C) Top panel: Distributions of tuning widths (left), amplitudes (middle), and means (right) for bimodal (filled bars, N = 13) and unimodal (open bars, N = 4) Purkinje cells. Bottom panel: For comparison, the same distributions are plotted for a population of rostral fastigial nucleus (rFN) neurons previously characterized using a comparable approach (Figure 6C has been adapted from Figure 5 from Brooks and Cullen, 2009). (D) Average tuning curves computed by aligning the peak of each individual neuron’s tuning curve. Average tuning curves are shown for bimodal and unimodal Purkinje cells (blue) for vestibular stimulation with the head oriented at different positions relative to the body. Again, for comparison, the average tuning curves of rFN neurons are superimposed (Figure 6D has been adapted from Figure 6 from Brooks and Cullen, 2009).
Figure 7 with 5 supplements
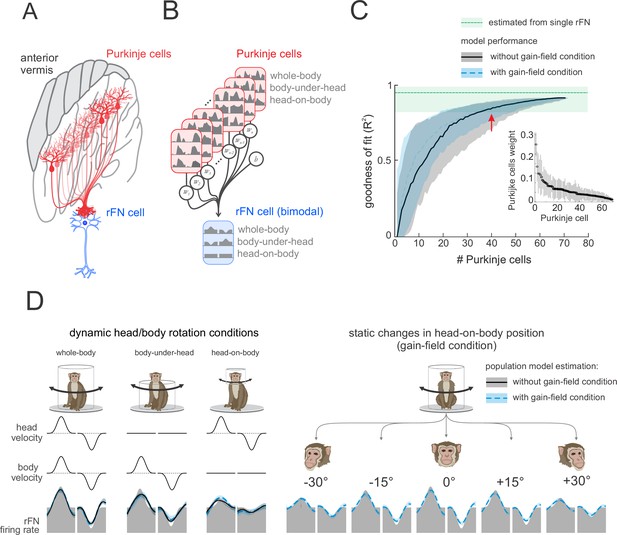
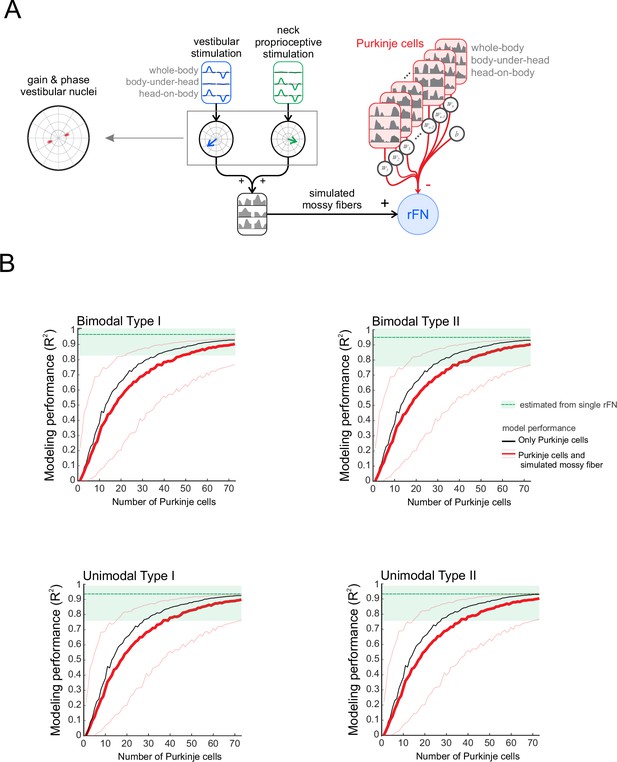
A simple linear population model of Purkinje cell integration can explain the responses of target bimodal neurons in deep cerebellar nuclei across all self-movement conditions.
(A) Illustration of the convergence of multiple Purkinje cells onto a single neuron in the rostral fastigial nucleus (rFN), with different shades of red representing theoretical differences in the weighing of each Purkinje cell’s synapse with the target rFN neuron. (B) Schematic of the linear summation population model used to estimate the firing rate of a target neuron in the rFN. Each Purkinje cell’s weight was optimized to generate the best estimate of the average bimodal rFN neuron across conditions (Brooks and Cullen, 2009). (C) Model performance as a function of the number of Purkinje cells. Black curve corresponds to model fit to the simple spike firing rates of all 73 Purkinje cells recorded during our three dynamic conditions (i.e., whole-body, body-under-head, and head-on-body movements). Blue curve corresponds to the model fit to simple spike firing rates of all 73 Purkinje cells during these same three dynamic conditions as well as simulated responses of these cells recorded in the gain-field condition (Figure 6). The variability estimated from a population of rFN bimodal neurons previously described by Brooks and Cullen, 2009, is represented by the green shaded band. Inset: the distribution of computed weights for each Purkinje cell modeled during our three dynamic conditions with 40 Purkinje cells, sorted based on average weight. (D) Estimated model firing rates based on a population of 40 Purkinje cells superimposed on the actual average firing rate of a bimodal rFN neuron (gray shaded region). Solid black lines versus dashed blue lines illustrate firing rate estimations from models that included (i) the three dynamic head/body rotation conditions (left) versus (ii) the three dynamic conditions as well as the gain-field condition (right).
Figure 7—figure supplement 1
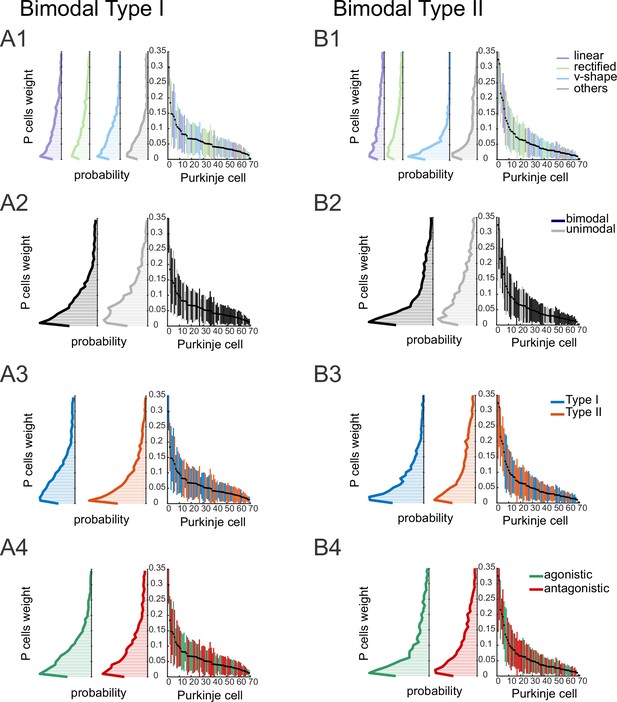
The distribution of the weights of the inputs to the model with 40 Purkinje cells projecting to a bimodal rostral fastigial nucleus (rFN) neuron.
The distribution of the Purkinje cell weights in a model with 40 Purkinje cells projecting to (A) Type I and (B) Type II bimodal rFN neuron that were classified as (A1, B1) linear versus v-shaped versus rectifying Purkinje cells, (A2, B2) bimodal versus unimodal Purkinje cells, (A3, B3) Type I versus Type II Purkinje cells, and (A4, B4) agonistic (i.e., same vestibular and proprioceptive sensitivity sign) versus antagonistic (i.e., opposite vestibular and proprioceptive sensitivity sign).
Figure 7—figure supplement 2
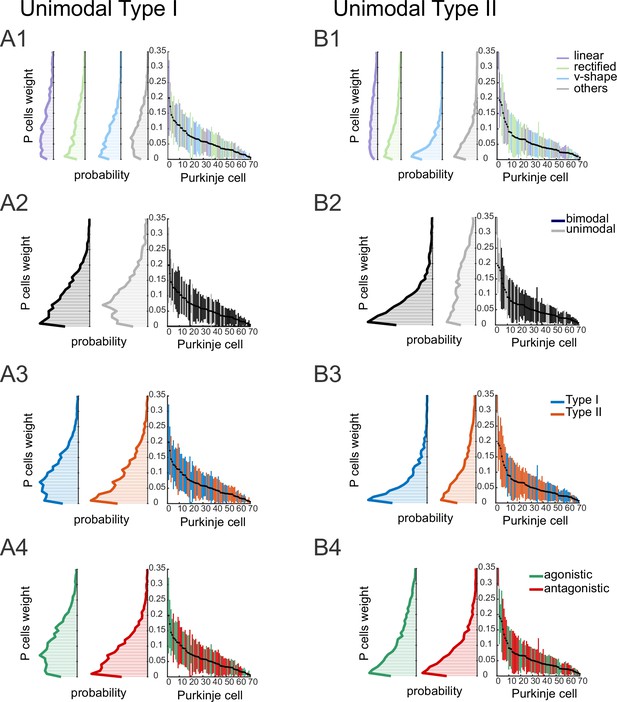
The distribution of the weights of the inputs to a model with 40 Purkinje cells projecting to a unimodal rostral fastigial nucleus (rFN) neuron.
The distribution of the Purkinje cell weights in a model with 40 Purkinje cells projecting to (A) Type I and (B) Type II unimodal rFN neuron that were classified as (A1, B1) linear versus v-shaped versus rectifying Purkinje cells, (A2, B2) bimodal versus unimodal Purkinje cells, (A3, B3) Type I versus Type II Purkinje cells, and (A4, B4) agonistic (i.e., same vestibular and proprioceptive sensitivity sign) versus antagonistic (i.e., opposite vestibular and proprioceptive sensitivity sign).
Figure 7—figure supplement 3
Modeling the mossy fiber inputs to unimodal fastigial neurons.
(A) Schematic of a model with a mossy fiber input that is simulated as the summation of random patterns of responses to vestibular and neck proprioceptive input. The gains and phases were randomly drawn from a distribution comparable to that previously reported in the vestibular nuclei (0.6 ± 0.1 (sp/s)/(°/s) and 20 ± 5°, respectively; Mitchell et al., 2017). (B) The performance of the Purkinje cell population in predicting the response of the bimodal (top) and unimodal (bottom) rostral fastigial nucleus (rFN) neurons in the presence (gray) and absence (red) of mossy fibers in (A).
Figure 7—figure supplement 4
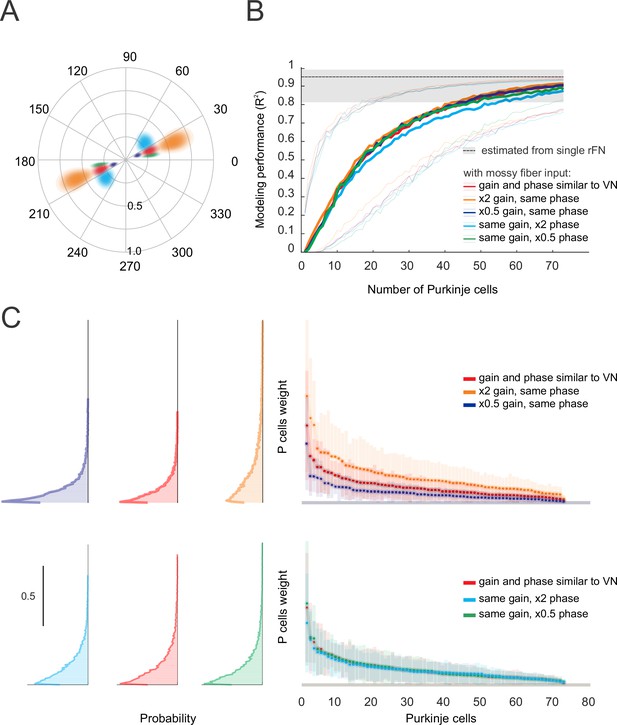
Exploring the effect of systematically altering the distribution of gain and phase values in this simulated mossy fiber input.
(A) Five different distributions of mossy fiber inputs. The reference distribution is similar to the neurons in the vestibular nuclei (red; gain: 0.6 ± 0.1 (sp/s)/(°/s), phase: 20 ± 5°). Four other distributions were generated by systematically altering the distribution of gain and phase values for the reference distribution by (i) doubling the gain (orange), (ii) reducing the gain by half (dark blue), (iii) doubling the phase (blue), and (iv) reducing the phase by half (green). (B) The performance of a population model of Purkinje cells projecting to a bimodal Type I rostral fastigial nucleus (rFN) neuron considering mossy fiber inputs with the five distributions shown in (A). The performance was similar for all distributions of mossy fibers. (C) The distribution of the weights of the Purkinje cells in the model with 40 Purkinje cells considering mossy fiber inputs with the distributions shown in (A). Changing the gain but not the phase of mossy fiber inputs affects the weighting of Purkinje cell inputs.
Figure 7—figure supplement 5
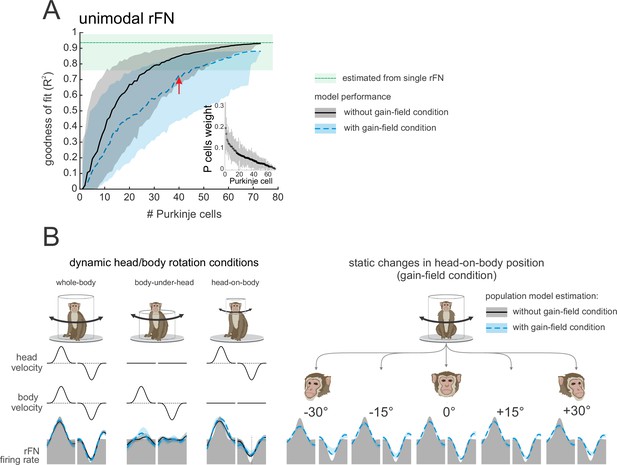
A simple linear population model of Purkinje cell integration can explain the responses of target unimodal neurons in deep cerebellar nuclei across all self-movement conditions.
(A) Model performance as a function of the number of Purkinje cells. Black curves correspond to the population modeling that was performed on the simple spike firing rate of all 73 Purkinje cells recorded during three dynamic conditions (i.e., whole-body, body-under-head, and head-on-body movements). Blue curves correspond to the modeling of the simple spike firing rate of all 73 Purkinje cells during these same three dynamic conditions as well as the gain-field condition (Figure 5). The variability estimated from population of rostral fastigial nucleus (rFN) unimodal neurons previously described by Brooks and Cullen, 2009, is represented by the green shaded band. Inset: the distribution of computed weights for each Purkinje cell in a model with 40 Purkinje cells during our three dynamic conditions, sorted based on average weight. (B) Typical firing rate of unimodal neurons in the rFN (gray shaded region) and the estimated firing rate based on a population of 50 Purkinje cells (mean ± SD) during three dynamic head/body rotation conditions (left) and the static changes in head-on-body position condition (right). We also performed population modeling on rFN Type II cells and found similar results.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Distinct representations of body and head motion are dynamically encoded by Purkinje cell populations in the macaque cerebellum
eLife 11:e75018.
https://doi.org/10.7554/eLife.75018
