Broad-scale variation in human genetic diversity levels is predicted by purifying selection on coding and non-coding elements
- Department of Biological Sciences, Columbia University, United States
- Genes and Human Disease Research Program, Oklahoma Medical Research Foundation, Oklahoma City, United States
- MyHeritage, Israel
- Flatiron Health Inc, United States
- Program for Mathematical Genomics, Columbia University, United States
Figures
Figure 1
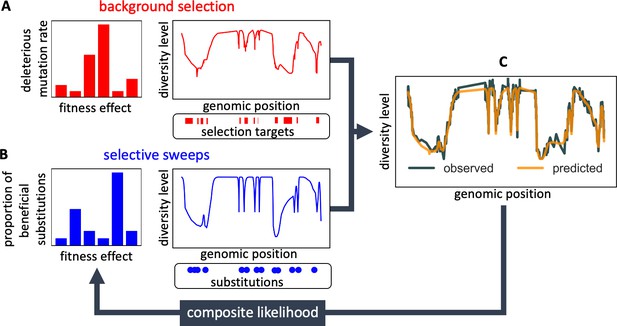
Modeling and inferring the effects of linked selection in humans.
Given the putative targets of selection and corresponding selection parameters (A and B), we calculate the expected neutral diversity levels along the genome (C). We infer the selection parameters by maximizing their composite likelihood given observed diversity levels (C). Based on these parameter estimates, we calculate a map of the expected effects of selection on linked diversity levels.
Figure 2
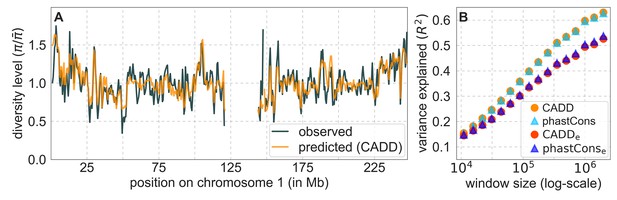
Comparison of diversity levels predicted by our best-fitting maps of background selection effects with observations.
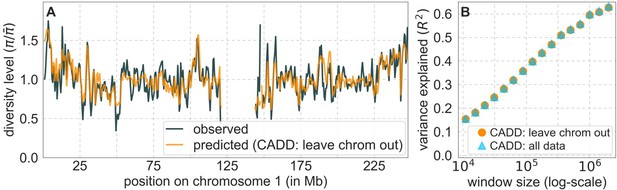
(A) Predicted and observed diversity levels along chromosome 1 in the YRI sample. Diversity levels are measured in 1 Mb windows, with a 0.5 Mb overlap, with the autosomal mean set to 1. (B) The proportion of variance in YRI diversity levels explained by background selection models at different spatial scales. Shown are the results for four choices of putative targets of selection: all sites with the highest 6% of CADD or phastCons scores (denoted CADD and phastCons, respectively) and the subset of these sites that are exonic (denoted CADDe and phastConse, respectively). The results shown for our best-fitting models (based on the 6% of sites with the highest CADD or phastCons scores) are based on out-of-sample predictions in non-overlapping, contiguous 2 Mb windows. See Appendix 1 Section 4 for similar graphs with other choices, and Appendix 1 Sections 7 and 9 for other populations.
Figure 3
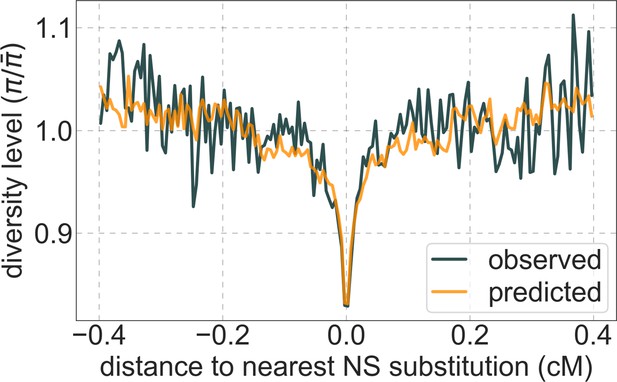
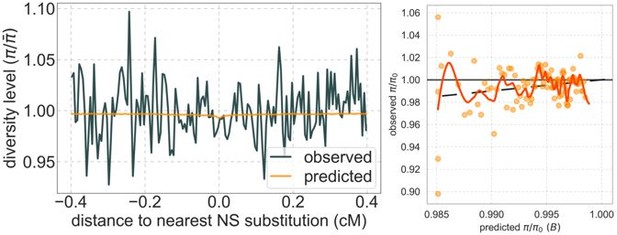
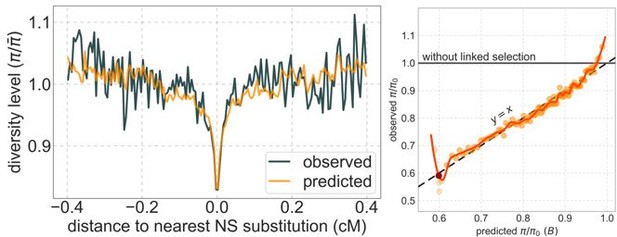
A background selection model predicts neutral diversity levels observed around human-specific nonsynonymous (NS) substitutions.
Shown are the results for putatively neutral sites as a function of their genetic distance to the nearest nonsynonymous substitution (in 160 bins, each spanning 0.005 cM). For observed values, we average diversity levels within each bin. For predicted values, we average diversity levels predicted by our best-fitting CADD-based model (using the out-of-sample predictions in non-overlapping, contiguous, 2 Mb windows) and correct for relative mutation rate in each bin (using substitution data; see Appendix 1 Section 3.3). Both observed and predicted diversity levels are plotted relative to the autosomal mean. See Appendix 1—figure 49 and Appendix 1—figure 51 for similar graphs for other genomic features and using data from other populations.
Figure 4
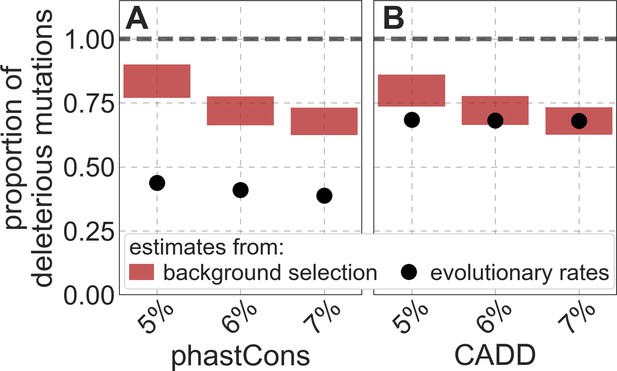
Estimates of the proportion of mutations at putatively selected sites that are deleterious.
Shown are the results using 5–7% of sites with the highest phastCons scores (A) and CADD scores (B) as selection targets. For estimates based on fitting background selection models, we divide our estimates of the deleterious mutation rate per selected site by the estimate of the total mutation rate per site, where the ranges correspond to the range of estimates of the total rate, that is, per base pair per generation (Appendix 1 Section 5.1). For estimates based on evolutionary rates (on the human lineage from the common ancestor of humans and chimpanzees), we take the ratio of the estimated rates at putatively selected sites and at matched sets of putatively neutral sites (see text and Appendix 1 Section 5.2 for details).
Figure 5
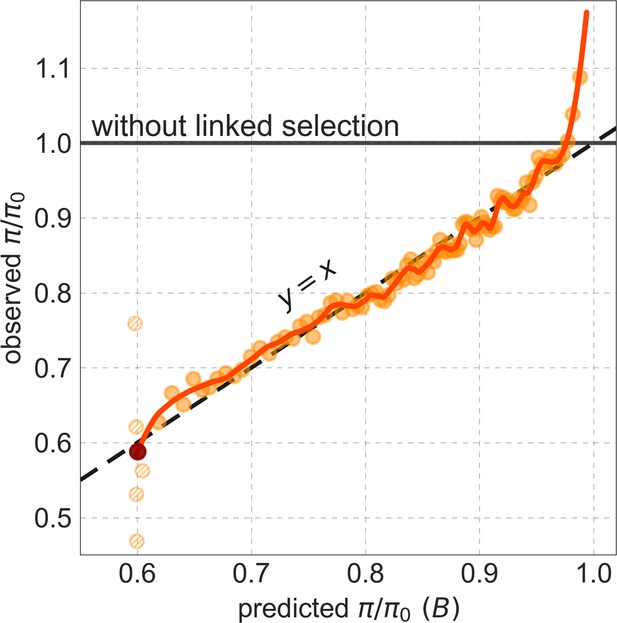
Observed vs. predicted neutral diversity levels across the autosomes.
Shown are the results for the best-fitting CADD-based model, using the out-of-sample predictions in non-overlapping, contiguous 2 Mb windows. Light orange scatter plot: we divide putatively neutral sites into 100 equally sized bins based on the predicted . For predicted values (x-axis), we average the predicted in each bin. For observed values (y-axis), we divide the average diversity level by the estimate of the average relative mutation rate (obtained from substitution data; see Appendix 1 Section 3.3) in each bin, and normalize by the autosomal average of (estimated from fitting the model; see Appendix 1 Section 1.1). Owing to a technical approximation (see Appendix 1 Section 1.5), our method forces the predictions for the 5 bins with the lowest predicted (open, hatched circles on the left) to be similar; we therefore also show the results for these bins grouped together (dark red circle). Dark orange curve: the LOESS fit for a similarly defined scatter plot but with 2000 rather than 100 bins (with span = 0.1). For similar graphs corresponding to other models and using data from other populations, see Appendix 1 Sections 4 and 9, respectively.
Appendix 1—figure 1
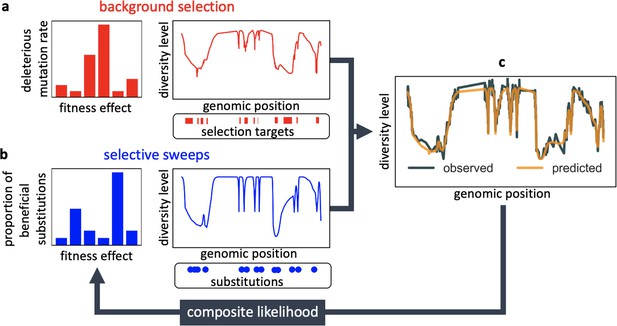
Modeling and inferring the effects of linked selection in humans.
Given the targets of selection and corresponding selection parameters (a and b), we calculate the expected neutral diversity levels along the genome (c). We infer the selection parameters by maximizing their composite-likelihood given observed diversity levels (c). Based on these parameter estimates, we calculate a map of the expected effects of linked selection on diversity levels.
Appendix 1—figure 2
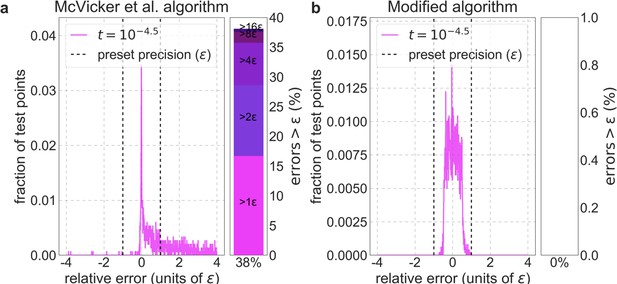
Distribution of relative errors in predictions before and after modifying calc_bkgd.
We consider the model in which autosomal sites with the top 6% of CADD scores are chosen as selection targets, the deleterious mutation rate is per bp per generation and the selection coefficient is the lowest in our grid (), because this is the case most prone to errors (see text). We calculate -values accurately (using Equation 10) at a million positions picked randomly from the 22 autosomes and use these values to calculate the relative errors based on the McVicker et al. algorithm (a) and on our modified algorithm (b). The side panel shows the proportion of sites in which the error exceeds (below), as well as its breakdown in multiples of .
Appendix 1—figure 3
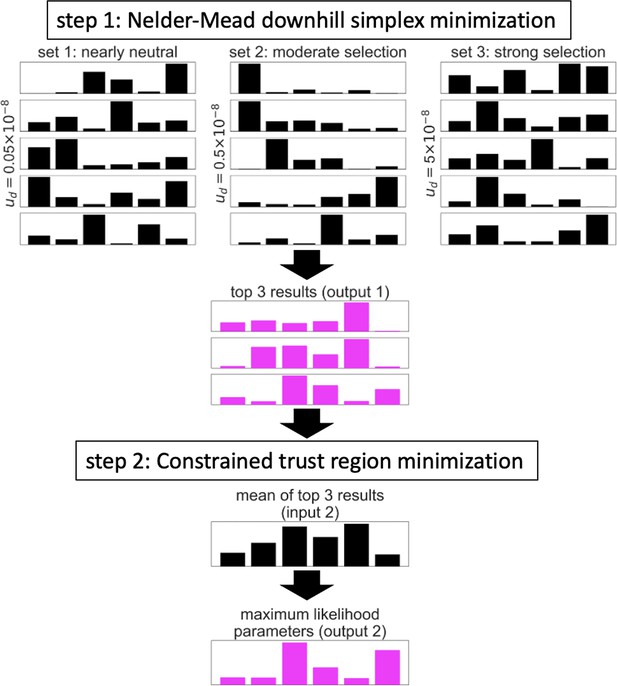
Illustration of the two-step algorithm.
In this example, the optimization is applied to a model of background selection with a single selected annotation and a grid of 6 selection coefficients. See text for details.
Appendix 1—figure 4
Comparison of inferred and ground-truth parameters for datasets simulated ‘deterministically’ under the best-fitting background selection model.
Panels a-d correspond to different simulated datasets. Boxed region in (c) highlights the small differences between inferred and ground truth parameters introduced by discretization.
Appendix 1—figure 5
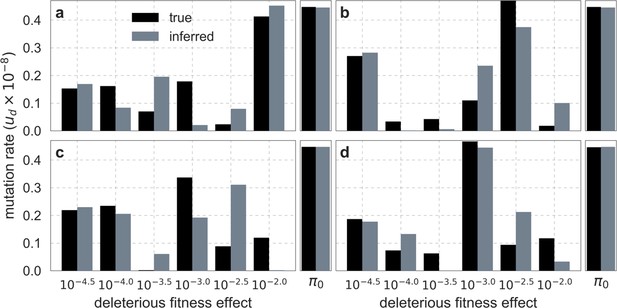
Comparison of inferred and ground-truth parameters for datasets simulated with noise under the best-fitting background selection model.
Panels a-d correspond to different simulated datasets.
Appendix 1—figure 6
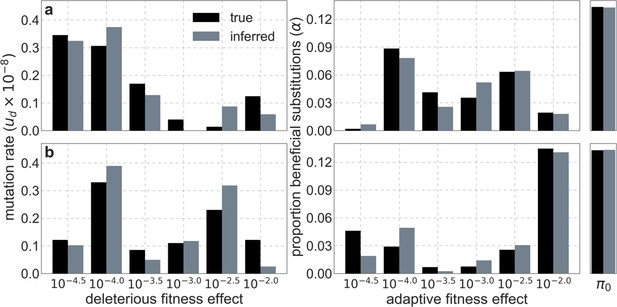
Comparison of inferred and ground-truth parameters for datasets simulated with noise under a joint model of background selection and selective sweeps.
Panels a and b correspond to different simulated datasets.
Appendix 1—figure 7
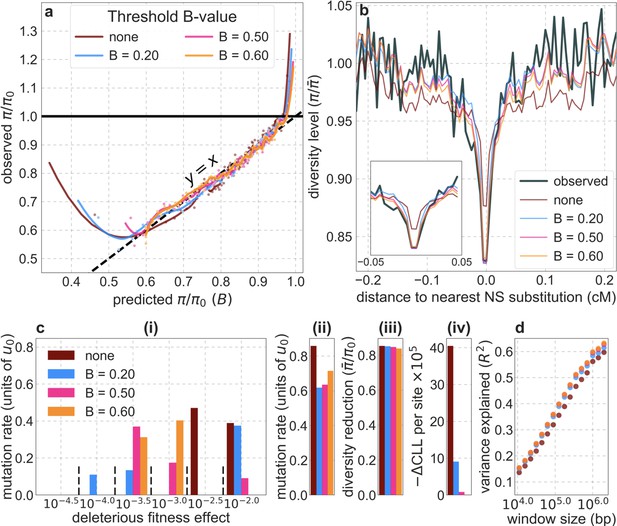
Comparison of inference results with and without thresholding.
The results shown correspond to our best-fitting CADD-based model (see Main Text), with threshold values of (without threshold, labeled ‘none’), , , and applied in the lookup tables. (a) Observed vs. predicted neutral diversity levels across the autosomes. The graph was generated as detailed in Figure 5. Note that the division of neutral sites among bins varies with the choices of thresholds because it is based on corresponding maps. (b) Observed vs. predicted neutral diversity levels as a function of genetic distance from human-specific nonsynonymous (NS) substitutions. The graph was generated as detailed in Figure 3, using a narrower range of genetic distances to NS substitutions to highlight differences among thresholds. (c) Parameter estimates and summaries of the inferences. From left to right: (i) The estimated distribution of fitness effects, described in terms of the rate of mutation per generation with a given selection coefficient. Mutation rates (throughout) are measured relative to the estimate of the total mutation rate in humans, per bp per generation (see Section 5). (ii) The total deleterious mutation rate () measured in units of . (iii) Our prediction of the mean reduction in neutral diversity level due to background selection, measured as the ratio of the average predicted level across the genome, , to the predicted level in the absence of selection at linked sites, . (iv) The reduction in composite log-likelihood (CLL) per site relative to the model with the highest CLL. Differences in CLL should be interpreted with caution, as this measure does not account for linkage disequilibrium. (d) The proportion of variance in diversity levels explained () on different spatial scales (measured in non-overlapping windows).
Appendix 1—figure 8
The proportion of variance explained in 10 kb, 100 kb, and 1 Mb windows using a range of thresholds applied to lookup tables (‘lookup’) or during maximization (‘maximization’).
Appendix 1—figure 9
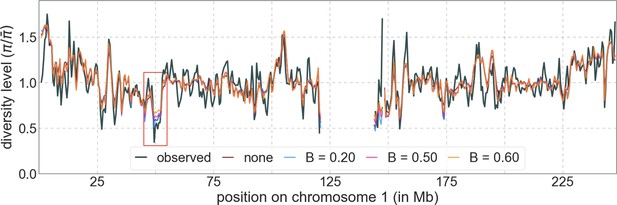
Predicted and observed diversity levels along chromosome 1 in the YRI sample.
Diversity levels are measured in 1 Mb windows, with a 0.5 Mb overlap, with the autosomal mean set to 1. Thresholds were applied in the lookup tables. Lower thresholds yield better predictions in regions with low diversity levels, for example, near 50 Mb (red box).
Appendix 1—figure 10
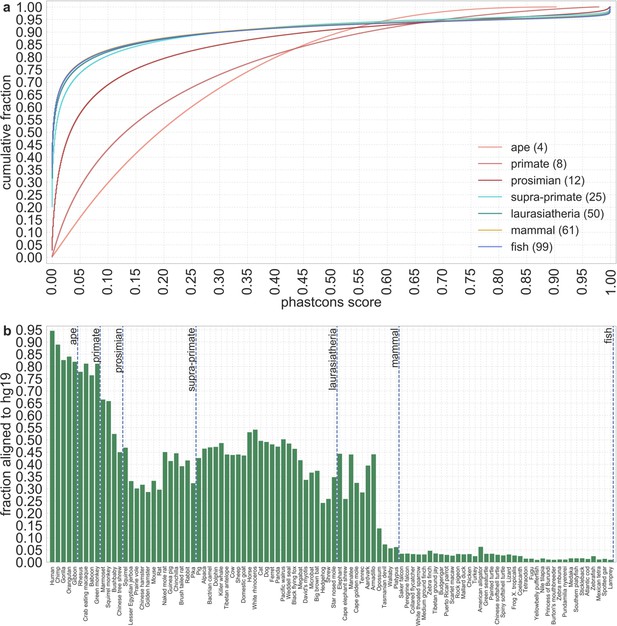
The distribution of phastCons scores across autosomes for varying phylogenetic distances from humans.
(a) The number of species included at each phylogenetic depth is noted in the caption. As the number of species in the alignment increases, the ability to distinguish between conserved and neutral sites increases. (b) The proportion of a species’ sequenced genome that aligns to the human reference (hg19) decreases with their phylogenetic distance from humans. The decrease is not monotonic because of other factors, for example, the quality of the sequencing. The proportion is not 1 for humans because of missing information in the reference genome.
Appendix 1—figure 11
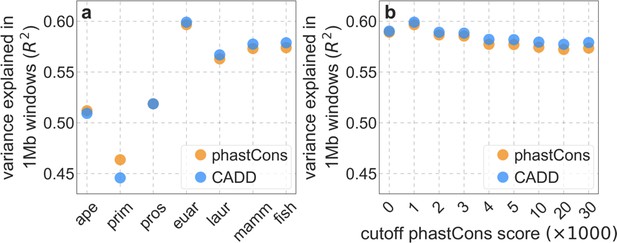
The variance in diversity levels explained by our two best-fitting models using different choices of putatively neutral sites.
In (a) we vary the phylogenetic depth of the multi-species alignment (i.e. the maximal phylogenetic distance from humans to any/all of the other species) and in (b) we vary the cutoff phastCons score for the least conserved sites included in our set. The best fit corresponds to the least conserved 35% of sites (phastCons scores ≤ 0.001) in the supra-primate alignment (euar).
Appendix 1—figure 12
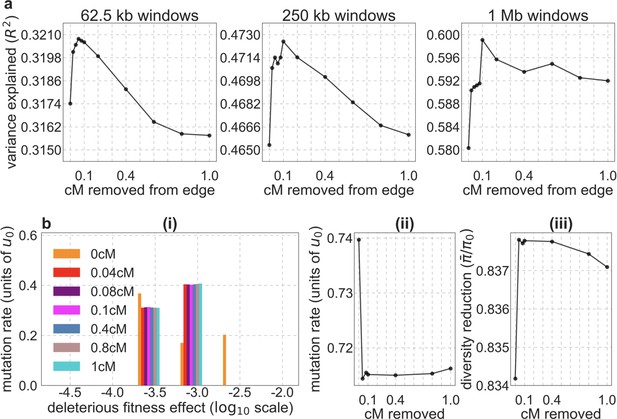
The effect of removing putatively neutral sites near telomeres on model fit and parameter estimates.
We show the result for our best-fitting CADD-based model; results for phastCons scores are highly similar (not shown). (a) The proportion of variance in diversity levels explained for different window sizes, as a function of the size of the removed region (in cM). (b) (i-iii) Estimates of model parameters as a function of the size of the removed region (in cM).
Appendix 1—figure 13
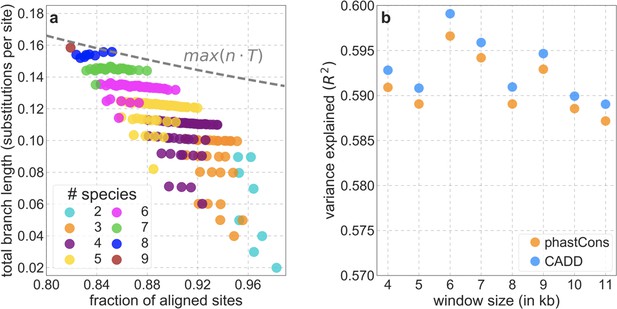
Choosing the parameters used in estimating the relative mutation rate at putatively neutral sites.
(a) The trade-off between the fraction of aligned sites and total branch length for subsets of the primate phylogeny. The fraction of aligned sites is estimated for our set of putatively neutral sites, and the total branch length is measured in terms of the average number of substitutions per site on the phylogeny, estimated by phyloFit. The maximum product of the fraction and branch length is attained by including all primates included in the 99-vertebrate alignment other than gibbon. (b) The variance in diversity levels explained by our best-fitting models across 1 Mb windows, for different choices of window sizes (i.e. the number of putatively neutral sites) used to control for variation in mutation rates at putatively neutral sites.
Appendix 1—figure 14
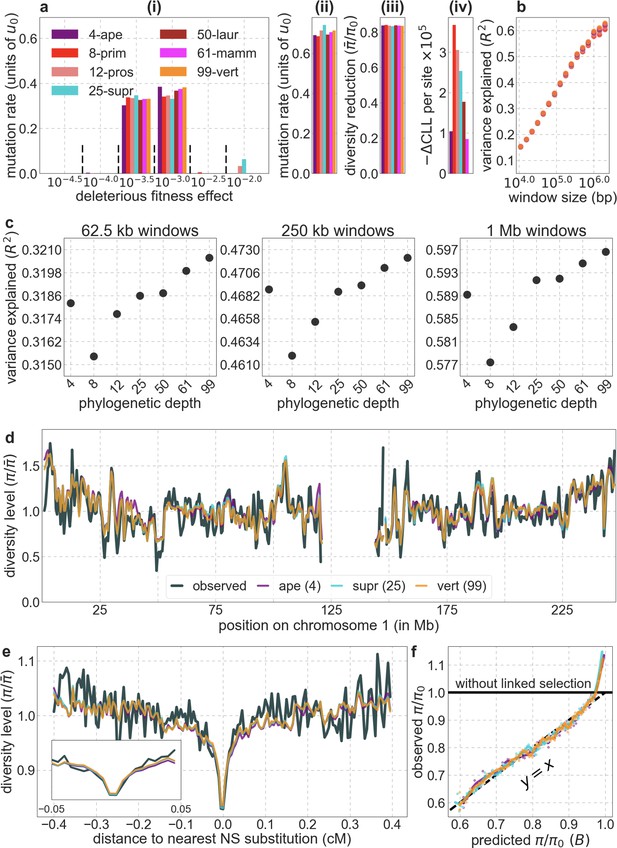
Comparison of background selection models based on phastCons conservation scores in phylogenies of difference depths.
Shown are results of models based on conservation in four apes, eight primates, 12 prosimians, 25 supra-primates, 50 laurasiatherians, 61 mammals, and 99 vertebrates extending out to lamprey. In all cases, we take the 6% of autosomal sites with the highest phastCons scores (excluding putatively neutral sites) as our targets of selection. Throughout Appendix 1, with the exception of Section 7, we show results using data from YRI. The panels describe: (a) Parameters and summaries of models (from left to right): (i) Estimated distribution of fitness effects, described in terms of the rate of mutations with given selection coefficients. Mutation rates throughout are measured relative to the estimate of the estimated average mutation rate per bp per generation in humans, (see Section 5). As detailed in Section 1.5, the inferred distribution of selection coefficients should be interpreted with caution. (ii) Estimated total deleterious mutation rate per selected site () measured in units of . (iii) Estimated autosomal average fold-reduction in neutral diversity levels due to selection at linked sites, i.e., the ratio of average predicted heterozygosity, , to average predicted heterozygosity in the absence of selection at linked sites, . (iv) The reduction in composite log-likelihood (CLL) per site relative to the model with the highest CLL. Differences in CLL should be interpreted with caution, as diversity levels at putatively neutral sites are not independent. (b) The proportion of variance in diversity levels explained () on different spatial scales (measured in non-overlapping contiguous windows). (c) Close-up on the variance explained for several window sizes. (d) Predicted and observed diversity levels along chromosome 1. Diversity levels are measured in 1 Mb windows, with 0.5 Mb overlap, and are normalized by the mean level (as detailed in Figure 2). The results here and in subsequent panels are shown for a subset of depths, including four apes, 25 supra-primates and 99 vertebrates. (e) Predicted and observed diversity levels as a function of genetic distance to the nearest human-specific nonsynonymous (NS) substitutions. The plot was generated as detailed in Figure 3. Inset shows closeup between –0.05 and 0.05 cM. (f) Observed vs. predicted neutral diversity levels across the autosomes. The plot was generated as detailed in Figure 5.
Appendix 1—figure 15
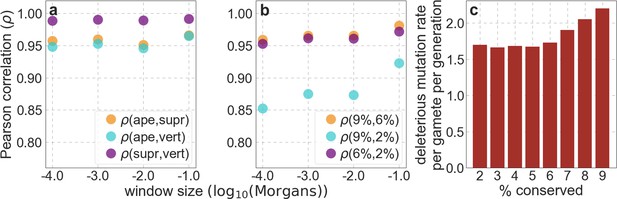
The spatial distribution of putatively selected sites remains similar when we vary the phylogenetic depth of the alignment used to infer conservation (shown in a), and the proportion of sites with the highest conservation scores included (in b).
We compare two choices of selection targets at a time, and show the Pearson correlations () between the numbers of putatively selected sites among windows of different genetic lengths (measured in Morgans). The range of window sizes roughly corresponds to the spatial scales over which selection affects linked neutral diversity for the estimated range of selection effects. When we vary the phylogenetic depth, we use the 6% of autosomal sites with the highest phastCons scores, and when we vary the conservation cutoff, we use phastCons scores based on the 99-vertebrate alignment. (c) The deleterious mutation rate per gamete per generation inferred as a function of assumed proportion of selected sites in autosomes.
Appendix 1—figure 16
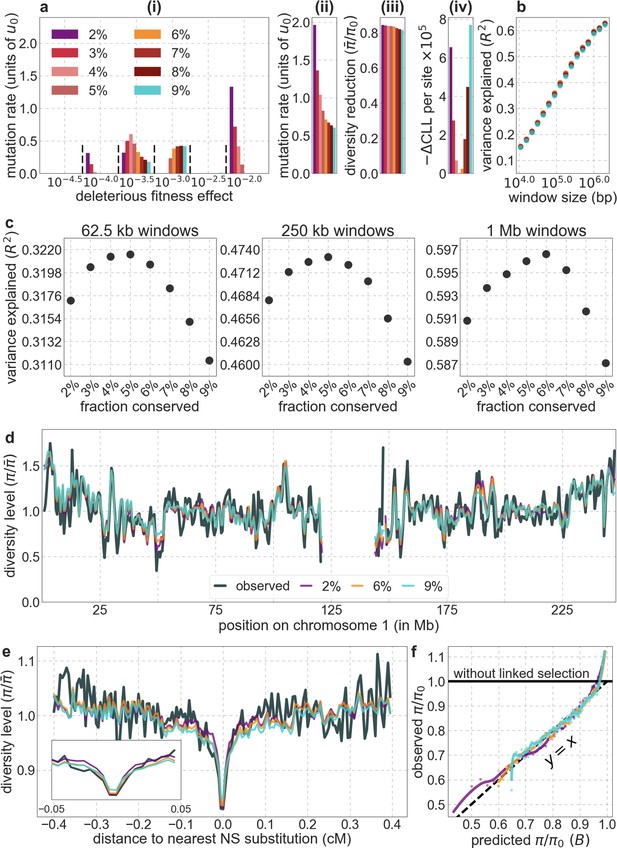
Comparison of background selection models based on phastCons scores using different proportions of autosomal sites as selection targets.
In all cases considered, we rely on conservation in 99 vertebrates. Otherwise, all panels are as described in Appendix 1—figure 14.
Appendix 1—figure 17
The background selection model based on simple genic annotations fits worse than our best-fitting phastCons-based model.
All the panels are as described in Appendix 1—figure 14 (but with the hatch-marked blue bars in a (i) and (ii) corresponding to different annotations of the genic model).
Appendix 1—figure 18
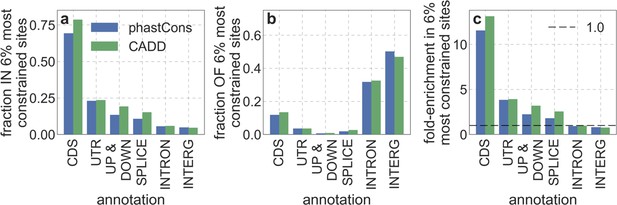
The relationship between simple genic annotations and our main measures of constraint.
Specifically, we examine the overlap of the 6% of autosomal sites with the highest phastCons or CADD scores with the genic annotation detailed in the text; we added intronic (INTRON) and intergenic (INTERG) annotations for completeness. (a) The fraction of each genic annotation within the 6% most constrained sites. (b) The fraction of the 6% most constrained within each genic annotation. (c) Enrichment of genic annotations in the 6% most constrained sites, i.e., the ratio of their proportion among constrained and all autosomal sites.
Appendix 1—figure 19
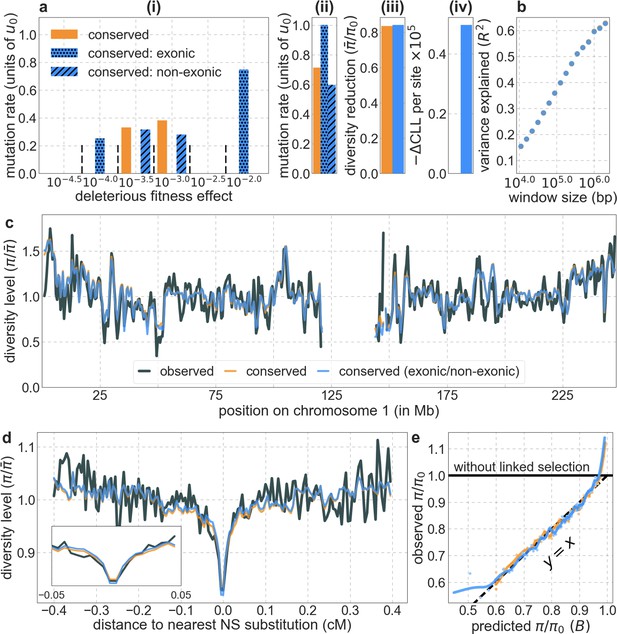
Dividing conserved sites into exonic and non-exonic sets leads to different estimates of selection parameters in each, but to little improvement in fit compared to the model based on conservation alone.
Our set of conserved sites consists of the 6% of sites with the highest phastCons scores in the 99-vertebrate alignment (see Section 4.1). All panels are as described in Appendix 1—figure 14. Because of thresholding (Section 1.5), the model based on conservation alone is not formally nested in the one with the division into exonic and non-exonic sets, explaining how its maximum composite-likelihood can be slightly greater.
Appendix 1—figure 20
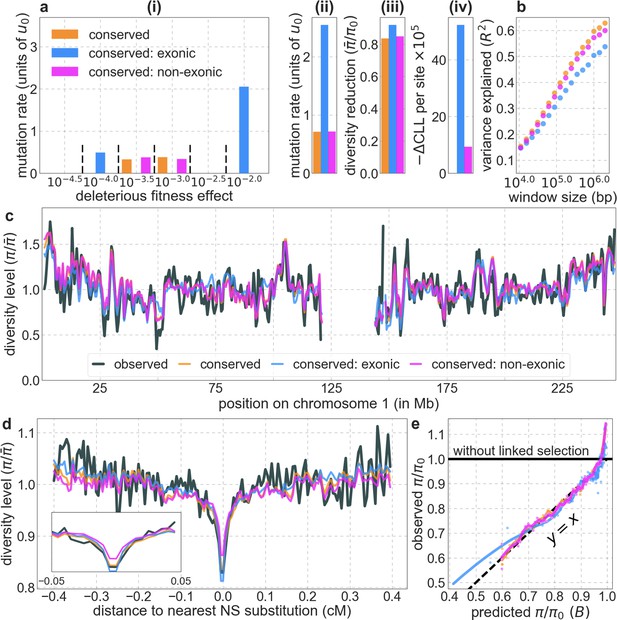
Comparison of background models using exonic, non-exonic and all conserved sites as targets of selection.
Our set of conserved sites consists of the 6% of sites with the highest phastCons scores in the 99-vertebrate alignment (see Section 4.1). All panels are as described in Appendix 1—figure 14.
Appendix 1—figure 21
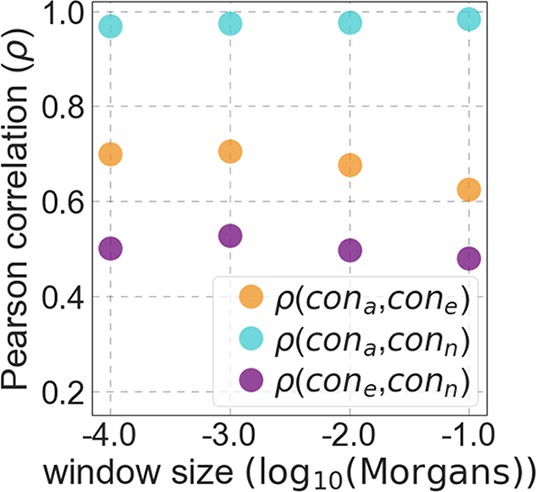
The spatial correlations of exonic, non-exonic and all conserved sites for varying window sizes (‘cone’, ‘conn’ and ‘cona‘, respectively).
Appendix 1—figure 22
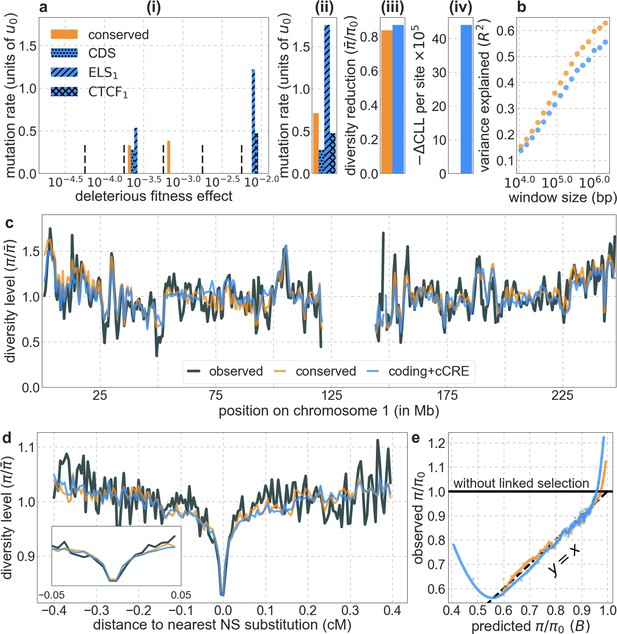
The model based on the ENCODE annotations of cCRE fit the data substantially worse than our best-fitting phastCons-based model using conservation in the 99-vertebrate alignment (conserved).
The results shown correspond to the model in which we split each type of cCREs into those that occur in few (subscript 1) and many biosamples (subscript 2). We infer a non-negligible deleterious mutation rate (i.e. ) in 2 of the 8 cCRE-based putative selection targets: enhancer like sequences and CTCF binding sites identified in few biosamples, ELS1 and CTCF1 respectively, as well as in protein coding regions (CDS). All the panels are as described in Appendix 1—figure 14.
Appendix 1—figure 23
The relationship between ENCODE cCRE annotations and our main measures of constraint.
Specifically, we examine the overlap of the 6% of autosomal sites with the highest phastCons or CADD scores with promoter like sequences (PLS), enhancer like sequences (ELS), CTCF-bound (CTCF), poised/DNAse-hypersensitive (H3K4me3), as well as sites that are not in any of these annotations (NONE). (a) The fraction of each cCRE annotation within the 6% most constrained sites. (b) The fraction of the 6% most constrained within each cCRE annotation. (c) Enrichment of cCRE annotations in the 6% most constrained sites, that is, the ratio of their proportion among constrained and all autosomal sites.
Appendix 1—figure 24
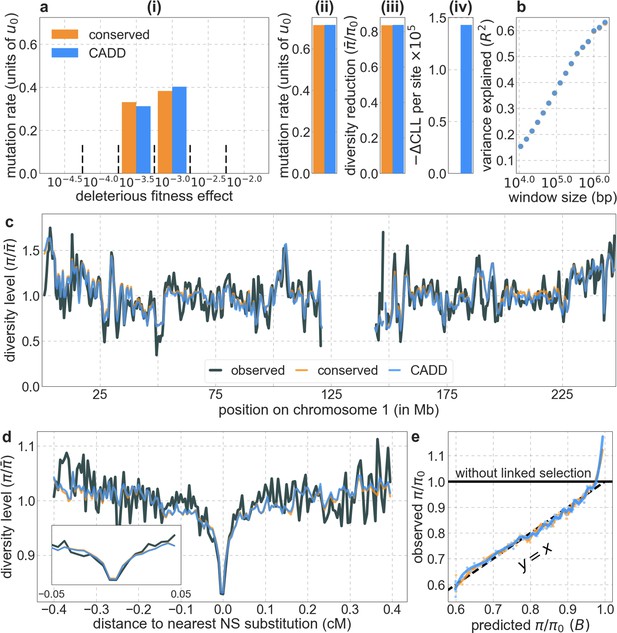
The model based on CADD scores offer little improvement over the model based on phastCons scores (based on the 99-vertebrate alignment).
In both cases, we take the 6% of sites with the highest scores. All the panels are as described in Appendix 1—figure 14.
Appendix 1—figure 25
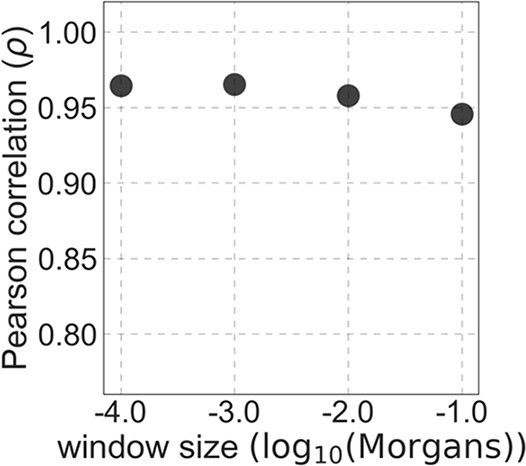
The spatial correlation between the 6% of sites with the highest CADD and phastCons scores.
Appendix 1—figure 26
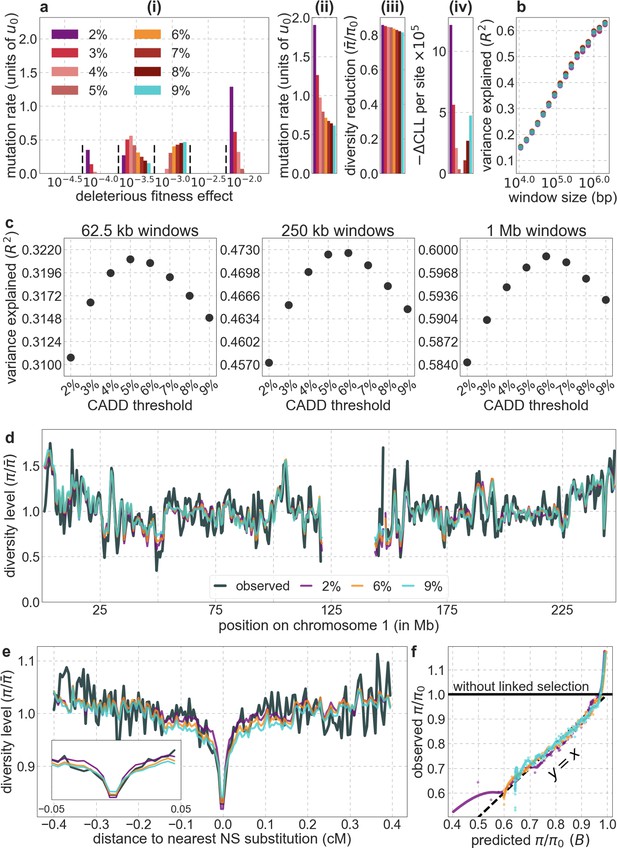
Comparison of background selection models based on CADD scores using different proportions of autosomal sites as selection targets.
All panels are as described in Appendix 1—figure 14.
Appendix 1—figure 27
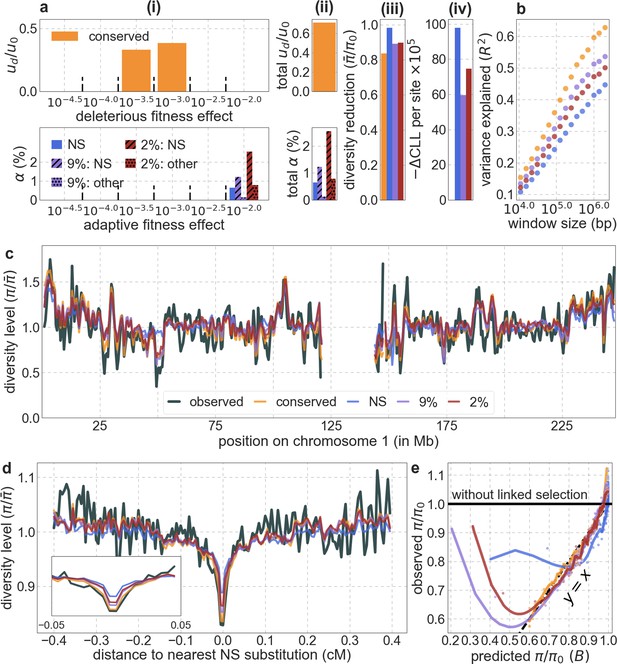
Models with sweeps alone fit substantially worse than models with background selection alone.
Shown are the results for sweep models based on either: all nonsynonymous substitutions (NS); nonsynonymous and other substitutions at sites within the top 9% of phastCons scores (9%: NS/other); or nonsynonymous and other substitutions at sites within the top 2% of phastCons scores (2%: NS/other). For comparison, we also show the results of our best-fitting phastCons-based background selection model (conserved). The panels are as described in Appendix 1—figure 14, with the exception of the bottom halves of panels a (i) and (ii), which show the proportions of substitutions that are estimated to be adaptive for a given selection coefficient (i) or in total (ii), for different annotations and sweeps models.
Appendix 1—figure 28
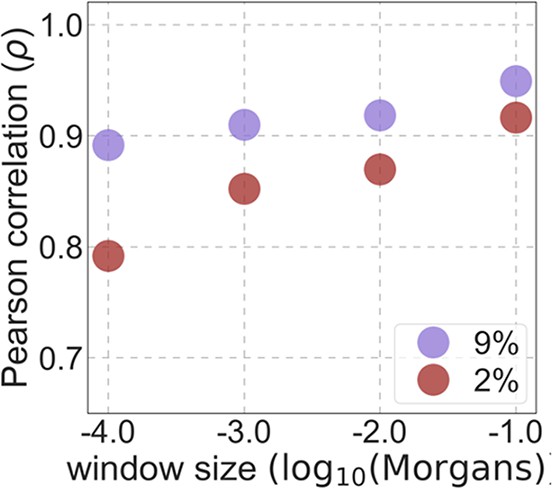
The spatial correlation between targets of selection in sweep models and in our best-fitting phastCons-based background selection model.
Results shown for sweep models based on human-specific substitutions at sites within the top 2% and 9% of phastCons scores (see text for details).
Appendix 1—figure 29
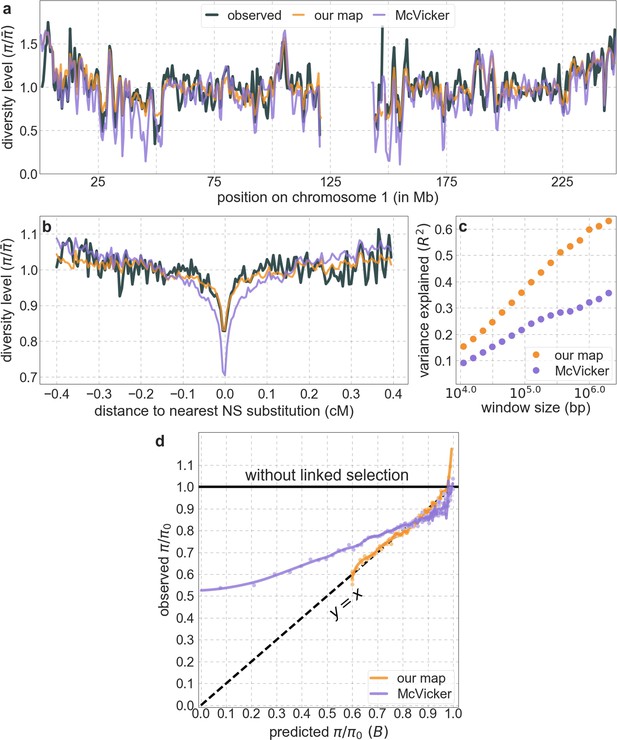
Our maps of the effects of background selection fit the data much better than the maps from McVicker et al., 2009.
Shown are the results for our best-fitting CADD-based model. All panels are as described for the corresponding ones in Appendix 1—figure 14.
Appendix 1—figure 30
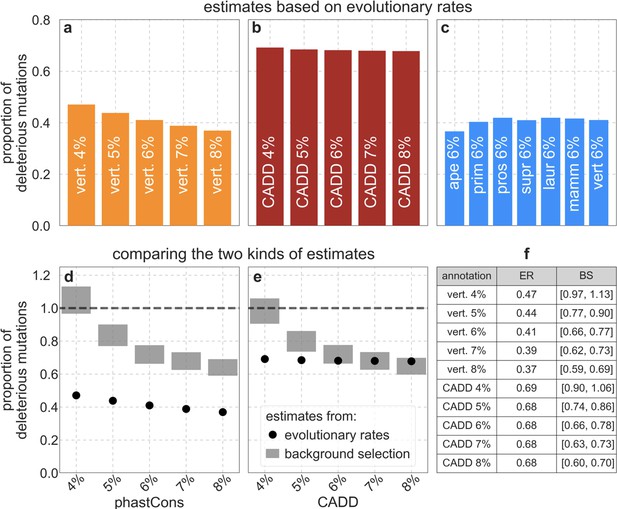
Different estimates of the deleterious mutation rate at putatively selected sites, measured relative to total mutation rates per site ().
Estimates based on evolutionary rates are shown for sets of selected sites chosen based on either: (a) the top 4–8% of phastCons scores for the 99-vertebrate alignment, (b) the top 4–8% of CADD scores, or (c) the top 6% of phastCons scores for alignments of varying phylogenetic depths. As expected, (see Section 4.1), the estimates are fairly insensitive to the phylogenetic depth (c). (d and e) Estimates based on evolutionary rates vs. those based on the effects of background selection, for sets of putatively selected sites based on phastCons scores for the 99-vertebrate alignment (d) and on CADD scores (e). (f) Estimates for different sets of putatively selected sites based on evolutionary rates (ER) and background selection effects (BS). The range of estimates based on background selection effects (in d-f) is due to the uncertainty about the total mutation rate per site (Section 5.1).
Appendix 1—figure 31
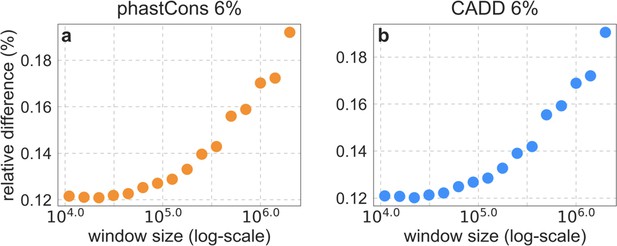
The relative difference between estimates using all the data and the exclusion approach described in the text, for our two best-fitting models.
Appendix 1—figure 32
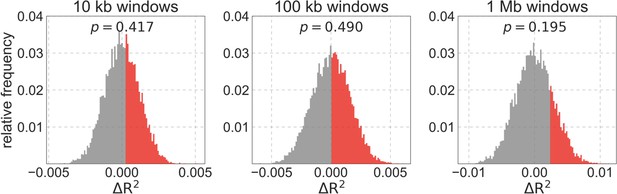
Assessing the differences in fit between our best-fitting models on three spatial scales.
We show the distribution of differences in explained variance () for 10,000 paired permutations of the best-fitting CADD and phastCons based maps. The part of the distributions with is in red, and the corresponding p-value is shown above.
Appendix 1—figure 33
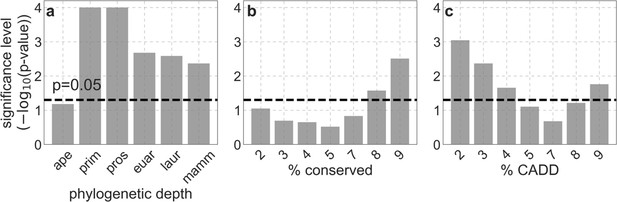
Significance level of differences in fit between our best-fitting models and variations on these models, on the 1 Mb spatial scale.
(a and b) Comparison of our best-fitting phastCons-based model with phastCons-based models with alternative phylogenetic depths (a) and conservation thresholds (b). (c) Comparisons of our best-fitting CADD-based model with CADD-based models with alternative thresholds.
Appendix 1—figure 34
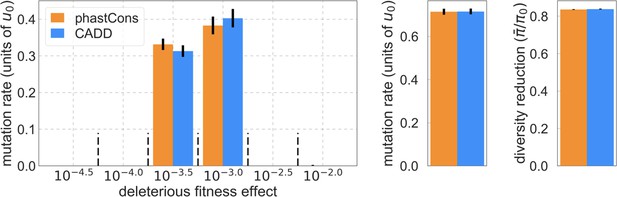
Estimates of the sampling errors of parameter estimates for our two best-fitting models.
The bars denote estimated using jackknife as described in the text.
Appendix 1—figure 35
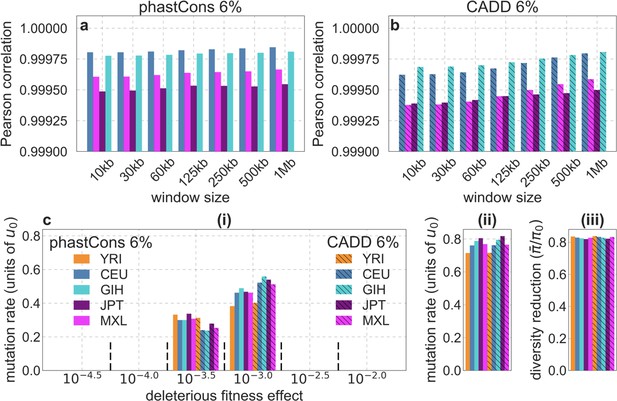
The maps and parameter estimates for different populations are remarkably similar.
Shown are the results for our best-fitting models using data for one of 1000 Genomes Project populations from each continental group: Africa – Yoruba (YRI), Europe – North-Western European (CEU), South Asia – Gujrati Indian (GIH), East Asia – Japanese (JPT), and Americas – Mexican (MXL). (a and b) The Pearson correlations between predictions of relative diversity levels (compared to the population mean) in YRI vs. the other populations for the models based on phastCons (a) and CADD (b) scores. (c) Comparison of parameter estimates using data from these populations (panels c (i-iii) as described in panels a (i-iii) in Appendix 1—figure 14).
Appendix 1—figure 36
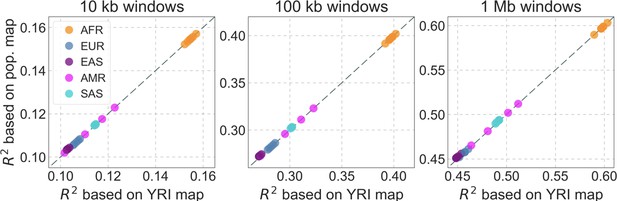
The proportion of variance in diversity levels explained () in different populations, using the population specific map vs. the YRI map.
We show the results for three window sizes (10 kb, 100 kb, and 1 Mb) based on our best-fitting CADD-based model. Each point corresponds to one of the 26 populations sampled in the 1000 genomes project and is colored based on continental origin, i.e., African (AFR), European (EUR), South Asian (SAS), East Asian (EAS), and American (AMR).
Appendix 1—figure 37
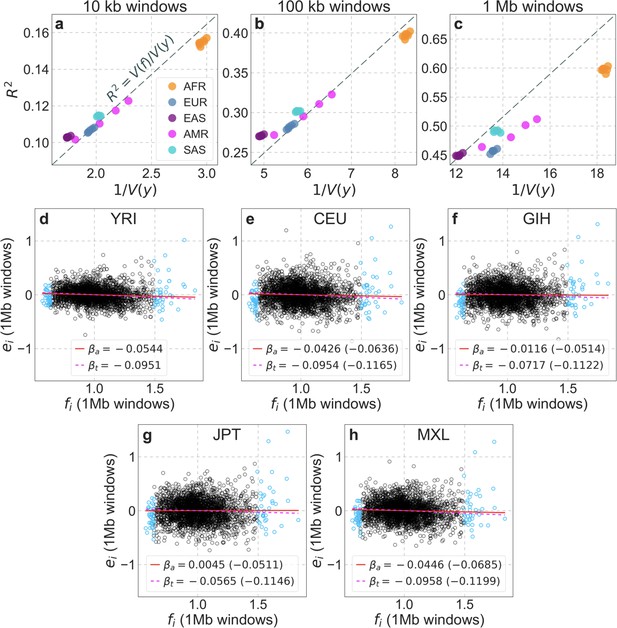
Differences among populations in the variance in diversity levels explained by our map of the effects background selection.
(a–c) The variance explained () as a function of (where is the total variance), for three choices of window size. If the interaction terms () were 0, we would expect populations to fall on the dashed line , with slope and differences in due to demographic history. The distances from the dashed line reflect the interaction terms (specifically, ; Equation 15). The points correspond to the 26 populations sampled in the 1000 genomes project (Auton et al., 2015) and are colored by continental origin as described in Appendix 1—figure 36. Here we base our predictions on our best-fitting CADD-based map in YRI, but using other population-specific maps yields almost identical results. (d-h) The relationship between the residuals () and predictions () in representative populations (same as in Appendix 1—figure 36) on the 1 Mb scale. The 1.5% of windows with lowest and highest predicted values, where our predictions are likely off for various reasons (see Sections 1.5 and 8), are marked in blue. The s for each population, with and without extreme points, are shown on the graph (denoted ‘a’ for ‘all’ and ‘t’ for ‘trimmed’, respectively). As above, we use the predictions in YRI, but other population maps yield qualitatively similar results (s obtained using the corresponding population specific maps are shown in parenthesis).
Appendix 1—figure 38
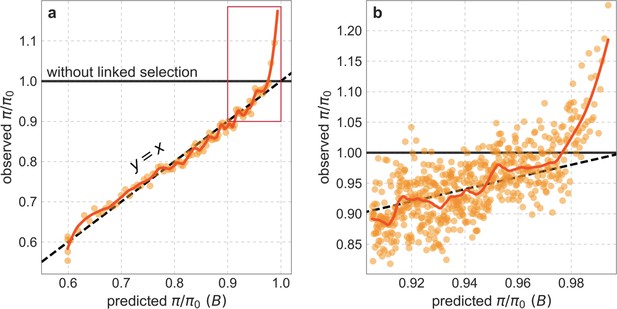
Observed vs. predicted neutral diversity levels across the autosomes (similar to Figure 5).
(a) Light orange scatter plot: We divide putatively neutral sites into 100 equally sized bins based on the predicted effect of background selection, , from the best-fitting CADD-based model. For predicted values (x-axis), we average the predicted in each bin. For observed values (y-axis), we divide the average diversity level in each bin by the average predicted diversity level in the absence of background selection, , after scaling each in bin by its estimated local (relative) mutation rate ( in Equation 8; Section 3.3). Dark orange curve: the LOESS curve for a similarly defined scatter plot but with 2000 rather than 100 bins (with span = 0.1). (b) A close-up near corresponding to the boxed region in (a). Here, the LOESS curve has span = 0.033 and the scatter plot corresponds to 2000 bins (showing the top 30%).
Appendix 1—figure 39
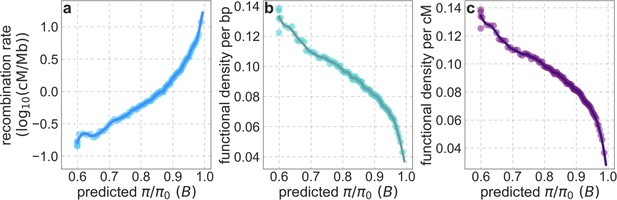
Average recombination rate (a) and functional density per bp (b) and per cM (c) as a function of predicted .
The predicted , binning of putatively neutral sites and LOESS fitting are as described in Appendix 1—figure 38a. We calculate the average recombination rate in each bin based on the African-American admixture map from Hinch et al., 2011 (Section 2.3). We measure functional density by calculating the mean phastCons score (based on the 99-vertebrate alignment) in a radius of 50 kb (b) or 0.05 cM (c) around each putatitively neutral site, and averaging these means over sites in each bin.
Appendix 1—figure 40
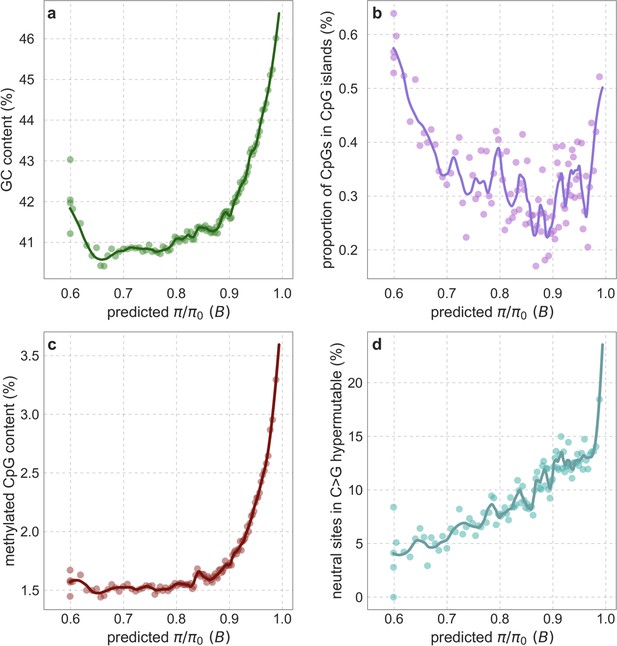
GC content (a), CpG sites in CpG islands (b), proportion of methylated CpGs in neutral sites (c), and proportion of neutral sites in C>G hypermutable regions (d) as a function of predicted .
Proportions and other quantities are measured for putatively neutral sites, whose type (i.e. GC and CpG) is defined based on the inferred state in the human-chimpanzee ancestor (Section 2.7). Data sources are detailed in Section 2.8. The predicted , binning of putatively neutral sites and LOESS fitting are as described for Appendix 1—figure 38a.
Appendix 1—figure 41
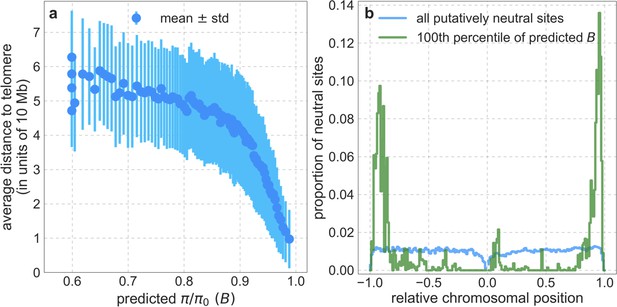
The relationship between chromosomal position and predicted .
(a) The distance to telomeres is measured on the same chromosome (see Section 2.8). (b) The distribution of putatively neutral sites by relative chromosomal position, defined as the ratio of a site’s distance to the centromere and the distance between centromere and telomeres on that chromosomal arm (see Section 2.8); relative distances corresponding to the shorter chromosome arm are shown on the left (in [–1, 0]) and to the longer arm on the right (in [0, 1]). The binning of putatively neutral sites by predicted is as described for Appendix 1—figure 38a.
Appendix 1—figure 42
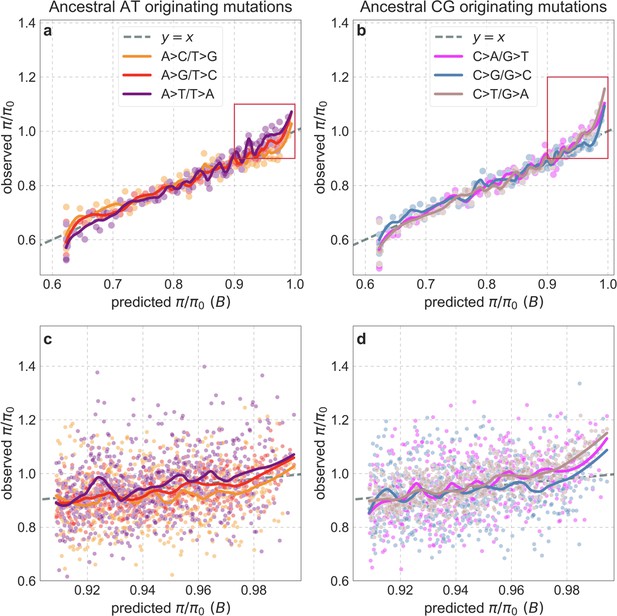
Rates of different types of substitutions as a function of predicted .
We bin putatively neutral sites by predicted as described in Appendix 1—figure 38a. We calculate the rate of X>Y substitutions in a bin by dividing the estimate of the number of X>Y substitutions at its sites in an 8-primate phylogeny by the estimated number of its sites with state X in the ancestor of that phylogeny (see Section 3.3). We obtain the relative rate by dividing the rate in a bin by the average rate across bins. We show the rates of substitutions with ancestral state AT in (a) and GC in (b).
Appendix 1—figure 43
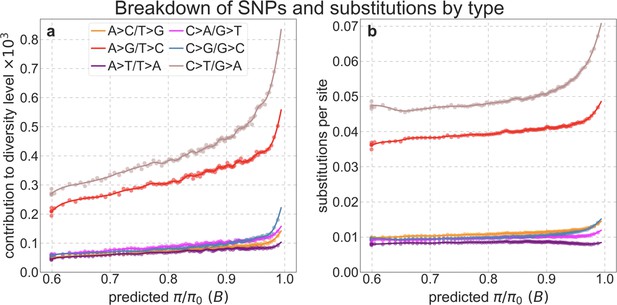
Contribution of different types of substitutions to diversity levels (a) and number of substitutions per site in the 8-primate phylogeny (b) as a function of predicted .
We bin putatively neutral sites by predicted as described in Appendix 1—figure 38a. (a) We define the ancestral state, that is, AT or GC, as the inferred state in the human-chimpanzee ancestor (see Section 2.7). We define the contribution of each type of substitution to the diversity level in a bin as the ratio of the number of pairwise differences of that type and the total number of pairwise comparisons in a bin; this way, the sum over types equals the observed diversity level in a bin (). (b) We calculate the number of substitutions of each type in a bin as described in Appendix 1—figure 42, but here we normalize it by the number of sites, such that the sum over types equals the observed number of substitutions per site in the 8-primate phylogeny.
Appendix 1—figure 44
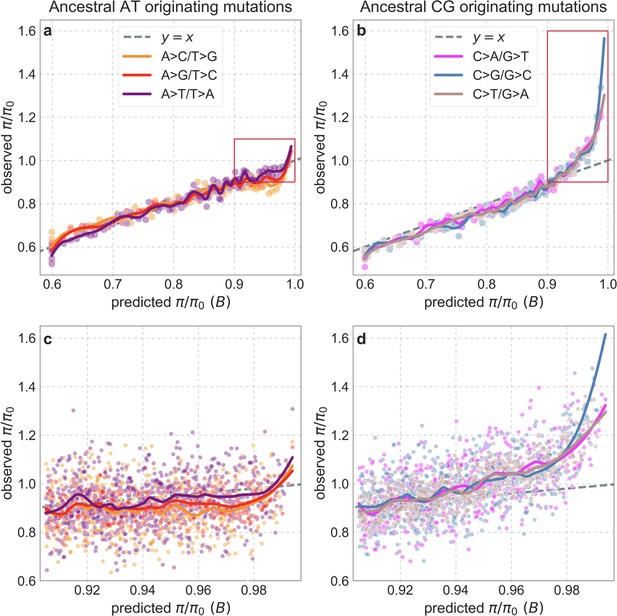
Observed vs. predicted neutral diversity levels for different types of substitutions.
Diversity levels are presented as in Appendix 1—figure 38, but here, we calculate diversity levels and substitution rates for sites with a given ancestral state, that is, AT (a and c) or CG (b and d), and for each of the three types of substitutions from the ancestral state, as in Appendix 1—figure 43.
Appendix 1—figure 45
Observed vs. predicted neutral diversity levels for different types of substitutions after removing C>G hypermutable regions (from both the inference and observations).
Other than removing ~12% of putatively neutral sites in these regions, the details are as in Appendix 1—figure 44. We note that while a greater proportion of sites is removed from bins near (~20% for the 100th percentile), this in itself has a minor effect on the departures from predictions in these bins.
Appendix 1—figure 46
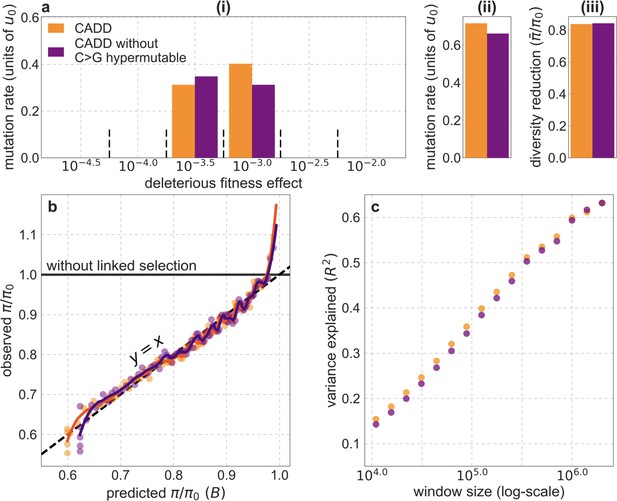
Comparison of the best-fitting CADD-based models with and without C>G hypermutable regions.
All panels are as described for the corresponding ones in Appendix 1—figure 14.
Appendix 1—figure 47
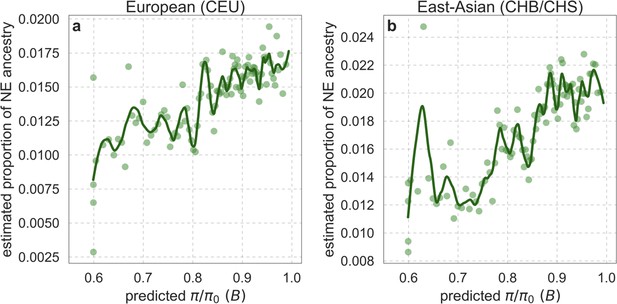
Estimated proportion of Neanderthal (NE) ancestry as a function of predicted in Europeans (CEU) (a) and East-Asians (CHB/CHS) (b).
See text for the estimation procedure. The bins and LOESS curves were calculated as in Appendix 1—figure 38.
Appendix 1—figure 48
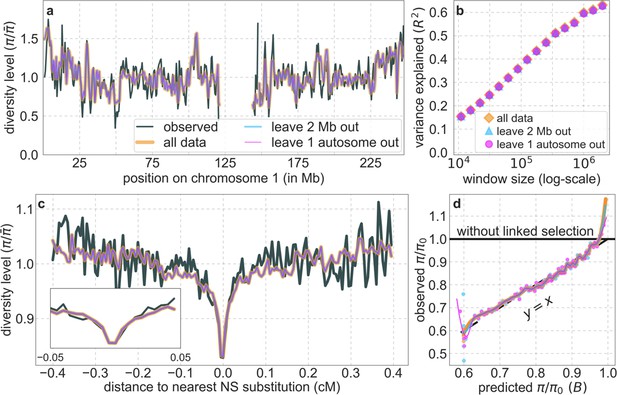
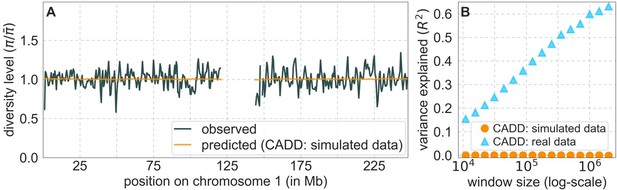
Overfitting has negligible effects on our results (see also Section 6.1).
As an illustration, we compare the results corresponding to our best-fitting CADD-based model, using all the data jointly (orange), out-of-sample predictions in non-overlapping, contiguous, 2 Mb windows (light blue) and out-of-sample predictions for each autosome (pink). (a) Predicted and observed diversity levels along chromosome 1 in the YRI sample; (details as in Figure 2A in Main Text). (b) The proportion of variance in YRI diversity levels explained by background selection at different spatial scales (details as in Figure 2B in Main Text). (c) Predicted and observed neutral diversity levels around human-specific nonsynonymous (NS) substitutions (details as in Figure 3 in Main Text). (d) Observed vs. predicted neutral diversity levels across the autosomes (details as in Figure 5 in Main Text). As an example, the explained variance in diversity levels over 1 Mb windows is 59.9% without excluding data, 59.8% when we exclude 2 Mb windows, and 59.5% when we leave out one chromosome at a time. Our statistical analysis in Section 6.2 suggests that these minute difference are not significant. Moreover, the reduction in explained variance in the case in which we exclude one autosome at a time is plausibly due to the reduced amount of data rather than overfitting (e.g. chromosomes 1 and 2 correspond to 8% and 9.3% of our putatively neutral sites, respectively).
Appendix 1—figure 49
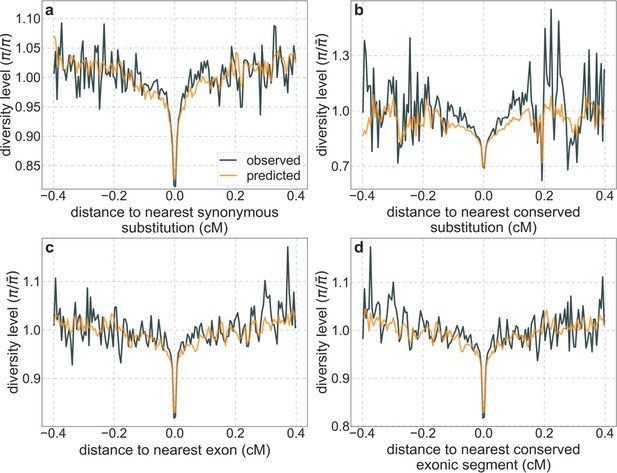
A background selection model predicts neutral diversity levels around different genomic features.
Here we use our best-fitting CADD-based model and show diversity levels around: (a) human-specific synonymous substitutions; (b) human-specific substitutions in conserved regions; (c) exons; and (d) conserved exonic regions. The inference of human-specific substitutions is described in Section 2.7. Conserved regions are based on autosomal sites with the top 6% phastCons scores in the 99-vertebrate alignment (Section 4.1). The set of exons is described in Section 2.4. The genetic distance to the nearest element (e.g. exon) is measured to its closest edge. Other details are similar to Figure 3.
Appendix 1—figure 50
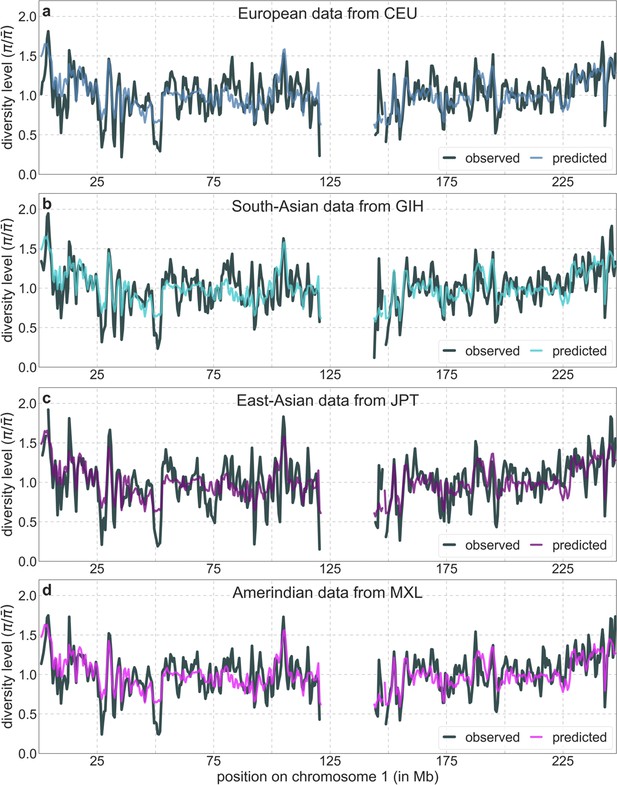
Predicted and observed neutral diversity levels along chromosome 1 based on data from representative continental populations.
Plots are generated as detailed in Figure 2A.
Appendix 1—figure 51
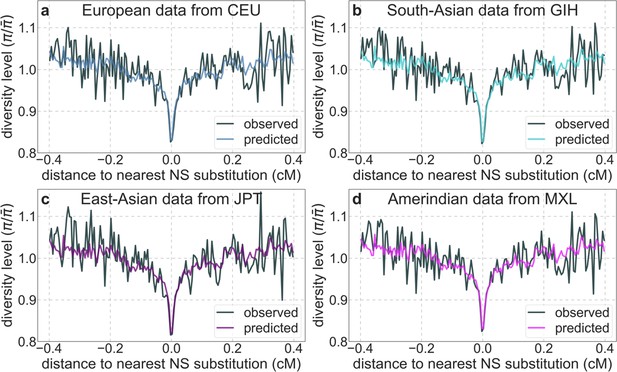
A background selection model predicts neutral diversity levels around human-specific nonsynonymous (NS) substitutions in representative continental populations.
Plots are constructed as detailed in Figure 3, using polymorphism data from each population for both inferences and observations.
Appendix 1—figure 52
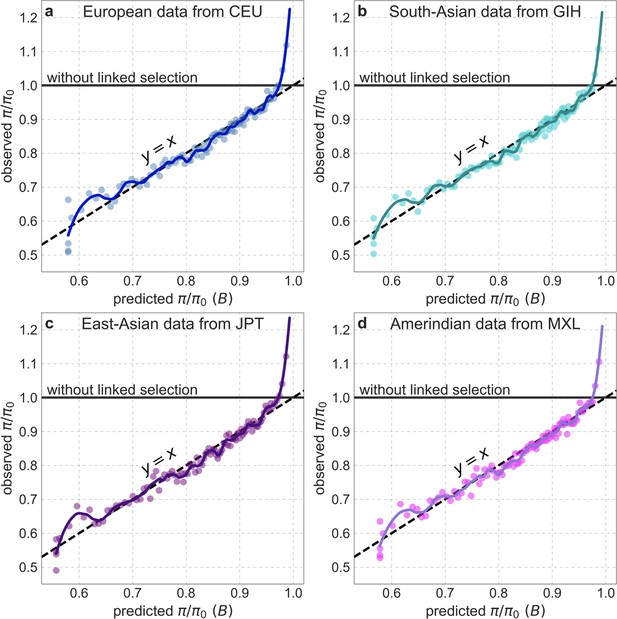
Observed vs. predicted neutral diversity levels across the autosomes in representative continental populations.
Plots are constructed as detailed in Figure 5, using polymorphism data from each population for both inferences and observations.
Author response image 1
Author response image 2
Author response image 3
Fig. 1 equivalent: orange curve (A) and points (B) correspond to predictions in which data from the focal chromosome was excluded.
Author response image 4
Figures 3 and 5 equivalents.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Broad-scale variation in human genetic diversity levels is predicted by purifying selection on coding and non-coding elements
eLife 12:e76065.
https://doi.org/10.7554/eLife.76065
