Self-configuring feedback loops for sensorimotor control
- Computational Neuroscience Unit, Okinawa Institute of Science and Technology, Japan
Figures
Figure 1
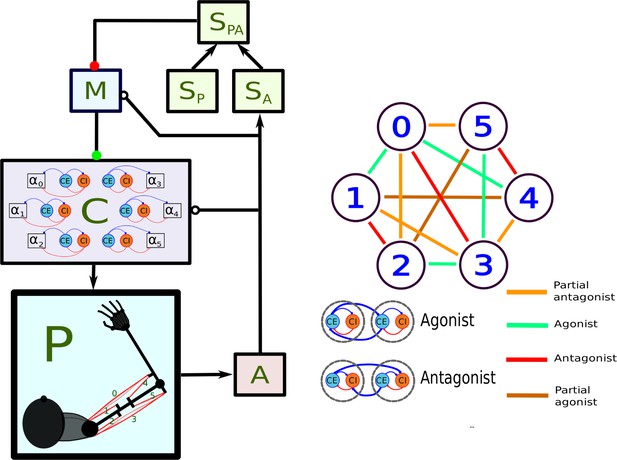
Main components of the model.
In the left panel, each box stands for a neural population, except for P, which represents the arm and the muscles. Arrows indicate static connections, open circles show input correlation synapses, and the two colored circles show possible locations of synapses with the learning rule in Verduzco-Flores et al., 2022. In the spinal learning model the green circle connections are plastic, and the red circle connections are static. In the cortical learning model the red circle connections are plastic, whereas the green circle connections are static. In the static network all connections are static. A : afferent population. : Somatosensory cortex, modulated by afferent input. : somatosensory cortex, prescribed pattern. : population signaling the difference between and : primary motor cortex. : spinal cord. Inside the box the circles represent the excitatory () and inhibitory () interneurons, organized into six pairs. The interneurons in each pair innervate an alpha motoneuron (), each of which stimulates one of the six muscles in the arm, numbered from 0 to 5. The trios consisting of , , units are organized into agonists and antagonists, depending on whether their motoneurons cause torques in similar or opposite directions. These relations are shown in the right-side panel.
Figure 2 with 4 supplements
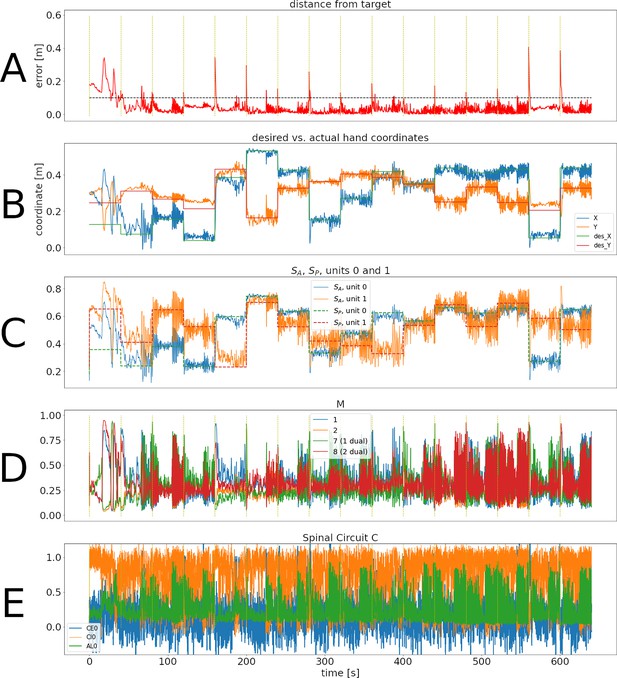
Representative training phase of a simulation for the spinal learning model.
(A) Distance between the target and the hand through 640 s of simulation, corresponding to 16 reaches to different targets. The horizontal dotted line corresponds to 10 cm. The times when changes are indicated with a vertical, dotted yellow line. Notice that the horizontal time axis is the same for all panels of this figure. The average error can be seen to decrease through the first two reaches. (B) Desired versus actual hand coordinates through the training phase. The straight lines denote the desired X (green) and Y (red) coordinates of the hand. The noisy orange and blue lines show the actual coordinates of the hand. (C) Activity of units 0 and 1 in and . This panel shows that the desired values in the units (straight dotted lines) start to become tracked by the perceived values. (D) Activity of units 1, 2, and their duals. Notice that even when the error is close to zero the activity in the units does not disappear. E: Activity of the trio for muscle 0. The intrinsic noise in the units causes ongoing activity. Moreover, the inhibitory activity (orange line) dominates the excitatory activity (blue line).
Figure 2—figure supplement 1
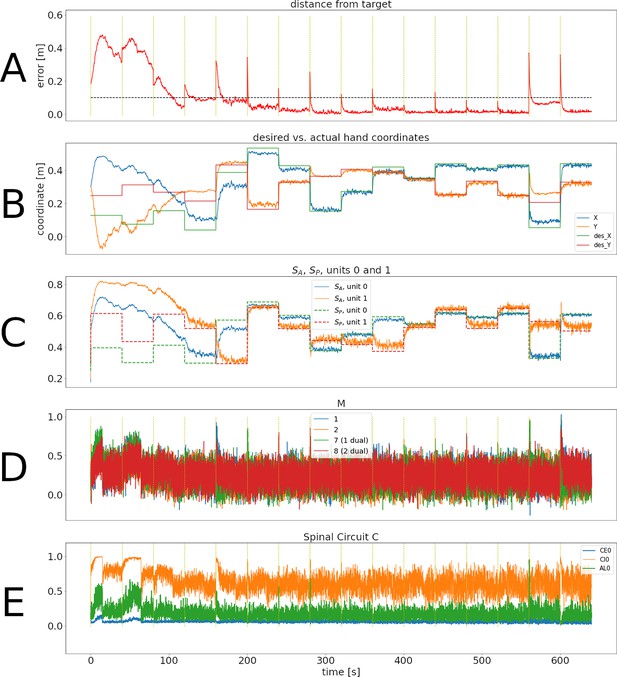
Representative training phase of the simulation for the cortical learning configuration.
Panels are as in Figure 2.
Figure 2—figure supplement 2
Representative training phase of the simulation for the static network.
Panels are as in Figure 2.
Figure 2—figure supplement 3
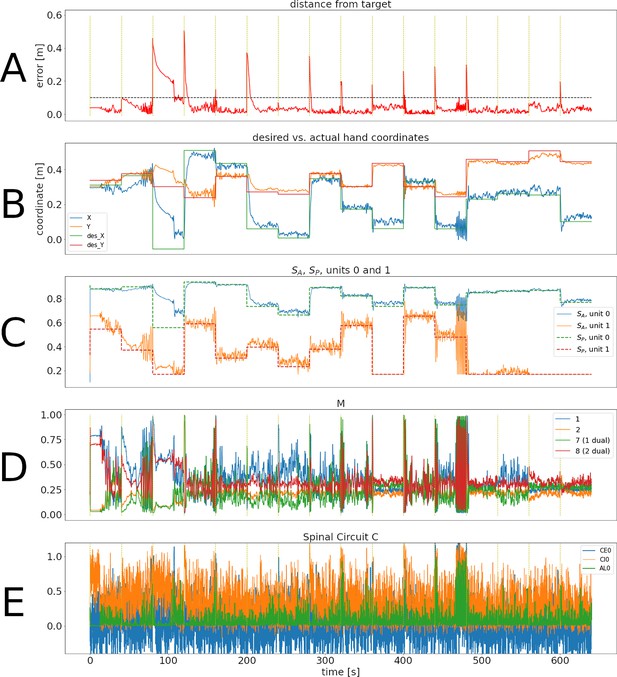
Representative training phase of the simulation for the synergistic network.
Panels are as in Figure 2.
Figure 2—figure supplement 4
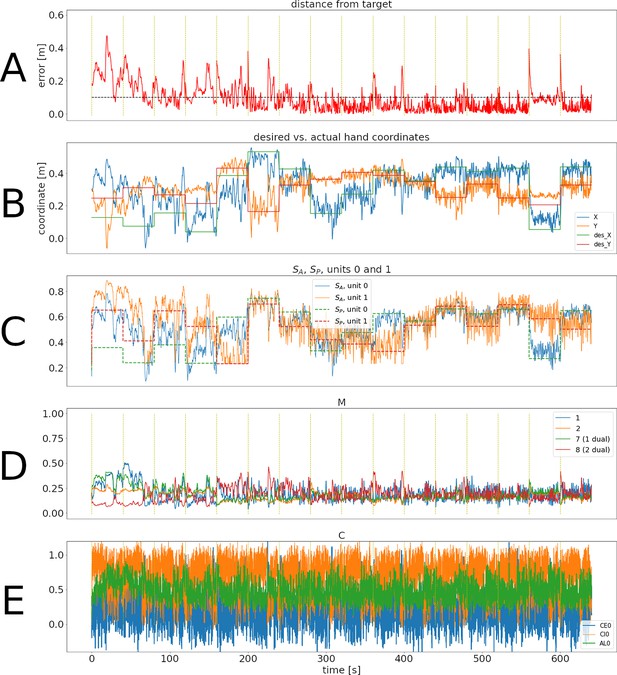
Representative training phase of the simulation for the mixed errors network.
Panels are as in Figure 2.
Figure 3 with 3 supplements
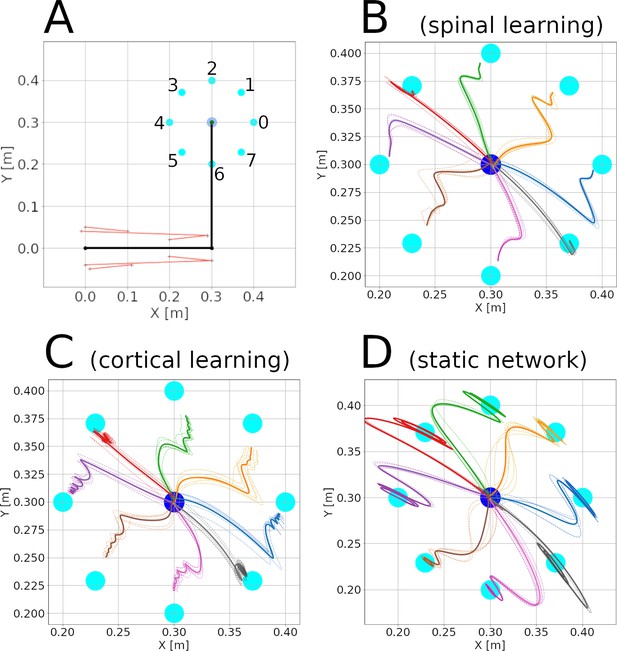
Center-out reaching.
(A) The arm at its resting position, with hand coordinates (0.3, 0.3) meters, where a center target is located. Eight peripheral targets (cyan dots) were located on a circle around the center target, with a 10 cm radius. The muscle lines, connecting the muscle insertion points, are shown in red. The shoulder is at the origin, whereas the elbow has coordinates (0.3, 0). Shoulder insertion points remain fixed. (B-F) Hand trajectories for all reaches in the three configurations. The trajectory’s color indicates the target. Dotted lines show individual reaches, whereas thick lines indicate the average of the 6 reaches.
Figure 3—figure supplement 1
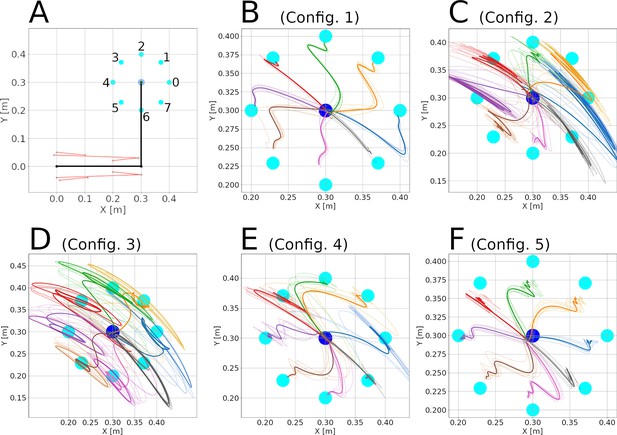
Center-out reaching before the control loop gain was adjusted.
Panels are as in Figure 3, with the two extra configurations presented in Appendix 1. The numbers in in panels B-F represent a particular configuration: Config. 1=spinal learning, Config. 2=cortical learning, Config. 3=static network, Config 4=synergistic network, Config. 5=mixed errors network.
Figure 3—figure supplement 2
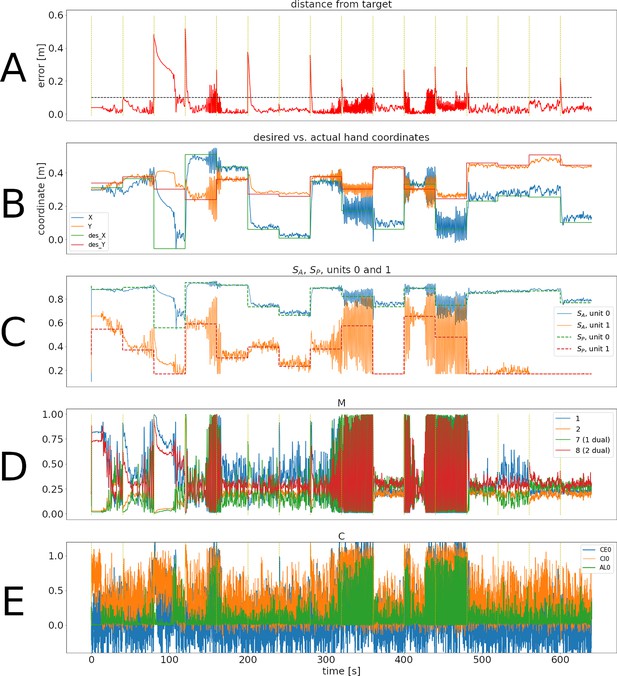
Training phase of the simulation for the static network before gain was reduced.
Panels are as in Figure 2.
Figure 3—figure supplement 3
Training phase of the simulation for the synergistic network before gain was reduced.
Panels are as in Figure 2.
Figure 4
Distance to target and reach velocity through time for the three configurations.
Thick lines show the average over 48 reaches (8 targets, 6 repetitions). Filled stripes show standard deviation. For the spinal and cortical learning configurations (left and center plots) the hand initially moves quickly to the target, but the direction is biased, so it needs to gradually correct the error from this initial fast approach; most of the variance in error and velocity appears when these corrections cause small-amplitude oscillations. In the case of the static network (right plots) oscillations are ongoing, leading to a large variance in velocity.
Figure 5
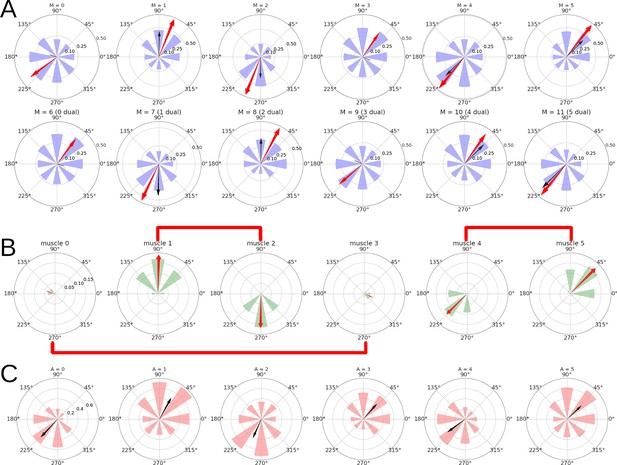
Directional tuning of the units in for a simulation with the spinal learning model.
(A) Average firing rate per target, and preferred direction (see Methods) for each of the 12 units in . Each polar plot corresponds to a single unit, and each of the 8 purple wedges corresponds to one of the 8 targets. The length of a wedge indicates the mean firing rate when the hand was reaching the corresponding target. The red arrow indicates the direction and relative magnitude of the PD vector. The black arrow shows the predicted PD vector, in this case just the corresponding arrows from panel B. (B) For each muscle and target, a wedge shows the muscle’s length at rest position minus the length at the target, divided by the rest position length. The red arrow comes from the sum of the wedges taken as vectors, and represents the muscle’s direction of maximum contraction. Plots corresponding to antagonist muscles are connected by red lines. (C) Average activity of the 6 units indicating muscle tension. The black arrows come from the sum of wedges taken as vectors, showing the relation between muscle tension and preferred direction.
Figure 6
Preferred direction vectors for the 12 units.
In all three plots the arrows denote the direction and magnitude of the preferred direction (PD) for an individual unit. The gray dotted lines shows the main axis of the distribution. The red dotted lines are a 45 degree rotation of the gray line, for comparison with Scott et al., 2001. It can be seen that all configurations display a strong bimodality, especially when considering the units with a larger PD vector. The axis where the PD vectors tend to aggregate is in roughly the same position for the three configurations.
Figure 7
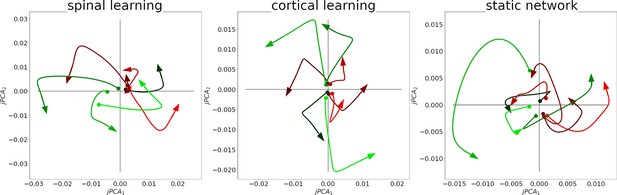
Rotational dynamics in the M population in a representative simulation for all configurations.
Each plot shows the first two jPCA components during 0.25 s, for each of the 8 conditions/targets. Traces are colored according to the magnitude of their initial component, from smallest (green) to largest (red).
Figure 8
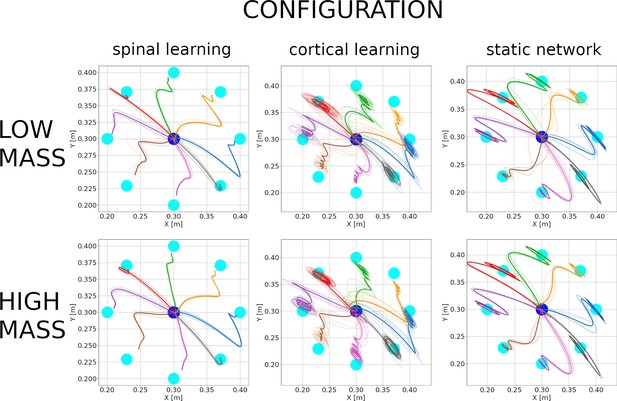
Hand trajectories with low mass (0.8 kg, top 3 plots) and high mass (1.2 kg, bottom 3 plots) for the 3 configurations.
Plots are as in Figure 3. The spinal learning model and the static network show qualitatively similar trajectories compared to those in Figure 3. In contrast, the cortical learning model began to display considerable endpoint oscillations for several targets after its mass was reduced. These oscillations persist after the mass has been increased.
Figure 9
Two sample direction fields and their linear addition for circuit C1.
(A) Direction Field (DF) from stimulation of the interneurons for muscle 0 (biarticular biceps). The approximate location of the fixed point is shown with a blue dot. (B) DF from stimulation of muscle 3 (biarticular triceps) interneurons. A red dot shows the fixed point. (C) Panels A and B overlapped. (D) In green, the DF from stimulating the interneurons for muscles 0 and 3 together. In purple, the sum of the DFs from panels A and B. Dots show the fixed points. The average angle between the green and purple vectors is 4 degrees.
Appendix 1—figure 1
Modified architecture of the population.
Each pair of units projects to two motoneurons (top). There are 15 possible pairs of muscles, corresponding to the blue lines for each arm in the figure. Three of the pairs (marked with red crosses) contain antagonist muscles, and are not included. The remaining 12 pairs can be arranged into 2 groups of 6 units each. The units in the group marked with green circles are the antagonists of the units with the same number, marked with pink circles.
Appendix 1—figure 2
A failure to learn for a simulation of configuration 1 (spinal learning) with no noise and no ACT unit.
Captions are as in Figure 2 of the main text.
Videos
Appendix 1—video 1
Visualization of the arm and the muscles during the learning phase for configuration 1.
Data comes from the simulation shown in Figure 2. Speed is roughly 4 X.
Appendix 1—video 2
Arm animation of the first 180 seconds of center-out reaching for the 5 configurations.
Speed is roughly 4 X.
Appendix 1—video 3
The learning phase for a simulation with configuration 1.
Both noise and the unit were removed, reducing exploration and disrupting learning. Data comes from the same simulation in Appendix 1—figure 2. Speed is 4 X.
Appendix 1—video 4
The first 180 seconds of center-out reaching for the 5 configurations before the gains were adjusted.
Speed is roughly 4 X. Configuration 2 shows target-dependent oscillations after 70 seconds.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Self-configuring feedback loops for sensorimotor control
eLife 11:e77216.
https://doi.org/10.7554/eLife.77216
