Coarsening dynamics can explain meiotic crossover patterning in both the presence and absence of the synaptonemal complex
- Computational and Systems Biology, John Innes Centre, Norwich Research Park, United Kingdom
- Cell and Developmental Biology, John Innes Centre, Norwich Research Park, United Kingdom
Figures
Figure 1 with 1 supplement
Mathematical model for HEI10 dynamics in a zyp1 synaptonemal complex (SC) mutant.
(A) Each cell contains Q = 5 chromosome pairs (purple line pairs). Recombination intermediates (RIs) (yellow stars) are placed randomly along the chromosome pairs immersed in the nucleoplasm (P). (B) HEI10 (red) is able to move from the nucleoplasmic pool into the RI compartments (rate α) and escape (rate β) from the RI compartments back into the pool. Cq,n is the HEI10 molecule number at the nth RI on the qth chromosome pair, which has length Lq. (C) Differential equations governing nucleoplasmic pool (P) and RI HEI10 (C) amounts, together with functional form of escape rate function , sigmoidal smoothing function Hs(s), and initial conditions for RI and nucleoplasmic HEI10 amounts. This sigmoidal smoothing function effectively switches off nucleoplasmic recycling for RIs with insufficient HEI10, without introducing a discontinuity in the system of equations, which would complicate numerical simulation. is a Normal distribution, truncated at 3 standard deviations away from its mean. (D) Graph showing RI escape rate function . (E) Default simulation parameter values. (F) Form of end-bias function . (G) Description of terms appearing in model equations.
-
Figure 1—source data 1
Default simulation parameter values for nucleoplasmic coarsening model.
- https://cdn.elifesciences.org/articles/79408/elife-79408-fig1-data1-v2.xlsx
Figure 1—figure supplement 1
Form of end-bias function from nucleoplasmic coarsening model (Figure 1F) and from the synaptonemal complex (SC)-mediated coarsening model (Morgan et al., 2021).
Note that the extra HEI10 loading in the nucleoplasmic coarsening model (up to 25% on the most distal 60% of each chromosome pair) is lower and more spread than that used in the SC-mediated coarsening model (up to 100% on the most distal 20%). Here, x/L is relative position along chromosome pair, with xe = 0.3 (left) and xe = 0.1 (right), specifying starting position of end bias, where fe = 1.25 (left) and fe = 2 (right).
Figure 2 with 2 supplements
Analysis of crossover (CO) number in zyp1 mutant.
(A, B) Experimental data from zyp1 null mutant plants (top) and nucleoplasmic coarsening model simulations (bottom). Results from simulating the model for 10,000 cells are shown. (A) Distribution of total CO number per cell. Experimental data is from pooled MLH1 foci counts from Capilla-Pérez et al., 2021. Sample mean (µ), estimated variance (), and sample size () inset. Green dots (joined by a line) show a Poisson distribution with the same mean. (B) Distribution of univalent number per cell. Experimental data is from univalent counts in metaphase I chromosomes from Capilla-Pérez et al., 2021. Again data from 10,000 simulated cells. (C) Simulation outputs showing the distribution of total CO numbers on the five individual chromosomes pairs. Green dots and lines again show Poisson distributions with same means as simulated data, with sample mean (µ) and estimated variance () inset. Chromosome mean lengths () and standard deviations () shown above each histogram. Simulation output from 10,000 cells. (D) Traces of HEI10 focus intensity against time, for all recombination intermediates (RIs) within a single simulated cell. Coloured lines indicate HEI10 amounts at each RI, in arbitrary units (a.u.). All simulation parameters are listed in Figure 1E.
Figure 2—figure supplement 1
zyp1 total crossover (CO) number per cell simulation without nonuniform initial loading.
zyp1 nucleoplasmic coarsening model simulation showing the distribution of total CO number per cell, where the model has uniform initial loading (no end bias). Results from simulating the model for 10,000 cells are shown. Sample mean (µ) and estimated variance () inset. Green dots (joined by a line) show a Poisson distribution with the same mean.
Figure 2—figure supplement 2
zyp1+HEI10 over-expression total crossover (CO) number per cell.
(A) Experimental distribution of total CO number per cell. Experimental data is from MLH1 foci counts from Durand et al., 2022. Sample mean (µ), estimated variance (), and sample size () inset. (B, C) zyp1+HEI10 over-expression nucleoplasmic coarsening model simulation outputs showing the distribution of total CO number per cell. Results shown from simulating the model for 10,000 cells with the same relative noise level as in the zyp1 mutant (σF = 263) (B) and with (C) additional noise in cellular HEI10 levels (σF = 862). Sample mean (µ) and estimated variance () inset. Green dots (joined by a line) show a Poisson distribution with the same mean.
Figure 3 with 1 supplement
3D-SIM imaging of late-prophase I cells.
Maximum intensity projections of 3D image stacks from wild-type (A) and zyp1a-2/zyp1b-1 mutants (B), labelled for SMC3 (green) and HEI10 (red) (scale bars = 5 µm). 3D models of segmented axial elements (with each chromosome axis labelled in a different colour), generated using the SNT plugin to FIJI, are also shown. Each nucleus contains five pairs of axes (bottom row, A, B), with individual axes in each pair having equivalent lengths and pairing tightly (A) or roughly (B) in 3D space. Zoomed-in regions (right-hand panels) from merged images (yellow dashed boxes) show the localisation of late-HEI10 foci between closely paired axes (scale bars = 0.2 µm).
Figure 3—figure supplement 1
3D-SIM imaging of early pachytene cells.
Maximum intensity projections of 3D image stacks from wild-type (A) and zyp1a-2/zyp1b-1 mutants (B), labelled for HEI10 (red), SMC3 (green) and DAPI (blue). Scale bars = 5 µm.
Figure 4 with 2 supplements
Analysis of late-HEI10 focus patterning and intensity data in wild-type and zyp1 mutant.
(A–C) Experimental data from wild-type plants (left), zyp1a-2/zyp1b-1 plants (middle), and from nucleoplasmic coarsening model simulation outputs (right). Model outputs from simulating 10,000 cells are shown. (A) Late-HEI10 focus positions along chromosome pairs, relative to the length of the chromosome pair. Experimental data are replicated and made symmetric about chromosome midpoints (N = 161,322 simulated foci). (B) Distribution of spacing between adjacent late-HEI10 foci, in µm (N = 113,278 simulated spaces between foci). (C) Violin plots of late-HEI10 foci intensities against the number of late-HEI10 foci on that chromosome pair. Focus intensities are relative to the mean intensity of all (on-chromosome) HEI10 foci within the same cell. Red lines show simple linear regression best fits, treating the number of foci on the chromosome as a continuous independent variable. For wild-type plants, slope = –0.1944, R2 = 0.188, F(1,88) = 20.36, p<0.001. For zyp1 mutant plants, slope = 0.0028, R2 < 0.001, F(1,260) = 0.04538, p=0.831. For simulated data, slope = 0.0004, R2 < 0.001, F(1,161320) = 0.7838, p=0.376. Simulation parameters are again as listed in Figure 1E, with simulated data from 10,000 cells (50,000 chromosome pairs).
Figure 4—figure supplement 1
A combined synaptonemal complex (SC)- and nucleoplasm-mediated coarsening model.
(A) Schematic representation of the combined coarsening model. (B) HEI10 (red) is able to move from the nucleoplasmic pool into the recombination intermediate (RI) compartments (rate α), and escape (rate β) from the RI compartments back into the nucleoplasm. HEI10 can also move from SC compartments into the RI compartments (rate ) and escape back onto the SC (rate ). HEI10 on the SC has concentration , and is able to diffuse along the SC with one-dimensional diffusion coefficient . Cq,n is the HEI10 molecule number at the nth RI on the qth chromosome pair, which has length Lq. (C) Differential equations and initial/boundary conditions governing simulations. (D) Default simulation parameter values for various scenarios: WT, original SC-mediated coarsening model with wild-type parameters (as implemented in ‘Materials and methods’), WT+nuc, combined SC- and nucleoplasm-mediated coarsening model with wild-type parameters. (E) Description of terms appearing in model equations.
-
Figure 4—figure supplement 1—source data 1
Default simulation parameter values for various scenarios: WT, original synaptonemal complex (SC)-mediated coarsening model with wild-type parameters (as implemented in ‘Materials and methods’), WT+nuc, combined SC- and nucleoplasm-mediated coarsening model with wild-type parameters.
- https://cdn.elifesciences.org/articles/79408/elife-79408-fig4-figsupp1-data1-v2.xlsx
Figure 4—figure supplement 2
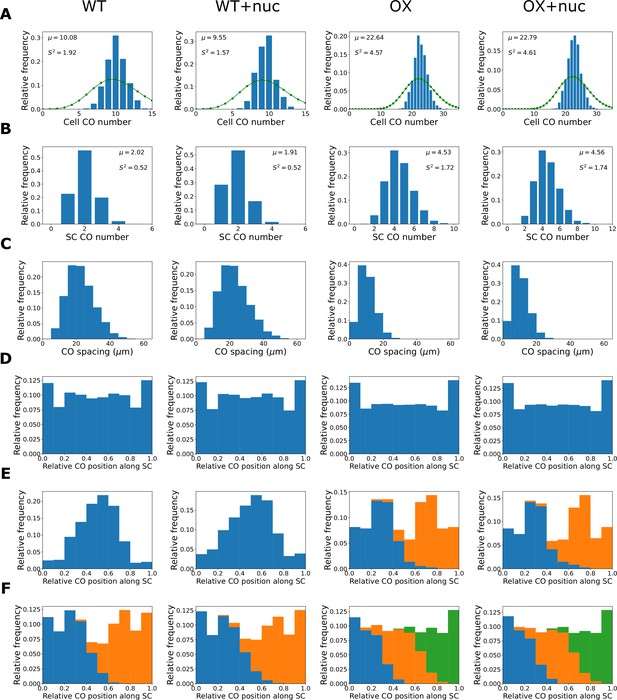
The combined synaptonemal complex (SC)- and nucleoplasm-mediated coarsening model can explain crossover patterning in wild-type and HEI10 over-expressor lines.
Columns show simulated results from the original SC-mediated coarsening model with wild-type parameters (WT, as implemented in ‘Materials and methods’), the combined SC- and nucleoplasm-mediated coarsening model with wild-type parameters (WT+nuc), the original SC-mediated coarsening model with HEI10 over-expressor parameters (OX, as implemented in ‘Materials and methods’), and the combined SC- and nucleoplasm-mediated coarsening model with HEI10 over-expressor parameters (OX+nuc). Results from simulating the model for 1000 cells are shown. Above simulations of WT and OX cases agree well with previously published experimental data (Morgan et al., 2021). Number of late-HEI10 foci per cell, green dots (joined by a line) show a Poisson distribution with the same mean, (A), number of late-HEI10 foci per SC (5000 simulated SC), (B), sample mean (µ) and estimated variance () inset (A, B), spacing between successive late-HEI10 foci (C), relative positions of late-HEI10 foci along SC (D), relative positions of single late-HEI10 foci (WT, WT+nuc) and double late-HEI10 foci (OX, OX+nuc) (E), and relative positions of double late-HEI10 foci (WT, WT+nuc) and triple late-HEI10 foci (OX, OX+nuc) (F). Parameters are as listed in Figure 4—figure supplement 1D, with parameters and controlling initial cellular HEI10 levels increased to 4.5× the WT values in the HEI10 over-expressor simulations.
Figure 5 with 1 supplement
Late-HEI10 focus patterning and intensity data in pch2-1.
(A) Maximum intensity projections of 3D image stacks from pch2-1 mutants labelled for HEI10, ZYP1, and SMC3. A 3D model of segmented synaptonemal complex (SC) segments (with each segment labelled in a different colour), generated using the SNT plugin to FIJI, is also shown. (B–G) Experimental data and combined coarsening model simulations showing; (B) late-HEI10 focus number per cell (1000 simulated cells), green dots (joined by a line) show a Poisson distribution with the same mean, (C) late-HEI10 focus number per SC segment (13870 simulated segments), (B, C) sample mean (µ) and estimated variance () inset, (D) positioning of all late-HEI10 foci along SC segments relative to total segment length (11,009 simulated foci), (E) spacing between neighbouring late-HEI10 foci on the same SC segment (2590 spaces between simulated foci), (F) SC segment length versus number of late-HEI10 foci per SC segment (same number of observations as in C), and (G) single late-HEI10 focus intensity (relative to the mean intensity of all HEI10 foci within the same cell) versus SC segment length, with a random sample of simulation output to match experimental dataset size.
Figure 5—figure supplement 1
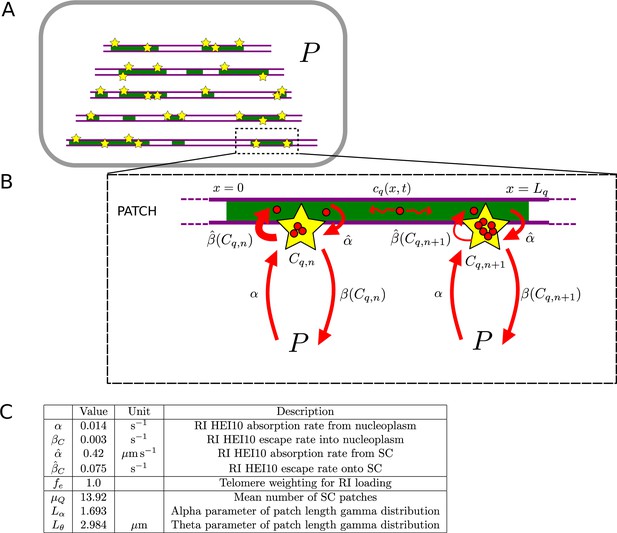
Model for pch2 simulations.
(A, B) Schematic of combined nucleoplasmic- and synaptonemal complex (SC)-mediated coarsening model used for pch2 simulations, where dynamics occur on patches of SC, rather than whole chromosomes. (C) Parameters for pch2 simulations that are different from those in Figure 4—figure supplement 1D. See ‘Materials and methods’ for more details.
-
Figure 5—figure supplement 1—source data 1
Parameters for pch2 simulations that are different from those in Figure 4—figure supplement 1—source data 1.
- https://cdn.elifesciences.org/articles/79408/elife-79408-fig5-figsupp1-data1-v2.xlsx
Tables
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Gene (Arabidopsis) | ZYP1A | TAIR | AT1G22260 | |
| Gene (Arabidopsis) | ZYP1B | TAIR | AT1G22275 | |
| Gene (Arabidopsis) | PCH2 | TAIR | AT4G24710 | |
| Strain, strain background (Arabidopsis) | zyp1a-2/zyp1b-1 | France et al., 2021 | Supplied by Dr James Higgins, University of Leicester | |
| Strain, strain background (Arabidopsis) | pch2-1 | Syngenta Arabidopsis Insertion Library (SAIL) | SAIL_1187_C06 | |
| Antibody | Anti-HEI10 (rabbit polyclonal) | Lambing et al., 2015 | Supplied by Prof Chris Franklin, University of Birmingham (1:500 dilution) | |
| Antibody | Anti-SMC3 (rat polyclonal) | Ferdous et al., 2012 | Supplied by Prof Chris Franklin, University of Birmingham (1:500 dilution) | |
| Antibody | Anti-ZYP1 (guinea-pig polyclonal) | France et al., 2021 | Supplied by Prof Chris Franklin, University of Birmingham (1:500 dilution) | |
| Antibody | Alexa Fluor 555 goat anti-rabbit (goat polyclonal) | Thermo Fisher | RRID:AB_2535849 | (1:200 dilution) |
| Antibody | Alexa Fluor plus 488 goat anti-rat (goat polyclonal) | Thermo Fisher | RRID:AB_2896330 | (1:200 dilution) |
| Antibody | Alexa Fluor 647 goat anti-guinea-pig (goat polyclonal) | Thermo Fisher | RRID:AB_2735091 | (1:200 dilution) |
| Sequence-based reagent | PCH2_1_FV | Lambing et al., 2015 | PCR primers | CAGTGCAAATAGCCGTCGCTGAG |
| Sequence-based reagent | PCH2_1_RV | Lambing et al., 2015 | PCR primers | CTCACATGGTCCTTCTTCAATGAGC |
| Sequence-based reagent | Sail LB2 | Lambing et al., 2015 | PCR primers | GCTTCCTATTATATCTTCCCAAATTACCAATACA |
| Sequence-based reagent | zyp1_ns_1 | France et al., 2021 | PCR primers | CTCGCATTTGCTGGTTTAAAGAGTC |
| Sequence-based reagent | zyp1b_sp_1 | France et al., 2021 | PCR primers | TGCGTATATTGCTAGGTTTATATTG |
| Sequence-based reagent | salk_lb2 | France et al., 2021 | PCR primers | GTGCTTTACGGCACCTCGAC |
| Sequence-based reagent | zyp1a_sp_1 | France et al., 2021 | PCR primers | GAATAGTTAGCAGATTCATATTTCAC |
| Peptide, recombinant protein | HindIII-HF | NEB | R3104S | |
| Chemical compound, drug | Cytohelicase | Sigma-Aldrich | C8274 | |
| Chemical compound, drug | Polyvinylpyrrolidone | Sigma-Aldrich | PVP40 | |
| Software, algorithm | FIJI | Schindelin et al., 2012 | 2.1.0/1.53f51 | |
| Software, algorithm | Zen Black | Zeiss | 14.0.12.201 | |
| Software, algorithm | Python | Python | RRID:SCR_008394 | https://www.python.org/ |
| Software, algorithm | R | R Project for Statistical Computing | RRID:SCR_001905 | http://www.r-project.org/ |
| Software, algorithm | Julia | Julia | RRID:SCR_021666 | https://julialang.org/ |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Coarsening dynamics can explain meiotic crossover patterning in both the presence and absence of the synaptonemal complex
eLife 12:e79408.
https://doi.org/10.7554/eLife.79408
