Figures and data in Resource allocation accounts for the large variability of rate-yield phenotypes across bacterial strains

Figures
Tables
Additional files

8 figures, 8 tables and 5 additional files

Figures

Figure 1

Download asset Open asset

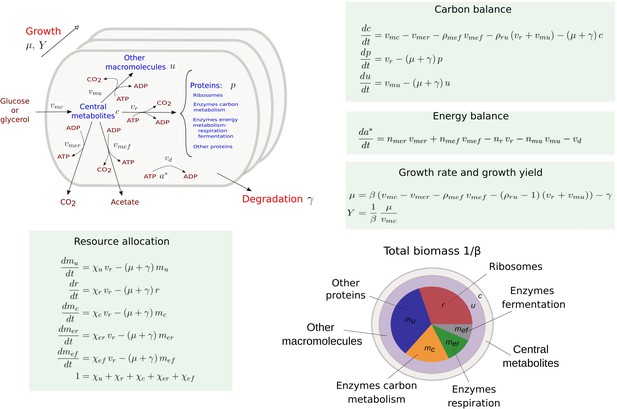
Coarse-grained model of microbial growth with coupled carbon and energy fluxes.

Upper left figure: schematic outline of the model, showing the biomass constituents and the macroreactions, as well as the growth and degradation of biomass. Green boxes: system of differential equations describing the carbon and energy balances, growth rate and growth yield, and resource allocation. The kinetic expressions for the reaction rates can be found in Appendix 1. The growth rate and growth yield are defined in terms of the fluxes of the macroreactions. Lower right figure: biomass composition, including the protein categories considered in resource allocation. The fluxes v_r, $v_{m u}$ , $v_{m c}$ , $v_{m e r}$ , $v_{m e f}$ , v_d [Cmmol or mmol gDW^-1 hr^-1], the variables $p$ , $r$ , m_u, m_c, $m_{e r}$ , $m_{e f}$ , $c$ , $u$ , $a^{*}$ [Cmmol or mmol gDW^-1], the resource allocation parameters $χ_{u}$ , $χ_{r}$ , $χ_{c}$ , $χ_{e r}$ , $χ_{e f}$ [dimensionless], the degradation rate constant $γ$ [hr^-1], the biomass density $β$ [Cmmol gDW^-1], the ATP yield and cost factors $n_{m e r}$ , $n_{m e f}$ , n_r, $n_{m u}$ [mmol Cmmol^-1], and the correction factors for CO₂ loss $ρ_{m e f}$ , $ρ_{r u}$ [dimensionless] are formally defined in Appendix 1. The values of the parameters are derived in Appendix 2.

Figure 2 with 4 supplements

Download asset Open asset

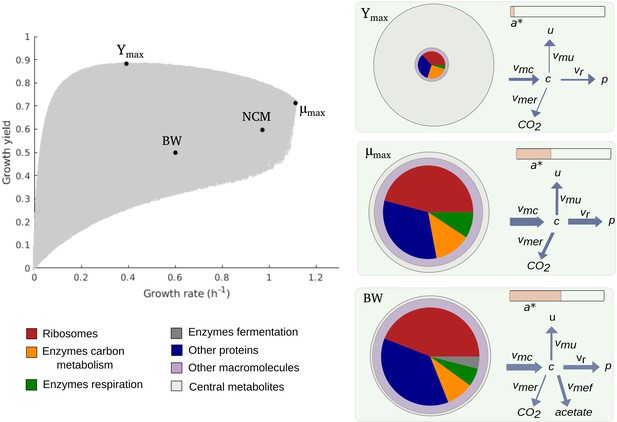
Predicted rate-yield phenotypes and underlying resource allocation strategies.

Predicted rate-yield phenotypes during balanced growth of *E. coli* on minimal medium with glucose (gray dots). The resource allocation strategy and growth physiology underlying the rate-yield phenotypes are shown for selected points, corresponding to the BW25113 reference strain (BW), predicted maximum growth rate ( $μ_{m a x}$ ), and predicted maximum growth yield (Y_max). The pictograms show the biomass composition, flux distribution, and energy charge. Note that by calibration, the predicted and observed resource allocation strategies for the reference strain are identical. We also indicate, for later reference, the rate-yield phenotype of the NCM3722 strain (NCM).

Figure 2—figure supplement 1

Download asset Open asset

Observed allocation of resources to the category of residual proteins in different growth conditions.

Using data for the *E. coli* BW25113 reference strain (Schmidt et al., 2016), we computed for a large variety of growth conditions the fraction of the proteome consisting of proteins other than ribosomes and translation-affiliated proteins, enzymes in central carbon metabolism, and enzymes in energy metabolism ( $m_{u} / p$ ). The considered conditions concern growth on different limiting carbon sources, different temperatures, different pH, etc. The computations were carried out in the same way as for model calibration (Materials and methods). The solid line corresponds to the mean of the value for $m_{u} / p$ over the different conditions and the broken lines to the upper and lower bound of the variation from the mean. In the simulations underlying Figures 2—4 in the main text, the value of $χ_{u}$ was sampled from the interval between the upper and lower bound, $[0.32, 0.41]$ .

Figure 2—figure supplement 2

Download asset Open asset

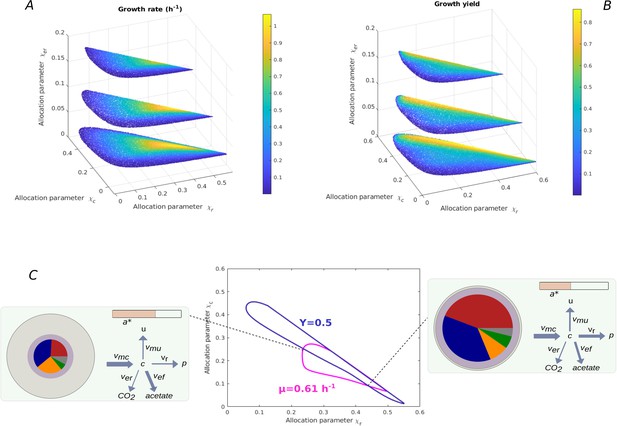
Relation between resource allocation strategies and rate-yield phenotypes.

(A) Predicted dependence of the growth rate on values for $(χ_{u}, χ_{r}, χ_{c}, χ_{e r}, χ_{e f})$ for batch growth in minimal medium with glucose. $χ_{u}$ was set to the constant value of 0.37 for the BW25113 reference strain (Appendix 2), while three different values for $χ_{e r}$ were explored (0.02, 0.1, 0.2). Note that each combination $(χ_{u}, χ_{r}, χ_{c}, χ_{e r})$ fixes the remaining value of $χ_{e f}$ due to the constraint that the resource allocation parameters sum to 1 (Appendix 1). (B) Idem for the growth yield. Each resource allocation strategy leads to a unique rate-yield phenotype. (C) Rate and yield isoclines in the $(χ_{r}, χ_{c})$ space for fixed values of $χ_{u}$ and $χ_{e r}$ . In particular, the isoclines correspond to a growth rate of 0.61 hr^-1 and a growth yield of 0.50, the BW25113 phenotype, for a value of $χ_{e r}$ set to 0.062 (Appendix 2). The two isoclines have four intersection points, that is, the specified growth rate and growth yield can be reached for four combinations of values of $χ_{r}$ and. $χ_{c}$ The growth physiology obtained at two of the intersection points is quantitatively different, as illustrated by the two pictograms (see Figure 2 for legend). When allowing $χ_{e r}$ to continuously vary over a range of values, an infinite number of resource allocation strategies can account for the specified rate and yield.

Figure 2—figure supplement 3

Download asset Open asset

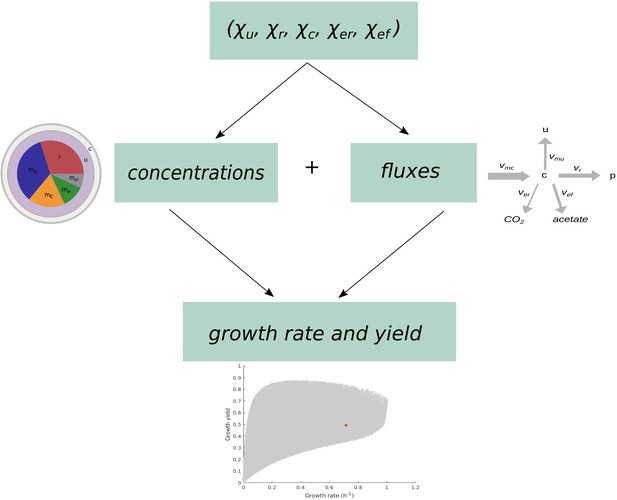
Schematic overview of the computation of growth rate and growth yield from resource allocation strategies.

The computational procedure takes a resource allocation strategy as input and simulates microbial growth until steady state is reached. The fluxes and concentrations at steady state are used to compute the growth rate and growth yield as output.

Figure 2—figure supplement 4

Download asset Open asset

Predicted fluxes, concentrations, and resource allocation along the Pareto frontier of growth rate and growth yield.

(A) Concentrations along the Pareto frontier in Figure 2. The concentrations of macromolecules increase, whereas the concentration of central carbon metabolites decreases. (B) Saturation of kinetic expressions for central carbon metabolites and energy cofactors (ADP, ATP), and loss of CO₂ during macromolecular synthesis. The latter loss is proportionally low as compared to the total flux of carbon through the growing bacteria. Whereas the concentrations of central carbon metabolites and ADP are saturating, this is not the case for ATP. (C) Fluxes along the Pareto frontier. All fluxes increase with the growth rate, as expected. (D) Resource allocation parameters along the Pareto frontier. Whereas the fraction of other proteins remains constant and low, the fraction of energy proteins increases and the fraction of enzymes in central metabolism decreases. Interestingly, the fraction of ribosomal proteins only increases at the highest growth rate. At lower growth rates, an increase of the protein synthesis rate is obtained by a higher ATP driving force.

Figure 3 with 1 supplement

Download asset Open asset

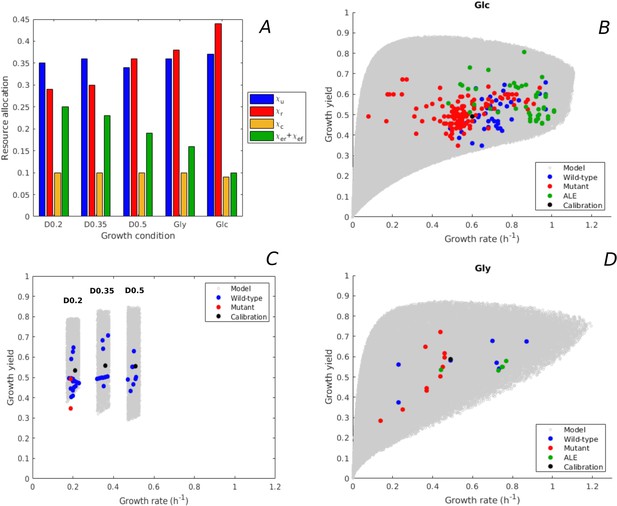
Predicted rate-yield phenotypes and comparison with experimental data.

(A) Measured proteome fractions of the protein categories in the model, corresponding to resource allocation strategies during balanced growth, for the BW25113 reference strain used for model calibration (Schmidt et al., 2016 and Appendix 2). (B) Predicted and observed combinations of growth rate and growth yield for balanced batch growth of *E. coli* in minimal medium with glucose. The rate-yield phenotypes concern the reference strain, other wild-type strains, mutant strains obtained by directed mutagenesis, and mutant strains from adaptive laboratory evolution (ALE) experiments. (C) Idem for continuous growth in a chemostat in minimal medium with glucose at different dilution rates (0.2, 0.35, and 0.5 hr^-1). The predicted yields are shown for the indicated dilution rates ±10%. (D) Idem for batch growth of *E. coli* in minimal medium with glycerol. All predictions were made using the model in Figure 1, calibrated for the different growth conditions, and varying the resource allocation parameters as described in the text (90,000–160,000 samples). The measurements of rate and yield reported in the source literature have been converted to units hr^-1 (growth rate) and a dimensionless unit corresponding to ${C m m o l}_{biomass}$ ${C m m o l}_{substrate}^{- 1}$ (growth yield) (see Materials and methods and Supplementary files 1 and 2 for details).

Figure 3—figure supplement 1

Download asset Open asset

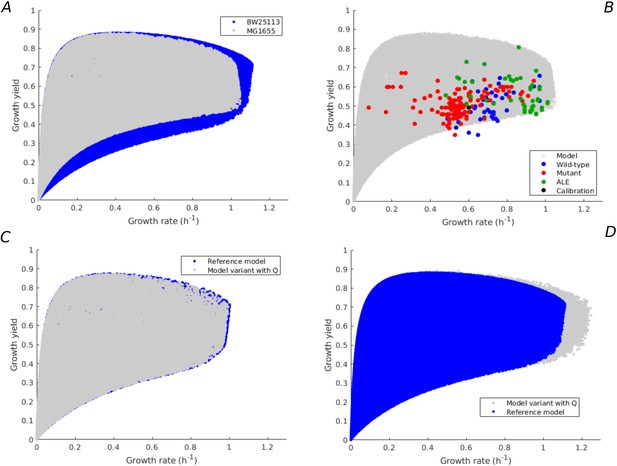
Robustness of rate-yield predictions for alternative model calibration and alternative model assumption.

(A) Rate-yield predictions (gray) for the same model as in Figure 1, but calibrated by means of experimental data for the MG1655 instead of BW25113 strain, in the case of minimal growth on glucose (see Appendix 2 for details). The blue dots correspond to the predictions for the model calibrated by means of data for the BW reference strain. (B) Comparison of the rate-yield predictions from the alternative model in panel A with the experimental data from Figure 3B. The rate-yield variability predicted by the model calibrated with the MG data agrees with both the predicted variability of the reference model and the observed rate-yield phenotypes. (C) Rate-yield predictions (gray) for a model variant having a growth-rate-independent protein category with fixed resource allocation parameter $χ_{q}$ (see Appendix 1 for details). The model was calibrated using data for the BW strain (Appendix 2—table 3), in the case of batch growth on glucose. The blue dots correspond to the predictions for the reference model in Figure 1. (D) Idem, when the value of $χ_{q}$ is allowed to vary by 10%, corresponding to the observed difference between the BW25113 and NCM3722 strains. In both cases the clouds of blue and gray dots largely overlap, indicating that the model predictions are robust for an alternative model hypothesis and an alternative model calibration.

Figure 4 with 2 supplements

Download asset Open asset

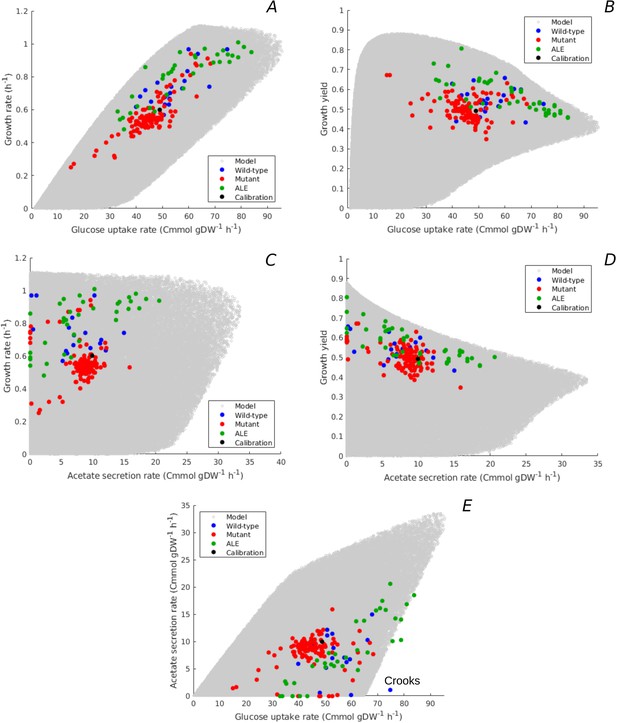
Predicted uptake-secretion phenotypes and comparison with experimental data.

(A) Predicted and observed glucose uptake rates and growth rates for the case of batch growth of *E. coli* on minimal medium with glucose. (B) Idem for glucose uptake rates and growth yields. (C) Idem for acetate secretion rates and growth rates. (D) Idem for acetate secretion rates and growth yields. (E) Idem for glucose uptake and acetate secretion rates. The predicted uptake-secretion phenotypes $v_{m c}$ and $v_{m e f}$ were taken from the simulations giving rise to Figure 3B. The measurements of glucose uptake and acetate secretion rates reported in the source literature have been converted to units Cmmol gDW^-1 hr^-1 (see Materials and methods and Supplementary files 1 and 2 for details). The Crooks strain, labeled in panel E, shows an uptake-secretion phenotype deviating from the range of predicted phenotypes.

Figure 4—figure supplement 1

Download asset Open asset

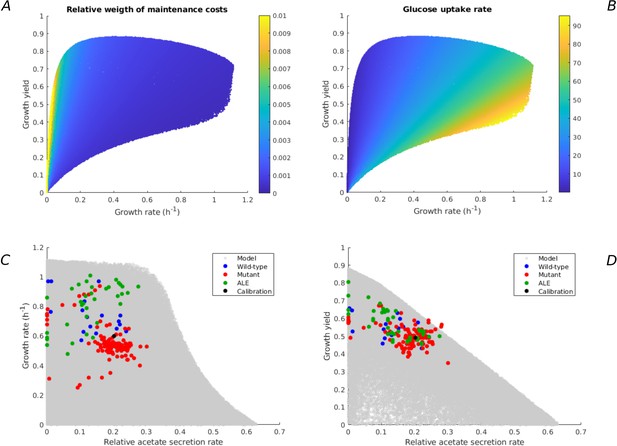
Additional model predictions of rate-yield and uptake-secretion phenotypes and their comparison with experimental data.

All predictions concern the case of *E. coli* growing on minimal medium with glucose (Figure 2). (A) Relative weight of maintenance costs due to degradation of macromolecules ( $γ / v_{m c}$ ) for predicted rate-yield phenotypes. (B) Glucose uptake rates $v_{m c}$ corresponding to predicted rate-yield phenotypes. (C) Predicted and observed relative acetate secretion rates $v_{m e f} / v_{m c}$ vs growth rates. (D) Predicted and observed relative acetate secretion rates $v_{m e f} / v_{m c}$ vs growth yields.

Figure 4—figure supplement 2

Download asset Open asset

Variation of normalized acetate secretion rate with growth rate in experiments with a single E. *coli* strain growing in different environments.

The plot shows data from Basan et al., 2015a, and Cheng et al., 2019, concerning batch growth of an NCM strain with a modified, titrable uptake system in minimal medium with glucose, data from Nanchen et al., 2006, concerning continuous growth in a chemostat of the MG1655 strain in minimal medium with glucose, data from Holms, 1996, concerning batch growth of the ML308 strain in minimal medium with various carbon sources, data from Gerosa et al., 2015, concerning batch growth of the BW25113 strain in minimal medium with various carbon sources, and data from Valgepea et al., 2010, and Peebo et al., 2015, concerning continuous growth in a chemostat of the MG1655 and BW25113 strains, respectively, in minimal medium with glucose. The relative acetate uptake rate, defined as the ratio of the acetate secretion rate (in unit Cmmol gDW^-1 hr^-1) and the glucose uptake rate (in the same unit), has a tendency to increase with the growth rate. This indicates a proportionally higher loss of carbon, and therefore lower yield, corresponding to a gradual shift of ATP production from respiration to fermentation.

Figure 5 with 1 supplement

Download asset Open asset

Resource allocation strategies underlying high-rate, high-yield phenotypes.

(A) Characterization of the physiology of the NCM3722 strain in comparison with the BW25113 strain during batch growth on glucose (data from Appendix 2—table 1 and Appendix 2—table 5). (B) Comparison of total protein and metabolic fractions in NCM and BW. The total protein fraction includes amino acids (Figure 1), which is indicated by the hatched pattern. (C) Predicted resource allocation strategies for a strain with the NCM phenotype, in the case of the model with fixed catalytic constants (blue boxplot) or a model variant in which catalytic constants are allowed to vary twofold (red boxplot). The observed resource allocation strategy for NCM (Schmidt et al., 2016, black dots) corresponds with the strategies predicting the NCM phenotype when catalytic constants are allowed to vary, that is, when metabolic regulation in addition to resource allocation is taken into account. The model predictions summarized in the boxplot concern strategies with simulated rate-yield and uptake-secretion phenotypes within 5% of the observed values for NCM. The black dots correspond to three independent replicates of the proteomic measurements (Schmidt et al., 2016). (D) Predicted and observed biomass composition for high-rate, high-yield growth of *E. coli*, with data for NCM (Appendix 2—table 5). Regulation of enzyme activity leads to a very good match of predicted and observed total protein and metabolite concentrations, here indicated as fractions of the total biomass ( $p β$ and $c β$ ).

Figure 5—figure supplement 1

Download asset Open asset

Relative changes in kinetic parameters for resource allocation strategies reproducing the observed phenotypes of the NCM3722 strain during minimal growth on glucose.

We repeated the sampling procedure explained in the Materials and methods section while allowing the values of the catalytic constants, $k_{m c}$ , $k_{m e r}$ , and $k_{m e f}$ to vary by maximally twofold (higher or lower). A total of 200,000 simulations were run. The plot shows the combinations of parameter values, relative to the values for the BW25113 reference strain (Appendix 2), that allow growth rate μ, growth yield $Y$ , glucose uptake rate, $v_{m c}$ , and acetate secretion rate $v_{m e f}$ of the NCM3722 strain to be reproduced (within a 5% margin) by resource allocation strategies that are close to those observed for NCM (within a 5% margin). The resource allocation strategy of NCM was computed from the data from Schmidt et al., 2016 (Materials and methods) and the phenotype data are shown in Figure 5A. Agreement between resource allocation strategies allowing the observed NCM growth phenotype to be reproduced is obtained for an increased value of $k_{m c}$ (higher activity of glycolytic enzymes). The increase in enzyme activity allows resources to be liberated for augmenting the concentrations of other proteins and central carbon metabolites ( $c$ ), thus increasing growth rate and growth yield. Changes in $k_{m e r}$ and $k_{m e f}$ may fine-tune these effects, but are not necessary.

Appendix 1—figure 1

Download asset Open asset

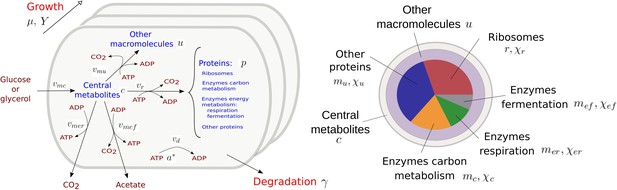
Resource allocation model of coupled carbon and energy fluxes in microorganisms.

The figure shows the biomass categories and macroreactions, together with the concentration variables, reaction rates, and growth and degradation rates.

Appendix 2—figure 1

Download asset Open asset

Protein dry mass fraction for different growth rates of E. *coli*.

The protein dry mass fraction (g gDW^-1) as a function of the steady-state growth rate was computed from data for the NCM3722 wild-type strain grown in different media (red dots) or for a strain carrying a plasmid for the gratuitous overexpression of a protein (blue dots) (Appendix Table S4 in Basan et al., 2015b). We interpolated the data (black line) to provide an estimate of the protein dry mass fractions at the growth rates corresponding to batch growth of the BW25113 strain in minimal medium with either glucose or glycerol ( $μ = 0.61$ hr^-1 or $μ = 0.49$ hr^-1, respectively).

Appendix 2—figure 2

Download asset Open asset

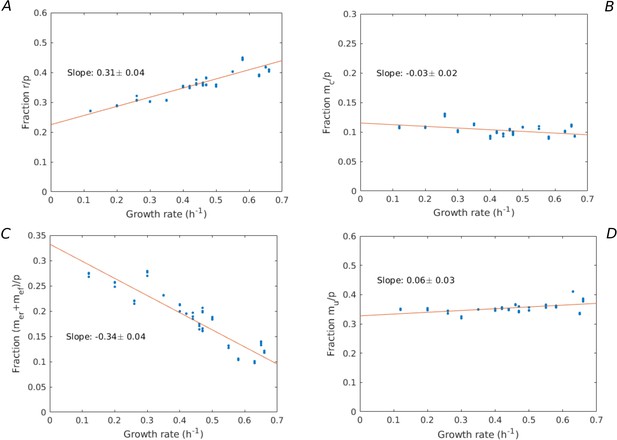
Growth-rate dependency of proteome fractions.

Using the data from Schmidt et al., 2016, the proteome fractions over a large variety of growth conditions (growth on different limiting carbon sources, different temperatures, different pH, etc.) are plotted for the categories: (A) ribosomes and translation-affiliated proteins ( $r / p$ ), (B) enzymes in central carbon metabolism ( $m_{c} / p$ ), (C) enzymes in energy metabolism ( $(m_{e r} + m_{e f}) / p$ ), and (D) other proteins ( $m_{u} / p$ ). A linear regression is performed, giving rise to slopes (A) 0.31 ± 0.04, (B) –0.03 ± 0.02, (C) –0.34 ± 0.04, and (D) 0.06 ± 0.03, showing that only the fraction $r / p$ significantly increases with the growth rate.

Tables

Appendix 1—table 1

Model variables and rates.

The units Cmmol and gDW refer to mmol carbon and gram dry weight, respectively.

Model	Description	Unit
	Macromolecule concentrations
$p$	Total proteins	Cmmol gDW^-1
$r$	Ribosomes	Cmmol gDW^-1
m_c	Enzymes in central carbon metabolism	Cmmol gDW^-1
$m_{e r}$	Enzymes in energy metabolism (respiration)	Cmmol gDW^-1
$m_{e f}$	Enzymes in energy metabolism (fermentation)	Cmmol gDW^-1
m_u	Other proteins	Cmmol gDW^-1
$u$	Other macromolecules	Cmmol gDW^-1
	Metabolite concentrations
$c$	Central carbon metabolites	Cmmol gDW^-1
$a$	ADP	mmol gDW^-1
$a^{*}$	ATP	mmol gDW^-1
	Reaction rates
$v_{m c}$	Carbon uptake and central metabolism	Cmmol gDW^-1 hr^-1
$v_{m e r}$	Energy metabolism (respiration)	Cmmol gDW^-1 hr^-1
$v_{m e f}$	Energy metabolism (fermentation)	Cmmol gDW^-1 hr^-1
v_r	Protein synthesis	Cmmol gDW^-1 hr^-1
$v_{m u}$	Synthesis of other macromolecules	Cmmol gDW^-1 hr^-1
v_d	Energy dissipation	mmol gDW^-1 hr^-1
	Other rates and yield
μ	Growth rate	hr^-1
γ	Degradation rate	hr^-1
Y	Growth yield	–

Appendix 1—table 2

Model parameters.

Model	Description	Unit
	Resource allocation parameters
$χ_{r}$	Fraction of ribosomal proteins	–
$χ_{c}$	Fraction of enzymes in central carbon metabolism	–
$χ_{e r}$	Fraction of enzymes in respiratory energy metabolism	–
$χ_{e f}$	Fraction of enzymes in fermentation energy metabolism	–
$χ_{u}$	Fraction of other proteins	–
	ATP factors
$n_{m e r}$	ATP yield from respiration	mmol Cmmol^-1
$n_{m e f}$	ATP yield from fermentation	mmol Cmmol^-1
n_r	ATP cost of protein synthesis	mmol Cmmol^-1
$n_{m u}$	ATP cost of synthesis of other macromolecules	mmol Cmmol^-1
	Correction factors
$ρ_{m e f}$	Correction for CO₂ loss during fermentation	–
$ρ_{r u}$	Correction for CO₂ loss during biosynthesis	–
$1 / β$	Total biomass concentration	Cmmol gDW^-1

Appendix 2—table 1

Reconstruction of growth and degradation rates, fluxes, and concentrations from published datasets for the case of batch growth of E. coli in minimal medium with glucose or glycerol, as explained in the text.

The uncertainty intervals for the rates, fluxes, and metabolite concentrations are standard deviations reported in the source publications, after unit conversion. The uncertainty interval for the total biomass concentration was obtained by propagating the errors of the measurements in the right-hand side of $1 / β = Y v_{m c} / μ$ (Morin et al., 2016). The uncertainty interval for the total protein concentration was obtained by combining the latter error with the standard error of the mean for the total protein fraction predicted by the linear model fitted to the data in Appendix 2—figure 1. The resulting error was distributed over the individual protein categories according to their mass fractions. References: $^{a}$ Haverkorn van Rijsewijk et al., 2011, $^{b}$ Gerosa et al., 2015, $^{c}$ Esquerré et al., 2014, $^{d}$ Farmer and Jones, 1976, $^{e}$ Morin et al., 2016, $^{f}$ Basan et al., 2015b, $^{g}$ Schmidt et al., 2016, $^{h}$ Park et al., 2016.

Rates	Unit	Glucose	Glycerol	Reference
$\hat{μ}$	${hr}^{- 1}$	$0.61 \pm 0.01$	$0.49 \pm 0.01$	$a, b$
$\hat{γ}$	${hr}^{- 1}$	0.027	0.032	$c, d$
Uptake, secretion, biosynthesis fluxes
${\hat{v}}_{m c}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	$49.6 \pm 5$	$33.9 \pm 1.0$	$a$
${\hat{v}}_{m e r}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	4.6	7.3	Derived
${\hat{v}}_{m e f}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	$9.8 \pm 3.0$	$1.2 \pm 0.4$	$a$
${\hat{v}}_{m u}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	6.5	5.3	Derived
${\hat{v}}_{r}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	19.2	15.8	Derived
Total biomass concentration
$1 / \hat{β}$	$Cmmol {gDW}^{- 1}$	$40.65 \pm 2.0$	$40.65 \pm 2.0$	$e$
Protein concentrations
$\hat{m_{u}}$	$Cmmol {gDW}^{- 1}$	$11.1 \pm 0.5$	$10.9 \pm 0.5$	$e, f, g$
$\hat{r}$	$Cmmol {gDW}^{- 1}$	$13.2 \pm 0.6$	$11.5 \pm 0.6$	$e, f, g$
${\hat{m}}_{c}$	$Cmmol {gDW}^{- 1}$	$2.7 \pm 0.1$	$3.0 \pm 0.1$	$e, f, g$
${\hat{m}}_{e r} + {\hat{m}}_{e f}$	$Cmmol {gDW}^{- 1}$	$3.0 \pm 0.1$	$4.8 \pm 0.2$	$e, f, g$
${\hat{m}}_{e r}$	$Cmmol {gDW}^{- 1}$	1.9	4.4	Derived
${\hat{m}}_{e f}$	$Cmmol {gDW}^{- 1}$	1.1	0.47	Derived
Metabolite concentrations
$\hat{c}$	$Cmmol {gDW}^{- 1}$	$0.35 \pm 0.002$	$0.20 \pm 0.002$	$b, h$
${\hat{a}}^{*}$	$mmol {gDW}^{- 1}$	$0.009 \pm 0.0002$	$0.005 \pm 0.0003$	$b$
$\hat{a}$	$mmol {gDW}^{- 1}$	$0.011 \pm 0.0006$	$0.010 \pm 0.0005$	$b$
${\hat{a}}_{0}$	$mmol {gDW}^{- 1}$	$0.020 \pm 0.0008$	$0.015 \pm 0.0008$	$b$
Concentration of other biomass
$\hat{u}$	$Cmmol {gDW}^{- 1}$	10.2	10.2	Derived

Appendix 2—table 2

Estimation of the values of the kinetic parameters in the model, in the case of batch growth of E. coli in minimal medium with glucose or glycerol, as explained in the text.

Parameter	Glucose	Glycerol	Unit
${\hat{ρ}}_{r u}$	1.17	1.17	–
${\hat{ρ}}_{m e f}$	1.5	1.5	–
${\hat{k}}_{r}$	2.9	3.6	${hr}^{- 1}$
${\hat{k}}_{m u}$	1.2	1.3	${hr}^{- 1}$
${\hat{e}}_{s}$	18.3	11.2	${hr}^{- 1}$
${\hat{k}}_{m e r}$	5.0	4.4	${hr}^{- 1}$
${\hat{k}}_{m e f}$	17.4	6.7	${hr}^{- 1}$
${\hat{k}}_{a}$	2279	6462	${hr}^{- 1}$
${\hat{K}}_{r}$	0.29	0.28	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{m u}$	0.29	0.28	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{m e r}$	0.29	0.28	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{m e f}$	0.29	0.28	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{a r}$	0.0009	0.0005	$mmol {gDW}^{- 1}$
${\hat{K}}_{a m e r}$	0.0011	0.001	$mmol {gDW}^{- 1}$
${\hat{K}}_{a m e f}$	0.0011	0.001	$mmol {gDW}^{- 1}$
${\hat{K}}_{a m u}$	0.0009	0.0005	$mmol {gDW}^{- 1}$
${\hat{n}}_{m e r}$	4.3	4.7	$mmol {Cmmol}^{- 1}$
${\hat{n}}_{m e f}$	2.0	2.3	$mmol {Cmmol}^{- 1}$
${\hat{n}}_{r}$	0.77	0.09	$mmol {Cmmol}^{- 1}$
${\hat{n}}_{m u}$	0.65	0.65	$mmol {Cmmol}^{- 1}$

Appendix 2—table 3

Reconstruction of growth and degradation rates, fluxes, and concentrations from published datasets for the case of continuous growth of E. coli in minimal medium with glucose at different dilution rates (D0.2: 0.2 hr^-1, D0.35: 0.35 hr^-1, D0.5: 0.5 hr^-1).

For the error bars, see Appendix 2—table 1. References: ^a Peebo et al., 2015, ^b Esquerré et al., 2014, ^c Morin et al., 2016, ^d Basan et al., 2015b, ^e Schmidt et al., 2016, ^f Gerosa et al., 2015, ^g Park et al., 2016.

Rates	Unit	D0.2	D0.35	D0.5	Reference
$\hat{μ}$	hr^-1	o.2	0.35	0.5	$a$
$\hat{γ}$	hr^-1	0.027	0.027	0.027	$b$
Uptake, secretion, and biosynthesis fluxes
${\hat{v}}_{m c}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	16.0	26.2	37.4	$a$
${\hat{v}}_{m e r}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	5.3	8.1	9.4	Derived
${\hat{v}}_{m e f}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	0.02	0.16	2.0	$a$
${\hat{v}}_{m u}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	1.9	3.4	5.2	Derived
${\hat{v}}_{r}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	7.3	11.8	16.1	Derived
Total biomass concentration
$1 / \hat{β}$	$Cmmol {gDW}^{- 1}$	$40.65 \pm 2.0$	$40.65 \pm 2.0$	$40.65 \pm 2.0$	$c$
Protein concentrations
$\hat{m_{u}}$	$Cmmol {gDW}^{- 1}$	$11.2 \pm 0.6$	$11.2 \pm 0.6$	$10.4 \pm 0.5$	$c, d, e$
$\hat{r}$	$Cmmol {gDW}^{- 1}$	$9.3 \pm 0.5$	$9.4 \pm 0.5$	$11.0 \pm 0.5$	$c, d, e$
${\hat{m}}_{c}$	$Cmmol {gDW}^{- 1}$	$3.5 \pm 0.2$	$3.4 \pm 0.2$	$3.3 \pm 0.2$	$c, d, e$
${\hat{m}}_{e r} + {\hat{m}}_{e f}$	$Cmmol {gDW}^{- 1}$	$8.0 \pm 0.4$	$7.2 \pm 0.4$	$5.8 \pm 0.3$	$c, d, e$
${\hat{m}}_{e r}$	$Cmmol {gDW}^{- 1}$	7.9	7.1	5.2	Derived
${\hat{m}}_{e f}$	$Cmmol {gDW}^{- 1}$	0.05	0.1	0.6	Derived
Metabolite concentrations
$\hat{c}$	$Cmmol {gDW}^{- 1}$	$0.35 \pm 0.002$	$0.35 \pm 0.002$	$0.35 \pm 0.002$	$f, g$
${\hat{a}}^{*}$	$mmol {gDW}^{- 1}$	0.005	0.006	0.008	$f$
$\hat{a}$	$mmol {gDW}^{- 1}$	0.011	0.015	0.016	$f$
${\hat{a}}_{0}$	$mmol {gDW}^{- 1}$	0.016	0.021	0.024	$f$
Concentration of other biomass
$\hat{u}$	$Cmmol {gDW}^{- 1}$	8.2	9.0	9.8	Derived

Appendix 2—table 4

Estimation of the values of the kinetic parameters in the model, in the case of continuous growth of E. coli in minimal medium with glucose at different dilution rates (D0.2: 0.2 hr^-1, D0.35: 0.35 hr^-1, D0.5: 0.5 hr^-1), as explained in the text.

Parameter	D0.2	D0.35	D0.5	Unit
${\hat{ρ}}_{r u}$	1.16	1.17	1.17	–
${\hat{ρ}}_{m e f}$	1.5	1.5	1.5	–
${\hat{k}}_{r}$	1.6	2.5	2.9	${hr}^{- 1}$
${\hat{k}}_{m u}$	0.33	0.61	1.0	${hr}^{- 1}$
${\hat{e}}_{s}$	4.5	7.6	11.2	${hr}^{- 1}$
${\hat{k}}_{m e r}$	1.3	2.3	3.6	${hr}^{- 1}$
${\hat{k}}_{m e f}$	0.77	2.98	6.8	${hr}^{- 1}$
${\hat{k}}_{a}$	3203	4001	3633	${hr}^{- 1}$
${\hat{K}}_{r}$	0.29	0.29	0.29	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{m u}$	0.29	0.29	0.29	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{m e r}$	0.29	0.29	0.29	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{m e f}$	0.29	0.29	0.29	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{a r}$	0.0005	0.0006	0.0008	$mmol {gDW}^{- 1}$
${\hat{K}}_{a m e r}$	0.0011	0.0015	0.0016	$mmol {gDW}^{- 1}$
${\hat{K}}_{a m e f}$	0.0011	0.0015	0.0016	$mmol {gDW}^{- 1}$
${\hat{K}}_{a m u}$	0.0005	0.0006	0.0008	$mmol {gDW}^{- 1}$
${\hat{n}}_{m e r}$	4.3	4.3	4.3	$mmol {Cmmol}^{- 1}$
${\hat{n}}_{m e f}$	2.0	2.0	2.0	$mmol {Cmmol}^{- 1}$
${\hat{n}}_{r}$	0.77	0.77	0.77	$mmol {Cmmol}^{- 1}$
${\hat{n}}_{m u}$	0.65	0.65	0.65	$mmol {Cmmol}^{- 1}$

Appendix 2—table 5

Reconstruction of growth and degradation rates, uptake and secretion fluxes, and protein and metabolite concentrations from published datasets for E. coli MG1655 and NCM3722 strains for the case of batch growth in glucose minimal medium.

The uncertainty intervals for the rates, fluxes, and metabolite concentrations are standard deviations reported in the source publications, after unit conversion. For the NCM3722 strain, as an example of a fast-growing strain with a higher growth yield than the BW25113 reference strain, we only use a subset of observed values in the main text. References: ^aCheng et al., 2019, ^bBasan et al., 2015a, ^cEsquerré et al., 2014, ^dFarmer and Jones, 1976, ^eMonk et al., 2017, ^fBasan et al., 2015b, ^gSchmidt et al., 2016, ^hPark et al., 2016, ⁱMcCloskey et al., 2018.

Rates	Unit	MG1655	NCM3722	Reference
$\hat{μ}$	${hr}^{- 1}$	$0.69 \pm 0.02$	$0.97 \pm 0.05$	$a, b$
$\hat{γ}$	${hr}^{- 1}$	0.027	–	$c, d$
Uptake, secretion, and biosynthesis fluxes
${\hat{v}}_{m c}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	$51.5 \pm 8.5$	$66.1 \pm 4$	$a, b, e$
${\hat{v}}_{m e r}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	5.7	–	Derived
${\hat{v}}_{m e f}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	$7.8 \pm 2.3$	$10.3 \pm 1.8$	$a, b, e$
${\hat{v}}_{m u}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	7.0	–	Derived
${\hat{v}}_{r}$	$Cmmol {gDW}^{- 1} {hr}^{- 1}$	21.7	–	Derived
Total biomass concentration
$1 / \hat{β}$	$Cmmol {gDW}^{- 1}$	$40.65 \pm 2.0$	–	$e$
Protein concentrations
$\hat{p}$	$Cmmol {gDW}^{- 1}$	$30.7 \pm 2.0$	$29.7 \pm 1.9$	$e, f$
$\hat{m_{u}}$	$Cmmol {gDW}^{- 1}$	$11.4 \pm 0.74$	–	$e, f, g$
$\hat{r}$	$Cmmol {gDW}^{- 1}$	$13.8 \pm 0.9$	–	$e, f, g$
${\hat{m}}_{c}$	$Cmmol {gDW}^{- 1}$	$2.4 \pm 0.2$	–	$e, f, g$
${\hat{m}}_{e r} + {\hat{m}}_{e f}$	$Cmmol {gDW}^{- 1}$	$3.1 \pm 0.2$	–	$e, f, g$
${\hat{m}}_{e r}$	$Cmmol {gDW}^{- 1}$	$2.2 \pm 0.1$	–	Derived
${\hat{m}}_{e f}$	$Cmmol {gDW}^{- 1}$	$0.9 \pm 0.04$	–	Derived
Metabolite concentrations
$\hat{c}$	$Cmmol {gDW}^{- 1}$	$0.5 \pm 0.09$	$0.8 \pm 0.03$	$h, i$
${\hat{a}}^{*}$	$mmol {gDW}^{- 1}$	0.046	–	$h, i$
$\hat{a}$	$mmol {gDW}^{- 1}$	0.008	–	$h, i$
${\hat{a}}_{0}$	$mmol {gDW}^{- 1}$	0.054	–	$h, i$
Concentration of other biomass
$\hat{u}$	$Cmmol {gDW}^{- 1}$	9.4	–	Derived

Appendix 2—table 6

Estimation of the values of the kinetic parameters in the model for the E. coli MG1655 strain during batch growth in glucose minimal medium from data in Appendix 2—table 5, as explained in the text.

Idem for a model variant with an additional category of growth-rate-independent proteins ( $Q$ ), using data for the BW25113 strain from Appendix 2—table 1.

Parameter	MG1655	Model variant with Q	Unit
${\hat{ρ}}_{r u}$	1.17	1.17	–
${\hat{ρ}}_{m e f}$	1.5	1.5	–
${\hat{k}}_{r}$	2.5	6.1	${hr}^{- 1}$
${\hat{k}}_{m u}$	0.9	2.5	${hr}^{- 1}$
${\hat{e}}_{s}$	21.0	38.0	${hr}^{- 1}$
${\hat{k}}_{m e r}$	4.1	10.3	${hr}^{- 1}$
${\hat{k}}_{m e f}$	20.4	36.1	${hr}^{- 1}$
${\hat{k}}_{a}$	412	2278	${hr}^{- 1}$
${\hat{K}}_{r}$	0.24	0.29	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{m u}$	0.24	0.29	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{m e r}$	0.24	0.29	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{m e f}$	0.24	0.29	$Cmmol {gDW}^{- 1}$
${\hat{K}}_{a r}$	0.005	0.0009	$mmol {gDW}^{- 1}$
${\hat{K}}_{a m e r}$	0.0008	0.0011	$mmol {gDW}^{- 1}$
${\hat{K}}_{a m e f}$	0.0008	0.0011	$mmol {gDW}^{- 1}$
${\hat{K}}_{a m u}$	0.005	0.0009	$mmol {gDW}^{- 1}$
${\hat{n}}_{m e r}$	4.3	4.3	$mmol {Cmmol}^{- 1}$
${\hat{n}}_{m e f}$	2.0	2.0	$mmol {Cmmol}^{- 1}$
${\hat{n}}_{r}$	0.77	0.77	$mmol {Cmmol}^{- 1}$
${\hat{n}}_{m u}$	0.65	0.65	$mmol {Cmmol}^{- 1}$

Additional files

Supplementary file 1 Database with reported rate-yield pairs for Escherichia coli grown on glucose minimal medium (excel file).: https://cdn.elifesciences.org/articles/79815/elife-79815-supp1-v2.xlsx
Download elife-79815-supp1-v2.xlsx
Supplementary file 2 Database with reported rate-yield pairs for Escherichia coli grown on glycerol minimal medium (excel file).: https://cdn.elifesciences.org/articles/79815/elife-79815-supp2-v2.xlsx
Download elife-79815-supp2-v2.xlsx
Supplementary file 3 Half-saturation constants for reactions in central carbon metabolism of Escherichia coli (excel file).: https://cdn.elifesciences.org/articles/79815/elife-79815-supp3-v2.xlsx
Download elife-79815-supp3-v2.xlsx
Supplementary file 4 Classification of energy proteins (excel file).: https://cdn.elifesciences.org/articles/79815/elife-79815-supp4-v2.xlsx
Download elife-79815-supp4-v2.xlsx
MDAR checklist: https://cdn.elifesciences.org/articles/79815/elife-79815-mdarchecklist1-v2.docx
Download elife-79815-mdarchecklist1-v2.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Valentina Baldazzi
Delphine Ropers
Jean-Luc Gouzé
Tomas Gedeon
Hidde de Jong

(2023)

Resource allocation accounts for the large variability of rate-yield phenotypes across bacterial strains

eLife 12:e79815.

https://doi.org/10.7554/eLife.79815

Figures

Coarse-grained model of microbial growth with coupled carbon and energy fluxes.

Predicted rate-yield phenotypes and underlying resource allocation strategies.

Observed allocation of resources to the category of residual proteins in different growth conditions.

Relation between resource allocation strategies and rate-yield phenotypes.

Schematic overview of the computation of growth rate and growth yield from resource allocation strategies.

Predicted fluxes, concentrations, and resource allocation along the Pareto frontier of growth rate and growth yield.

Predicted rate-yield phenotypes and comparison with experimental data.

Robustness of rate-yield predictions for alternative model calibration and alternative model assumption.

Predicted uptake-secretion phenotypes and comparison with experimental data.

Additional model predictions of rate-yield and uptake-secretion phenotypes and their comparison with experimental data.

Variation of normalized acetate secretion rate with growth rate in experiments with a single E. coli strain growing in different environments.

Resource allocation strategies underlying high-rate, high-yield phenotypes.

Relative changes in kinetic parameters for resource allocation strategies reproducing the observed phenotypes of the NCM3722 strain during minimal growth on glucose.

Resource allocation model of coupled carbon and energy fluxes in microorganisms.

Protein dry mass fraction for different growth rates of E. coli.

Growth-rate dependency of proteome fractions.

Tables

Model variables and rates.

Model parameters.

Reconstruction of growth and degradation rates, fluxes, and concentrations from published datasets for the case of batch growth of E. coli in minimal medium with glucose or glycerol, as explained in the text.

Estimation of the values of the kinetic parameters in the model, in the case of batch growth of E. coli in minimal medium with glucose or glycerol, as explained in the text.

Reconstruction of growth and degradation rates, fluxes, and concentrations from published datasets for the case of continuous growth of E. coli in minimal medium with glucose at different dilution rates (D0.2: 0.2 hr^-1, D0.35: 0.35 hr^-1, D0.5: 0.5 hr^-1).

Estimation of the values of the kinetic parameters in the model, in the case of continuous growth of E. coli in minimal medium with glucose at different dilution rates (D0.2: 0.2 hr^-1, D0.35: 0.35 hr^-1, D0.5: 0.5 hr^-1), as explained in the text.

Reconstruction of growth and degradation rates, uptake and secretion fluxes, and protein and metabolite concentrations from published datasets for E. coli MG1655 and NCM3722 strains for the case of batch growth in glucose minimal medium.

Estimation of the values of the kinetic parameters in the model for the E. coli MG1655 strain during batch growth in glucose minimal medium from data in Appendix 2—table 5, as explained in the text.

Additional files

Supplementary file 1

Supplementary file 2

Supplementary file 3

Supplementary file 4

MDAR checklist

Download links

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Be the first to read new articles from eLife

Share this article

Cite this article

Coarse-grained model of microbial growth with coupled carbon and energy fluxes.

Predicted rate-yield phenotypes and underlying resource allocation strategies.

Observed allocation of resources to the category of residual proteins in different growth conditions.

Relation between resource allocation strategies and rate-yield phenotypes.

Schematic overview of the computation of growth rate and growth yield from resource allocation strategies.

Predicted fluxes, concentrations, and resource allocation along the Pareto frontier of growth rate and growth yield.

Predicted rate-yield phenotypes and comparison with experimental data.

Robustness of rate-yield predictions for alternative model calibration and alternative model assumption.

Predicted uptake-secretion phenotypes and comparison with experimental data.

Additional model predictions of rate-yield and uptake-secretion phenotypes and their comparison with experimental data.

Variation of normalized acetate secretion rate with growth rate in experiments with a single E. coli strain growing in different environments.

Resource allocation strategies underlying high-rate, high-yield phenotypes.

Relative changes in kinetic parameters for resource allocation strategies reproducing the observed phenotypes of the NCM3722 strain during minimal growth on glucose.

Resource allocation model of coupled carbon and energy fluxes in microorganisms.

Protein dry mass fraction for different growth rates of E. coli.

Growth-rate dependency of proteome fractions.

Model variables and rates.

Model parameters.

Reconstruction of growth and degradation rates, fluxes, and concentrations from published datasets for the case of batch growth of E. coli in minimal medium with glucose or glycerol, as explained in the text.

Estimation of the values of the kinetic parameters in the model, in the case of batch growth of E. coli in minimal medium with glucose or glycerol, as explained in the text.

Reconstruction of growth and degradation rates, fluxes, and concentrations from published datasets for the case of continuous growth of E. coli in minimal medium with glucose at different dilution rates (D0.2: 0.2 hr-1, D0.35: 0.35 hr-1, D0.5: 0.5 hr-1).

Estimation of the values of the kinetic parameters in the model, in the case of continuous growth of E. coli in minimal medium with glucose at different dilution rates (D0.2: 0.2 hr-1, D0.35: 0.35 hr-1, D0.5: 0.5 hr-1), as explained in the text.

Reconstruction of growth and degradation rates, uptake and secretion fluxes, and protein and metabolite concentrations from published datasets for E. coli MG1655 and NCM3722 strains for the case of batch growth in glucose minimal medium.

Estimation of the values of the kinetic parameters in the model for the E. coli MG1655 strain during batch growth in glucose minimal medium from data in Appendix 2—table 5, as explained in the text.

Supplementary file 1

Supplementary file 2

Supplementary file 3

Supplementary file 4

MDAR checklist

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Reconstruction of growth and degradation rates, fluxes, and concentrations from published datasets for the case of continuous growth of E. coli in minimal medium with glucose at different dilution rates (D0.2: 0.2 hr^-1, D0.35: 0.35 hr^-1, D0.5: 0.5 hr^-1).

Estimation of the values of the kinetic parameters in the model, in the case of continuous growth of E. coli in minimal medium with glucose at different dilution rates (D0.2: 0.2 hr^-1, D0.35: 0.35 hr^-1, D0.5: 0.5 hr^-1), as explained in the text.