Single spikes drive sequential propagation and routing of activity in a cortical network
- Max Planck Institute for Brain Research, Germany
- School of Life Sciences, Technical University of Munich, Germany
Figures
Figure 1
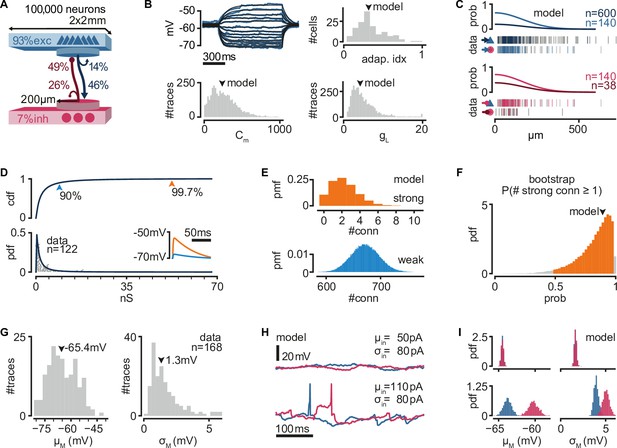
A biologically inspired model of turtle visual cortex.
(A) Schematic of the network with the size, proportion of E and I populations, and connection probabilities within a disc of 200 μm radius (see C). Mean number of outgoing connections per cell: E-to-E: 750, I-to-I: 110, E-to-I: 190, I-to-E: 2690. Blue triangles: excitatory neurons. Red circles: inhibitory neurons. (B) Top left: example of fit (black) of membrane potential responses to current injection in a recorded neuron (blue). Bottom left and right: distributions of fitted membrane capacitance (Cm) and leak conductance (gL) (n = 3886 traces). Top right: distribution of adaptive indices for 145 recorded neurons. Arrowheads indicate parameters of model neurons (median). (C) Gaussian profiles of distance-dependent connection probabilities for different connection types (top: exc, bottom: inh). The profiles were fitted from the fraction of pairs of patched neurons that showed a connection from all tested pairs. Vertical bars below (data) indicate connected (colored) or disconnected (gray) pairs of neurons for different connection types. (D) Lognormal fit to peak excitatory synaptic conductances. Top: cumulative distribution function (cdf). Bottom: probability density function (pdf). Conductances were estimated from excitatory postsynaptic potential (EPSP) amplitudes experimentally obtained from recorded pairs of connected neurons (gray dots). Inset: example of modeled EPSPs for different synaptic weights (top arrowheads) in an isolated postsynaptic neuron at resting potential. (E) Probability mass function (pmf) of number of strong (top 0.3%) or weak (bottom 90%) excitatory-to-excitatory connections per model neuron. (F) Bootstrap estimate of the probability of an excitatory neuron having at least one strong excitatory-to-excitatory connection. Colored area: 95% confidence interval. Arrowhead: fit with the original dataset in (D). (G) Experimentally measured mean and standard deviation of the membrane potential of 168 patched neurons in ex vivo preparations. Arrowheads indicate medians. (H) Membrane potential of two model neurons (blue: exc; red: inh) under different white noise current parameters. Note the presence of action potentials and EPSPs under a high mean current (μin). (I) Distributions of membrane potential mean and standard deviation for model neurons (blue: exc; red: inh) under the white noise current parameters in (H).
Figure 2 with 1 supplement
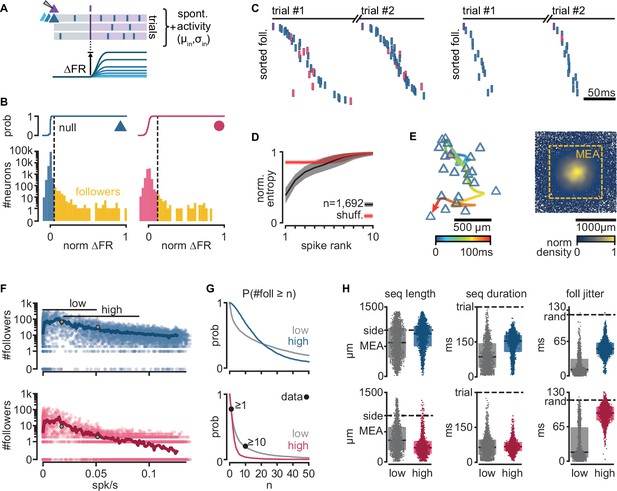
Repeatable sequential activation of follower neurons in the model network.
(A) Schematic of the stimulation protocol in the model. One neuron (top) was driven to produce one action potential, and all other neurons in the network were tested for resulting changes in their firing rate. (B) Distribution of single-cell firing rate modulation (∆FR) for one representative simulation. Top: cumulative mass function of the null distribution. Dashed: threshold for follower classification (p = 10−7). Bottom: ∆FR for followers (yellow) and other neurons in the network (blue: exc, red: inh). ∆FR is normalized to the modulation of a perfect follower (exactly one spike per trial). (C) Left: sequence of spikes from followers in two consecutive trials in an example simulation. Y-axis: followers sorted by median spike time across all trials. Same sorting in both trials. Spikes from non-followers are not shown. Right: same for a different simulation with a higher mean firing rate (left: 0.017 spk/s, right: 0.051 spk/s). See Figure 2—figure supplement 1C for full rasters. (D) Normalized spike rank entropy of sequences with at least 10 followers (black: mean; gray: std), compared to shuffled sequences (red). (E) Left: spatial evolution of the center-of-mass of follower activations during the first 100 ms of the first sequence in (C). Trigger neuron in purple outline. Exc followers in blue outlines. Right: spatial location of excitatory followers pooled from all simulations, colored by local density (n = 117,427). All simulations are aligned so that the trigger neuron is in the center. Stippled square: size of the MEA used in experiments. (F) Number of followers detected for each simulation as a function of the mean level of activity in the network. Blue: exc; red: inh; thick line: moving average; gray dots: sequences in (C). (G) Probability of generating a minimum number of followers for excitatory and inhibitory populations in high- and low-activity simulations. Dots: experimental ex vivo estimates. (H) Statistics of excitatory- or inhibitory-follower activations by activity level. Left: distance from trigger neuron to farthest detected follower in each simulation (side: half-width of the model network; MEA: half-width of MEA used in experiments). Middle: delay to median spike time of the last activated follower in each simulation (trial: maximum detectable duration under protocol in A). Right: standard deviation of follower spike times, averaged over all followers in each simulation (rand: expected standard deviation of randomly distributed spike times). Boxes: median and [25th, 75th] percentiles.
Figure 2—figure supplement 1
Network firing rates.
(A) Input–output curve of the model. Each dot corresponds to one simulation. Y-axis indicates the mean firing rate over all neurons in the simulation. X-axis and color indicate the mean and standard deviation of the random spontaneous current. Highlighted in blue and orange (s1, s2) are the simulations containing the sequences shown in Figure 2C. Highlighted in green (s3) is the simulation containing the sequence shown in (B). (B) Sequence of spikes in two trials of an example simulation with firing rates above in vivo estimates (green s3 in (A) 0.13 spk/s). Neurons are sorted by median spike time across all trials. Same sorting in both trials. Spikes from non-followers are not shown (see C). Purple: trigger spike. (C) Spike raster of the three simulations highlighted in (A). Each raster shows all spikes for all neurons in the network for 1 s in the middle of the simulation, containing two consecutive trials. Arrowheads indicate the initiation of a trial. Purple circles highlight injected spikes. Blue: exc; pink: inh. (D) Spatial distribution of population firing rates for three consecutive time bins in the middle of an example simulation (green s3 in A). Spikes are counted in a 2D grid of 1 μm. Counts are convolved with a 100-μm Gaussian filter and divided by the duration of the time bins (20 ms). Blue: exc. spikes. Pink: inh. spikes. (E) Distributions of mean firing rates per cell for the three simulations highlighted in A. Dashed lines indicate Poisson fits. Blue: exc; pink: inh.
Figure 3 with 1 supplement
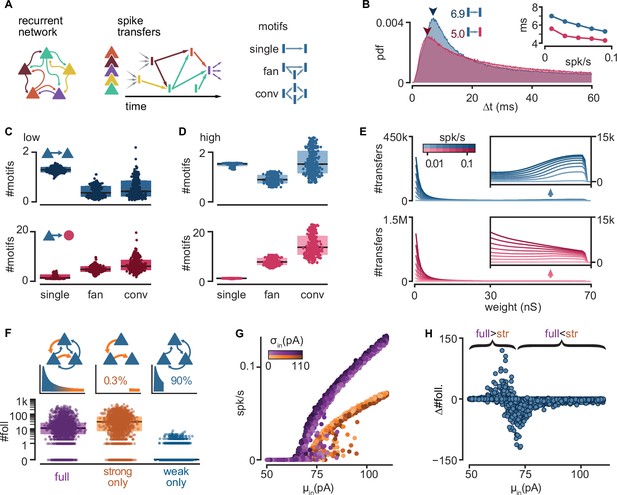
Connectivity underlying activity propagation in the network.
(A) Schematic. Left: the recurrent network structure and spiking activity are combined to produce a directed graph of spike transfers. Right: motifs of spike transfers detected in this graph (conv: convergence). (B) Distribution of delays of excitatory-to-inhibitory (red) and excitatory-to-excitatory (blue) spike transfers. Average of all low-activity simulations ([0, 0.05] spk/s). Arrowheads: mode of each distribution. Inset: most common delay as a function of mean firing rate. (C) Number of motifs leading to an excitatory (blue) or inhibitory (red) neuron spike. Motifs defined in (A). Each dot represents the mean for all spikes in each simulation. Low-activity simulations. Boxes: median and [25th, 75th] percentiles. (D) Same as (C) for high-activity simulations. (E) Histograms of strengths of synapses leading to excitatory (blue) or inhibitory (red) neuron spikes. Insets: zoomed-in tails. Each line averages 25–100 simulations grouped in equal bins of mean firing rate (color bar). (F) Top: schematic of alternative network models and their truncated distribution of synaptic strengths. Bottom: number of detected excitatory followers per simulation (n = 2000 each). Boxes: median and [25th, 75th] percentiles. (G) Input–output curves for the full (purple) and strong-only (orange) models. (H) Difference between the number of followers detected in full and strong-only models under the same input. Brackets indicate regimes where the presence of weak connections increases (full >str) or decreases (full <str) the follower count. 2000 simulations.
Figure 3—figure supplement 1
Properties of full, strong-only, and weak-only models.
(A) Input–output curves for the full (purple), strong-only (orange), and weak-only (blue) models. Note that the weak-only model produced firing rates only when driven with very strong depolarizations (rheobase current of a model neuron in isolation ~150 pA). (B) Number of followers as a function of firing rate for each model. (C) Probability of obtaining at least n followers for each model.
Figure 4
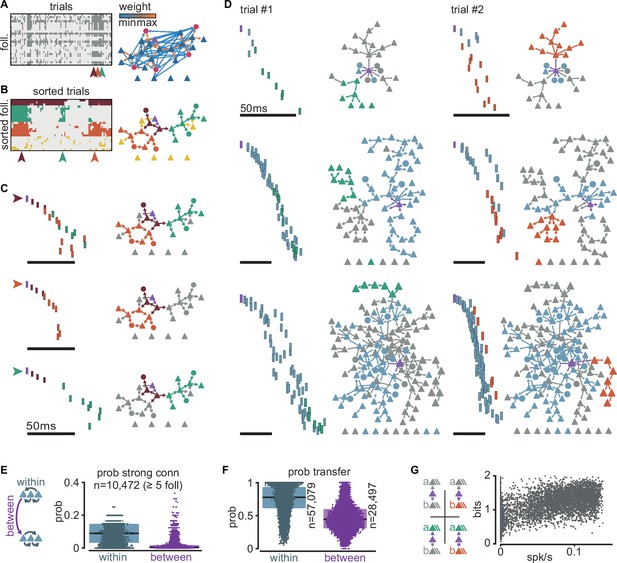
Clusters of sequential spikes reflect sub-networks of strongly connected followers.
(A) Left: matrix of followers (rows) and trials (columns) of a representative simulation indicating follower activation (dark entries). Colored arrowheads indicate trials in (C). Right: graph of excitatory follower-to-follower connections colored by strength. Trigger neuron in purple. Neurons identified as followers but not directly connected are aligned below. (B) Left: matrix in (A) after sorting followers and trials according to k-modes clustering. Right: same graph as in (A) with only top 5% connections. Colors according to follower clustering. Note that members of orange, green, and brown clusters are connected to one another. (C) The three trials indicated in (A) and (B). Left: firing sequence with spikes colored according to follower cluster. Right: same graph as in (B) with inactive followers in gray. (D) Two trials (columns) of three different simulations to illustrate selective sub-network activation. Top to bottom: different trigger neurons with 28, 68, and 145 followers. Only the top 5% connections are shown. Followers were clustered as in (B). Green and orange: example active sub-networks. Blue: other active sub-networks. Gray: inactive followers. (E) Relationship between connectivity and follower clusters. Left: schematic illustrating connections between (purple) and within (blue) clusters. Right: estimated probability (measured frequency) of strong (top 0.3%) excitatory-to-excitatory connection within or between clusters for 10,472 clusters of at least 5 followers pooled across all 6000 simulations. (F) Estimated probability (measured frequency) of postsynaptic activation conditioned on presynaptic activation in the same trial, for excitatory-to-excitatory connections, pooled across all 6000 simulations. Boxes: median and [25th, 75th] percentiles. (G) Relationship between entropy and baseline firing rate. Left: schematic of four possible propagation scenarios in a simplified scheme where only two sub-networks are considered per simulation. Right: entropy over trials for each simulation with at least two sub-networks (n = 5371) as a function of network mean firing rate.
Figure 5 with 1 supplement
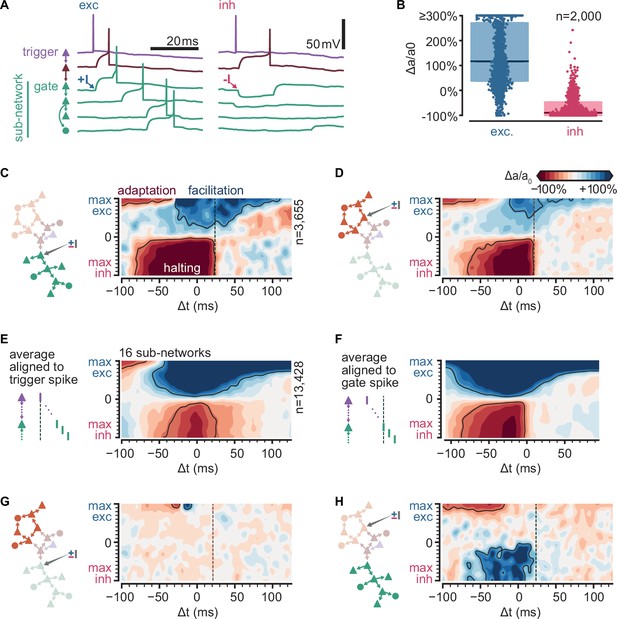
Sub-sequence activations depend on the state of gate neurons.
(A) Voltage traces for six neurons in a sequence (network and colors as in Figure 4B) in two trials of simulations where the first neuron in the green sub-network receives a single excitatory (left,+I) or inhibitory (right, −I) input from an external source (arrows). (B) Fold change of sub-network activation above baseline (∆a/a0, %) for sub-networks randomly selected across all 6000 original simulations. The model gate neuron of each sub-network received an additional single input from an external source at the beginning of each trial. (C) Schematic of protocol and map of the fold change in activation (∆a/a0, %) for a sub-network when manipulating its gate (same network as Figure 4A). Arrow in schematic indicates stimulated gate. Solid outlines indicate combinations of strength and timing leading to halting (bottom, −50% ∆a/a0), facilitation (top right,+50% ∆a/a0), and adaptation (top left, −50% ∆a/a0). ∆t indicates the delay from trigger spike to external input. Dashed lines indicate the median spike time of the gate. (D) Same as (C) for a different sub-network. (E) Average map of the change in activation (∆a/a0, %, same as C) computed from 16 sub-networks of 8 different networks spanning 5–462 followers and 0.01–0.1 spk/s baseline firing rate (networks in C) and (Figure 5—figure supplement 1B). Maps were aligned relative to trigger spike as in (C) before averaging. Solid outlines indicate ±50% ∆a/a0. Color bar as in (C). (F) Same as (E) but maps were aligned to each gate median spike time (dashed line in C) before averaging. (G) Same as (C) for the orange sub-network when manipulating the green gate. (H) Same as (D) for the green sub-network when manipulating the orange gate.
Figure 5—figure supplement 1
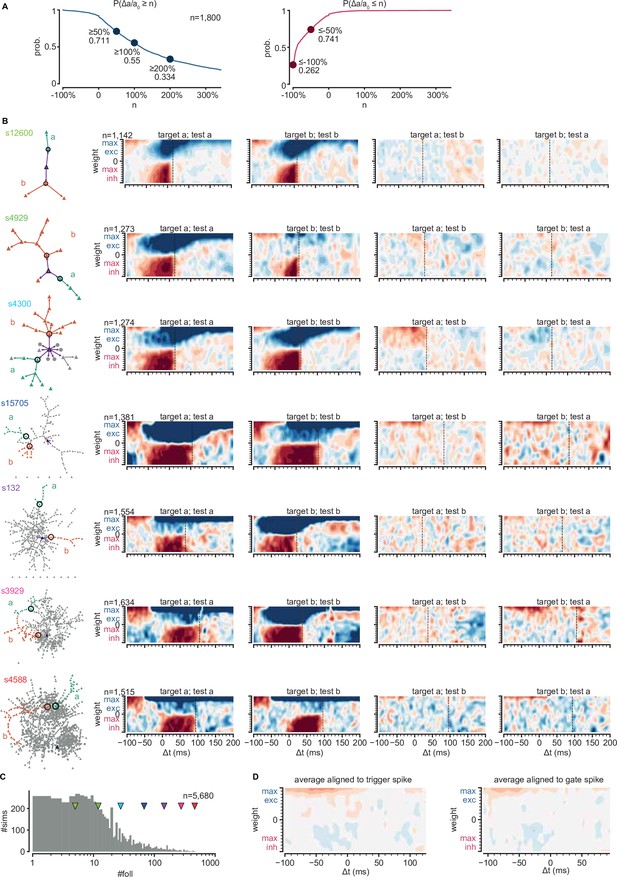
Gating sub-sequence activations.
(A) Top: probability of an excitatory input onto a gate neuron producing at least an n-fold increase of activation probability on its respective sub-network. Bottom: same for inhibitory inputs. (B) Left column: graphs of strong connections between followers for seven networks with an increasing number of followers. Sub-networks are colored and labeled a and b. Circles indicate sub-network gates. Other columns: change of sub-network activation on sub-network a or b (test) as a function of external input strength and timing onto the gate of sub-network a or b (target). (C) Number of followers for all networks with at least two sub-networks. Arrowheads indicate networks in (B). (D) Left: average change of all maps of sub-network activation in two rightmost columns (B). Right: average but aligning all maps to the median spike time of their respective gate.
Figure 6 with 1 supplement
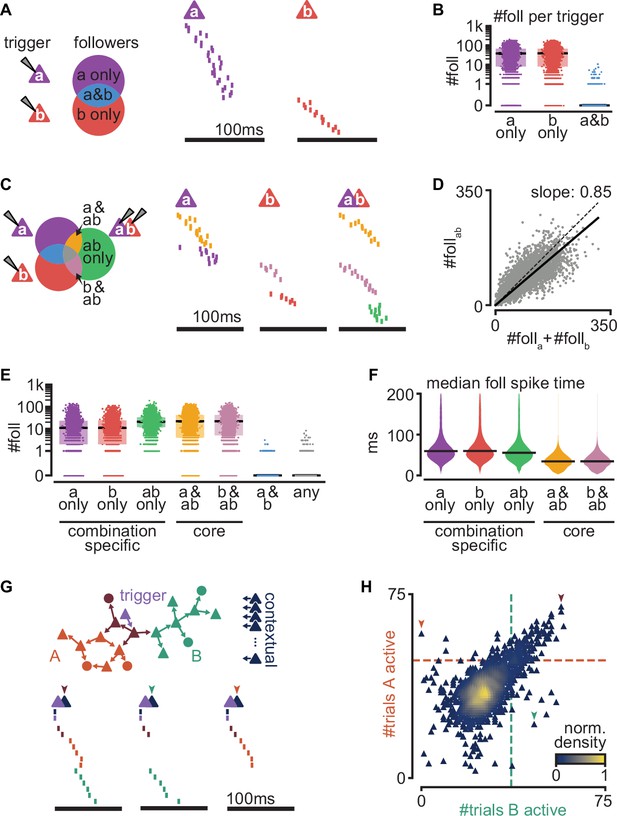
Interaction of sequences from multiple triggers reliably route activity.
(A) Left: schematic of follower classes as a function of trigger neuron (purple: follower to a; red: follower to b; blue: follower to both a and b). Right: example sequences produced by the activation of a or b. Followers are sorted by trigger class (left) and median spike time. Triggers do not share any followers (blue trigger class). (B) Number of followers for each trigger class in (A) for all random pairs of simulations (n = 5000). Boxes: median and [25th, 75th] percentiles. (C) Left: schematic of follower classes as a function of trigger: single-trigger neuron (a or b) or simultaneous coactivation (ab). Blue, purple, and red as in (A). Right: same trials as in (A), and a trial under coactivation. Followers are sorted by trigger class (left) and median spike time. Same follower sorting in all trials. (D) Number of followers presents under trigger coactivation as a function of the sum of followers for single triggers. Dashed line: diagonal. Solid line: linear fit with zero intercept. (E) Number of followers for each trigger class in (C) for all random pairs of triggers (n = 5000). (F) Median follower spike time for each trigger class in (C) after pooling followers from all simulations (5000 simulations; 532,208 followers). Lines indicate median. (G) Top: trigger neuron (purple), followers, strong connections between them (arrows), and other neurons in the network (dark blue). Follower colors as in Figure 4B. Bottom: sequences triggered under simultaneous coactivation of trigger (purple) and one additional contextual neuron that facilitates propagation in both sub-networks (left), only in the green sub-network (middle), or only in the orange sub-network (right). (H) Effect on green and orange sub-network activation (G top) when the trigger neuron is coactivated with each of 2000 randomly selected contextual neurons. Dashed lines indicate baseline activation of each sub-network. Neurons are colored by local density. Colored arrows correspond to sequences in (G).
Figure 6—figure supplement 1
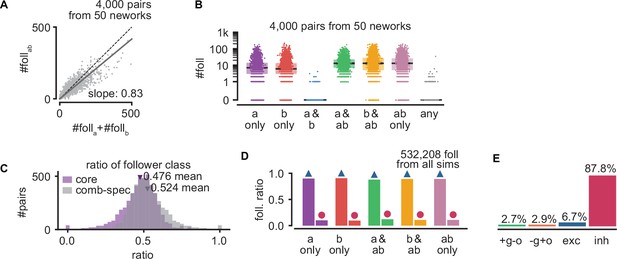
Interactions between sequences.
(A) Number of model followers presents under trigger coactivation as a function of the sum of followers for each trigger alone. Same as Figure 6D but with follower pairs pooled across 50 randomly picked networks (800 pairs per network). (B) Number of followers for each trigger class for all simulations. Same as Figure 6E but with follower pairs pooled as in (A). (C) Ratio of core and combination-specific followers for every pair of random triggers for the network in Figure 6. (D) Ratio of excitatory and inhibitory followers for each trigger class, pooling all followers from the network shown in Figure 6. (E) Ratio of random triggers for each one of the quadrants in Figure 6H. Bottom right: +g o; top left: −g+o; top right: exc; bottom left: inh.
Figure 7
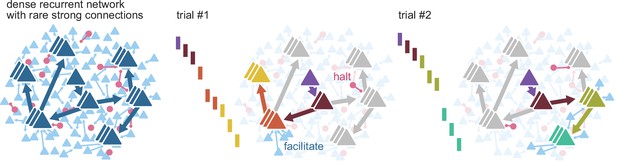
Routing using sparse strong connectivity.
As activity propagates in cortex, a spike will preferentially propagate through strong connections. The strength of those connections ensures reliable propagation, while their sparsity enables flexibility, creating sub-networks with gates where propagation can be halted or facilitated. The halting of activity can appear as partial failures of the expected sequence of spikes over a different history of neuron activations. The spiking state of other neurons in the recurrent network, together with external inputs, form a context that determines the final path for each spike.
Author response image 1
Sequence evolution at super-high firing rates.
(A) Input-output curve of the network, including new simulations at higher firing rates. Original simulations explored the area in purple (same as Figure 2 —figure supplement 1). New simulations as colored dots. Input standard deviation for new simulations: 110 pA. (B) Spike raster of a simulation with 2.28 spk/s mean rate (red dot in A). All spikes for all neurons in the network for 1 second in the middle of the simulation. Arrowheads indicate the initiation of a trial. Purple circles highlight injected spikes. Blue: exc.; pink: inh. (C) Distribution of single-cell mean firing rate for an example simulation with mean network rate of 2.28 spk/s (red dot in A, mean exc. rate of 0.36 spk/s). Only excitatory neurons are shown. Dashed line indicates a Poisson fit. (D) Evolution of sequences as firing rates increase above turtle in vivo estimates. Each row corresponds to one of the three original simulations in Figure 2 —figure supplement 1 (s1, s2, s3). Left column: example trials from original simulations. Other columns: example trials of each simulation re-run at an increased mean firing rate (indicated at the top; colored dots as in A). Only spikes from excitatory followers are shown. Purple: trigger spike. Within each row, we show spikes from the same neurons with the same sorting. (E) Distribution of single-cell firing rate modulation (∆FR) for an example simulation with 2.28 spk/s mean rate (red dot in A). Yellow: ∆FR for excitatory followers as detected in original simulations. Blue: other excitatory neurons in the network.
Author response image 2
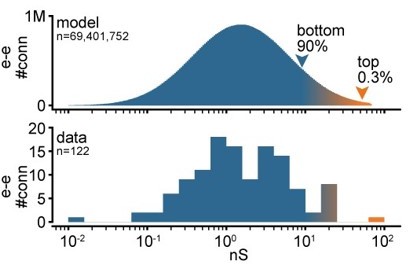
Log-scale distribution of connection strengths.
Top: histogram of conductances for all excitatory-to-excitatory connections in an example model network. Bottom: histogram of synaptic conductances estimated from EPSP amplitudes experimentally obtained from recorded pairs of connected neurons.
Author response image 3
Sequences without inhibitory neuron adaptation.
(A) Number of followers in a network with non-adaptive inhibitory neurons detected for each simulation as a function of the mean level of activity in the network. Blue: exc; red: inh; thick line: moving average; Gray dots: sequences in B. (B) Top to bottom: sequences of follower spikes in two trials for three example simulations (gray dots in A). Y-axis: Followers sorted by median spike-time. Same sorting in both trials. Spikes from non-follower spikes are not shown.
Tables
Table 1
Neuron and synapse model parameters.
Asterisk (*) indicates parameters fitted from experimental data (Hemberger et al., 2019). Parameters of excitatory synaptic conductance are for a truncated lognormal distribution.
| Variable | Value |
|---|---|
| Excitatory reversal potential () | 10 mV |
| Inhibitory reversal potential () | −75 mV |
| Synaptic conductance time constant* | 1.103681 ms |
| Excitatory synaptic conductance (mean)* | 3.73 nS |
| Excitatory synaptic conductance (std)* | 6.51 nS |
| Excitatory synaptic conductance (max)* | 67.8 nS |
| Leak reversal potential () | −70.6 mV |
| Spike detection threshold | 0 mV |
| Membrane reset potential | −60 mV |
| Spike initiation threshold () | −50.4 mV |
| Membrane capacitance* () | 239.8 pF |
| Leak conductance* () | 4.2 nS |
| Subthreshold adaptation () | 4 nS |
| Spike-triggered adaptation () | 80.5 pA |
| Adaptation time constant () | 144 ms |
| Slope factor () | 2 mV |
| Refractory period | 2 ms |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Single spikes drive sequential propagation and routing of activity in a cortical network
eLife 12:e79928.
https://doi.org/10.7554/eLife.79928
