Sparse dimensionality reduction approaches in Mendelian randomisation with highly correlated exposures
Figures
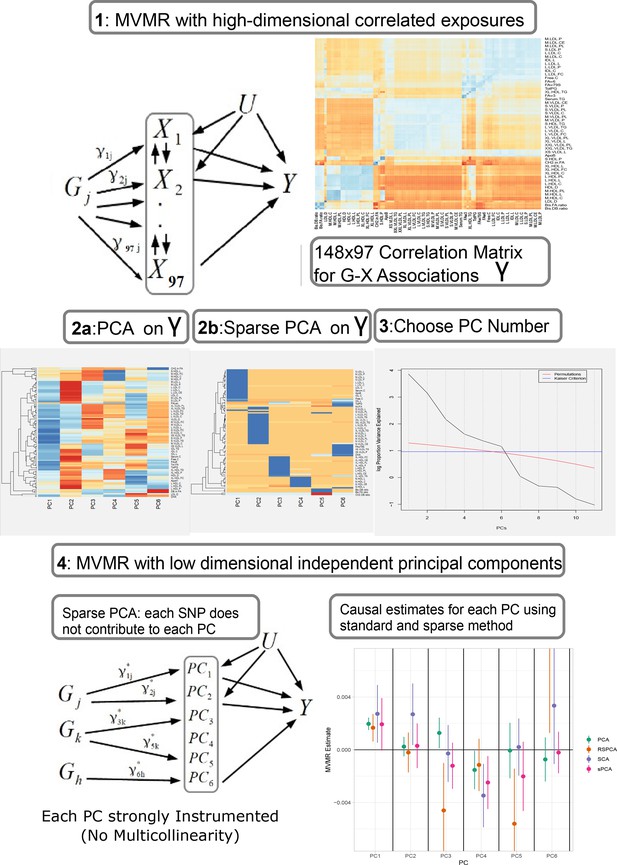
Proposed workflow.
Step 1: MVMR on a set of highly correlated exposures. Each genetic variant contributes to each exposure. The high correlation is visualised in the similarity of the single-nucleotide polymorphism (SNP)-exposure associations in the correlation heatmap (top right). Steps 2 and 3: PCA and sparse PCA on . Step 4. MVMR analysis on a low dimensional set of principal components (PCs). X: exposures; Y: outcome; k: number of exposures; PCA: principal component analysis; MVMR: multivariable Mendelian randomisation.

Heatmaps for the loadings matrices in the Kettunen dataset for all methods (one with no sparsity constraints [a], four with sparsity constraints under different assumptions [b–e]).
The number of the exposures plotted on the vertical axis is smaller than as the exposures that do not contribute to any of the sparse principal components (PCs) have been left out. Blue: positive loading; red: negative loading; yellow: zero.
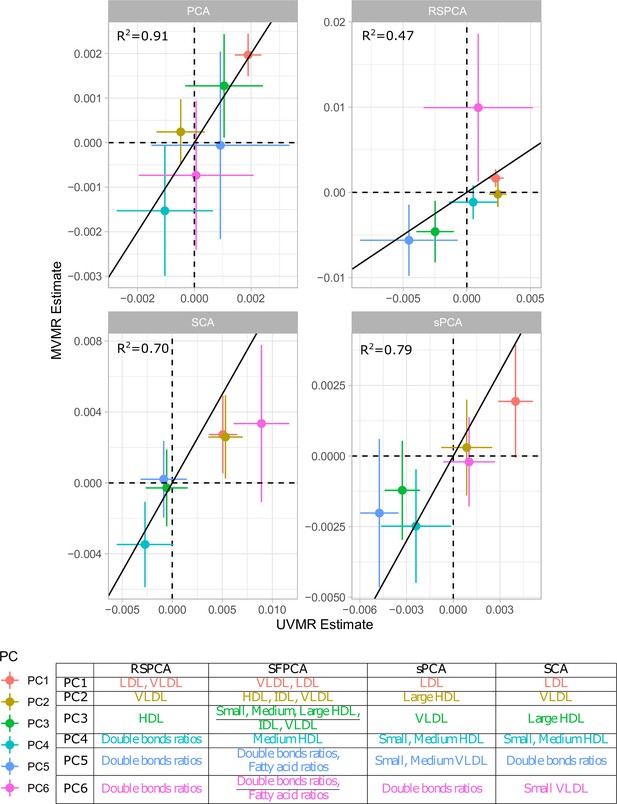
Comparison of univariable Mendelian randomisation (UVMR) and multivariable MR (MVMR) estimates and presentation of the major group represented in each principal component (PC) per method.
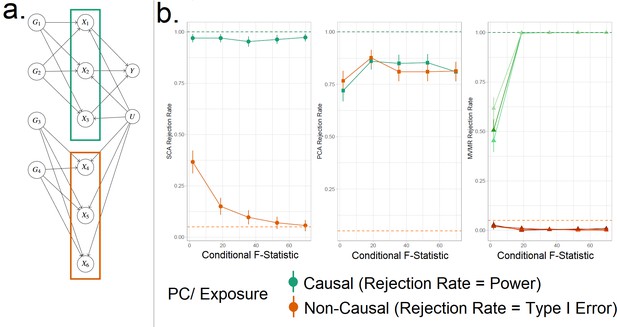
Simulation Study Outline.
(a) Data generating mechanism for the simulation study, illustrative scenario with six exposures and two blocks. In red boxes, the exposures that are correlated due to a shared genetic component are highlighted. (b) Simulation results for six exposures and three methods (sparse component analysis [SCA] [Chen and Rohe, 2021], principal component analysis [PCA], multivariable Mendelian randomisation [MVMR]). The exposures that contribute to () are presented in shades of green colour and those that do not in shades of red (). In the third panel, each exposure is a line. In the first and second panels, the PCs that correspond to these exposures are presented as single lines in green and red. Monte Carlo SEs are visualised as error bars. Rejection rate: proportion of simulations where the null is rejected.
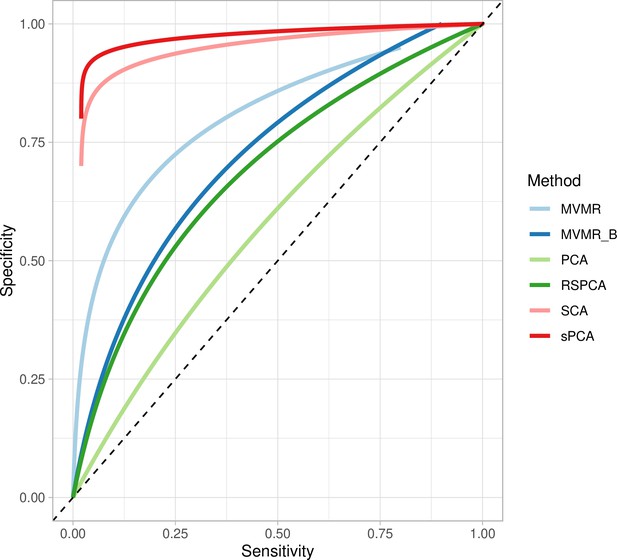
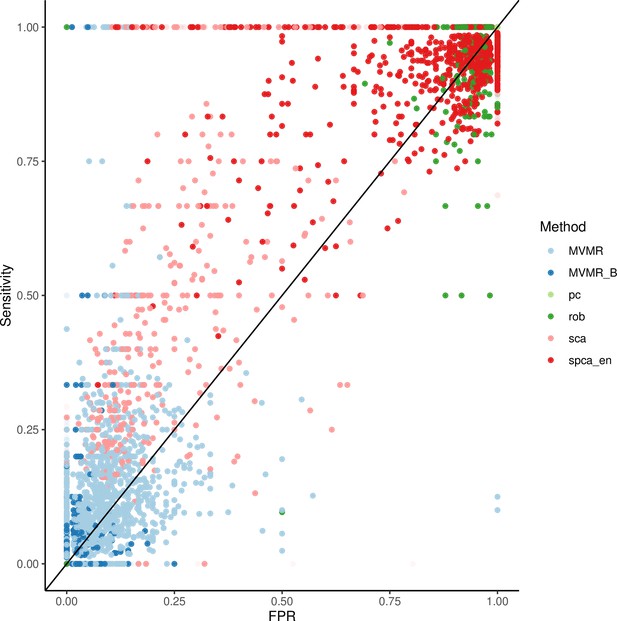
Extrapolated receiver-operating characteristic (ROC) curves for all methods.
SCA: sparse component analysis (Chen and Rohe, 2021) sPCA: sparse PCA (Zou et al., 2006) RSPCA: robust sparse PCA (Croux et al., 2013); PCA: principal component analysis; MVMR: multivariable Mendelian randomisation; MVMR_B: MVMR with Bonferroni correction.
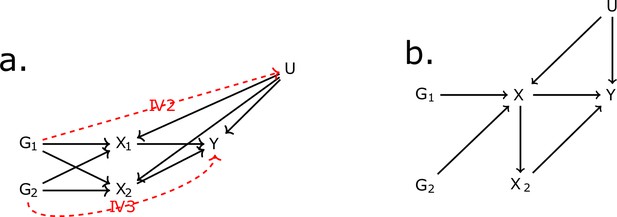
Directed acyclic graph (DAG) for the multivariable Mendelian randomisation (MVMR) assumptions.
IV2, IV3: instrumental variable assumptions 2 and 3.
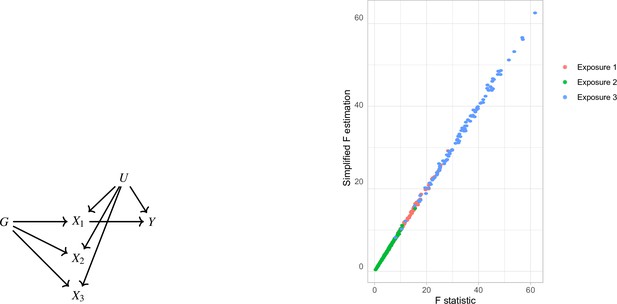
Simplified F-statistic Estimation.
(a) Data generating mechanism. Three exposures with different degrees of strength of association with are generated . (b) -statistic for the three exposures as estimated by the formulae in Equation 5 (horizontal axis) and Equation 4 (vertical axis).
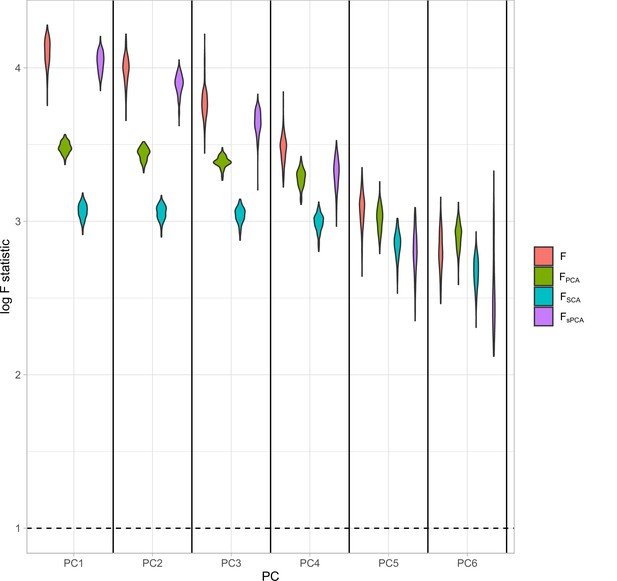
Distributions of the F-statistics in principal component analysis (PCA) methods and individual (not transformed) exposures.
Exposure data in different blocks are simulated with a decreasing strength of association and the correlated blocks map to principal components (PCs). Each distribution represents the F-statistics for each PC. In the case of the individual exposures (red), the distributions represent the F-statistics for the corresponding exposures. Individual: individual exposures without any transformation; PCA: F-statistics for PCA; SCA: sparse component analysis (Chen and Rohe, 2021) sPCA: sparse PCA as described by Zou et al., 2006.
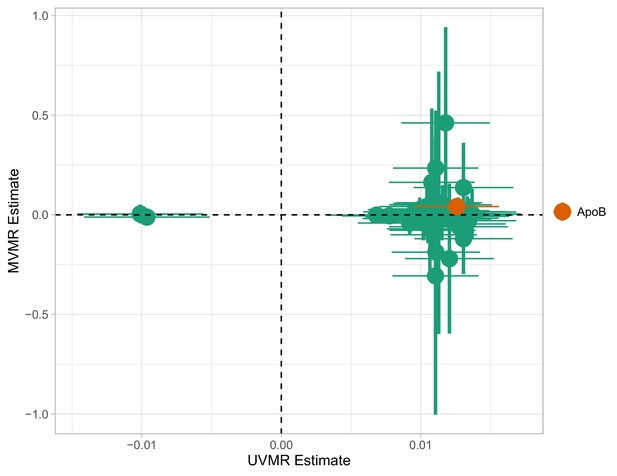
Multivariable Mendelian randomisation (MVMR) and univariable MR (UVMR) estimates.
Only ApoB is strongly associated with coronary heart disease (CHD). All SEs are larger in the MVMR model (range of ).
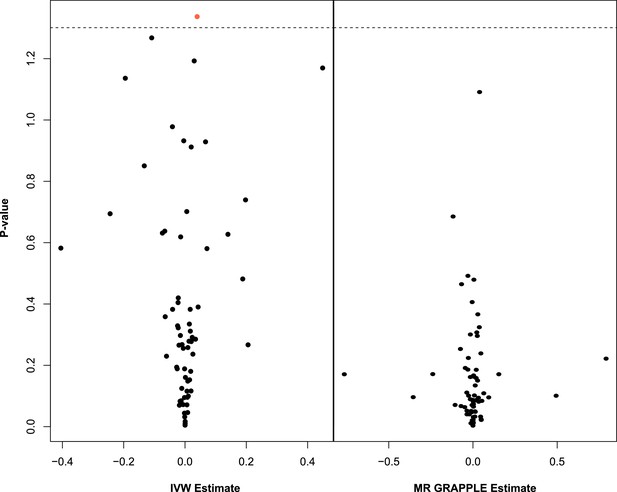
Multivariable Mendelian randomisation (MVMR) with IVW (left) and MVMR with GRAPPLE (Zhao et al., 2021) (right).
Only the 66 exposures. that are significant in univariable MR (UVMR) are put forward in these models. In IVW (left), ApoB shows nominal significance. In MR GRAPPLE (right), apolipoprotein B has the lowest p-value but no trait reaches nominal significance.
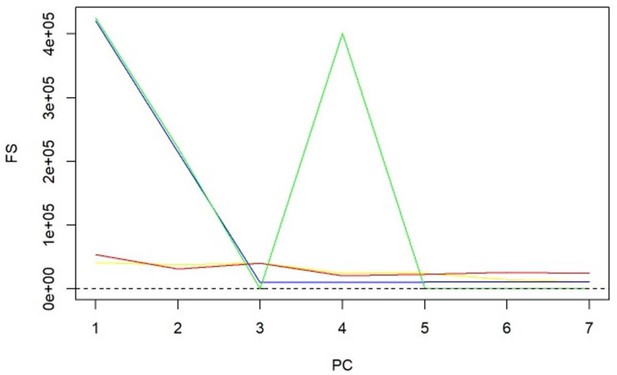
-statistics for principal components (PCs) and sparse PCs.
The formula derived in Equation 5 is used. Black: principal component analysis (PCA) (no sparsity constraints); yellow: sparse component analysis (SCA); red: sparse PCA (Zou); blue: sparse robust PCA; green: sparse fused PCA. The dashed line represents the cutoff of 10 that is considered the minimum desired -statistic for an exposure to be considered well instrumented. The green line diverges from the pattern of decreasing instrument strength but, when referring to the loadings heatmap (Figure 2), it can be observed that the 4th sparse PC in the fused sPCA receives negative loadings from multiple very low-density lipoprotein (VLDL)- and low-density lipoprotein (LDL)-related traits. This may in turn cause the large -statistic.
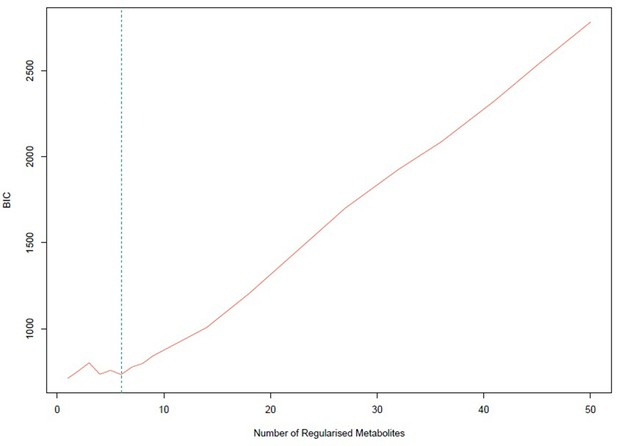
Bayesian information criterion (BIC) for different numbers of metabolites regularized to 0.
The lowest value is achieved for one non-zero exposure per component. However, six non-zero exposures per component also achieved a similar low BIC and this was selected.
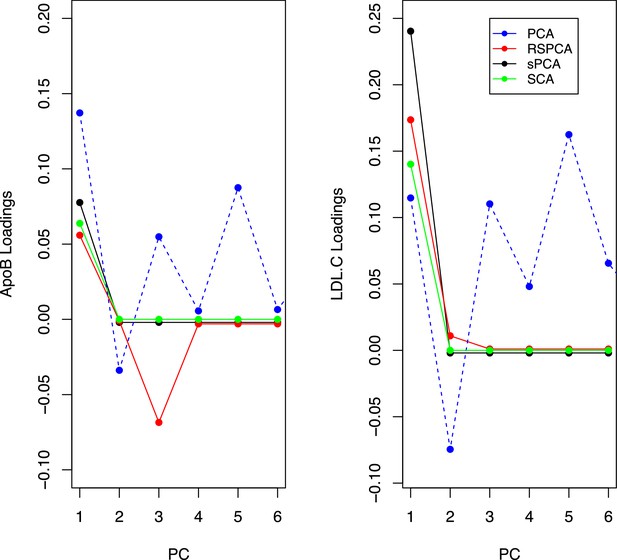
Trajectories for the loadings of total cholesterol in low-density lipoprotein (LDL) and ApoB in all methods.
Principal component analysis (PCA) loadings imply a contribution of LDL.c and ApoB to all principal components (PCs). In the sparse methods, this is limited to one PC (two for RSPCA).
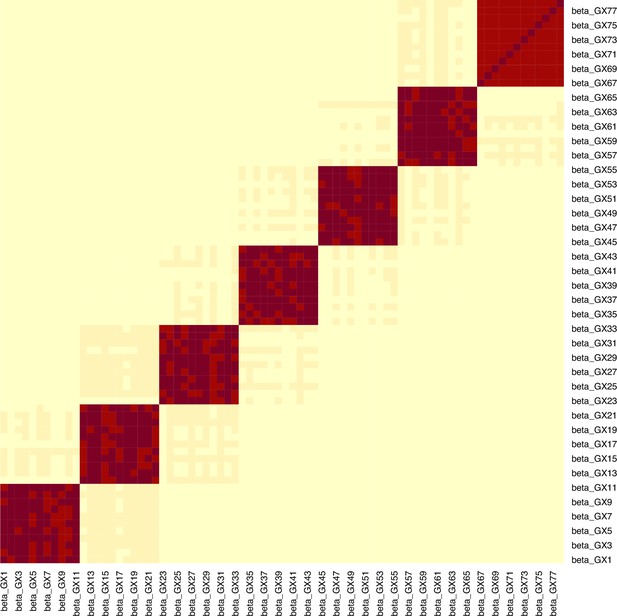
Example for the block correlation in (, ) induced by the data generating mechanism in Figure 4.
In this example, the mean -statistic is 231.2 and the mean is 3.21.
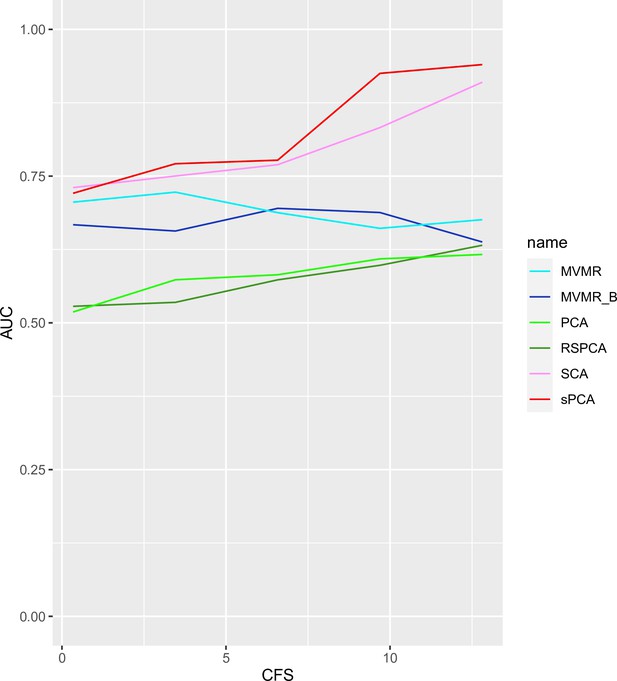
AUC performance of multivariable Mendelian randomisation (MVMR) and dimensionality reduction methods for increasing sample sizes.
Two sparse methods (sparse component analysis [SCA], sparse principal component analysis [sPCA]) perform better compared with PCA and MVMR, with improving performance as the sample size increases. CFS: conditional F-statistic.
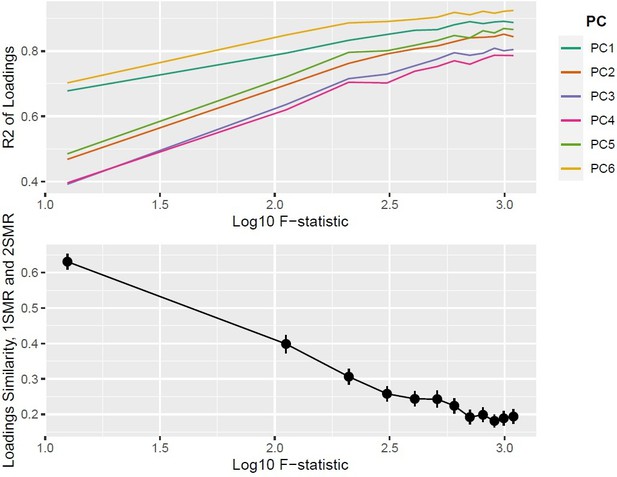
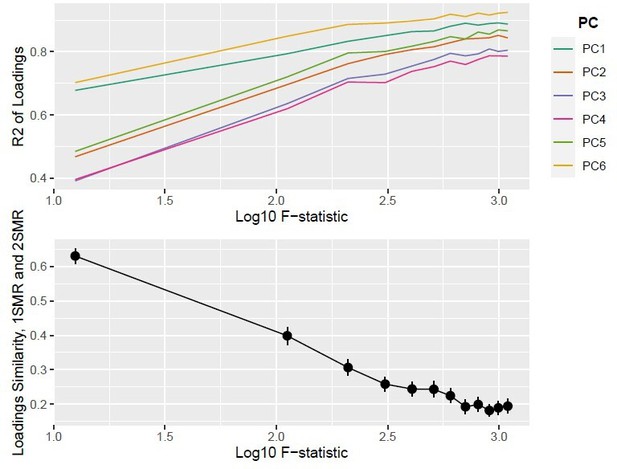
Top panel: ; bottom panel: similarity of loadings () between one-sample Mendelian randomisation (MR) and two-sample MR ().
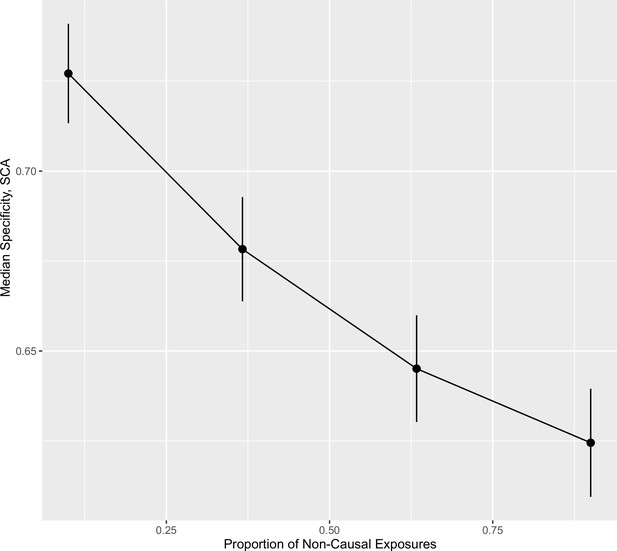
Specificity (ability to accurately identify true negative exposures) of sparse component analysis (SCA) as a different proportion of exposures in each block are causal for .
Tables
Univariable Mendelian randomisation (MR) results for the Kettunen dataset with coronary heart disease (CHD) as the outcome.
Positive: positive causal effect on CHD risk; Negative: negative causal effect on CHD risk.
| Positive | Negative | |
|---|---|---|
| VLDL | AM.VLDL.C, M.VLDL.CE, M.VLDL.FC, M.VLDL.L,M.VLDL.P, M.VLDL.PL, M.VLDL.TG, XL.VLDL.L,XL.VLDL.PL, XL.VLDL.TG, XS.VLDL.L, XS.VLDL.P, XS.VLDL.PL,XS.VLDL.TG, XXL.VLDL.L, XXL.VLDL.PL,L.VLDL.C, L.VLDL.CE, L.VLDL.FC, L.VLDL.L, L.VLDL.P,L.VLDL.PL, L.VLDL.TG, SVLDL.C, S.VLDL.FC,S.VLDL.L, S.VLDL.P, S.VLDL.PL, S.VLDL.TG | None |
| LDL | ALDL.C, L.LDL.C, L.LDL.CE, L.LDL.FC, L.LDL.L, L.LDL.P, L.LDL.PL,M.LDL.C, M.LDL.CE, M.LDL.L, M.LDL.P,M.LDL.PL, S.LDL.C, S.LDL.L, S.LDL.P | None |
| HDL | S.HDL.TG, XL.HDL.TG | M.HDL.C, M.HDL.CE |
Overview of sparse principal component analysis (sPCA) methods used.
KSS: Karlis-Saporta-Spinaki criterion. Package: R package implementation; Features: short description of the method; Choice: method of selection of the number of informative components in real data; PCs: number of informative PCs.
| Method | Package | Authors | Features | Choice | PCs |
|---|---|---|---|---|---|
| RSPCA | pcaPP | Croux et al., 2013 | Robust sPCA (RSPCA), different measure of dispersion () | Permutation KSS | 6 |
| SFPCA | Code in publication, Supplementary Material | Guo et al., 2010 | Fused penalties for block correlation | KSS | 6 |
| sPCA | elasticnet | Zou et al., 2006 | Formulation of sPCA as a regression problem | KSS | 6 |
| SCA | SCA | Chen and Rohe, 2021 | Rotation of eigen vectors for approximate sparsity | Permutation KSS | 6 |
Results for principal component analysis (PCA) approaches.
Overlap: Percentage of metabolites receiving non-zero loadings in ≥1 component. Overlap in PC1, PC2: overlap as above but exclusively for the first two components which by definition explain the largest proportion of variance. Very low-density lipoprotein (VLDL), low-density lipoprotein (LDL), and high-density lipoprotein (HDL) significance: results of the IVW regression model with CHD as the outcome for the respective sPCs (the sPCs that mostly received loadings from these groups). The terms VLDL and LDL refer to the respective transformed blocks of correlated exposures; for instance, VLDL refers to the weighted sum of the correlated VLDL-related associations, such as VLDL phospholipid content and VLDL triglyceride content. †: RSPCA projected VLDL- and LDL-related traits to the same PC (sPC1). ‡: SCA discriminated HDL molecules in two sPCs, one for traits of small- and medium-sized molecules and one for large- and extra-large-sized.
| PCA | RSPCA | SFPCA | sPCA | SCA | |
|---|---|---|---|---|---|
| Overlap | 1 | 0.938 | 1 | 0.187 | 0.196 |
| Overlap in PC1,PC2 | 1 | 0.433 | 1 | 0.010 | 0 |
| Sparse % | 0 | 0.474 | 0.082 | 0.835 | 0.796 |
| VLDL significance in MR† | Yes | No | Yes | No | Yes |
| LDL significance in MR | No | Yes | No | No | Yes |
| HDL significance in MR‡ | Yes | Yes | Yes | No | No |
| Small, medium HDL significance in MR | Yes | No | Yes | Yes | Yes |
Sensitivity and specificity presented as median and interquartile range across all simulations.
Presented as median sensitivity/specificity and interquartile range across all simulations; AUC: area under the receiver-operating characteristic (ROC) curve.
| PCA | SCA | sPCA | RSPCA | MVMR_B | MVMR | |
|---|---|---|---|---|---|---|
| AUC | 0.56 | 0.919 | 0.941 | 0.644 | 0.660 | 0.712 |
| Sensitivity | 1,0.1 | 1,0.21 | 1, 0.047 | 0.667, 0.251 | 0.222, 0.2 | 0, 0.076 |
| Specificity | 0,0.02 | 0.925,0.772 | 0.936, 0.097 | 0.192, 0.104 | 0.960, 0.048 | 1,0 |
| Youden’s J | 0 | 0.584 | 0.778 | –0.061 | 0.192 | 0.044 |
Two-sample Mendelian randomisation (MR).
Study characteristics.
| First author | Year | PMID | N | Cases | Controls | Study name (population) | |
|---|---|---|---|---|---|---|---|
| Metabolites | Kettunen | 2016 | 27005778 | 24,925 | NMR GWAS (European) | ||
| CHD | Nelson | 2017 | 28714975 | 453,595 | 113,937 | 339,658 | CARDIoGRAMplusC4D (European) |
Estimated causal effects of principal components (PCs) on coronary heart disease (CHD) risk.
PCA: principal component analysis; SCA: sparse component analysis; sPCA: sparse PCA (Zou et al., 2006); RSPCA: robust sparse PCA.
| PC | Method | OR | LCI | UCI |
|---|---|---|---|---|
| PC1 | PCA | 1.002 | 1.0015 | 1.0024 |
| PC2 | PCA | 1.0002 | 0.9995 | 1.001 |
| PC3 | PCA | 1.0013 | 1.0001 | 1.0024 |
| PC4 | PCA | 0.9985 | 0.997 | 0.9999 |
| PC5 | PCA | 0.9999 | 0.9978 | 1.002 |
| PC6 | PCA | 0.9993 | 0.9976 | 1.0009 |
| PC1 | SCA | 1.0027 | 1.0005 | 1.0049 |
| PC2 | SCA | 1.0027 | 1.0004 | 1.005 |
| PC3 | SCA | 0.9997 | 0.9976 | 1.0019 |
| PC4 | SCA | 0.9965 | 0.9941 | 0.9989 |
| PC5 | SCA | 1.0002 | 0.998 | 1.0024 |
| PC6 | SCA | 1.0034 | 0.9989 | 1.0078 |
| PC1 | sPCA | 1.0019 | 0.9999 | 1.0039 |
| PC2 | sPCA | 1.0003 | 0.9986 | 1.002 |
| PC3 | sPCA | 0.9988 | 0.997 | 1.0005 |
| PC4 | sPCA | 0.9975 | 0.9955 | 0.9995 |
| PC5 | sPCA | 0.998 | 0.9954 | 1.0006 |
| PC6 | sPCA | 0.9998 | 0.9982 | 1.0014 |
| PC1 | RSPCA | 1.0017 | 1.0006 | 1.0027 |
| PC2 | RSPCA | 0.9998 | 0.9983 | 1.0013 |
| PC3 | RSPCA | 0.9954 | 0.9918 | 0.999 |
| PC4 | RSPCA | 0.9989 | 0.9969 | 1.0008 |
| PC5 | RSPCA | 0.9944 | 0.9903 | 0.9986 |
| PC6 | RSPCA | 1.01 | 1.0013 | 1.0188 |
| PC1 | SFPCA | 1.002 | 1.0015 | 1.0025 |
| PC2 | SFPCA | 0.9991 | 0.9979 | 1.0004 |
| PC3 | SFPCA | 0.9998 | 0.9991 | 1.0006 |
| PC4 | SFPCA | 0.9982 | 0.9967 | 0.9997 |
| PC5 | SFPCA | 1.0001 | 0.9977 | 1.0025 |
| PC6 | SFPCA | 1.0009 | 0.9985 | 1.0033 |
Simulation study on only four exposures (out of the total ) contributing to the outcome .
A drop in sensitivity and specificity is observed for sparse component analysis (SCA) and sparse principal component analysis (sPCA) compared with the simulation configuration in Table 4.
| PCA | SCA | sPCA | RSPCA | MVMR | MVMR_B | |
|---|---|---|---|---|---|---|
| AUC | 0.799 | 0.714 | 0.859 | 0.492 | 0.511 | 0.675 |
| SNS | 1,0.03 | 0.75,0.25 | 1,0.17 | 0.5,0.25 | 0.25,0.25 | 0,0 |
| SPC | 0,0.2 | 0.76,0.46 | 0.66,0.18 | 0.37,0.15 | 0.94,0.07 | 1,0 |
| Youden’s J | 0 | 0.428 | 0.625 | –0.029 | 0.105 | 0.032 |