Arguments for the biological and predictive relevance of the proportional recovery rule
- Department of Biostatistics, Columbia Mailman School of Public Health, United States
- Burke Neurological Institute, United States
- Weill Cornell Medicine, United States
- Cereneo, Center for Neurology and Rehabilitation, Switzerland
- Vascular Neurology and Neurorehabilitation, Department of Neurology, University Hospital Zurich, University of Zurich, Switzerland
- Department of Medicine, University of Auckland, New Zealand
- Department of Exercise Sciences, University of Auckland, New Zealand
- Rehabilitation Research Centre, Reade, Netherlands
- Rehabilitation Medicine, Amsterdam UMC - Location VUMC, Amsterdam Movement Sciences, Netherlands
- Department of Neurology, Johns Hopkins University, United States
- Department of Neuroscience, Johns Hopkins University, United States
- Department of Physical Medicine and Rehabilitation, United States
- Santa Fe Institute, United States
Figures
Figure 1
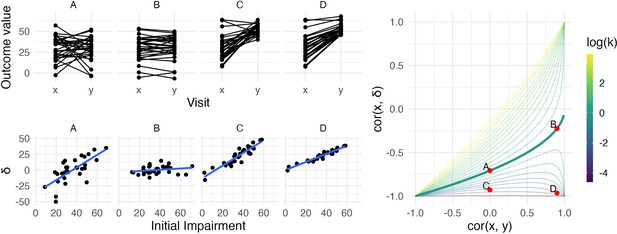
The left panels show four generated datasets, labeled A, B, C, and D.
In the top row, panels show outcome values and baseline (x) and follow-up (y). In the bottom row, panels show change () against initial impairment (66 − x). The right panel shows a contour plot of Equation 1, with contours corresponding to values of the variance ratio k and the contour for k=1 highlighted. Points on this surface show correlation values obtained for Datasets A through D. A figure similar to the contour plot is shown in Hope et al., 2018, with different axes and orientations.
Figure 2
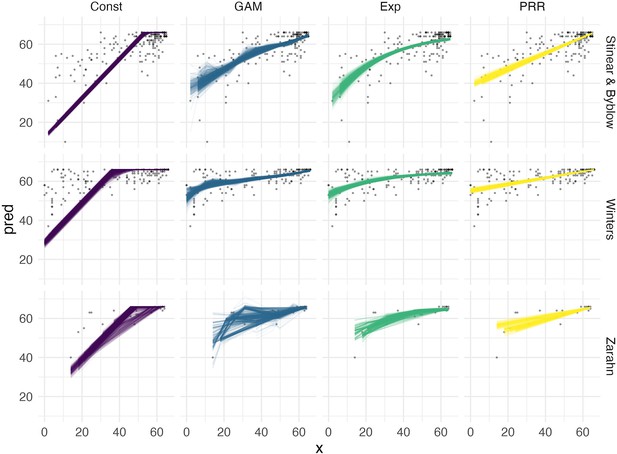
The top panels show three generated datasets with true outcome values and baseline (x) and follow-up (y); a horizontal line indicates a ceiling on observed values.
In the bottom row, panels show the observed (ceiled) value at follow-up against the baseline value. Fitted values from an intercept-only model (Int), a generalized additive model (GAM), and the proportional recovery rule (PRR) are shown in the bottom row.
Figure 3
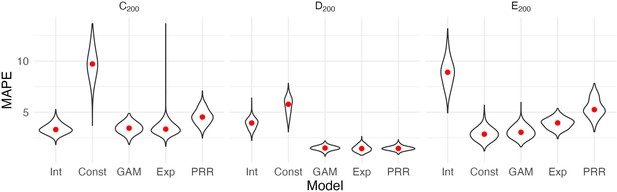
Each panel shows the distribution of median absolute prediction errors (MAPE) obtained using cross validation for each of five models.
Panels correspond to the generated datasets shown in Figure 2. Models compared are an intercept-only model (Int), a generalized additive model (GAM), and the proportional recovery rule (PRR).
Figure 4
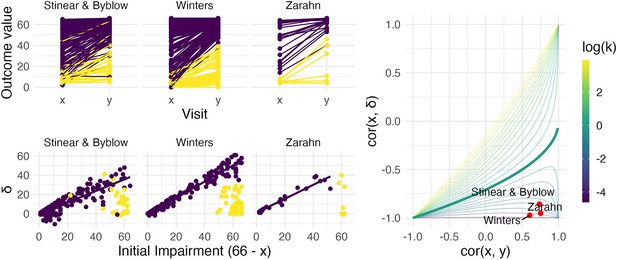
The left panels show three real datasets.
In the top row, panels show outcome values and baseline (x) and follow-up (y); points are colored to indicate recoverers (purple) and non-recoverers (yellow) using the definitions from each paper describing the data. In the bottom row, panels show change (delta) against initial impairment (66 − x), again separating recoverers and non-recoverers. The right panel shows a contour plot of Equation 1, with contours corresponding to values of the variance ratio k and the contour for k=1 highlighted. Points on this surface show correlation values obtained for the real datasets.
Figure 5
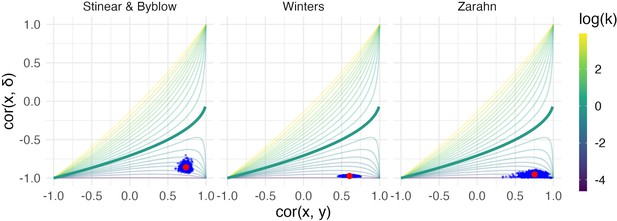
Each panel shows the results of the bootstrap procedure used to obtain inferences about the value of correlations and variance ratio.
Red points are the values obtained for the full dataset, and blue points are values obtained in each of 1000 bootstrap samples; points are overlaid on the contour plot of Equation 1.
Figure 6
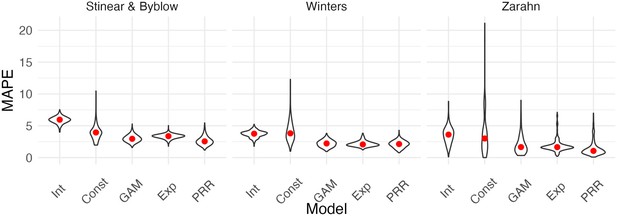
Each panel shows the distribution of median absolute prediction errors (MAPEs) obtained using cross validation for each of five models.
Panels correspond to the datasets shown in Figure 4. Models compared are an intercept-only model, a generalized additive model, and the proportional recovery rule (PRR).
Figure 7
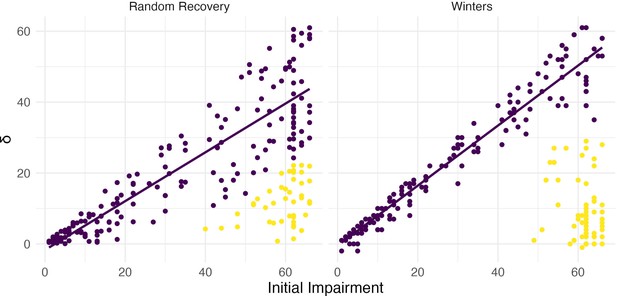
Both panels show change between baseline and follow-up against initial impairment (66 – baseline).
Left panel shows data generated under a ‘random recovery’ process, in which outcome values are drawn from a uniform distribution over the baseline value and ceiling. Right panel presents again data from Winters et al., 2015.
Appendix 1—figure 1
Fitted values for each of four models, obtained within separate training / testing splits as part of the cross validation procedure.
Tables
Table 1
Values and 95% confidence intervals for and for each of three datasets.
Confidence intervals are obtained through a bootstrap procedure with 1000 bootstrap samples.
| Dataset name | ||
|---|---|---|
| Stinear and Byblow | 0.39 [0.27, 0.54] | 0.73 [0.66, 0.79] |
| Winters | 0.07 [0.05, 0.09] | 0.59 [0.49, 0.69] |
| Zarahn | 0.13 [0.03, 0.24] | 0.75 [0.55, 0.92] |
Table 2
The proportion of follow-up () variation explained by the proportional recovery rule (PRR) for each of three datasets.
Follow-up fitted values are obtained by adding predicted change from the PRR to observed baseline values, and we compute .
| Dataset name | Percent of outcome variation explained |
|---|---|
| Stinear and Byblow | 0.55 |
| Winters | 0.35 |
| Zarahn | 0.56 |
Additional files
-
MDAR checklist
- https://cdn.elifesciences.org/articles/80458/elife-80458-mdarchecklist1-v2.pdf
-
Source data 1
The zip file contains two data sets ("Winters"and "Zarahn"), as well as code that can be used to reproduce all analyses of these datasets.
- https://cdn.elifesciences.org/articles/80458/elife-80458-data1-v2.zip
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Arguments for the biological and predictive relevance of the proportional recovery rule
eLife 11:e80458.
https://doi.org/10.7554/eLife.80458
