Selection and the direction of phenotypic evolution
- Institut de Biologie de l’École Normale Supérieure, CNRS UMR 8197, Inserm U1024, PSL Research University, France
Figures
Figure 1 with 1 supplement
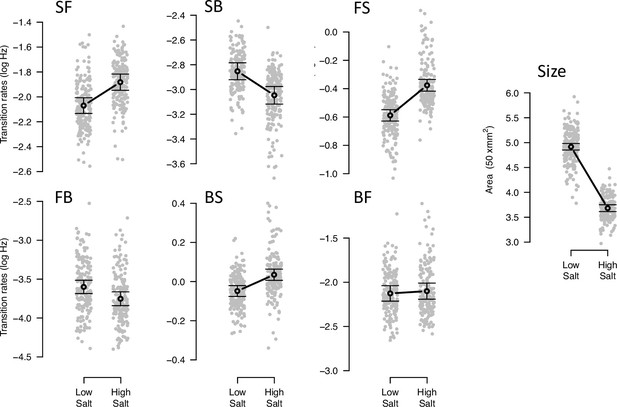
Phenotypic plasticity of the ancestral population.
Gray dots indicate the trait values (BLUPs) estimated for each inbred line in the low and high salt environments: F for ‘forward,’ B for ‘backward’, and S for ‘still,’ left to right order indicating movement direction. Gray circles and bars indicate the mean 95% confidence intervals least-square estimates using the univariate approach (see Methods). Significant differences between environments are indicated with a line, when using the multivariate approach (Table 2). Figure source code is linked here - Multivariate analysis of variance (MANOVA) and figures/tables export scripts.
-
Figure 1—source data 1
Raw data for analysis including all design and environmental covariates.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig1-data1-v2.txt
-
Figure 1—source data 2
Sample sizes, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig1-data2-v2.pdf
-
Figure 1—source data 3
Multivariate analysis of variance (MANOVA) results, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig1-data3-v2.pdf
-
Figure 1—source data 4
Multivariate analysis of variance (MANOVA) results for the ancestral population by each trait, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig1-data4-v2.pdf
-
Figure 1—source data 5
Eigendecomposition of the MANOVA SSCP matrix for the environment factor, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig1-data5-v2.pdf
Figure 1—figure supplement 1
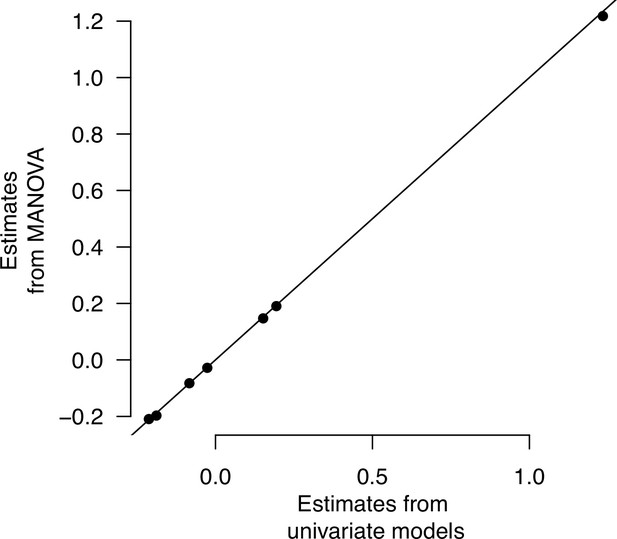
Multivariate and univariate models’ environmental effects.
The least-square mean estimates of high salt environmental effects for each of the seven traits in the ancestral population are shown.
-
Figure 1—figure supplement 1—source code 1
See Figure script.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig1-figsupp1-code1-v2.zip
-
Figure 1—figure supplement 1—source data 1
Univariate models’ contrasts. See table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig1-figsupp1-data1-v2.pdf
Figure 2 with 3 supplements
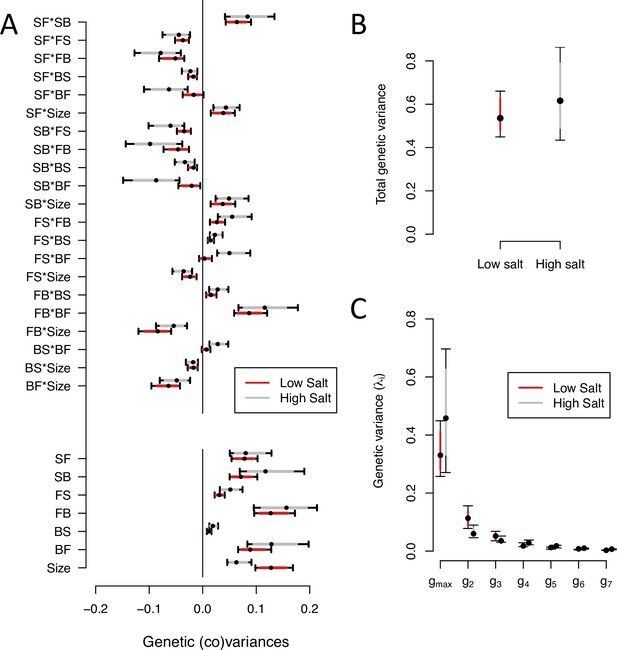
-matrix of the ancestral population in low salt and high salt environments.
(A). The bottom seven estimates indicate the genetic variances in transition rates and body size, top 15 estimates are the genetic covariances between the seven traits. (B). Total genetic variance in each environment is the trace of the -matrices (C). Eigenvalues of the six eigenvectors for each -matrix. For all panels, red (gray) indicates estimates in low (high) salt, with dots, and colored intervals the mode and the 83% or 95% credible intervals of the posterior distribution.
-
Figure 2—source code 1
See G-matrix computation, Figure 2 and table export scripts.
Figure 2 script also produces Figure 2—figure supplements 2 and 3.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig2-code1-v2.zip
-
Figure 2—source data 1
Ancestral -matrix in low and high salt environments, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig2-data1-v2.pdf
-
Figure 2—source data 2
Eigendecomposition of the ancestral -matrices, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig2-data2-v2.pdf
Figure 2—figure supplement 1
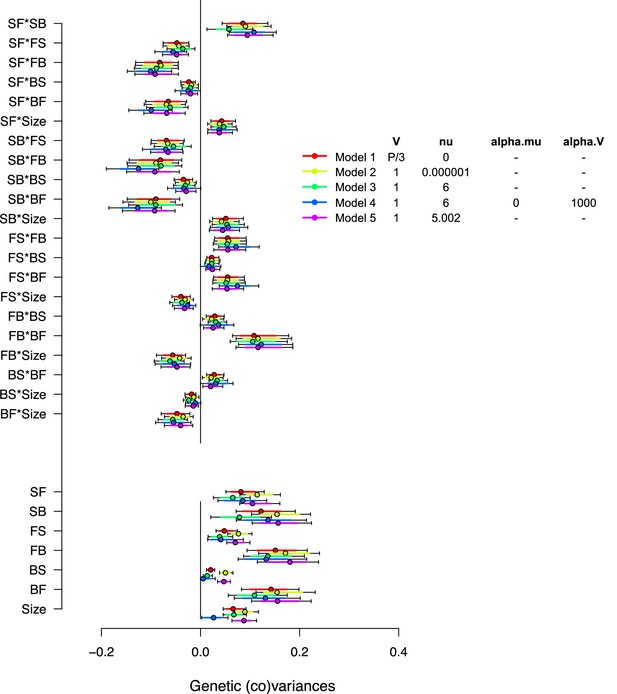
Varying priors for -matrix estimation in the ancestral population.
Varying prior distributions for -matrix estimation. Inset shows the parameters used to specify the priors for all matrices estimated with the model (i.e. both random effect matrices and the residual). is the expected value and the ‘degree of belief’ for the Inverse-Wishart distribution. Model 1 uses a flat improper prior, retained for all analysis. Models 2, 3, and 5 use inverse-Wishart distributions as priors with different degrees of belief. Model 4 uses parameter-expanded algorithms with and being the prior means and covariances, respectively. Dots show the modes with 83% and 95% of the posterior high salt -matrix distribution.
-
Figure 2—figure supplement 1—source code 1
See Figure script.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig2-figsupp1-code1-v2.zip
Figure 2—figure supplement 2
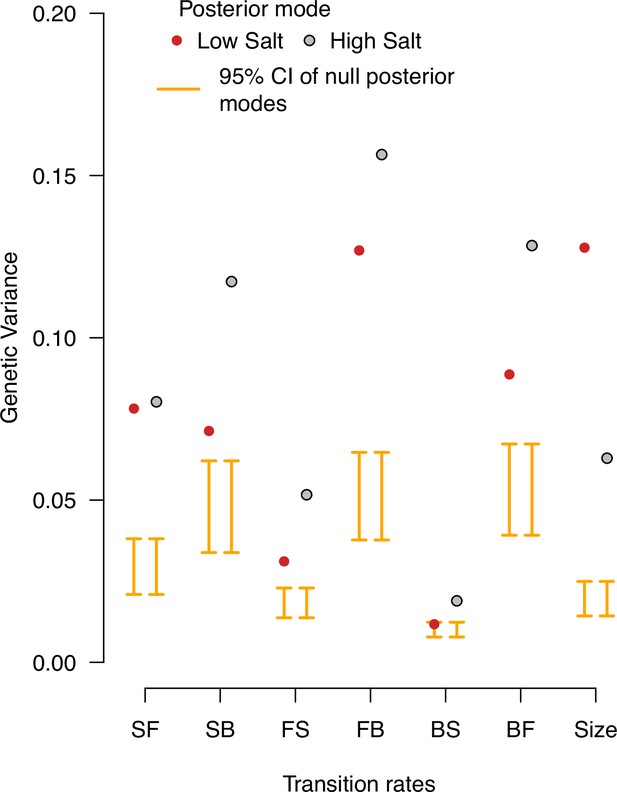
Null distributions of genetic variances in the ancestral population.
Genetic variance estimates in the ancestral population’s low salt and high salt environments. The posterior modes are compared with 95% CI of the posterior modes distribution of 1,000 randomized -matrices by inbred line and block identities (orange bars). Red (gray) indicates the posterior mode estimates in low (high) salt from Figure 2.
Figure 2—figure supplement 3
Eigendecomposition of null distributions of the ancestral -matrix.
-matrix eigenvalues in low salt (red) and high salt (gray) environments for the ancestral population. The posterior modes are compared with the 95% CI of randomized -matrices using two methods. Orange bars show the 95% CI of the distribution of posterior modes of 1000 randomized -matrices. Green bars show the 95% CI posterior distribution of the genetic variance in the observed eigenvectors (Figure 2A).
Figure 3
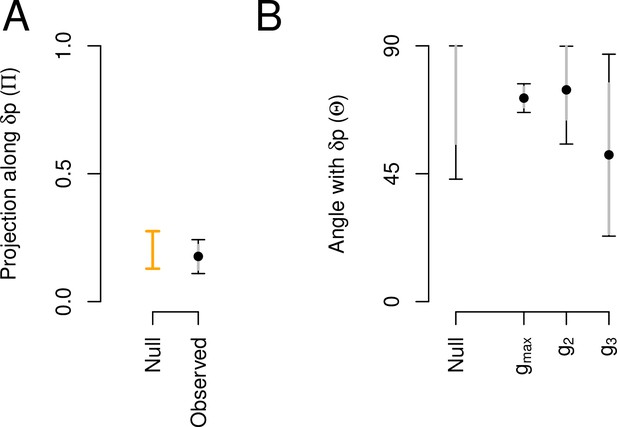
Aligment between phenotypic plasticity and standing genetic variation in high salt for the ancestral population.
(A) Projection of the high salt -matrix along the phenotypic plasticity canonical trait . Dots show the mean estimate with bars the 83% and 95% credible interval of the posterior -matrix distribution. Orange bar shows the null 95% CI of the posterior distribution of modes of 1000 -matrix randomized by inbred line and block identities (see Methods). (B). The angle (, Equation 3) between and the first three eigenvectors of the ancestral -matrix (, g2, and g3). does not differ from the random expectations. Dots show the mean estimate with bars the 83% and 95% credible interval of the posterior -matrix distribution. The null expectation was obtained by computing the angle between pairs of random vectors sampled from a uniform distribution (see Methods).
-
Figure 3—source code 1
See Figure 3 script.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig3-code1-v2.zip
-
Figure 3—source data 1
Projections and angles (including CI) are shown in Figure 3 as a table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig3-data1-v2.pdf
Figure 4 with 2 supplements
Selection differentials in the ancestral population.
Ancestral genetic covariances between transition rates and body size measured in high salt (gray) or low salt (red) with high salt self-fertility. Dots and colored intervals show the mode and the 83% or 95% credible intervals of the posterior distribution.
-
Figure 4—source code 1
See Gqw computation and Figure 4 scripts.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig4-code1-v2.zip
-
Figure 4—source data 1
Selection differentials’ estimates, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig4-data1-v2.pdf
Figure 4—figure supplement 1
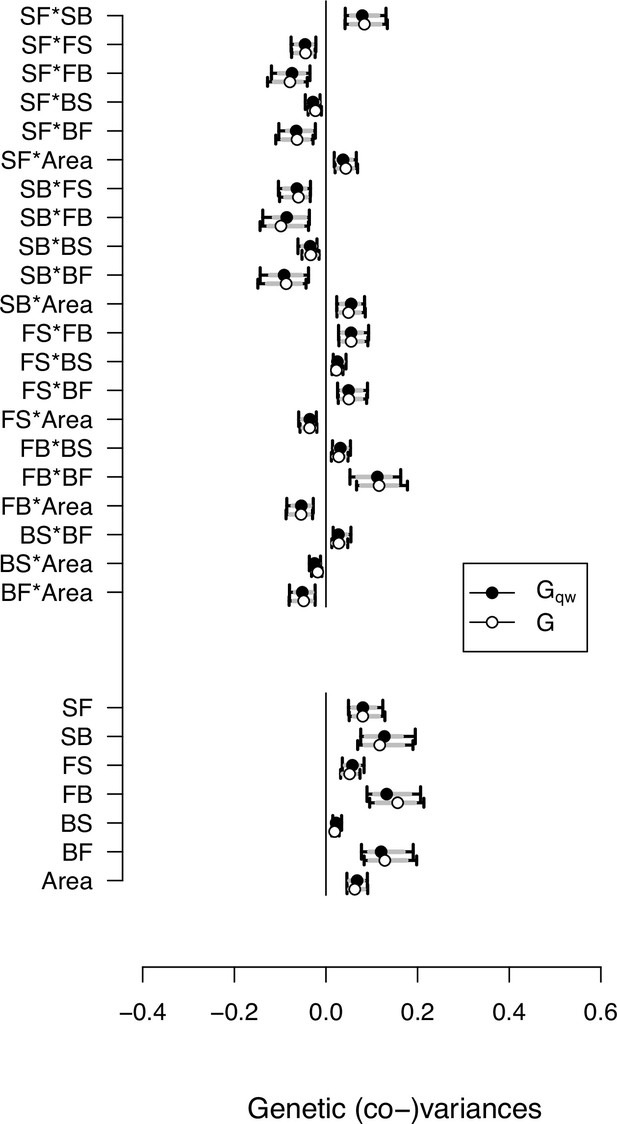
Genetic (co)variances estimate from the - and -matrices.
Selection differentials were estimated as the last column of the -matrix. This plot shows that the genetic (co)variance estimates of locomotion traits and body size are robust to adding an 8th trait (self-fertility) to the -matrix. Circles show the mode and 83% and 95% CI of the posterior distributions.
-
Figure 4—figure supplement 1—source code 1
See Figure script.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig4-figsupp1-code1-v2.zip
Figure 4—figure supplement 2
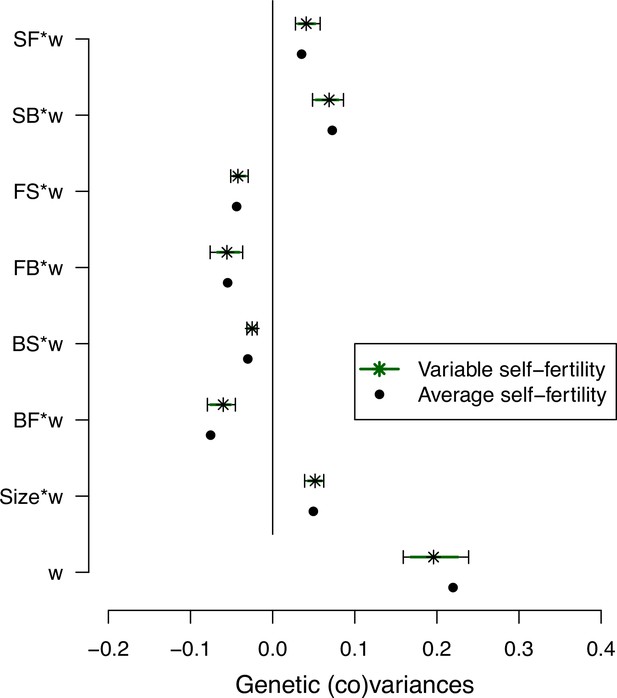
Self-fertility variation effects on selection differentials’ estimates.
Effect of self-fertility variation in selection differentials estimates for the ancestral population (high salt environment only). We generated 500 matrices while generating variable self-fertility measurements for each set of measured transition rates based on the standard deviation of the means estimates for each line fecundity (stars; see Methods). Dots show the mean posterior estimates (Figure 4).
-
Figure 4—figure supplement 2—source code 1
See Figure script.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig4-figsupp2-code1-v2.zip
Figure 5
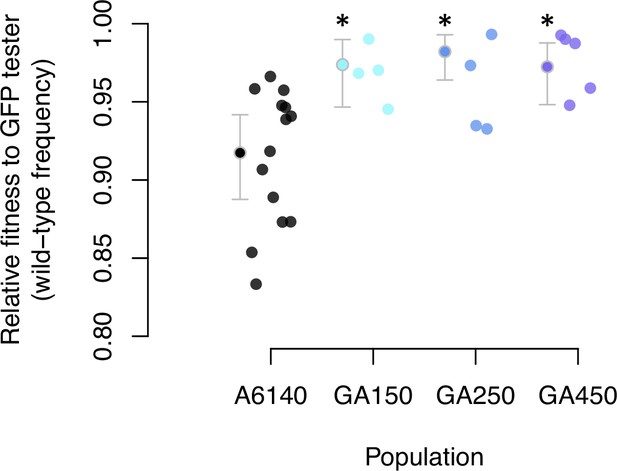
Adaptation to the high salt environment.
Colored dots show the ratio of wild-type to green-fluorescent protein (GFP) alleles after one generation of pairwise competitions between the outbred experimental populations with a GFP-tester strain. Filled circles indicate the least-square mean estimates with 95% confidence intervals; asterisks indicate significant differences between each replicate population relative to the ancestral population.
-
Figure 5—source code 1
See data analysis and figure script.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig5-code1-v2.zip
-
Figure 5—source data 1
Data for analysis, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig5-data1-v2.txt
-
Figure 5—source data 2
Population contrasts, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig5-data2-v2.txt
Figure 6 with 2 supplements
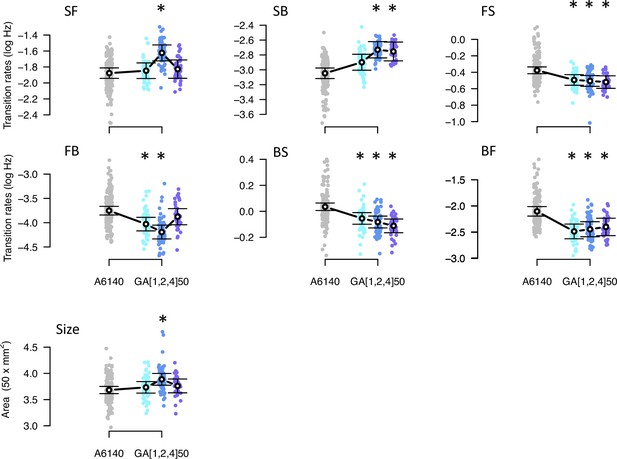
Phenotypic divergence in the high salt environment.
Each panel shows the transition rates and body size as in Figure 1. Dots indicate the values estimated for each inbred line in a high salt environment, gray for the ancestral population, blues for the evolved replicate populations. Circles and bars indicate the mean and the 95% confidence intervals least-square estimates. Line shows significant differentiation between all four populations using the multivariate MANOVA approach (Table 2). Significant differences between each of the evolved populations and the ancestral population using the univariate approach are shown with asterisks (Figure 6—source data 2).
-
Figure 6—source code 1
Multivariate analysis of variance (MANOVA) and figures/tables export scripts (as for Figure 1, also produces Figure 6—figure supplement 2).
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig6-code1-v2.zip
-
Figure 6—source data 1
Multivariate analysis of variance results, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig6-data1-v2.pdf
-
Figure 6—source data 2
Contrasts between evolved and ancestral populations in high salt, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig6-data2-v2.pdf
-
Figure 6—source data 3
Eigendecomposition of the MANOVA SSCP matrix of the phenotypic divergence, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig6-data3-v2.pdf
Figure 6—figure supplement 1
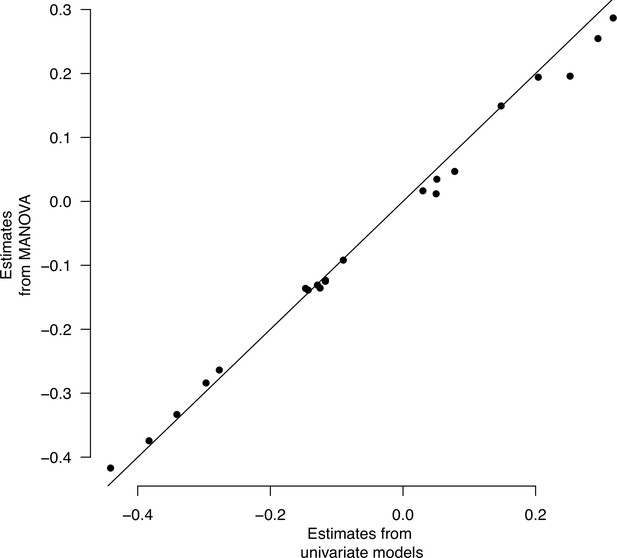
Multivariate and univariate models’ population estimates.
Multivariate and univariate models’ population effects. Least-square mean estimates for each of the seven traits are plotted.
-
Figure 6—figure supplement 1—source code 1
See Figure script.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig6-figsupp1-code1-v2.zip
Figure 6—figure supplement 2
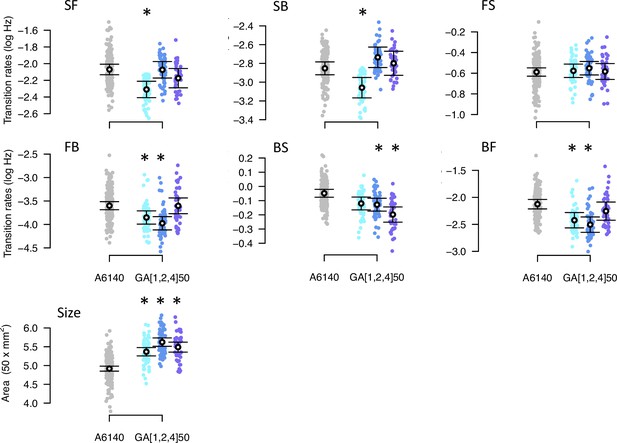
Phenotypic divergence in the low salt environment.
Each panel shows the transition rates and body size. Dots indicate the values estimated for each inbred line, gray for the ancestral population, blues for the evolved GA populations. Circles and bars indicate the mean and the 95% confidence intervals least-square estimates. Significant differences between each evolved population relative to the ancestral population are shown with an asterisk, using the univariate modeling approach.
-
Figure 6—figure supplement 2—source data 1
Contrasts between evolved and ancestral populations in low salt, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig6-figsupp2-data1-v2.pdf
Figure 7 with 3 supplements
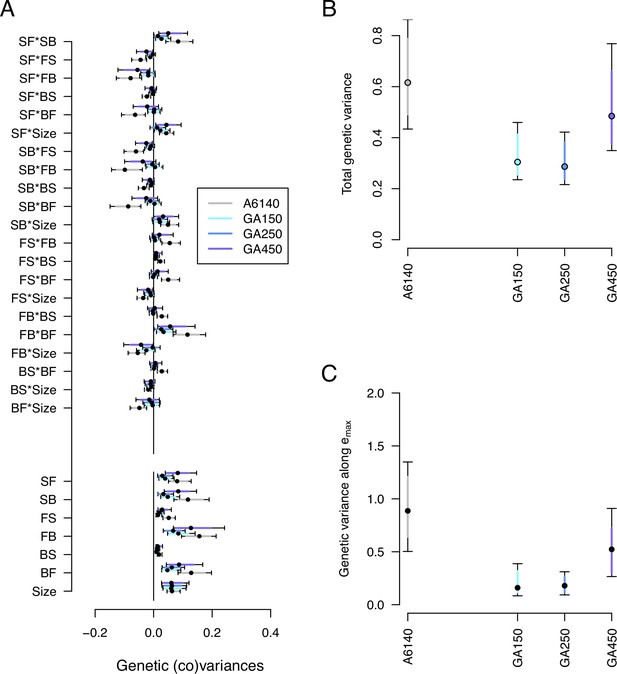
Genetic divergence in the high salt environment.
(A) High salt -matrix evolution of ancestral (gray) and evolved GA populations (blues). Eigendecomposition of the ancestral -matrix (gray) can be found in Figure 2, those of the evolved GA populations in Figure 7—figure supplement 2. (B) Total -matrix variance for each experimental population. (C) Genetic variance along , the main canonical trait of genetic differentiation obtained after the random skewers analysis (see Methods, Table 1). Dots and colored bars show the mode and the 83% or 95% credible intervals of the posterior distribution. Figure 7 sources linked here - matrix computation, random skewers analysis, and Figure 7 scripts. The Figure 7 scripts also produces all three figure supplements.
-
Figure 7—source data 1
-matrices of evolved populations in the high salt environment, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig7-data1-v2.pdf
Figure 7—figure supplement 1
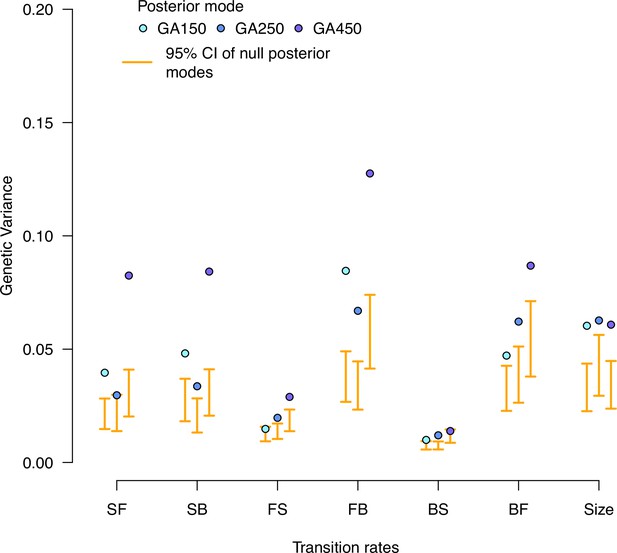
Null distributions of high salt genetic variances in the evolved populations.
Genetic variance estimates for each experimentally evolved population in the high salt environment. Blue dots indicate the posterior mode for each replicate. These values are compared with the posterior mode distribution obtained from randomizing the -matrices by inbred line and assay block identities (orange).
-
Figure 7—figure supplement 1—source data 1
Eigendecomposition of the evolved -matrices.
See table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig7-figsupp1-data1-v2.pdf
Figure 7—figure supplement 2
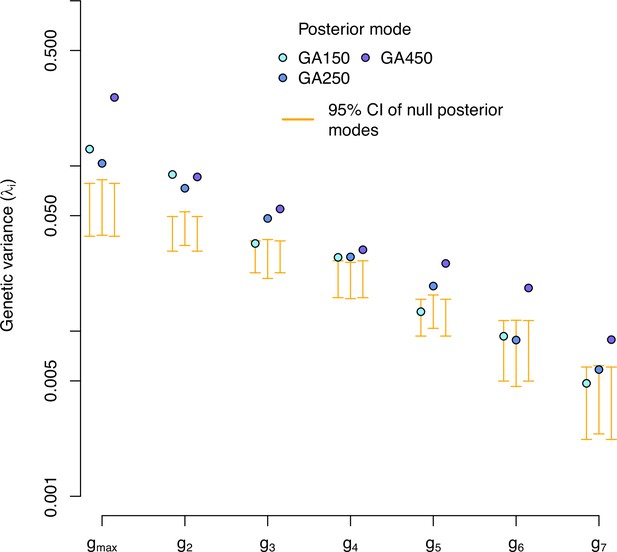
Eigendecomposition of the high salt -matrix of the evolved populations.
-matrix eigenvalues for each experimentally evolved population in the high salt environment. Blue dots indicate the posterior mode for each replicate. These values are compared with the posterior mode distribution obtained from randomizing the -matrices by inbred line and assay block identities (orange).
Figure 7—figure supplement 3
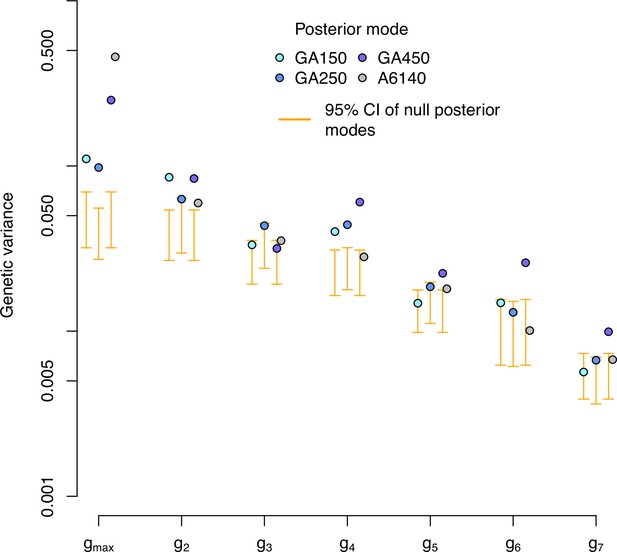
Genetic variance of the high salt -matrix in the evolved populations along the eigentraits of the ancestral population.
Genetic variance in the high salt environment for each experimentally evolved population and their ancestral population in the eigentraits of the ancestral populations. Blue and gray dots indicate the posterior mode for each replicate. These values are compared with the posterior mode distribution obtained from randomizing the -matrices by inbred line and assay block identities (orange, for the evolved populations only).
Figure 8
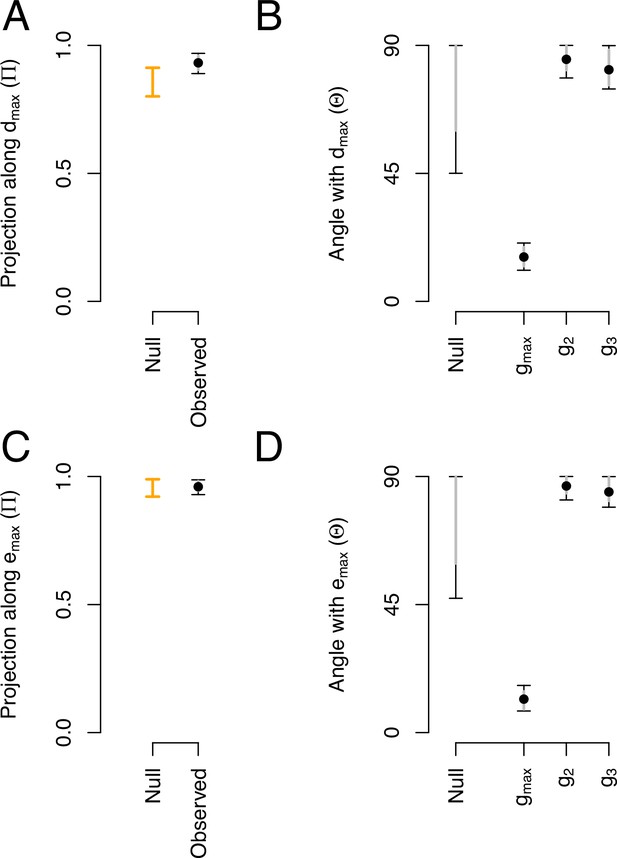
Phenotypic and genetic divergence alignments with ancestral standing variation.
(A) Projection of the total ancestral genetic variance along the phenotypic divergence canonical trait . Dots show the mean estimate with bars the 95% CI. Orange bar shows the null 95% CI after randomizing the -matrix (see Methods). Mean of the observed posterior distribution (0.93) is outside the 95% CI of the randomized posterior modes (0.80–0.91). (B). The angle () between and the first three eigenvectors of the ancestral -matrix (). The null expectation was obtained by computing the angle between 1000 pairs of random vectors. (C and D) Similar projection and angles as shown in (A) and (B) but with - the vector of the main genetic divergence - instead of . In (C), the null and observed projections do not differ. Because and are almost aligned, both the observed and the null are very close to one (as is estimated relatively to , see Equation 5) and the relative phenotypic variance between traits is conserved in the randomized -matrices.
-
Figure 8—source code 1
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig8-code1-v2.zip
-
Figure 8—source data 1
Projections and angles (including CI) shown in Figure 8 as a table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig8-data1-v2.pdf
Figure 9 with 2 supplements
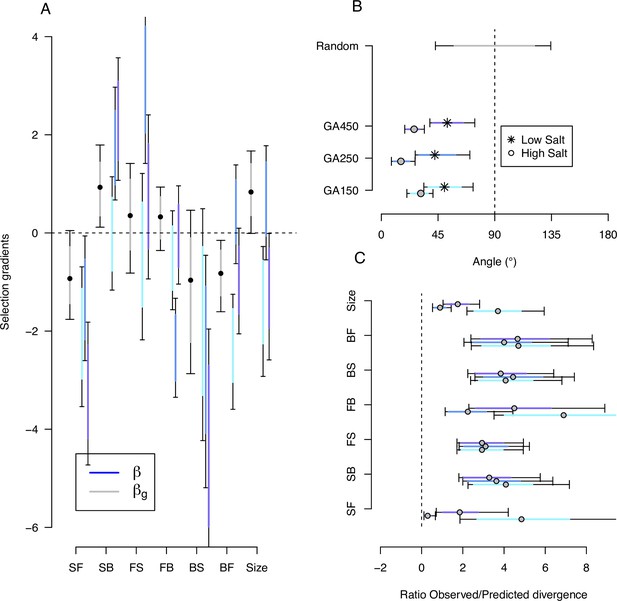
Predicting phenotypic evolution with Lande’s equation.
(A) Indirect and direct selection. Genetic selection gradients (gray) and phenotypic selection gradients (blues) for each replicate population, see Equation 6 and Equation 7, respectively. were divided by 3.5 for scaling (the average ratio observed/predicted divergence, panel C) rather than by 140 (the total number of generations in the experiment) for visual convenience. (B) The direction of phenotypic evolution. Angle between the expected phenotypic divergence (selection differentials, sk; Figure 4) and the observed phenotypic divergence at each replicate (; Figure 6). Circles show the results in the high salt environment and stars in the low salt environment. The expected angle by chance is in gray and was generated by computing 1000 angles between pairs of randomly generated vectors from a uniform distribution . (C) The magnitude of phenotypic evolution. The ratio phenotypic divergence at each replicate () with expected divergence (sk). For all panels, dots/circles/stars and colored bars show the mode and the 83% or 95% credible intervals of the posterior distributions obtained by sampling in posterior distribution of the ancestral high salt -matrix (Figure 2).
-
Figure 9—source code 1
See Figure 9 script that includes Figure 9—figure supplement 1 and Figure 9—figure supplement 2.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig9-code1-v2.zip
-
Figure 9—source data 1
Genetic selection gradients, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig9-data1-v2.pdf
-
Figure 9—source data 2
Phenotypic selection gradients, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig9-data2-v2.pdf
Figure 9—figure supplement 1
Genetic selection gradients bias due to low variance traits.
Estimates of genetic selection gradients , as in Figure 9, obtained by sampling the posterior distribution of the ancestral high salt -matrix with (gray) or without (red) traits with low genetic variance (from Figure 2—figure supplement 2, the forward-to-still (FS) and back-to-still (BS) traits).
Figure 9—figure supplement 2
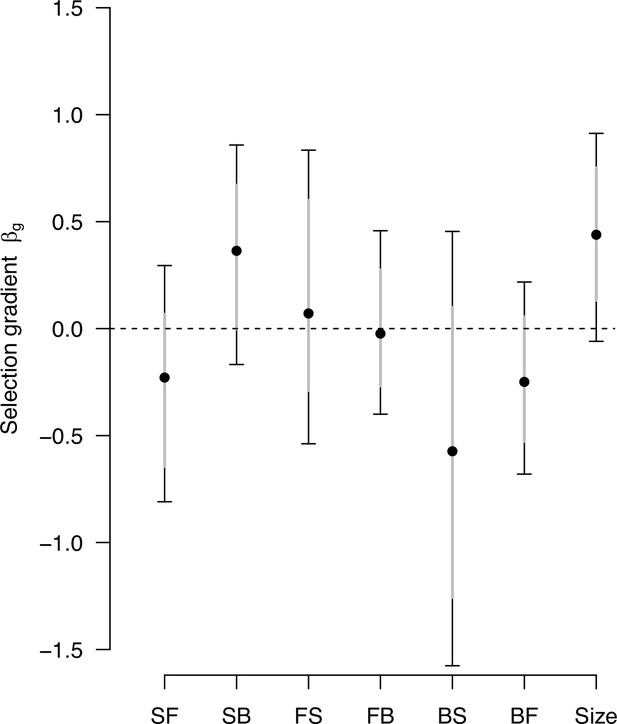
Genetic selection gradients with a sampling of -matrix and differentials.
Estimates of genetic selection gradients , as in Figure 9, obtained by sampling the posterior distribution of the ancestral high salt -matrix and the posterior distribution of sk.
-
Figure 9—figure supplement 2—source data 1
Genetic selection gradients, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-fig9-figsupp2-data1-v2.txt
Author response image 1
Selection gradients estimated with all 7 traits (gray, as shown in Figure 9 of the manuscript), a subset of 5 traits (red) or separately (green) using ββgg = GG-1sk.
CI are all obtained from sampling the posterior of the ancestral G-matrix and using fixed selection differentials.
Tables
Table 1
Notation.
| Variable | Definition |
|---|---|
| relative fitness in high salt, the self-fertility of hermaphrodites; from Chelo et al., 2019 | |
| transition rates between the movement states and ; see Equation 1 | |
| genetic (co)variance matrix of transition rates and body size; see Equation 2 | |
| genetic (co)variance matrix of transition rates, body size, and self-fertility | |
| ancestral selection differentials in high salt, with the salt environment where traits were measured; last column of | |
| vector of genetic selection gradients; see Equation 6 | |
| vector of phenotypic selection gradients; see Equation 7 | |
| SSCP | Sum-of-Squares and Cross-Product matrices for the environment and population factors; from MANOVA |
| 1st eigenvector of the population factor SSCP-matrix in high salt | |
| 1st eigenvector of the environment factor SSCP-matrix, for the ancestral population | |
| 1st eigenvector of the ancestral -matrix, one for each salt environment | |
| first eigenvector of the random skewer -matrix representing the main canonical trait differentiating the four -matrices in high salt | |
| Mean difference of the GA[1,2,4]50 populations from A6140, with the salt environment where traits were measured; from MANOVA | |
| eigenvalue of the th eigenvector | |
| the angle between eigenvectors of ancestral genetic variation and ,, or ; see Equation 3 | |
| proportion of -matrix variance along , , or ; see Equation 5 |
Table 2
MANOVA results for ancestral phenotypic plasticity and phenotypic differentiation.
| Factor | Df | Wilks | approx.F | num.DF | den.Df | Prob(>F) |
|---|---|---|---|---|---|---|
| Environment | 1 | 0.137 | 523.4 | 7 | 583 | 2.20E-16 |
| Population | 3 | 0.310 | 40.2 | 21 | 1674.6 | 2.20E-16 |
| Environment:Population | 3 | 0.828 | 5.4 | 21 | 1674.6 | 3.99E-14 |
| Residuals | 589 |
-
Notes: The Environment factor refers to the phenotypic difference between high and low salt environments for the ancestral population (Figure 1). The Population factor refers to the phenotypic differences between the four populations in the high salt environment (A6140 and GA[1,2,4]50); (Figure 6). The interaction between Environment and Population refers to the change in phenotypic difference between the four populations between the two environments, that is, to the evolution of phenotypic plasticity (Figure 6—figure supplement 2). The intercept in this MANOVA model is the ancestral population trait values in the high salt environment. Full model results, including the effects of assay design and environmental covariates (block, temperature, density, etc.), can be found in Figure 1—source data 3.
Table 3
Canonical traits of ancestral standing variation, divergence, and selection in high salt.
| Trait | (1) | (1) | g2(1) | g3(1) | (1) | (1) | (2) | (3) | m2(3) |
|---|---|---|---|---|---|---|---|---|---|
| SF | 0.148 | –0.360 | –0.388 | 0.241 | –0.225 | –0.331 | –0.93 | –0.402 | –0.125 |
| SB | –0.103 | –0.459 | –0.409 | 0.394 | –0.365 | –0.502 | 0.93 | –0.224 | –0.209 |
| FS | 0.161 | 0.267 | 0.303 | 0.129 | 0.284 | 0.378 | 0.35 | 0.607 | 0.257 |
| FB | –0.039 | 0.532 | –0.502 | –0.117 | 0.517 | 0.459 | 0.32 | 0.632 | –0.518 |
| BS | 0.094 | 0.142 | 0.153 | 0.035 | 0.253 | 0.145 | –0.96 | 0.077 | 0.106 |
| BF | 0.062 | 0.467 | –0.496 | 0.150 | 0.473 | 0.498 | –0.82 | –0.096 | –0.765 |
| Size | –0.963 | –0.258 | –0.264 | –0.856 | –0.425 | –0.132 | 0.83 | 0.069 | –0.102 |
| 99% | 76% | 9% | 6% | 95% | - | - | 39% | 37% |
-
Notes: (1) trait loadings of eigenvectors defined in Table 1, for the high salt environment; (2) modes of genetic selection gradients posterior distributions from Figure 9; (3) trait loadings of the first two eigenvectors of the mutational (co)variances matrix in low salt, re-analysis of locomotion behavior data with body size, from mutation accumulation lines reported in Mallard et al., 2023 (see Discussion). The bottom row shows the percent variation each eigenvector explains, when relevant.
-
Table 3—source data 1
Eigendecomposition of environmental effects in the ancestral population, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-table3-data1-v2.pdf
-
Table 3—source data 2
Eigendecomposition of the high salt -matrix, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-table3-data2-v2.pdf
-
Table 3—source data 3
Eigendecomposition of phenotypic differentiation, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-table3-data3-v2.pdf
-
Table 3—source data 4
Genetic selection gradients for traits measured in high salt, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-table3-data4-v2.pdf
-
Table 3—source data 5
Eigendecomposition of the mutation variance-covariance matrix, see table.
- https://cdn.elifesciences.org/articles/80993/elife-80993-table3-data5-v2.pdf
Appendix 1—key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Strain, strain background (C. elegans, male and hermaphro dite) | A6140 | DOI: 10.1186/s12915-014-0093-1 | A6140 | Ancestor, outbred population |
| Strain, strain background (C. elegans, hermaphro dite) | A6140L# | DOI: 10.1534/ genetics.117.300406 | A6140L# | A6140 inbred lines |
| Strain, strain background (C. elegans, male and hermaphro dite) | GA150 | DOI: 10.1186/ s12915-014-0093-1 | GA150 | Outbred population |
| Strain, strain background (C. elegans, hermaphro dite) | GA150L# | DOI: 10.1534/genetics.117.300406 | GA150L# | GA150 inbred lines |
| Strain, strain background (C. elegans, male and hermaphro dite) | GA250 | DOI: 10.1186/s12915-014-0093-1 | GA250 | Derived from A6140 |
| Strain, strain background (C. elegans, hermaphro dite) | GA250L# | DOI: 10.1534/genetics.117.300 406 | GA250L# | GA250 inbred lines |
| Strain, strain background (C. elegans, male and hermaphro dite) | GA450 | DOI: 10.1186/ s12915-014-0093-1 | GA450 | Outbred population |
| Strain, strain background (C. elegans, hermaphro dite) | GA450L# | DOI: 10.1534/genetics.117.300406 | GA450L# | GA250 inbred lines |
| Strain, strain background (C. elegans, hermaphro dite) | EEV1402 | DOI : 10.1038/ncomms3417 | EEV wormbase lab line 1402 | A6140 inbred line with GFP transgene ccIs4251 |
| Software, algorithm | MTW | DOI: 10.1038/nmeth.1625 | - | - |
| Software, algorithm | R | http://www.Rproject.org | - | version 3.3.2 |
| Software, algorithm | RStan | http://mc-stan.org/ | - | R package version 2.18.2 |
| Software, algorithm | stats | https://www.Rproject.org/ | - | R package version 3.3.2 |
| Software, algorithm | lme4 | doi: 10.18637/jss.v067.i01 | - | R package version 1.1-32 |
| Software, algorithm | emmeans | doi:10.1080/00031305.1980.10483031 | - | R package version 1.7.1-1 |
| Software, algorithm | multcomp | 10.1002/bimj.200810425 | - | R package version 1.4-23 |
| Software, algorithm | msm | DOI: 10.18637/jss.v038.i08. | - | R package version 1.7 |
| Software, algorithm | MCMCgl mm | DOI: 10.18637/jss.v033.i02. | - | R package version 2.34 |
| Software, algorithm | R scripts | https://github.com/ExpEvolWormLab/Mallard_Robertson | - | This paper |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Selection and the direction of phenotypic evolution
eLife 12:e80993.
https://doi.org/10.7554/eLife.80993
