Isometric spiracular scaling in scarab beetles—implications for diffusive and advective oxygen transport
Figures
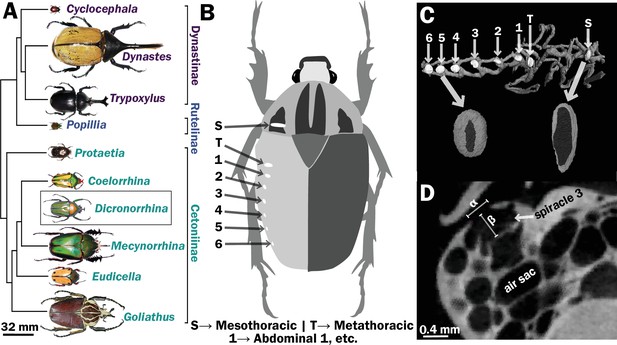
Scarab beetles include large bodied individuals and have eight spiracles.
(A) Phylogenetic tree for the scarab beetles used in this study showing size distribution among clades (branch lengths are meaningless). (B) Location of the eight spiracles in the scarab body. (C) 3D reconstruction of the tracheal trunks in the thorax, legs, and abdomen of Dicronorrhina derbyana; spiracles are shown in white. The larger images of spiracles show the size of the opening (dark in color) compared to the mushroom-shaped (white) atrium behind and the differences in spiracle shape. (D) Transverse X-ray slice through the third abdominal spiracle with diameter, α, and depth, β, measures illustrated.
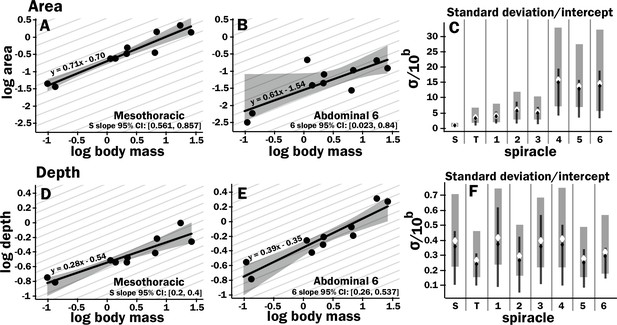
Isometric scaling of scarab beetle spiracles.
Spiracle area scales with geometric isometry (A, B), with much tighter distribution about the isometric model for the large anterior spiracles compared to the smaller posterior spiracles. In A, B, D, and E, the light gray lines show isometric scaling (slopes of 0.67 for area and 0.33 for depth). (C) shows estimates for the variability for regression models for the various spiracles (S mesothoracic, T metathoracic, 1–6 abdominal), calculated as the standard deviation divided by 10regression intercept, which represents the spiracle area for a 1 g beetle. Black diamond and line show the median and 2.5th–97th residual standard deviation divided by 10regression intercept calculated on nonparametric bootstrap samples. The white diamond and gray interval represent the median and 3rd–97th highest posterior density interval for the standard deviation divided by 10regression intercept calculated from parameter samples from the Bayesian regression. We see a trend toward much higher variability in posterior spiracle area as compared to anterior. In contrast to spiracle area, spiracle depth shows similar variability in all spiracles (D–F) regardless of position.
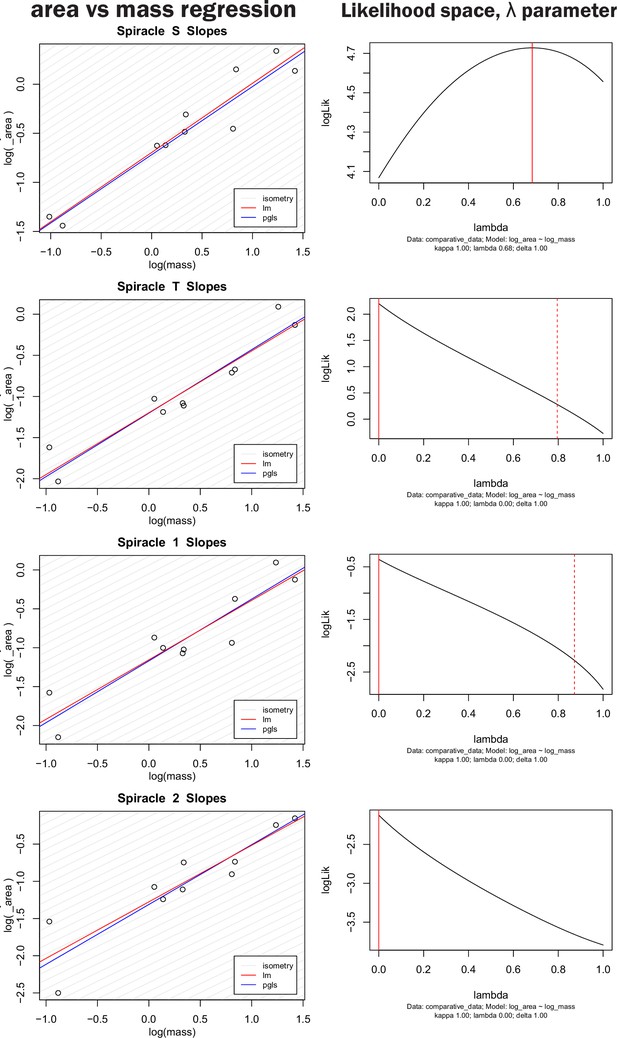
Nonidentifiability of phylogenetic signal parameter in pGLS regression model.
The left-hand column shows both OLS regression and pGLS regression models plotted for log spiracle area versus log of mass for the four largest spiracles. The right-hand column shows the log likelihood space for the parameter λ, which scales the off-diagonal covariance terms of the regression model thereby providing an indication of how strongly phylogeny influences the pattern of data distribution. A λ of one indicates strong phylogenetic signal whereas a value of zero indicates no sign of covariance in the data due to phylogeny. The solid red line indicates the maximum likelihood for the parameter used in the model on the left, the dashed red line indicates confidence interval estimates for the parameter value. Note that the log likelihood for the parameter is fairly flat across large section of the possible parameter space, and all confidence intervals on the parameter include zero (no phylogenetic signal). Similar results were found for all spiracles and for depth, area/depth, and area2/depth. Together, these indicate that many values for λ are similarly likely, and that the strength of the phylogenetic signal is hence nonidentifiable (our data do not strongly inform the parameter). Given the weakly to nonpeaked likelihood distributions, selecting a particular value for λ to use in the model is a largely arbitrary choice, poorly supported by the data.
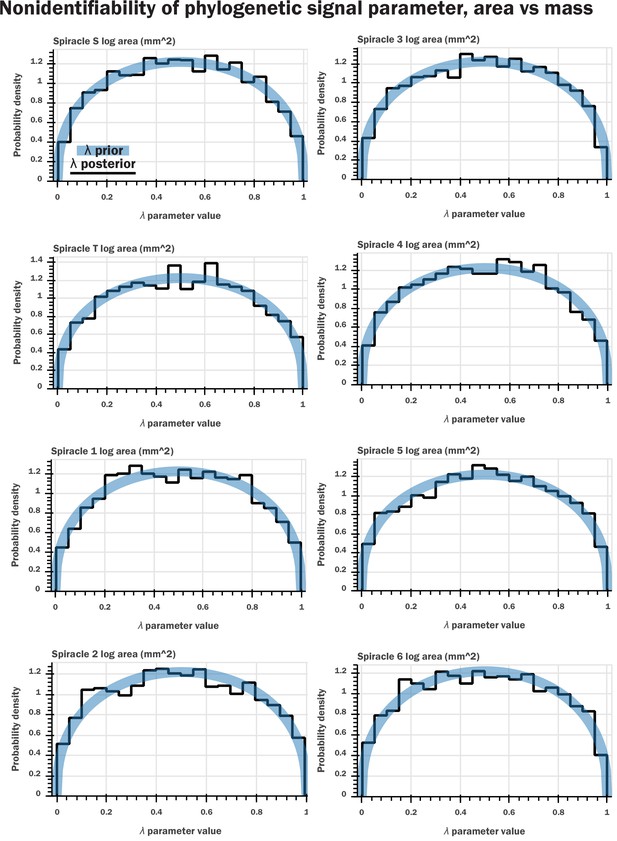
Nonidentifiability of the phylogenetic signal parameter as indicated by Bayesian modeling.
We constructed a generative model for our data (a multivariate normal distribution with covariance matrix given by the phylogenetic signal) which is analogous to the model assumed in pGLS regression. We included a parameter for λ that scaled the off-diagonal terms of the covariance matrix, analogous to pGLS, and sampled from our model for the various regressions of log spiracle morphology versus log mass. We then plotted the prior for the λ parameter (a beta distribution with shape parameters 1.4 and 1.4) against the samples from HMC sampling; shown here are plots for log spiracle area vs. log body mass. This indicated that the samples for this parameter had no shrinkage: the posterior samples for the parameter matched the prior. This indicates that the data do not inform this parameter, a clear indication that the parameter is entirely nonidentifiable given our data. Similar results were found for spiracular depth, area/depth, and area2/depth. Together, with Figure 2—figure supplement 1, this indicates that the phylogenetic signal is not informative for our models and does not provide useful information or insight to our analysis.
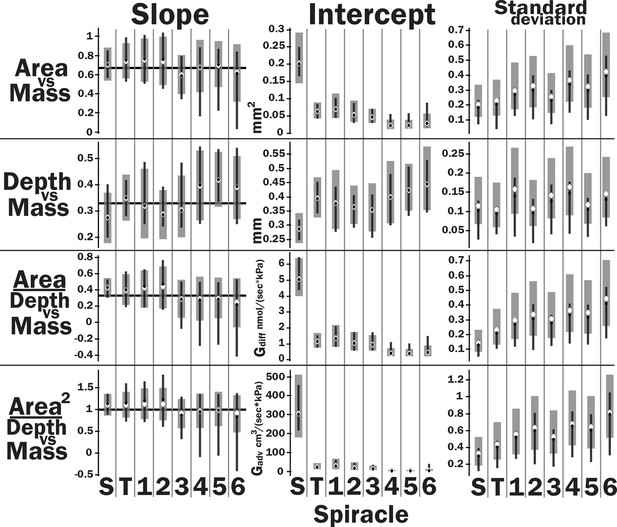
Slopes, intercepts, standard deviations, and quasi-coefficient of variation with confidence intervals generated via nonparametric bootstrapping or Bayesian regression for all spiracles and area, depth, area/depth, or area2/depth versus mass.
All spiracles scaled isometrically. The anterior spiracles are much larger than the posterior ones and hence provide much of the gas exchange capacity for the animal. They also exhibit a much tighter distribution for their area and gas exchange capacity than the posterior ones. The spiracle depth, however, did not show the same level of variation in dimension; all spiracular depths had similar degree of variation. This suggests there may be tighter selective regulation on the morphology of the large spiracles that likely supply the airflow needed for highly metabolically demanding tissue like the flight muscle, legs, and brain.
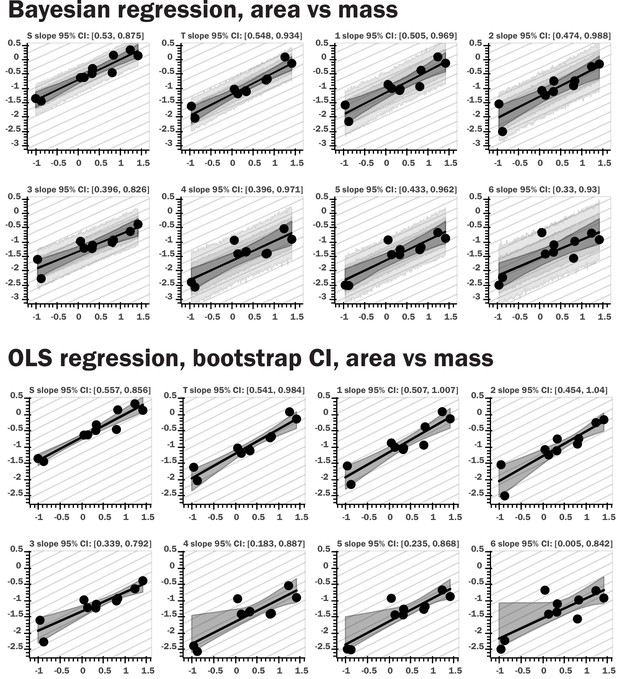
Regression plots for both Bayesian and nonparametric bootstrap analyses.
The top set of panels provide results for Bayesian linear regression for log area vs log body mass; the light gray bands provide the 80th and 95th percentile for the posterior predictive distribution for the regression model, the dark gray interval shows the 95th percentile for regression line ranges given by the slope and intercept samples, the black line the 10th percentile for these regression lines. The bottom panels show regression results from nonparametric bootstrap replicates drawn from the data, with ordinary least squares regression as the summary statistic applied to the subsamples. The gray interval shows the 95th percentile for the regression lines generated by the bootstrap sampling. The repeated light gray lines in both sets of figures indicate the theoretical isometric slope value for the regression of a given morphological trait. Very similar results were obtained with the two methods, and the same pattern was observed for spiracular depth, area/depth, and area2/depth.
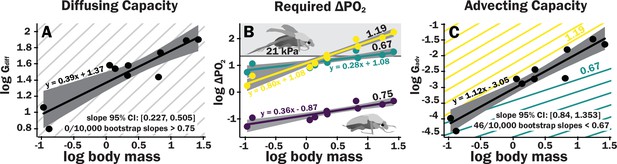
Scaling of the spiracles is insufficient for diffusive capacities across the spiracles to match expected increases in metabolic rate, so for pure diffusive gas exchange, the required partial pressure for oxygen must increase with size.
In contrast, advective capacities through the spiracles likely match or exceed the scaling of flight metabolic rate. (A) The log10 of total spiracular diffusive capacity per beetle (nmol s–1 kPa–1) increases with beetle size, with a slope estimated as 0.39. This slope was not significantly different from the 0.33 predicted from isometric scaling. The upper 95% confidence limit for the slope was 0.505, lower than any reported metabolic scaling slopes for insects. A metabolic rate slope of 0.75, commonly found for resting insects and animals more generally, is shown in light gray. (B) The log10 PO2 gradient (kPa) across the spiracles required to diffusively supply the oxygen demand of beetles increases with beetle size. The lower, purple line shows the estimated PO2 gradient across the spiracles to support diffusive gas exchange at rest; this increases from approximately 0.05–0.49 kPa as beetles increase in body size across this range. The less steeply upward sloping greenish and steeper yellow lines shows the estimated PO2 gradient across the spiracles during flight, assuming a 90× aerobic scope if flight metabolic rates scale with an exponent of 0.67 or 1.19, as found for large insects and small insects, respectively (Duell et al., 2022). The upper gray band indicates where the partial pressure of oxygen needed for calculated beetle metabolic demand exceeds the 21 kPa atmospheric oxygen level. (C) Hypermetric scaling of log10 summed advective capacity (m3 s–1 kPa–1) versus log10(body mass). There are uncertainties in the scaling of metabolic rate in flying insects: depending on size and study, slopes have ranged from 0.67 to 1.19. Confidence limits for advecting capacity include 1.19 but not 0.67. Equations of regression lines and confidence intervals for the slopes are shown for each plot.
Additional files
-
Supplementary file 1
The measurements made on each spiracle for each beetle.
- https://cdn.elifesciences.org/articles/82129/elife-82129-supp1-v3.xls
-
Supplementary file 2
Area and depth measurements for each spiracle for each beetle.
- https://cdn.elifesciences.org/articles/82129/elife-82129-supp2-v3.xlsx
-
Supplementary file 3
Conductances for diffusion and advection for each spiracle for each beetle.
- https://cdn.elifesciences.org/articles/82129/elife-82129-supp3-v3.xlsx
-
Supplementary file 4
Intercepts and slopes for scaling relationships (log–log plots) for morphologies (spiracular areas and depths), conductances, and PO2 gradients across the spiracles, including confidence limits, for each spiracle and for all spiracles combined.
- https://cdn.elifesciences.org/articles/82129/elife-82129-supp4-v3.xlsx
-
Supplementary file 5
Summed spiracular areas and average spiracular depths, summed conductances, and estimated average PO2 gradients across all the spiracles, for each beetle species, estimated at rest and during flight if flight metabolic rate scale with mass0.67 or mass1.19.
- https://cdn.elifesciences.org/articles/82129/elife-82129-supp5-v3.xlsx
-
Supplementary file 6
Reconstruction of the spiracles and connecting tracheal trunks on one side of the scarab beetle Dicronorhina derbyana.
- https://cdn.elifesciences.org/articles/82129/elife-82129-supp6-v3.zip
-
MDAR checklist
- https://cdn.elifesciences.org/articles/82129/elife-82129-mdarchecklist1-v3.docx





