Balancing true and false detection of intermittent sensory targets by adjusting the inputs to the evidence accumulation process
- School of Electrical and Electronic Engineering and UCD Centre for Biomedical Engineering, University College Dublin, Ireland
- Department of Statistics, University of Warwick, United Kingdom
- Trinity College Institute of Neuroscience and School of Psychology, Trinity College Dublin, Ireland
Figures
Figure 1
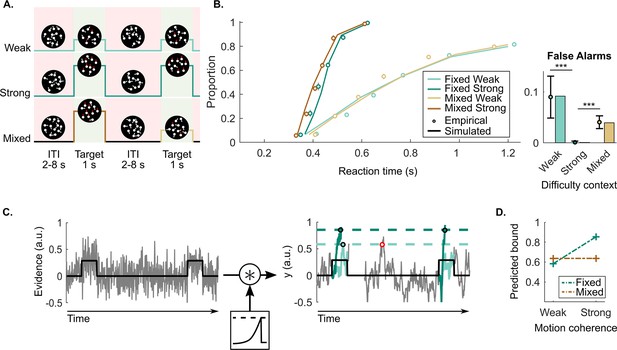
Continuous random dot motion (RDM) detection task and behaviour.
(A) Participants continuously monitored a cloud of moving dots to detect targets defined by a step change to coherent upward motion for 1 s. The inter-target interval (ITI) duration varied between 2, 4, 6, and 8 s. In each block of 24 targets, participants would perform a weak fixed context condition (step increase of 25%), a strong fixed context condition (step increase of 70%), or a mixed context condition (25% and 70% equally likely). (B) Reaction time (RT) cumulative quantile probability functions and the proportions of a 2 s ITI period containing a false alarm as a function of difficulty context (dots in cumulative quantile probability and false alarm plots). Each plot includes simulated data from a fitted leaky accumulator model with bound adjustment (solid lines in cumulative quantile probability plot and bars in the false alarm plot). (C) Schematic representation of the leaky accumulator model with adjustable bound parameters. Noisy evidence, which steps up during targets, is accumulated () until it reaches a context-dependent bound. Leaky accumulation is represented as a convolution with an exponential decay kernel. The degree of leakage is a free parameter but constrained to be equal (not adjusted) across contexts. When the target evidence is weak, a more liberal (lower) bound needs to be set to avoid misses; this comes however at the cost of more false alarms (example indicated in red). (D) Bound parameter values estimated by the best fitting bound-adjustment model. All figures represent a sample size of N = 14. Error bars represent the 95% confidence interval. p-Values resulting from the GMM are indicated by the asterisks; *p<0.05, **p<0.01, and ***p<0.001.
Figure 2 with 2 supplements
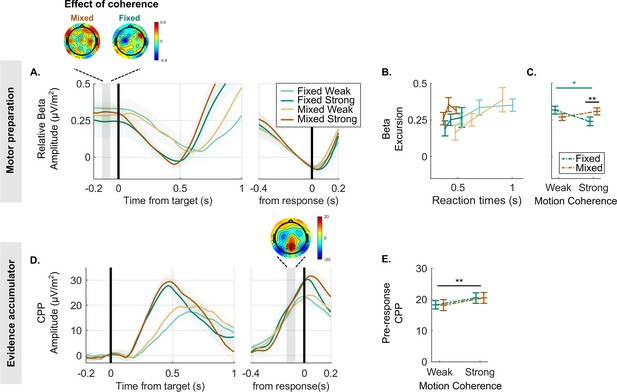
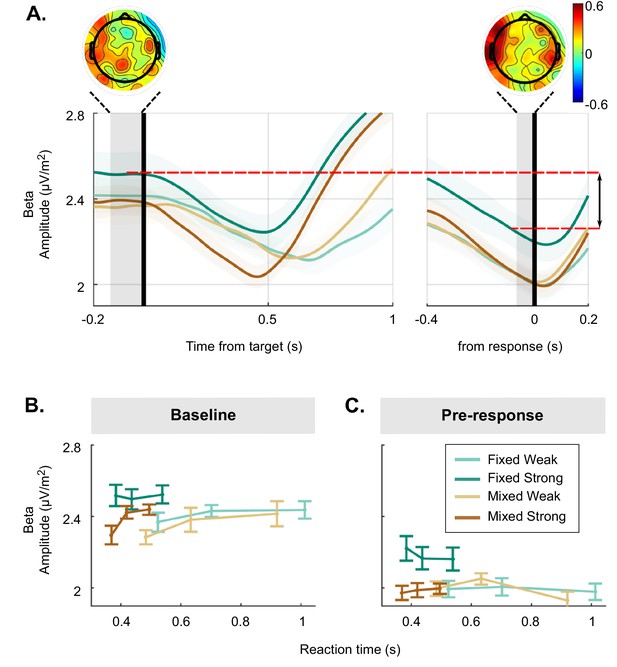
Decreases in beta amplitude track motor preparation and reveal a lower decision bound for the strong context.
(A) Beta amplitude (15–30 Hz) over the motor cortex, aligned to the target (left) and to the response (right), averaged for each condition and expressed as a difference relative to the corresponding pre-response level taken to reflect motor execution threshold (i.e. threshold level is indicated by zero). To ensure that the beta rebound effect following false alarms (see Figure 2—figure supplement 1) could not artificially drive the differences in excursion across conditions, targets occurring within 1.2 s of a false alarm were excluded from these data. The scalp topography shows the distribution of the difference between weak and strong targets in the baseline amplitude (again relative to the motor execution threshold; blue corresponds with more negative amplitude for strong relative to weak motion coherence). This highlights that the difference in beta excursion in the fixed strong relative to fixed weak context is maximal over the motor cortex. (B) The average beta excursion (i.e. difference of pre-target beta amplitude minus pre-response beta amplitude), plotted for three equal-size reaction time (RT) bins per condition. Smaller beta excursion predicts faster RTs as found in previous studies linking beta to a motor-level decision variable. (C) Grand-average beta excursion for all conditions, reflecting the neural index of bound settings. These show an obvious qualitative difference to the bound parameter values estimated in the behavioural data fit of the leaky accumulator model with adjustable bound in Figure 1D. (D) Centro-parietal positivity (CPP) signals averaged for each condition, target-locked (left) and response-locked (right). The topography of the indicated pre-response time window shows the cluster of electrodes used for plotting average waveforms. (E) Average pre-response CPP amplitude for each condition. All figures represent a sample size of N = 14. Error bars represent the 95% confidence interval. p-Values resulting from the GMM are indicated by the asterisks; *p<0.05, **p<0.01, and ***p<0.001.
Figure 2—figure supplement 1
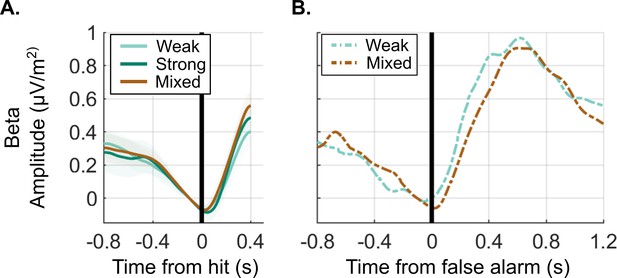
Beta waveforms aligned to (A) a true detection and to (B) a false alarm, both plotted as a function of context (weak, strong, and mixed).
Note, false alarm waveforms of the strong context could not be plotted as there were close to zero false alarms in this condition. Despite a common baseline correction to the pre-response level for hits, the level reached just prior to a false alarm aligned to that of the hits indicating that offset levels did not differ during inter-target interval (ITI) from during targets.
Figure 2—figure supplement 2
Posterior N2 component.
(A) Target-locked N2 waveform and (B) N2 amplitude around 300 ms after target onset, plotted as a function of reaction time (RT) for each condition. There are main effects of both target motion coherence ((1)=4.7, p=0.006), with lower N2 for strong targets as well as in the mixed condition. Furthermore, there is a main effect of RT ((1)=–2.6, p=0.002), where faster RTs have lower N2s. All figures represent a sample size of N = 14. Error bars represent the 95% confidence interval. (C) The scalp topography shows the distribution of the difference between mixed and fixed contexts. Blue would correspond with more negative amplitude in the mixed relative to fixed context.
Figure 3 with 2 supplements
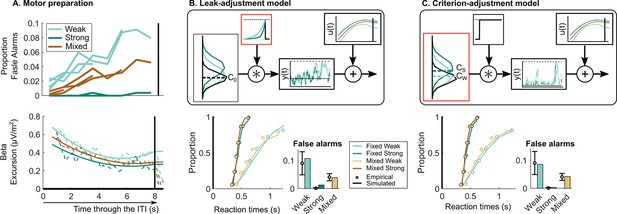
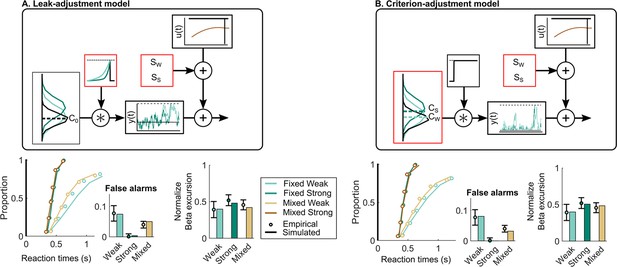
Neurally informed modelling.
(A) Motor preparation throughout the inter-target interval (ITI), showing a dynamic urgency trend. The proportion of false alarms (per 1 s period) increases throughout the ITI (upper; four ITIs superimposed). This corresponds to an increase in motor preparation throughout the ITI reflected in decreasing beta amplitude (lower). Beta amplitude is plotted for the 8 s ITI relative to the corresponding pre-response level taken to reflect motor execution threshold. After normalisation, beta amplitude is used to model urgency () through the ITI generating the observed increase in false alarms. Model evaluation for the neurally informed (B) leak-adjustment and (C) sensory criterion-adjustment model comparing empirical and predicted reaction time (RT) cumulative quantile probability distributions and false alarm rates (per 2 s ITI period). Above are model schematics illustrating the different mechanisms of continuous accumulation and context-dependent adjustment. In (B) the leak-adjustment model, evidence is referenced to the centre of the noise distribution (C0, equal to zero) and accumulated () with a leak. Leak is represented in the time constant of a convolution kernel and is free to change across contexts. Meanwhile in (C) the criterion-adjustment model, evidence is referenced to a criterion ‘zero’ so that is adjustable across contexts (, , and with two shown for illustration) and fed to a non-leaky accumulator with a lower reflecting bound at zero to preclude negative accumulation. All figures represent the empircical data of N = 14. Error bars represent the 95% confidence interval.
Figure 3—figure supplement 1
Neurally informed models fit simultaneously to behaviour and beta excursion.
As a control, the neurally informed model fitting procedure was adjusted so that the temporal profile of dynamic urgency during the inter-target interval (ITI) was fixed and the static urgency offset between conditions was governed by two additional free parameters (here referred to as ). In this way, the predicted motor-level decision variable is more precisely linked to the sum of cumulative evidence plus urgency, and not just the urgency component. This is important in the criterion-adjustment model where due to the reflecting lower bound cumulative evidence () asymptotes to different levels depending on criterion settings. This leads to the misestimation of the predicted motor-level decision variable in that case, and thus breaking its linking proposition with beta excursion. Specifically, behaviour and beta excursion data were fit simultaneously by minimising G2+beta penalty. This beta penalty term was added to the cost function to quantify the divergence between the real and simulated pre-target beta excursion summed across condition, for example with as a scaling factor. The dynamic urgency throughout the ITI was anchored to the mixed condition, while the static for the other conditions ( and ) are fitted for the neurally informed (A) leak-adjustment and (B) sensory criterion-adjustment model. Above are the revised model schematics illustrating the mechanism of adding free parameters to determine urgency offsets . All figures represent the empircical data of N = 14. Error bars represent the 95%
Figure 3—figure supplement 2
Simulated single-trial example of the motor-level decision variable during the inter-target interval (ITI).
This example illustrates how, in the weak context, despite the decision variable lying at a tonically lower level due to the lower urgency, the lower sensory criterion in this case causes short-term bursts of cumulative noise to occur more often, leading to increased false alarms.
Figure 4 with 1 supplement
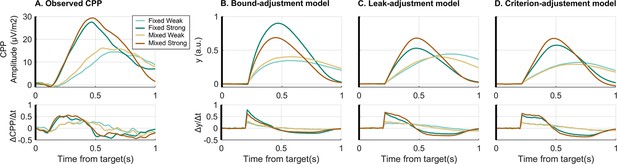
Comparison of empirical and simulated evidence accumulation waveforms.
(A) Empirical average target-locked centro-parietal positivity (CPP) signals (upper row) for each condition as well as their first derivative (lower row). This can be compared to the simulated accumulator process, , for (B) the bound-adjustment model, and the neurally informed (C) leak-adjustment and (D) criterion-adjustment models. The build-up rate of the CPP does not immediately begin to fall steeply in the way predicted by the leaky accumulator model. In these simulations, CPP is simulated as the cumulative evidence without direct urgency influence (Kelly et al., 2021). Without loss of generality for the behavioural responses, we assumed that after reaching commitment, there is a delay of 80 ms before the CPP stops accumulating and over 416 ms falls linearly back to zero, implemented identically in all contexts and in both models. This was based on observed post-response dynamics in the real CPP.
Figure 4—figure supplement 1
Comparison of empirical response-locked centro-parietal positivity (CPP) with the simulated pre-response evidence accumulation waveforms.
(A) Empirical average response-locked CPP waveforms (upper row) for each condition as well as the average pre-response CPP (lower row). Figure represent the empircical data of N = 14. Error bars represent the 95%. These are compared to the simulated accumulator process, for the (B) bound-adjustment, (C) leak-adjustment, and (D) criterion-adjustment models. All three models predict an interaction in pre-response cumulative evidence levels (see lower rows), but whereas the bound-adjustment model predicts the fixed strong condition to stand out as the highest, the neurally informed models, by design, predict cumulative evidence levels that mirror the decision bounds estimated from empirically observed beta excursion, where the fixed strong condition is instead the lowest.
Figure 5
Detailed analysis of raw beta amplitude in the baseline and pre-response time frames.
(A) Beta amplitude (15–30 Hz) over the motor cortex without any baseline or threshold subtraction, aligned to the target (left) and to the response (right), averaged for each condition. Additionally, a visual representation of excursion is shown with the red lines. Scalp topographies show the distribution of the difference between strong targets in the mixed and fixed condition, more red indicating higher activity in the fixed condition. (B) Baseline beta activity and (C) pre-response beta plotted for each condition and three equal-size reaction time (RT) bins. Error bars for all plots represent the 95% confidence interval.
Author response image 1
Simulations of the original criterion-adjustment model showing the traces throughout the longest ITI (8 sec).
Here showing, (A) the urgency constrained by the Β data, (B) “evidence” (zero-mean noise during ITI) accumulation and (C) the sum of the urgency component plus evidence accumulation. These figures show that within the original criterion-adjustment model the noise accumulates to a context-dependent average asymptotic level, which contributes alongside urgency to the context-dependent offsets seen in the motor-level decision variable reflecting the sum urgency + evidence accumulation.
Author response image 2
Simulation from the control analysis where the Criterion-adjustment model was forced to reproduce the static shifts observed in baseline Β amplitude as well as the observed behavioural patterns simultaneously.
Traces in the Longest ITI are plotted, from left to right: (A) Urgency traces, where the Mixed condition is constrained by the observed Β signals and the Weak and Strong conditions are statically shifted by two free parameters relative to the Mixed condition; (B) the evidence (zero-mean noise during ITI) accumulation; (C) the sum of the urgency component and evidence accumulation.
Tables
Table 1
Parameter values estimated for the leaky accumulator model with adjustable bound fit to behaviour alone, and for the neurally informed models featuring leak adjustment and criterion adjustment. ’Noise’ refers to the standard deviation (σ) for the Gaussian sensory evidence noise. ’Bound’ refers to the threshold set on the decision variable for triggering a response. ’Leak’ refers to the proportion of the current cumulative evidence total that leaks away on the following sample (note a 16.7 ms time step is used). No leak was fitted for the criterion-adjustment model. ‘Tnd’ refers to the non-decision time in ms. ‘Drift’ refers to drift rate, corresponding to the mean of the sensory evidence during targets. The goodness-of-fit metric, G2, is listed for each model. Note that, if comparing parameter values between models directly, it must be taken into account that whereas the bound-adjustment model set a scaling parameter of noise σ = 0.1 and allowed bounds to vary freely with respect to this. In contrast, the neurally constrained models were scaled directly by the normalised urgency signals relative to the ultimate action-triggering bound taken to be equal to 1. These fixed parameters are indicated in red.
| Noise | Variable parameters | Tnd | Drift | G2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bound-adjustment | 0.1 | Bound | Leak | 238 | W | S | MW | MS | 16 | |||
| W | S | M | 0.14 | |||||||||
| 0.58 | 0.85 | 0.63 | 0.05 | 0.14 | 0.05 | 0.12 | ||||||
| Leak-adjustment | 0.05 | Leak | Bound | 238 | W | S | MW | MS | 23 | |||
| W | S | M | 1 | |||||||||
| 0.02 | 0.08 | 0.04 | 0.02 | 0.06 | 0.03 | 0.07 | ||||||
| Criterion-adjustment | 0.07 | Criterion | 1 | 230 | W | S | MW | MS | 16 | |||
| W | S | M | ||||||||||
| 0.02 | 0.06 | 0.03 | 0.03 | 0.10 | 0.04 | 0.09 | ||||||
Table 2
Parameter values estimated for neurally informed models fitting behaviour and beta excursion simultaneously (see Figure 3—figure supplement 1). Neurally informed models were revised to directly constrain the temporal profile of the urgency signal during the inter-target interval (ITI) in the mixed condition only. Two free additional parameters were added for the additive offsets (’shift’) in urgency for the weak and strong context condition relative to the mixed context. Additionally, goodness-of-fit metrics are reported as G2+beta penalty.
| Noise | Variable parameters | Tnd | Drift | Shift | G2 + Penalty | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Leak-adjustment | 0.05 | Leak | 238 | W | S | MW | MS | W | S | 33 | |||
| W | S | M | |||||||||||
| 0.03 | 0.08 | 0.04 | 0.03 | 0.07 | 0.03 | 0.07 | 0.02 | 0.03 | |||||
| Criterion-adjustment | 0.09 | Criterion | 248 | W | S | MW | MS | W | S | 16 | |||
| W | S | M | |||||||||||
| 0.02 | 0.10 | 0.014 | 0.04 | 0.14 | 0.05 | 0.10 | –0.14 | 0.06 | |||||
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Balancing true and false detection of intermittent sensory targets by adjusting the inputs to the evidence accumulation process
eLife 12:e83025.
https://doi.org/10.7554/eLife.83025
