Conformational and oligomeric states of SPOP from small-angle X-ray scattering and molecular dynamics simulations
- Linderstrøm-Lang Centre for Protein Science, Department of Biology, University of Copenhagen, Denmark
- Department of Structural Biology, St. Jude Children’s Research Hospital, United States
Figures
Figure 1 with 1 supplement
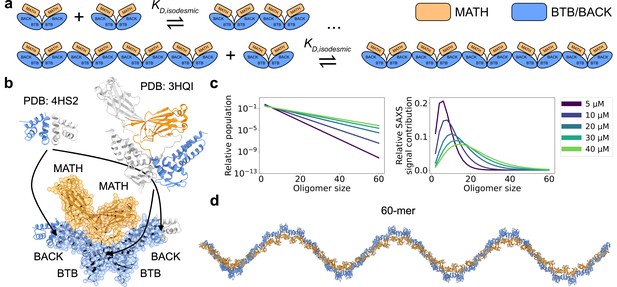
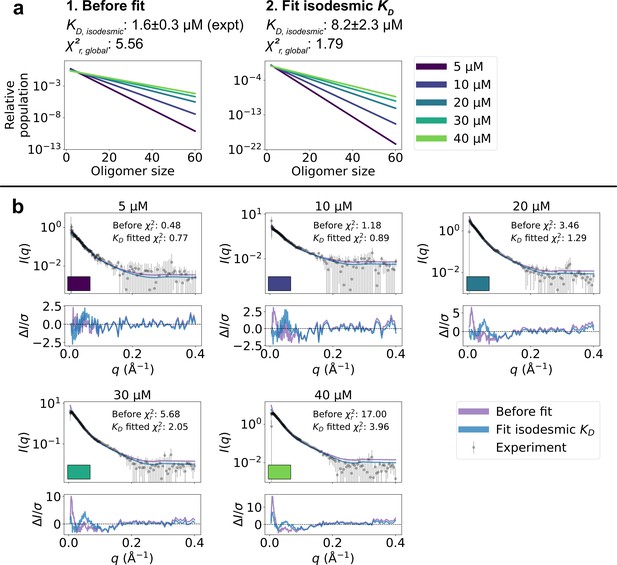
SPOP forms higher-order oligomers through isodesmic self-association.
(a) The SPOP BTB-BTB homodimer forms with nanomolar affinity, and is the unit of higher-order oligomerization through BACK-BACK homodimerization. Higher-order SPOP oligomerization follows an isodesmic model, where the equilibrium between oligomer and +1 is described by a single equilibrium constant, , which is independent of oligomer size. (b) Crystal structures of homodimers of the BACK (left, PDB: 4HS2) and MATH-BTB (right, PBD: 3HQI) domains of SPOP. Below, the structure of a SPOP28–359 dimer constructed based on crystal structures. The cartoon model is overlaid with the coarse-grained representation used in the Martini simulations. The BACK domains of the two neighbouring subunits in the oligomer are also shown (without Martini bead overlay). (c) Left: Populations of SPOP oligomers given by the isodesmic model with =1.6 µM, determined from CG-MALS, for the protein concentrations used in our SAXS experiments. Note the logarithmic scale. Right: Relative contribution of each oligomer to the average SAXS signal given by the populations in left panel. (d) Structure of a SPOP28–359 60-mer constructed based on structures in panel b. MATH domains are coloured orange and BTB/BACK domains are coloured blue in all panels.
Figure 1—figure supplement 1
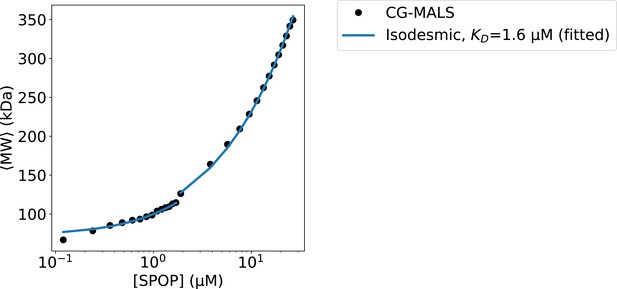
Fit of isodesmic model to CG-MALS.
Composition gradient multi-angle light scattering (CG-MALS) data from Marzahn et al., 2016. Fit of isodesmic model (blue) to CG-MALS data (black). The isodesmic and monomer molecular weight, , were treated as free fitting parameters. was fitted individually for each of the two merged data-sets (shown as line-break). The fitted parameters were =39±2.6 kDa, =36±1.3 kDa, and =1.6±0.3 µM, in good agreement with the 37.6 kDa theoretical mass of a SPOP28–359.
Figure 2
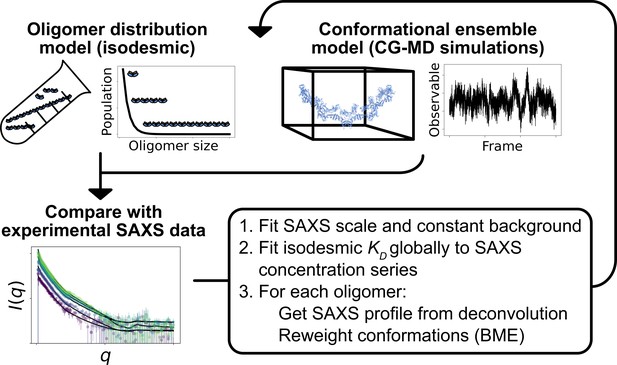
Overview of the self-consistent approach used to fit conformational ensembles of SPOP oligomers to SAXS data.
Small-angle X-ray scattering (SAXS) data on SPOP represents an average over a range of oligomeric species present in solution. Here, the distribution of oligomeric species and the conformational ensemble of each oligomer were self-consistently fitted to a concentration series of SAXS data by iteratively fitting the scale and constant background of the SAXS data and the isodesmic , followed by reweighting of the conformational ensemble of each oligomer.
Figure 3 with 9 supplements
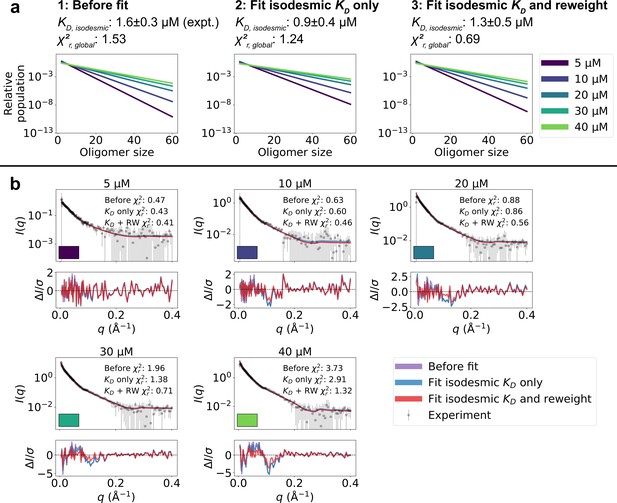
Refining oligomer populations and conformational ensembles against SAXS data.
(a) Relative populations of oligomers for the protein concentrations used in SAXS experiments. Note the logarithmic scale. Populations are given by the isodesmic model with the noted above the plot, which is either (1) previously determined by CG-MALS or (2–3) fitted globally to the SAXS data in panel b. quantifies the agreement with SAXS data in panel b for the three scenarios. (b) Agreement between experimental SAXS data and averaged SAXS data calculated from conformational ensembles of SPOP oligomers with populations given by the isodesmic model (as shown in panel a). SAXS profiles are shown for three different scenarios: (1) calculated from the conformational ensembles generated by MD simulations with the isodesmic previously determined with CG-MALS, (2) calculated from the conformational ensembles generated by MD simulations with the isodesmic fitted to the SAXS data, and (3) calculated from conformational ensembles refined against the SAXS data using Bayesian/MaxEnt reweighting, and with the isodesmic self-consistently fitted to the SAXS data. Error-normalized residuals are shown below the SAXS profiles and to each SAXS profile is shown on the plot.
Figure 3—figure supplement 1
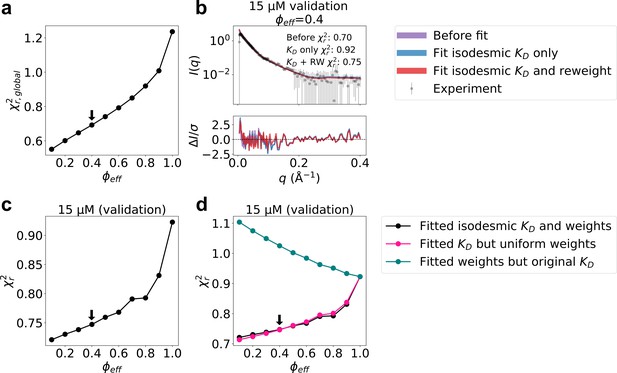
Selection of and model validation.
(a) calculated from the concentration series of SAXS data as a function of the fraction of effective frames, , retained after BME reweighting. The arrow shows the selected value of =1 corresponds to the MD simulations before reweighting. (b) Agreement between calculated and experimental SAXS data recorded using 15 µM protein, which was not used for optimization. Calculated SAXS profiles are shown before fitting (isodesmic =1.6 µM) (purple), with isodesmic optimized (isodesmic =0.9 µM) (blue), and with isodesmic and ensemble weights optimized with =0.4 (isodesmic =1.3 µM) (red). Error-normalized residuals are shown below the SAXS profile and for the three cases are shown on the plot. (c) Validation using SAXS data at 15 µM protein. to the SAXS data at 15 µM, which was not used for optimization, using the ensemble weights and determined from the optimization as a function of . Only SAXS scale and constant background were fitted to the 15 µM SAXS data. The arrow shows the selected value of . (d) Same as panel c (black), but also showing the agreement given by using only the fitted isodesmic with uniform weights (unbiased MD ensemble; red) or using only the fitted weights but the isodesmic of 0.9 µM determined before reweighting (green).
Figure 3—figure supplement 2
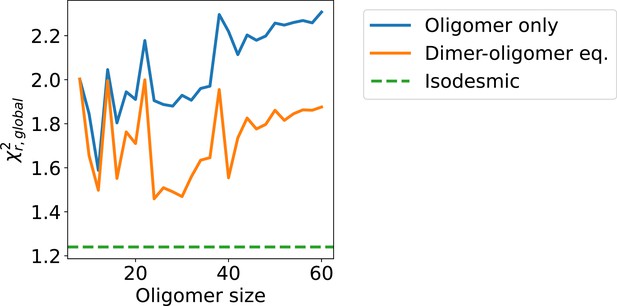
Agreement with SAXS for other self-association models.
to SAXS concentration series given by SPOP conformational ensembles of individual oligomers (blue) and dimer-oligomer equilibria (orange) for even oligomers ranging from octamer to 60-mer. The and SAXS scale and constant background were fitted to the SAXS data for each dimer-oligomer equilibrium. given by an isodesmic distribution of oligomers with isodesmic fitted to SAXS is shown as green dashed line.
Figure 3—figure supplement 3
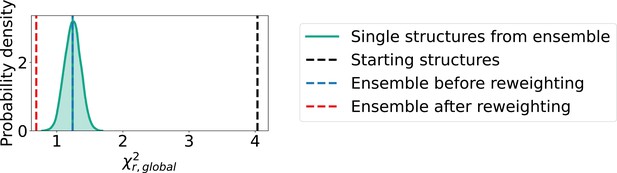
Comparison of static structures and ensembles.
to SAXS concentration series given by starting structures constructed based on crystal structure (black), single structure for each oligomer drawn from conformational ensemble (green), conformational ensembles before reweighting (blue) and conformational ensembles after reweighting (red). In all cases, the populations of oligomers were given by the isodesmic model, and the and SAXS scale and constant background were fitted to the SAXS data independently for each set of structures. The distribution of single structures drawn from the ensemble represents 10,000 sets of randomly selected structures.
Figure 3—figure supplement 4
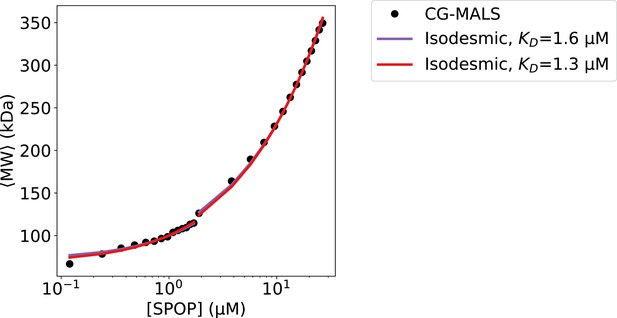
Agreement with CG-MALS for isodesmic model fitted to SAXS.
Composition gradient multi-angle light scattering (CG-MALS) data from Marzahn et al., 2016. Comparison of isodesmic model with fitted to CG-MALS (purple) and fitted to SAXS (red) in agreement with CG-MALS data (black). The monomer molecular weight, , was treated as a free fitting parameter. was fitted individually for each of the two merged data-sets (shown as line-break). The fitted parameters with =1.6 µM were =39.4±0.22 kDa and =36.5±0.55 kDa, and the fitted parameters with =1.3 µM were =36.1±0.22 kDa and =34.9±0.59 kDa. The theoretical mass of SPOP28–359 is 37.6 kDa.
Figure 3—figure supplement 5
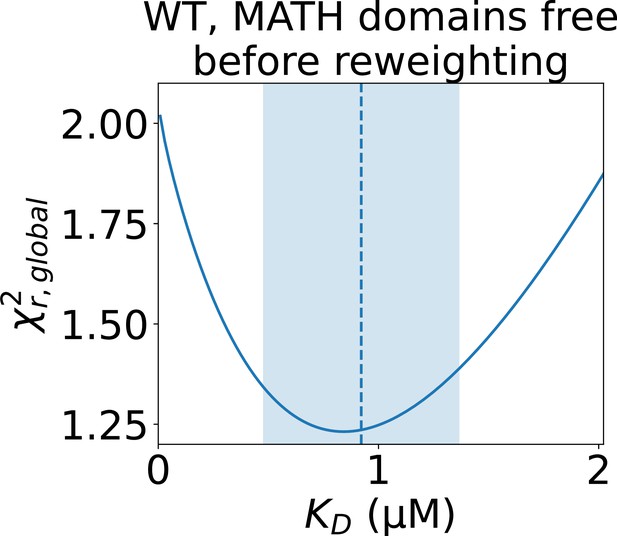
Determining the error of the fitted isodesmic before reweighting.
to the concentration series of SAXS data given by the conformational ensemble shown above the plot with oligomer populations given by a range of isodesmic values around the fitted with simulated annealing. Only the SAXS scale and constant background were fitted for each . The fitted with simulated annealing is shown as a dashed line and the selected error is shaded. The error was selected to include all values that give a no more than 10% greater than the minimum .
Figure 3—figure supplement 6
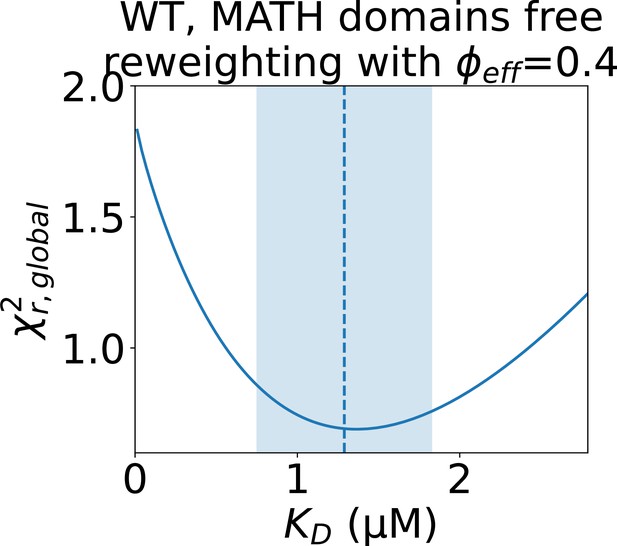
Determining the error of the fitted isodesmic after reweighting.
to the concentration series of SAXS data given by the conformational ensemble shown above the plot with oligomer populations given by a range of isodesmic values around the fitted with simulated annealing. Only the SAXS scale and constant background were fitted for each . The fitted with simulated annealing is shown as a dashed line and the selected error is shaded. The error was selected to include all values that give a no more than 10% greater than the minimum .
Figure 3—figure supplement 7
Fit to SAXS data for SPOP R221C.
(a) Relative populations of oligomers for the protein concentrations used in SAXS experiments (note the logarithmic scale). Populations are given by the isodesmic model with the value noted above the plot, which is either (1) previously determined with CG-MALS or (2) fitted globally to the SAXS data in panel b. quantifies the agreement with SAXS data in panel b for the two scenarios. (b) Agreement between experimental SAXS data on SPOP R221C and averaged SAXS data calculated from conformational ensembles of SPOP oligomers with populations given by the isodesmic model (as shown in panel a). Error-normalized residuals are shown below the SAXS profiles and to each SAXS profile is shown on the plot.
Figure 3—figure supplement 8
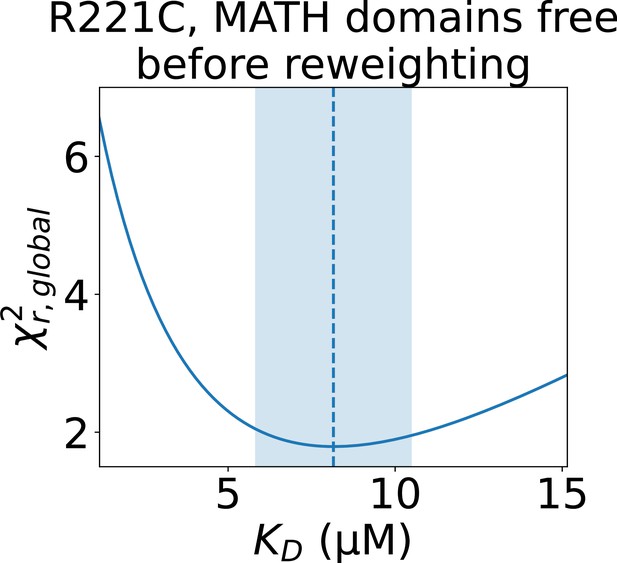
Determining the error of the fitted isodesmic for R221C.
to the concentration series of SAXS data on SPOP R221C given by the conformational ensemble shown above the plot with oligomer populations given by a range of isodesmic values around the fitted with simulated annealing. Only the SAXS scale and constant background were fitted for each . The fitted with simulated annealing is shown as a dashed line and the selected error is shaded. The error was selected to include all values that give a no more than 10% greater than the minimum .
Figure 3—figure supplement 9
Averaging the conformational weights from different SAXS experiments.
Left: relative oligomer populations given by the isodesmic model with fitted =1.3 µM for each protein concentration in the SAXS concentration series. Middle: relative contribution of each oligomer to the averaged SAXS signal given the populations in left plot. Right: weight given to conformational weights obtained with each SAXS experiment when averaging to get a single set of conformational weights for each oligomer.
Figure 4 with 3 supplements
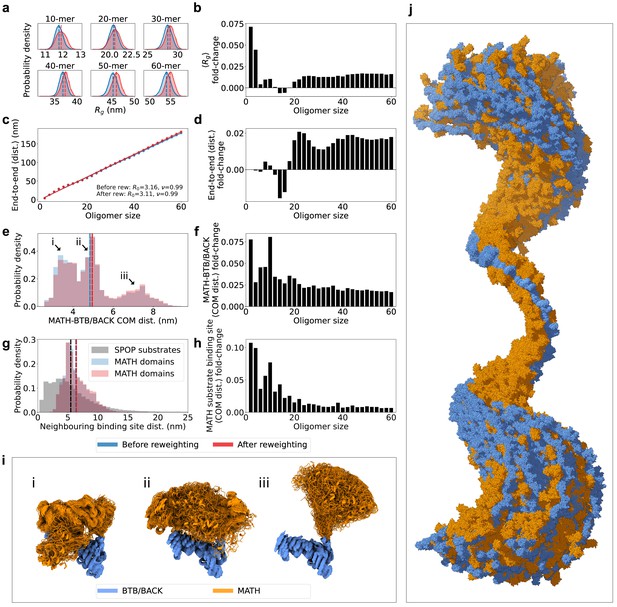
SPOP forms rigid, linear oligomers with flexible MATH domains in solution.
(a) Probability distribution of the radius of gyration () calculated from ensembles of six representative SPOP oligomers before and after reweighting (see Figure 1 for distributions for all oligomers). Dashed lines show the average values. (b) The fold-change in average after reweighting for all SPOP oligomers. (c) The average end-to-end distance calculated from ensembles of SPOP oligomers before and after reweighting (see Figure 2 for distributions for all oligomers). Solid lines show the fit of a power law: , where is the average end-to-end distance, R0 is the subunit segment size, is the number of subunits in the oligomer, and is a scaling exponent. The fit gave R0=3.16 nm, =0.99 before reweighting and R0=3.11 nm, =0.99 after reweighting. (d) The fold-change in average end-to-end distance after reweighting for all SPOP oligomers. (e) Normalized histogram of distances between the center-of-mass (COM) of the MATH domain and the COM of the BTB/BACK domains in the same subunit before and after reweighting. The histogram contains the distances from every conformation of every subunit in every oligomer. (f) The fold-change in average MATH-BTB/BACK COM distance after reweighting for all SPOP oligomers. (g) Normalized histogram of COM distances between MATH substrate binding sites in neighbouring subunits (blue and red). The histogram contains the distances from every conformation of every subunit in every oligomer. In black, distances between neighbouring SPOP binding sites in seven SPOP substrate IDRs calculated from CALVADOS simulations. (h) The fold-change in average COM distance between neighbouring MATH substrate binding sites after reweighting for all SPOP oligomers. (i) Overlay of conformational ensembles corresponding to the three populations in panel (e) The structures are from all non-terminal subunits of the SPOP dodecamer and are superposed on the BTB/BACK domains. (j) Overlay of 151 randomly selected frames from the conformational ensemble of the SPOP 60-mer with atoms represented as spheres. Structures were superposed to the BTB/BACK domains in the four middle subunits. MATH domains are shown in orange and BTB/BACK domains are shown in blue.
Figure 4—figure supplement 1
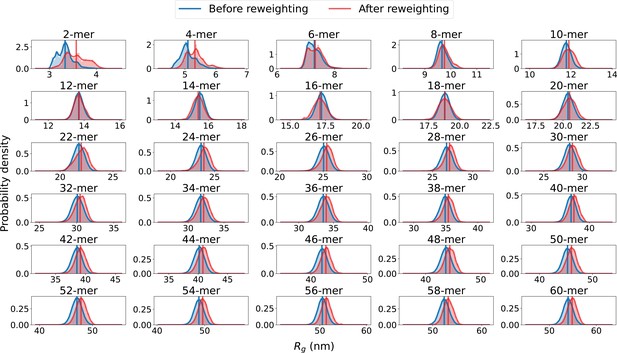
distributions before and after reweighting.
Probability distribution of the radius of gyration (), calculated from ensembles of SPOP oligomers before and after reweighting against SAXS data. Average values are shown as vertical lines.
Figure 4—figure supplement 2
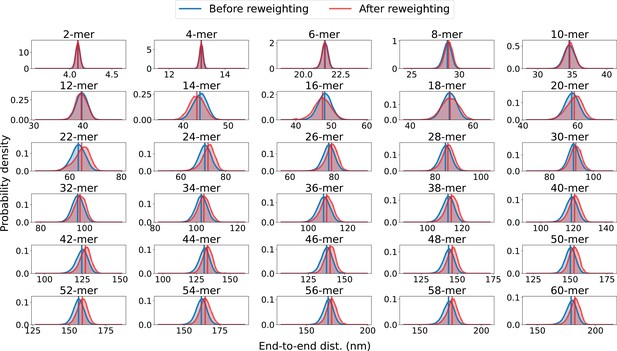
End-to-end distance distributions before and after reweighting.
Probability distribution of the end-to-end distance, calculated from ensembles of SPOP oligomers before and after reweighting against SAXS data. Average values are shown as vertical lines.
Figure 4—figure supplement 3
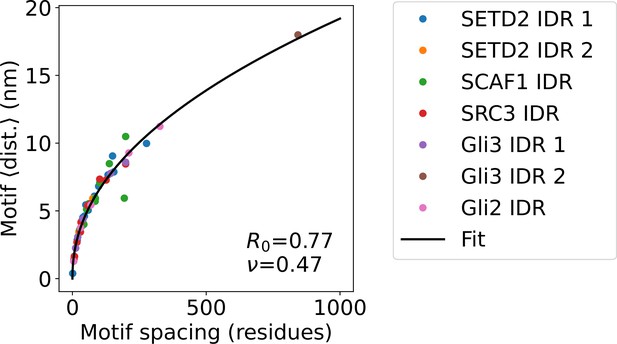
SPOP substrate motif-motif distances and motif-motif spacing.
Average distance between neighbouring SPOP binding motifs in disordered SPOP substrates calculated from CALVADOS simulations as a function of sequence distance. The relationship was fitted with a power law , where R0 is the segment size, is the number of residues spacing the two motifs, and is a scaling exponent. Fitted parameters are shown on the plot.
Figure 5 with 6 supplements
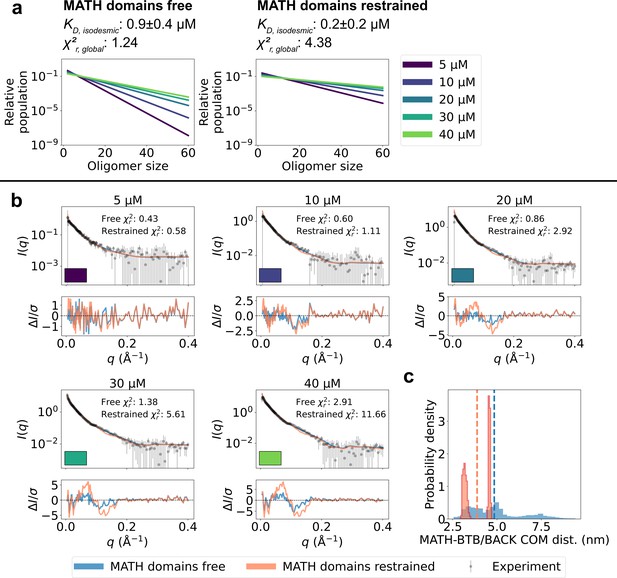
Unrestrained MATH domains give better agreement with SAXS data.
Comparison of conformational ensembles with MATH domains either unrestrained (blue) or restrained to BTB/BACK domains based on the configuration in the crystal structure (orange). (a) Relative populations of oligomers for the protein concentrations used in SAXS experiments. Note the logarithmic scale. Populations are given by the isodesmic model with the noted above the plot. was fitted globally to the SAXS data in panel (b). quantifies the agreement with SAXS data in panel b for the two setups. (b) Agreement between experimental SAXS data and averaged SAXS data calculated from conformational ensembles of SPOP oligomers generated with the two setups. Oligomer populations are given by the isodesmic model (as shown in panel a). Error-normalized residuals are shown below the SAXS profiles and to each SAXS profile is shown on the plot. (c) Histogram of center-of-mass distances between MATH and BTB/BACK domains in the same subunit calculated from all conformations of all subunits of all oligomers. Average values are shown as dashed lines.
Figure 5—figure supplement 1
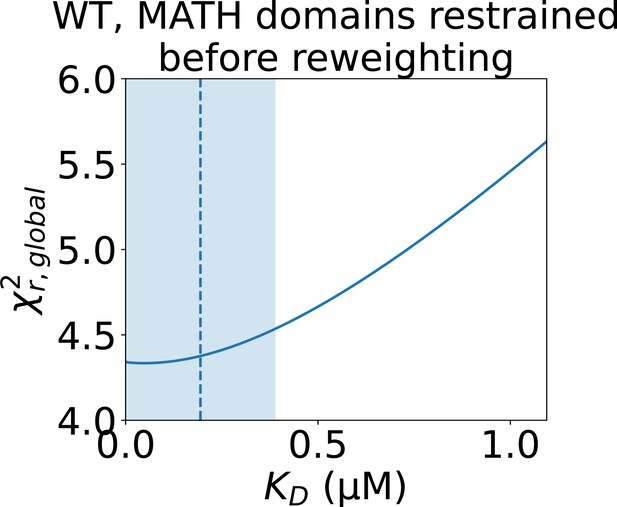
Determining the error of the fitted isodesmic with ensembles with MATH restrained.
to the concentration series of SAXS data given by the conformational ensemble shown above the plot with oligomer populations given by a range of isodesmic values around the fitted with simulated annealing. Only the SAXS scale and constant background were fitted for each . The fitted with simulated annealing is shown as a dashed line and the selected error is shaded. The error was selected to include all values that give a no more than 10% greater than the minimum .
Figure 5—figure supplement 2
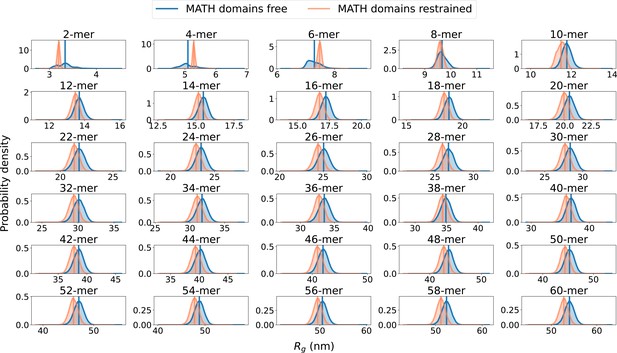
distributions from simulations with MATH free and MATH restrained.
Probability distribution of the radius of gyration (), calculated from ensembles of SPOP oligomers generated with MATH domains unrestrained (blue, free) or restrained to the BTB/BACK domains based on the configuration in the crystal structure using the Martini elastic network model (orange, restrained). Average values are shown as vertical lines.
Figure 5—figure supplement 3
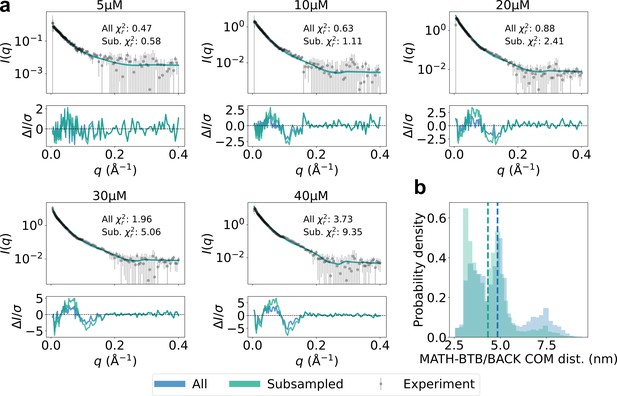
Subsampling compact MATH domains.
(a) Agreement with experimental SAXS data for original SPOP ensembles (blue) and SPOP ensembles subsampled to have lower MATH-BTB/BACK center-of-mass (COM) distance (green). Populations of oligomers were given by isodesmic model with =1.6 µM. (b) Histogram of MATH-BTB/BACK COM distances within the same subunit calculated from all conformations of all subunits of all oligomers for original ensembles (blue) and subsampled ensembles (green). Average values are shown as dashed lines.
Figure 5—figure supplement 4
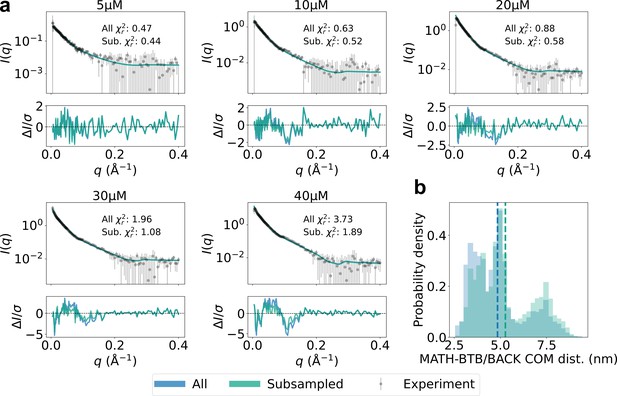
Subsampling extended MATH domains.
(a) Agreement with experimental SAXS data for original SPOP ensembles (blue) and SPOP ensembles subsampled to have higher MATH-BTB/BACK center-of-mass (COM) distance (green). Populations of oligomers were given by isodesmic model with =1.6 µM. (b) Histogram of MATH-BTB/BACK COM distances within the same subunit calculated from all conformations of all subunits of all oligomers for original ensembles (blue) and subsampled ensembles (green). Average values are shown as dashed lines.
Figure 5—figure supplement 5
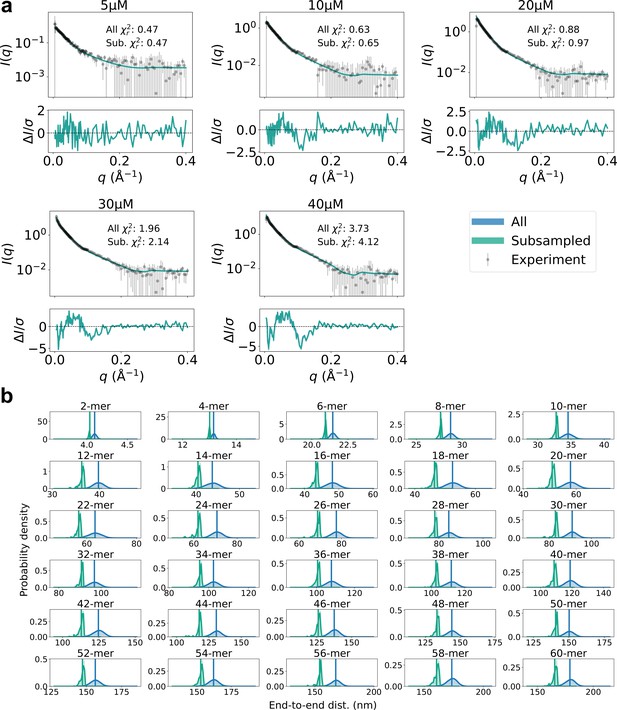
Subsampling low end-to-end distance.
(a) Agreement with experimental SAXS data for original SPOP ensembles (blue) and SPOP ensembles subsampled to have lower end-to-end distance (green). Populations of oligomers were given by isodesmic model with =1.6 µM. (b) Probability distribution of the end-to-end distance, calculated from original ensembles (blue) and subsampled ensembles (green). Average values are shown as vertical lines.
Figure 5—figure supplement 6
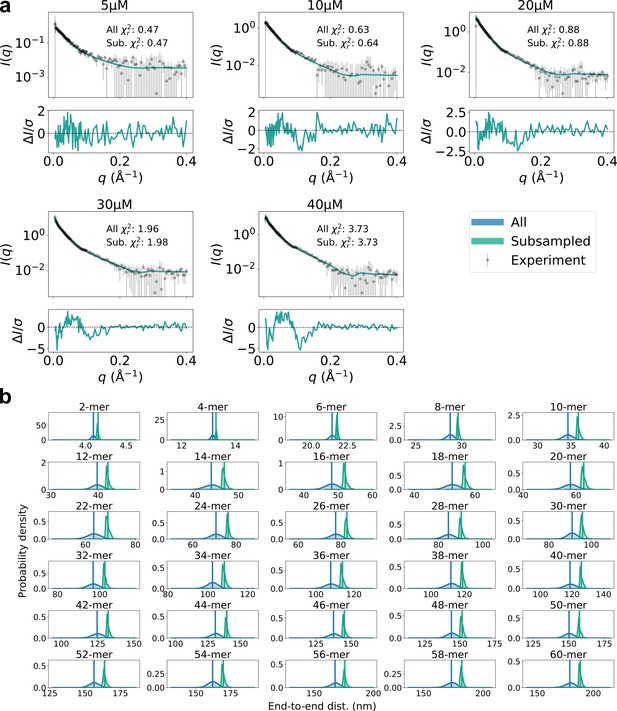
Subsampling high end-to-end distance.
(a) Agreement with experimental SAXS data for original SPOP ensembles (blue) and SPOP ensembles subsampled to have higher end-to-end distance (green). Populations of oligomers were given by isodesmic model with =1.6 µM. (b) Probability distribution of the end-to-end distance, calculated from original ensembles (blue) and subsampled ensembles (green). Average values are shown as vertical lines.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Conformational and oligomeric states of SPOP from small-angle X-ray scattering and molecular dynamics simulations
eLife 12:e84147.
https://doi.org/10.7554/eLife.84147
