Figures and data in Are single-peaked tuning curves tuned for speed rather than accuracy?

Figures
Tables
Additional files

9 figures, 3 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

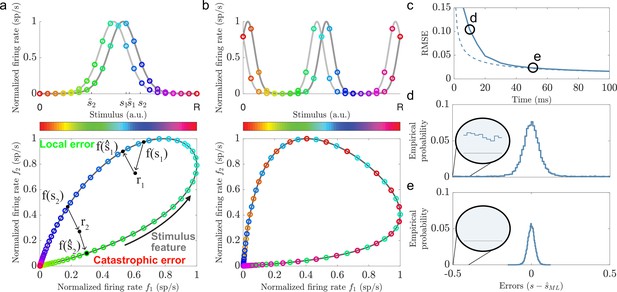
Illustrations of local and catastrophic errors.

(a) Top: A two-neuron system encoding a single variable using single-peaked tuning curves ( $λ = 1$ ). Bottom: The tuning curves create a one-dimensional activity trajectory embedded in a two-dimensional neural activity space (black trajectory). Decoding the two stimulus conditions, s₁ and s₂, illustrates the two types of estimation errors that can occur due to trial-by-trial variability, local ( ${\hat{s}}_{1}$ ) and catastrophic ( ${\hat{s}}_{2}$ ). (b) Same as in (a) but for periodic tuning curves ( $λ = 0.5$ ). Notice that the stimulus conditions are intermingled and that the stimulus can not be determined from the firing rates. (c) Time evolution of the root mean squared error (RMSE) using maximum likelihood estimation (solid line) and the Cramér-Rao bound (dashed line) for a population of single-peaked tuning curves ( $N = 600$ , $w = 0.3$ , average evoked firing rate $\bar{f_{s t i m}} = 20 \exp (- 1 / w) B_{0} (1 / w)$ sp/s, and $b = 2$ sp/s). For about 50 ms the RMSE is significantly larger than the predicted lower bound. (d) The empirical error distributions for the time point indicated in (c), where the RMSE strongly deviates from the predicted lower bound. Inset: A non-zero empirical error probability spans the entire stimulus domain. (e) Same as in (d) when the RMSE roughly converges to the Cramér-Rao bound. Notice the absence of large estimation errors.

Figure 2

Download asset Open asset

(Very) Short decoding times when both Fisher information and MSE fails.

(a) Time evolution of root mean squared error (RMSE), averaged across trials and stimulus dimensions, using maximum likelihood estimation (solid lines) for two populations (blue: $λ_{1} = 1$ , $c = 1$ , red: $λ_{1} = 1$ , $c = 1 / 1.44$ ). Dashed lines indicate the lower bound predicted by Cramér-Rao. The black circle indicates the point where the periodic population has become optimal in terms of MSE. (b) The empirical distribution of errors for the time indicated by the black circle in (a). The single-peaked population (blue) has a wider distribution of errors centered around 0 compared to the periodic population (red), as suggested by having a higher MSE. Inset: Zooming in on rare error events reveals that while the periodic population has a narrower distribution of errors around 0, it also has occasional errors across large parts of the stimulus domain. (c) The empirical CDF of the errors for the same two populations as in (b). Inset: a zoomed-in version (last 1%) of the empirical CDF highlights the heavy-tailed distribution of errors for the periodic population. Parameters used in the simulations: stimulus dimensionality $D = 2$ , the number of modules $L = 5$ , number of neurons $N = 600$ , average evoked firing rate $\bar{f_{s t i m}} = 20 \exp (- 1 / w) B_{0} (1 / w)$ sp/s, ongoing activity $b = 2$ sp/s, and width parameter $w = 0.3$ . Note that the estimation errors for the two stimulus dimensions are pooled together.

Figure 3 with 2 supplements

Download asset Open asset

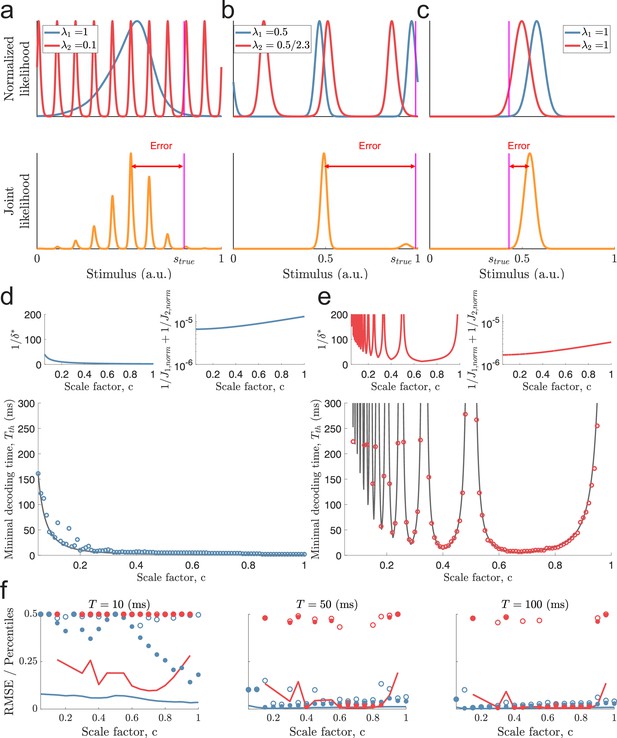
Catastophic errors and minimal decoding times in populations with two modules.

(a) Top: Sampled individual likelihood functions of two modules with very different spatial periods. Bottom: The sampled joint likelihood function for the individual likelihood functions in the top panel. (**b–c**) Same as in (a) but for spatial periods that are similar but not identical and for a single-peaked population, respectively. (d) Bottom: The dependence of the scale factor c on the minimal decoding time for $λ_{1} = 1$ . Blue circles indicate the simulated minimal decoding times, and the black line indicates the estimation of the minimal decoding times according to Equation 8, with $p_{e r r o r} = 10^{- 4}$ . Top left: The predicted value of $1 / δ^{*}$ . Top right: The inverse of the Fisher information. (e) Same as (d) but for $λ_{1} = 1 / 2$ . (f) RMSE (lines), the 99.8th percentile (filled circles), and the maximal error (open circles) of the error distribution for several choices of scale factor, $c$ , and decoding time. The color code is the same as in panels (**d-e**). The parameters used in (**d-f**) are: population size $N = 600$ , number of modules $L = 2$ , scale factors $c = 0.05 - 1$ , width parameter $w = 0.3$ , average evoked firing rate $\bar{f_{s t i m}} = 20 \exp (- 1 / w) B_{0} (1 / w)$ sp/s, ongoing activity $b = 0$ sp/s, and threshold factor $α = 2$ .

Figure 3—figure supplement 1

Download asset Open asset

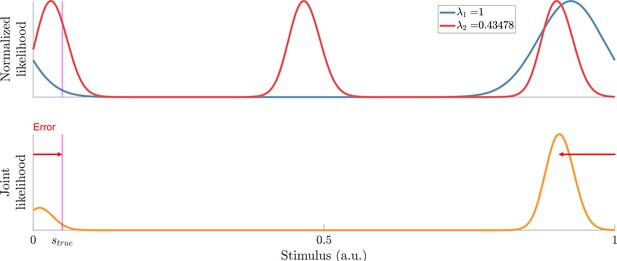
Example of decoding a stimulus close to the periodic edge.

Top: Sampled likelihood functions of two modules with $λ_{1} = 1$ and $λ_{2} = 1 / 2.3$ . Bottom: The joint likelihood function is shifted across the periodic boundary. Such shifts across the periodic boundary can become more pronounced when $λ_{2}$ is slightly below a multiple of $λ_{1}$ .

Figure 3—figure supplement 2

Download asset Open asset

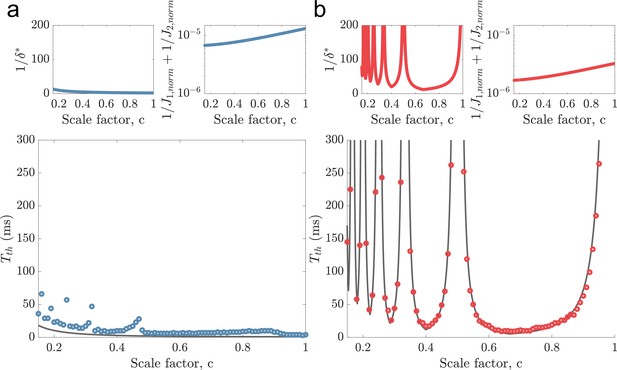
Same as (Figure 2d–e) but using threshold factor $α = 1.2$ .

Notice the stronger deviations from the predicted minimal decoding time for $λ_{1} = 1$ when c is slightly below $1 / 2, 1 / 3, 1 / 4, \dots$ , etc.

Figure 4 with 6 supplements

Download asset Open asset

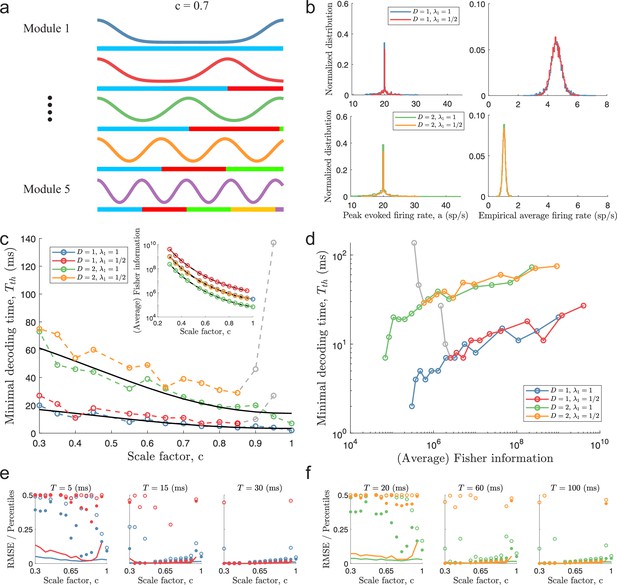
Minimal decoding times for populations with five modules.

(a) Illustration of the likelihood functions of a population with $L = 5$ modules using scale factor $c = 0.7$ . (b) The peak stimulus-evoked amplitudes of each neuron (left column) were selected such that all neurons shared the same expected firing rate for a given stimulus condition (right column). (c) Inset: Plot of average Fisher information as a function of the scale factor $c$ (colored lines: estimations from simulation data, black lines: theoretical approximations). Main plot: Plot of minimal decoding time as a function of scale factor $c$ . Minimal decoding time tends to increase with decreasing grid scales (colored lines: estimated minimal decoding time from simulations, black lines: fitted theoretical predictions using Equation 47). The gray color corresponds to points with large discrepancies between the predicted and the simulated minimal decoding times. (d) Plot of the average Fisher information against the minimal decoding time. Points colored in gray are the same as in panel (c). (e) RMSE (lines), the 99.8^th percentile (filled circles), and the maximal error (open circles) of the error distribution when decoding a 1-dimensional stimulus for several choices of decoding time. The color code is the same as above. (f) same as (e) but for a two-dimensional stimulus. Note that the error distributions across stimulus dimensions are pooled together. Parameters used in panels (**a-d**): population size $N = 600$ , number of modules $L = 5$ , scale factors $c = 0.3 - 1$ , width parameter $w = 0.3$ , average evoked firing rate $\bar{f_{s t i m}} = 20 \exp (- D / w) B_{0} {(1 / w)}^{D}$ sp/s, ongoing activity $b = 0$ sp/s, and threshold factor $α = 2$ .

Figure 4—figure supplement 1

Download asset Open asset

Scaling of minimal decoding time with stimulus dimensionality and tuning width.

(a) The predicted minimal decoding time from $D = 1$ scaled by $\frac{\exp (1 / w)}{B_{0} (1 / w)}$ provides a reasonable prediction of the minimal decoding time for $D = 2$ . The data used is the same as in Figure 4c (solid lines with circles, color code the same as in the main figure). (**b–d**) Minimal decoding times for various width parameters $w$ . As in Figure 4c, there is a trend of increasing minimal decoding time with decreasing scale factor $c$ . However, the range of minimal decoding times decreases with decreasing widths (for $D = 1$ ).

Figure 4—figure supplement 2

Download asset Open asset

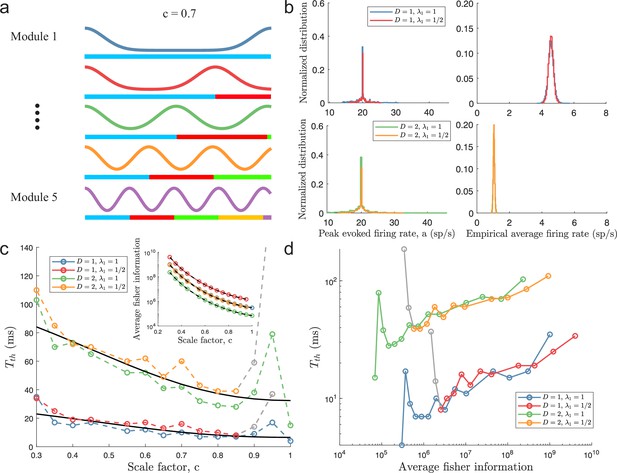
Minimal decoding times using a different threshold factor.

Same as Figure 4a–d in the main text, but simulated using threshold factor. For each $T$ , the MSE is evaluated based on 15,000 random stimulus samples.

Figure 4—figure supplement 3

Download asset Open asset

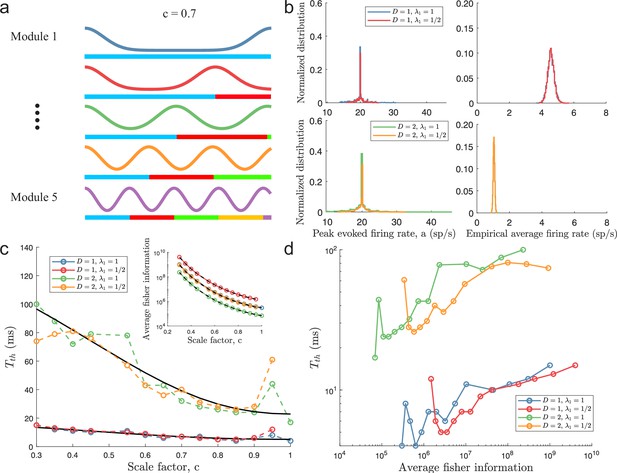
Minimal decoding times based on one-sided KS-tests.

Same as Figure 4a–d in the main text, but simulated using the one-sided KS-test for determining minimal decoding time (see main text for details). For each $T$ , the MSE is evaluated based on 15,000 random stimulus samples.

Figure 4—figure supplement 4

Download asset Open asset

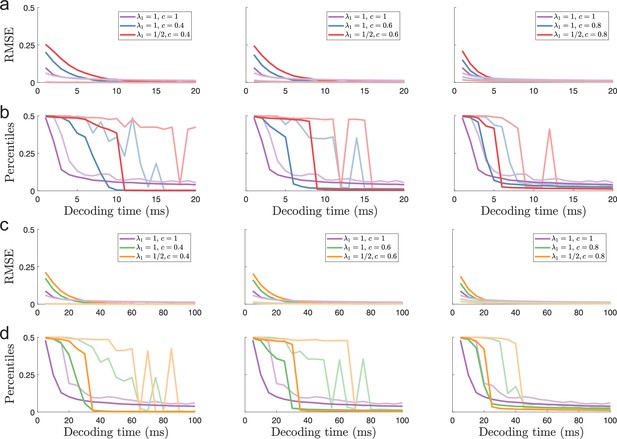
Time evolution of MSE and outlier errors.

(a) Time evolution of the RMSE (non-transparent lines) for periodic and single-peaked populations and the lower bound set by the Cramér-Rao bound (transparent lines) when decoding a $D = 1$ stimulus. (b) Same as in (a) but for the 99.8^th (non-transparent lines) and the 100^th (transparent lines) percentiles of the root squared error distributions. (**c–d**) same as (**a-b**) but for a $D = 2$ stimulus. For each decoding time $T$ , the RMSE and outliers are evaluated based on 15,000 random stimulus samples.

Figure 4—figure supplement 5

Download asset Open asset

Spike counts required for removing catastrophic errors.

Plot of the mean spike counts (summed over the population) required to remove catastrophic errors for the populations in Figure 4. Each circle indicates the minimal spike count for a single population with a constant scale factor encoding either a one-dimensional (x-axis) or a two-dimensional stimulus (y-axis). Blue circles indicate $λ_{1} = 1$ and red circles $λ_{1} = 1 / 2$ . Being on the grey line corresponds to having the same required spike count for both stimulus cases.

Figure 4—figure supplement 6

Download asset Open asset

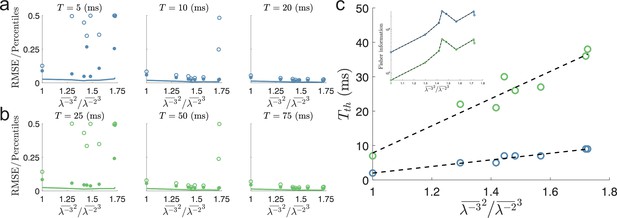
Minimal decoding times for populations without scale factors.

Same as Figure 4c, e and f, but only using tuning curves with an integer number of peaks, that is, being all integers. Thus, there is no common scale factor relating the spatial frequencies of the modules within a population. The populations here have $1 / λ = [1]$ , $[1, 2]$ , $[1, 3]$ , $[1, 4]$ , $[1, 2, 3]$ , $[1, 2, 4]$ , $[1, 3, 4]$ , or $[1, 2, 3, 4]$ . Note that for the single-peaked population, ${\bar{λ^{- 3}}}^{2} / {\bar{λ^{- 2}}}^{3} = 1$ . (a) Shows the RMSE (solid lines) and the outliers, 99.8th (filled circles) and 100th (open circles) percentiles, for a $D = 1$ stimulus. (b) Same as (a) but for a $D = 2$ stimulus. (c) Same as Figure 4c but for the integer peaked populations listed above (blue: $D = 1$ , green: $D = 2$ ).

Figure 5

Download asset Open asset

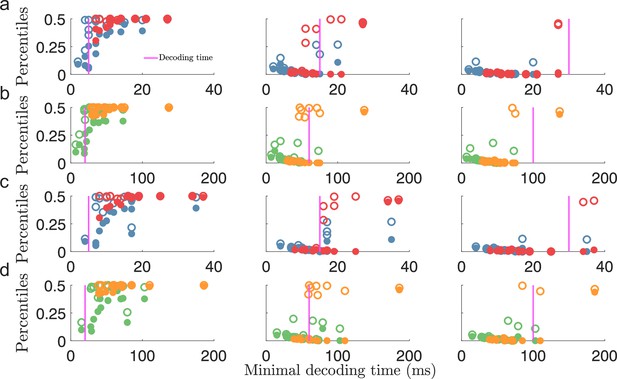
Minimal decoding time predicts the removal of large estimation errors.

(a) The 99.8th percentile (filled circles) and the maximal error (i.e., 100th percentile, open circles) of the root squared error distributions for $D = 1$ against the estimated minimal decoding time for the corresponding populations ( $α = 2$ ) for various choices of decoding time, $T$ (indicted by the vertical magenta lines). (b) same as (a) but for $D = 2$ . (c-d) Same as for (**a-b**) but for $α = 1.2$ . Note that the plots (a) and (c), or (b) and (d), illustrate the same percentile data only remapped on the x-axis by the different minimal decoding times from the different threshold factors $α$ . Color code: same as in Figure 4.

Figure 6 with 2 supplements

Download asset Open asset

Ongoing activity increases minimal decoding time.

(a) The case of encoding a one-dimensional stimulus ( $D = 1$ ) with or without ongoing activity at 2 sp/s (diamond and circle shapes, respectively). (b) The case of a two-dimensional stimulus ( $D = 2$ ) under the same conditions as for (a). In both conditions, ongoing activity increases the time required for all populations to produce reliable signals, but the effect is strongest for $c ≪ 1$ . The parameters used in the simulations are: population size $N = 600$ , number of modules $L = 5$ , scale factors $c = 0.3 - 1$ , width parameter $w = 0.3$ , average evoked firing rate $\bar{f_{s t i m}} = 20 \exp (- D / w) B_{0} {(1 / w)}^{D}$ sp/s, ongoing activity $b = 2$ sp/s, and threshold factor $α = 2$ .

Figure 6—figure supplement 1

Download asset Open asset

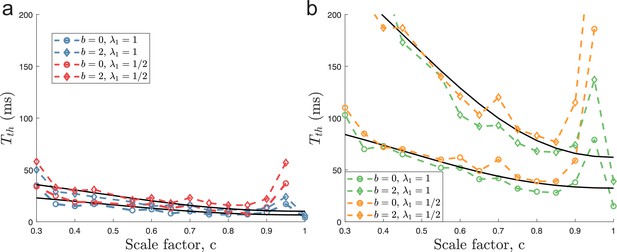
Minimal decoding times using a different threshold factor.

Same as Figure 6 in the main text, but using $α = 1.2$ .

Figure 6—figure supplement 2

Download asset Open asset

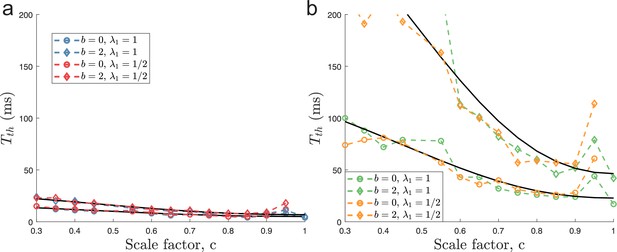
Minimal decoding times based on one-sided KS-test.

Same as Figure 6 in the main text, but using the one-sided KS-test criterion described before (see Figure 4—figure supplement 4).

Figure 7

Download asset Open asset

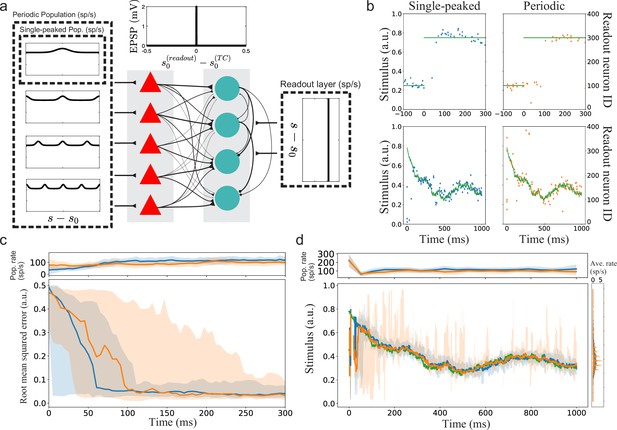
Implications for a simple spiking neural network with suboptimal readout.

(a) Illustration of the spiking neural networks (SNNs). (b) Example of single trials. Top row: Two example trials for step-like change in stimulus (green line). The left and right plots show the readout activity for the single-peaked (blue) and periodic SSNs (orange), respectively. Note that the variance around true stimulus is larger for the single-peaked SNN (i.e. larger local errors) but that there are fewer very large errors than for the periodic SNN. Bottom row: Same as for the top row but with a continuously time-varying stimulus. (c) Bottom: The median RMSE (thick lines) over all trials in a sliding window (length 50ms) for the single-peaked (blue) and periodic (orange) SNNs. The shadings correspond to the regions between the 5th and 95th percentiles. Top: The instantaneous population firing rates of the readout layers and the standard deviations (same color code as in the bottom panel). (d) Bottom left: The median estimated stimulus across trials in a sliding window (length 10ms) for the single-peaked (blue) and periodic (orange) SNNs. Shaded areas again correspond to the regions between the 5th and 95th percentiles. The true stimulus is shown in green. Bottom right: the average firing rate of each neuron, arranged according to the preferred stimulus condition. Top: The instantaneous population firing rates of the readout layers and the standard deviations. See Materials and methods for simulation details and Table 1, Table 2, Table 3 for all parameters used in the simulation.

Figure 8

Download asset Open asset

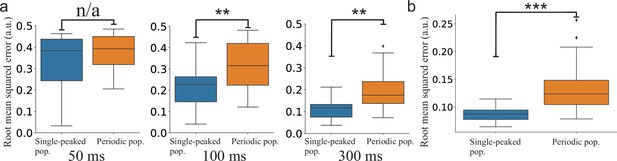
Statistical comparison of the SNN models.

(a) Step-like change: Comparison between the distributions of accumulated RMSEs at different decoding times ( $p = 0.4$ , $9.0 \cdot 10^{- 4}$ , and $8.7 \cdot 10^{- 5}$ , respectively). (b) OU-stimulus: The distributions of RMSE across trials for the two SNNs ( $p = 4.3 \cdot 10^{- 8}$ ). All statistical comparisons in (a) and (b) were based on two-sample Kolmogorov–Smirnov (KS) tests using 30 trials per network.

Figure 9

Download asset Open asset

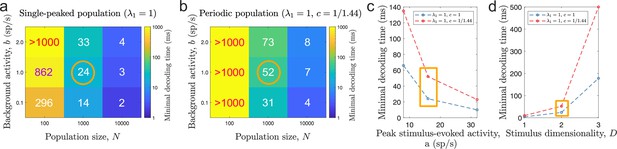
Minimal decoding time for various tuning and stimulus parameters.

(**a-b**) Minimal decoding time for different combinations of population sizes ( $N$ ) and levels of ongoing background activity ( $b$ ) for the single-peaked population (a) and the periodic population (b). (c) Minimal decoding time as a function of average stimulus-evoked firing rate (x-axis re-scaled to the corresponding peak amplitude, $a$ , for single-peaked tuning curves for easier interpretation). The corresponding amplitudes are $a = 8, 16,$ and $32$ sp/s, respectively. (d) Minimal decoding time as a function of stimulus dimensionality. Unless indicated on the axes, the parameters are set according to the orange circles and rectangles in (**a-d**). Auxiliary parameters: number of modules $L = 5$ , width parameter $w = 0.3$ , and threshold factor $α = 1.2$ .

Tables

Table 1

Parameters and parameter values for O-U stimulus.

Parameters	Parameter values
$τ_{s}$	0.5 (s)
$σ_{s}$	0.1

Table 2

Parameters and parameter values for LIF neurons.

Parameters	Parameter values
Membrane time constant, $τ_{m e m b}$ (ms)	20
Threshold memb. potential, $V_{t h}$ (mV)	20
Reset memb. potential (mV)	10
Resting potential, V₀ (mV)	0
Refractory period, $τ_{r p}$ (ms)	2

Table 3

Spiking network parameters and parameter values.

Parameters	Parameter values
Number of neurons 1st layer, N₁	500
Number of neurons 2nd layer, N₂	400
Maximal stimulus-evoked input rate, $a$ (sp/s)	750
Baseline input rate, $b$ (sp/s)	4250
Spatial periods, $λ_{j}$	[1] or [1,2,3,4]
Width parameter, $w$	0.3
Width parameter (readout layer), $w_{r o}$	$\frac{(π / N_{2})^{2}}{2 \log (2)}$
Input EPSP (1st layer), $J_{E}$ (mV)	0.2
Maximal EPSP (2nd layer), $J_{E E}$ (mV)	2
Maximal IPSP (2nd layer), $J_{I I}$ (mV)	2
Synaptic delays, $d$ (ms)	1.5