Figures and data in Homeostasis, injury, and recovery dynamics at multiple scales in a self-organizing mouse intestinal crypt

Figures
Videos
Tables
Additional files

12 figures, 3 videos, 1 table and 2 additional files

Figures

Figure 1

Download asset Open asset

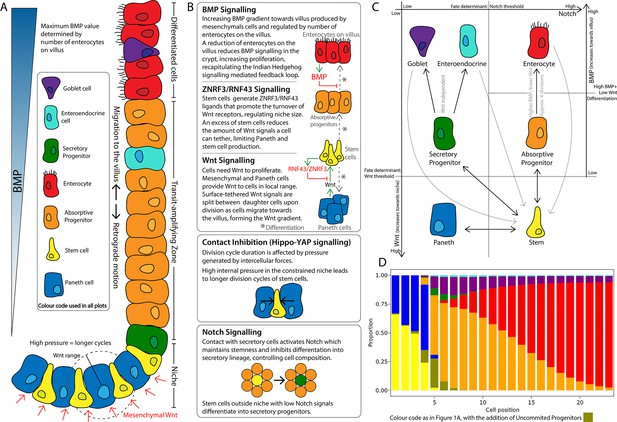
Schematics of the small intestinal crypt composition and cell fate signalling pathways included in the agent-based model (ABM).

(A) Depiction of the crypt highlighting key signalling features and cell types in each crypt region. (B) Details of signalling pathways including the formation of the Wnt signalling gradient with high levels of Wnt in the stem cell niche generated by Paneth and mesenchymal cells. Intercellular pressure regulates the duration of the division cycle (YAP-Hippo pathway-mediated contact inhibition of proliferation) which impacts on the accumulation of cell surface-tethered Wnt signals. Notch signalling maintains the balance between Paneth and stem cells through lateral inhibition. A ZNRF3/RNF43-mediated feedback mechanism modulates Wnt signalling in the niche restricting the number of stem and Paneth cells. BMP signals generated by mature villus cells form a feedback loop that regulates maturation and proliferation of absorptive progenitors. (C) Cell fate determination. High Wnt signalling and activation of Notch are required to maintain stemness. Low Notch signalling determines differentiation into secretory fates, including Paneth cells in high Wnt signalling regions, or goblet/enteroendocrine progenitors in low Wnt regions. Absorptive progenitors develop from stem cells in low Wnt conditions and divide 3–5 times, before becoming terminally differentiated when Wnt signal levels are decreased and cells find sufficient BMP signals. (D) Average composition of a simulated healthy/homeostatic crypt (over 100 simulated days), showing the relative proportion of cells at each position.

Figure 2

Download asset Open asset

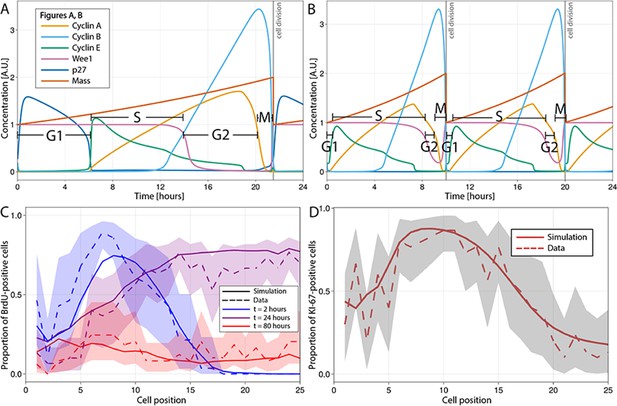
Multiscale modelling of cell division in single cells of the agent-based model (ABM).

(**A, B**) Modelled dynamics of the main cell cycle proteins across the phases of division in each single cell over a 24 hr period, according to the cell cycle regulatory protein network model of Csikasz-Nagy (Csikász-Nagy et al., 2006). The protein interaction diagram can be found in the original report of Csikasz-Nagy (Csikász-Nagy et al., 2006). Stem cells in the crowded niche (A) exhibit longer cycles, up to 21.5 hr on average, with elevated levels of p27 regulating the duration of G1 and the starting of S-phase. Cells in the transit-amplifying compartment (B) have shorter cycles, up to 10 hr on average, due to low levels/lack of p27 expression which leads to G1 shortening and early start of the S-phase. A.U., arbitrary units. (C) Observed (dashed line) and simulated (solid line) proportions of BrdU-positive cells at each crypt position at 2 hr (blue), 24 hr (purple), and 80 hr (red) after a single pulse of BrdU. (D) Observed and simulated Ki-67-positive cells at each crypt position assuming that Ki-67 is detected in cycling cells at all phases except G1 and in any recently differentiated and arrested cells. Shadows depict the 95% confidence interval of our simulated staining results assuming that the proportion of staining cells has a beta distribution and estimating its error from experimental data.

Figure 3

Download asset Open asset

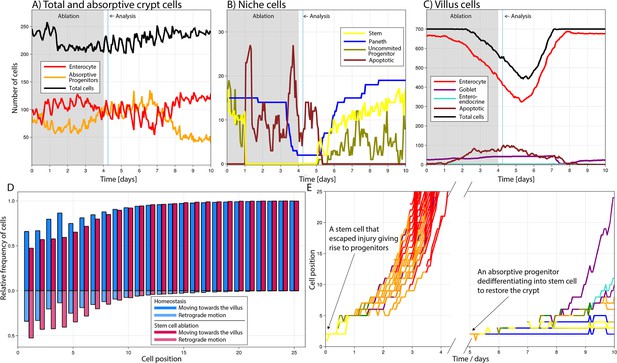
Simulated cell dynamics in the epithelium subjected to continuous ablation of stem cells for four consecutive days (grey block) resembling a previously published experiment **(A–C**) (Tan et al., 2021).

Analysis time denotes 6 hr after ablation interruption for comparison with reported results (Tan et al., 2021). All cell lineages are recorded during treatment and few days after recovery of the simulated crypt for comparison with homeostasis. A simulated 3D image of a crypt in homeostasis can be found in Figure 4A. (A) shows the total number of cells, absorptive progenitors, and enterocytes in the crypt; (B) shows the number of Paneth, stem cells, and uncommitted progenitors, mostly found in the niche; and (C) shows villus cells. (D) Relative frequency of crypt cells moving towards the villus (darker colour) and towards the crypt base, that is, retrograde motion (lighter colour), in homeostasis (blue) and during stem cell ablation (red) at each cell position, showing increased retrograde cellular motion in the niche following stem cell ablation. (E) Leftmost: trajectories (cell position on crypt–villus longitudinal axis vs time) of the progeny of one stem cell, with both daughters leaving the niche and giving rise to a cascade of absorptive and secretory cells that eventually leave the crypt. Rightmost: trajectories of the progeny of an absorptive progenitor dedifferentiating into a stem cell during recovery after stem cell ablation.

Figure 4

Download asset Open asset

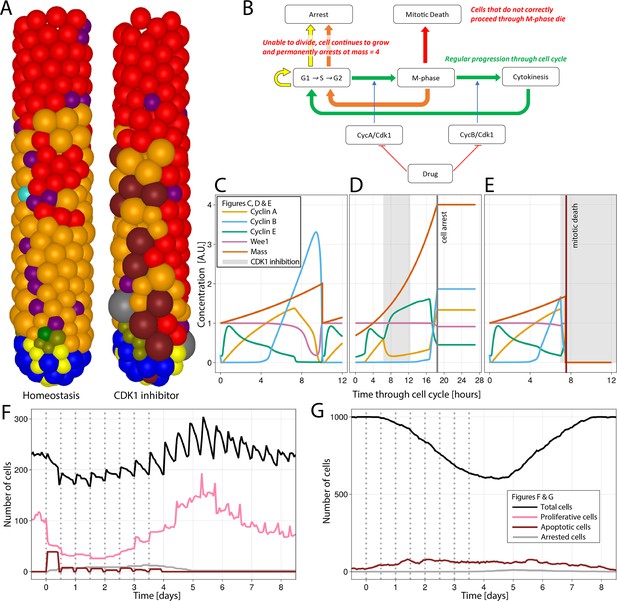
Simulation of CDK1 inhibition for 6 hr, every 12 hr for four consecutive days in the agent-based model (ABM) and impact on the cell cycle and crypt and villus organization.

All cell lineages are recorded during treatment and a few days after recovery of the simulated crypt for comparison with homeostasis.

(A) A simulated 3D image of a crypt in homeostasis (left) and a crypt subjected to CDK1 inhibition (right). Following CDK1 inhibition, the simulated crypt exhibits apoptotic cells and oversized cells unable to correctly complete the cell cycle and eventually undergo cell cycle arrest. Colour code provided here for apoptotic and arrested cells and in Figure 1A for the rest of cells. (B) Flowchart showing the regular progression through the cell cycle (green path) disturbed by CDK1 inactivation. A disorderly restart of the cycle, leading to enlarged cells, is observed when CDK1 inhibition prevents cells from entering (yellow path) or completing M-phase (orange path) by early reduction of cyclin B, with premature restart of G1 (orange path). Cells in M-phase subjected to greater reduction of cyclins A and B that completely disrupts the protein network undergo mitotic death (red path). (C) Cell cycle protein dynamics in homeostasis. (**D, E**) Altered cell cycle protein profile by CDK1 inhibition, resulting in premature restart of G1 and arrest of enlarged cell (D) and in disruption of the protein network and cell death (E). Protein concentrations given in arbitrary units (A.U.). Cell dynamics in simulated crypts (F) and villi (G) during CDK1 inhibition period and recovery. The dynamics of all cell lineages are reported in Appendix 1—figure 1. Discontinuous bars denote the beginning of CDK1 inhibition period.

Figure 5

Download asset Open asset

Modelling 5-fluorouracil (5-FU) (50 mg/kg twice a day for 4 d) induced injury at several scales in mouse small intestinal epithelium.

(A) Diagram showing the implemented mechanism in the agent-based model (ABM) to describe DNA and RNA damage and cell cycle disruption driven by 5-FU metabolites. Cells trigger the apoptotic pathway if relatively high levels of RNA and/or DNA damage are detected at the cycle checkpoints. Lower levels of DNA damage induced P21 activation, which, together with RNA damage, slow down and could eventually arrest the cycle. (B) Predicted concentration (ng/ml) of 5-FU, FUTP, and FdUTP in plasma in mouse (pharmacokinetics model of 5-FU described in Gall et al., 2023). (**C, D**) Cell cycle protein dynamics and fate decision when 5-FU challenge starts (C) prior to or at the beginning of S-phase, leading to DNA damage and cell death at the G2-M-phase checkpoint, and (D) at the end of S-phase, resulting in not enough DNA damage, the cell finishes the cycle. (E) Predicted (solid line) and observed (dashed line) proportions of Ki-67-positive cells along the crypt axis at 6 hr, 1 d, 4 d, and 6 d during the 5-FU treatment period. Shadows depict the 95% confidence interval of our simulated staining results assuming that the proportion of staining cells has a beta distribution and estimating its error from experimental data. (**F, G**) Predicted (lines) and observed (symbols) number of cells in the crypt (F) and villus (G). Vertical bars represent dosing times. Symbols represent cell counts from individual mice.

Appendix 1—figure 1

Download asset Open asset

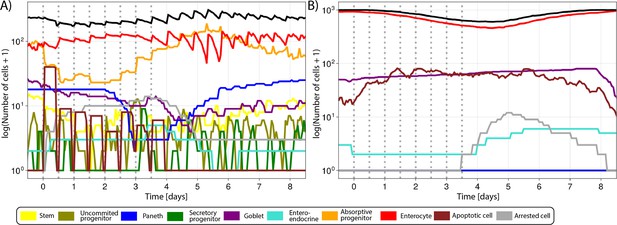
Simulated cell lineages in the crypt (A) and villus (B) during a 4-day CDK1 inhibition treatment for 6 hr, every 12 hr for four consecutive days and following recovery in the agent-based model (ABM) as described in Figure 4.

Appendix 1—figure 2

Download asset Open asset

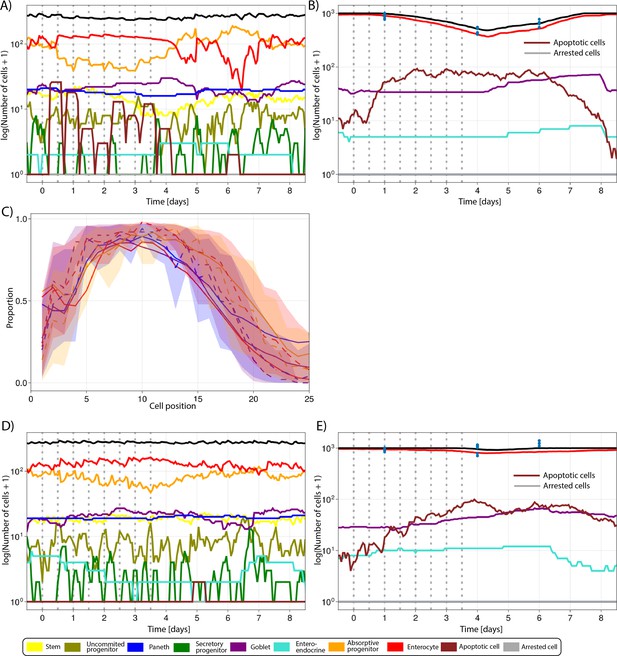
Simulated (lines) and observed (symbols) number of cells in the crypt.

(A) and villus (B) during the administration of 50 mg/kg of 5-fluorouracil (5-FU) twice a day for 4 d and following recovery as described in Figure 5. (C) Predicted (continuous lines) and observed (dashed line) proportions of Ki-67-positive cells along the crypt axis at 6 hr, 1 d, 4 d, and 6 d following the administration of 20 mg/kg of 5-FU twice a day for 4 d. Shadows depict the 95% confidence interval of our simulated staining results assuming that the proportion of staining cells has a beta distribution and estimating its error from experimental data. (**D, E**) Predicted (lines) and observed (symbols) number of cells in the crypt (D) and villus (E) during the administration of 20 mg/kg of 5-FU twice a day for 4 d and subsequent recovery. Vertical bars represent dosing times. Symbols represent cell counts from individual mice.

Appendix 1—figure 3

Download asset Open asset

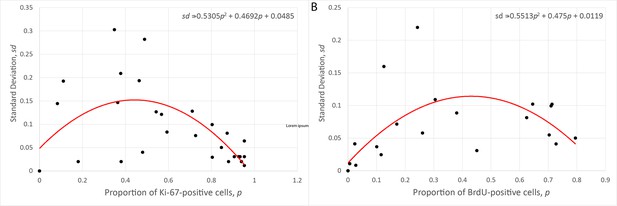
Relationship between the mean and the standard deviation of the proportion of Ki-67- (A) and BrdU-positive (B) cells observed at several crypt positions in three replicated control experiments.

Appendix 1—figure 4

Download asset Open asset

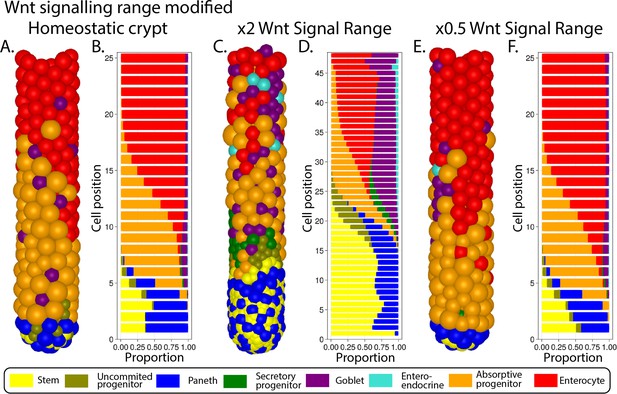
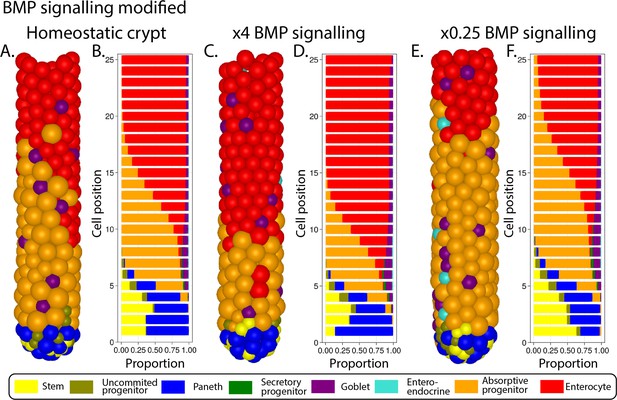
Simulated ileal mouse crypt with modified Wnt signalling.

Three-dimensional image (A) and cell composition (B) by position in homeostasis and likewise after doubling (**C, D**) and halving (**E, F**) Paneth cell generated Wnt signals, maintaining homeostatic levels of Wnt of mesenchymal sources.

Appendix 1—figure 5

Download asset Open asset

Simulated ileal mouse crypt with modified ZNRF3/RNF43 signalling.

Three-dimensional image (A) and cell composition (B) by position in homeostasis and likewise after doubling (**C, D**) and halving (**E, F**) ZNRF3/RNF43 signalling strength.

Appendix 1—figure 6

Download asset Open asset

Simulated ileal mouse crypt with modified Notch signalling.

Three-dimensional image (A) and cell composition (B) by position in homeostasis and likewise after increasing (**C, D**) and decreasing (**E, F**) the Notch threshold by 1 A.U.

Appendix 1—figure 7

Download asset Open asset

Simulated ileal mouse crypt with modified BMP signalling.

Three-dimensional image (A) and cell composition (B) by position in homeostasis and likewise after a fourfold increase (**C, D**) and a fourfold decrease (**E, F**, respectively) of BMP signalling strength.

Videos

Video 1

Download asset

posterframe for video — Simulated cell dynamics in the epithelium subjected to continuous ablation of stem cells for four consecutive days resembling a previously published experiment (Tan et al., 2021).

Plots depict changes in the number of cells in the crypt and villus during the simulation. Colour code of cell types is included below plots.

Video 2

Download asset

Video 3

Download asset

Tables

Appendix 1—table 1

Parameter values of the agent-based model (ABM) model of the mouse small intestinal crypt.

Parameter		Value		Source/justification
		Jejunum	Ileum	Source/justification
Geometry
$C_{h}$ , maximum fold-increase of the height of the crypt		1.2		Calibration of ABM to experimental data in drug-injured crypt
$q$ , Hill coefficient of height scaling		3.5		Calibration of ABM to experimental data in drug-injured crypt
Crypt circumference		9 distance units*		Calibration of ABM to experimental data in a homeostatic crypt Due to cell compression, this results in a crypt circumference of 10 cells
Villus length		1000 cells (700 for cell ablation)
Biochemical signalling
BMP/Indian hedgehog feedback
$z_{0}$ , z coordinate at the top of the crypt in homeostatic conditions (measured from the edge of stem cell niche in the direction of the longitudinal crypt–villus z-axis)		18 distance units*.	16 distance units*.	Calibration of ABM to experimental data in homeostatic and drug-injured crypt Due to cell compression, this results in a homeostatic crypt height of 22–26 (jejunum) and 20–24 (ileum) measured in cell positions
$z_{50 .}$ z coordinate at which the number of mature enterocytes becomes greater than the number of absorptive progenitors in homeostatic conditions (measured from the edge of stem cell niche in the direction of the longitudinal crypt–villus z-axis)		14.5 distance units*.	13 distance units*.	Calibration of ABM to experimental data in a homeostatic crypt Due to cell compression, this corresponds to cell position 18 (jejunum) and 16 (ileum)
$E_{h}$ , homeostatic enterocyte count		940 cells	920 cells (644 for cell ablation experiment)	Calibration of ABM to experimental data in homeostatic and drug-injured crypt (Umar, 2010) Cell ablation experiment scaled using 0.7× reduction in villus length
$p$ , Hill coefficient of Hedgehog/BMP feedback		8.5	4	Calibration of ABM to experimental data in a drug-injured crypt
$A$ , level of BMP signals at height z_top		64		Calibration of ABM to experimental data in homeostatic crypt
$B$ , exponential transformation of the diffusion coefficient of BMP signals		8		Calibration of ABM to experimental data in homeostatic crypt
Wnt signalling
$k_{W n t}$		152.80		Calibration of ABM to experimental data in homeostatic crypt
WntRange, Wnt signalling short-range field around Paneth cells and Wnt-emitting mesenchymal cells where Wnt signals tethered to receptive cells		0.35 distance units*		Calibration of ABM to experimental data in homeostatic crypt
$M e s e n c h y m a l_{n i c h e}$ , number of Wnt emitting mesenchymal cells surrounding the stem cell niche		32 cells		Assumed equal to the total number of epithelial cells in the niche in homeostatic conditions (Wright and Alison, 1984; Snippert et al., 2010)
$M_{W n t}$ , maximum number of Wnt signals a cell can have tethered		128		Calibration of ABM to experimental data in homeostatic crypt Value chosen to be a power of 2 to facilitate dividing Wnt signals in half upon cellular division
Notch signalling
$k_{n o t c h}$		200		Calibration of ABM to experimental data in homeostatic crypt
Notch range		0 during homeostasis, increasing to one cell unit with drop in local cell density		Calibration of ABM to experimental data in homeostatic and drug-injured crypt
ZNRF3/RNF43 signalling
$Z$ , maximum signal strength immediately around the emitting cell		1		Calibration of ABM to experimental data in homeostatic crypt
$L_{Z N R F 3}$ , length scale of ZNRF3 signalling.		1 distance units*		Calibration of ABM to experimental data in homeostatic crypt
$K$ , regulates the dependence of the decay rate of cell surface-tethered Wnt molecules on ZNRF3/RNF43 signals		19.1		Calibration of ABM to experimental data in homeostatic crypt
$Z N R F 3_{}$ , ZNRF3 signal strength experienced at the edge of niche		3.5		Calibration of ABM to experimental data in homeostatic crypt. Maintains homeostatic number of stem cells, ≈14-16 (Snippert et al., 2010)
$u$ , Hill coefficient of ZNRF3 feedback.		1		Calibration of ABM to experimental data in a drug-injured crypt
Contact inhibition and mechanical parameters
$p_{0}$		3.2		Calibration of ABM to experimental data in homeostatic crypt
$ϵ_{P a n e t h - P a n e t h}$ , adhesive constant for Paneth–Paneth interactions		0.1111		Calibration of ABM to experimental data in homeostatic crypt
$ϵ$ , adhesive constant for all other interactions		0.01111		Calibration of ABM to experimental data in homeostatic crypt
$ν$ , Poisson ratio		0.4		Based on published data (Geissler and Hecht, 1981; Mokbel et al., 2020; Mahaffy et al., 2004)
$E$ , Young’s modulus		25 kPa (Paneth), 4 kPa (all others)		Pin et al., 2015
$μ_{f r i c .}$		$\frac{π (r^{2} - p_{i j}^{2})}{10000}$		Calibration of ABM to experimental data in homeostatic crypt Maintains published cell transfer velocity of 1 cell/hr (Potten, 1998)
$μ$		$\frac{1 + 2 π r_{c e l l}^{2}}{3000}$ (multiplied by 10,000 for Paneth cells)		Calibration of ABM to experimental data in homeostatic crypt Maintains published cell transfer velocity of 1 cell/hr (Potten, 1998)
Cell timescales
$t_{c y c l e}^{s h o r t}$		10 hr		Wright and Alison, 1984
$t_{c y c l e}^{l o n g}$		21.5 hr		Schepers et al., 2011
Paneth cell lifespan		54 d		Ireland et al., 2005
Other cell lifespan		6 d (jejunum), 6.5 d (ileum) (4 d for villus cells in Barker experiment)		Calibration of ABM to experimental data in drug-injured crypt
Apoptosis duration		12 hr		Sundquist et al., 2006
Paneth ->Stem de-differentiation duration		48 hr (reversible for first 36 hr)		Calibration of ABM to experimental data in homeostatic crypt (Tan et al., 2021)
Absorptive progenitor ->Enterocyte differentiation duration		0 hr		Calibration of ABM to experimental data in homeostatic crypt
All other differentiations duration		4 hr		Stamataki et al., 2011
Duration of Ki-67 positivity		6 hours post-differentiation. 6/8/10/12 hr after drug-induced cell cycle interruption in G1/S/G2/M-phase		Calibration of ABM to experimental data in homeostatic and drug-injured crypt.(Miller et al., 2018)
$K_{B r d U},$ theoretical maximum level of BrdU		5.7		Calibration of ABM to experimental data in homeostatic crypt
Cell fate decision parameters
Stem ->Paneth Notch threshold		3		Calibration of ABM to experimental data in homeostatic crypt
Absorptive/secretory Notch threshold		2		Calibration of ABM to experimental data in homeostatic and drug-injured crypt
Paneth ->Stem emergency Notch threshold		5		Calibration of ABM to experimental data in homeostatic crypt. Qualitatively reproduces (Yu et al., 2018)
Paneth/stem Wnt threshold		64		Arbitrary parameterization
Cell cycle modifications
$c_{m a s s}$	$c_{m a s s}^{s h o r t}$	0.962		Calibrated to enable variable division time responding to mechanical cues
$c_{m a s s}$	$c_{m a s s}^{l o n g}$	1.175
$c_{V s i}$	$c_{V s i}^{s h o r t}$	0.1		Calibrated to modify G1-phase duration for variable division time
$c_{V s i}$	$c_{V s i}^{l o n g}$	1
$K A_{W e e 1 p}$	${K A}_{W e e 1 p}^{s h o r t}$	2.76		Calibrated to maintain S-phase duration for variable division time
$K A_{W e e 1 p}$	${K A}_{W e e 1 p}^{l o n g}$	0.97
DNA/RNA module
$v_{1}$		2		Calibration of ABM to experimental data in homeostatic crypt
$v_{2}$		5		Calibration of ABM to experimental data in drug-injured crypt
$s$		3		Calibration of ABM to experimental data in drug-injured crypt
$K_{V s i}$		5		Calibration of ABM to experimental data in drug-injured crypt
$t$		2		Calibration of ABM to experimental data in drug-injured crypt
Drug simulation parameters
Cdk1 inhibitor
$k_{d r u g, C y c A}$		70		N/A
$k_{d r u g, C y c B}$		140		N/A
Mass threshold		4		Mass of cell determining cycle arrest for cells unable to undergo mitosis
5-FU simulation
$d_{D N A}$		50.8		Calibration of ABM to experimental data in drug-injured crypt
$K_{F d U T P}$		13100		Calibration of ABM to experimental data in drug-injured crypt
$n$		5.82		Calibration of ABM to experimental data in drug-injured crypt
$d_{R N A}$		30.3		Calibration of ABM to experimental data in drug-injured crypt
$K_{F U T P}$		1610		Calibration of ABM to experimental data in drug-injured crypt
$m$		1.940		Calibration of ABM to experimental data in drug-injured crypt
Computational parameters
$d t$ , timestep for movement		0.0001 d		N/A
$d t_{c y c l e}$ , timestep for cell cycle		0.00001 d		N/A

*

All distances are normalized such that an average, isolated cell has a diameter of one distance unit. We have assumed cells are deformable and hence lose the spherical shape upon compression so that the cell diameters, in both the z-axis direction (longitudinal crypt–villus axis), as well as in the y–x plane (crypt transversal circumference), are smaller than one unit and result in inequality between the number of cells and the distance units.

Additional files

MDAR checklist: https://cdn.elifesciences.org/articles/85478/elife-85478-mdarchecklist1-v2.pdf
Download elife-85478-mdarchecklist1-v2.pdf
Source code 1 Julia implementation of the agent-based model.: https://cdn.elifesciences.org/articles/85478/elife-85478-code1-v2.zip
Download elife-85478-code1-v2.zip

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Louis Gall
Carrie Duckworth
Ferran Jardi
Lieve Lammens
Aimee Parker
Ambra Bianco
Holly Kimko
David Mark Pritchard
Carmen Pin

(2023)

Homeostasis, injury, and recovery dynamics at multiple scales in a self-organizing mouse intestinal crypt

eLife 12:e85478.

https://doi.org/10.7554/eLife.85478

Figures

Schematics of the small intestinal crypt composition and cell fate signalling pathways included in the agent-based model (ABM).

Multiscale modelling of cell division in single cells of the agent-based model (ABM).

Simulated cell dynamics in the epithelium subjected to continuous ablation of stem cells for four consecutive days (grey block) resembling a previously published experiment (A–C) (Tan et al., 2021).

Simulation of CDK1 inhibition for 6 hr, every 12 hr for four consecutive days in the agent-based model (ABM) and impact on the cell cycle and crypt and villus organization.

Modelling 5-fluorouracil (5-FU) (50 mg/kg twice a day for 4 d) induced injury at several scales in mouse small intestinal epithelium.

Simulated cell lineages in the crypt (A) and villus (B) during a 4-day CDK1 inhibition treatment for 6 hr, every 12 hr for four consecutive days and following recovery in the agent-based model (ABM) as described in Figure 4.

Simulated (lines) and observed (symbols) number of cells in the crypt.

Relationship between the mean and the standard deviation of the proportion of Ki-67- (A) and BrdU-positive (B) cells observed at several crypt positions in three replicated control experiments.

Simulated ileal mouse crypt with modified Wnt signalling.

Simulated ileal mouse crypt with modified ZNRF3/RNF43 signalling.

Simulated ileal mouse crypt with modified Notch signalling.

Simulated ileal mouse crypt with modified BMP signalling.

Videos

Simulated cell dynamics in the epithelium subjected to continuous ablation of stem cells for four consecutive days resembling a previously published experiment (Tan et al., 2021).

Simulated cell dynamics in the epithelium subjected to CDK1 inhibition for 4 d.

Simulated cell and signalling molecular dynamics in the epithelium following the administration of 50 mg/kg of 5-fluorouracil (5-FU) twice a day for 4 d in mouse.

Tables

Parameter values of the agent-based model (ABM) model of the mouse small intestinal crypt.

Additional files

MDAR checklist

Source code 1

Download links

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Be the first to read new articles from eLife

Share this article

Cite this article

Schematics of the small intestinal crypt composition and cell fate signalling pathways included in the agent-based model (ABM).

Multiscale modelling of cell division in single cells of the agent-based model (ABM).

Simulated cell dynamics in the epithelium subjected to continuous ablation of stem cells for four consecutive days (grey block) resembling a previously published experiment (A–C) (Tan et al., 2021).

Simulation of CDK1 inhibition for 6 hr, every 12 hr for four consecutive days in the agent-based model (ABM) and impact on the cell cycle and crypt and villus organization.

Modelling 5-fluorouracil (5-FU) (50 mg/kg twice a day for 4 d) induced injury at several scales in mouse small intestinal epithelium.

Simulated cell lineages in the crypt (A) and villus (B) during a 4-day CDK1 inhibition treatment for 6 hr, every 12 hr for four consecutive days and following recovery in the agent-based model (ABM) as described in Figure 4.

Simulated (lines) and observed (symbols) number of cells in the crypt.

Relationship between the mean and the standard deviation of the proportion of Ki-67- (A) and BrdU-positive (B) cells observed at several crypt positions in three replicated control experiments.

Simulated ileal mouse crypt with modified Wnt signalling.

Simulated ileal mouse crypt with modified ZNRF3/RNF43 signalling.

Simulated ileal mouse crypt with modified Notch signalling.

Simulated ileal mouse crypt with modified BMP signalling.

Simulated cell dynamics in the epithelium subjected to continuous ablation of stem cells for four consecutive days resembling a previously published experiment (Tan et al., 2021).

Simulated cell dynamics in the epithelium subjected to CDK1 inhibition for 4 d.

Simulated cell and signalling molecular dynamics in the epithelium following the administration of 50 mg/kg of 5-fluorouracil (5-FU) twice a day for 4 d in mouse.

Parameter values of the agent-based model (ABM) model of the mouse small intestinal crypt.

MDAR checklist

Source code 1

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)