A theory of hippocampal theta correlations accounting for extrinsic and intrinsic sequences

Version of Record

The authors declare this version of their article to be the Version of Record.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: October 4, 2023 (This version)
Reviewed preprint version 3: September 18, 2023 (Go to version)
Reviewed preprint version 2: August 14, 2023 (Go to version)
Reviewed preprint version 1: May 17, 2023 (Go to version)
Sent for peer review: March 2, 2023
Preprint posted: February 5, 2023 (Go to version)

1. Of interest
Similar excitability through different sodium channels and implications for the analgesic efficacy of selective drugs

Yu-Feng Xie, Jane Yang ... Steven A Prescott

Research Article Apr 30, 2024
Further reading

Abstract
eLife assessment
Introduction
Results
Discussion
Methods
Data availability
References
Article and author information
Metrics

Abstract

Hippocampal place cell sequences have been hypothesized to serve as diverse purposes as the induction of synaptic plasticity, formation and consolidation of long-term memories, or navigation and planning. During spatial behaviors of rodents, sequential firing of place cells at the theta timescale (known as theta sequences) encodes running trajectories, which can be considered as one-dimensional behavioral sequences of traversed locations. In a two-dimensional space, however, each single location can be visited along arbitrary one-dimensional running trajectories. Thus, a place cell will generally take part in multiple different theta sequences, raising questions about how this two-dimensional topology can be reconciled with the idea of hippocampal sequences underlying memory of (one-dimensional) episodes. Here, we propose a computational model of cornu ammonis 3 (CA3) and dentate gyrus (DG), where sensorimotor input drives the direction-dependent (extrinsic) theta sequences within CA3 reflecting the two-dimensional spatial topology, whereas the intrahippocampal CA3-DG projections concurrently produce intrinsic sequences that are independent of the specific running trajectory. Consistent with experimental data, intrinsic theta sequences are less prominent, but can nevertheless be detected during theta activity, thereby serving as running-direction independent landmark cues. We hypothesize that the intrinsic sequences largely reflect replay and preplay activity during non-theta states.

eLife assessment

This important work presents an interesting perspective for the generation and interpretation of phase precession in the hippocampal formation. Through numerical simulations and comparison to experiments, the study provides a convincing theoretical framework explaining the segregation of sequences reflecting navigation and sequences reflecting internal dynamics in the DG-CA3 loop. This study will be of interest for researchers in the spatial navigation and computational neuroscience fields.

https://doi.org/10.7554/eLife.86837.4.sa0

About eLife assessments

Introduction

As a rat navigates in an environment, place cells fire sequentially during one theta cycle (∼100 ms) and form time-compressed representations of behavioral experiences (Skaggs et al., 1996), called theta sequences. Theta sequences were proposed to be driven by extrinsic (extrahippocampal) sensorimotor input (Foster and Wilson, 2007; Huxter et al., 2008; Romani and Tsodyks, 2015; Yiu et al., 2022), since they are played out in the direction of travel during locomotion and, hence, represent current behavioral trajectories. In contrast, various types of hippocampal sequences have also been proposed to arise from intrinsic hippocampal connectivity. Non-local activation of place sequences during immobile periods was observed in replay of past locations after the space has been explored (Skaggs and McNaughton, 1996; Lee and Wilson, 2002) as well as in preplay (Dragoi and Tonegawa, 2011) of prospective locations before the animal explores a novel environment. In addition, some CA3 place cells exhibit out-of-field firing at reward locations (Sasaki et al., 2018). These remote activations of place cells reflect the underlying circuit connectivity rather than the actual location and movement of the animal. Furthermore, a subset of CA3 cell pairs shows rigid theta correlations with peak lags that are independent of the traversal order of their place fields (Yiu et al., 2022), suggesting the existence of hard-wired sequences even when sensorimotor drive is present. Such intrinsic sequences that are driven by intrahippocampal connectivity (Tsodyks et al., 1996), although less predominantly observed during theta (Yiu et al., 2022), are generally interpreted as reflecting spatial memories or planning (Kay et al., 2020).

Existing models for theta sequences are, however, either fully extrinsic or intrinsic. The former often employ short-term plasticity (Romani and Tsodyks, 2015; Thurley et al., 2008), which creates synaptic couplings that are temporally stronger along the instantaneous forward direction. In contrast, intrinsic models, such as the Tsodyks et al., 1996 model, use a fixed asymmetrical weight matrix pre-designed to align with one movement trajectory (for review see Maurer and McNaughton, 2007; Jaramillo and Kempter, 2017). Neither of these models alone can explain the simultaneous presence of rigid and flexible correlations in theta sequences. Here we present a network model that accounts for both types of correlations by separating their generation into two anatomically distinct layers: CA3 and dentate gyrus (DG). Extrinsic sequences are generated in the CA3 layer by short-term synaptic plasticity mechanisms, while the intrinsic sequences are evoked by the CA3-DG feedback loop with fixed asymmetrical weights, as inspired by the experimental evidence that lesions of DG abolish non-local activation of CA3 place cells (Sasaki et al., 2018) and CA3 theta correlations (Ahmadi et al., 2022).

In this paper, we present a model for theta correlations that unifies both extrinsic and intrinsic mechanisms. Extrinsic and intrinsic sequences can propagate simultaneously in separate directions, along the movement trajectory and the pre-designed CA3-DG feedback loops, respectively. As a result, spike correlations display directionality as the two sequences cross each other at various angles: The more parallel they are, the stronger the correlation. Our simulations are in quantitative agreement with directionality properties found in experimental data (Yiu et al., 2022) and propose that rigid correlation structure can serve as a stable temporal pattern, which is recognizable across multiple movement directions. This temporal ‘landmark’ pattern allows spatial encoding even if sensory-motor experience is lacking and may reflect the mechanistic basis for replay in non-theta states.

Results

Dependence of theta sequences on heading directions: Extrinsic and intrinsic sequences

Theta-scale correlations of place cells have been explained by previous models using two different types of network mechanisms, intrinsic and extrinsic ones. For intrinsic models spike correlations are explained by only the recurrent connectivity of the neuronal network (Figure 1A). For extrinsic models, the spike correlation is defined by sensory-motor parameters such as movements (Figure 1B). We first illustrate how these mechanisms work for two exemplary representatives of these two major model classes.

Figure 1

Download asset Open asset

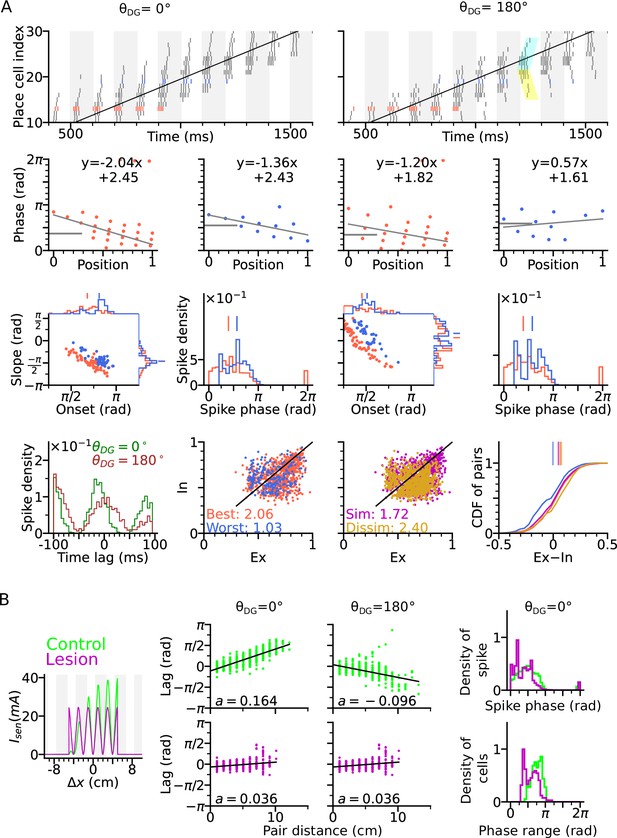
Phase precession depends on running direction in intrinsic models but not extrinsic models.

(A) Left: Schematic illustration of the intrinsic Tsodyks et al., 1996 model. When the animal runs through a series of place fields (solid circles) in 1-D, the place cells fire action potentials in sequence at the theta timescale (spike raster with corresponding colors). Recurrent connectivity is pre-configured and asymmetrical (connection strengths indicated by arrow sizes). Right: Cross-correlation function between the red and magenta cell, which remains the same for both running directions. (B) Left: Schematic illustration of the extrinsic Romani and Tsodyks, 2015 model. Recurrent connections behind the animal are temporarily depressed by short-term plasticity, and thereby, become movement-dependent. Right: Cross-correlation flips sign in the opposite running direction. (C) Simulated trajectories (duration 2 s) in a 2-d environment (80×80 cm) with speed 20 cm/s in left and right (left column), diagonal (middle), and up and down (right) directions. (**D–F**) Simulation results from the intrinsic model (with fixed asymmetrical connectivity inspired by the Tsodyks et al., 1996 model). Place cells only project synapses to their right neighbors. (D) Spike raster plots of place cells along the orange (left panel) and light green (right panel) trajectories (colors defined in C). Theta sequence order remains the same in the reversed running direction. Black line indicates animal position. (E) Phase-position relation for the spikes colored in C. Linear-circular regression (gray line) parameters are indicated on top. Positions of the animal at the first and last spike are normalized to 0 and 1, respectively. (F) Averaged cross-correlation of all cell pairs separated by 4 cm along the trajectory. Reversal of running direction does not flip the sign of the peak lags. (**G–I**) Same as D-F, but for the extrinsic model (spike-based variant of Romani and Tsodyks, 2015 model). Correlation peaks flip after reversal of running direction.

For intrinsic models, we refer to the Tsodyks et al., 1996 model where phase precession is generated by the fixed asymmetrical connectivity between place cells. Spike phases of the place cells ahead of the animal decrease as the excitatory drive is gradually increasing, but only along the direction in which the connection strength is asymmetrically stronger (e.g. rightward in Figure 1A), called the asymmetry direction. Here we simulate a network of CA3 place cells with fixed asymmetrical connectivity (see Methods section: CA3 recurrent connections) as suggested in the Tsodyks et al., 1996 model and applied our model to behavioral running trajectories in a 2-d open space (Figure 1C). Phase precession and spike correlations (Figure 1D–E) are compared for opposite running directions. In our simulations, all place cells project excitatory synapses to their counterparts with rightward neighboring place fields. Phase precession therefore is determined by how closely the running direction matches the asymmetry direction imposed by the intrinsic connections. The closer the trajectory angle aligns with this asymmetry direction, the more negative is the slope of phase precession (Figure 1E). Since in this case, the theta sequence only propagates rightwards as place cells are sequentially activated from left to right, the signs of spike correlations between cell pairs remain invariant to the movement direction (Figure 1F, see Methods section: Cross-correlation analysis). Intrinsic models thus cannot explain experimentally observed directional independence of phase precession and directional dependence of theta spike correlations (Huxter et al., 2008).

Our example of an extrinsic model is based on our spiking simulations of the originally rate-based model by Romani and Tsodyks, 2015, where phase precession was explained by symmetric recurrent connections that undergo running direction-dependent attenuation by short-term synaptic depression (STD): place fields with centers behind the current animal position on the trajectory thereby received largely reduced recurrent input resulting in recurrently driven theta sequences to play out only in forward direction (see Methods section: CA3 recurrent connections). We simulated our spiking variant of the Romani and Tsodyks, 2015 model with the same trajectories as the intrinsic model (Figure 1G–I), and recovered direction-independent phase precession (Figure 1H). Since now, the theta sequences are played out in the same direction as the movement, theta spike correlations are symmetrically reversed (Figure 1I) as shown experimentally in CA1 neurons (Huxter et al., 2008; Yiu et al., 2022).

In area CA3, however, theta spike correlations are neither solely extrinsic (Yiu et al., 2022; Kay et al., 2020), since phase precession properties change in relation to running directions, nor are they solely intrinsic since reversal of correlation is still observed in most of the sequences (Huxter et al., 2008; Yiu et al., 2022). We therefore propose a new theory of phase precession for CA3 incorporating both intrinsic and extrinsic factors.

Directional sensory input

To, however, fully explain directional properties of theta phase precession and theta spike correlations by a model, also directional modulations of firing rates (Yiu et al., 2022) need to be taken into account.

We therefore included both directional and positional modulation of the sensory input to the model place cells (Figure 2A–B) with randomized preferred heading directions (see Methods section: Spatial input). The sensory input is assumed to arise from MEC, and hence, it is also theta-modulated and phase-shifted by $70^{\circ}$ with respected to the peak of theta cycle (Mizuseki et al., 2009). Furthermore, since the precession slope observed in the Romani and Tsodyks, 2015 model is limited (-1.13 radians per field size, see Figure 1H) as compared to the experimental reports (-4.44 radians (Yiu et al., 2022) and about -2.0 radians (Harris et al., 2002) per field size), we introduced short-term synaptic facilitation (STF) to the sensory input (Berretta and Jones, 1996; Thurley et al., 2008) generating temporally asymmetric depolarization as suggested by intracellular recordings in vivo (Harvey et al., 2009; Figure 2B). STF amplifies the sensory current at the later part of the field, thus creating phase precession with steeper slopes thereby extending the phase range (see Methods section: Spatial input). Finally, we designated the synaptic weights to be stronger between place cells with similar preferred heading directions (Figure 2C) as has been proposed (Brunel and Trullier, 1998) as a result of Hebbian plasticity applied to directional firing fields.

Figure 2

Download asset Open asset

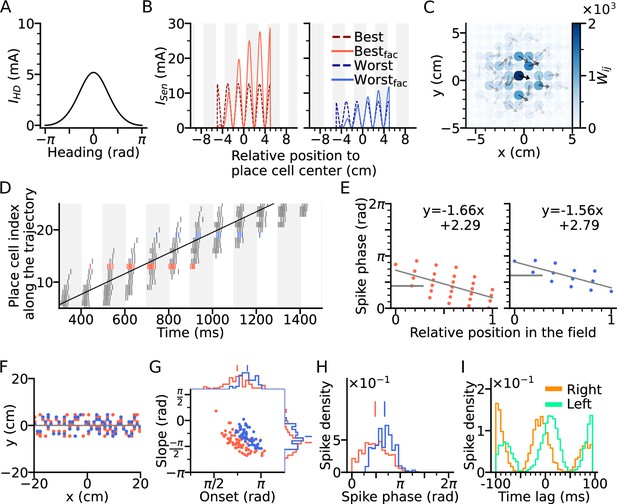
Directional input gives rise to spikes at lower theta phase.

(A) Directional input component of an example place cell. (B) Total sensory input as the sum of directional and positional drive of an example place cell for the animal running along (red dashed line, left) and opposite (blue dashed line, right) the preferred heading direction of the cell, respectively named as *best* and *worst* direction. The sensory input is modelled by oscillatory currents arriving with +70° phase shift relative to theta peaks (gray vertical lines). Place fields are defined by a 5 cm rectangular envelope. Solid lines depict the input current including short-term synaptic facilitation. (C) Synaptic weights ( $W_{i j}$ , color) from the place cell at the center (the darkest dot) to its neighbors in the 2-d environment. Each dot is a place field center in 2-d space. Arrows depict their preferred heading directions. (D) Spike raster plot sorted by visiting order of the place fields along the trajectory. Spikes of the cells with best and worst direction are colored in red and blue, respectively. (E) Phase position plots for the cells with best and worst direction from D (labels as in Figure 1E). The mean phase is marked as horizontal gray bar. (F) Example place cell centers with best (<30° different from the trajectory; red) and worst (>150°; blue) directions relative to the rightward trajectory (gray line). Only centers of cells that fire more than 5 spikes are shown. (G) Slopes and onsets of phase precession of the population from (F). Marginal slope and onset distributions are plotted on top and right, respectively. Note higher phase onset in the worst-direction case. (H) Spike phase distributions. Higher directional inputs generate lower spike phases. (I) Average spike correlation between all pairs with 4 cm of horizontal distance difference when the animal runs rightwards and leftwards. Peak lags are flipped as expected from an extrinsic model.

A simulation of the place cell network was performed for a rightward trajectory through the arena based on our variant of the extrinsic Romani and Tsodyks, 2015 model (Figure 2D). We focus on two sets of place cells, one for which the trajectory aligns with the preferred heading direction of the field (red, denoted as best direction) and one for which the trajectory runs opposite the preferred heading direction (denoted as worst direction; Figure 2F). Phase precession has a lower onset and marginal spike phase along best direction than along the worst (Figure 2G–H), which is consistent with experimental data (Yiu et al., 2022 report mean spike phases ± SEM for best and worst direction of 1.61 ± 0.02 and 2.22 ± 0.03 in radians respectively), reflects that larger depolarizations generally yield shorter latencies. Directionality of the input, although it yields lower spike phases through higher depolarization, does not affect spike pair correlations, which remains solely extrinsic (Figure 2I). Thus, even though rate directionality and directional bias in recurrent connectivity can render phase precession directionally dependent, they are not sufficient to account for intrinsic sequences.

Generation of intrinsic sequences by the DG-CA3 recurrent network

To explain the expression of intrinsic sequences in CA3, we propose them to be generated by the interaction of two networks, CA3 and DG (Figure 3A). DG is a good candidate region to be involved in phase precession, since lesions of it were shown to reduce prospective spiking (Sasaki et al., 2018) and to lower the onset phase of phase precession (Ahmadi et al., 2022). In our model, the neurons in DG receive excitatory synaptic inputs from CA3 place cells (putatively via hilar mossy cells) and project back to the CA3 cells with place field centers at a different location (Equation 3) to induce propagation of intrinsic sequences along a specific spatial direction. The CA3 cells at the target location of DG input are then activated and evoke higher depolarization in cells with place fields at the next DG target locations through the feedback. This scheme produces a rigid sequence whose activation order is independent of the movement direction. The connection pattern of DG-CA3 projections (for brevity, we also refer to it as ‘DG loop’ in the subsequent text) could be determined by pre-existing network structure or past experience through associative learning, or both.

Figure 3 with 2 supplements see all

Download asset Open asset

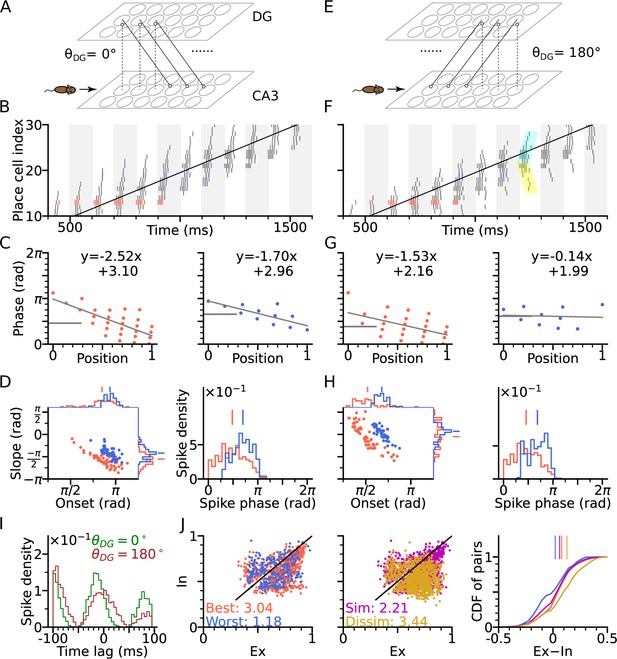
DG-CA3 loop introduces directionality of theta sequences.

(A) Illustration of synaptic connections from CA3 place cells to DG and vice versa. DG layer mirrors the place cell population in CA3 and redirects the CA3 inputs back to different locations. Here, DG cells project into CA3 place cells with fields 4 cm displaced to the right of the pre-synaptic CA3 cells. $θ_{DG}$ denotes the angular difference between the DG projection direction and the animal’s movement direction. (B) Spike raster plots sorted by cell indices along the trajectory (2 s duration) from x=-20 cm to x=20 cm. Cells with best and worst angles are marked by red and blue colors, respectively. (C) Phase-position plots as is Figure 2E. (D) Distributions of precession slopes, onsets and spike phases as in Figure 2G–H. (**E–H**) Same as A-D, but with DG cells projecting opposite to the animal’s movement direction ( $θ_{DG} = 180^{\circ}$ ). In F, cyan and yellow shaded regions indicate the examples of forward sequence induced by the movement (extrinsic), and backward sequence induced by the DG recurrence (intrinsic), respectively. (I) Average spike correlations for $θ_{DG} = 0^{\circ}$ and $θ_{DG} = 180^{\circ}$ for pairs separated by 4 cm along the trajectory. Note that for $θ_{DG} = 180^{\circ}$ , there is a relative excess of spike-pairs with positive lags. (J) Left: Intrinsicity and extrinsicity (see Methods) for all pairs from the populations with best (red) and worst (blue) direction. Pair correlations above and below the identity line are classified as intrinsic and extrinsic, respectively. Numbers are the ratios of extrinsically to intrinsically correlated field pairs. Note that the red best direction pairs are more extrinsic than the blue worst direction pairs due to higher sensory input. Middle: Ex/Intrinsicity of pairs with similar (<30°) and dissimilar (>150°) preferred heading angles. Pairs with similar preferred heading angle s are more intrinsic due to stronger DG-CA3 recurrence. Right: Cumulative distribution of the differences between extrinsicity and intrinsicity. Dissimilar and best direction pairs have higher bias to extrinsicity than similar and worst direction pairs, respectively.

Figure 3, provides schematic illustrations, for a DG layer that either only projects CA3 activity to their rightward neighbours ( $θ_{DG} = 0^{\circ}$ , Figure 3A) or only to their leftward neighbors ( $θ_{DG} = 180^{\circ}$ , Figure 3E). Simulations for both cases ( $θ_{DG} = 0^{\circ}$ and $θ_{DG} = 180^{\circ}$ ) assume a rightward trajectory. Apart from the addition of the DG layer, the model architecture and parameters of CA3 layer are the same as in Figure 2 (including best and worst direction in place field firing rate), which only generates extrinsic sequences through STD in the CA3 recurrent synaptic connections. DG-loop connectivity is additionally modulated by firing rate directionality of the CA3 place fields. Fields with similar preferred heading directions are more strongly connected via the loop than those with opposite preferred heading directions (see Methods section: DG layer).

We found that, when the simulated animal is running in the same direction as the DG-CA3 projection, phase precession starts from a higher phase (Figure 3C–D) due to the forward activation of place cells through DG layer (recovering the effect of asymmetric connectivity in the original Tsodyks et al., 1996 model), as compared to the model without DG layer (Figure 2G–H). Spike phases in best direction remain lower than along the worst direction (Figure 3D). When, however, the animal is running against the DG-CA3 projection (Figure 3E), extrinsic sequences are still present in forward direction, evoked by the movement of the animal, but the intrinsic sequences are played out backward as determined by the direction of fixed recurrence (see cyan and yellow shaded regions in Figure 3F). The latter is reflected by the higher phase at the end of the phase position plots (Figure 3G) which leads to flatter precession slopes and decreases the fraction of phase precession (slope <0) of all traversal trials (Figure 3H). A closer look into pair correlation reveals that for trajectories opposite to the DG-loop projection ( $θ_{DG} = 180^{\circ}$ ), spike probability is added to positive time lags (Figure 3I). Therefore, introducing fixed recurrence through DG loops elicits both extrinsic and intrinsic sequences and qualitatively changes theta sequences.

To quantify the degrees of extrinsic and intrinsic sequence firing in a way allowing comparison to experimental reports, we use the measures extrinsicity and intrinsicity (Yiu et al., 2022) that are based on pairs of place cells with overlapping place fields (see Methods section: Extrinsicity and intrinsicity, and Discussion). In our simulation, extrinsically and intrinsically driven cell pairs are both present in the population (Figure 3J), indicating a coexistence of extrinsic and intrinsic sequences. Our model reproduces a greater extrinsicity for cell pair activity when running direction aligns with both best place field directions as compared to when it aligns to both worst field directions, since along the best direction, cells receive more sensory depolarization, and thus, the movement-dependent extrinsic sequences are more activated. The model also explains, why pairs with similar preferred heading directions may be less extrinsic than pairs with approximately opposite preferred heading direction (dissimilar pairs), since the DG loop preferentially connects CA3 place cells with similar preferred heading directions. Both of the results follow the same trend as found in experimental data (Yiu et al., 2022 report ratios of extrinsically to intrinsically correlated CA3 field pairs of 1.57 for both-best directions, 0.41 for both-worst directions, 0.87 for similar pairs and 2.43 for dissimilar pairs).

Thus, by introducing feedback excitation via the DG layer, intrinsic sequences are able to propagate in fixed directions on top of the movement-dependent extrinsic sequences. Theta sequence directionality is reflected through the change in spike correlation, which varies as a function of the difference between the direction of DG feedback and movement direction. The combination of extrinsic and intrinsic theta sequence activity is robust regarding changes of the parameters of short-term synaptic plasticity (Figure 3—figure supplement 1), as well as running speed (Figure 3—figure supplement 2), as long as place fields are wide enough to allow spikes in sufficiently many theta cycles.

Lesion of DG reduces theta compression and phase precession range

One prediction of the DG-loop model, consistent with findings from DG lesion experiments (Ahmadi et al., 2022), is that DG would contribute to the temporal organization of spike sequences in CA3. To verify this hypothesis also in the model, we implemented a lesion of DG by disabling activity in the DG layer. To compensate for reduced excitatory drive caused by the lesion, we then increased probability of release of the sensory inputs thereby increasing the initial input amplitudes but removing short-term synaptic facilitation (Figure 4A).

Figure 4

Download asset Open asset

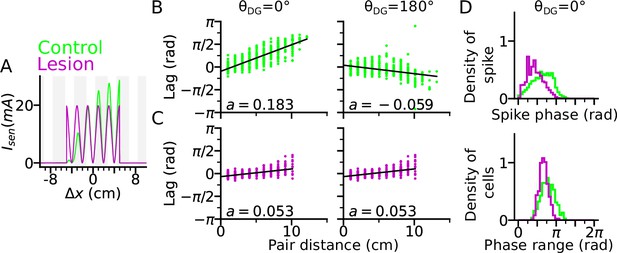
DG lesion reduces theta compression and phase precession range.

DG recurrence is turned off to simulate the lesion condition. (A) Positional sensory inputs into a place cell in lesion (purple) and control (green) cases. The control case is identical to Figure 3. In the lesion case, DG input is compensated by increased sensory input with increased probability of synaptic release, hence reduced short-term synaptic facilitation. (B) Theta compression, that is correlation between peak correlation lag and distance of field centers in the control case. Each dot represents a field pair. Linear-circular regression line is indicated in black. Note that the sign of regression slope ( $a$ in radians/cm) is determined by the directions of DG loop (negative in $θ_{DG} = 180^{\circ}$ ). (C) same as B, but for the lesion case. Theta compression is reduced as compared to the control condition. (D) Top: Distribution of spike phase during phase precession in all active (spike count > 5) cells in control and lesion case. Bottom: Distribution of phase precession range for all active cells.

We found that a DG lesion would reduce theta compression in sequence activity. Theta compression (Dragoi and Buzsáki, 2006) refers to the compression of seconds-long behavioural experience of place-field crossing into a neural representation of spike sequences at a shorter (theta) timescale. To quantify the strength of theta compression, we plotted the pair correlation lags versus the distance between the centers of two fields (abbreviated as ‘lags’ and ‘pair distance’ respectively), after simulating a rightward trajectory (Figure 4B–C). The magnitude of the linear-circular regression slope $a$ measures how much theta phase encodes a certain interval in space, and therefore, the strength of theta compression. As a result, theta compression is reduced for the DG-lesioned case ( $a = 0.053$ radians/cm for both $θ_{DG} = 0^{\circ}$ and $θ_{DG} = 180^{\circ}$ ), as compared to the control case ( $a = 0.183$ radians/cm for $θ_{DG} = 0^{\circ}$ and $a = - 0.059$ radians/cm for $θ_{DG} = 180^{\circ}$ ) reproducing the finding (Ahmadi et al., 2022) that spatial encoding via theta sequences crucially depends on intact DG and suggesting that the loss of DG inputs could be compensated for by the increase of release probability in the spared afferent synapses from the MEC. The DG lesion also reduces the spike phase and phase range of phase precession (Figure 4D), which indicates the participation of DG loops in high-phase spiking. Both weaker phase precession and theta compression stress the important role of DG in temporal organization of CA3 sequences.

Theta sequences in 2-d and out-of-field firing

So far, the model was only evaluated on bidirectional linear tracks, where running directions completely overlapped with the orientation of the DG loop connectivity. Now, we extend our analysis to 2-d space by examining oblique trajectories which cross the orientation of DG-loop projection at certain angles.

We first arrange the DG-loop connections such that the DG-loop orientation crosses a rightward trajectory at 45° and 225° (Figure 5A–F). Similar to the cases of $θ_{DG} = 0^{\circ}$ and $θ_{DG} = 180^{\circ}$ (Figure 3D and H), precession slopes are steeper and onsets higher when the trajectory direction aligns more with the orientation of the DG-loop, but with a smaller effect size for oblique crossings (Figure 5A and C) since DG-loop connectivity area only overlaps with part of the trajectory near the intersection. We further resolve the precession slope, onset and marginal phase for each place cell into 2-d maps (Figure 5B and D). Intrinsic sequences with a higher marginal spike phase can be clearly seen along the belt of DG-loop projections and are even extended to the outside of trajectory predicting ‘off-track’ spikes at high phases. Depending on the alignment between movement direction and DG-loop orientation, the slope becomes either more negative ( $θ_{DG} = 45^{\circ}$ ) or more positive ( $θ_{DG} = 225^{\circ}$ ). Analysis of extrinsicity and intrinsicity was conducted for all field pairs and confirmed the same trend as in Figure 3 that best and dissimilar pairs are more extrinsic than worst and similar pairs, respectively (Figure 5E). As a quantitative prediction, we computed the angle differences between field centers of cell pairs for the extrinsic and intrinsic populations, and observe that place field center differences in extrinsically correlated field pairs are mostly oriented horizontally (along the running direction) while place field center differences from intrinsically correlated field pairs are oriented along the DG-loop orientation $θ_{DG} = 45^{\circ}$ , as by design (Figure 5F).

Figure 5

Download asset Open asset

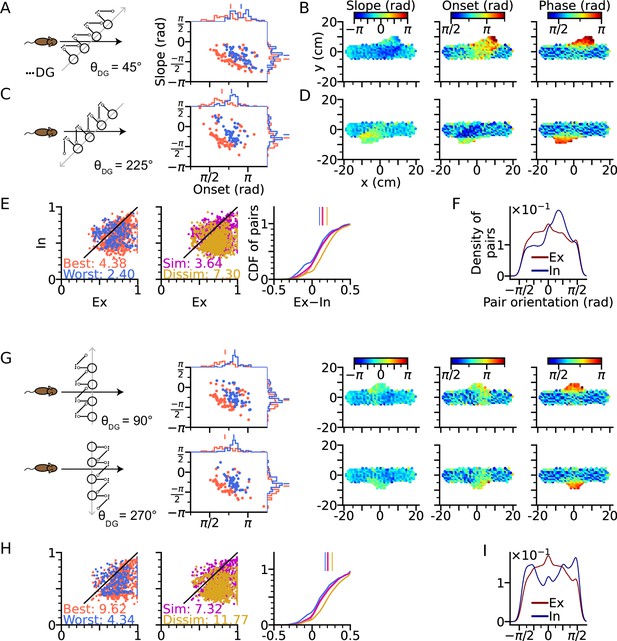
Intrinsic sequences lead to direction dependent 2-d phase precession and out-of-field firing (A) Left: Schematic illustration of DG-loop projection being tilted by 45° relative to the trajectory.

Right: Distributions of phase precession onsets and slopes from the place cells along the trajectory as in Figure 2G. (B) Slopes (left), onsets (middle) and mean spike phases (right) of phase precession from the place cells as a function of field center. High spike phases and onsets occur along the DG-loop orientation where intrinsic spiking dominates and yield out-of-field firing (see the extrusions from horizontal dot clouds) with late onsets and phases. (**C–D**) Same as A-B, but DG-loop projection is at 225° relative to trajectory direction. (D) For DG loops pointing opposite to the sensorimotor drive, prospective firing along the DG loop yields less steep precession slopes and lower onset. (E) Extrinsicity and intrinsicity of all place field pairs along the trajectory as in Figure 3J. Some pairs are totally extrinsic (Ex = 1) because DG projection is absent at those parts of the trajectory. (F) Density of field pairs with extrinsic/intrinsic correlation as a function of the orientation of field center difference vector relative to the x axis. Intrinsic fields peak at 45°. (G) Same as A-D, but DG-loop orientations are perpendicular to the trajectory direction at 90° (top) and 270°. Prospective spikes from intrinsic sequences are initiated in the perpendicular directions. (H) Same as E, but with higher Ex-In ratios. (I) Field pairs with intrinsic correlations are at ±90°.

The analysis above is repeated for the geometric configurations that DG-loop connectivity is minimally interacting with the place cell activity induced by movement, that is when DG-loop orientation and the movement direction are perpendicular to each other ( $θ_{DG} = 90^{\circ}$ and $θ_{DG} = 270^{\circ}$ , Figure 5G). Similar effects as in Figure 5B and D on precession slope, onset and marginal phases are also observed in the 2-d map, except that the effects are further restricted to the intersection area in the middle. Also, the whole population has become more extrinsic as compared to the 45° and 225° cases (Figure 5H, see the numbers for extrinsic-intrinsic ratios) due to the smaller overlapping area between DG-loop projection and the trajectory. Lastly, the pair center difference orientation confirms that field pairs with extrinsic correlations follow the trajectory direction while those with intrinsic correlation are biased towards the DG-loop orientations (90°).

The results demonstrate the distinct roles of extrinsic and intrinsic sequences in 2-d spatial encoding. The former represents trajectory direction while the latter the associative memory towards specific locations. They can be played out at the same time separately in different directions and only interact with each other when they overlap. The interaction is reflected in directional dependence of phase precession properties, most notably the higher spike phases from the DG-CA3 recurrent input, as well as increased intrinsicity of pair correlation and extended firing fields along the orientation of the DG-loop projections. Intrinsic sequences also triggered out-of-field firing (Figure 5B, D and G) at late theta phases. In this case, the DG-loop connects to cells with remote place fields. These cells could even display multiple separated place fields, with high spike phases indicating the target location of the intrinsic sequence.

Topology-free mechanisms of extrinsic phase precession

A well-known problem of phase precession models based on recurrent connectivity that applies to both, the original intrinsic Tsodyks et al., 1996 and Romani and Tsodyks, 2015 model, is that they do not explain how the topological connectivity matrix (in our case $W^{CA3}$ ) is generated (Lisman and Redish, 2009; Jaramillo and Kempter, 2017). Extrinsic theta sequences in a first exposure to a novel environment should therefore be missing. Although Feng et al., 2015 find that theta sequences on a first exposure of a novel linear track are indeed much weaker (maybe only reflecting intrinsic sequences), their results nevertheless indicate a very fast learning time scale that is hard to reconcile with recurrent learning of a full spatial topology (particularly the generalization to 2-d). Also their result might be hampered by place field plasticity that biases the decoder towards backward-shifted place maps of later trials (Parra-Barrero and Cheng, 2023). We therefore explored, whether extrinsic 2-d sequences could also be generated by a model that is not relying on 2-d topology in the recurrent weights. To this end, we disabled the CA3 recurrence and compensated the missing level of excitation by an increased strength of the spatial input and the DG loops (see Methods section: Parameters of the models). Our simulations show that extrinsic sequences can still be generated by spatial input alone (Figure 6A), relying only on the short-term facilitation mechanism. Simulating CA3 activity with lesioned DG similarly abolishes the temporal organization of theta sequence and reduces the phase range (Figure 6B). The results demonstrate that the temporal order of extrinsic sequences could be coordinated solely by sensorimotor drive and does not necessarily require CA3 recurrence.

Figure 6

Download asset Open asset

Extrinsically driven theta correlations can be temporally organized by sensorimotor drive alone without CA3-CA3 recurrence.

Simulations were performed without CA3-CA3 recurrence but with stronger spatial input. (A) Same as Figure 3. Extrinsically driven theta correlations and phase precession are still present. (B) Same as Figure 4. DG is still integral to the theta compression in a network model without CA3-CA3 recurrence.

Functional role of intrinsic sequences

While the function of extrinsic theta sequences in encoding the actual trajectory of an animal (connecting the recent past, present and near future locations) is obvious, the potential role of the less readily apparent intrinsic sequences is not straight forward. Simulations of trajectories in 2-d (Figure 5) suggest intrinsic activity may serve a role to identify certain location-direction pairs independent of the current trajectory. Here, we follow this idea by evaluating the hypothesis that the intrinsic sequences signal a stable ‘landmark’ (location/direction pair) cue by a temporal code that is invariant to different directions of approach.

To test our hypothesis, we constructed a downstream readout neuron that would reliably identify the presence of the intrinsic sequence independently of the animal’s running direction, whereas it would not be able to do so for only extrinsic sequences. To this end, we trained the synaptic weights using the tempotron learning rule (Gütig and Sompolinsky, 2006), which is able to implement binary classification based on temporal relations of input spike patterns (see Methods section: Tempotron). Two tempotrons were trained to recognize the spike patterns from the place cells, one taking input from a model with DG-loop connectivity at $θ_{DG} = 0^{\circ}$ , and one without DG-loop connectivity to serve as a control only having access to extrinsic sequences (Figure 7A). Non-moving spatial inputs were applied to the CA3 place cells at the centers of with-loop and no-loop populations and their spike patterns in subsequent theta cycle were used as training patterns, mimicking a situation in which network activity is evoked without sensory-motor input as, for example in a offline situation before the animal walks or maybe even has seen the environment. The training patterns have only (+) labels, which the tempotrons are trained to recognize by firing a spike (Figure 7B). We then test the tempotrons with spike patterns induced by the animal running on different trajectories through the trained location with running directions varying between 0° to 360° (Figure 7C). All spikes in each training and testing pattern are individually jittered by adding a noise term $σ \sim N (0, (2 m s)^{2})$ for 100 times, producing 100 samples for each pattern. The tempotron is said to successfully recognize the sequence of a trajectory direction if any of the theta cycles throughout the trajectory elicits a spike, that is while running, the readout cell would evaluate the place cell sequence in every theta cycle for information on the trained landmark.

Figure 7 with 1 supplement see all

Download asset Open asset

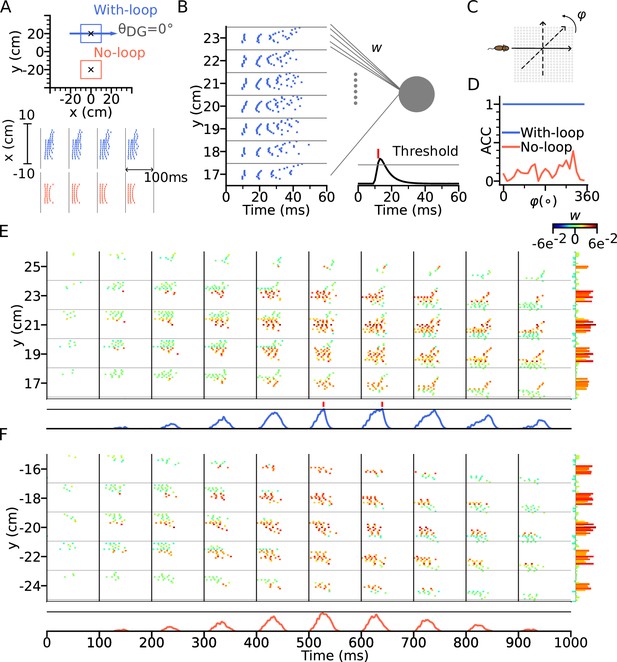
Intrinsic sequences provide a stable landmark for positional decoding using a tempotron.

(A) Top: Two tempotrons are trained for place cell populations within the top (with DG loop; blue) and bottom (no DG loop; red) squares, to recognize the presence of the corresponding sequence activities. DG-loop rightward projection is indicated by blue arrow and only exists in the blue square. Non-moving spatial inputs are applied to the CA3 network centered at the two locations (marked by black crosses) to evoke spike sequences for training. Bottom: Resulting spikes of the place cell network zoomed in to the subset of field centers from x=-10 to x=10 for y=+20 (with-loop, top raster plot) and y=-20 (no-loop, bottom). Each theta cycle is one (+) training pattern, which the tempotron is trained to detect by eliciting a spike. (B) Example training pattern with spikes of place cells from x=-10 to x=10 (in each rectangular row) fixed at different values of y. Only one theta cycle is shown. Each place cell delivers spikes to the dendrite of the tempotron, producing post-synaptic potentials (PSPs) at the soma (line plot at the bottom). Synaptic weights are adapted by the tempotron learning rule such that PSPs can cross the threshold (gray line) and fire for the detection of the sequence. After the tempotron has fired, the PSPs will be shunted. (C) Sequence detection is tested while the simulated animal ran on a trajectory with varying direction ( $φ$ ) from 0° to 360° with a 15° increment to detect the presence of the sequence. (D) Detection accuracies (ACC) for with-loop (red line) and no-loop (blue) input populations. Note that the tempotron cannot detect the no-loop sequences when tested on trajectories at various angles. (E) Detection of the intrinsic sequence for a trajectory $φ = 180^{\circ}$ for the DG-loop condition. Spike raster is shown for every two horizontal rows of place cells in the arena and color-coded by the synaptic weights (see color bar on the right). Tempotron soma potential is shown at the bottom for each pattern. (F) Same as E, but for no-loop inputs. The tempotron remains silent.

We found that the tempotron trained on the intrinsic sequence from the DG loop is able to recognize the sequence patterns produced for all running directions, while the tempotron trained without a DG-loop fails to identify the extrinsic sequences most of the time (see accuracies in Figure 7D). The reason is that the spike patterns induced by intrinsic sequences remain similar to the training pattern despite being approached in other directions (see sequential contributions in Figure 7E), while spike patterns for the no-loop condition are different between training and testing (Figure 7F). The distinction is further illustrated in Figure 8, where 2-d maps of spike time gradients in one theta cycle are plotted with respect to running direction/training condition. Sequences always contain components that propagate along the projection direction of DG loop, while, without such a loop, they only propagate along the running direction. Moreover, during training, the no-loop condition evokes concentric waves, reflecting the 2-d topology of the recurrent weights. Similar results were also achieved without CA3-CA3 recurrence (Figure 7—figure supplement 1 and Figure 8C).

Figure 8

Download asset Open asset

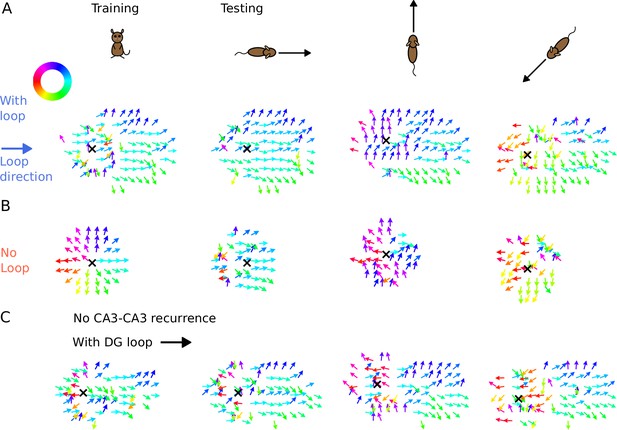
Illustration of spike time gradients in one theta cycle (500–600 ms) with and without DG loop.

(A) Time gradients with a DG loop projecting to the rightward direction ( $θ_{D G} = 0^{\circ}$ ). Each arrow is located at a CA3 place field center. The arrow direction indicates the spike time gradient, equivalently the ‘travelling direction’ of sequence activity, which is calculated as the sum of the directions to the 8 neighbouring field centers, weighted by the difference between their mean spike times in one theta cycle. Arrow direction is color-coded according to the color wheel. Black cross marks the instantaneous position of the animal. The first column shows the training condition when a non-moving spatial stimulus is applied. The three columns on the right show the testing condition when the rat is running in various directions. The sequence mostly propagates rightwards, following the DG-loop direction even when the animal runs in different directions. (B) Same as A without a DG loop. Sequences propagate outward from the animal position as a concentric travelling wave during training. During testing, spike time gradients follow the running direction. (C) Same as A, using the network model without CA3 recurrence. As in Figure 6, the extrinsic sequence is driven solely by the STF mechanism of the spatial input. Intrinsic sequences in this model still remain invariant to running directions and function as spatial landmarks.

Our results show that intrinsic sequences can provide a stable correlation signal which allows reliable decoding of locations through temporal correlations. The intrinsic temporal code remains detectable even when mixed with extrinsic sequences.

Discussion

We presented a model of hippocampal theta sequences in 2-d environments, suggesting that both extrinsic and intrinsic mechanisms are required to explain experimental reports that phase precession and spike timing correlations are non-homogeneous across running directions. Although phase precession already becomes directional by including direction-dependent sensory input into a purely extrinsic model, directionality of spike timing correlations cannot be explained by such a model. We, however, demonstrated that the correlation preference could be implemented by fixed recurrent loops via a model DG layer. We further supported the model assumptions by showing that DG lesions plus compensatory sensory drive can abolish the theta compression effect in CA3 spiking activity (Ahmadi et al., 2022). By employing a spike-based temporal pattern decoder (tempotron), we showed that the intrinsic sequences could function as stable signatures that act as anchors of the spatial code.

Early intrinsic models (Tsodyks et al., 1996) were challenged owing to their inability to generate phase precession in backward travel (Figure 1E, also see Cei et al., 2014), as well as the predominantly extrinsic correlations observed in CA1 (Huxter et al., 2008). In our hybrid model, phase precession still occurs during backward travel ( $θ_{D G} = 180^{\circ}$ ) but at a lower probability as indicated by the larger fraction of positive phase-position slopes (Figure 3H). Also, extrinsic sequences still dominate over intrinsic sequences as indicated by the majority of field pairs being extrinsic (Figure 3J). Both the reduced expression of phase precession in reverse runs and the dominance of extrinsic sequences are in accordance with the experimental data (Yiu et al., 2022).

The mixture of extrinsic and intrinsic mechanisms in our theory, naturally gives rise to the directionality of spike correlations and phase distributions. As the trajectory aligns itself with the DG loops, the ratio of intrinsic to extrinsic sequences increases. As a result, spike correlations become more rigid and the phase distribution is shifted upward due to the accumulated synaptic transmission delay from the reverberating activity between CA3 and DG populations. Adding directional sensory input activates extrinsic sequences in the best direction more strongly, and hence, leads to an association between best-angle (worst-angle) pairs and extrinsicity (intrinsicity). These predictions of our model are corroborated by past reports of higher spike phases in the non-preferred arm of a T-maze (Kay et al., 2020) as well as the association of rigid correlations with upward shifts in spike phases and an increase in worst-angle pairs (Yiu et al., 2022). The experimental distinction between extrinsic and intrinsic components in theta sequences has so far only been achieved in pairs of place cells, owing to the limited number of simultaneously recorded place cells with overlapping fields. Our model predicts that similar distinctions should also be observable in higher-order statistics, obtained from overlapping fields of a larger number of cells. Instead of correlation lags, we suggest to use temporal pattern detection methods (e.g. Chenani et al., 2019) to unveil the respective sequence contributions.

Since intrinsic sequences can also propagate outside the trajectory (out-of-field firing in Figure 5) and activate place cells non-locally, our model predicts direction-dependent expansion of place fields, or even multiple place fields, with the intrinsic sequence’s target location exhibiting late spike phases and higher phase precession onsets. Remote activation during locomotion has already been observed in a previous study (Sasaki et al., 2018) where CA3 place cells preferentially firing at one arm of the maze were also activated at reward locations at other arms. In our model, only short-range intrinsic connectivity was considered, thus, place field boundaries expand locally but in a skewed manner matching the sequence direction. Skewness of place fields has been reported by a number of studies (Mehta et al., 1997; Shen et al., 1997; Mehta et al., 2000; Ekstrom et al., 2001; Lee et al., 2004; Burke et al., 2008; Cei et al., 2014; Roth et al., 2012; Dong et al., 2021) showing place fields to be asymmetrically expanded opposite to the direction of travel. This effect was connected to plasticity as it develops after repeated traversal, and due to its dependence on NMDA receptor activation (Ekstrom et al., 2001; Burke et al., 2008; Shen et al., 1997). These plasticity studies show that the hippocampal place code is shaped by intrinsic synaptic computations including temporal activation patterns in theta sequences (Feng et al., 2015). Apart from being conducted on linear tracks and not 2-d environments, most of this work focused on CA1 and associated Schaffer collateral plasticity. Yet some prior studies (Lee et al., 2004; Roth et al., 2012) did show that place fields in CA3 were more skewed than in CA1, which our model would explain by CA3 expressing more intrinsic sequences than CA1 consistent with prior experimental observations (Yiu et al., 2022 reported ratios of extrinsically to intrinsically driven cell pairs of 1.44 in CA1 and 1.23 in CA3).

A further prediction of hard-wired DG loops is that the resulting activity patterns (intrinsic sequences) should not remap under conditions of global or partial remapping (Leutgeb et al., 2004). Instead the same intrinsic sequence components should be observable in multiple environments, however, they might only be seen in a small fraction and thus this prediction is potentially hard to test.

The back-projection from CA3 to DG is a crucial anatomical prerequisite of our model, but was rarely explored compared to the feed-forward inputs via the perforant pathway. The proposed CA3-DG recurrent structure of this model, albeit simplified, is consistent with the anatomical evidence. Pyramidal cells in CA3 innervate the mossy cells at the DG hilus (Scharfman, 1994; Scharfman, 2016), which then project to granule cells through both excitatory and inhibitory pathways (Hsu et al., 2016; Scharfman, 1995; Larimer and Strowbridge, 2008; Soriano and Frotscher, 1994), and subsequently back to CA3 pyramidal cells. An optogenetic study (Hsu et al., 2016) showed that the net effect of mossy cells on granule cells was predominantly inhibitory, suggesting that the DG ensembles excited by mossy cell synaptic drive are sparsified by suppressing unwanted out-of-ensemble activity. Indeed, past studies showed that reliable excitatory effect could be observed when granule cells were depolarized (Scharfman, 1995) and when they received back-propagation of sharp wave bursts from CA3 population (Penttonen et al., 1998). This indicates that the excitatory recurrent pathway from CA3 via DG exists and might allow activity reverberation between two layers. While our model, owing to its simplicity and generality does not require any DG specific pathways and would work equally well with any other anatomical interpretation of the CA3 feedback, we hypothesize the intrinsic feedback connectivity to arise via the DG, particularly because DG lesions were shown to eliminate the coordinated temporal structure of CA3 activity and to be instrumental to sequence organization (Figure 4 and Ahmadi et al., 2022).

Our model assumed a connectivity pattern in the DG loops, in which neurons activate the neighbours along a specific direction, as inspired by Hebb’s phase sequences (Hebb, 1949) and, hence, replay of the loop would activate a spatially plausible virtual trajectory. The loop connectivity could either arise from previous learning, or might be present already beforehand (Dragoi and Tonegawa, 2013), with spatial topology inherited by associating 2-d sensory features to cell ensembles in the loop (Leibold, 2020). The resulting topology can exhibit discontinuous long-range jumps to other locations (Sasaki et al., 2018) or consist of a discrete set of (behaviorally relevant) locations (Pfeiffer, 2022).

Different from other phase precession models, we also included heading direction as part of the sensory input, as inspired by past literature that CA1 (Markus et al., 1995; Acharya et al., 2016; Stefanini et al., 2020), CA3 (Mankin et al., 2019), and DG place cells (Stefanini et al., 2020) exhibit directional selectivity in firing rates, potentially inherited from the upstream head-direction cells in the medial entorhinal cortex (Giocomo et al., 2014) and postsubiculum (Taube et al., 1990). As a result, the directional drive immediately translates to phase directionality in theta sequences, partly contributing to the upward shift of the phase distribution in the worst angles. Such phase directionality arises naturally from the intracellular dynamics of a spike-based model, where stronger depolarization causes earlier spiking. This phase-rate dependence has already been used in previous models (Harris et al., 2002; Mehta et al., 2002; Thurley et al., 2008), where the increasing depolarization within place fields directly relates to decreasing spike phases. The causal effect of firing rate on spike phases, however, was disputed by Huxter et al., 2003 as they showed that precession slopes and spike phases remained the same between high- and low-spiking runs, suggesting that the phase is not single-handedly determined by firing rate. In our model, firing rate is determined by both low-phase spiking from sensory input and high-phase spike arrivals of DG-CA3 loops, both producing opposing effects on the phase distribution. Thus, depending on the strength and geometry of the DG-CA3 connectivity, spike phases are not fully determined by firing rate.

By using a tempotron to decode the spike patterns, we show that the spike patterns of intrinsic sequences can serve as a stable landmark which remains decodable across multiple running directions. The invariant temporal patterns could serve as anchors of spatial memories in a novel environment, since place fields only stabilize after the animal becomes familiar with the environment (Wilson and McNaughton, 1993). The pre-existing sequence motifs, even at times when the spikes of the neurons are not spatially tuned to a location, can still encode the position based on their temporal relations alone. The idea has previously been spelled out (Cheng, 2013) and numerically verified (Leibold, 2020; Parra-Barrero and Cheng, 2023) with multiple fixed sequences that form a decodable spatial representation.

Intrinsic sequences may thus act as a scaffold around which a new spatial code can be built for new but similar behavioral contexts, where similarity could for example be identified by a salient feature. Once the behavioral context of a situation changes, new intrinsic sequences would be observable. These intrinsic landmarks need to be stable across time, as shown for some dentate gyrus representations (Hainmueller and Bartos, 2018). We speculate that offline sequences observed during replay and preplay (for review see Buhry et al., 2011; Dragoi and Tonegawa, 2014), would correspond to the intrinsic activity patterns and indicate the context expectation of an animal (which can be detected by a tempotron). The functional roles of intrinsic sequences may thus not be limited to spatial memories. While, in the spatial domain, intrinsic sequences could be interpreted as spatial trajectories (Kay et al., 2020; Sasaki et al., 2018), virtual non-spatial trajectories could represent working memories contents (Jensen et al., 1996) available for general decision making processes.

Methods

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Software, algorithm	Python	Python Software Foundation	https://www.python.org/ RRID:SCR_008394
Software, algorithm	Linear-circular regression	Kempter et al., 2012		The algorithm is customized to our analyses
Software, algorithm	Tempotron	Gütig and Sompolinsky, 2006		The algorithm is customized to our analyses

Neuronal model

Generation of neuronal action potentials is modelled according to Izhikevich, 2003. The soma potential $v$ and the adaptation variable $u$ of unit $i$ at time $t$ (in ms) follows the equations:

{\dot{v}}_{i} (t) = 0.04 v_{i}^{2} (t) + 5 v_{i} (t) + 140 - u_{i} (t) + I_{i} (t)

{\dot{u}}_{i} (t) = a [b v_{i} (t) - u_{i} (t)]

I_{i} (t) = I_{i}^{R} (t) + I_{i}^{S} (t) - I^{θ} (t)

Any time $v (t)$ crosses the threshold 30 mV from below, we register a spike for the neuron and reset the soma potential by $v (t) \leftarrow c$ and the adaptation variable by $u (t) \leftarrow u (t) + d$ . For the excitatory pyramidal place cells, we use parameters $a = 0.035$ , $b = 0.2$ , $c = - 60$ mV, $d = 8$ , which provides the neuron with burst firing characteristics. For the inhibitory interneurons, the parameters were $a = 0.02$ , $b = 0.25$ , $c = - 65$ mV, and $d = 2$ , which corresponds to fast spiking patterns. $I (t)$ is the total sum of recurrent $I^{R} (t)$ , sensory $I^{S} (t)$ and oscillatory theta input

I^{θ} (t) = 7 [1 + \cos (\frac{2 π t}{100 m s})] / 2

We chose to use the phenomenological spike generation model of Izhikevich, 2003, since it allows to adjust burst firing properties with only few parameters that efficiently emulate the bifurcation structure of spike generation. Synaptic integration below threshold is not affected by the spike generation model and will thus be treated by conventional synaptic models.

Spatial input

The place field centers $p_{i}^{C A 3} = [x_{i}^{C A 3} (t), y_{i}^{C A 3} (t)]$ of $80 \times 80 = 6400$ excitatory CA3 cells equally tile the 80 by 80 cm square arena. Place cell firing rates are modelled direction-sensitive, with preferred heading directions $ψ_{i}^{C A 3}$ semi-randomized among each 2×2 tile of place cells by randomly rotating a set of four equally spaced direction angles by a uniformly distributed angle $ξ$ , that is

[ψ_{i}^{C A 3}, ψ_{i + 1}^{C A 3}, ψ_{i + 2}^{C A 3}, ψ_{i + 3}^{C A 3}] = [0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}] + ξ \mod 360^{\circ} .

The sensory input $J_{i}^{S} (t)$ into the $i$ -th neuron depends on the instantaneous position, $p (t) = [x (t), y (t)]$ , and heading direction $ψ (t)$ of the animal as

\begin{array}{ll} J_{i}^{S} (t) & = {\begin{cases} A_{i}^{S} (t) I^{M E C} (t) & if d (p (t), p_{i}^{C A 3}) ≦ 5 cm \\ 0 & if d (p (t), p_{i}^{C A 3}) > 5 cm \end{cases} \end{array}

A_{i}^{S} (t) = A^{p o s} + A^{d i r} \exp (\cos (ψ (t) - ψ_{i}^{C A 3}) - 1)

I^{M E C} (t) = \frac{1}{2} [1 + \cos (\frac{2 π t}{100 m s} + 70^{\circ} \frac{π}{180^{\circ}})],

where $A^{pos}$ is the amplitude of positional tuning and $d (\cdot)$ computes the Euclidean distance between two positions. The positional tuning curve is implemented as a rectangular box function, where the place cell only receives sensory input if the animal is within 5 cm from the field center. Directional tuning is implemented as an additional amplitude gain $A^{dir}$ to the positional current depending on the circular difference between the animal’s heading and the neuron’s preferred heading direction $ψ_{i}^{CA3}$ . The sensory input is assumed to be modulated by theta oscillations from medial entorhinal cortex (MEC) $I^{MEC} (t)$ with a phase shift of 70° (Mizuseki et al., 2009).

The sensory input $J^{S}$ is subsequently transformed to the input current $I^{S}$ via short-term facilitation (STF)

{\dot{s}}_{i}^{F} (t) = \frac{(S_{0}^{F} - s_{i}^{F} (t))}{τ^{F}} + (S_{1}^{F} - s_{i}^{F} (t)) Φ^{F} J_{i}^{S} (t)

I_{i}^{S} = J_{i}^{S} (t) [s_{i}^{F} (t)]^{2},

where the facilitation variable $s_{i}^{F}$ decays to $S_{0}^{F}$ with a time constant $τ^{F} = 500 m s$ and increases to $S_{1}^{F}$ when the sensory input $J_{i}^{S}$ is present. The time constant $τ^{F}$ of facilitation of neocortical synapses was in the range suggested by Tsodyks et al., 1998 following previous experimental reports (Mejías and Torres, 2008; Zucker and Regehr, 2002). $Φ^{F}$ controls the strength of the STF. The facilitation variable is squared to include non-linear interactions in presynaptic calcium dynamics. As a result, facilitated sensory input $I_{i}^{S}$ increases over time and becomes stronger in the later part of the field, thus effectively generating a spatially graded input strength.

Note that only the CA3 place cells receive the sensory input. $I_{i}^{S} (t)$ is not applied to the place cells in DG and all of the inhibitory interneurons.

CA3 recurrent connections

Place cells in CA3 connect with each other by excitatory synapses. The excitatory synaptic current $I_{i}^{E} (t)$ is conductance-based, and follows the equations:

{\dot{g}}_{i}^{E} (t) = \frac{- g_{i}^{E} (t)}{τ^{E}} + \frac{1}{N_{J}} \sum_{j, f} W_{i j} s_{j}^{D} (t) δ (t - t_{j}^{(f)} - τ_{0})

I_{i}^{E} (t) = [V^{E} - v_{i} (t)] g_{i}^{E} (t)

The conductance $g_{i}^{E}$ of a post-synaptic cell $i$ is increased by the spike arrivals at times $t_{j}^{(f)}$ from the pre-synaptic cell $j$ , and decay with a time constant $τ^{E} = 12 m s$ . $N_{J} = 6, 400$ is the number of presynaptic place cells, $V^{E} = 0 m V$ is the reversal potential of the excitatory synapses and $τ_{0} = 2 m s$ is the synaptic transmission delay.

The synaptic weights $W_{i j}$ from cell $j$ to cell i depend on the distance between place cell centers and on the similarity of their preferred heading angles, i.e.,

W_{i j}^{C A 3} = J_{i j} {B^{p o s} + B^{d i r} \exp [K^{C A 3} (\cos (ψ_{i}^{L} - ψ_{j}^{L}) - 1)]} \exp (\frac{- d (p_{i}^{C A 3}, p_{j}^{C A 3})^{2}}{2 σ^{2}}),

where $B^{pos}$ and $σ = 2 c m$ correspond to the maximum strength and width of the location-specific interaction, respectively. $B^{dir}$ and $K^{CA3}$ control the maximum strength and the concentration of the directional dependence, respectively. $J_{i j}$ models the rightward asymmetry of the cell connections, which was only turned on when we simulated the 2-d variant of Tsodyks et al., 1996 model in Figure 1C–F and otherwise turned off in the rest of our analysis.

\begin{array}{ll} I f r i g h t w a r d a s y m m e t r y i s O N, & J_{i j} = 1 i f x_{j}^{C A 3} < x_{i}^{C A 3}, e l s e 0 \\ I f r i g h t w a r d a s y m m e t r y i s O F F, & J_{i j} = 1 \end{array}

Furthermore, the recurrent synaptic conductances underwent short-term synaptic depression (STD), as was proposed in Romani and Tsodyks, 2015 to serve as sequence generator in 2-d space. The mechanism penalizes the recurrent input into the place cells behind the animal. As a result, the differential recurrence strengths translate to a gradient of spike phases and produces extrinsic sequences in the direction of travel. We model the STD by the variable $s_{i}^{D} (t)$ which represents the available synaptic resource and follows the dynamics:

{\dot{s}}_{i}^{D} (t) = \frac{1 - s_{i}^{D} (t)}{τ^{D}} - U^{D} δ (t - t_{i}^{(f)}),

where $s_{i}^{D}$ recovers to 1 with a time constant $τ^{D} = 500$ ms and is depleted by a fraction $U^{D}$ every time a spike occurs. The recovery time constant is comparable to experimentally obtained values of cortical neurons (200–800 ms in Tsodyks and Markram, 1997; Markram et al., 1998; Abbott et al., 1997; Zucker and Regehr, 2002) and previous modelling work (450–800 ms in Romani and Tsodyks, 2015; Haga and Fukai, 2018; Tsodyks and Markram, 1997; Tsodyks et al., 1998). The STD only applies to synaptic connections when presynaptic cells are CA3 place cells. $s_{i}^{D} (t)$ is fixed at 1 when the pre-synaptic cells are inhibitory interneurons or DG place cells.

DG layer

We simulated $N_{DG} = 40 \times 40 = 1600$ place cells in the DG layer, with place field centers equally tiling the environment. The DG cells do not receive sensory input. Their positional ( $x_{i}^{DG}, y_{i}^{DG}$ ) and directional ( $ψ_{i}^{DG}$ ) tunings are determining synaptic strengths to and from the CA3 layer. The directional tuning is semi-randomized as described for CA3. The synaptic current dynamics follow Equations (1) and (2). Excitatory synaptic weights from CA3 place cells to DG place cells are defined as

W_{i j}^{C A 3 - D G} = C_{j}^{C A 3} B^{D G} \exp [K^{D G} (\cos (ψ_{i}^{D G} - ψ_{j}^{C A 3}) - 1)] \exp (\frac{- d (p_{i}^{D G}, p_{j}^{C A 3})^{2}}{2 σ^{2}}),

which are dependent on the differences in the place field centers and preferred heading angles between the CA3 and DG populations. The variable $C_{j}^{CA3}$ strengthens outgoing connections from CA3 place cells on the path corresponding to the intrinsic sequence by choosing

C_{j}^{C A 3} = {m a x}_{k \in [- 10, 10]} {\exp (\frac{- d (p_{k}^{C}, p_{j}^{C A 3})^{2}}{2 σ^{2}})},

where $p_{k}^{C}$ varies with the intrinsic path direction $θ_{D G}$ as $p_{k}^{C} = [2 k \cos (θ_{D G}), 2 k \sin (θ_{D G})]$ .

The excitatory synaptic strengths from DG to CA3 are chosen such that DG cells project back to CA3 cells with place field centers shifted by a vector $r = [4 \cos (θ_{D G}), 4 \sin (θ_{D G})]$ of fixed length of 4 cm along the intrinsic path, that is

W_{i j}^{D G - C A 3} = B^{D G} \exp [K^{D G} (\cos (ψ_{i}^{C A 3} - ψ_{j}^{D G}) - 1)] \exp (\frac{- d (p_{i}^{C A 3} - r, p_{j}^{D G})^{2}}{2 σ^{2}}) .

The model has no synaptic connections between DG excitatory neurons.

Inhibitory synapses

The model additionally contains $N_{I} = 250$ inhibitory interneurons (denoted as Inh) each for the CA3 and the DG layer. They provide inhibitory feedback separately to the excitatory cells within each layer (CA3-Inh-CA3 and DG-Inh-DG). The dynamics of their synaptic currents mirrors the excitatory synapses, that is

{\dot{g}}_{i}^{I} (t) = \frac{- g_{i}^{I} (t)}{τ^{I}} + \frac{1}{N_{I}} \sum_{j}^{N_{I}} W_{i j}^{X - Y} δ (t - t_{j}^{(f)} - τ_{0})

I_{i}^{I} (t) = [V^{I} - v_{i} (t)] g_{i}^{I} (t),

with $τ^{I} = 10 m s$ , $V^{I} = - 80 m V$ . CA3 and DG have all-to-all connections to their inhibitory populations with uniformly randomized strengths, i.e. $W_{i j}^{X - Y} = W_{0}^{X - Y} ξ$ , with $ξ \sim U (0, 1)$ is the maximum synaptic strength, and the notation X-Y corresponds to Inh-CA3 and Inh-DG connections. There is no synaptic connection between inter-neurons, that is $W^{Inh - Inh} = 0$ .

The total recurrent current entering each excitatory neuron is thus the sum of the excitatory and inhibitory current:

I_{i}^{R} (t) = I_{i}^{I} (t) + I_{i}^{E} (t)

Excitatory synapses to interneurons

Interneurons only receive all-to-all excitatory currents from their respective layer. Those currents are modelled according to Equations 1; 2. The synaptic weights are constant and denoted by $W_{0}^{CA3 - Inh}$ and $W_{0}^{DG - Inh}$ .

Parameters of the models

Model parameters that are adjusted in different analyses are listed in Table 1. The values of the synaptic weights and spatial input were chosen to allow for a large range of phase precession and stability of the network activity. For the analyses including the DG layer, weights are adjusted to allow coexistence of extrinsic and intrinsic sequences.

Table 1

Model parameters used in simulations according to Figure panels.

In, Ex, C. and L. refer to intrinsic, extrinsic, control and lesion respectively.

Name \Figure	1 (In)	1 (Ex)	2	3	4 (L.)	5	6A	6B (C.)	6B (L.)	7
$A^{pos}$	7.5	9.0	6.5				9.5	7.5		6.5
$A^{dir}$	0		6				9	8		6
$S_{0}^{F}$	1		0		1.25	0	0.25	0	1.25	0
$S_{1}^{F}$	1		2		1.25	2	1.5	2	1.25	2
$Φ^{F}$	0		0.001		0	0.001			0	0.001
$B^{pos}$	1100		0
$B^{dir}$	0		2000	1500		2000	0			1500
$K^{CA3}$	0		1
$J_{i j}$	ON	OFF
$U^{D}$	0	0.9	0.7
$N_{DG}$	0			40×40 = 1600
$B^{DG}$	0			3000	0	4000		4000	0	4000
$K^{DG}$	0			1
$N_{I}$	0		250
$W_{0}^{CA3 - Inh}$	0		50
$W_{0}^{Inh - CA3}$	0		5
$W_{0}^{DG - Inh}$	0			350
$W_{0}^{Inh - DG}$	0			35

Cross-correlation analysis

Cross-correlation represents the probability that a spike of one place cell would occur following a certain time lag from the spike of the another cell. Cross-correlation is always empirically computed as a histogram of time lags between spike pairs with a resolution of 5ms in a window of 200ms. Throughout the present study, the direction of a time lag is designated as the lag of the first encountered cell relative to the next cell along the trajectory, except in Figure 1, where the direction of time lag follows the cell order along the $0^{\circ}$ , $45^{\circ}$ , and $90^{\circ}$ trajectory in each comparison group, and in Figure 2, where the time lag direction is from left to right cells.

Correlation lag is derived by band-pass (4–12 Hz) filtering the cross-correlation histogram and applying a Hilbert transform on the filtered signal. The phase of the analytic signal at time lag 0 is the correlation lag.

Extrinsicity and intrinsicity

We apply quantitative measures for the extrinsic or intrinsic nature of cross-correlations in a pair of place fields following Yiu et al., 2022. We compare the cross-correlation histograms of a field pair for a running direction along the DG loop ( $θ_{D G}$ ) and opposite to the loop ( $θ_{D G} + 180^{\circ}$ ). Extrinsicity (Ex) is computed as the Pearson’s correlation ( $r$ ) between two cross-correlation histograms, and intrinsicity (In) between the histogram of $θ_{D G}$ and the horizontally flipped histogram of $θ_{D G} + 180^{\circ}$ . The Pearson’s correlation is then transformed ( $r^{'} = (r + 1) / 2$ ) to be in the range of 0 and 1. An extrinsic correlation would give an extrinsicity near 1, since the effect of DG loop is minimal and correlation histograms are similar in both $θ_{D G}$ and $θ_{D G} + 180^{\circ}$ directions. A pair of place fields with intrinsic correlation would see cross-correlation horizontally flipped in the $θ_{D G} + 180^{\circ}$ condition due to the large effect of DG loop, and hence, give an intrinsicity near 1. We classify a pair as extrinsic if its extrinsicity exceeds intrinsicity, and vice versa.

Tempotron

A tempotron is a neuronally inspired classifier (readout neuron) whose dendritic synaptic weights can be adapted to recognize temporal patterns of spikes arriving at the afferents (for details, see Gütig and Sompolinsky, 2006). Briefly, the soma potential of the tempotron follows the equations

V (t) = \sum_{i} w_{i} \sum_{i, f} K (t - t_{i}^{(f)})

K (t - t_{i}^{(f)}) = V_{0} (\exp [- (t - t_{i}^{(f)}) / τ] - \exp [- (t - t_{i}^{(f)}) / τ_{r}]),

where w_i is the adaptable weight of the afferent fiber conveying spikes from place cell $i$ to the tempotron. $K (t - t_{i}^{(f)})$ is a post-synaptic potential (PSP) kernel with decay and rising time constants of $τ = 5 m s$ and $τ_{r} = 1.25 m s$ respectively. V₀ is a factor which normalizes the PSP kernel to 1. A spike is said to occur if $V (t)$ crosses the firing threshold $V_{Θ} = 2$ from below. After threshold crossing, the afferents will be shunted and spike arrivals will not evoke more PSPs for the rest of the pattern. A pattern is defined as the set of spike times of all the pre-synaptic place cells in a theta cycle (100 ms).

The weight w_i follows the update rule

Δ w_{i} = 0.01 \sum_{t_{i}^{(f)} < t_{m a x}} K (t_{m a x} - t_{i}^{(f)})

w_{i} \leftarrow w_{i} + Δ w_{i} I f a (+) p a t t e r n d o e s n o t e l i c i t a s p i k e, w_{i} \leftarrow w_{i} - Δ w_{i} I f a (-) p a t t e r n d o e s n o t e l i c i t a s p i k e,

where t_max is the time at the peak of the soma potential $V (t)$ . The learning rule assigns credit to the afferents based on spike timing. Spike times closer to the peak are considered to have higher contribution to the tempotron firing, hence their afferents are incremented by a larger step. After training, spike times with similar temporal correlations as the (+) patterns would be able to evoke enough PSP in the tempotron’s soma and elicit a spike as a positive response of binary classification, while those similar to (-) patterns would not elicit a spike from the tempotron.

We trained the tempotrons to identify the spike patterns of place cells at locations with and without intrinsic connectivity separately. To this end, we modified our network such that DG loops are present at the upper half of the arena, spanning the space from x=-20cm to x=+20 cm at y=+20 cm in direction $θ_{D G} = 0^{\circ}$ , while the loop is absent in the lower half of the arena.

During training, we applied ‘non-moving’ spatial inputs to the CA3 place cells at the with-loop (0 cm, 20 cm) and no-loop (0 cm, –20 cm) locations for 1 s, as if the animal were standing still at the locations, evoking the activities representing the two location cues. For computational efficiency, we restricted our analysis to the populations of CA3 place cells within the 20 cm squared boxes centered at the two locations. Each population contains 400 pre-synaptic cells, forming the input space for the tempotron. The spikes from the with-loop population will train the first tempotron and those from the no-loop population will train the second tempotron. Prior to training, the input spikes are sub-divided to 10 patterns based on their theta cycles. Each pattern has a window of 100 ms. We added noise to the patterns by jittering the spikes with Gaussian noise $N \sim (0, (2 m s)^{2})$ for 100 times. As a result, each tempotron receives 10×100 = 1,000 training patterns from the activity evoked by the location. All training patterns are (+) patterns and there is no (-) pattern.

After training, trajectories (20 cm long, 1 s duration) with running directions from 0° to 360° with 15° increment were simulated to cross each of the locations. The trajectories produce a mix of extrinsic and intrinsic sequences in the with-loop population and only extrinsic sequences in the no-loop population. The patterns evoked by the running trajectories were separately applied to the tempotrons. The input spikes for testing were also subdivided into theta cycles and jittered in the same manner as during training, forming 1000 testing patterns for each running direction. A sequence is said to be correctly identified if the tempotron fires at at least 1 out of 10 theta cycles along the trajectory. The accuracy rate for each running direction of trajectory is computed across the 100 jittered realizations.

Code availability

We used Python 3 for simulations and visualization. The codes are available from a github repository (https://github.com/yyhhoi/directionalnet, copy archived at Yiu, 2023).

Data availability

The current manuscript is a computational study, so no data have been generated for this manuscript. We used Python 3 for simulations and visualization. The codes are available from https://github.com/yyhhoi/directionalnet (copy archived at Yiu, 2023).

References

1. Abbott LF
2. Varela JA
3. Sen K
4. Nelson SB
(1997) Synaptic depression and cortical gain control
Science 275:220–224.
https://doi.org/10.1126/science.275.5297.221
- PubMed
- Google Scholar
1. Acharya L
2. Aghajan ZM
3. Vuong C
4. Moore JJ
5. Mehta MR
(2016) Causal influence of visual cues on Hippocampal Directional selectivity
Cell 164:197–207.
https://doi.org/10.1016/j.cell.2015.12.015
- PubMed
- Google Scholar
Preprint
1. Ahmadi S
2. Sasaki T
3. Sabariego M
4. Leibold C
5. Leutgeb S
6. Leutgeb JK
(2022) Distinct Roles of Dentate Gyrus and Medial Entorhinal Cortex Inputs for Phase Precession and Temporal Correlations in the Hippocampal CA3 Area
bioRxiv.
https://doi.org/10.1101/2022.06.07.491859
- Google Scholar
1. Berretta N
2. Jones RS
(1996) Tonic facilitation of glutamate release by presynaptic N-methyl-D-aspartate autoreceptors in the entorhinal cortex
Neuroscience 75:339–344.
https://doi.org/10.1016/0306-4522(96)00301-6
- PubMed
- Google Scholar
1. Brunel N
2. Trullier O
(1998) Plasticity of directional place fields in a model of rodent CA3
Hippocampus 8:651–665.
https://doi.org/10.1002/(SICI)1098-1063(1998)8:6<651::AID-HIPO8>3.0.CO;2-L
- PubMed
- Google Scholar
1. Buhry L
2. Azizi AH
3. Cheng S
(2011) Reactivation, replay, and preplay: how it might all fit together
Neural Plasticity 2011:203462.
https://doi.org/10.1155/2011/203462
- PubMed
- Google Scholar
1. Burke SN
2. Maurer AP
3. Yang Z
4. Navratilova Z
5. Barnes CA
(2008) Glutamate receptor-mediated restoration of experience-dependent place field expansion plasticity in aged rats
Behavioral Neuroscience 122:535–548.
https://doi.org/10.1037/0735-7044.122.3.535
- PubMed
- Google Scholar
1. Cei A
2. Girardeau G
3. Drieu C
4. Kanbi KE
5. Zugaro M
(2014) Reversed theta sequences of hippocampal cell assemblies during backward travel
Nature Neuroscience 17:719–724.
https://doi.org/10.1038/nn.3698
- PubMed
- Google Scholar
(2019) Hippocampal CA1 replay becomes less prominent but more rigid without inputs from medial entorhinal cortex
Nature Communications 10:1341.
https://doi.org/10.1038/s41467-019-09280-0
- PubMed
- Google Scholar
1. Cheng S
(2013) The CRISP theory of hippocampal function in episodic memory
Frontiers in Neural Circuits 7:88.
https://doi.org/10.3389/fncir.2013.00088
- PubMed
- Google Scholar
(2021) Distinct place cell dynamics in CA1 and CA3 encode experience in new environments
Nature Communications 12:2977.
https://doi.org/10.1038/s41467-021-23260-3
- PubMed
- Google Scholar
1. Dragoi G
2. Buzsáki G
(2006) Temporal encoding of place sequences by hippocampal cell assemblies
Neuron 50:145–157.
https://doi.org/10.1016/j.neuron.2006.02.023
- PubMed
- Google Scholar
1. Dragoi G
2. Tonegawa S
(2011) Preplay of future place cell sequences by hippocampal cellular assemblies
Nature 469:397–401.
https://doi.org/10.1038/nature09633
- PubMed
- Google Scholar
1. Dragoi G
2. Tonegawa S
(2013) Distinct preplay of multiple novel spatial experiences in the rat
PNAS 110:9100–9105.
https://doi.org/10.1073/pnas.1306031110
- Google Scholar
1. Dragoi G
2. Tonegawa S
(2014) Selection of preconfigured cell assemblies for representation of novel spatial experiences
Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 369:20120522.
https://doi.org/10.1098/rstb.2012.0522
- PubMed
- Google Scholar
(2001) NMDA receptor antagonism blocks experience-dependent expansion of hippocampal “place fields.”
Neuron 31:631–638.
https://doi.org/10.1016/s0896-6273(01)00401-9
- PubMed
- Google Scholar
1. Feng T
2. Silva D
3. Foster DJ
(2015) Dissociation between the experience-dependent development of hippocampal theta sequences and single-trial phase precession
The Journal of Neuroscience 35:4890–4902.
https://doi.org/10.1523/JNEUROSCI.2614-14.2015
- PubMed
- Google Scholar
1. Foster DJ
2. Wilson MA
(2007) Hippocampal theta sequences
Hippocampus 17:1093–1099.
https://doi.org/10.1002/hipo.20345
- PubMed
- Google Scholar
(2014) Topography of head direction cells in medial entorhinal cortex
Current Biology 24:252–262.
https://doi.org/10.1016/j.cub.2013.12.002
- PubMed
- Google Scholar
1. Gütig R
2. Sompolinsky H
(2006) The tempotron: a neuron that learns spike timing-based decisions
Nature Neuroscience 9:420–428.
https://doi.org/10.1038/nn1643
- PubMed
- Google Scholar
1. Haga T
2. Fukai T
(2018) Recurrent network model for learning goal-directed sequences through reverse replay
eLife 7:e34171.
https://doi.org/10.7554/eLife.34171
- PubMed
- Google Scholar
1. Hainmueller T
2. Bartos M
(2018) Parallel emergence of stable and dynamic memory engrams in the hippocampus
Nature 558:292–296.
https://doi.org/10.1038/s41586-018-0191-2
- PubMed
- Google Scholar
1. Harris KD
2. Henze DA
3. Hirase H
4. Leinekugel X
5. Dragoi G
6. Czurkó A
7. Buzsáki G
(2002) Spike train dynamics predicts theta-related phase precession in hippocampal pyramidal cells
Nature 417:738–741.
https://doi.org/10.1038/nature00808
- PubMed
- Google Scholar
(2009) Intracellular dynamics of hippocampal place cells during virtual navigation
Nature 461:941–946.
https://doi.org/10.1038/nature08499
- PubMed
- Google Scholar
Book
1. Hebb DO
(1949)
The Organization of Behavior: A Neuropsychological Theory

New York: Wiley.
- Google Scholar
1. Hsu TT
2. Lee CT
3. Tai MH
4. Lien CC
(2016) Differential recruitment of dentate Gyrus Interneuron Types by Commissural Versus Perforant Pathways
Cerebral Cortex 26:2715–2727.
https://doi.org/10.1093/cercor/bhv127
- PubMed
- Google Scholar
(2003) Independent rate and temporal coding in hippocampal pyramidal cells
Nature 425:828–832.
https://doi.org/10.1038/nature02058
- PubMed
- Google Scholar
(2008) Theta phase–specific codes for two-dimensional position, trajectory and heading in the hippocampus
Nature Neuroscience 11:587–594.
https://doi.org/10.1038/nn.2106
- Google Scholar
1. Izhikevich EM
(2003) Simple model of spiking neurons
IEEE Transactions on Neural Networks 14:1569–1572.
https://doi.org/10.1109/TNN.2003.820440
- PubMed
- Google Scholar
1. Jaramillo J
2. Kempter R
(2017) Phase precession: a neural code underlying episodic memory?
Current Opinion in Neurobiology 43:130–138.
https://doi.org/10.1016/j.conb.2017.02.006
- PubMed
- Google Scholar
(1996) Physiologically realistic formation of autoassociative memory in networks with theta/gamma oscillations: role of fast NMDA channels
Learning & Memory 3:243–256.
https://doi.org/10.1101/lm.3.2-3.243
- Google Scholar
1. Kay K
2. Chung JE
3. Sosa M
4. Schor JS
5. Karlsson MP
6. Larkin MC
7. Liu DF
8. Frank LM
(2020) Constant sub-second cycling between representations of possible futures in the Hippocampus
Cell 180:552–567.
https://doi.org/10.1016/j.cell.2020.01.014
- PubMed
- Google Scholar
1. Kempter R
2. Leibold C
3. Buzsáki G
4. Diba K
5. Schmidt R
(2012) Quantifying circular-linear associations: hippocampal phase precession
Journal of Neuroscience Methods 207:113–124.
https://doi.org/10.1016/j.jneumeth.2012.03.007
- PubMed
- Google Scholar
1. Larimer P
2. Strowbridge BW
(2008) Nonrandom local circuits in the dentate gyrus
The Journal of Neuroscience 28:12212–12223.
https://doi.org/10.1523/JNEUROSCI.3612-08.2008
- PubMed
- Google Scholar
1. Lee AK
2. Wilson MA
(2002) Memory of sequential experience in the hippocampus during slow wave sleep
Neuron 36:1183–1194.
https://doi.org/10.1016/s0896-6273(02)01096-6
- PubMed
- Google Scholar
1. Lee I
2. Rao G
3. Knierim JJ
(2004) A double dissociation between hippocampal subfields: differential time course of CA3 and CA1 place cells for processing changed environments
Neuron 42:803–815.
https://doi.org/10.1016/j.neuron.2004.05.010
- PubMed
- Google Scholar
1. Leibold C
(2020) A model for navigation in unknown environments based on A reservoir of hippocampal sequences
Neural Networks 124:328–342.
https://doi.org/10.1016/j.neunet.2020.01.014
- PubMed
- Google Scholar
1. Leutgeb S
2. Leutgeb JK
3. Treves A
4. Moser MB
5. Moser EI
(2004) Distinct ensemble codes in hippocampal areas CA3 and CA1
Science 305:1295–1298.
https://doi.org/10.1126/science.1100265
- PubMed
- Google Scholar
1. Lisman J
2. Redish AD
(2009) Prediction, sequences and the hippocampus
Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 364:1193–1201.
https://doi.org/10.1098/rstb.2008.0316
- PubMed
- Google Scholar
1. Mankin EA
2. Thurley K
3. Chenani A
4. Haas OV
5. Debs L
6. Henke J
7. Galinato M
8. Leutgeb JK
9. Leutgeb S
10. Leibold C
(2019) The hippocampal code for space in Mongolian gerbils
Hippocampus 29:787–801.
https://doi.org/10.1002/hipo.23075
- PubMed
- Google Scholar
(1998) Differential signaling via the same axon of neocortical pyramidal neurons
PNAS 95:5323–5328.
https://doi.org/10.1073/pnas.95.9.5323
- Google Scholar
1. Markus EJ
2. Qin YL
3. Leonard B
4. Skaggs WE
5. McNaughton BL
6. Barnes CA
(1995) Interactions between location and task affect the spatial and directional firing of hippocampal neurons
The Journal of Neuroscience 15:7079–7094.
https://doi.org/10.1523/JNEUROSCI.15-11-07079.1995
- PubMed
- Google Scholar
(2005) Self-motion and the origin of differential spatial scaling along the septo-temporal axis of the hippocampus
Hippocampus 15:841–852.
https://doi.org/10.1002/hipo.20114
- PubMed
- Google Scholar
1. Maurer AP
2. McNaughton BL
(2007) Network and intrinsic cellular mechanisms underlying theta phase precession of hippocampal neurons
Trends in Neurosciences 30:325–333.
https://doi.org/10.1016/j.tins.2007.05.002
- Google Scholar
(1997) Experience-dependent, asymmetric expansion of hippocampal place fields
PNAS 94:8918–8921.
https://doi.org/10.1073/pnas.94.16.8918
- Google Scholar
(2000) Experience-dependent asymmetric shape of hippocampal receptive fields
Neuron 25:707–715.
https://doi.org/10.1016/s0896-6273(00)81072-7
- PubMed
- Google Scholar
(2002) Role of experience and oscillations in transforming a rate code into a temporal code
Nature 417:741–746.
https://doi.org/10.1038/nature00807
- PubMed
- Google Scholar
1. Mejías JF
2. Torres JJ
(2008) The role of synaptic facilitation in spike coincidence detection
Journal of Computational Neuroscience 24:222–234.
https://doi.org/10.1007/s10827-007-0052-8
- PubMed
- Google Scholar
(2009) Theta oscillations provide temporal windows for local circuit computation in the entorhinal-hippocampal loop
Neuron 64:267–280.
https://doi.org/10.1016/j.neuron.2009.08.037
- PubMed
- Google Scholar
1. Parra-Barrero E
2. Cheng S
(2023) Learning to predict future locations with internally generated theta sequences
PLOS Computational Biology 19:e1011101.
https://doi.org/10.1371/journal.pcbi.1011101
- PubMed
- Google Scholar
1. Penttonen M
2. Kamondi A
3. Sik A
4. Acsády L
5. Buzsáki G
(1998) Feed-forward and feed-back activation of the dentate gyrus in vivo during dentate spikes and sharp wave bursts
Hippocampus 7:437–450.
https://doi.org/10.1002/(SICI)1098-1063(1997)7:4<437::AID-HIPO9>3.0.CO;2-F
- Google Scholar
1. Pfeiffer BE
(2022) Spatial learning drives Rapid Goal representation in Hippocampal ripples without place field Accumulation or Goal-Oriented Theta Sequences
The Journal of Neuroscience 42:3975–3988.
https://doi.org/10.1523/JNEUROSCI.2479-21.2022
- PubMed
- Google Scholar
(1996) Changes in hippocampal cell discharge patterns and theta rhythm spectral properties as a function of walking velocity in the guinea pig
Experimental Brain Research 108:113–118.
https://doi.org/10.1007/BF00242908
- PubMed
- Google Scholar
1. Romani S
2. Tsodyks M
(2015) Short-term plasticity based network model of place cells dynamics
Hippocampus 25:94–105.
https://doi.org/10.1002/hipo.22355
- PubMed
- Google Scholar
1. Roth ED
2. Yu X
3. Rao G
4. Knierim JJ
(2012) Functional differences in the backward shifts of CA1 and CA3 place fields in novel and familiar environments
PLOS ONE 7:e36035.
https://doi.org/10.1371/journal.pone.0036035
- PubMed
- Google Scholar
1. Sasaki T
2. Piatti VC
3. Hwaun E
4. Ahmadi S
5. Lisman JE
6. Leutgeb S
7. Leutgeb JK
(2018) Dentate network activity is necessary for spatial working memory by supporting CA3 sharp-wave ripple generation and prospective firing of CA3 neurons
Nature Neuroscience 21:258–269.
https://doi.org/10.1038/s41593-017-0061-5
- PubMed
- Google Scholar
1. Scharfman HE
(1994) Evidence from simultaneous intracellular recordings in rat hippocampal slices that area CA3 pyramidal cells innervate dentate hilar mossy cells
Journal of Neurophysiology 72:2167–2180.
https://doi.org/10.1152/jn.1994.72.5.2167
- PubMed
- Google Scholar
1. Scharfman HE
(1995) Electrophysiological evidence that dentate hilar mossy cells are excitatory and innervate both granule cells and interneurons
Journal of Neurophysiology 74:179–194.
https://doi.org/10.1152/jn.1995.74.1.179
- PubMed
- Google Scholar
1. Scharfman HE
(2016) The enigmatic mossy cell of the dentate gyrus
Nature Reviews. Neuroscience 17:562–575.
https://doi.org/10.1038/nrn.2016.87
- PubMed
- Google Scholar
(1997) The effect of aging on experience-dependent plasticity of hippocampal place cells
The Journal of Neuroscience 17:6769–6782.
https://doi.org/10.1523/JNEUROSCI.17-17-06769.1997
- PubMed
- Google Scholar
1. Skaggs WE
2. McNaughton BL
(1996) Replay of neuronal firing sequences in rat hippocampus during sleep following spatial experience
Science 271:1870–1873.
https://doi.org/10.1126/science.271.5257.1870
- PubMed
- Google Scholar
(1996) Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences
Hippocampus 6:149–172.
https://doi.org/10.1002/(SICI)1098-1063(1996)6:2<149::AID-HIPO6>3.0.CO;2-K
- PubMed
- Google Scholar
1. Soriano E
2. Frotscher M
(1994) Mossy cells of the rat fascia dentata are glutamate-immunoreactive
Hippocampus 4:65–69.
https://doi.org/10.1002/hipo.450040108
- PubMed
- Google Scholar
1. Stefanini F
2. Kushnir L
3. Jimenez JC
4. Jennings JH
5. Woods NI
6. Stuber GD
7. Kheirbek MA
8. Hen R
9. Fusi S
(2020) A distributed Neural Code in the dentate Gyrus and in CA1
Neuron 107:703–716.
https://doi.org/10.1016/j.neuron.2020.05.022
- PubMed
- Google Scholar
(1990) Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis
The Journal of Neuroscience 10:420–435.
https://doi.org/10.1523/JNEUROSCI.10-02-00420.1990
- PubMed
- Google Scholar
(2008) Phase precession through synaptic facilitation
Neural Computation 20:1285–1324.
https://doi.org/10.1162/neco.2008.07-06-292
- PubMed
- Google Scholar
(1996) Population dynamics and theta rhythm phase precession of hippocampal place cell firing: A spiking neuron model
Hippocampus 6:271–280.
https://doi.org/10.1002/(SICI)1098-1063(1996)6:3<271::AID-HIPO5>3.0.CO;2-Q
- PubMed
- Google Scholar
1. Tsodyks MV
2. Markram H
(1997) The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability
PNAS 94:719–723.
https://doi.org/10.1073/pnas.94.2.719
- PubMed
- Google Scholar
(1998) Neural networks with dynamic synapses
Neural Computation 10:821–835.
https://doi.org/10.1162/089976698300017502
- PubMed
- Google Scholar
1. Wilson MA
2. McNaughton BL
(1993) Dynamics of the hippocampal ensemble code for space
Science 261:1055–1058.
https://doi.org/10.1126/science.8351520
- PubMed
- Google Scholar
(2022) Directional tuning of phase precession properties in the Hippocampus
The Journal of Neuroscience 42:2282–2297.
https://doi.org/10.1523/JNEUROSCI.1569-21.2021
- PubMed
- Google Scholar
Software
1. Yiu YH
(2023) Directionalnet, version swh:1:rev:7d87577ddb437b0c5941a29fae1b2f1bed909b33
Software Heritage.

https://archive.softwareheritage.org/swh:1:dir:fc7e003de3035b1738384de92550691dc47192b0;origin=https://github.com/yyhhoi/directionalnet;visit=swh:1:snp:e48933641593f2607bf458b9c564be6f773d2abf;anchor=swh:1:rev:7d87577ddb437b0c5941a29fae1b2f1bed909b33
1. Zucker RS
2. Regehr WG
(2002) Short-term synaptic plasticity
Annual Review of Physiology 64:355–405.
https://doi.org/10.1146/annurev.physiol.64.092501.114547
- PubMed
- Google Scholar

Article and author information

Author details

Yuk-Hoi Yiu
1. Fakultät für Biologie & Bernstein Center Freiburg Albert-Ludwigs-Universität Freiburg, Freiburg, Germany
2. Graduate School of Systemic Neurosciences, Ludwig-Maximilians-Universität München, Munich, Germany
Contribution
Conceptualization, Data curation, Software, Writing - original draft, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-1997-9277
Christian Leibold
1. Fakultät für Biologie & Bernstein Center Freiburg Albert-Ludwigs-Universität Freiburg, Freiburg, Germany
2. BrainLinks-BrainTools, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany
Contribution
Conceptualization, Supervision, Funding acquisition, Writing - original draft, Writing - review and editing

For correspondence
christian.leibold@biologie.uni-freiburg.de

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-4859-8000

Funding

Deutsche Forschungsgemeinschaft (LE2250/13-1)

Christian Leibold

Deutsche Forschungsgemeinschaft (INST 39/963-1 FUGG)

Christian Leibold

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Version history

Preprint posted: February 5, 2023 (view preprint)
Sent for peer review: March 2, 2023
Preprint posted: May 17, 2023 (view preprint)
Preprint posted: August 14, 2023 (view preprint)
Preprint posted: September 18, 2023 (view preprint)
Version of Record published: October 4, 2023 (version 1)

Cite all versions

You can cite all versions using the DOI https://doi.org/10.7554/eLife.86837. This DOI represents all versions, and will always resolve to the latest one.

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

1,049

views
70

downloads
0

citations

Views, downloads and citations are aggregated across all versions of this paper published by eLife.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Yuk-Hoi Yiu
Christian Leibold

(2023)

A theory of hippocampal theta correlations accounting for extrinsic and intrinsic sequences

eLife 12:RP86837.

https://doi.org/10.7554/eLife.86837.4

Share this article

Cite this article

Phase precession depends on running direction in intrinsic models but not extrinsic models.

Directional input gives rise to spikes at lower theta phase.

DG-CA3 loop introduces directionality of theta sequences.

DG lesion reduces theta compression and phase precession range.

Intrinsic sequences lead to direction dependent 2-d phase precession and out-of-field firing (A) Left: Schematic illustration of DG-loop projection being tilted by 45° relative to the trajectory.

Extrinsically driven theta correlations can be temporally organized by sensorimotor drive alone without CA3-CA3 recurrence.

Intrinsic sequences provide a stable landmark for positional decoding using a tempotron.

Illustration of spike time gradients in one theta cycle (500–600 ms) with and without DG loop.

Model parameters used in simulations according to Figure panels.

Author details

Yuk-Hoi Yiu

Contribution

Competing interests

Christian Leibold

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Further reading