Uncovering circuit mechanisms of current sinks and sources with biophysical simulations of primary visual cortex
- Department of Informatics, University of Oslo, Norway
- Department of Physics, University of Oslo, Norway
- Department of Data Science, Norwegian University of Life Sciences, Norway
- MindScope Program, Allen Institute, United States
- Department of Physics, Norwegian University of Life Sciences, Norway
Figures
Figure 1
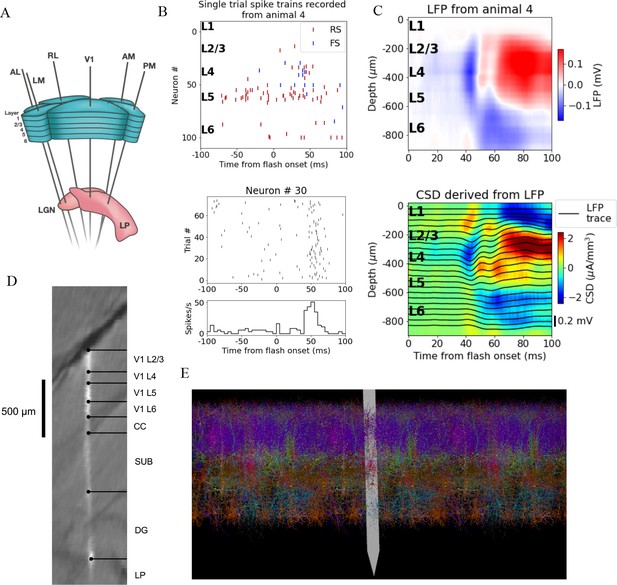
Illustration of experimental data and the biophysical model for mouse primary visual cortex (V1).
(A) Schematic of the experimental setup, with six Neuropixels probes inserted into six cortical (V1, latero-medial [LM], rostro-lateral [RL], antero-lateral [AL], postero-medial [PM], AM) and two …
Figure 2 with 3 supplements
Variability in experimentally recorded current source density (CSD).
(A) Evoked CSD response to a full-field flash averaged over 75 trials, from five animals in the dataset. (B) The first principal component (PC) computed from the CSD of all n = 44 animals, …
Figure 2—figure supplement 1
Trial-averaged current source density (CSD) during presentation of full-field flashes for all 44 animals in this study.
Figure 2—figure supplement 2
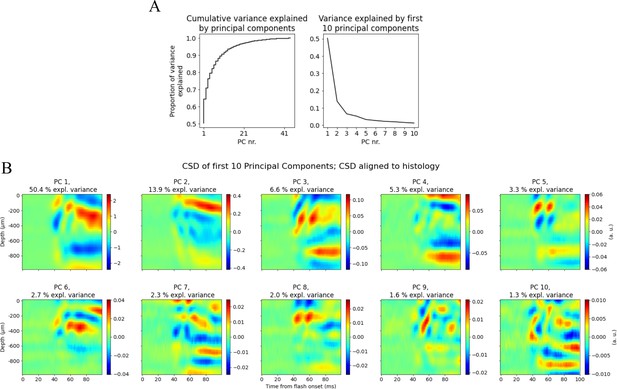
Principal component analysis (PCA) on histology-aligned current source density (CSD).
(A) Left: cumulative variance explained by principal components. Right: variance explained by first 10 components. (B) CSD plots of the first 10 principal components explaining in total >90% of the …
Figure 2—figure supplement 3
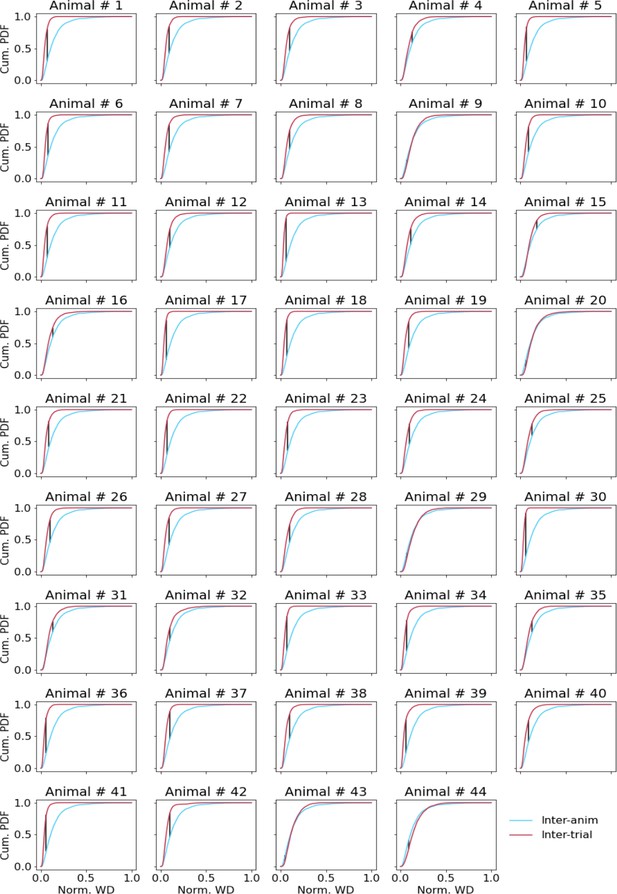
Comparing inter-trial and inter-animal pairwise Wasserstein distances (WDs).
Cumulative distributions of pairwise WDs between trial-averaged current source density (CSD) of individual animals (blue line) and pairwise WDs between single trial CSD in each animal (red lines). …
Figure 3 with 2 supplements
Variability in experimentally recorded spikes.
(A) Trial-averaged laminar population firing rates of regular-spiking (RS) cells, differentiated by layer, and fast-spiking (FS) cells across all layers in response to full-field flash. Black line: …
Figure 3—figure supplement 1
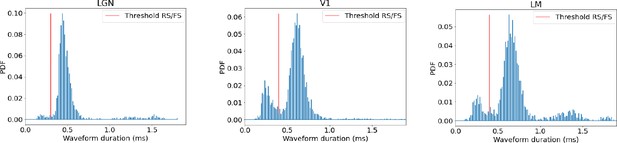
Classifying cell types in experimental data.
Distributions of waveform duration in cells from lateral geniculate nucleus (LGN), V1, and latero-medial (LM) and the threshold (red line) between classifying as regular-spiking (RS) or fast-spiking …
Figure 3—figure supplement 2
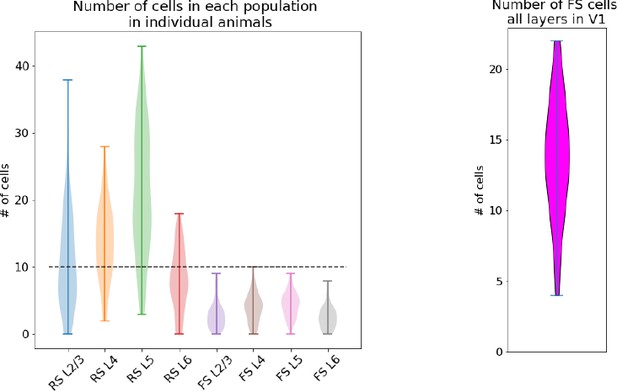
Number of cells in each population in experimental data.
Left: number of regular-spiking (RS) and fast-spiking (FS) in each layer in individual animals. Right: number of FS cells across all layers in V1 in individual animals.
Figure 4 with 1 supplement
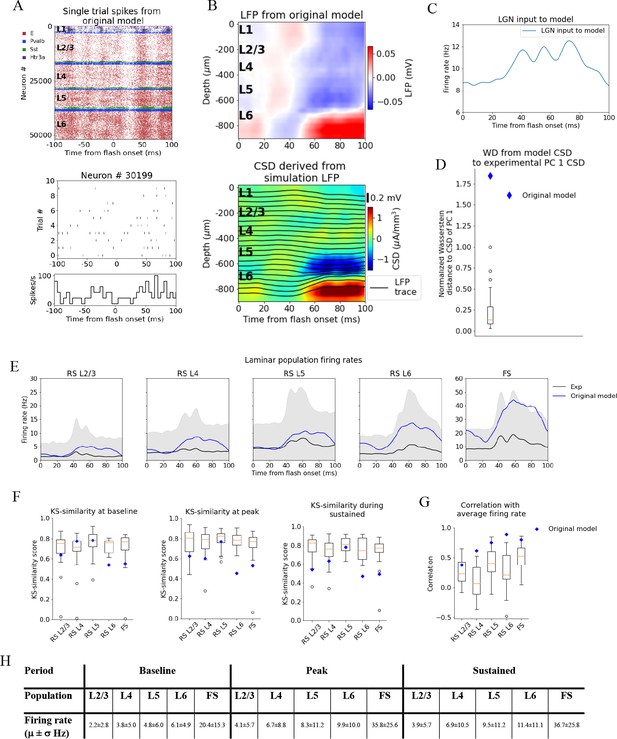
Local field potential (LFP), current source density (CSD), and spikes from simulations with the original model.
(A) Top: raster plot of all ~50,000 cells in the model’s 400 μm radius ‘core’ region spanning all layers, in a simulation of a single trial with the flash stimulus. Bottom: raster plot and histogram …
Figure 4—figure supplement 1
Effect of reducing recurrent inhibition.
Laminar population firing rates in the original model (blue line), in the model after reduction of recurrent excitatory synaptic weights to all Pvalb cells by 30% (brown line), and in experiments …
Figure 5 with 4 supplements
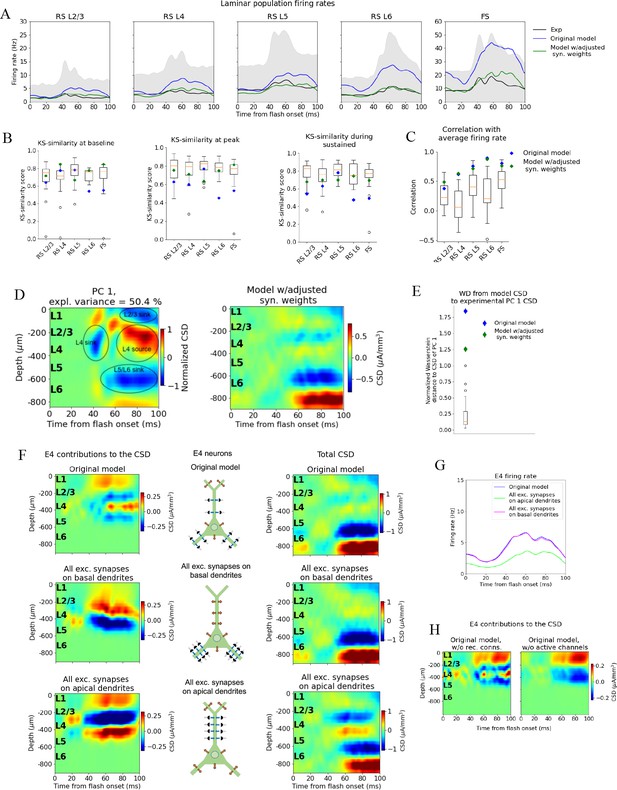
Adjusting the model to fit spikes or current source density (CSD).
(A) Average experimentally (black) and simulated firing rates of experiments in the model with adjusted recurrent synaptic weights (green) and original model (blue). Synaptic adjustments included …
Figure 5—figure supplement 1
Quantifying change in simulated current source density (CSD) with adjustments to synaptic weights.
(A) CSD of original model. (B) CSD of intermediate model where synaptic weights between populations in V1 have been adjusted. (C) CSD of final model. (D) Pairwise Wasserstein distance between CSD …
Figure 5—figure supplement 2
Quantifying change in spiking of L4 excitatory cells after adjusting synaptic placement.
(A) Blue line: original model where excitatory synapses onto L4 excitatory cells were placed on both basal and apical dendrites. Green line: all excitatory synapses onto L4 excitatory cells were …
Figure 5—figure supplement 3
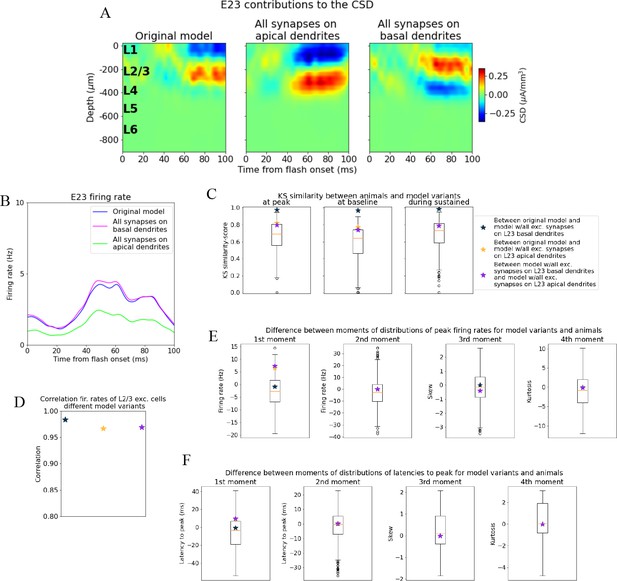
Effects of manipulating synaptic placement onto L2/3 excitatory cells on population current source density (CSD) and spiking.
(A) CSD generated by L2/3 excitatory cells in (left) the original configuration with synapses on both apical and basal dendrites, (middle) all excitatory synapses placed on apical dendrites, and …
Figure 5—figure supplement 4
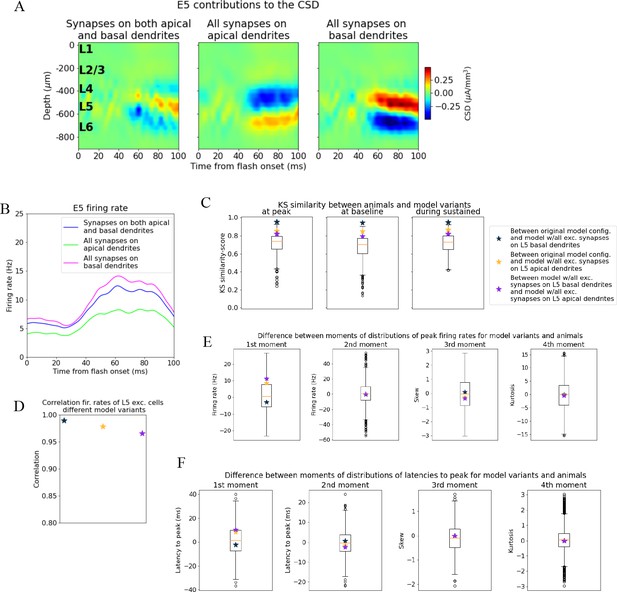
Effects of manipulating synaptic placement onto L5 excitatory cells on population current source density (CSD) and spiking.
(A) CSD generated by L5 excitatory cells in (left) the original configuration with synapses on both apical and basal dendrites, (middle) all excitatory synapses placed on apical dendrites, and …
Figure 6 with 9 supplements
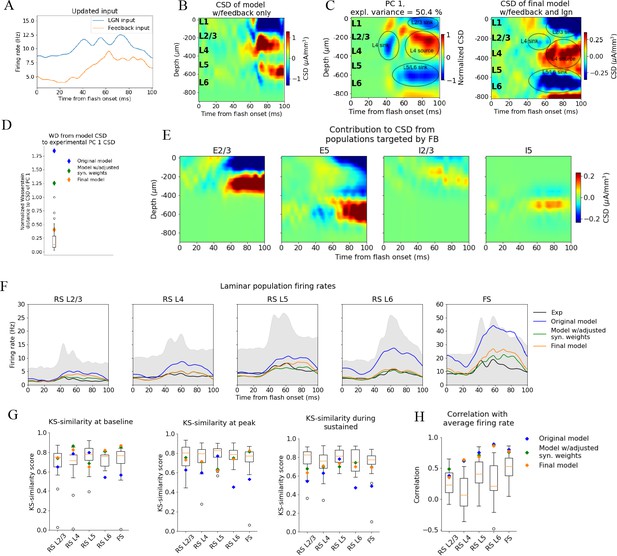
Introducing feedback from latero-medial (LM) to V1 in the model.
(A) Firing rate of the experimentally recorded lateral geniculate nucleus (LGN) and LM units used as input to the model. (B) Total current source density (CSD) resulting from simulation with input …
Figure 6—figure supplement 1
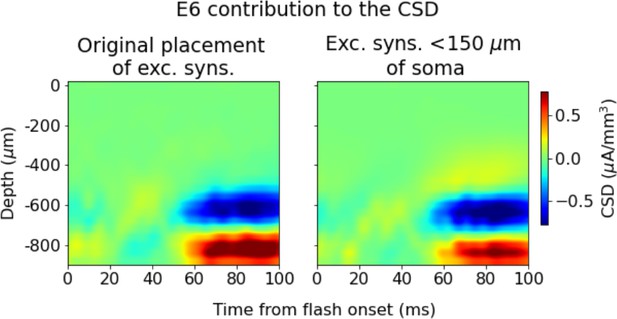
Effect of adjusting synaptic placement onto L6 excitatory cells.
Contributions to the total current source density (CSD) from L6 excitatory cells with the original placement of recurrent excitatory synapses uniformly along the whole length of their dendrites …
Figure 6—figure supplement 2
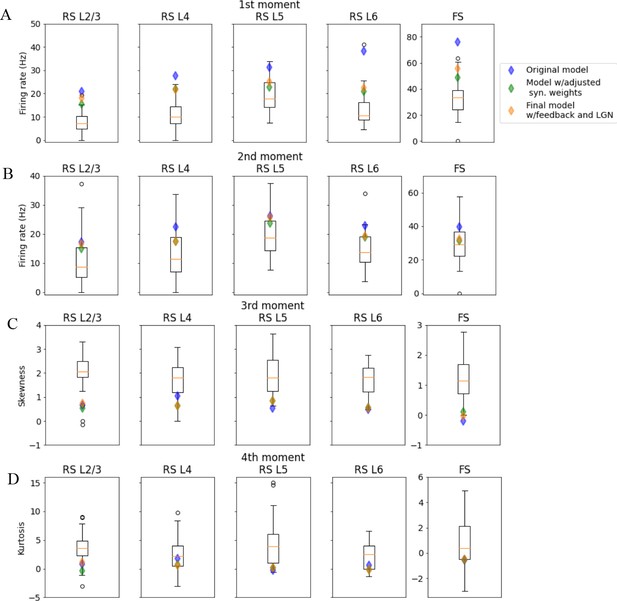
Moments of distributions of peak firing rate in model versions and experiments for different populations.
Boxplots represent data for different animals, diamonds represent model versions. (A) First moment (mean). (B) Second moment (standard deviation). (C) Third moment (skewness). (D) Fourth moment …
Figure 6—figure supplement 3
Moments of distributions of latency to peak of firing rates in model versions and experiments in different populations.
Boxplots represent data for different animals, diamonds represent model versions. (A) First moment (mean). (B) Second moment (standard deviation). (C) Third moment (skewness). (D) Fourth moment …
Figure 6—figure supplement 4
Relative change in peak firing rates between neighboring populations.
(A) From regular-spiking (RS) cells in L2/3 to RS cells in L4. (B) From RS cells in L4 to RS cells in L5. (C) From RS cells in L5 to RS cells in L6. (D) From all RS cells in V1 to all FS cells in …
Figure 6—figure supplement 5
Moments of distributions of greatest curvature in firing rate across cells.
Diamonds represent model versions and boxplots represent moments calculated for different animals. (A) First moment (mean). (B) Second moment (standard deviation). (C) Third moment (skew). (D) …
Figure 6—figure supplement 6
Orientation and direction selectivity in final model.
Rate at preferred direction (A), direction selectivity index (B), and orientation selectivity index (C) in layer populations of model (blue) and in experiments (gray).
Figure 6—figure supplement 7
Current source density (CSD) analysis after aligning experimental CSD plots to landmarks rather than histology.
(A) Example CSD plot with landmarks used for alignment marked (white stars). (B) Top: PC 1 CSD after application of principal component analysis (PCA) on trial-averaged CSD from all animals. Bottom: …
Figure 6—figure supplement 8
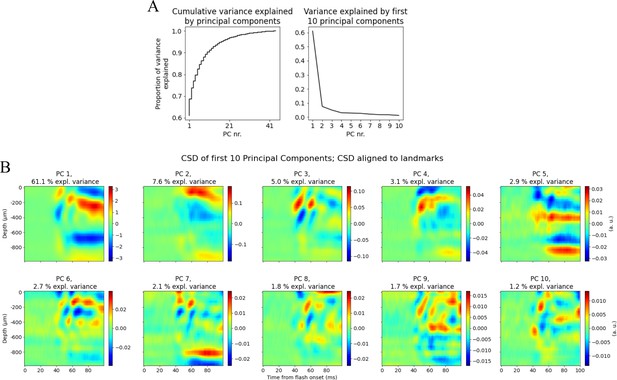
Priincipal component analysis (PCA) on landmark aligned current source density (CSD).
(A) Left: cumulative variance explained by components. Right: variance explained by first 10 components. (B) CSD plots of the first 10 principal components explaining in total >90% of the variance …
Figure 6—figure supplement 9
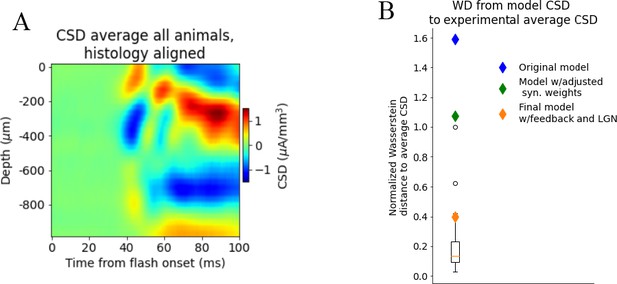
Effect of using plain average of trial-averaged current source density (CSD) from all animals instead of first principal component as target.
Wasserstein distance from model versions and individual animal CSD to plain average of trial-averaged CSD from all animals. (A) CSD averaged over trial-averaged CSD from all animals. CSD aligned to …
Figure 7 with 3 supplements
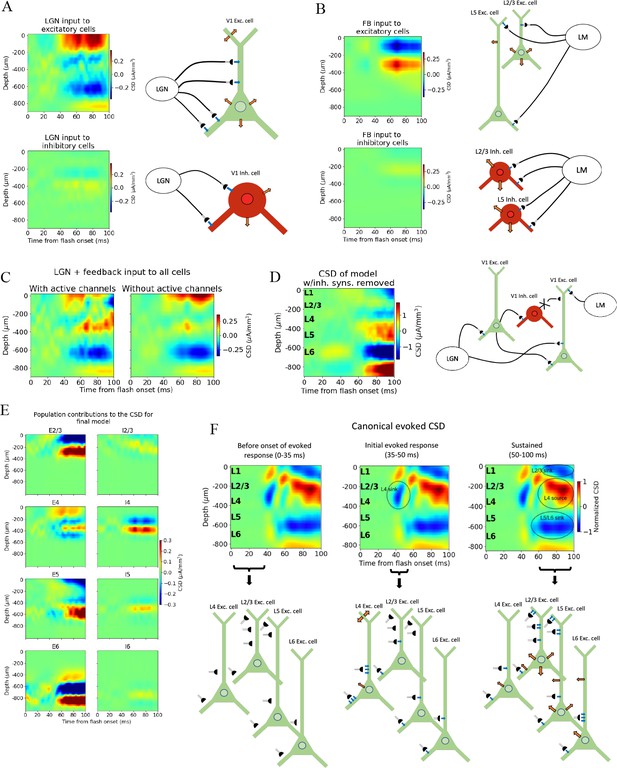
Biophysical origin of canonical current source density (CSD).
(A) Sinks and sources generated from thalamocortical and (B) feedback synapses. The schematics illustrate which synapses cause the observed sinks and sources. Blue arrows indicate inflowing current …
Figure 7—figure supplement 1
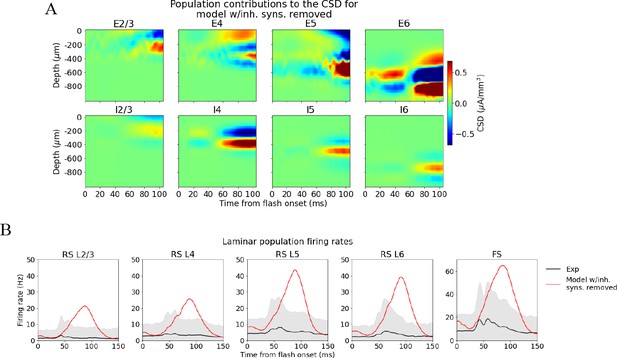
Effects of removing recurrent inhibition on population current source density (CSD) and firing rates.
(A) Population contributions to the total CSD and (B) laminar population firing rates in a simulation where all inhibitory synapses have been removed.
Figure 7—figure supplement 2
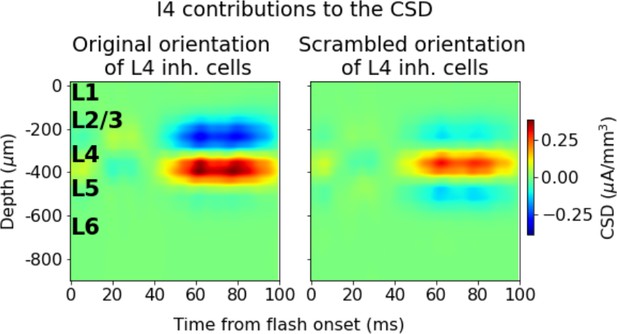
Effect of cell orientation on current source density (CSD) contributions of L4 inhibitory cells.
CSD contribution of L4 inhibitory cells with original orientation (left) and scrambled orientation (right).
Figure 7—figure supplement 3
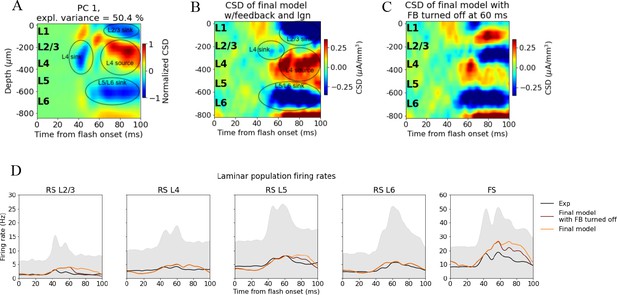
Silencing feedback from latero-medial (LM) in model during evoked response.
Current source density (CSD) of (A) PC 1 computed from experiments, (B) final model, and (C) final model with feedback turned off at 60ms. (D) Trial-averaged population firing rates in experiments …
Appendix 1—figure 1
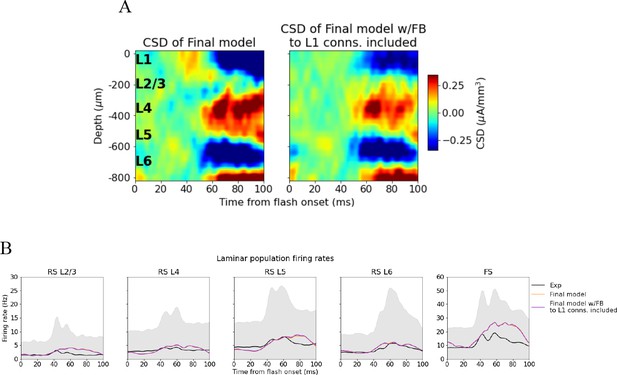
Effect of adding feedback connections from latero-medial (LM) to L1 inhibitory cells.
(A) Left: current source density (CSD) from simulation of final model version without connections from LM to L1 inhibitory cells. Right: CSD from simulation of final model version with connections …
Author response image 1
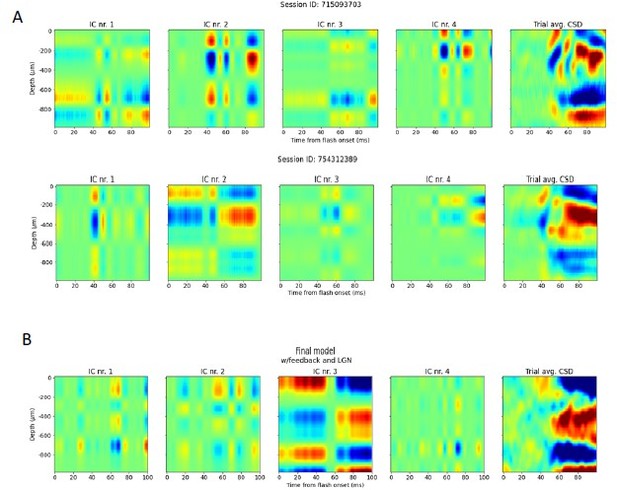
ICA decomposition of experimental CSD and simulated CSD.
(A) Two examples of applying ICA on trial averaged CSD of animals. Four resulting independent components are displayed from left to right, and the trial averaged CSD of the example animal is shown …
