Quantifying gliding forces of filamentous cyanobacteria by self-buckling
- Max Planck Institute for Dynamics and Self-Organization (MPI-DS), Germany
- Experimental Physics V, University of Bayreuth, Germany
- Max Planck School Matter to Life, University of Göttingen, Germany
- Institute for Dynamics of Complex Systems, University of Göttingen, Germany
- Department of Experimental Phycology and SAG Culture Collection of Algae Albrecht-von-Haller Institute for Plant Science, University of Göttingen, Germany
- Fachbereich Physik, University of Konstanz, Germany
Figures
Figure 1
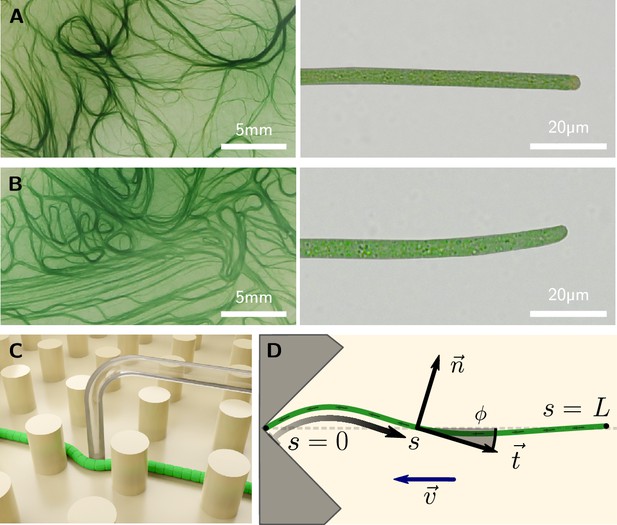
Colony and filament morphology of gliding filamentous cyanobacteria, bending, and buckling tests.
(A, B) Colonies on agar plates (left) and individual filaments in liquid medium (right) of K. animale and O. lutea, respectively. (C) Schematic of a microscopic three-point bending test, pushing a filament into the gap between SU-8 pillars using a glass micropipette. (D) Schematic of a self-buckling test in a microfluidic chip: A filament glides into a V-shaped obstacle and buckles if its contour length exceeds the self-buckling threshold .
Figure 2 with 1 supplement
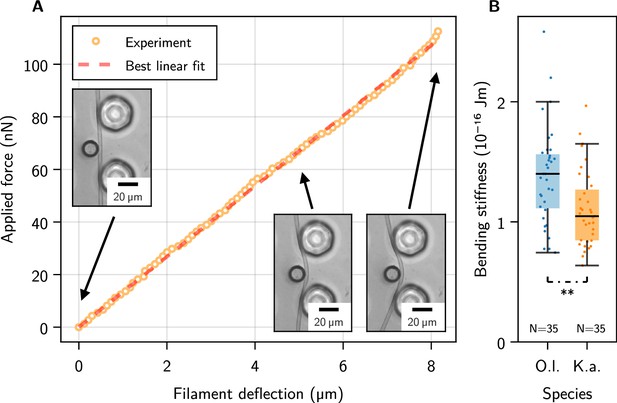
Single-filament bending measurements using micropipette force sensors.
(A) Representative force-deflection measurement for K. animale. Insets: Bottom-view micrographs of the same experiment. (B) Box plot of the bending moduli for individuals of K. animale and O. lutea, shown as points (each tested 2-10 times). Box limits denote the first and third quartile, whiskers the last measurement within the inter-quartile distance away from the respective box limit. A p-value of 6.87 suggests different typical moduli for the two species.
Figure 2—figure supplement 1
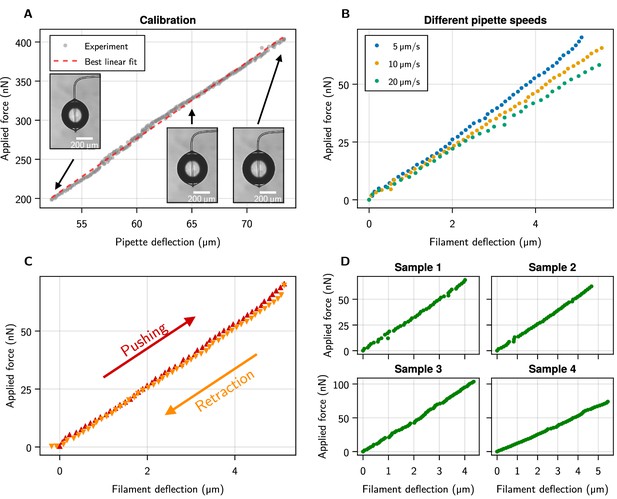
Details on the microscopic three-point bending tests.
(A) Calibration of the force-sensing micropipette by the weight of an evaporating water droplet. (B) Testing the same filament with three different actuation speeds shows a negligible speed dependence of the force-deflection curves as compared to the spread between individual measurements. (C) Force-deflection curves for increasing (‘pushing’) and decreasing (‘retraction’) deflection, showing the absence of hysteresis. (D) Force-deflection measurements for four individual filaments of K. animale.
Figure 3 with 3 supplements
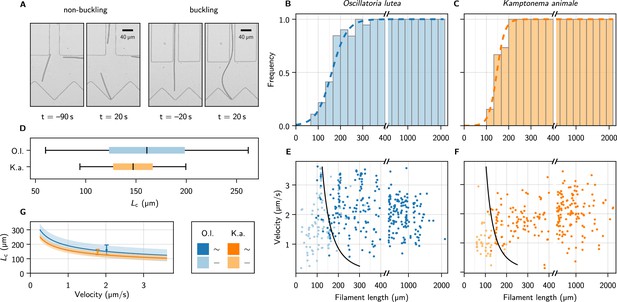
Self-buckling experiments and statistics.
(A) Snapshots of K. animale, before and after hitting the obstacle at . Left, short filament with , right, long filament with . (B, C) Bar plot of the buckling frequency vs. filament length for O. lutea (B, totally events) and K. animale (C, totally events), together with the logistic regression (dashed curve). (D) Box plot of the quantiles of the critical length distribution from the logistic regression . Box limits denote first and third quartiles, whiskers the 5th and 95th percentile. (E, F) Velocity immediately before hitting the obstacle vs. filament length for O. lutea and K. animale, respectively, distinguishing buckling (dark) and non-buckling (light). The velocity-dependent median critical length , as derived from a logistic regression with and as independent explanatory variables, is indicated by black lines. Note that axes in (B, C, E, F) are broken around to emphasize the critical region. (G) (lines) and inter-quartile region (shaded), together with the simple logistic regression from (D), located at the mean velocity of the population (symbols & error bars).
Figure 3—figure supplement 1
Collection of buckling events with different shapes of the traps.
Snapshots of K. animale (top row) and O. lutea (bottom row), before and after hitting the obstacle at time . Left, four short filaments with length below the critical length, right, six long filaments above the critical length.
Figure 3—figure supplement 2
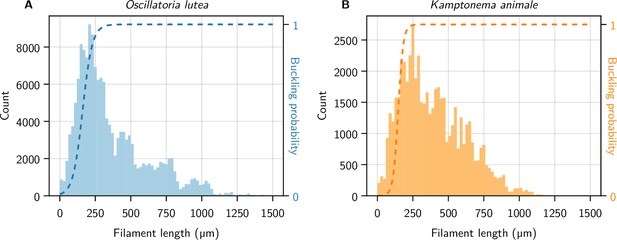
Natural length distributions and buckling probability.
Length distributions of O. lutea (A) and K. animale (B), together with the buckling probability estimated by the logistic regression. Colonies were grown in quiescent liquid medium and then gently squeezed in between agar solidified medium and glass. Filaments glide from the colony into the glass-agar contact and form a sub-monolayer. After ∼ 6 hr, the layer is then analyzed by our modified U-Net segmentation procedure. Filaments remain intact and alive in this configuration for days, as inferred from their gliding velocity.
Figure 3—figure supplement 3
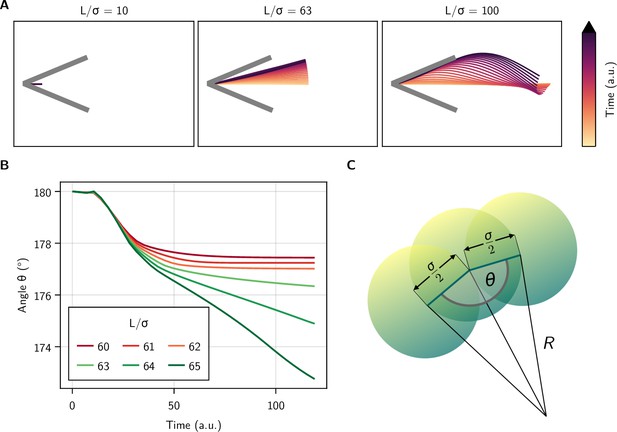
Simulations of self-buckling semi-flexible chains of active overdamped particles.
Chains of particles of diameter and separation are connected by torsional springs to generate an effective bending modulus. Each particle self-propels along the tangent of the particle chain, defined by the mean orientation of its two bonds. (A) Trajectory of active particle chains of 21, 127, and 201 particles, corresponding to filament lengths of 10 σ, 63 σ, and 100 σ, respectively. (B) Front-Mid-End angle of particle chains as a function of time, after hitting the obstacle. Active force and torsional spring constant were chosen to obtain, from the analytical expression,. The chain hits the obstacle slightly off-center, to induce a non-singular initial condition for self-buckling. For (red colors), curvature stagnates and then relaxes very slowly. For (green colors), curvature increases further. (C) Definition of the Geometry of the particle chains.
Figure 4 with 2 supplements
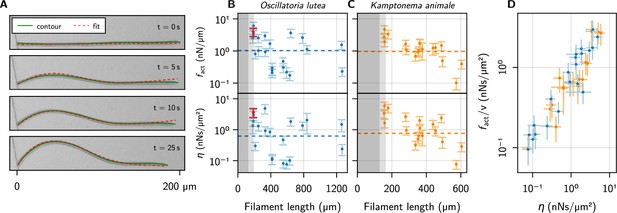
Kirchhoff theory compared to experimental contours.
(A) Time series of a characteristic buckling event of O. lutea, overlaying the contour extracted from the images (green) and the best fit of the solution to Equation 5 (red). (B, C) and vs. filament length , as determined from the fit, for O. lutea and K. animale, respectively. Light gray indicates (see Figure 3D), dark gray , where buckling is not observed. The dashed lines are obtained from of logistic regression. The filament from (A) is indicated in red. (D) Free-gliding friction coefficient against from the buckling profile fit.
Figure 4—figure supplement 1
Active force and friction coefficient vs.filament velocity.
Velocities were measured immediately before hitting the obstacle. Neither nor appears to be correlated with the velocity.
Figure 4—figure supplement 2
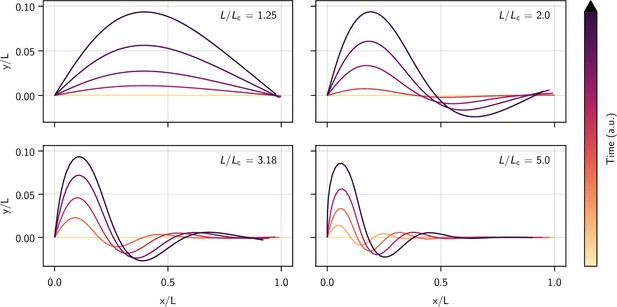
Numerical results for the full non-linear Kirchhoff theory.
Equation 5 is discretized according to the scheme described in Methods and integrated over time, starting from a small-amplitude analytical solution to the linearized equations.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Quantifying gliding forces of filamentous cyanobacteria by self-buckling
eLife 12:RP87450.
https://doi.org/10.7554/eLife.87450.3
