Modeled grid cells aligned by a flexible attractor
- Leloir Institute – IIBBA/CONICET, Argentina
- Department of Mathematics, Durham University, United Kingdom
Figures
Figure 1 with 1 supplement
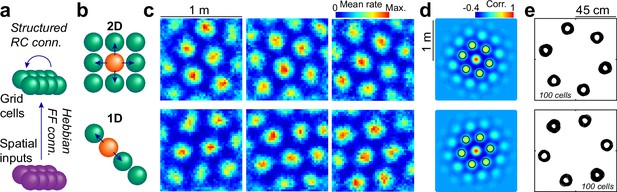
Attractors with a 2D or 1D architecture align grid maps.
(a) Schematics of the network model, including an input layer with place cell-like activity (purple), feedforward all-to-all connections with Hebbian plasticity and a grid cell layer (green) with global inhibition and a set of excitatory recurrent collaterals of fixed structure. (b) Schematics of the recurrent connectivity from a given cell (orange) to its neighbors (green) in a 2D (top) or 1D (bottom) setup. (c) Representative examples of maps belonging to the same 2D (top) or 1D (bottom) network at the end of training. (d) Average of all autocorrelograms in the same two simulations, highlighting the 6 maxima around the center (black circles). (e) Superposition of the 6 maxima around the center (as in d) for all individual autocorrelograms in the same two simulations.
Figure 1—figure supplement 1
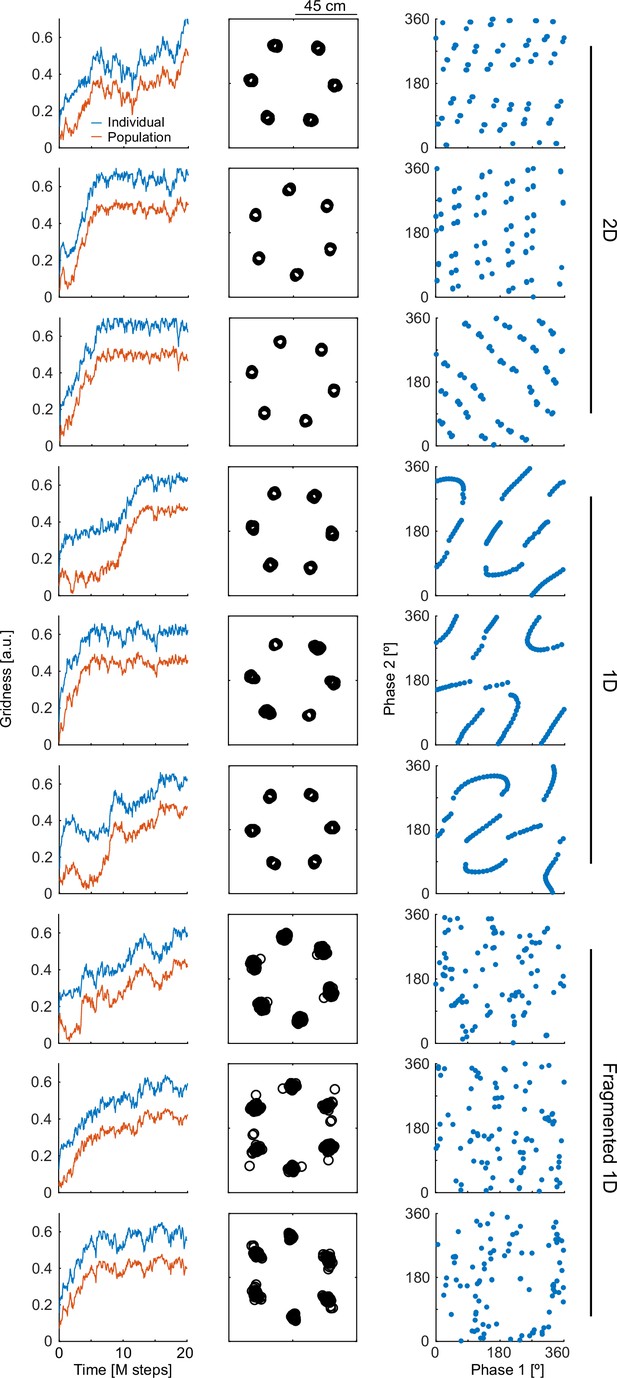
Spatial phases present characteristic patterns for simple attractors, although this is not a necessary feature for slightly more complex architectures.
For simulations (one per row) organized in groups of three for each condition (indicated) columns show from left to right: evolution of individual and population gridness throughout learning (as in Figure 2c), superposition of autocorrelation maxima (as in Figure 1e) and spatial phase along two grid axes. The conditions are 2D (top), 1D (center) and a recurrent architecture with 20 overlapping 1 DL attractors, each one recruiting 10 randomly selected cells among the 100 available (Fragmented 1D). While all conditions reach high levels of alignment (slightly lower in the Fragmented 1D case), only 1D and 2D show characteristic organization patterns. The fact that the Fragmented 1D condition does not present any visible organization pattern for spatial phases demonstrates that, although observable in the simplest cases, this phenomenon is not a necessary outcome of flexible attractors.
Figure 2 with 2 supplements
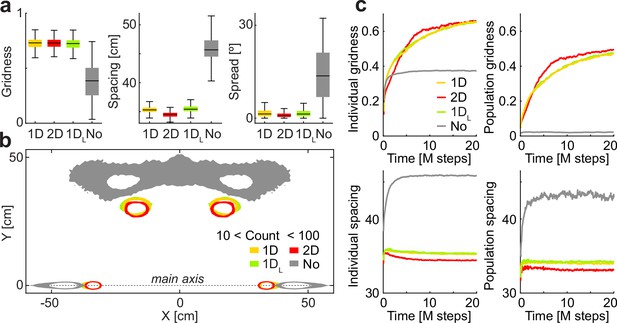
Quantification of the alignment and contraction of grid maps by different attractor architectures.
(a) Distribution (i.q.r., n = 10000) of gridness (left), spacing (center), and spread (right) at the end of the learning process across conditions (quartiles; identical simulations except for the architecture of recurrent collaterals). (b) Smoothed distribution of maxima relative to the main axis of the corresponding autocorrelogram. (c) Mean evolution of gridness (top) and spacing (bottom) in transient maps along the learning process, calculated from individual (left) or average (right) autocorrelograms. Individual spacing negatively correlates with time for the 2D (R: –0.78, p: 10–84), 1D (R: –0.77, p: 10–79), and 1 DL (R: –0.74, p: 10–71).
Figure 2—figure supplement 1
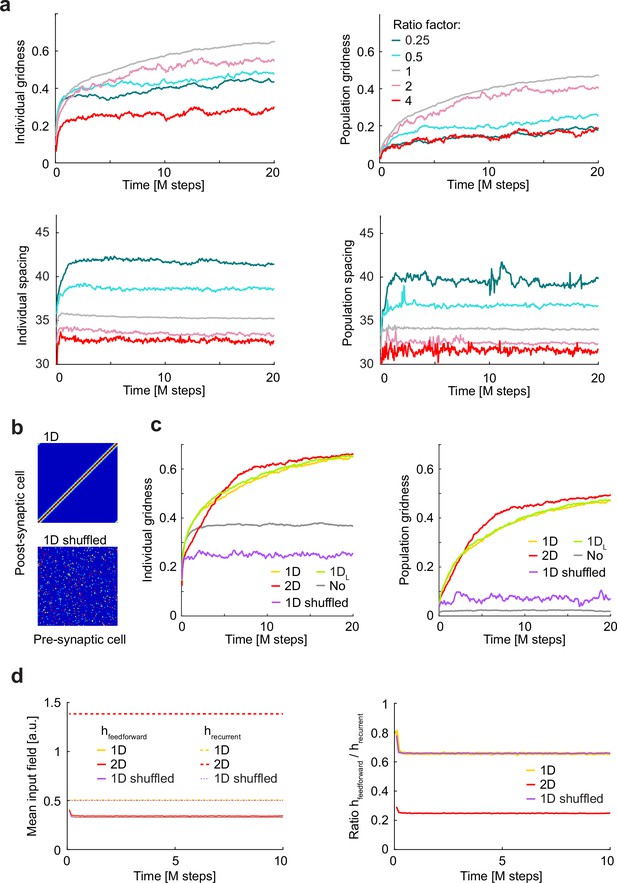
Too weak, too strong or shuffled attractors fail to align grid cells.
(a) Individual (left) or population (right) gridness (top) and spacing (bottom) for the 1D condition is repeated from Figure 2 (grey; ratio arbitrarily defined as 1), together with the results of 10 simulations for each value of a range of ratios between recurrent and feedforward synaptic strength (color code; ratios: 0.25, 0.5, 2, and 4 relative to the 1D condition). Note that gridness decreases if the attractor is too strong or too weak, while spacing is inversely related to the stregth of the attractor. (b) Recurrent connectivity matrix for the 1D condition (top) and for a condition where the recurrent input weights for each neuron are shuffled (bottom). (c) Plots in Figure 2c are repeated here but adding the average of 10 simulations in the shuffled condition. (d) Left: mean input feedforward (solid lines) and recurrent (dashed lines) fields throughout learning for the 1D, 2D and shuffled conditions (color coded). Mean input fields are the sum of all inputs of a given kind entering a neuron at a given moment in time, averaged across cells and time. Right: for the same conditions, feedforward to recurrent mean field ratio.
Figure 2—figure supplement 2
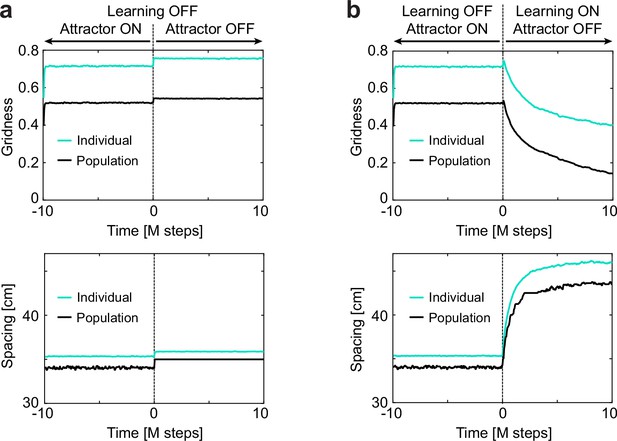
Instant improvement in gridness by turning off recurrent collaterals is reverted by learning.
(a) Individual (green) and population (black) gridness (top) and spacing (bottom) for a trained 1D network where feedforward Hebbian learning has been turned off. At time t=0 the attractor is also turned off, resulting in an improvement in gridness and an increase in spacing. (b) Similar to (a) but this time Hebbian learning is turned on at time = 0. While instantaneously gridness and spacing increase, as in (a) in the long run the network progresses toward the equilibrium corresponding to the condition with no attractor, showing that learning is reversible and that the attractors plays a role in aligning and contracting grid maps.
Figure 3 with 1 supplement
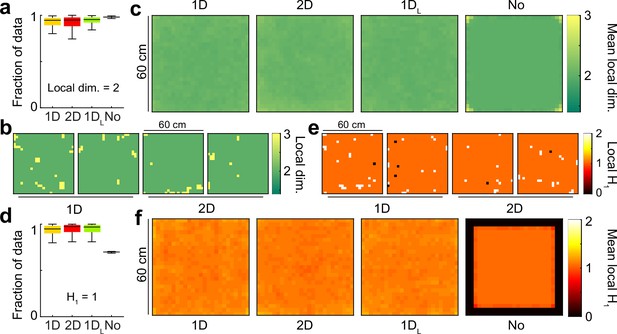
The population activity in all attractor conditions is locally two-dimensional, with no boundary or singularities.
(a) Distribution across conditions of the fraction of the data with local dimensionality of 2 (i.q.r., n = 100). (b) Distribution of local dimensionality across physical space in representative examples of 1D and 2D conditions. (c) Average distribution of local dimensionality for all conditions (same color code as in (b)). (d-f) As (a–c) for but exploring deviations of the local homology H1 from a value of 1, the value expected away from borders and singularities.
Figure 3—figure supplement 1
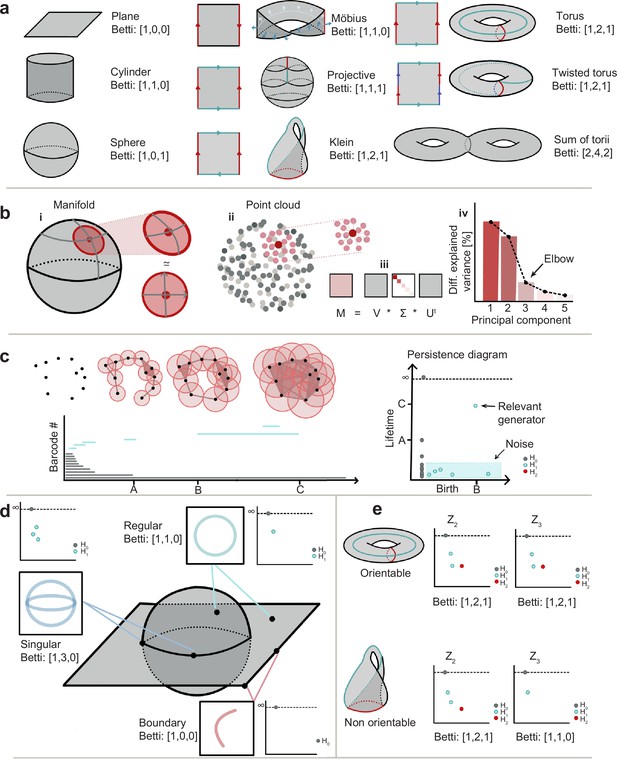
Methods in topological data analysis and examples.
(a) Basic representation of different geometries (indicated) and their corresponding Betti numbers. (b) Local dimensionality of a sphere (i) and a local neighborhood (ii), computed by obtaining its local principal components (iii) and finding and elbow on the rate of explained variance (iv). (c) Left, top: Birth and death of a generator in H1 (a cycle) for the same collection of datapoints and increasing radius. Left, bottom: barcode diagram indicating the birth and death of all generators. Right: Lifetime diagram indicating the birth and length of bars in (b) distinctively indicating relevant generators and noise. (d) Local homology in different locations of a locally two-dimensional object. Deviations from the Betti number B1=1 can indicate boundaries (B1=0) or singularities (B1 >1) as exemplified. (e) Orientable (top, torus) and non-orientable (bottom, Klein bottle) objects with Betti numbers [1, 2, 1] in Z2 but different Betti numbers in Z3 (indicated).
Figure 4 with 1 supplement
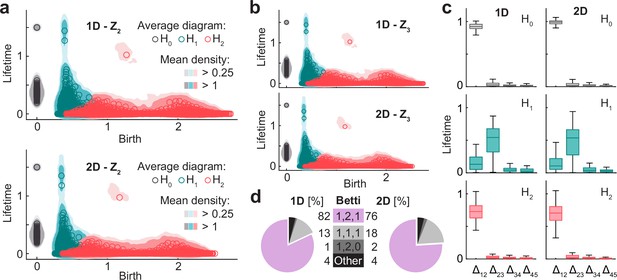
For 1D and 2D architectures, the population activity is an orientable manifold with the homology of torus.
(a) Smoothed density of pooled data (colored areas) and average across simulations (circles) of persistence diagrams with coefficients in Z2 for H0 (grey), H1 (blue), and H2 (red) corresponding to simulations in the 1D (top) and 2D (bottom) conditions. (b) As (a) but with coefficients in Z3. Similarity with (a) implies that population activity lies within an orientable surface. (c) Distribution (i.q.r., n = 100) across simulations of lifetime difference between consecutive generators ordered for each simulation from longest to shortest lifetime for 1D (left) and 2D (right). Maxima coincide with Betti numbers. (d) Pie plot and table indicating the number of simulations (out of 100 in each condition) classified according to their Betti numbers.
Figure 4—figure supplement 1
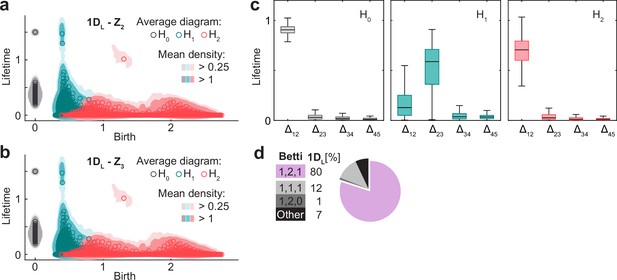
Persistent homology and Betti numbers for condition 1 DL.
(a) Smoothed density of pooled data (colored areas) and average across simulations (circles) of persistence diagrams with coefficients in Z2 for H0 (grey), H1 (blue), and H2 (red) corresponding to simulations in the 1 DL condition. (b) as (a) but in Z3. (c) Distribution (i.q.r., n = 100) across simulations of lifetime difference between consecutive generators ordered for each simulation from longest to shortest lifetime. (d) Pie plot and table indicating the number of simulations (out of 100) classified according to their Betti numbers.
Figure 5
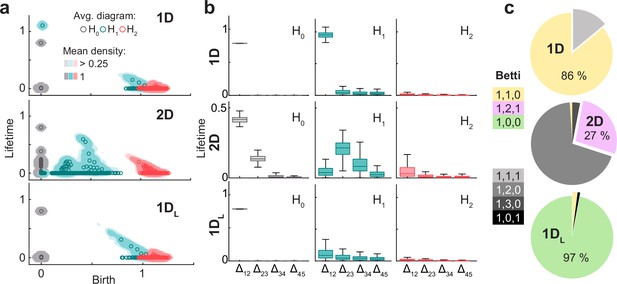
Features of the attractor architecture observed in the persistent homology of neural activity.
(a) From top to bottom, diagrams as in Figure 4a but for the point cloud of neurons in conditions 1D, 2D, and 1 DL. Each panel shows smoothed density of pooled data (colored areas) and average (circles) persistence diagrams for H0 (gray), H1 (blue), and H2 (red) with coefficients in Z2. (b) As in Figure 4c, distribution of the difference between consecutive generators ordered for each simulation from longest to shortest lifetime (i.q.r., n = 100). (c) Pie plots showing the percentage of simulations in which each combination of Betti numbers was found.
Figure 6
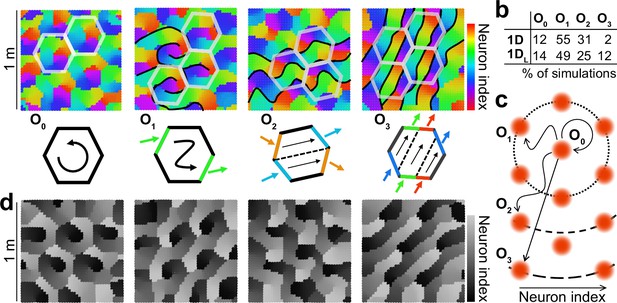
Multiple configurations for the alignment of grid maps by one-dimensional attractors.
(a) Top: Population map for 4 representative examples of 1D simulations with increasing configuration order (indicated) from left to right. Color indicates the region of the ring attractor best describing the mean population activity at each position. Schematics of some of the frontiers, defined by abrupt changes in color (black), and hexagonal tiles maximally coinciding with these frontiers (semi-transparent white) are included for visualization purposes. Bottom: Schematic representation of the order of the solution as the minimum number of colors traversing the perimeter of the hexagonal tile or, equivalently, the minimum number of hexagonal tiles whose perimeter is traversed by one cycle of the attractor. (b) Table indicating the number of simulations out of 100 in which each configuration order was found. (c) Schematic representation of the ring attractor extending in space from a starting point to different order neighbors in a hexagonal arrangement. (d) As (a) but for the 1 DL condition. Gray scale emphasizes the lack of connections between extremes of the stripe attractor.
Figure 7
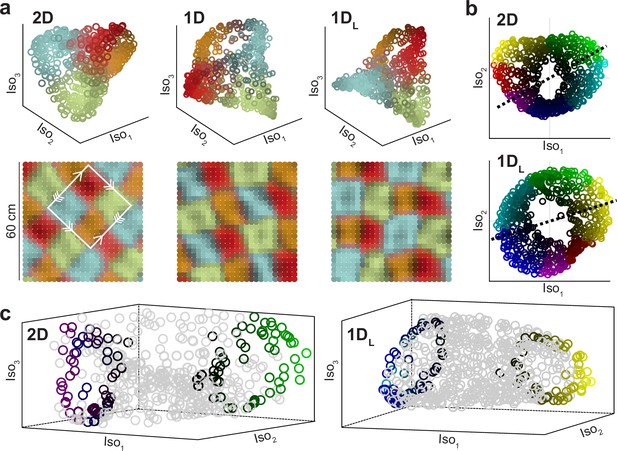
Two different visualizations of the twisted torus obtained with Isomap.
(a) Top: Representative examples of dimensionality reduction into a structure resembling a tetrahedron for different conditions (indicated). Data points are colored according to the distance to one of the four cluster centers obtained with k-means (each one close to tetrahedron vertices; k=4). Bottom: Same data and color code but plotted in physical space. The white square indicates the minimal tile containing all colors, with correspondence between edges, indicated by arrows, matching the basic representation of the twisted torus. (b) Representative examples of dimensionality reduction into a torus structure squeezed at two points, obtained in other simulations using identical Isomap parametrization. Hue (color) and value (from black to bright) indicate angular and radial cylindrical coordinates, respectively. (c) For the same two examples (indicated), three-dimensional renderings. To improve visualization of the torus cavity, color is only preserved for data falling along the corresponding dashed lines in (b).
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Modeled grid cells aligned by a flexible attractor
eLife 12:RP89851.
https://doi.org/10.7554/eLife.89851.3
