Deciphering the genetic code of neuronal type connectivity through bilinear modeling
- LinkedIn, United States
Figures
Figure 1
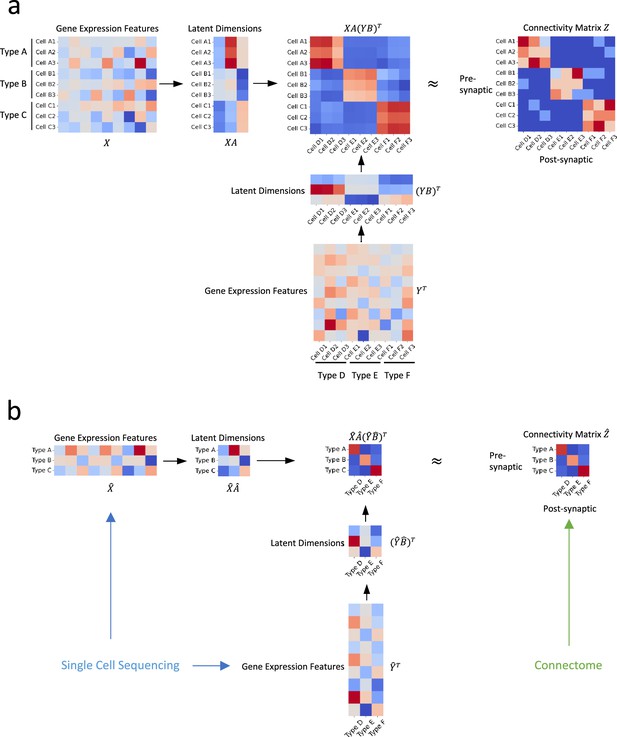
Illustration of our approach.
(a) In an ideal scenario where gene expression profiles and connectivity data of individual cells are available simultaneously, we establish the relationship between connectivity and gene expression profiles via two transformation matrices and (b) In practical situations where the gene expression profiles are derived from distinct sources, such as single-cell transcriptomic and connectomic data, we propose that the connectivity of individual cells and their latent gene expression features can be approximated by the averages of their corresponding cell types, and establish their relationship through transformation matrices and .
Figure 2 with 1 supplement
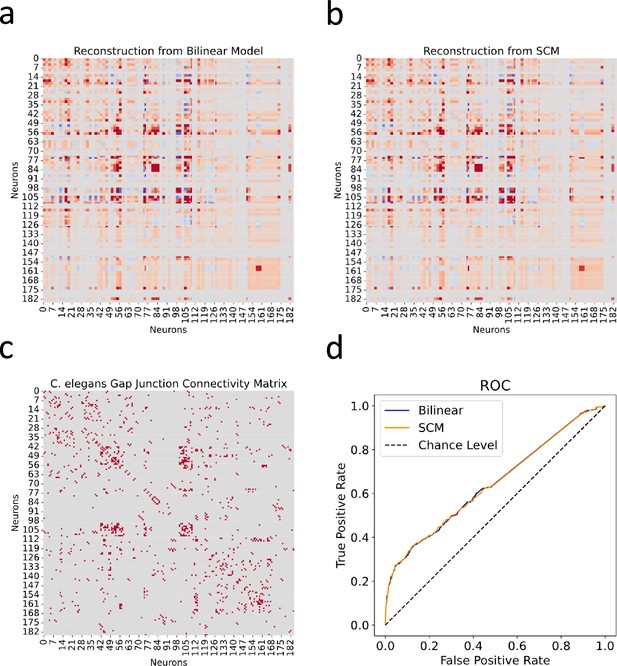
Reconstructed gap junction connectivity from innexin expression data.
(a) Connectivity matrix predicted by the bilinear model. (b) Connectivity matrix modeled from Kovács et al.’s SCM. (c) Observed gap junction connectivity matrix, serving as ground truth. The color spectrum from red to gray denotes the spectrum from strong connections to weak or no connections. (d) ROC curves from both the bilinear model and the SCM. Dashed line indicates the chance level.
Figure 2—figure supplement 1
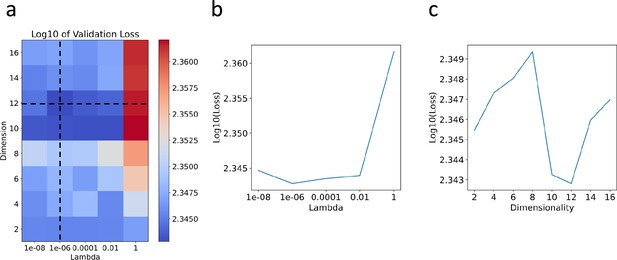
Hyperparameter selection through cross-validation for the C. elegans neuronal dataset.
(a) Heatmap plot of the logarithm (base 10) of the validation loss, showing variations with respect to across [10−8, 10−6, 0.0001, 0.01, 1] and dimensionality across [2, 4, 6, 8, 10, 12, 14, 16]. (b) Plot showing the logarithm (base 10) of the validation loss against over the range [10−8, 10−6, 0.0001, 0.01, 1]. (c) Plot displaying the logarithm (base 10) of the validation loss against dimensionality over the range [2, 4, 6, 8, 10, 12, 14, 16].
Figure 3 with 1 supplement
Genetic rules from the bilinear model and the SCM.
(a) The rule matrix derived from the bilinear model. (b) The rule matrix from the SCM. Black boxes highlight entries with substantial differences.
Figure 3—figure supplement 1
Detailed discrepancy analysis between the bilinear model and SCM genetic rules.
(a) Discrepancy scores (DS) identifying divergences between the models’ rule matrices. (b, c) Significant entries from the bilinear model’s rule matrix (b) and the SCM’s rule matrix (c), respectively, with DS exceeding 0.5 and matrix entries no less than 0.1.
Figure 4 with 3 supplements
Reconstruction of connectivity map from gene expression profiles.
(a) The reconstructed connectivity matrix, derived from the shared latent feature space projections. (b) The connectivity matrix obtained from connectomic data. Differences in color intensity represent the strength of connections, with dark red indicating strong connections and dark blue indicating weak or no connections.
Figure 4—figure supplement 1
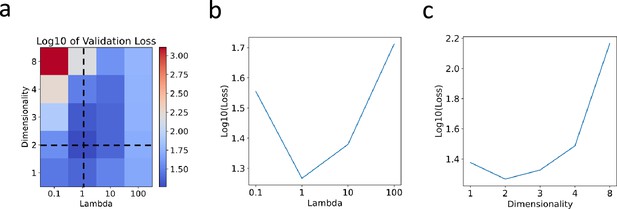
Hyperparameter selection through cross-validation for the mouse retinal neuronal dataset.
(a) Heatmap plot of the logarithm (base 10) of the validation loss, showing variations with respect to across [0.1, 1, 10, 100] and dimensionality across [1, 2, 3, 4, 8]. (b) Plot showing the logarithm (base 10) of the validation loss against over the range [0.1, 1, 10, 100]. (c) Plot displaying the logarithm (base 10) of the validation loss against dimensionality over the range [1, 2, 3, 4, 8].
Figure 4—figure supplement 2
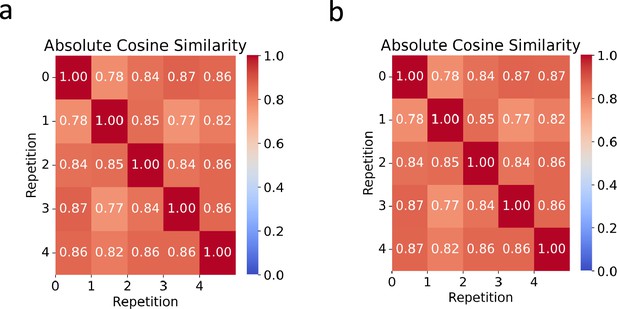
Heatmaps showcasing the average absolute cosine similarities across five optimization repetitions for (a) and (b) .
The color scale reflects value of the metric.
Figure 4—figure supplement 3
Detailed discrepancy analysis between the reconstructed and the target connectivity matrices.
(a) Discrepancy scores (DS) identifying divergences between the two matrices. (b, c) Specific connections present in the target matrix (c) that were not captured in the reconstructed matrix (b), with DS exceeding 0.5, indicating notable deviations.
Figure 5
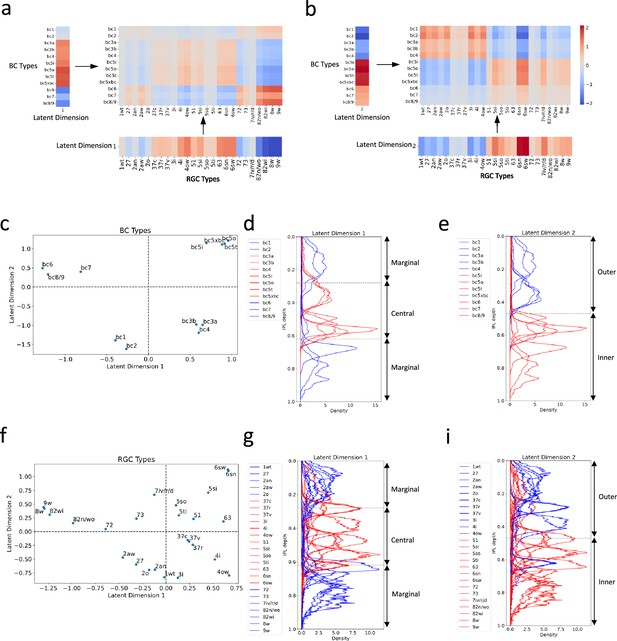
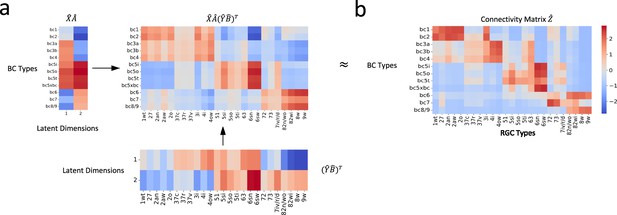
Distinct connectivity motifs revealed by the two latent dimensions.
(a, b) The reconstructed connectivity using only latent dimension 1 or 2, respectively. Differences in color intensity represent the strength of connections. (c) BC types plotted in the latent feature space, with each point representing a specific BC type. Dashed lines indicate zero values for latent dimensions 1 and 2. (d, e) Stratification profiles of BC types in IPL, color-coded based on their positions along the first (d) or second (e) latent dimension. Red indicates BC types on the positive half, while blue indicates BC types on the negative half. (f) RGC types plotted in the latent feature space, with each point representing a specific RGC type. (g, h) Stratification profiles of RGC types in IPL, color-coded based on their positions along the first (g) or second (h) latent dimension. Dashed lines in (d) and (g) mark the positions of ON and OFF SACs (Bae et al., 2018). BCs and RGCs stratifying between them tend to exhibit more transient responses, and those stratifying outside them exhibit more sustained responses. Dashed lines in (e) and (h) denote the boundary of the outer and inner IPL (Bae et al., 2018). Synapses between BCs and RGCs in the outer retina mediate OFF responses, while those in the inner retina mediate ON responses.
Figure 6
Gene signatures associated with the two latent dimensions.
(a, b) Weight vectors of the top 50 genes for latent dimension 1, along with their expression patterns in BC types (a) and RGC types (b). The weight value is indicated in the color bar, with the sign represented by color (red: positive and blue: negative), and the magnitude by saturation. The expression pattern is represented by the size of each dot (indicating the percentage of cells expressing the gene) and the color saturation (representing the gene expression level). BC and RGC types are sorted by their positions along latent dimension 1, as shown in Figure 5c and f, with the dashed line separating the positive category from the negative category. (c, d) Weight vectors of the top 50 genes for latent dimension 2, and their expression patterns in BC types (c) and RGC types (d), depicted in the same manner as in (a) and (b). BC and RGC types are sorted by their positions along latent dimension 2.
Figure 7
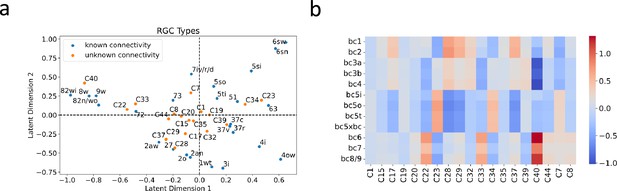
BC partner prediction of transcriptionally-defined RGC types.
(a) Projection of transcriptionally-defined RGC types with unknown connectivity into the same latent space as those with known connectivity. (b) The resulting predicted connectivity matrix between these RGC types and BC types. Transcriptionally-defined RGC types are named according to Tran et al., 2019.
Figure 8
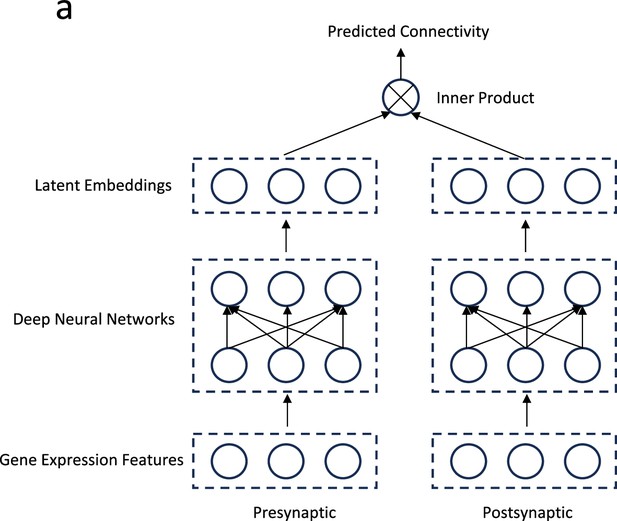
Future direction: A two-tower deep learning model.
(a) Gene expression profiles of pre- and post-synaptic neurons are transformed into latent embedding representations via deep neural networks. The connectivity metric between the pre- and post-synaptic neurons is predicted by taking the inner product of their respective latent embeddings.
Additional files
-
Supplementary file 1
Correspondence of Mouse BC Types from Greene et al., 2016; Shekhar et al., 2016.
- https://cdn.elifesciences.org/articles/91532/elife-91532-supp1-v1.xlsx
-
Supplementary file 2
Correspondence of Mouse RGC Types from Bae et al., 2018; Tran et al., 2019; Goetz et al., 2022.
- https://cdn.elifesciences.org/articles/91532/elife-91532-supp2-v1.xlsx
-
Supplementary file 3
Additional Correspondence of Mouse RGC types (Bae et al., 2018; Tran et al., 2019; Goetz et al., 2022).
- https://cdn.elifesciences.org/articles/91532/elife-91532-supp3-v1.xlsx
-
Supplementary file 4
Gene Ontology (GO) Terms Associated with Latent Dimensions in BCs and RGCs.
- https://cdn.elifesciences.org/articles/91532/elife-91532-supp4-v1.xlsx
-
Supplementary file 5
Predicted BC Partners of Transciptionally-defined RGC Types.
- https://cdn.elifesciences.org/articles/91532/elife-91532-supp5-v1.xlsx
-
MDAR checklist
- https://cdn.elifesciences.org/articles/91532/elife-91532-mdarchecklist1-v1.pdf
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Deciphering the genetic code of neuronal type connectivity through bilinear modeling
eLife 12:RP91532.
https://doi.org/10.7554/eLife.91532.3
