Theoretical principles explain the structure of the insect head direction circuit
- Institute of Neuroinformatics, University of Zürich and ETH Zürich, Switzerland
- School of Informatics, University of Edinburgh, United Kingdom
Figures
Figure 1
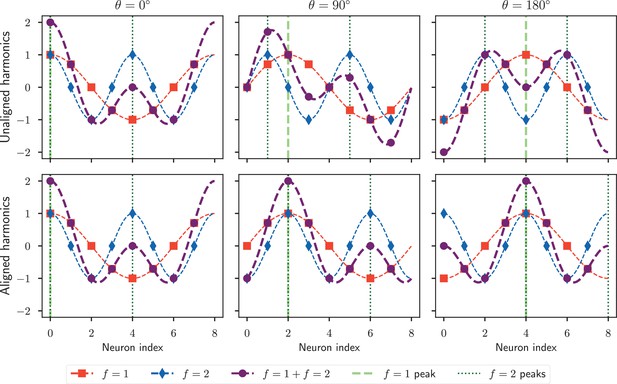
Encoding heading with multiple harmonics.
Each panel shows the activity profiles encoding a particular heading value. Curves , , and respectively denote the waveform of the first harmonic, second harmonic, and the sum of the two. The vertical dashed ( peak) and dotted lines ( peaks) indicate the neurons which respond maximally for the first and second harmonic, respectively. Top row: Encoding the heading as the sum of two independent harmonics causes the waveform to change shape as the insect rotates, because the waveform for each harmonic can only rotate a distance of as the insect rotates a full revolution to ensure an unambiguous representation. Bottom row: If all harmonics are aligned to rotate at the same speed, the combined waveform shape does not change. However, this alignment implies that higher harmonic waveforms cannot be uniquely mapped back to a heading: here the encoding is the same for θ = 0° and 180°.
Figure 2
Increased number of harmonics introduces more noise.
Increasing the number of active harmonic frequencies increases the effect of errors in the network. (A) Weight matrix profiles, , for networks with increasing numbers of harmonics. (B) Normally distributed noise with zero mean and standard deviation 0.3 was added to the network activity, then the network state updated until it reached steady state. Networks with fewer harmonics better filtered out noise. (C) Noise variance increases linearly as the number of active harmonics increases, as predicted by Equation 12. The sample size was n=1000 trials for each active harmonics set, and the error bars show the standard deviation over trials.
Figure 3
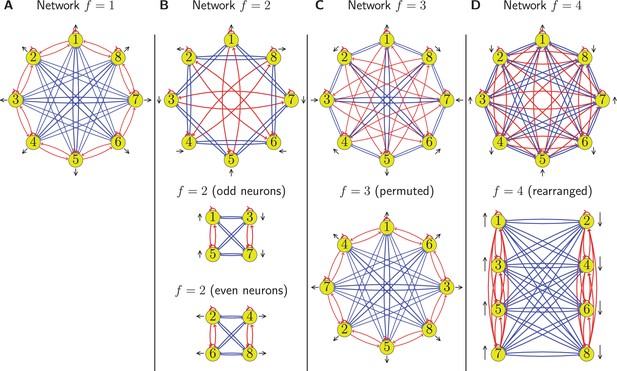
Circuits for encoding with different harmonics.
We show four circuits corresponding to each of the individual harmonics in panels (A, B, C, and D), respectively. Excitatory synapses are marked in red and inhibitory in blue. Neurons are shown in yellow with each having a black arrow that marks the direction to which it is tuned from Equation 16. The circuit is the simplest and constitutes our baseline. For the other cases we plot the original connectivity in the upper row and the rearranged network in the lower row. We find that the circuit consists of two independent subnetworks encoding orthogonal directions, the case is identical to after permuting neuron indices, and the case results in two connected groups of neurons inhibiting each other, hence it can only encode one direction. As such, all cases either have a degenerate ring structure () or are equivalent to after permutation.
Figure 4
Comparison to biological data.
The biological network models of (A) the locust and (B) the fruit fly, with four distinct neural populations each were simplified to equivalent networks with one population by counting paths of lengths 1, 2, and 3 between EPG neurons (which encode the integrated heading) and using the net signed path count as a proxy for connectivity strength. The average connectivity profile for each neuron to its neighbours around the ring was compared to the sinusoidal connectivity predicted by our theory. The locust network has no standard deviation because the data in Pisokas et al., 2020, are based on light microscopy which couldn’t resolve variations between columns. Excitatory connections are shown in red and inhibitory connections in blue, while the strength of a connection is indicated by the line width.
Figure 5
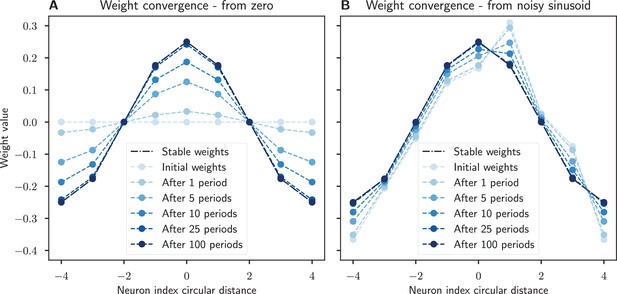
Recovery of synaptic weights with a Hebbian learning rule.
The synaptic weights converge to a sinusoidal pattern under our modified Oja’s rule when the network activity is dynamic and a sinusoidal input is provided. (A) The weights start at zero and slowly converge to the prescribed sinusoidal profile, showing that this connectivity can emerge from scratch. (B) The sinusoidal weights are perturbed by noise but learning ensures that the weight profile is corrected. In both cases the network’s initial activity is corrupted with zero mean Gaussian noise. Noisy sinusoidal input is provided to rotate the activity bump around the network at a constant speed of 1/8 neurons per timestep. The simulation runs for 100 periods. Parameters: integration timestep .
Figure 6
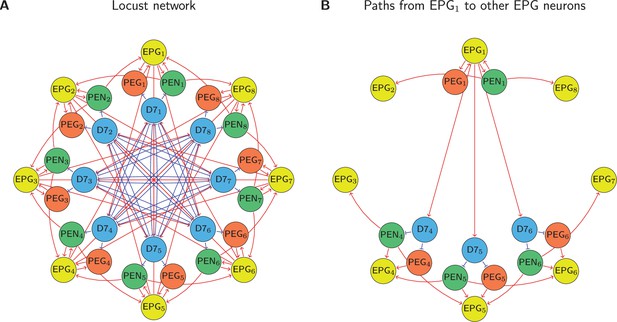
Path counting.
(A) The full locust connectivity network from Pisokas et al., 2020, and (B) the connections with path lengths 2 and 3 from to all other neurons in the network. Because the network is rotationally symmetric these path counts generalise to all neurons as shown in Table 3.
Figure 7
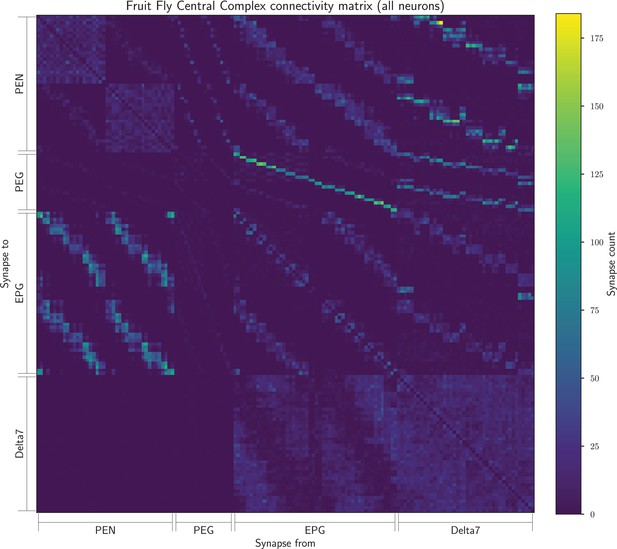
The connectivity matrix for the fruit fly containing all 152 neurons.
On the horizontal axis are the names of the pre-synaptic neurons while on the vertical axis the names of the post-synaptic neurons. Neurons of each cell type are ordered by the glomerulus they innervate and arbitrarily within glomerulus.
Figure 8
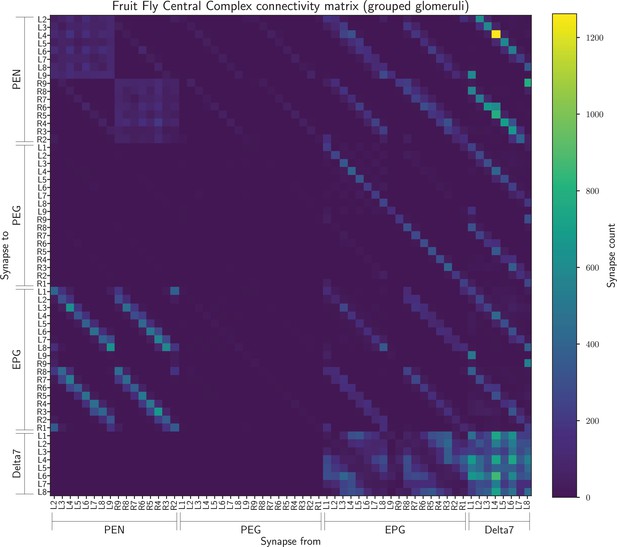
The connectivity matrix for the fruit fly neurons grouped by innervated glomerulus so containing 60 groups.
On the horizontal axis are the names of the pre-synaptic neurons while on the vertical axis the names of the post-synaptic neurons. Neuron groups are ordered by the glomerulus they innervate.
Figure 9
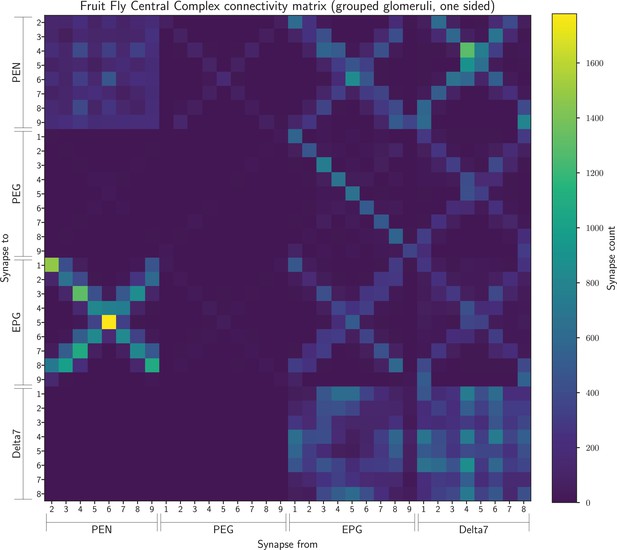
The connectivity matrix for the fruit fly neurons grouped by glomerulus and aggregated from both hemispheres, so containing 34 groups.
On the horizontal axis are the names of the pre-synaptic neuron groups while on the vertical axis are the names of the post-synaptic neuron groups. Neuron groups are ordered by the glomerulus they innervate.
Figure 10
The connectivity matrix for the fruit fly neurons grouped by glomerulus and aggregated from both hemispheres, with PEG9 and PEG1 neurons and EPG9 and EGP1 neurons grouped, so containing 32 groups in total.
On the horizontal axis are the names of the pre-synaptic neuron groups while on the vertical axis the names of the post-synaptic neuron groups. Neuron groups are ordered by the glomerulus they innervate.
Figure 11
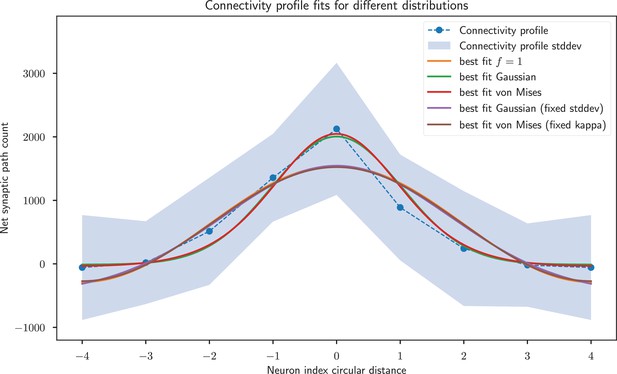
Gaussian and von Mises distributions provide a better fit than the weight profile with sinusoidal weights of frequency 1, but the former two distributions have an extra model parameter.
When fixing the width parameters of these distributions to match the sinusoid, all three distributions provide a very similar fit. Note that the –4 and 4 neuron indices are the same and just duplicated for visualisation purposes.
Figure 12
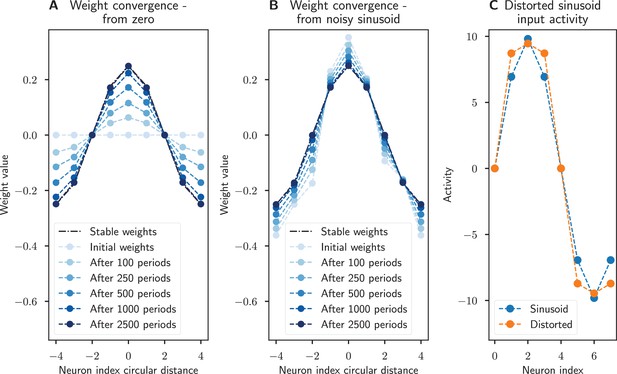
Recovery of synaptic weights with a Hebbian learning rule.
The synaptic weights converge to a sinusoidal pattern under Oja’s rule when the neurons have a nonlinear () activation function and a distorted (more square wave-like) sinusoidal input is provided. (A) The weights start at zero and slowly converge to the prescribed sinusoidal profile, showing that this connectivity can emerge from scratch. (B) The sinusoidal weights are perturbed by noise but learning ensures that the weight profile is corrected. (C) The distorted sinusoidal input (orange) compared to a sinusoid profile (blue). Noise was added to the initial activity, weights, and input with the same parameters as in Figure 5, the only difference being that these simulations were run for 2500 periods.
Tables
Table 1
Requirements for a heading integration circuit.
 |  |  |
|---|---|---|
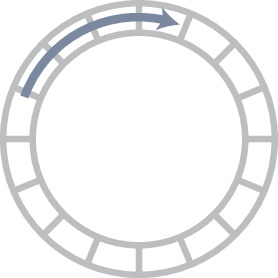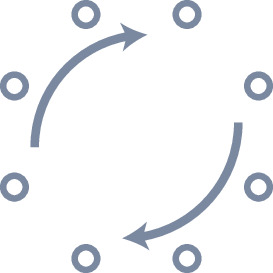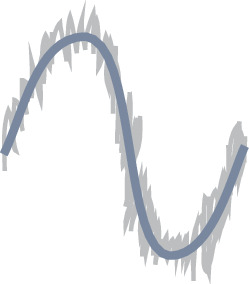| Circular topology | Rotational symmetry | Noise minimisation |
| The activity should have the same topology as the variable it is encoding to prevent discontinuities. To encode heading, the activity should have the topology of a 1D circle. | The heading integration circuit should work similarly, irrespective of the direction in which the insect travels. There should not be a bias for any direction. | The circuit should minimise the noise of the neural representation so the insect can navigate as precisely as possible. |
Table 2
Distribution of neural activity phases for different harmonics.
We computed for and and found that all possible phases appear for any odd number. This happens because the operation imposes an abelian group structure, namely and any coprime with 8 will be a generator of the whole group. If we use instead or we have that we can divide and by 2 and we get the abelian group which has four elements. The same argument applies to , leaving only two elements, and for we get a single element.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | |
| 0 | 2 | 4 | 6 | 0 | 2 | 4 | 6 | 2 | |
| 0 | 3 | 6 | 1 | 4 | 7 | 2 | 5 | 1 | |
| 0 | 4 | 0 | 4 | 0 | 4 | 0 | 4 | 4 | |
| 0 | 5 | 2 | 7 | 4 | 1 | 6 | 3 | 1 | |
| 0 | 6 | 4 | 2 | 0 | 6 | 4 | 2 | 2 | |
| 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 |
Table 3
Net path count profile between neurons in the locust circuit.
| Excitatory path count | 0 | 0 | 0 | 1 | 2 | 1 | 0 | 0 |
| Inhibitory path count | 4 | 3 | 1 | 0 | 0 | 0 | 1 | 3 |
| Net path count | –4 | -3 | –1 | 1 | 2 | 1 | –1 | –3 |
Table 4
Neuron types and their numbers in the fruit fly connectome dataset (Scheffer et al., 2020).
| Neuron class | Number |
|---|---|
| PEN_a(PEN1) | 20 neurons |
| PEN_b(PEN2) | 22 neurons |
| PEG | 18 neurons |
| EPG | 46 neurons |
| EPGt | 4 neurons |
| Delta7 (Δ7) | 42 neurons |
Table 5
List of the Delta7 neuron sub-types in the fruit fly connectome dataset (Scheffer et al., 2020).
These differ in the glomeruli their pre- and post-synaptic terminals innervate. We are referring to those altogether as Delta7 neurons in the present account.
| Delta7 neuron sub-types | Glomerulus group |
|---|---|
| Delta7(PB15)_L1L9R8_R | Delta7 L1 |
| Delta7(PB15)_L2R7_R | Delta7 L2 |
| Delta7(PB15)_L3R6_R | Delta7 L3 |
| Delta7(PB15)_L4R5_R | Delta7 L4 |
| Delta7(PB15)_L4R6_R | Delta7 L4 |
| Delta7(PB15)_L5R4_L | Delta7 L5 |
| Delta7(PB15)_L6R3_L | Delta7 L6 |
| Delta7(PB15)_L6R4_L | Delta7 L6 |
| Delta7(PB15)_L7R2_L | Delta7 L7 |
| Delta7(PB15)_L7R3_L | Delta7 L7 |
| Delta7(PB15)_L8R1R9_L | Delta7 L8 |
Table 6
Quality of fit for different possible weight structures.
The root mean square error (RMSE) is weighted by the variance attached to each connection (in units of standard deviations). The corrected Akaike information criterion (AICc) is also shown for the weight profiles in Figure 11. The best fit after correcting for model size is the Gaussian with fixed standard deviation, but it is very closely matched by the von Mises with fixed kappa and .
| Curve | RMSE | AICc |
|---|---|---|
| 0.3213 | 8.05 | |
| Gaussian | 0.1941 | 12.60 |
| von Mises | 0.1854 | 12.55 |
| Gaussian (fixed stddev) | 0.3142 | 7.98 |
| von Mises (fixed kappa) | 0.3178 | 8.02 |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Theoretical principles explain the structure of the insect head direction circuit
eLife 13:e91533.
https://doi.org/10.7554/eLife.91533
