Predictive learning rules generate a cortical-like replay of probabilistic sensory experiences
- Okinawa Institute of Science and Technology Graduate University, Japan
- RIKEN Center for Brain Science, RIKEN ECL Research Unit, Japan
- RIKEN Pioneering Research Institute (PRI), Japan
Figures
Figure 1
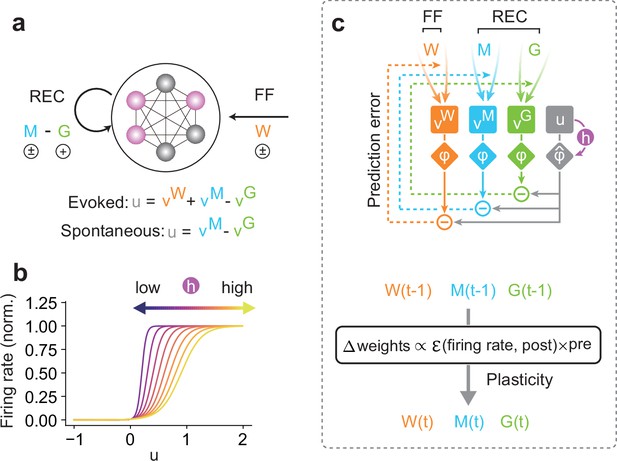
Unsupervised prior learning in a recurrent neural network.
(a) A schematic of a network model is shown. The interconnected circles denote the model neurons, of which the activities are controlled by two types of inputs: feedforward (FF) and recurrent (REC) inputs. Colored circles indicate active neurons. Here, vW denote FF, and vM denote REC connections. We considered two modes of activity (i.e., evoked and spontaneous activity). In the evoked mode, the membrane potential u of a network neuron was calculated as a linear combination of inputs across all different connections (vW, vM, and vG). This evoked mode is considered during the learning phase, when all synapses attempt to predict the network activity, as we will explain in the main text. Once all synapses are sufficiently learned, all FF inputs are removed, and the network is driven spontaneously (spontaneous mode). Our interest lies in the statistical similarity of the network activity in these two modes. (b) The gain and threshold of output response function was controlled by a dynamic variable, h, which tracks the history of the membrane potential. (c) A schematic of the learning rule for a network neuron is shown (top). During learning, for each type of connection on a postsynaptic neuron, synaptic plasticity minimizes the error between output (gray diamond) and synaptic prediction (colored diamonds). Note that all types of synapses share the common plasticity rule, where weight updates are calculated as the multiplication of the error term and the presynaptic activities (bottom). Our hypothesis is that such plasticity rule allows a recurrent neural network to spontaneously replay the learned stochastic activity patterns without external input.
Figure 2
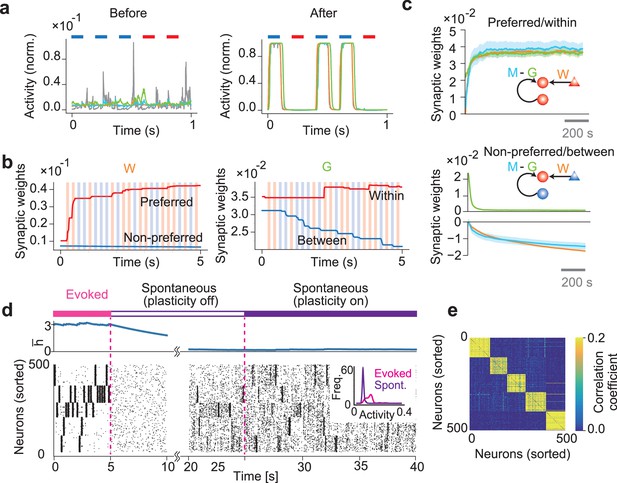
Formation of stimulus-selective assemblies in a recurrent network.
(a) Example dynamics of neuronal output and synaptic predictions are shown before (left) and after (right) learning. Colored bars at the top of the figures represent periods of stimulus presentations. (b) Example dynamics of feedforward connection W and inhibitory connection G are shown. W-connections onto neurons organizing to encode the same or different input patterns are shown in red and blue, respectively. Similarly, the same colors are used to represent G connections within and between assemblies. (c) Dynamics of the mean connection strengths are shown on neuron in cell assembly 1. Shaded areas represent SDs over 10 samples. In the schematic, triangles indicate input neurons and circles indicate network neurons. The color of each neuron indicates the stimulus preference of each neuron. (d) Example dynamics of the averaged dynamical variable (top) and the learned network activity (bottom) are shown. The dynamical variables are averaged over the entire network. Neurons are sorted according to their preferred stimuli. During the spontaneous activity, afferent inputs to the network were removed. The inset shows the firing rate distribution of the evoked and the spontaneous activity. (e) Correlation coefficients of spontaneous activities of every pair of neurons are shown.
Figure 3 with 2 supplements
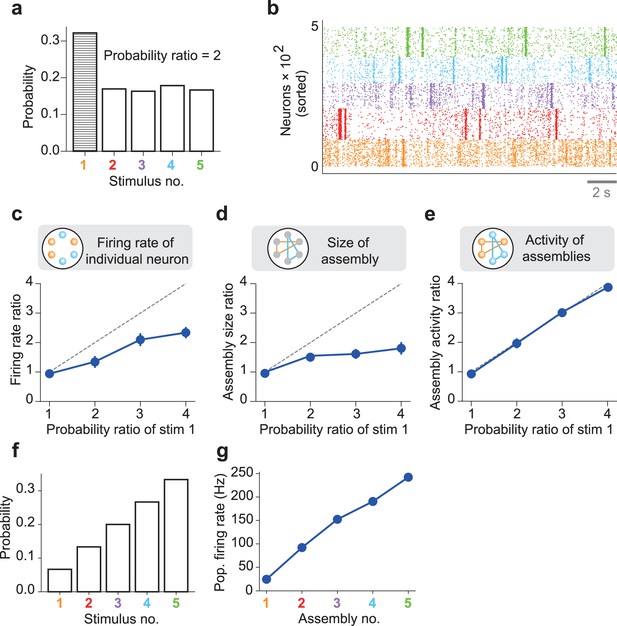
Priors coded in spontaneous activity.
An nDL network was trained with five probabilistic inputs. (a) Stimulus 1 appeared twice as often as the other four stimuli during learning. The example empirical probabilities of the stimuli used for learning are shown. (b) The spontaneous activity of the trained network shows distinct assembly structures. (c) The mean ratio of the population-averaged firing rate of assembly 1 to those of the other assemblies is shown for different values of the occurrence probability of stimulus 1. Vertical bars show SDs over five trials. A diagonal dashed line is a ground truth. (d) Similarly, the mean ratios of the size of assembly 1 to those of the other assemblies are shown. (e) The mean ratios of the total activities of neurons in assembly 1 to those of the other assemblies are shown. (f) Five stimuli occurring with different probabilities were used for training the nDL model. (g) The population firing rates are shown for five self-organized cell assemblies encoding the stimulus probabilities shown in (f).
Figure 3—figure supplement 1
Prior encoding by the nDL model.
As in Figure 3f and g, the nDL model was trained with a set of stimuli. (a) The five stimuli occurred with different probabilities during training. (b) The spontaneously replayed cell assemblies exhibited population firing rates proportional to the occurrence probabilities of the corresponding stimuli. (c) Similar to a, but with seven stimuli. (d) The spontaneous population activities of seven assemblies are shown. The activities were proportional to the occurrence probabilities of stimuli shown in c. Error bars show SDs over five independent simulations. A dashed line is a regression line.
Figure 3—figure supplement 2
Learning occurrence probabilities of overlapped input patterns.
(a) Two input patterns were presented with 30% (blue) and 70% (red) probabilities of which 50% of input neurons were shared (purple horizontal area). (b) The spontaneous activity of the trained network shows distinct assembly structures. (c) The ratio of the activities of two learned assemblies in spontaneous activity showed a strong similarity to the stimulus probabilities.
Figure 4 with 6 supplements
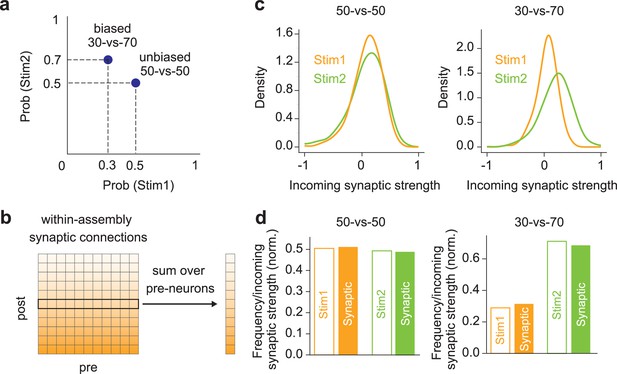
Probability encoding by learned within-assembly synapses.
(a) Two input stimuli were presented in two protocols: uniform (50% vs. 50%) or biased (30% vs. 70%). (b) The total incoming synaptic strength on each neuron was calculated within each cell assembly. (c) left, The distributions of incoming synaptic strength are shown for the learned assemblies in the 50-vs-50 case. right, Same as in the left figure, but in the 30-vs-70 case. (d) left, The empirical probabilities of stimuli 1 and 2 and the normalized excitatory incoming weights within assemblies are compared in the 50-vs-50 case. right, Same as in the left figure, but in the 30-vs-70 case.
Figure 4—figure supplement 1
Within-assembly connections encode the probability structures.
The mean ratios of spontaneous population firing rates without between-assembly connections are shown. The connections were removed after the network learned to encode the stimulus probabilities shown in Figure 3f. Error bars indicate the SDs over five trials.
Figure 4—figure supplement 2
Inhibitory plasticity during learning is necessary to stabilize spontaneous activity.
(a) Spontaneous activity of learned network with non-plastic inhibitory connections during learning. (b) Same as in a, but with plastic inhibitory connections.
Figure 4—figure supplement 3
Crucial roles of inhibitory plasticity in prior learning.
We first trained the network models with five external stimuli. (a) Then, we terminated the stimuli at −50 s and waited until 0 s for the recovery of network activity through the renormalization process (Equation 10) with all plasticity rules turned off. We turned on the plasticity of M at time 0 s. We kept the plasticity of G turned off in the truncated model (blue), while we turned on the G-plasticity in the control model (magenta). (b) Left, the time evolution of the difference between the average within-assembly coherence and the average between-assembly coherence was plotted for the control (magenta) and truncated (blue) models. Larger differences imply more robust cell assemblies. Error bars indicate the SDs over five trials. Right, activity coherences between neurons are shown at the indicated times. (c) The time-varying normalized firing rate of a neuron (gray) and the values predicted by recurrent synaptic inputs (top) and lateral inhibition (bottom) are shown for the control model. (d) Similar plots are shown for the truncated model. (e) Changes in prediction errors in the control (magenta) and truncated (blue) models are shown for recurrent synaptic inputs (top) and lateral inhibition (bottom).
Figure 4—figure supplement 4
Distinct assembly replay after sequence.
(a) The network was trained repetitively with a fixed sequence (i.e., 1–2–3–4–5). (b) An example of spontaneous activity after learning. The assemblies are reactivated almost independently. (c) The learned recurrent connection matrix shows stronger intra-assembly and weaker inter-assembly connections.
Figure 4—figure supplement 5
Role of dynamical variable h in spontaneous replay of assemblies.
(a) An example of assembly dynamics (solid) and dynamical variables h (dashed) are shown. Each color refers to one of the five assemblies, and red curves are highlighted for visualization purposes. The dynamical variables show an abrupt increase when the corresponding assembly has peak activity, and a slow decrease otherwise. Note that the dynamics of h corresponding to assemblies that do not show large activity peaks decay slowly almost everywhere without showing a significant increase (e.g., the green dashed line). Curves show the averaged values over the individual assemblies, and shaded areas show the standard error. (b) The mean ratios of spontaneous population firing rates calculated with fixed h variables are shown. The network was first trained to encode the stimulus probabilities shown in Figure 3f and the h values were then fixed during spontaneous activity. The ratios capture the increasing tendency of the true probability distribution in Figure 3f with degraded accuracies, especially in assemblies 4 and 5. Error bars indicate the SDs over five trials.
Figure 4—figure supplement 6
Learning of multivariate priors with assemblies.
(a) Network neurons were separated into two populations receiving different groups of feedforward inputs (left). Subnetwork A received stimuli 1 (S1) and 2 (S2), each presented one at a time with probability 1/2. Subnetwork B received stimuli 3 (S3) or 4 (S4) exclusively when subnetwork A was also stimulated. S3 or S4 was sampled at each presentation according to the probability distribution conditioned on the stimulus presented to subnetwork A (middle and right). (b) Raster plot of evoked activity after training. Each subnetwork formed two assemblies responding to different preferred stimuli. Shaded areas with four colors indicate the duration of stimuli given to the two subnetworks. (c) The connection matrix self-organized among the cell assemblies is shown. (d) The activities of the four assemblies in the presence of S1 and S2 but not S3 and S4 are shown. Despite the absence of stimuli, subnetwork B replayed the assemblies encoding S3 and S4 when subnetwork A was activated by S1 or S2. (e) Activities of assemblies 3 and 4 in subnetwork B varied with the stimulus presented to subnetwork A. Each data point corresponds to one of 20 independent stimulus presentations. Error bars represent SDs.
Figure 5
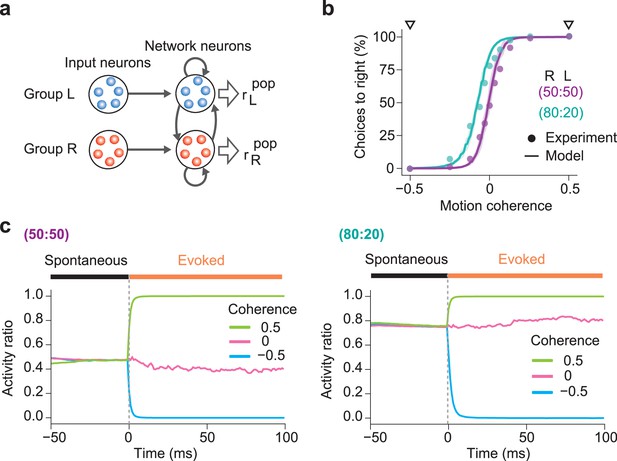
Simulations of biased perception of visual motion coherence.
(a) The network model simulated perceptual decision-making of coherence in random dot motion patterns. In the network shown here, network neurons have already learned two assemblies encoding leftward or rightward movements from input neuron groups L and R. The firing rates of input neuron groups were modulated according to the coherence level Coh of random dot motion patterns (Materials and Methods). (b) The choice probabilities of monkeys (circles) and the network model (solid lines) are plotted against the motion coherence in two learning protocols with different prior probabilities. The experimental data were taken from Hanks et al., 2011. In the 50:50 protocol, moving dots in the “R” (Coh = 0.5) and “L” (Coh = -0.5) directions were presented randomly with equal probabilities, while in the 80:20 protocol, the “R” and “L” directions were trained with 80% and 20% probabilities, respectively. Shaded areas represent SDs over 20 independent simulations. The computational and experimental results show surprising coincidence without curve fitting. (c) Spontaneous and evoked activities of the trained networks are shown for the 50:50 (left) and 80:20 (right) protocols. Evoked responses were calculated for three levels of coherence: Coh = -50%, 0%, and 50%. In both protocols, the activity ratio in spontaneous activity matches the prior probability and gives the baseline for evoked responses. In the 80:20 protocol, the biased priors of “R” and “L” motion stimuli shift the activity ratio in spontaneous activity to an “R”-dominant regime.
Figure 6
A network model with distinct excitatory and inhibitory connections.
(a) Strong excitatory connections were formed within assemblies. (b) The first type of recurrent inhibitory connections, Minh, became stronger between assemblies, enhancing assembly competition. (c) The second type of inhibitory connections G were strengthened within assemblies to balance the strong excitatory inputs.
Figure 7 with 1 supplement
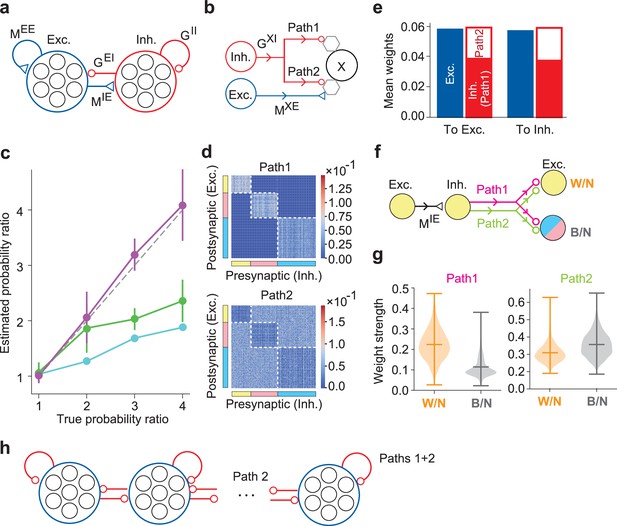
The DL model of excitatory and inhibitory cell assemblies.
(a) This model consists of distinct excitatory and inhibitory neuron pools, obeying Dale’s law. (b) Each inhibitory neuron projects to another neuron X through two inhibitory paths, path 1 and path 2, where the index X refers to an excitatory or an inhibitory postsynaptic neuron. Hexagons represent minimal units for prediction and learning in the neuron model and may correspond to dendrites, which were not modeled explicitly. (c) The probability ratios estimated by numerical simulations are plotted for the assembly activity ratios (purple), firing rate ratios (cyan), and assembly size ratios (green) as functions of the true probability ratio of external stimuli. Error bars indicate SEs calculated over five simulation trials with different initial states of neurons and synaptic weights in each parameter setting. (d) Inhibitory connection matrices are shown for path 1 and path 2. (e) The mean weights of self-organized synapses on excitatory and inhibitory postsynaptic neurons are shown. (f) Within-assembly and between-assembly connectivity patterns of excitatory and inhibitory neurons are shown. Colors indicate three cell assemblies self-organized. (g) The strengths of lateral inhibitions within-(W/N) and between-assemblies (B/N) are shown for paths 1 and 2. Horizontal bars show the medians and quartiles. (h) The resultant connectivity pattern suggests an effective competitive network between excitatory assemblies with self-(within-assembly) and lateral (between-assembly) inhibition.
Figure 7—figure supplement 1
The coexistence of the two inhibitory paths is crucial for learning.
(a) A typical spike raster of stimulus-evoked responses is presented for the elaborate network model shown in Figure 7 . (b) A spike raster of stimulus-evoked responses is shown for simulations of the elaborate model without inhibitory path 2. Inhibitory connections were modifiable in path 1. (c) A similar spike raster is presented for simulations of the elaborate model without inhibitory path 1. Inhibitory connections were modifiable in path 2. The results shown in b and c demonstrate that the network model fails to self-organize the cell assemblies encoding the different stimuli when it lacks one of the two inhibitory paths.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Predictive learning rules generate a cortical-like replay of probabilistic sensory experiences
eLife 13:RP92712.
https://doi.org/10.7554/eLife.92712.3
