1. Computational and Systems Biology
  2. Physics of Living Systems

Overflow metabolism originates from growth optimization and cell heterogeneity

  1. Xin Wang  Is a corresponding author
  1. School of Physics, Sun Yat-sen University, China
https://doi.org/10.7554/eLife.94586.4
Share this article
Cite this article
  1. Xin Wang
(2025)
Overflow metabolism originates from growth optimization and cell heterogeneity
eLife 13:RP94586.
https://doi.org/10.7554/eLife.94586.4
  2. Download BibTeX
  3. Download .RIS
10 figures, 3 tables and 3 additional files

Figures

Figure 1
Download asset Open asset
Model and results of overflow metabolism in E. coli.

(A) The central metabolic network of carbon source utilization. The Group A carbon sources (Wang et al., 2019) are labeled with green squares. (B) Coarse-grained model for Group A carbon source utilization. (C) Model predictions (see Equations S47 and S160) and experimental results (Basan et al., 2015; Holms, 1996) of overflow metabolism, covering the data for all the Group A carbon sources shown in (A). (D) Growth rate dependence of respiration and fermentation fluxes (see Equations S47 and S160). (E) The proteome efficiencies for energy biogenesis in the respiration and fermentation pathways vary with growth rate as functions of the nutrient quality of a Group A carbon source (see Equations S31 and S36). See Appendices 9 and 11 for model parameter settings and experimental data sources (Basan et al., 2015; Holms, 1996; Hui et al., 2015) for Figures 1—4 of E. coli.

Figure 2
Download asset Open asset
Influence of protein overexpression on overflow metabolism in E. coli.

(A) A 3D plot of the relations among fermentation flux, growth rate, and the expression level of useless proteins. In this plot, both the acetate excretion rate and growth rate vary as bivariate functions of the nutrient quality of a Group A carbon source (denoted as κA) and the useless protein expression encoded by lacZ gene (denoted as ϕZ perturbation; see Equations S57 and S160). (B) Growth rate dependence of the acetate excretion rate upon ϕZ perturbation for each fixed nutrient condition (see Equations S58 and S160). (C) Growth rate dependence of the acetate excretion rate as κA varies (see Equations S58 and S160), with each fixed expression level of LacZ.

Figure 3
Download asset Open asset
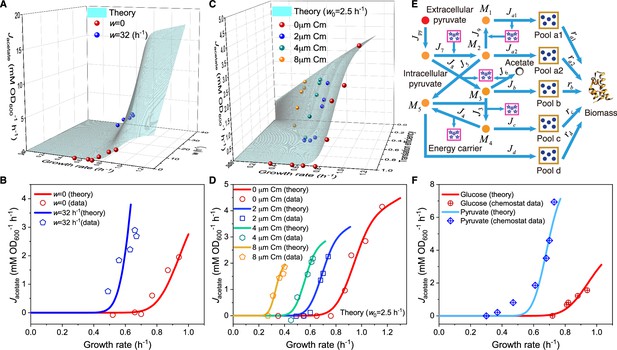
Influence of energy dissipation, translation inhibition, and carbon source category alteration on overflow metabolism in E. coli.

(A) A 3D plot of the relations among fermentation flux, growth rate, and the energy dissipation coefficient (see Equations S70 and S160). (B) Growth rate dependence of the acetate excretion rate as the nutrient quality κA varies, with each fixed energy dissipation coefficient determined by or fitted from experimental data. (C) A 3D plot of the relations among fermentation flux, growth rate, and the translation efficiency (see Equations 85 and S160). Here, the translation efficiency is adjusted by the dose of chloramphenicol (Cm). (D) Growth rate dependence of the acetate excretion rate as κA varies, with each fixed dose of Cm. (E) Coarse-grained model for pyruvate utilization. (F) The growth rate dependence of fermentation flux in pyruvate (see Equations 105 and S160) significantly differs from that of the Group A carbon sources (see Equations 47 and S160).

Figure 4
Download asset Open asset
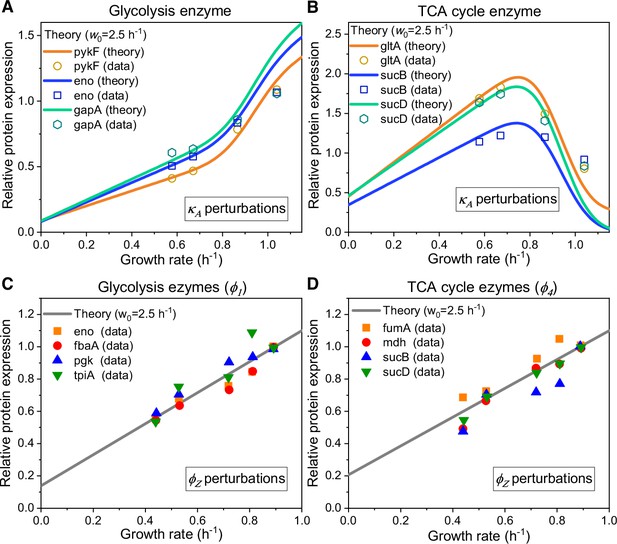
Relative protein expression of central metabolic enzymes in E. coli under carbon limitation and proteomic perturbation.

(A, C) Relative protein expression of representative genes from glycolysis. (B, D) Relative protein expression of representative genes from the TCA cycle. (A, B) Results of the perturbation through changes in nutrient quality κA (see Equation S119). (C, D) Results of proteomic perturbation via varied levels of expression of the useless protein LacZ (i.e. ϕZ perturbation; see Equation S121).

Figure 5
Download asset Open asset
Model comparison with data on the Crabtree effect in yeast and the Warburg effect in tumors.

(A) A linear scale representation on the y-axis. (B) A log scale representation on the y-axis. In (A–B), ⟨εr⟩ and ⟨εf⟩ represent the population averages of εr and εf, while χεr and χεf are the coefficients of variation (CVs) of εr and εf⋅⟨εr⟩/⟨εf⟩ represents the ratio of proteome efficiency between respiration and fermentation at the population-averaged level, while Jf(E)/(Jf(E)+Jr(E)) stands for the fraction of energy flux generated by the fermentation pathway (see Equation 6). The data for yeast in batch culture and chemostat were calculated from experimental data of S. cerevisiae and I. orientalis (Shen et al., 2024). The data for mouse tumors were calculated from in vivo experimental data of pancreatic ductal adenocarcinoma (PDAC) and leukemic spleen of mice (Bartman et al., 2023; Shen et al., 2024). See Appendix 11 for detailed information on the experimental data sources (Bartman et al., 2023; Shen et al., 2024).

Appendix 1—figure 1
Download asset Open asset
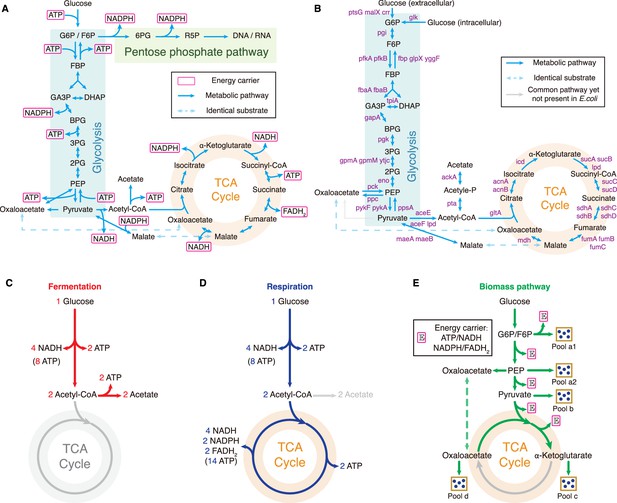
Central metabolic network and carbon utilization pathways of E. coli.

(A) Energy biogenesis details in the central metabolic network. In E. coli, NADPH and NADH are interconvertible (Sauer et al., 2004), and all energy carriers can be converted to ATP through ADP phosphorylation. The conversion factors are: NADH = 2 ATP, NADPH = 2 ATP, FADH2=1 ATP (Neidhardt et al., 1990). (B) Relevant genes encoding enzymes in the central metabolic network of E. coli. (C–E) Three independent fates of glucose metabolism in E. coli. (C) For energy biogenesis through fermentation, a molecule of glucose generates 12 ATPs. (D) For energy biogenesis via respiration, a molecule of glucose generates 26 ATPs. (E) For biomass synthesis, glucose is converted into precursors of biomass. Note that biomass synthesis is accompanied by ATP production (see Appendix 3.1).

Appendix 1—figure 2
Download asset Open asset
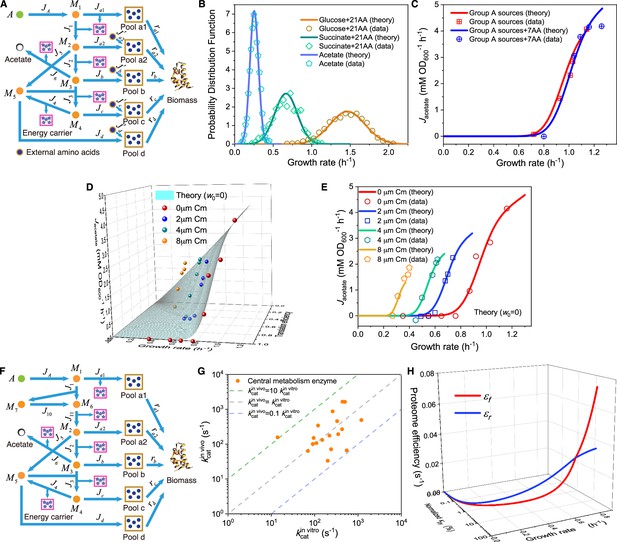
Model and results for experimental comparison of E. coli.

(A–C) Model analysis for carbon utilization in mixtures with amino acids. (A) Coarse-grained model for the case of a Group A carbon source mixed with extracellular amino acids. (B) Model predictions (Equations S157, S164-S165) and single-cell reference experimental results (Wallden et al., 2016) showing growth rate distributions for E. coli in three culturing conditions. (C) Comparison of the growth rate-fermentation flux relation for E. coli in Group A carbon sources between minimal media and enriched media (those with 7AA). (D–E) Influence of translation inhibition on overflow metabolism in E. coli. (D) A 3D plot illustrating the relations among fermentation flux, growth rate, and translation efficiency (Equations S79 and S160). (E) Growth rate dependence of acetate excretion rate as κA varies, with each fixed dose of Cm. Translation efficiency is tuned by the dose of Cm, and the maintenance energy coefficient is set to 0 (i.e. w0=0). (F) Coarse-grained model for Group A carbon source utilization, which includes more details to compare with experiments. (G) Comparison of in vivo and in vitro catalytic rates for enzymes of E. coli within glycolysis and the TCA cycle (see Appendix 1—table 1 for details). (H) The proteome efficiencies for energy biogenesis in the respiration and fermentation pathways vary with growth rate as functions of the substrate quality of pyruvate (Equations S93 and S96)

Appendix 1—figure 3
Download asset Open asset
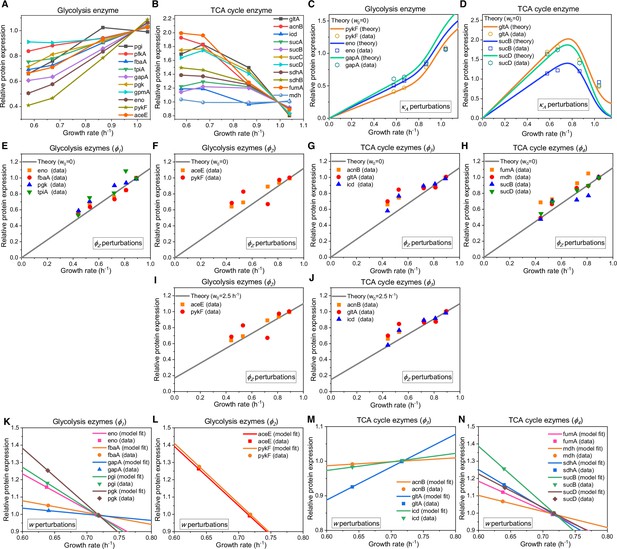
Relative protein expression of central metabolic enzymes in E. coli under various types of perturbations.

(A–D) Relative protein expression under κA perturbation. (A) Experimental data (Hui et al., 2015) for the catalytic enzymes at each step of glycolysis. (B) Experimental data (Hui et al., 2015) for the catalytic enzymes at each step of the TCA cycle. (C) Model predictions (Equation S118, with w0=0) and experimental data (Hui et al., 2015) for representative glycolytic genes. (D) Model predictions (Equation S118, with w0=0) and experimental data (Hui et al., 2015) for representative genes from the TCA cycle. (E–J) Relative protein expression under ϕZ perturbation. (E, F, I) Model predictions and experimental data (Basan et al., 2015) for representative glycolytic genes. (G, H, J) Model predictions and experimental data (Basan et al., 2015) for representative genes from the TCA cycle. (E–H) Results of ϕZ perturbation with w0=0 (Equation S120). (I–J) Results of ϕZ perturbation with w0=2.5(h−1) (Equation S121). (K–N) Relative protein expression upon energy dissipation. (K–L) Model fits (Equations S127 and S123) and experimental data (Basan et al., 2015) for representative glycolytic genes. (M–N) Model fits (Equations S127 and S123) and experimental data (Basan et al., 2015) for representative genes from the TCA cycle.

Appendix 1—figure 4
Download asset Open asset
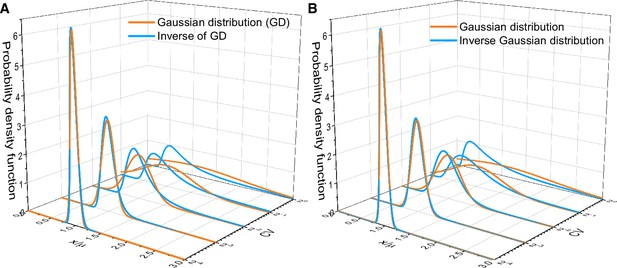
Asymptotic distributions of inverse Gaussian distribution and the inverse of Gaussian distribution.

(A) Comparison between the inverse of Gaussian distribution and the corresponding Gaussian distribution for various values of the coefficient of variation (CV) (Equations S140 and S145). (B) Comparison between the inverse Gaussian distribution and the corresponding Gaussian distribution for various values of CV (Equations S142 and S146). Both the inverse Gaussian distribution and the inverse of Gaussian distribution converge to Gaussian distributions when CV is small.

Appendix 1—figure 5
Download asset Open asset
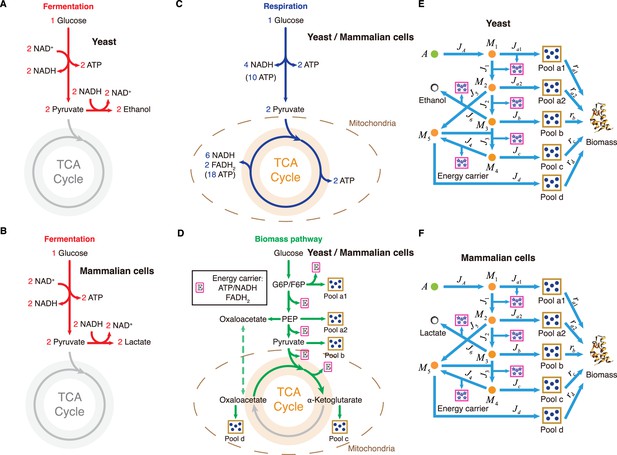
Carbon utilization in yeast and mammalian cells.

(A–D) Three independent fates of glucose metabolism in yeast and mammalian cells. (A–B) For energy biogenesis through fermentation, one molecule of glucose generates 2 ATPs. (C) For energy biogenesis through respiration, one molecule of glucose generates 32 ATPs. (D) For biomass synthesis, glucose is converted into biomass precursors, with ATP produced as a byproduct. In yeast and mammalian cells, the energy stored in NADH and FADH2 converts ADP into ATP in the mitochondria, with higher conversion factors than in E. coli: NADH = 2.5 ATP, FADH2=1.5 ATP (Nelson and Cox, 2008). (E) Coarse-grained model for Group A carbon source utilization in yeast. (F) Coarse-grained model for Group A carbon source utilization in mammalian cells.

Tables

Appendix 1—table 1
Molecular weight (MW) and in vivo/in vitro kcat data for E. coli.
No.*ReactionEnzymeGene nameECMW (kDa)In vitro kcat (s-1)ReferencesIn vivo†kcat (s-1)Selected kcat (s-1)
J1Glucose-6P ↔ Fructose-6PGlucose-6-phosphate isomerasepgiEC:5.3.1.91.2×1022.6×102PMID:7004378;
DOI:https://doi.org/10.1016/j.ijms.2004.09.017		8.7×1028.7×102
Fructose-6P → Fructose-1,6PPhosphofructokin-asepfkA‡EC:2.7.1.111.4×1024.4×102PMID:6218375; 702261.7×1031.7×103
Fructose-1,6P ↔ Glyceraldehyde 3-phosphate+Dihydroxyacetone phosphateFructose-bisphosphate aldolasefbaA†EC:4.1.2.137.8×101.4×10PMID:8939754; 155316271.6×1021.6×102
Dihydroxyacetone phosphate ↔ Glyceraldehyde 3-phosphateTriosephosphate IsomerasetpiAEC:5.3.1.15.4×104.3×102PMID:3887397; 60928572.7×1022.7×102
Glyceraldehyde 3-phosphate ↔ 1,3-BisphosphoglycerateGlyceraldehyde-3-phosphate dehydrogenasegapAEC:1.2.1.121.4×1029.5×10PMID:4932978; 22009291.5×1021.5×102
1,3-Bisphosphoglycerate ↔ 3-PhosphoglyceratePhosphoglycerate kinasepgkEC:2.7.2.34.4×103.5×102PMID:367367; 1662741.9×1021.9×102
3-Phosphoglycerate ↔ 2-PhosphoglyceratePhosphoglycerate mutasegpmA‡EC:5.4.2.114.9×103.3×102PMID:104378014.5×1024.5×102
2-Phosphoglycerate ↔ PhosphoenolpyruvateEnolaseenoEC:4.2.1.119.0×102.2×102PMID:1094232; 49423261.7×1021.7×102
J2Phosphoenolpyruvate → PyruvatePyruvate kinasepykF‡EC:2.7.1.402.4×1025.0×102PMID:67598521.6×1031.6×103
Pyruvate → Acetyl-CoAPyruvate dehydrogenaseaceE‡EC:1.2.4.11.0×1021.2×102PMID:230884223.4×1023.4×102
J3Oxaloacetate +Acetyl CoA → CitrateCitrate synthasegltAEC:2.3.3.19.7×102.4×102PMID:4900996; 239543057.1×107.1×10
Citrate ↔ IsocitrateAconitate hydrataseacnB‡EC:4.2.1.39.4×107.0×10PMID:15963579; 159635796.3×106.3×10
Isocitrate→ α-KetoglutarateIsocitrate dehydrogenaseicdEC:1.1.1.429.5×102.0×102PMID:8141; 36923; 22009293.3×103.3×10
J4α-Ketoglutarate → Succinyl-CoAα-Ketoglutarate dehydrogenase complex E1 componentsuc A suc B‡EC:1.2.4.2, EC:2.3.1.611.9×1021.5×102PMID:6380583; 45886791.3×1021.3×102
Succinyl-CoA ↔ SuccinateSuccinyl-CoA synthetasesuc C suc DEC:6.2.1.51.6×1029.1×10PMID:53381301.0×1021.0×102
Succinate → FumarateSuccinate dehydrogenasesdh A sdh B‡EC:1.3.5.11.0×1021.1×102PMID:4334990; 164842321.1×1021.1×102
Fumarate ↔ MalateFumarasefumA‡EC:4.2.1.22.0×1021.2×103PMID:3282546; 120214534.9×1024.9×102
Malate ↔ OxaloacetateMalate dehydrogenasemdhEC:1.1.1.376.1×105.5×102doi:https://doi.org/10.1016/0076-6879(69)13029-36.6×106.6×10
J5Phosphoenolpyruvate →OxaloacetatePhosphoenolpyru-vate carboxylaseppcEC:4.1.1.314.0×1021.5×102PMID:9927652; 4932977/1.5×102
J6Acetyl-CoA ↔ Acetyl phosphatePhosphate acetyltransferaseptaEC:2.3.1.87.7×103.0×10PMID:202363193.7×1023.7×102
Acetyl phosphate↔ AcetateAcetate kinaseackAEC:2.7.2.14.3×103.6×103EcoCyc:
EG10027;
PMID:24801996		3.3×1023.3×102
Acetate (intracellular) ↔ Acetate (extracellular)Acetate transporteractP/2×104.7×102PMID:31405984 (Estimated)/4.7×102
J7Pyruvate → PhosphoenolpyruvatePyruvate, water dikinaseppsAEC:2.7.9.22.5×1023.5×10PMID:4319237/3.5×10
JAGlucose-6P (extracellular) → Glucose-6P (intracellular)Glucose-6-phosphate transporterUhpT/5×102×102PMID:3283129; 2197272;
20018695
(Estimated)		/2×102
Glucose (extracellular) → Glucose-6PGlucose-specific PTS enzymeptsGEC:
2.7.1.199		5×101×102PMID:9575173; 20018695; 12146972/1×102
Lactose (extracellular) → Lactose (intracellular)Lactose transporterlacY/4.6×106×10PMID:6444453; 20018695/6×10
Lactose →Glucose +Galactoseβ-galactosidaselacZEC:3.2.1.234.6×1026.4×102PMID:8008071;
23011886
(Estimated)		/6.4×102
JpyPyruvate (extracellular) → Pyruvate (intracellular)Pyruvate transporterbtsT CstA/8×106×10PMID:20018695; 33260635;
EcoCyc: G7942; EG10167
(Estimated)		/6×10
  1. *

    The classification of Ji follows the coarse-grained models shown in Figures 1B and 3E.

  2. †

    In vivo kcat values were obtained using the experimental data shown in Appendix 1—table 2, combined with Equations S134-S135.

  3. ‡

    See Appendix 1—figure 1B for additional genes that may play a secondary role.

Appendix 1—table 2
Proteome and flux data (Basan et al., 2015) used to calculate the in vivo kcat of E. coli.
Culture 1Culture 2Culture 3Culture 4
Growth rate λ (h–1)*0.820.870.971.03
Jacetate (mM OD600–1 h–1)†0.391.182.682.84
JCO2, r (mM OD600–1 h–1) †7.446.054.303.04
Gene nameProteomic mass fractions obtained using absolute abundance (ϕi)
pgi0.09%0.09%0.10%0.11%
pfkA0.06%0.06%0.06%0.06%
fbaA0.32%0.35%0.35%0.39%
tpiA0.12%0.15%0.13%0.18%
gapA1.19%1.29%1.33%1.47%
pgk0.30%0.31%0.32%0.36%
gpmA0.15%0.15%0.15%0.16%
eno0.63%0.70%0.75%0.83%
pykF0.15%0.15%0.18%0.21%
aceE0.30%0.32%0.34%0.41%
gltA0.88%0.80%0.61%0.48%
acnB0.92%0.84%0.66%0.57%
icd1.55%1.55%1.31%1.39%
suc A suc B0.71%0.75%0.64%0.55%
suc C suc D0.88%0.84%0.66%0.52%
sdh A sdh B0.49%0.45%0.42%0.35%
fumA0.24%0.21%0.17%0.13%
mdh0.45%0.45%0.41%0.39%
pta0.10%0.10%0.10%0.10%
ackA0.06%0.07%0.06%0.06%
  1. *

    For calibration purposes, a factor of 1.03/0.97 was multiplied by the reference data (Basan et al., 2015)‡.

  2. †

    For calibration purposes, a factor of 2.84/3.24 was multiplied by the reference data (Basan et al., 2015)‡.

  3. ‡

    Here, (1.03, 2.84) and (0.97, 3.24) are both the data points for (λ h-1, Jacetate mM OD600-1 h-1) for E. coli strain NCM3722 cultured with lactose in the same reference (Basan et al., 2015). The former is specified in the source data of the reference’s figure 1 (Basan et al., 2015), while the latter is recorded in the reference’s extended data figure 3a (Basan et al., 2015). With the calibrations above, the data for the Jacetate(M)−λ relation shown here align with the curve depicted in Figure 1C.

Appendix 1—table 3
Illustrations of symbols in this manuscript.
SymbolsIllustrations/DefinitionsModel variable/parameter settings for E. coli*
A (in the figures)A Group A carbon source joining the metabolic network from the upper part of glycolysis.NA †
Mi (in the figures)A metabolite in the metabolic network that serve as intermediate node.NA
Ji (in the figures)The stoichiometric flux delivering carbon flux, an extensive variable‡; see Equation S7.see Equations S7-S8.
ri (in the figures)The mass fraction of carbon flux drawn from a precursor pool.ra1=24%; ra2=24%; rb = 28%; rc = 12%; rd = 12%
(Nelson and Cox, 2008).
λGrowth rate of the cell population; see Equation S36 for the optimal model solution.see Equations S4 and S36.
Jr, JfJr and Jf are stoichiometric fluxes of respiration and fermentation, extensive variables.Jr = J4; Jf = J6 (see Equation S22)
m0 The weighted average carbon mass of metabolite molecules at the entrance of precursor pools.See Equation S17.
McarbonThe carbon mass of the cell population, an extensive variable.NA
MproteinThe protein mass of the cell population; an extensive variable.NA
MQ(P), MR(P), MC(P)The mass of Q-class, R-class, or C-class proteome.See Equation S2.
fQ, fR, fCThe ribosome allocation fraction for protein synthesis of Q-class, R-class, or C-class.fQ=ϕQ.
mAAThe average molecular weight of amino acids.A reducible parameter for the results.
kTTranslation speed of ribosomes.kT=20.1 aa/s (Scott et al., 2010).
ϕQ, ϕR, ϕCThe mass fraction of Q-class, R-class, or C-class proteome; see Appendix 2.1.ϕQ=52% (Scott et al., 2010).
ϕmaxThe maximum proteomic mass fraction of proteome allocation for fermentation, respiration, and biomass generation, with ϕmax≡1−ϕQ.ϕmax=48% (Scott et al., 2010).
mRThe protein mass of a single ribosome.mR=7336mAA
(Neidhardt et al., 1990).
VcellThe cell volume of the cell population (the ‘big cell’); an extensive variable.NA
NR, Mrp(P)The number or the total protein mass of ribosomes in the big cell; extensive variables.NA
ςThe ratio of the mass of R-class proteome to the protein mass of ribosomes: ς≡MR(P)/Mrp(P).ς=1.67 (Scott et al., 2010).
[Ei], [Si]The concentration of enzyme Ei or substrate Si; intensive variables.NA
ai, di, bi, ciai and di are reaction parameters; bi and ci are stoichiometric coefficients. See Appendix 2.3.NA
KiThe Michaelis constant, defined as Ki≡(di+kicat)/ ai.Obtainable from Bennett et al., 2009, yet unused in practice since [Si]>Ki
(see Appendix 2.5).
viThe reaction rate per volume of a biochemical reaction catalyzed by Ei; an intensive variable.See Equation S6.
NEi, MEiThe copy number or the total weight enzyme Ei in the cell population; extensive variables.NEi=Vcell⋅[Ei];
MEi=NEi⋅mEi.
mcarbonThe mass of a carbon atom.mcarbon=12NAvogadrog, where g represents gram and NAvogadro is the Avogadro constant.
ΦiThe enzyme cost of all Ei molecules in the cell population; an extensive variable.Φi≡NEi⋅nEi.
ξiξi is defined such that ξi=Ji/Φi.ξi≡kicatnEi⋅[Si][Si]+Ki.
Ji(N)The normalized flux, i.e., flux per unit of biomass; an intensive variable§Ji(N)≡Ji⋅m0/Mcarbon
see Equations S15-S16.
Jr(N), Jf(N)Jr(N) and Jf(N) are the normalized fluxes of respiration and fermentation, intensive variables.Jr(N)=J4(N); Jf(N)=J6(N).
NEPicarbonThe number of carbon atoms in the entry point metabolite molecule of Precursor Pool i.NEPa1carbon=6; NEPa2carbon=3; NEPbcarbon=3; NEPccarbon=5; NEPdcarbon=4 (Nelson and Cox, 2008).
kcat, kicatThe turnover number of a catalytic enzyme.See Appendix 1—table 1.
mEi, nEimEi and nEi are the molecular weight and the enzyme cost of an Ei molecule, respectively.See Appendix 1—table 1.
rcarbon, rproteinrcarbon and rprotein are the mass fractions of all carbon and protein within a cell, respectively.rprotein=0.55; rcarbon=0.48
(Neidhardt et al., 1990).
κiSubstrate quality of a metabolite in a biochemical reaction; see Equation S12 and S20.Calculated from the values of kicat, mEi, m0, rprotein, rcarbon.
κASubstrate quality of a Group A carbon source; see Equation S27.Calculated from the values of kAcat, mEA, m0, rprotein, rcarbon, KA and the concentration of the Group A carbon source [A].
ϕiThe proteomic mass fraction of enzyme Ei: ϕi≡MEi/Mprotein; an intensive variable.See Equation S9.
ηiThe fraction of stoichiometric flux drawn from a precursor pool; see Equations S13, S14 and S18.ηa1=15%; ηa2=30%; ηb=35%; ηc=9%; ηd=11% (calculated from the values of ri and NEPicarbon).
ϕr, ϕf, ϕBMϕf, ϕf, ϕBM are the proteomic mass fraction of enzymes dedicated to fermentation, respiration, and biomass generation, respectively.NA
κtA parameter determined by the translation rate, defined as κt≡kT⋅mAA/(ς⋅mR).κt=1/610 (s–1) (calculated from the values of kT, ς and mR).
JBMThe carbon flux of biomass production; an extensive variable.See Equation S10.
JEThe energy demand for cell growth, expressed as the stoichiometric energy flux in ATP; an extensive variable.See Equation S25.
JE(N)The normalized flux of energy demand in ATP; an intensive variable.JE(N)≡JE⋅m0/Mcarbon.
rE, ηErE and ηE are energy coefficients. rE is the slope of JE versus JBM; ηE=rE⋅[∑iri/NEPicarbon].See Appendix 9.2.
βiThe stoichiometric coefficient of ATPs in biochemical reactions shown in Figures 1B and 3E (for E. coli) or Appendix 1—figure 5E and F (for yeast and mammalian cells).β1=4, β2=3, β3=2, β4=6, β6=1, βa1=4, β7=1, β8=2, β9=6 (E. coli); β1=5, β2=1, β3=5, β4=7.5, β6=2.5, βa1=5 (eukaryotic cells) (Neidhardt et al., 1990; Sauer et al., 2004).
βr(A), βf(A)βr(A) and βf(A) are the stoichiometric coefficients of ATP production per glucose in respiration and fermentation, respectively.βr(A)=26, βf(A)=12 (E. coli); βr(A)=32, βf(A)=2 (eukaryotic cells) (Neidhardt et al., 1990).
Jr(E), Jf(E)Jr(E) and Jf(E) are normalized energy fluxes of respiration and fermentation, intensive variables.Jr(E)≡βr(A)2⋅Jr(N);Jf(E)≡βf(A)2⋅Jf(N).
εr, εf
εr(dt), εf(dt)		εr (or εr(dt)) and εf (or εf(dt)) are the proteome efficiencies for energy biogenesis in the respiration and fermentation pathways: εr≡Jr(E)/ϕr and εf≡Jf(E)/ϕf.Calculated from the values of κA, κi, βr(A) and βf(A) with Equations S132 and S161.
φφ is an energy demand coefficient, defined in Equation S33 and mainly determined by ηE.Calculated from the values of ηE, βi, ηi with Equation S33. See Appendix 9.2.
ψ, ψdtψ-1 (or ψdt−1) is the proteome efficiency for biomass generation in the biomass pathway, with ψ−1≡/λ/ϕBM.Calculated from the values of ηi, κA, κi, Ω, κt with Equations S133 and S162.
κrA, κf(A)κrA and κfA are parameters defined as κr(A)≡[1κ1+2κ2+2κ3+2κ4]−1 and
κf(A)≡[1κ1+2κ2+2κ6]−1.		Calculated from the values of κi.
ΩΩ is a composite parameter defined as Ω≡1/κt+∑ia1,a2,b,c,dηi/κi.See Appendix 9.2.
κglucose(ST),κlactose(ST)The substrate quality of glucose or lactose at saturated concentration.Calculated using Equation S27 and the approximation used in Equation S20.
ΔΔ is a function of κA defined as Δ(κA)≡εf(κA)/εr(κA) .Δ≡εf/εr.
κA(C)The critical value of κA which satisfy Δ(κA)=1 and thus εf(κA)=εr(κA);
See Equation S42 (for E. coli) and S176 (for yeast and mammalian cells).		Calculated from the values of βi and κi with Equation S42.
λCThe critical growth rate at the transition point: λC≡λ(κA(C)); See Equations S43 and S177.Calculated from the values of ϕmax, φ, βi, κi, κA(C), Ω, ηi with Equations S43, S32 and S162.
θThe Heaviside step function.NA
Jacetate,JCO2,rJacetate and JCO2,r are the stoichiometric fluxes of acetate from the fermentation pathway and CO2 from the respiration pathway; extensive variables.Jacetate=Jf; JCO2,r=3⋅Jr. See Appendix 9.1 and Equations S158.
Jacetate(M),JCO2,r(M)Jacetate(M) and JCO2,r(M) are the fluxes of Jacetate and JCO2,r (per biomass) in the unit of mM/OD600/h, which are measurable in experiment. Intensive variables.Jacetate(M)≈2⋅Jf(N); JCO2,r(M)≈6⋅Jr(N). See Appendix 9.1 and Equation S160.
κAmaxThe maximum value of κA available across different Group A carbon sources.Approximated by the max κA across Group A carbon sources, calculated with Equation S27 and the approximation used in Equation S20.
λmaxThe population cell growth rate for the maximum value of κA: λmax=λκAmax.Calculated from the maximum of Equation S36 with the values of βi, κi, κAmax, φ, Ω, κt, and Equations S32, S132, Equation S161 and S162.
N(μ,σ2)A Gaussian distribution with a mean of μ and a standard deviation of σ.The probability density function is f(x)=1σ2πe−12(x−μσ)2.
μλC, σλCμλC and σλC are the mean and standard deviation of λC, respectively.μλC is approximated by the deterministic value of λC; see Appendix 3.3 for σλC settings. See Appendix 9.2 for the values.
erfThe error function in mathematics.erf(x)=2π∫0xexp(−t2)dt
ϕZThe proteomic mass fraction of useless proteins encoded by the LacZ gene.See Appendix 4.1.
wAn energy dissipation coefficient.See Appendix 4.2.
w0The maintenance energy coefficient.w0=0 or 2.5 (h–1) as specified in Figures 3–4, Appendix 1—figures 2 and 3. See Appendices 4.3 and 9.2.
ιι is the inhibition coefficient such that (1+ι)−1 represents the translation efficiency.See Appendices 4.3 and 9.2
ιw0=0(2μmCm), ιw0=0(4μmCm), ιw0=0(8μmCm), ιw0=2.5(2μmCm), ιw0=2.5(4μmCm), ιw0=2.5(8μmCm)The values for ι in the cases with 2 μm , 4 μm, or 8 μm of chloramphenicol and the maintenance energy coefficient w0 chosen as 0 or 2.5 (h–1).ιw0=0(2μmCm)=1.15;ιw0=0(4μmCm)=2.33; ιw0=0(8μmCm)=6.25; ιw0=2.5(2μmCm)=1.05; ιw0=2.5(4μmCm)=2.00; ιw0=2.5(8μmCm)=5.40. See Appendix 9.2.
κpyThe substrate quality of pyruvate; see Equation S89.Calculated from the values of kpycat, mEpy, m0, rprotein, rcarbon, Kpy and the external concentration of pyruvate [py].
βr(py), βf(py)βr(py) and βf(py) are the stoichiometric coefficients of ATP production per pyruvate in respiration and fermentation, respectively.βr(py)=10; βf(py)=3.
(Neidhardt et al., 1990).
Jr(E,py), Jf(E,py)Jr(E,py) and Jf(E,py) are the normalized energy fluxes of respiration and fermentation for pyruvate utilization; intensive variables.The corresponding variables of Jr(E) and Jf(E) in the case of pyruvate utilization.
εr(py),εf(py)εr(py) and εf(py) are the proteome efficiencies for energy biogenesis using pyruvate in the respiration and fermentation pathways.The corresponding variables of εr and εf in the case of pyruvate utilization.
ΩGg′Ω`Gg is a composite parameter defined as ΩGg′≡(ηb+ηc)/κ8+ηa1/κ9.See Appendix 9.2.
ψpy, φpy, κpy(ST)κpy(C), λmax(py)ψpy, φpy, κpy(ST), κpy(C) and λmax(py) are the corresponding variables/parameters of ψ, φ, κAmax, κAC and λmax in the case of pyruvate utilization.See Appendices 5.1 and 9.2.
λC(py), μλC(py), σλC(py)λC(py), μλC(py) and σλC(py) are the corresponding variables/parameters of λC, μλC and σλC in the case of pyruvate utilization.See Appendices 5.1 and 9.2.
NPicarbonThe number of carbon atoms in a molecule of Pool i.The value of NPicarbon is approximated by NEPicarbon (Equation S107).
κi(21AA)The substrate quality of the external supplied amino acids identical to those in Pool i.See Appendices 5.2 and 9.2.
Ω21AAΩ21AA is a composite parameter defined as Ω21AA≡1/κt+ηa1/κa1+∑ia2,b,c,dηi/κi(21AA).See Appendices 5.2 and 9.2.
ψ21AA, φ21AA, λmax(21AA), λC(21AA), μλC(21AA), σλC(21AA)ψ21AA, φ21AA, λmax(21AA), λC(21AA), μλC(21AA) and σλC(21AA) are the corresponding variables/parameters of ψ, φ, λmax, λC, μλC and σλC in the case of a Group A carbon source is mixed with 21 types of amino acids at saturated concentrations.See Appendices 5.2 and 9.2.
Ω7AA, φ7AA, μλC(7AA),σλC(7AA)Ω7AA, φ7AA, μλC(7AA) and σλC(7AA) are the corresponding parameters of Ω, φ, μλC and σλC in the case of a Group A carbon source is mixed with 7 types of amino acids.See Appendices 5.2 and 9.2.
Jin(N), ϑJin(N) is the normalized stoichiometric influx of a Group A carbon source (Equation S136). ϑ is a parameter defined as ϑ=ηa1+ηc+(ηa2+ηb+ηd)/2 for the model shown in Figure 1B.See Appendix 7.3
χext, χint, χtotχext, χint and χtot are the level of extrinsic noise, intrinsic noise and total noise in a system.See Appendix 8.1
μkicat, σkicat, μ1/kicat, σ1/kicat, μ1/kicat′, σ1/kicat′μkicat and σkicat are the mean and standard deviation of kicat. μ1/kicat (or μ1/kicat′) and σ1/kicat (or σ1/kicat′) are the mean and standard deviation of 1/kicat. See Appendix 8.1.μkicat is approximated by the deterministic value of kicat. The CV of kicat is set to 25%. μ1/kicat≈1/μkicat; σ1/kicat/μ1/kicat≈σkicat/μkicat.
IG(x;μ,ζ)The inverse Gaussian (IG) distribution: variable x>0 with parameters μ and ζ. See Equation S142.The probability density function is ζ2πx3exp-ζx-μ22μ2x.
IOGx;μ,ζThe positive inverse of Gaussian (IOG) distribution: variable x>0 with parameters μ and ζ. See Equation S140 and Appendix 8.1.The probability density function is ζ2πx4exp-ζx-μ22μ2x2.
ζ1/kicat, ζ1/kicat′Distributional parameters of 1/kicat corresponding to ζ in an IG or IOG distribution.See Appendix 8.1
GkThe characteristic function of IG distribution. See Equation S147.Gk=∫-∞∞eikx⋅IGx;μ,ζdx
Xi, αi, Θ, TΘ,Γi(t)Xi, αi, Θ and Γi(t) are variables and parameters used to calculate the first passage time TΘ of a stochastic process that mimics the duration of an enzyme to finishing a catalytic job.See Appendix 8.1.
γi, Ξ, μΞ, σΞγi is a real number; Ξ is a variable defined as Ξ≡∑i=1nγi/kicat; μΞ and σΞ are the mean and standard deviation of Ξ.See Equation S153 and Appendix 8.1.
μκi, σκi, μ1/κi, σ1/κiμκi and σκi are the mean and standard deviation of κi; μ1/κi and σ1/κi are the mean and standard deviation of 1/κi.See Equation S154 and Appendices 8.1 and 9.2.
λr, λf, μλr, σλr, μλf, σλf, ρrfλr and λf are the growth rates when cells choose respiration or fermentation; μλr, μλf and σλr, σλf are the means and standard deviations of λr and λf; ρrf is the correlation of λr and λf.See Equation S36 and Appendices 8.1 and 9.2.
λsuccinate(21AA), λacetate,μλsuccinate(21AA), μλacetate,σλsuccinate(21AA), σλacetateλsuccinate(21AA) and λacetate are the growth rates for succinate mixed with 21AA or acetate as the sole carbon source; μλsuccinate(21AA), μλacetate and σλsuccinate(21AA), σλacetate are the means and standard deviations of λsuccinate(21AA) and λacetate.See Appendix 9.2.
ϕMT, κMTϕMT and κMT are the proteomic mass fraction of the enzymes and the effective substrate quality of related metabolites in the mitochondria for yeast and mammalian cells, respectively.NA
PrfThe proportion of ATP generated from fermentation: Prf≡Jf(E)Jf(E)+Jr(E).See Equations S180, S189 and Appendix 10.
Δ¯The proteome efficiency difference between respiration and fermentation: Δ¯≡1/εr−1/εf.See Equations S181, S187 and Appendix 10.
μεr, μεf, μ1/εr, μ1/εfμεr, μεf, μ1/εr and μ1/εf are the mean values of εr , εf, 1/εr and 1/εf, respectively.See Equations S182-S184 and Appendix 10.
σεr, σεf, σ1/εr, σ1/εfσεr, σεf, σ1/εr, and σ1/εf are the standard deviations of εr , εf, 1/εr and 1/εf, respectively.See Equations S182, S185 and Appendix 10.
χεr, χεf, χ1/εr, χ1/εfχεr, χεf, χ1/εr, and χ1/εf are the coefficients of variation of εr , εf, 1/εr and 1/εf, respectively.See Equations S185-S186 and Appendix 10.
μΔ¯, σΔ¯μΔ¯ and σΔ¯ are the mean and standard deviation of Δ¯, respectively.See Equations S187-S188 and Appendix 10.
εr,⟨εf⟩εr and εf are the population-averaged values of εr and εf, respectively.Measurable from experiments.
See Equations S183-S184 and Appendix 10.
  1. *

    Parameter settings for yeast and mammalian cells are specifically labeled as ‘eukaryotic cells.’

  2. †

    ‘NA’ represents ‘Not applicable.’

  3. ‡

    Extensive variables scale with the size of the cell population.

  4. §

    Intensive variables are scale-invariant with respect to the cell population.

Additional files

Source data 1

Source data for the theoretical results generated in this study and the experimental data from prior studies, as shown in Figures 1—5.

https://cdn.elifesciences.org/articles/94586/elife-94586-data1-v2.xlsx
Source data 2

Source data for the theoretical results generated in this study and the experimental data from prior studies, as shown in Appendix 1—figures 2–4.

https://cdn.elifesciences.org/articles/94586/elife-94586-data2-v2.xlsx
MDAR checklist
https://cdn.elifesciences.org/articles/94586/elife-94586-mdarchecklist1-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Xin Wang
(2025)
Overflow metabolism originates from growth optimization and cell heterogeneity
eLife 13:RP94586.
https://doi.org/10.7554/eLife.94586.4