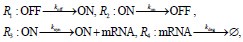Deep learning linking mechanistic models to single-cell transcriptomics data reveals transcriptional bursting in response to DNA damage

Joint Public Review:

In this work, the authors present DeepTX, a computational tool for studying transcriptional bursting using single-cell RNA sequencing (scRNA-seq) data and deep learning. The method aims to infer transcriptional burst dynamics-including key model parameters and the associated steady-state distributions-directly from noisy single-cell data. The authors apply DeepTX to datasets from DNA damage experiments, revealing distinct regulatory patterns: IdU treatment in mouse stem cells increases burst size, promoting differentiation, while 5FU alters burst frequency in human cancer cells, driving apoptosis or survival depending on dose. These findings underscore the role of burst regulation in mediating cell fate responses to DNA damage.

The main strength of this study lies in its methodological contribution. DeepTX integrates a non-Markovian mechanistic model with deep learning to approximate steady-state mRNA distributions as mixtures of negative binomial distributions, enabling genome-scale parameter inference with reduced computational cost. The authors provide a clear discussion of the framework's assumptions, including reliance on steady-state data and the inherent unidentifiability of parameter sets, and they outline how the model could be extended to other regulatory processes.

The revised manuscript addresses many of the original concerns, particularly regarding sample size requirements, distributional assumptions, and the biological interpretation of inferred parameters. However, the framework remains limited by the constraints of snapshot data and cannot yet resolve dynamic heterogeneity or causality. The manuscript would also benefit from a broader contextualisation of DeepTX within the landscape of existing tools linking mechanistic modelling and single-cell transcriptomics. Finally, the interpretation of pathway enrichment analyses still warrants clarification.

Overall, this work represents a valuable contribution to the integration of mechanistic models with high-dimensional single-cell data. It will be of interest to researchers in systems biology, bioinformatics, and computational modelling.

Author response:

The following is the authors’ response to the original reviews

Joint Public Review:

In this work, the authors develop a new computational tool, DeepTX, for studying transcriptional bursting through the analysis of single-cell RNA sequencing (scRNA-seq) data using deep learning techniques. This tool aims to describe and predict the transcriptional bursting mechanism, including key model parameters and the steady-state distribution associated with the predicted parameters. By leveraging scRNA-seq data, DeepTX provides high-resolution transcriptional information at the single-cell level, despite the presence of noise that can cause gene expression variation. The authors apply DeepTX to DNA damage experiments, revealing distinct cellular responses based on transcriptional burst kinetics. Specifically, IdU treatment in mouse stem cells increases burst size, promoting differentiation, while 5FU affects burst frequency in human cancer cells, leading to apoptosis or, depending on the dose, to survival and potential drug resistance. These findings underscore the fundamental role of transcriptional burst regulation in cellular responses to DNA damage, including cell differentiation, apoptosis, and survival. Although the insights provided by this tool are mostly well supported by the authors' methods, certain aspects would benefit from further clarification.

The strengths of this paper lie in its methodological advancements and potential broad applicability. By employing the DeepTXSolver neural network, the authors efficiently approximate stationary distributions of mRNA counts through a mixture of negative binomial distributions, establishing a simple yet accurate mapping between the kinetic parameters of the mechanistic model and the resulting steady-state distributions. This innovative use of neural networks allows for efficient inference of kinetic parameters with DeepTXInferrer, reducing computational costs significantly for complex, multi-gene models. The approach advances parameter estimation for high-dimensional datasets, leveraging the power of deep learning to overcome the computational expense typically associated with stochastic mechanistic models. Beyond its current application to DNA damage responses, the tool can be adapted to explore transcriptional changes due to various biological factors, making it valuable to the systems biology, bioinformatics, and mechanistic modelling communities. Additionally, this work contributes to the integration of mechanistic modelling and -omics data, a vital area in achieving deeper insights into biological systems at the cellular and molecular levels.

We thank the reviewers for their positive opinion on our manuscript. As reflected in our detailed responses to the reviewers’ comments, we will make significant changes to address their concerns comprehensively.

This work also presents some weaknesses, particularly concerning specific technical aspects. The tool was validated using synthetic data, and while it can predict parameters and steady-state distributions that explain gene expression behaviour across many genes, it requires substantial data for training. The authors account for measurement noise in the parameter inference process, which is commendable, yet they do not specify the exact number of samples required to achieve reliable predictions. Moreover, the tool has limitations arising from assumptions made in its design, such as assuming that gene expression counts for the same cell type follow a consistent distribution. This assumption may not hold in cases where RNA measurement timing introduces variability in expression profiles.

Thank reviewers for detailed and constructive feedback on our work. We will address the key concerns raised from the following points:

(1) Clarification on the required sample size: We tested the robustness of our inference method on simulated datasets by varying the number of single-cell samples. Our results indicated that the predictions of burst kinetics parameters become accurate when the number of cells reaches 500 (Supplementary Figure S3d, e). This sample size is smaller than the data typically obtained with current single-cell RNA sequencing (scRNA-seq) technologies, such as 10x Genomics and Smart-seq3 (Zheng GX et al., 2017; Hagemann-Jensen M et al., 2020). Therefore, we believed that our algorithm is well-suited for inferring burst kinetics from existing scRNA-seq datasets, where the sample size is sufficient for reliable predictions. We will clarify this point in the main text to make it easier for readers to use the tool.

(2) Assumption-related limitations: One of the fundamental assumptions in our study is that the expression counts of each gene are independently and identically distributed (i.i.d.) among cells, which is a commonly adopted assumption in many related works (Larsson AJM et al., 2019; Ochiai H et al., 2020; Luo S et al., 2023). However, we acknowledged the limitations of this assumption. The expression counts of the same gene in each cell may follow distinct distributions even from the same cell type, and dependencies between genes could exist in realistic biological processes. We recognized this and will deeply discuss these limitations from assumptions and prospect as an important direction for future research.

The authors present a deep learning pipeline to predict the steady-state distribution, model parameters, and statistical measures solely from scRNA-seq data. Results across three datasets appear robust, indicating that the tool successfully identifies genes associated with expression variability and generates consistent distributions based on its parameters. However, it remains unclear whether these results are sufficient to fully characterise the transcriptional bursting parameter space. The parameters identified by the tool pertain only to the steady-state distribution of the observed data, without ensuring that this distribution specifically originates from transcriptional bursting dynamics.

We appreciate reviewers’ comments and the opportunity to clarify our study’s contributions and limitations. Although we agree that assessing whether the results from these three realistic datasets can represent the characterize transcriptional burst parameter space is challenging, as it depends on data property and conditions in biology, we firmly believe that DeepTX has the capacity to characterize the full parameter space. This believes stems from the extensive parameters and samples we input during model training and inference across a sufficiently large parameter range (Method 1.3). Furthermore, the training of the model is both flexible and scalable, allowing for the expansion of the transcriptional burst parameter space as needed. We will clarify this in the text to enable readers to use DeepTX more flexibly.

On the other hand, we agree that parameter identification is based on the steady-state distribution of the observed data (static data), which loses information about the fine dynamic process of the burst kinetics. In principle, tracking the gene expression of living cells can provide the most complete information about real-time transcriptional dynamics across various timescales (Rodriguez J et al., 2019).

However, it is typically limited to only a small number of genes and cells, which could not investigate general principles of transcriptional burst kinetics on a genome-wide scale. Therefore, leveraging the both steady-state distribution of scRNA-seq data and mathematical dynamic modelling to infer genome-wide transcriptional bursting dynamics represents a critical and emerging frontier in this field. For example, the statistical inference framework based on the Markovian telegraph model, as demonstrated in (Larsson AJM et al., 2019), offers a valuable paradigm for understanding underlying transcriptional bursting mechanisms. Building on this, our study considered a more generalized non-Mordovian model that better captures transcriptional kinetics by employing deep learning method under conditions such as DNA damage. This provided a powerful framework for comparative analyses of how DNA damage induces alterations in transcriptional bursting kinetics across the genome. We will highlight the limitations of current inference using steady-state distributions in the text and look ahead to future research directions for inference using time series data across the genome.

A primary concern with the TXmodel is its reliance on four independent parameters to describe gene state-switching dynamics. Although this general model can capture specific cases, such as the refractory and telegraph models, accurately estimating the parameters of the refractory model using only steadystate distributions and typical cell counts proves challenging in the absence of time-dependent data.

We thank reviewers for highlighting this critical concern regarding the TXmodel's reliance on four independent parameters to describe gene state-switching dynamics. We acknowledge that estimating the parameters of the TXmodel using only steady-state distributions and typical single-cell RNA sequencing (scRNA-seq) data poses significant challenges, particularly in the absence of timeresolved measurements.

As described in the response of last point, while time-resolved data can provide richer information than static scRNA-seq data, it is currently limited to a small number of genes and cells, whereas static scRNA-seq data typically capture genome-wide expression. Our framework leverages deep learning methods to link mechanistic models with static scRNA-seq data, enabling the inference of genome-wide dynamic behaviors of genes. This provides a potential pathway for comparative analyses of transcriptional bursting kinetics across the entire genome.

Nonetheless, the refractory model and telegraphic model are important models for studying transcription bursts. We will discuss and compare them in terms of the accuracy of inferred parameters.

Certainly, we agree that inferring the molecular mechanisms underlying transcriptional burst kinetics using time-resolved data remains a critical future direction. We will include a brief discussion on the role and importance of time-resolved data in addressing these challenges in the discussion section of the revised manuscript.

The claim that the GO analysis pertains specifically to DNA damage response signal transduction and cell cycle G2/M phase transition is not fully accurate. In reality, the GO analysis yielded stronger p-values for pathways related to the mitotic cell cycle checkpoint signalling. As presented, the GO analysis serves more as a preliminary starting point for further bioinformatics investigation that could substantiate these conclusions. Additionally, while GSEA analysis was performed following the GO analysis, the involvement of the cardiac muscle cell differentiation pathway remains unclear, as it was not among the GO terms identified in the initial GO analysis.

We thank the reviewer for this valuable feedback and for pointing out the need for clarification regarding the GO and GSEA analyses. We agree that the connection between the cardiac muscle cell differentiation pathway identified in the GSEA analysis and the GO terms from the initial analysis requires further clarification. This discrepancy arises because GSEA examines broader sets of pathways and may capture biological processes not highlighted by GO analysis due to differences in the statistical methods and pathway definitions used. We will revise the manuscript to address this point, explicitly discussing the distinct yet complementary nature of GO and GSEA analyses and providing a clearer interpretation of the results.

As the advancement is primarily methodological, it lacks a comprehensive comparison with traditional methods that serve similar functions. Consequently, the overall evaluation of the method, including aspects such as inference accuracy, computational efficiency, and memory cost, remains unclear. The paper would benefit from being contextualised alongside other computational tools aimed at integrating mechanistic modelling with single-cell RNA sequencing data. Additional context regarding the advantages of deep learning methods, the challenges of analysing large, high-dimensional datasets, and the complexities of parameter estimation for intricate models would strengthen the work.

We greatly appreciate your insightful feedback, which highlights important considerations for evaluating and contextualizing our methodological advancements. Below, we emphasize our advantages from both the modeling perspective and the inference perspective compared with previous model. As our work is rooted in a model-based approach to describe the transcriptional bursting process underlying gene expression, the classic telegraph model (Markovian) and non-Markovian models which are commonly employed are suitable for this purpose:

Classic telegraph model: The classic telegraph model allows for the derivation of approximate analytical solutions through numerical integration, enabling efficient parameter point estimation via maximum likelihood methods, e.g., as explored in (Larsson AJM et al., 2019). Although exact analytical solutions for the telegraph model are not available, certain moments of its distribution can be explicitly derived. This allows for an alternative approach to parameter inference using moment-based estimation methods, e.g., as explored in (Ochiai H et al., 2020). However, it is important to note that higher-order sample moments can be unstable, potentially leading to significant estimation bias.

Non-Markovian Models: For non-Markovian models, analytical or approximate analytical solutions remain elusive. Previous work has employed pseudo-likelihood approaches, leveraging statistical properties of the model’s solutions to estimate parameters ,e.g., as explored in (Luo S et al., 2023).

However, the method may suffer from low inference efficiency.

In our current work, we leverage deep learning to estimate parameters of TXmodel, which is nonMarkovian model. First, we represent the model's solution as a mixture of negative binomial distributions, which is obtained by the deep learning method. Second, through integration with the deep learning architecture, the model parameters can be optimized using automatic differentiation, significantly improving inference efficiency. Furthermore, by employing a Bayesian framework, our method provides posterior distributions for the estimated dynamic parameters, offering a comprehensive characterization of uncertainty. Compared to traditional methods such as moment-based estimation or pseudo-likelihood approaches, we believe our approach not only achieves higher inference efficiency but also delivers posterior distributions for kinetics parameters, enhancing the interpretability and robustness of the results. We will present and emphasize the computational efficiency and memory cost of our methods the revised version.

Recommendations for the authors:

There are various noise sources in biological progress. How transcriptional bursting fits within those as well as the reasons to focus only on this source needs to be clearly discussed in the introduction of the manuscript. Related to this last point, transcriptional bursting might not be the only mechanism to take advantage of the stochastic nature of biomolecular processes to make decisions. Once again, what are the implications of assuming this as the underlying mechanism?

Thank the reviewer for this valuable comment. We fully agree that biological systems are subject to multiple stochastic sources, which arise from both intrinsic and extrinsic noise (Eling N et al., 2019). Intrinsic noise is primarily driven by the stochastic biochemical effects that directly influence mRNA and protein expression in a gene-specific manner, such as DNA, epigenetic, transcription, and translation levels. Extrinsic noise arises from fluctuations in cell-specific manners, such as changes in cell size, cell cycle, or cell signaling. Given that DNA damage most directly perturbs transcription and translation processes, focusing on intrinsic noise sources is appropriate for mechanistically modeling gene-specific expression variability, particularly since this variability can be captured at the genome-wide scale by scRNA-seq data.

Among various intrinsic noise sources, transcriptional bursting offers a mechanistically wellcharacterized and quantifiable representation of gene expression variability (Tunnacliffe E & Chubb JR, 2020). It reflects the dynamic switching between active and inactive gene states and has been observed consistently across prokaryotic and eukaryotic cells (Eling N et al., 2019). Moreover, transcriptional bursting kinetics, defined by burst size and frequency, can be inferred from scRNA-seq data at the singlegene level using steady-state assumptions, making it an analytically tractable and biologically meaningful feature for large-scale inference (Rodriguez J & Larson DR, 2020).

We acknowledge that transcriptional bursting is not the only mechanism through which cells can utilize stochasticity for fate decisions. Other processes, such as translational noise and chromatin accessibility, may also contribute. However, given the data modality (static scRNA-seq) and the established theoretical framework for bursting, we assume transcriptional bursting as a representative and interpretable proxy of stochastic regulation. This assumption enables us to extract meaningful insights while remaining open to future model extensions, incorporating additional regulatory layers as more data types become available.

In this version of the manuscript, we have revised the introduction section to better clarify the rationale of this assumption and to more explicitly emphasize the important role of transcriptional bursting within stochastic noise.

More careful discussion of how the proposed method differentiates from previous work that employs scRNA-seq to elucidate the diverse sources of noise (pp.3).

Thank the reviewer for this suggestion. Our proposed method differs significantly from previous work that utilizes scRNA-seq data to study diverse noise sources from several aspects (Ochiai H et al., 2020; Eling N et al., 2019; Morgan MD & Marioni JC, 2018). Specifically, DeepTX infers genomewide burst kinetics by directly matching the full steady-state distribution of a mechanistic stochastic model to the observed scRNA-seq data, rather than relying solely on low-order statistics such as mean and variance. Moreover, by adopting a non-Markovian process that allows multi-step promoter switching, DeepTX extends beyond the classic telegraph model to better capture the complex molecular events underlying transcriptional activation and repression. Crucially, we used a deep-learning–based solver to obtain these intractable steady-state distributions rapidly and accurately. This combination of richer data usage, more realistic mechanistic assumptions, and scalable neural-network–accelerated computation lays the groundwork for incorporating additional noise sources into a unified inference framework in future work.

In this version of the manuscript, we have revised the discussion section to highlight the difference with previous works.

The paper could benefit from being contextualised alongside other computational tools that aim to integrate mechanistic modelling with single-cell RNA sequencing data. This is an active area of research, and works such as Sukys and Grima (bioRxiv, 2024), Garrido-Rodriguez et al. (PLOS Computational Biology, 2021), Maizels (2024), and others could provide valuable context.

Thank the reviewer for suggesting these relevant works. Garrido-Rodriguez et al. (PLOS Comput. Biol., 2021) integrated single-cell and bulk transcriptomic data into mechanistic pathway models to infer signaling dynamics, an approach complementary to our mapping of burst kinetic parameters onto pathway enrichment for linking transcriptional bursting to functional outcomes. Sukys and Grima et al. (bioRxiv, 2024; Now in Nucleic Acids Res., 2025) demonstrated that cell-cycle stage and cellular age significantly modulate burst frequency and size, highlighting the potential to enhance DeepTX by incorporating cell-cycle–dependent variability into genome-wide burst inference. Maizels et al. (Philos. Trans. R. Soc. Lond. B. Biol. Sci., 2024) reviewed methods for capturing single-cell temporal dynamics across multi-omic modalities, underscoring how higher time-resolved data could refine and validate steady-state burst inference frameworks to better resolve causal gene-expression mechanisms.

We have cited these studies on the contextual relevance to DeepTX in the discussion sections.

As the advancement is primarily methodological, it lacks a comprehensive comparison with traditional methods that serve similar functions. Consequently, the overall evaluation of the method, including aspects such as inference accuracy, computational efficiency, and memory cost, remains unclear. We suggest incorporating these experiments to provide readers with a more complete understanding of the proposed method's performance.

Thank the reviewer for constructive suggestion regarding a comprehensive comparison with other previous methods. To address this problem, in this version, we compared DeepTX with our previous work, txABC, that utilized approximate Bayesian computation to infer parameters from the generalized telegraph model (Luo S et al., 2023). As a result, DeepTX achieved improvements in inference accuracy and computational efficiency (Supplementary Figure S4.). For memory cost during single-gene inference, DeepTX requires an average memory usage of approximately 70 MB, whose memory consumption accounts for only a small fraction of the total available memory on standard computing devices (typically exceeding 10 GB), while exhibiting superior inference efficiency compared to txABC. We have mentioned in the third result section.

Discuss the validity of the assumption of the static snapshot provided by the scRNA-seq data as in steadystate (i.e., stationary distribution), and the implications of this assumption being untrue (for the proposed method).

We thank the reviewer for the comment regarding the stationary assumption. We assume that each scRNA-seq snapshot approximates the steady-state (stationary) distribution of transcript counts because (i) typical single-cell experiments sample large, asynchronously dividing populations that collectively traverse many transcriptional burst cycles, and (ii) in the absence of a synchronized perturbation, mRNA production and degradation reach a dynamic balance on timescales much shorter than overall cell-type changes. Under these conditions, the empirical count distribution closely mirrors the model’s stationary solution, justifying steady-state inference of burst size and frequency from a single time point. This assumption is commonly adopted in probabilistic models of transcriptional bursting (Larsson AJM et al., 2019; Raj A & van Oudenaarden A, 2008).

However, this steady-state assumption has some limitations. First, in some scenarios, the cell system may exhibit highly transient transcriptional programs that do not satisfy stationarity, leading to biased or misleading parameter estimates. For example, immediately following a synchronized developmental stimulus—such as serum shock–induced activation of immediate-early genes. Second, because DeepTX infers the mean burst frequency and size across the population, it cannot recover the underlying time-resolved dynamics or distinguish heterogeneous kinetic subpopulations.

We have added a statement in the discussion to acknowledge these limitations and suggest future extensions—such as incorporating time-series measurements or latent pseudo time covariates—to address non-stationarity and recover temporal burst dynamics.

On page 3, "traditional telegraph model" is mentioned without any context. This model, and particularly the implications for the current work, might not be obvious to the reader. Take one or two sentences to give the reader context.

Thank the reviewer for this helpful comment. We acknowledge that the mention of the "traditional telegraph model" on page 3 may not be immediately clear to all readers. The traditional telegraph model is a mathematical framework commonly used to describe gene expression burst dynamics, in which genes stochastically switch between active (ON) and inactive (OFF) states, with exponentially distributed waiting times for state transitions. To provide the necessary context, we added a brief introduction to the traditional telegraph model and its relevance to our work in the revised manuscript.

A primary concern with the model used in Figure 2a (TXmodel) is its reliance on four independent parameters to describe gene state switching dynamics. While this general model can encompass specific cases such as the refractory model (Science 332, 472 (2011)) and the telegraph model, accurately estimating the parameters of the refractory model using only steady-state distributions and typical cell numbers (10³-10⁴) is challenging without time-dependent data. To address this, we suggest that the authors provide parameter inference results for each individual parameter, rather than only for burst size and burst frequency, based on synthetic data. This would help clarify the model's effectiveness and improve understanding of its estimation precision.

Thank the reviewer for highlighting this important concern. We agree that the lack of timeresolved measurements may affect the accuracy of inferences about dynamic parameters, especially the unidentifiability of parameters inferred from steady-state distributions, i.e., multiple parameters leading to the same steady-state distribution. The unidentifiability of individual parameters is a common and critical problem in systems biology studies. To address this issue, for example, Trzaskoma et al. developed StochasticGene, a computationally efficient software suite that uses Bayesian inference to analyze arbitrary gene regulatory models and quantify parameter uncertainty across diverse data types (Trzaskoma P et al., 2024). Alexander et al. adopt a Bayesian approach to parameter estimation by incorporating prior knowledge through a prior distribution and classify a parameter as practically nonidentifiable if it cannot be uniquely determined beyond the confidence already provided by the prior (Browning AP et al., 2020). Hence, in DeepTX, we employed a Bayesian approach based on loss potential to infer the posterior distributions of the parameters (Figure 3E).

Although DeepTX also encounters the issue of unidentifiability for individual parameters (Supplementary Figure S11), the multimodal nature of the posterior distribution suggests that multiple distinct parameter sets can produce similarly good fits to the observed data, highlighting the inherent non-identifiability of the model. Nevertheless, in the multimodal posterior distribution, at least one of the posterior peaks aligns closely with the ground truth, thereby demonstrating the validity of the inferred result. Moreover, inference results on synthetic data confirm that the BS and BF can be accurately estimated (Supplementary Figure S3b and S3c). We also performed robustness analyses on synthetic datasets. As shown in Supplementary Figure S3d and S3e, our model reliably recovers the ground-truth burst kinetics of models when the number of cells reaches ~1000, which is within the range of typical single-cell RNA-seq experiments.

We have explicitly pointed out the potential issue of unidentifiability due to the lack of temporal resolution information in the discussion section.

Noteworthy, transcriptional is always a multi-step process (depending on the granularity with which the process is described). What do the authors mean by saying that "DNA damage turns transcription into a multi-step process rather than a single-step process"?

Thank the reviewer for pointing out the lack of precision in our original statement. We agree that the phrasing could be misleading. Transcription is inherently a multi-step process, but most mechanistic studies simplify it to a single-step “telegraph” model for tractability. In the context of DNA damage, however, damage-induced pausing and repair-mediated delays introduce additional intermediary states in the transcription cycle that cannot be approximated by a single step. To capture these damage-specific interruptions, DeepTX explicitly consider a multi-step promoter switching framework rather than combining all transitions into one. What we originally wanted to express was the necessity of multi-step process modeling. We have replaced the original sentence in introduction with: “However, the presence of DNA damage necessitates modeling the transcriptional process as a multistep process, rather than a single-step process, to capture the additional complexity introduced by the damage”.

It is unclear why the authors have chosen a different definition in Equation (2) rather than the commonly used burst frequency, 1/(k_deg * tau_off), as reported in the literature. Unlike the traditional definition, which is unit-free, the definition in Eq. (2) includes units, raising questions about its interpretability and consistency with established conventions. Clarifying this choice would improve the understanding and consistency of the methodology.

Thank the reviewer for raising this important point. We acknowledge that there are multiple definitions of burst frequency (BF) in the literature. Here, we provide a detailed explanation, clarifying the differences between these definitions, including the one used 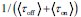and the traditional definition .

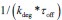First, the definition of burst frequency we adopt has been widely used in recent literatures, such as Benjamin Zoller et al. (Zoller B et al., 2018), Caroline Hoppe et al. (Hoppe C et al., 2020) and Daniel Ramsköld (Ramsköld D et al., 2024). And its quantity represents the average time it takes for the promoter to complete one full stochastic cycle between its active and inactive states 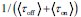. Secondly, the traditional definition 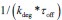can be regarded as a simplified version of our definition, under the assumptions that τ_on is negligible and k_deg =1 (i.e., rate parameters are normalized to be unit-free). Although it is reasonable to neglecting activate time τ_on, as it is typically much shorter than inactive time under some conditions, we chose a more complete way to define the burst frequency so that it is applicable to more general situations. In addition, by defining the burst frequency as 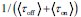, the mean transcription level can be analytically represented as the product of burst size and burst frequency.

This explanation has been clarified in the methods 1.2 section.

The authors mention the need to model "more realistic gene expression processes". How is this exactly being incorporated into the model?

Thank the reviewer for raising this important question. To incorporate "more realistic gene expression processes" into our model, we considered two critical aspects into DeepTX that are often oversimplified in traditional approaches:

(1) Integration of gene expression and sequencing processes: Observations from scRNA-seq data are influenced by both the intrinsic gene expression processes and the subsequent sequencing procedure. Traditional models often focus solely on gene expression, neglecting the stochastic effects introduced by the sequencing process. Our model explicitly incorporates both the gene expression and sequencing processes, providing a more comprehensive and realistic representation of the observed data.

(2) Modeling gene expression as a multi-step process: Gene expression is inherently a multi-step process. However, traditional telegraph models typically simplify gene state switching as a single-step process for tractable analysis, often assuming Markovian dynamics where transition waiting times follow exponential distributions. In contrast, our model accounts for the multi-step nature of gene state transitions by allowing the waiting times to follow non-exponential (non-Markovian) distributions. This model is more suitable for gene expression dynamics that cannot be simplified to a single-step process, such as DNA damage, which may introduce an intermediate state to represent pausing and repair in the transcription process.

By addressing these factors, our model better reflects the complexity and stochastic nature of gene expression processes, aligning more closely with the data generated from biological systems. We have added detailed explanations after this sentence for clarification in the first result section.

Better explanation of the previously developed TXmodel, and the assumption of a non-Markovian system. In particular, it isn't clear how using arbitrary distributions for the waiting times implies a non-Markovian process (as the previous state(s) of the system is not used to inform the transition probability, at least as explained in pp. 4). Without a clear discussion of the so-called arbitrary waiting time distribution, it isn't clear how these represent a mechanistic model. In general, a more careful discussion of the "mechanistic" model is needed.

Thank the reviewer for this thoughtful comment. In this revised version, we provided a more detailed explanation of the relationship between the TXmodel and the non-Markovian system in the revised manuscript. Specifically, we will clarify the following points:

(1) Why non-Markovian system: In a Markovian system, the waiting times for events are exponentially distributed, meaning that the state transitions depend solely on the current state and are memoryless (Van Kampen NG, 1992). However, when the waiting times follow non-exponential distributions, such as Gamma or Weibull distributions, the state transitions are no longer independent of the system's previous states. This introduces memory into the system, making it non-Markovian.

(2) Why mechanistic model: First, it is important to clarify that regardless of whether the waiting time is arbitrary or exponential (corresponding to non-Markovian and Markovian systems), our TXmodel is a mechanistic model because it models the dynamic process of transcription bursts with interpretable kinetic parameters. Second, although we introduced arbitrarily distributed waiting times, reasonable selection of waiting time distributions can still make the distribution parameters mechanistically interpretable. For example, in the context of modeling ON and OFF state switching times using a Gamma distribution, the two parameters have clear interpretations: the shape parameter represents the number of sequential exponential (memoryless) steps required for the transition to occur, capturing the complexity or multi-step nature of the switching process, while the scale parameter denotes the average duration of each of these steps. We have added the explanation in methods 1.2 section.

Include a brief discussion about the metric used to compare distributions (and introduce KL abbreviation).

Thank the reviewer for this suggestion. In the second result and methods 1.3 section of revised manuscript, we have included a brief discussion to introduce and clarify the metric used to compare distributions. Specifically, we have given more explanation for the Kullback-Leibler (KL) divergence, which is a widely used metric for quantifying the difference between two probability distributions. We also ensured that the abbreviation "KL" is properly introduced when it first appears in the text, along with a concise description of its mathematical definition and interpretation within the context of our analysis.

What does the "CTM" model stand for (in supplementary information)? And "TX" model?

Thank the reviewer for highlighting this point. We revised the supplementary information to explicitly define the "CTM" and "TX" models and clarify their distinctions.

CTM model: The "CTM" model refers to the classic telegraph model, a widely used model for capturing Markovian gene expression burst kinetics. The CTM describes stochastic gene expression as a sequence of four biochemical reactions involving two gene states (ON and OFF), mRNA transcription and degradation:

k_off as the rate at which the gene switches from OFF to ON, k_on as the rate at which the gene switches from ON to OFF, k_syn as the rate of mRNA synthesis and k_deg as the rate of mRNA degradation. In this model, gene switching between active and inactive states is governed by a memoryless Markovian process, where the waiting times for transitions follow exponential distributions (Van Kampen NG, 1992).

TX model: In contrast, the "TX" model is a more generalized telegraph model for transcriptional processes.

Different from the CTM, the waiting times for state transitions between ON and OFF in the TX model follow arbitrary waiting time distributions. This implies that the future state of the system depends not only on the current state but may also be influenced by its historical trajectories. Consequently, the TX model exhibits non-Markovian behavior. We have added more detailed description on these two models in section 1.1 of supplementary text.

Leaky transcription (in the OFF promoter state) is not considered. What would be the implications of its presence in the data?

Thank the reviewer for pointing out the potential role of leaky transcription in our analysis. We acknowledge that leaky transcription, occurring in the promoter OFF state, was not explicitly considered in our current model. Our decision to exclude it assumed that the leaky transcription rate is relatively small and its impact on the observed data is negligible. This assumption is consistent with previous studies that similarly disregard leaky transcription in gene expression modeling due to its minimal contribution to the overall dynamics (Larsson AJM et al., 2019).

However, we recognize that the leaky transcription should be considered, particularly in systems where the leaky rate is significant relative to the active transcription rate. In such cases, it may introduce additional variability to the observed expression levels or obscure the distinction between ON and OFF states. We have added relevant statements in the discussion section.

In the main text, the waiting time for state transitions is described by two parameters, while in the methods/supplementary information only one parameter is considered per distribution (without a clear discussion of the so-called "dwell time distributions").

Thank the reviewer for this comment. We recognize the need to clarify the discrepancy between the descriptions of waiting times in the main text and supplementary materials.

Dwell time distribution refers to the probability distribution of the time in which a gene remains in a particular transcriptional state (ON or OFF) before transitioning to the other state. While in Markovian models the dwell time follows an exponential distribution, more complex or non-Markovian regulatory mechanisms may give rise to Gamma, Weibull, or other non-exponential dwell time distributions.

In our model, we denote the dwell time distributions in the OFF and ON states by 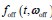and 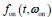, respectively, where w represents a vector of parameters characterizing the distribution, the dimensionality of which depends on the specific form of the distribution. For example, when an exponential distribution is assumed, w consists of a single rate parameter; in contrast, for distributions such as the Gamma or Weibull, w includes two parameters. In the main text, both 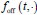and 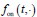are modeled using Gamma distributions, whereas in the Supplementary Materials, we assume exponential distributions for both, resulting in a single-parameter representation. We have added relevant statements in the methods 1.2 section.

Related, but more general, across the manuscript there are problems with the consistency in terminology. This is especially problematic with the figures. It makes it incredibly hard to follow the work. Better integration of the information, and consistency with the terminology, would improve the understanding for the reader.

Thank the reviewer for the valuable feedback. To enhance clarity and readability, we have carefully revised the manuscript to ensure consistent terminology throughout the text and figures e.g., unifying terms such as "untreatment" and "control" under the consistent label "control"—across both the text and figures.

One of the four main assumptions behind the model is that "the solution of the model can be explained by a mixed negative binomial distribution". The logic and implications of this assumption need to be discussed in the paper. (Methods, pp.13.) All four assumptions need to be carefully argued in the paper.

We appreciate the reviewer’s comment regarding the assumptions underlying our model. Here, we would like to clarify the rationale and implications of each assumption.

Assumption 1 (The gene expression of cells was in a stationary distribution during sequencing.) has been extensively used in previous studies for the inference and modeling of scRNA-seq data, demonstrating effectiveness in capturing mRNA expression distributions and inferring underlying dynamic parameters (Larsson AJM et al., 2019; Luo S et al., 2023; Ramsköld D et al., 2024; Gupta A et al., 2022).

For Assumption 2 (Gene expression counts of the same cell type follow the same distribution.) is as follows: cell types are typically defined based on gene expression profiles or functional characteristics. Cells with similar functions often exhibit consistent transcriptional programs, leading to approximately identical gene expression distributions. This assumption has been widely adopted in previous research (Larsson AJM et al., 2019; Gupta A et al., 2022).

Regarding Assumption 3 (The solution of the model can be approximated by a mixed negative binomial distribution.), in the most general formulation, a chemical master equation (CME) model of biological systems converges to a stationary distribution P(n;θ) over n∈ℕ. And P(n;θ) afford a real Poisson representation (Gardiner CW & Chaturvedi S, 1977): 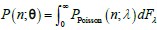where F is a mixing cumulative distribution function (CDF). If such a Poisson representation exists, we can always write down a finite approximation over K Poisson kernels: 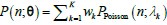, where w_k are weights on a K-dimensional simplex. Further, as k →∞,Q→P . More problematically, convergence in the number of kernels in K is typically slow. Negative binomial kernels P_Poisson (n m _k,l_k), which are continuous Poisson mixtures with a gamma mixing density can accelerate convergence in K (Gorin G et al., 2024). Hence, the solution of the TX model can be approximated by a mixed negative binomial distribution.

For Assumption 4 (The state space sampled from a sufficiently long single simulation is statistically equivalent to that obtained from multiple simulations at steady state in gene expression models.), when a sample trajectory of the model is simulated for a sufficiently long period, it is assumed to have traversed the entire stationary state space (Kuntz J et al., 2021). Therefore, by performing truncated statistical analysis on the trajectory, the corresponding stationary distribution of the model can be obtained. We have added the explanation in methods 1.1 section.

The authors propose that the waiting times between promoter states follow a non-exponential distribution, but the choice of gamma distribution and the implications for the method and the biological conclusions need to be discussed.

We thank the reviewer for this comment. To account for the impact of DNA damage on the transcription process, our model assumes that both the "ON" and "OFF" states of the promoter consist of multiple underlying sub-states. When a promoter switches from the "ON" state to the "OFF" state, the transition is governed by multiple distinct waiting time distributions that follow exponential distributions. Similarly, when a promoter switches from the "OFF" state to the "ON" state, there may be multiple transitions from different "OFF" sub-states. Consequently, the waiting times for the transitions from the "OFF" state to the "ON" state, and vice versa, must account for multiple exponential waiting time distributions associated with each "ON" state transition. We can map a multiple exponential-waiting-times reaction process to a single-step reaction process with a non-exponential waiting time distribution. Therefore, we use a Gamma distribution for dwell time of promoter switching, which can be expressed as the convolution of multiple exponential distributions (corresponding to a sum of multiple exponential variables). Additionally, other non-exponential distributions, such as those discussed in our previous studies (Zhang J & Zhou T, 2019), may also be considered, and we recognize that alternative choices could be made depending on the specific characteristics of the system. We have added the explanation in methods 1.2 section.

BF - burst frequency; BS - burst size. These terms represent the main data output, but they are only mathematically defined in the methods, and never the intuition of the specific expression explained (e.g., why not using tON/(tON+tOFF) as BF instead of 1/(tON+tOFF), and why not kSYN*tON as BS instead of kSYN*tON).

We appreciate the reviewer’s comment and agree that clarifying the biological intuition behind the mathematical definitions of burst frequency (BF) and burst size (BS) is important. Below, we provide a more detailed explanation of these definitions.

BF: The definition of burst frequency 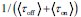we adopt has been widely used in previous literature, such as Benjamin Zoller et al (Zoller B et al., 2018), Caroline Hoppe et al (Hoppe C et al., 2020) and Daniel Ramsköld (Ramsköld D et al., 2024). And its quantity represents the average time it takes for the promoter to complete one full stochastic cycle between its active and inactive states.

BS: The definition of burst size BS = 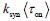we adopt is consistent with the definition proposed by the reviewer. Burst size refers to the average number of mRNA transcripts produced during a single transcriptional activation event of a gene. It reflects the quantity of gene product synthesized per activation and is influenced by the rate of transcription and the duration of the active state of the gene. Our definition aligns with this biological interpretation and is mathematically formulated as BS = 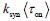, where k_syn is the transcription rate and 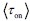is the average duration of the active state.

In addition, the mean transcription level can be analytically represented as the product of burst size and burst frequency. This analytical result has been included in the methods 1.2 section of revised manuscript.

One can assume from the methods that omegaON and omegaOFF are the vector of (2) parameters describing the distribution, but the reader would benefit from some clarity here. The authors claim that they proved that the distribution moments can be obtained through an iterative process. How much does this rely on the assumption of an underlying binomial distribution?

Thank the reviewer for this helpful suggestion. To clarify, the vectors omegaON and omegaOFF represent the parameters characterizing the waiting time distributions of the promoter's active and inactive states, respectively. The exact form and interpretation of these vectors depend on the specific distributional choice for the waiting times. For instance, when the waiting time distribution follows a Gamma distribution with shape parameter α>0 and scale parameter β>0 , denoted as 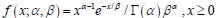, then w_on = (α,β) . Conversely, when the waiting time distribution follows a Weibull distribution, denoted as 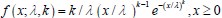, with shape parameter k >0 and scale parameter l>0, then w_on = (l,k) . We have clarified it in the Methods 1.2 section of the revised manuscript.

For the question about the binomial distribution, in our work, we use the binomial moment method to compute distributional statistics of chemical master equation (Zhang J et al., 2016). Binomial moments of the mRNA stationary distribution P(m) are defined as 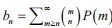, where the symbol 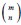represents the combinatorial number. This technique refers to a mathematical tool for moment calculation and is not based on the assumption that the underlying distribution is binomial distribution (Luo S et al., 2023). Hence, our approach is general and does not require the distribution itself to follow a binomial form.

More details about the parameter sampling are required. For instance, why are the specific ranges chosen and their implications? And is the space explored in logarithmic scale?

Thank the reviewer for the insightful comment regarding parameter sampling. In our study, we considered five parameters: 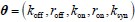. The parameters k_off and k_on represent the number of intermediate reaction steps involved in transcriptional state transitions. These values were sampled uniformly from the range 1 to 15, which aligns with biological evidence indicating that most genes undergo either direct (single-step) transitions or a small number of intermediate steps, typically fewer than ten (Tunnacliffe E & Chubb JR, 2020). This range is sufficient to capture both widely used singlestep models and more detailed multi-step mechanisms without introducing biologically implausible complexity.

Among these parameters, r_off and r_on denote the rate constants governing stochastic transitions between the OFF and ON transcriptional states, respectively. The mean duration of the OFF state, which corresponds to the time between transcriptional bursts, is given by 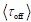= k_off / r_off , and falls within the range 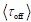∈(0.1,150).Experimental measurements report a median value of 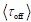approximately 3.7 (Gupta A et al., 2022), which is well contained within this range. Similarly, the mean duration of the ON state, referred to as the burst duration, is defined by 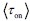= k_on / r_on , and spans the interval 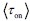∈(0.1,1500). The experimentally observed median value of 0.12 (Gupta A et al., 2022) confirms that the parameter range adequately captures biologically realistic dynamics.

The parameter k_syn represents the normalized synthesis rate after accounting for molecular degradation. Its range was chosen based on empirical observations of transcriptional burst sizes, which typically vary from single molecules to several dozen (Gupta A et al., 2022). Considering the relationship BS = k_syn * 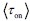, the selected range of k_syn ensures that the experimentally observed burst sizes are well represented within the defined parameter space. We have added the explanation in methods 1.2 section and supplementary text 4.

We fully recognize the advantages of logarithmic sampling, particularly when parameters span several orders of magnitude. Logarithmic scaling ensures balanced exploration across wide ranges and prevents sampling bias towards larger values. However, in our work, we applied Sobol sampling directly within the original (linear) parameter space. Although we did not explicitly transform parameters into logarithmic scale, Sobol sequences provide low-discrepancy, quasi-random coverage, which promotes uniform sampling across bounded domains (Sobol IM, 1967). Further, if necessary, we can increase the parameter range adaptively, and perform simulation algorithm to obtain sample and train a new model to solve a larger parameter range.

On page 15, the rationale for selecting the parameter space is unclear. This is crucial, as fully connected neural networks typically exhibit poor extrapolation beyond their training parameter space. If the parameter space of an experimental dataset significantly differs from the training range, the inference results may become unreliable. We suggest further clarification on how the alignment between the parameter spaces of the experimental data and the training dataset can be ensured to maintain inference accuracy.

We appreciate the reviewer’s insightful comment regarding the extrapolation limitations of fully connected neural networks. To address this concern, we have implemented a truncation strategy during inference, which constrains the inferred parameters to remain within the bounds of the training parameter space. This ensures that the neural network operates within a regime where its predictive accuracy has been validated, thereby enhancing the robustness of our results. Additionally, we have carefully selected the training parameter space to be reasonable, based on the characteristics of the experimental data. These ranges have been validated through domain knowledge and data analysis, ensuring that even when the experimental data approaches the boundaries of the training range, the inference results remain reliable and accurate.

On page 16, it is unclear why the authors chose to incorporate the Fano factor instead of using the coefficient of variation or variance. Clarifying the reasoning behind the selection of the Fano factor over these other statistical measures would provide better insight into its relevance for their analysis.

We thank the reviewer for raising this point. Although the loss term is described using the Fano factor, its formulation actually involves both the variance and the mean. Specifically, the loss we use is: 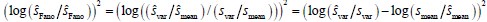. We chose to use the Fano factor because it is particularly well-suited for quantifying transcriptional noise in systems where the mean expression level varies across conditions or parameters. Unlike variance, the Fano factor normalizes variability by the mean, making it more robust for comparing noise levels across genes or regulatory regimes with different expression levels. Compared to the coefficient of variation (CV), which normalizes by the square of the mean, the Fano factor tends to be less sensitive to low expression regimes and is commonly used in stochastic gene expression studies, especially when the distribution is skewed or over dispersed (i.e., variance exceeds the mean). This makes it a more appropriate metric in our context, where transcriptional bursting often leads to over dispersed expression distributions. We have added an explanation in the methods 1.3 of revised manuscript to explain this choice.

On page 17, the definition of "sample" is unclear. Does it refer to the number of parameters sets or to the simulated trajectories generated by stochastic simulation algorithms?

Thank reviewers for your valuable feedback. The term "sample" in this context refers to the data points used in the neural network training set. To eliminate any ambiguity, we included a precise mathematical definition of "sample" (θ_i,P_simulation,i ) in the methods 1.3 section of revised manuscript.

Additionally, it is unclear how the authors determined the number of simulated trajectories per parameter set to ensure training accuracy. Furthermore, it would be relevant to address whether including moments during neural network training is beneficial.

We appreciate the reviewer’s insightful questions regarding the simulation and training process. To clarify, for each parameter set, we did not simulate multiple trajectories to obtain the corresponding distribution. Instead, we simulated the system for a sufficiently long period to ensure that the system reached a steady-state distribution. From this steady-state data, we then used interpolation methods to derive the corresponding distribution for each parameter set.

On the other hand, the moments were calculated theoretically without any approximations, providing higher accuracy. By incorporating the moments into the training process, we can effectively mitigate potential biases arising from insufficient sampling of the simulated data. Moreover, our experiments on the synthetic dataset demonstrate that introducing the moments as a loss function significantly enhances the model's performance on the test set (Figure 2E).

What is the intuition behind the choice of alpha_cg? On page 18, the rationale for setting the sampling probability to 0.5 is unclear. Could this parameter be inferred rather than being preset?

We thank the reviewer for the insightful comment regarding the choice of α_cg. We acknowledge that the typical values of this parameter in related literature often fall within a narrower range (e.g., 0.06–0.32) (Zheng GX et al., 2017; Macosko EZ et al., 2015). However, our decision to set α_cg was based on a trade-off between sampling efficiency and computational tractability in our specific application context. While it is indeed possible to infer α_cg as a learnable parameter, we opted for a fixed value in this work to reduce model complexity and avoid unidentifiability issues. In addition, we conducted inference under different capture efficiencies (0.5, 0.3, and 0.2), and found that the inferred burst size (BS) and burst frequency (BF) remained strongly correlated across these conditions (Supplementary Figure S12). This indicates that variations in capture efficiency do not significantly impact the outcomes of downstream enrichment analyses. Nevertheless, we agree that adaptively learning α_cg could be a promising direction, and we plan to explore this in future work. We have added the explanation in methods 1.4 section.

On page 19, the authors employed gradient descent for parameter inference. However, as this method is sensitive to initial values, it is unclear how the starting points were selected.

We sincerely thank the reviewer for highlighting the sensitivity of gradient-based optimization methods to initial values. To address this concern, we adopted a black-box optimization strategy in the form of the adaptive differential evolution (DE) algorithm (Das S & Suganthan PN, 2010) to derive robust initial parameters for the parameter inference. The adaptive DE algorithm enables global exploration across a broad parameter space, thereby reducing the risk of convergence to suboptimal local minima. This yielded reasonably good initial estimates, which were subsequently refined using gradient-based optimization to identify high-quality solutions characterized by a vanishing gradient norm. This hybrid strategy, which combines global and local search, is widely adopted in optimization literature to alleviate the risk of entrapment in local optima (Ahandani MA et al., 2014). We have clarified this detail in the third result of the revised manuscript.

Furthermore, clarification on how the gradients were computed - whether through finite difference approximation or other methods - would offer additional insight into the robustness and accuracy of their approach.

Thank reviewers for valuable feedback. Regarding the computation of gradients, we use the chain rule in neural networks, and the gradients are computed through backpropagation. Specifically, we rely on automatic differentiation to efficiently calculate the gradients. Unlike finite difference approximation, automatic differentiation directly computes the derivative of the loss function with respect to each parameter, ensuring accurate gradient calculations (Baydin AG et al., 2018). We have clarified this detail in the discussion section of the revised manuscript.

The paper presents several comparisons between continuous and discrete distributions in Figure 2B and Supplementary Figures S4, S6, and S8, described as a "comparison between mRNA distribution and inferred distribution by DeepTX for scRNA-seq data" or a "comparison between SSA results and DeepTX prediction results." This may lead to confusion for the reader, as the paper focuses on transcriptional bursting, a process where we would typically expect the distributions to be discrete. Clarifying this point would help align the figures with the main topic and enhance the reader's understanding.

We sincerely thank the reviewer for this insightful comment. We understand the concern that the distributions shown in Figure 2B and Supplementary Figures S4, S6, and S8 may appear to be continuous, which could be confusing given that transcriptional bursting naturally results in discrete mRNA count distributions.

We have clarified that in all these figures, both the empirical mRNA distributions derived from scRNAseq data and the model-predicted distributions from DeepTX are inherently discrete. To visualize the empirical distributions, we used histograms where the x-axis corresponds to discrete mRNA copy numbers and the y-axis represents the normalized frequency (density). To illustrate the DeepTX-inferred probability mass function, we plotted the predicted probabilities at each integer count as points and connected them with lines for clarity. While the connecting lines give the appearance of continuity, this is a standard graphical convention used to better show trends and model fit in discrete distributions.

We suggest that Figure 3E could present the error as a percentage of the parameter value, as this would provide a more equitable comparison and better illustrate the relative accuracy of the parameter estimation.

Thank reviewers for suggestion regarding Figure 3E. We agree that presenting the error as a percentage of the parameter value would offer a more equitable basis for comparison and better highlight the relative accuracy of our parameter estimation. Accordingly, we have revised Figure 3E to include the relative percentage error for each parameter.

Figure 4A could be improved for better legibility. The contour plots are somewhat confusing, and the light blue points are difficult to distinguish. Additionally, the x-axis label "Untreatment" appears throughout the manuscript-could this term be referring to the control experiment?

Thank reviewers for constructive feedback. We have revised Figure 4A to improve its clarity and legibility. Specifically, we adjusted the display style of the contour plots and enhanced the visibility of the light green points to make them more distinguishable.

Additionally, we recognize the potential confusion caused by the term "Untreatment" and have replaced it with "Control" throughout the revised manuscript to ensure consistency and accuracy in terminology.

Figure 4B was unclear, and further explanation would be helpful for understanding its purpose.

Thank reviewers for feedback. The purpose of Figure 4B is to illustrate the relationship between bursting kinetics and the mean and variance of the model. In the revised manuscript, we will provide a more detailed explanation of how the figure captures these relationships, highlighting the key insights it offers into the underlying dynamics.

Figure 4B illustrates the quantitative relationships among BS, BF, and gene expression noise within the framework of the transcriptional model. In this log-log-log 3D space, the mean expression level is constrained on a blue plane defined by the equation log(BS)+log(BF) = log(Mean), highlighting that the product of burst size and burst frequency determines the mean expression level. The orange plane represents a scaling relationship between expression noise and burst kinetics, expressed as log(BS)+log(BF) = klog(Noise), where k is a constant indicating how the burst kinetics co-vary with noise. Notably, the trajectory of the green sphere demonstrates that, under a fixed mean expression level (i.e., remaining on the blue plane), an increase in gene expression noise arises primarily from an increase in burst size. We have revised the caption of Figure 4B.

In Figure 4D, two of the GO analysis terms are highlighted in red, but the meaning behind this emphasis is not clear. The same question applies to Figure 5E, where the green dots are missing from the plot.

Clarification on these points would enhance the overall clarity.

We appreciate the reviewer’s thoughtful comments. We have added further clarification regarding the enrichment analysis results presented in Figure 4D. Specifically, we highlighted the "cell cycle G2/M phase transition" pathway because a delay in the G2/M phase transition has been shown to increase the probability of cell differentiation, which is a key aspect of our study. In addition, since IdU treatment is known to induce DNA damage, we emphasized the DNA damage-related pathway to support the biological relevance and consistency of our enrichment results. Similarly, in Figure 5E, we highlighted the apoptosis-related pathway. Apoptosis in this context is closely associated with cellular responses to toxic substances and mitochondrial dynamics. The enrichment of pathways related to these processes enables us to hypothesize the underlying mechanisms driving apoptosis in our system. Further, the absence of green dots in Figure 5E was due to an error in the figure caption. We have revised the figure caption accordingly to accurately describe all elements presented in the figure.

Clarify axis labels in figures, particularly the y-axis in Figure 5A and the x-axis in Figure 6G. In the first case, it isn't clear what this "value" represents. In the second case, the x-label is very confusing. As I understand the figure description, in these plots you are always comparing the G0 arrested genes between control and treated cells. But the x-label says "G0 (0 D)", "Cycle (50 D)".

Thank reviewers for pointing out the issues with the axis labels. We have made the necessary revisions to eliminate any confusion. In Figure 5A, the label for the y-axis has been changed from "value" to "log2 (value)" for clarity. The “value” in y-axis represents the value of statistical measure indicated at top of each panel. In Figure 6G, the x-axis label "Cycle (50 D)" has been updated to "G0 (50 D)" to accurately reflect the comparison between the G0-arrested genes in control and treated cells. We have revised the text of Figure 5A and Figure 6G.

Figure 6 uses a QS metric (quality score), but the definition of this metric is not provided. Including a brief explanation of its meaning would be helpful for clarity.

Thank reviewers for feedback. In this version, we provided explanation of the QS (Quality Score) metric in the supplementary text 3 for better clarity. The QS is calculated based on the difference in z-scores derived from GSVA (Gene set variation analysis) of gene sets upregulated and downregulated during the quiescent phase, and is defined as QS = z(up genes)− z(down genes) , as described in the literature (Wiecek AJ et al., 2023). z(up genes) represents the standardized enrichment score of the gene set upregulated during quiescence in each sample. A higher value indicates that the quiescenceassociated upregulated genes are actively expressed, suggesting that the sample is more likely to be in a quiescent (G0) state. z(down genes) corresponds to the standardized enrichment score of genes downregulated during quiescence. A lower value implies effective suppression of these genes, which is also consistent with quiescence. The difference score QS serves as an integrated indicator of the quiescent state: A higher value reflects simultaneous activation of quiescence-associated upregulated genes and repression of downregulated genes, indicating a gene expression profile that strongly aligns with the G0/quiescent state. A lower or negative value suggests a deviation from the quiescent signature, potentially reflecting a proliferative state or failure to enter quiescence.

In Figure 6G, light grey lines are shown, but their significance is unclear. It would be useful to specify what these lines represent.

Thank reviewers for observation. In Figure 6G, each point represents a single gene, and the light grey lines indicate the trend of changes in the corresponding bursting kinetics values, mean and variance for genes. We have added the explanation in the caption of Figure 6G.

Additionally, the manuscript should include references to the specific pathways used in the GO analysis to provide more context for the reader.

Thank reviewers for the suggestion. We have included references to the specific pathways used in the GO analysis in the revised manuscript to provide additional context for the readers.

In the discussion, sentences like "IdU drug treatment-induced BS enhancement delays the cell mitosis phase transition, impacting cell reprogramming and differentiation" are problematic as they imply causality, which I believe cannot be determined through the present analysis. The strength of the conclusions needs to be better argued (or toned down).

We acknowledge that the original sentence lacked precision and may have conveyed a misleading implication of causality not fully supported by our current analysis. In the discussion section of revised manuscript, we have rephrased the statement to present a more nuanced interpretation: IdU drug treatment-induced BS enhancement of genes may be associated with a delayed transition in the cell mitosis phase, which could potentially influence cell reprogramming and differentiation.

Other (minor) comments:

On pp. 10, "the BS down-regulates differential genes were mainly enriched..." appears to have a grammatical error/typo, "down-regulated"?

We have made correction. We have revised “down-regulates” to “down-regulated” for grammatical consistency.

Equation 2 doesn't match Figure 1A.

We have made correction. The definition of BF = 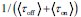in Equation 2 is correct. We have revised the definition of BF in Figure 1A to ensure consistency with Equation 2.

Reference

Zheng, G.X., Terry, J.M., Belgrader, P., Ryvkin, P., Bent, Z.W., Wilson, R., Ziraldo, S.B., Wheeler, T.D., McDermott, G.P., Zhu, J., Gregory, M.T., Shuga, J., Montesclaros, L., Underwood, J.G., Masquelier, D.A., Nishimura, S.Y., Schnall-Levin, M., Wyatt, P.W., Hindson, C.M., Bharadwaj, R., Wong, A., Ness, K.D., Beppu, L.W., Deeg, H.J., McFarland, C., Loeb, K.R., Valente, W.J., Ericson, N.G., Stevens, E.A., Radich, J.P., Mikkelsen, T.S., Hindson, B.J., Bielas, J.H. 2017. Massively parallel digital transcriptional profiling of single cells. Nature Communications 8: 14049. DOI: https://dx.doi.org/10.1038/ncomms14049, PMID: 28091601

Hagemann-Jensen, M., Ziegenhain, C., Chen, P., Ramsköld, D., Hendriks, G.J., Larsson, A.J.M., Faridani, O.R., Sandberg, R. 2020. Single-cell RNA counting at allele and isoform resolution using Smart-seq3. Nature Biotechnology 38: 708714. DOI: https://dx.doi.org/10.1038/s41587-020-0497-0, PMID: 32518404

Larsson, A.J.M., Johnsson, P., Hagemann-Jensen, M., Hartmanis, L., Faridani, O.R., Reinius, B., Segerstolpe, A., Rivera, C.M., Ren, B., Sandberg, R. 2019. Genomic encoding of transcriptional burst kinetics. Nature 565: 251-254. DOI: https://dx.doi.org/10.1038/s41586-018-0836-1, PMID: 30602787

Ochiai, H., Hayashi, T., Umeda, M., Yoshimura, M., Harada, A., Shimizu, Y., Nakano, K., Saitoh, N., Liu, Z., Yamamoto, T., Okamura, T., Ohkawa, Y., Kimura, H., Nikaido, I. 2020. Genome-wide kinetic properties of transcriptional bursting in mouse embryonic stem cells. Science Advances 6: eaaz6699. DOI: https://dx.doi.org/10.1126/sciadv.aaz6699, PMID: 32596448

Luo, S., Wang, Z., Zhang, Z., Zhou, T., Zhang, J. 2023. Genome-wide inference reveals that feedback regulations constrain promoter-dependent transcriptional burst kinetics. Nucleic Acids Research 51: 68-83. DOI: https://dx.doi.org/10.1093/nar/gkac1204, PMID: 36583343

Rodriguez, J., Ren, G., Day, C.R., Zhao, K., Chow, C.C., Larson, D.R. 2019. Intrinsic dynamics of a human gene reveal the basis of expression heterogeneity. Cell 176: 213-226.e218. DOI: https://dx.doi.org/10.1016/j.cell.2018.11.026, PMID: 30554876

Luo, S., Zhang, Z., Wang, Z., Yang, X., Chen, X., Zhou, T., Zhang, J. 2023. Inferring transcriptional bursting kinetics from single-cell snapshot data using a generalized telegraph model. Royal Society Open Science 10: 221057. DOI: https://dx.doi.org/10.1098/rsos.221057, PMID: 37035293

Eling, N., Morgan, M.D., Marioni, J.C. 2019. Challenges in measuring and understanding biological noise. Nature Reviews Genetics 20: 536-548. DOI: https://dx.doi.org/10.1038/s41576-019-0130-6, PMID: 31114032

Tunnacliffe, E., Chubb, J.R. 2020. What is a transcriptional burst? Trends in Genetics 36: 288-297. DOI: https://dx.doi.org/10.1016/j.tig.2020.01.003, PMID: 32035656

Rodriguez, J., Larson, D.R. 2020. Transcription in living Cells: molecular mechanisms of bursting. Annual Review of Biochemistry 89: 189-212. DOI: https://dx.doi.org/10.1146/annurev-biochem-011520-105250, PMID: 32208766

Morgan, M.D., Marioni, J.C. 2018. CpG island composition differences are a source of gene expression noise indicative of promoter responsiveness. Genome Biology 19: 81. DOI: https://dx.doi.org/10.1186/s13059-018-1461-x, PMID: 29945659

Raj, A., van Oudenaarden, A. 2008. Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135: 216-226. DOI: https://dx.doi.org/10.1016/j.cell.2008.09.050, PMID: 18957198

Trzaskoma, P., Jung, S., Pękowska, A., Bohrer, C.H., Wang, X., Naz, F., Dell’Orso, S., Dubois, W.D., Olivera, A., Vartak, S.V. 2024. 3D chromatin architecture, BRD4, and Mediator have distinct roles in regulating genome-wide transcriptional bursting and gene network. Science Advances 10: eadl4893. DOI: https://dx.doi.org/https://www.science.org/doi/10.1126/sciadv.adl4893, PMID:

Browning, A.P., Warne, D.J., Burrage, K., Baker, R.E., Simpson, M.J. 2020. Identifiability analysis for stochastic differential equation models in systems biology. Journal of the Royal Society Interface 17: 20200652. DOI: https://dx.doi.org/10.1098/rsif.2020.0652, PMID: 33323054

Zoller, B., Little, S.C., Gregor, T. 2018. Diverse spatial expression patterns emerge from unified kinetics of transcriptional bursting. Cell 175: 835-847.e825. DOI: https://dx.doi.org/10.1016/j.cell.2018.09.056, PMID: 30340044

Hoppe, C., Bowles, J.R., Minchington, T.G., Sutcliffe, C., Upadhyai, P., Rattray, M., Ashe, H.L. 2020. Modulation of the promoter activation rate dictates the transcriptional response to graded BMP signaling levels in the drosophila embryo. Dev Cell 54: 727-741.e727. DOI: https://dx.doi.org/10.1016/j.devcel.2020.07.007, PMID: 32758422

Ramsköld, D., Hendriks, G.J., Larsson, A.J.M., Mayr, J.V., Ziegenhain, C., Hagemann-Jensen, M., Hartmanis, L., Sandberg, R. 2024. Single-cell new RNA sequencing reveals principles of transcription at the resolution of individual bursts. Nature Cell Biology 26: 1725-1733. DOI: https://dx.doi.org/10.1038/s41556-024-01486-9, PMID: 39198695 Van Kampen, N.G. 1992. Stochastic Processes in Physics and Chemistry. Elsevier.

Gupta, A., Martin-Rufino, J.D., Jones, T.R., Subramanian, V., Qiu, X., Grody, E.I., Bloemendal, A., Weng, C., Niu, S.Y., Min, K.H., Mehta, A., Zhang, K., Siraj, L., Al' Khafaji, A., Sankaran, V.G., Raychaudhuri, S., Cleary, B., Grossman, S., Lander, E.S. 2022. Inferring gene regulation from stochastic transcriptional variation across single cells at steady state. Proceedings of the National Academy of Sciences 119: e2207392119. DOI: https://dx.doi.org/10.1073/pnas.2207392119, PMID: 35969771

Gardiner, C.W., Chaturvedi, S. 1977. The Poisson representation. I. A new technique for chemical master equations. Journal of Statistical Physics 17: 429-468. DOI: https://dx.doi.org/https://doi.org/10.1007/BF01014349, PMID:

Gorin, G., Carilli, M., Chari, T., Pachter, L. 2024. Spectral neural approximations for models of transcriptional dynamics. Biophysical Journal 123: 2892-2901. DOI: https://dx.doi.org/10.1016/j.bpj.2024.04.034, PMID: 38715358

Kuntz, J., Thomas, P., Stan, G.-B., Barahona, M. 2021. Stationary distributions of continuous-time Markov chains: a review of theory and truncation-based approximations. SIAM Review 63: 3-64. DOI:

Zhang, J., Zhou, T. 2019. Computation of stationary distributions in stochastic models of cellular processes with molecular memory. bioRxiv: 521575. DOI: https://dx.doi.org/https://doi.org/10.1101/521575, PMID:

Zhang, J., Nie, Q., Zhou, T. 2016. A moment-convergence method for stochastic analysis of biochemical reaction networks. The Journal of chemical physics 144. DOI:

Sobol, I.M. 1967. On the distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 7: 784-802. DOI: https://dx.doi.org/10.1016/0041-5553(67)90144-9, PMID:

Macosko, E.Z., Basu, A., Satija, R., Nemesh, J., Shekhar, K., Goldman, M., Tirosh, I., Bialas, A.R., Kamitaki, N., Martersteck, E.M., Trombetta, J.J., Weitz, D.A., Sanes, J.R., Shalek, A.K., Regev, A., McCarroll, S.A. 2015. Highly parallel genome-wide expression profiling of individual cells using nanoliter dsroplets. Cell 161: 1202-1214. DOI: https://dx.doi.org/10.1016/j.cell.2015.05.002, PMID: 26000488

Das, S., Suganthan, P.N. 2010. Differential evolution: A survey of the state-of-the-art. IEEE transactions on evolutionary computation 15: 4-31. DOI: https://dx.doi.org/10.1109/TEVC.2010.2059031, PMID:

Ahandani, M.A., Vakil-Baghmisheh, M.-T., Talebi, M. 2014. Hybridizing local search algorithms for global optimization. Computational Optimization and Applications 59: 725-748. DOI: https://dx.doi.org/https://doi.org/10.1007/s10589014-9652-1, PMID:

Baydin, A.G., Pearlmutter, B.A., Radul, A.A., Siskind, J.M. 2018. Automatic differentiation in machine learning: a survey. Journal of machine learning research 18: 1-43. DOI: https://dx.doi.org/https://dl.acm.org/doi/abs/10.5555/3122009.3242010, PMID:

Wiecek, A.J., Cutty, S.J., Kornai, D., Parreno-Centeno, M., Gourmet, L.E., Tagliazucchi, G.M., Jacobson, D.H., Zhang, P., Xiong, L., Bond, G.L., Barr, A.R., Secrier, M. 2023. Genomic hallmarks and therapeutic implications of G0 cell cycle arrest in cancer. Genome Biology 24: 128. DOI: https://dx.doi.org/10.1186/s13059-023-02963-4, PMID: 37221612