Peer review process
Not revised: This Reviewed Preprint includes the authors’ original preprint (without revision), an eLife assessment, public reviews, and a provisional response from the authors.
Read more about eLife’s peer review process.Editors
- Reviewing EditorPeter LathamUniversity College London, London, United Kingdom
- Senior EditorPanayiota PoiraziFORTH Institute of Molecular Biology and Biotechnology, Heraklion, Greece
Joint Public Reviews:
Summary:
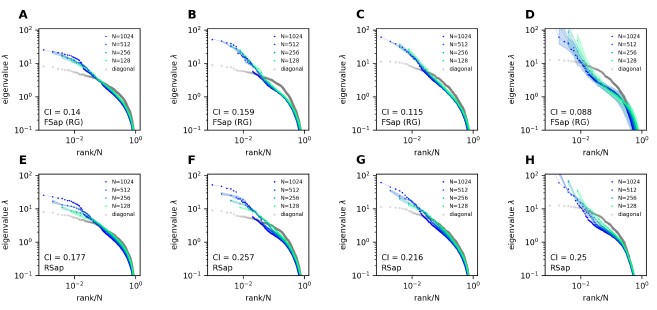
The authors examine the eigenvalue spectrum of the covariance matrix of neural recordings in the whole-brain larval zebrafish during hunting and spontaneous behavior. They find that the spectrum is approximately power law, and, more importantly, exhibits scale-invariance under random subsampling of neurons. This property is not exhibited by conventional models of covariance spectra, motivating the introduction of the Euclidean random matrix model. The authors show that this tractable model captures the scale invariance they observe. They also examine the effects of subsampling based on anatomical location or functional relationships. Finally, they briefly discuss the benefit of neural codes which can be subsampled without significant loss of information.
Strengths:
With large-scale neural recordings becoming increasingly common, neuroscientists are faced with the question: how should we analyze them? To address that question, this paper proposes the Euclidean random matrix model, which embeds neurons randomly in an abstract feature space. This model is analytically tractable and matches two nontrivial features of the covariance matrix: approximate power law scaling, and invariance under subsampling. It thus introduces an important conceptual and technical advance for understanding large-scale simultaneously recorded neural activity.
Weaknesses:
The downside of using summary statistics is that they can be hard to interpret. Often the finding of scale invariance, and approximate power law behavior, points to something interesting. But here caution is in order: for instance, most critical phenomena in neural activity have been explained by relatively simple models that have very little to do with computation (Aitchison et al., PLoS CB 12:e1005110, 2016; Morrell et al., eLife 12, RP89337, 2014). Whether the same holds for the properties found here remains an open question.