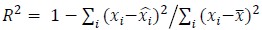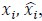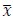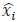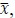Author Response
The following is the authors’ response to the previous reviews.
To the Senior Editor and the Reviewing Editor:
We sincerely appreciate the valuable comments provided by the reviewers, the reviewing editor, and the senior editor. After carefully reviewing and considering the comments, we have addressed the key concerns raised by the reviewers and made appropriate modifications to the article in the revised manuscript.
The main revisions made to the manuscript are as follows:
We have added comparison experiments with TNDM (see Fig. 2 and Fig. S2).
We conducted new synthetic experiments to demonstrate that our conclusions are not a by-product of d-VAE (see Fig. S2 and Fig. S11).
We have provided a detailed explanation of how our proposed criteria, especially the second criterion, can effectively exclude the selection of unsuitable signals.
We have included a semantic overview figure of d-VAE (Fig. S1) and a visualization plot of latent variables (Fig. S13).
We have elaborated on the model details of d-VAE, as well as the hyperparameter selection and experimental settings of other comparison models.
We believe these revisions have significantly improved the clarity and comprehensibility of the manuscript. Thank you for the opportunity to address these important points.
Reviewer #1
Q1: “First, the model in the paper is almost identical to an existing VAE model (TNDM) that makes use of weak supervision with behaviour in the same way [1]. This paper should at least be referenced. If the authors wish they could compare their model to TNDM, which combines a state space model with smoothing similar to LFADS. Given that TNDM achieves very good behaviour reconstructions, it may be on par with this model without the need for a Kalman filter (and hence may achieve better separation of behaviour-related and unrelated dynamics).”
Our model significantly differs from TNDM in several aspects. While TNDM also constrains latent variables to decode behavioral information, it does not impose constraints to maximize behavioral information in the generated relevant signals. The trade-off between the decoding and reconstruction capabilities of generated relevant signals is the most significant contribution of our approach, which is not reflected in TNDM. In addition, the backbone network of signal extraction and the prior distribution of the two models are also different.
It's worth noting that our method does not require a Kalman filter. Kalman filter is used for post hoc assessment of the linear decoding ability of the generated signals. Please note that extracting and evaluating relevant signals are two distinct stages.
Heeding your suggestion, we have incorporated comparison experiments involving TNDM into the revised manuscript. Detailed information on model hyperparameters and training settings can be found in the Methods section in the revised manuscripts.
Thank you for your valuable feedback.
Q2: “Second, in my opinion, the claims regarding identifiability are overstated - this matters as the results depend on this to some extent. Recent work shows that VAEs generally suffer from identifiability problems due to the Gaussian latent space [2]. This paper also hints that weak supervision may help to resolve such issues, so this model as well as TNDM and CEBRA may indeed benefit from this. In addition however, it appears that the relative weight of the KL Divergence in the VAE objective is chosen very small compared to the likelihood (0.1%), so the influence of the prior is weak and the model may essentially learn the average neural trajectories while underestimating the noise in the latent variables. This, in turn, could mean that the model will not autoencode neural activity as well as it should, note that an average R2 in this case will still be high (I could not see how this is actually computed). At the same time, the behaviour R2 will be large simply because the different movement trajectories are very distinct. Since the paper makes claims about the roles of different neurons, it would be important to understand how well their single trial activities are reconstructed, which can perhaps best be investigated by comparing the Poisson likelihood (LFADS is a good baseline model). Taken together, while it certainly makes sense that well-tuned neurons contribute more to behaviour decoding, I worry that the very interesting claim that neurons with weak tuning contain behavioural signals is not well supported.”
We don’t think our distilled signals are average neural trajectories without variability. The quality of reconstructing single trial activities can be observed in Figure 3i and Figure S4.
Neural trajectories in Fig. 3i and Fig. S4 show that our distilled signals are not average neural trajectories. Furthermore, if each trial activity closely matched the average neural trajectory, the Fano Factor (FF) should theoretically approach 0. However, our distilled signals exhibit a notable departure from this expectation, as evident in Figure 3c, d, g, and f.
Regarding the diminished influence of the KL Divergence: Given that the ground truth of latent variable distribution is unknown, even a learned prior distribution might not accurately reflect the true distribution. We found the pronounced impact of the KL divergence would prove detrimental to the decoding and reconstruction performance. As a result, we opt to reduce the weight of the KL divergence term. Even so, KL divergence can still effectively align the distribution of latent variables with the distribution of prior latent variables, as illustrated in Fig. S13. Notably, our goal is extracting behaviorally-relevant signals from given raw signals rather than generating diverse samples from the prior distribution. When aim to separating relevant signals, we recommend reducing the influence of KL divergence.
Regarding comparing the Poisson likelihood: We compared Poisson log-likelihood among different methods (except PSID since their obtained signals have negative values), and the results show that d-VAE outperforms other methods.
Author response image 1.
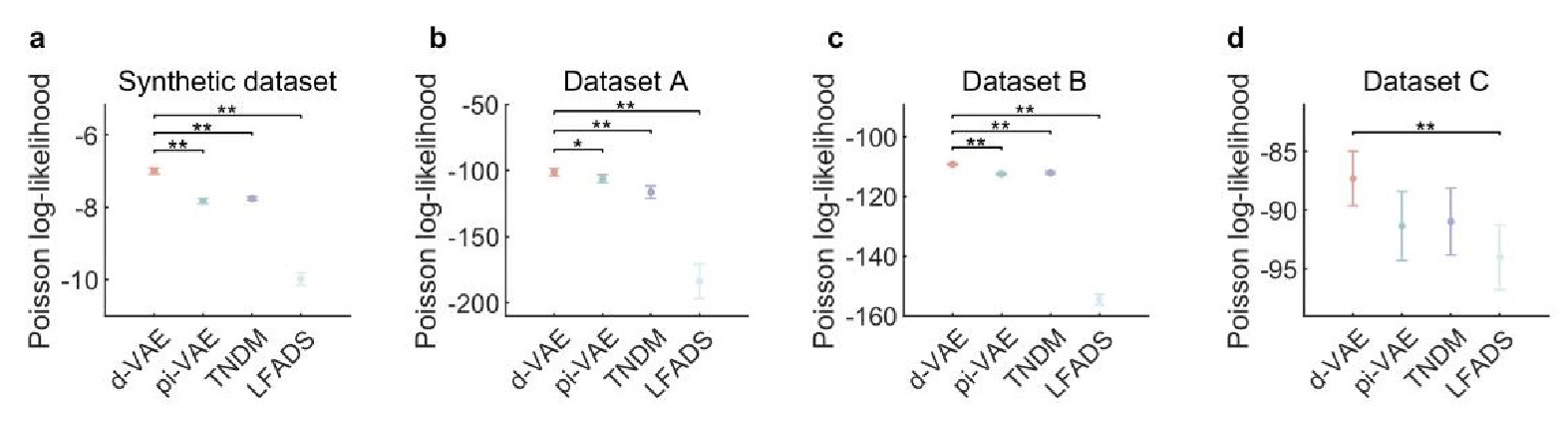
Regarding how R2 is computed: 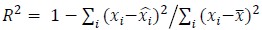 , where
, where 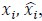 and
and 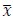 denote ith sample of raw signals, ith sample of distilled relevant signals, and the mean of raw signals. If the distilled signals exactly match the raw signals, the sum of squared error is zero, thus R2=1. If the distilled signals
denote ith sample of raw signals, ith sample of distilled relevant signals, and the mean of raw signals. If the distilled signals exactly match the raw signals, the sum of squared error is zero, thus R2=1. If the distilled signals 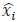 always are equal to
always are equal to 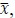 R2=0. If the distilled signals are worse than the mean estimation, R2 is negative, negative R2 is set to zero.
R2=0. If the distilled signals are worse than the mean estimation, R2 is negative, negative R2 is set to zero.
Thank you for your valuable feedback.
Q3: “Third, and relating to this issue, I could not entirely follow the reasoning in the section arguing that behavioural information can be inferred from neurons with weak selectivity, but that it is not linearly decodable. It is right to test if weak supervision signals bleed into the irrelevant subspace, but I could not follow the explanations. Why, for instance, is the ANN decoder on raw data (I assume this is a decoder trained fully supervised) not equal in performance to the revenant distilled signals? Should a well-trained non-linear decoder not simply yield a performance ceiling? Next, if I understand correctly, distilled signals were obtained from the full model. How does a model perform trained only on the weakly tuned neurons? Is it possible that the subspaces obtained with the model are just not optimally aligned for decoding? This could be a result of limited identifiability or model specifics that bias reconstruction to averages (a well-known problem of VAEs). I, therefore, think this analysis should be complemented with tests that do not depend on the model.”
Regarding “Why, for instance, is the ANN decoder on raw data (I assume this is a decoder trained fully supervised) not equal in performance to the relevant distilled signals? Should a well-trained non-linear decoder not simply yield a performance ceiling?”: In fact, the decoding performance of raw signals with ANN is quite close to the ceiling. However, due to the presence of significant irrelevant signals in raw signals, decoding models like deep neural networks are more prone to overfitting when trained on noisy raw signals compared to behaviorally-relevant signals. Consequently, we anticipate that the distilled signals will demonstrate superior decoding generalization. This phenomenon is evident in Fig. 2 and Fig. S1, where the decoding performance of the distilled signals surpasses that of the raw signals, albeit not by a substantial margin.
Regarding “Next, if I understand correctly, distilled signals were obtained from the full model. How does a model perform trained only on the weakly tuned neurons? Is it possible that the subspaces obtained with the model are just not optimally aligned for decoding?”:Distilled signals (involving all neurons) are obtained by d-VAE. Subsequently, we use ANN to evaluate the performance of smaller and larger R2 neurons. Please note that separating and evaluating relevant signals are two distinct stages.
Regarding the reasoning in the section arguing that smaller R2 neurons encode rich information, we would like to provide a detailed explanation:
After extracting relevant signals through d-VAE, we specifically selected neurons characterized by smaller R2 values (Here, R2 signifies the proportion of neuronal activity variance explained by the linear encoding model, calculated using raw signals). Subsequently, we employed both KF and ANN to assess the decoding performance of these neurons. Remarkably, our findings revealed that smaller R2 neurons, previously believed to carry limited behavioral information, indeed encode rich information.
In a subsequent step, we employed d-VAE to exclusively distill the raw signals of these smaller R2 neurons (distinct from the earlier experiment where d-VAE processed signals from all neurons). We then employed KF and ANN to evaluate the distilled smaller R2 neurons. Interestingly, we observed that we could not attain the same richness of information solely through the use of these smaller R2 neurons.
Consequently, we put forth and tested two hypotheses: First, that larger R2 neurons introduce additional signals into the smaller R2 neurons that do not exist in the real smaller R2 neurons. Second, that larger R2 neurons aid in restoring the original appearance of impaired smaller R2 neurons. Our proposed criteria and synthetic experiments substantiate the latter scenario.
Thank you for your valuable feedback.
Q4: “Finally, a more technical issue to note is related to the choice to learn a non-parametric prior instead of using a conventional Gaussian prior. How is this implemented? Is just a single sample taken during a forward pass? I worry this may be insufficient as this would not sample the prior well, and some other strategy such as importance sampling may be required (unless the prior is not relevant as it weakly contributed to the ELBO, in which case this choice seems not very relevant). Generally, it would be useful to see visualisations of the latent variables to see how information about behaviour is represented by the model.”
Regarding "how to implement the prior?": Please refer to Equation 7 in the revised manuscript; we have added detailed descriptions in the revised manuscript.
Regarding "Generally, it would be useful to see visualizations of the latent variables to see how information about behavior is represented by the model.": Note that our focus is not on latent variables but on distilled relevant signals. Nonetheless, at your request, we have added the visualization of latent variables in the revised manuscript. Please see Fig. S13 for details.
Thank you for your valuable feedback.
Recommendations: “A minor point: the word 'distill' in the name of the model may be a little misleading - in machine learning the term refers to the construction of smaller models with the same capabilities.
It should be useful to add a schematic picture of the model to ease comparison with related approaches.”
In the context of our model's functions, it operates as a distillation process, eliminating irrelevant signals and retaining the relevant ones. Although the name of our model may be a little misleading, it faithfully reflects what our model does.
I have added a schematic picture of d-VAE in the revised manuscript. Please see Fig. S1 for details.
Thank you for your valuable feedback.
Reviewer #2
Q1: “Is the apparently increased complexity of encoding vs decoding so unexpected given the entropy, sparseness, and high dimensionality of neural signals (the "encoding") compared to the smoothness and low dimensionality of typical behavioural signals (the "decoding") recorded in neuroscience experiments? This is the title of the paper so it seems to be the main result on which the authors expect readers to focus. ”
We use the term "unexpected" due to the disparity between our findings and the prior understanding concerning neural encoding and decoding. For neural encoding, as we said in the Introduction, in previous studies, weakly-tuned neurons are considered useless, and smaller variance PCs are considered noise, but we found they encode rich behavioral information. For neural decoding, the nonlinear decoding performance of raw signals is significantly superior to linear decoding. However, after eliminating the interference of irrelevant signals, we found the linear decoding performance is comparable to nonlinear decoding. Rooted in these findings, which counter previous thought, we employ the term "unexpected" to characterize our observations.
Thank you for your valuable feedback.
Q2: “I take issue with the premise that signals in the brain are "irrelevant" simply because they do not correlate with a fixed temporal lag with a particular behavioural feature hand-chosen by the experimenter. As an example, the presence of a reward signal in motor cortex [1] after the movement is likely to be of little use from the perspective of predicting kinematics from time-bin to time-bin using a fixed model across trials (the apparent definition of "relevant" for behaviour here), but an entire sub-field of neuroscience is dedicated to understanding the impact of these reward-related signals on future behaviour. Is there method sophisticated enough to see the behavioural "relevance" of this brief, transient, post-movement signal? This may just be an issue of semantics, and perhaps I read too much into the choice of words here. Perhaps the authors truly treat "irrelevant" and "without a fixed temporal correlation" as synonymous phrases and the issue is easily resolved with a clarifying parenthetical the first time the word "irrelevant" is used. But I remain troubled by some claims in the paper which lead me to believe that they read more deeply into the "irrelevancy" of these components.”
In this paper, we employ terms like ‘behaviorally-relevant’ and ‘behaviorally-irrelevant’ only regarding behavioral variables of interest measured within a given task, such as arm kinematics during a motor control task. A similar definition can be found in the PSID[1].
Thank you for your valuable feedback.
[1] Sani, Omid G., et al. "Modeling behaviorally relevant neural dynamics enabled by preferential subspace identification." Nature Neuroscience 24.1 (2021): 140-149.
Q3: “The authors claim the "irrelevant" responses underpin an unprecedented neuronal redundancy and reveal that movement behaviors are distributed in a higher-dimensional neural space than previously thought." Perhaps I just missed the logic, but I fail to see the evidence for this. The neural space is a fixed dimensionality based on the number of neurons. A more sparse and nonlinear distribution across this set of neurons may mean that linear methods such as PCA are not effective ways to approximate the dimensionality. But ultimately the behaviourally relevant signals seem quite low-dimensional in this paper even if they show some nonlinearity may help.”
The evidence for the “useless” responses underpin an unprecedented neuronal redundancy is shown in Fig. 5a, d and Fig. S9a. Specifically, the sum of the decoding performance of smaller R2 neurons and larger R2 neurons is significantly greater than that of all neurons for relevant signals (red bar), demonstrating that movement parameters are encoded very redundantly in neuronal population. In contrast, we can not find this degree of neural redundancy in raw signals (purple bar).
The evidence for the “useless” responses reveal that movement behaviors are distributed in a higher-dimensional neural space than previously thought is shown in the left plot (involving KF decoding) of Fig. 6c, f and Fig. S9f. Specifically, the improvement of KF using secondary signals is significantly higher than using raw signals composed of the same number of dimensions as the secondary signals. These results demonstrate that these dimensions, spanning roughly from ten to thirty, encode much information, suggesting that behavioral information exists in a higher-dimensional subspace than anticipated from raw signals.
Thank you for your valuable feedback.
Q5: “there is an apparent logical fallacy that begins in the abstract and persists in the paper: "Surprisingly, when incorporating often-ignored neural dimensions, behavioral information can be decoded linearly as accurately as nonlinear decoding, suggesting linear readout is performed in motor cortex." Don't get me wrong: the equivalency of linear and nonlinear decoding approaches on this dataset is interesting, and useful for neuroscientists in a practical sense. However, the paper expends much effort trying to make fundamental scientific claims that do not feel very strongly supported. This reviewer fails to see what we can learn about a set of neurons in the brain which are presumed to "read out" from motor cortex. These neurons will not have access to the data analyzed here. That a linear model can be conceived by an experimenter does not imply that the brain must use a linear model. The claim may be true, and it may well be that a linear readout is implemented in the brain. Other work [2,3] has shown that linear readouts of nonlinear neural activity patterns can explain some behavioural features. The claim in this paper, however, is not given enough”
Due to the limitations of current observational methods and our incomplete understanding of brain mechanisms, it is indeed challenging to ascertain the specific data the brain acquires to generate behavior and whether it employs a linear readout. Conventionally, the neural data recorded in the motor cortex do encode movement behaviors and can be used to analyze neural encoding and decoding. Based on these data, we found that the linear decoder KF achieves comparable performance to that of the nonlinear decoder ANN on distilled relevant signals. This finding has undergone validation across three widely used datasets, providing substantial evidence. Furthermore, we conducted experiments on synthetic data to show that this conclusion is not a by-product of our model. In the revised manuscript, we added a more detailed description of this conclusion.
Thank you for your valuable feedback.
Q6: “Relatedly, I would like to note that the exercise of arbitrarily dividing a continuous distribution of a statistic (the "R2") based on an arbitrary threshold is a conceptually flawed exercise. The authors read too much into the fact that neurons which have a low R2 w.r.t. PDs have behavioural information w.r.t. other methods. To this reviewer, it speaks more about the irrelevance, so to speak, of the preferred direction metric than anything fundamental about the brain.”
We chose the R2 threshold in accordance with the guidelines provided in reference [1]. It's worth mentioning that this threshold does not exert any significant influence on the overall conclusions.
Thank you for your valuable feedback.
[1] Inoue, Y., Mao, H., Suway, S.B., Orellana, J. and Schwartz, A.B., 2018. Decoding arm speed during reaching. Nature communications, 9(1), p.5243.
Q7: “I am afraid I may be missing something, as I did not understand the fano factor analysis of Figure 3. In a sense the behaviourally relevant signals must have lower FF given they are in effect tied to the temporally smooth (and consistent on average across trials) behavioural covariates. The point of the original Churchland paper was to show that producing a behaviour squelches the variance; naturally these must appear in the behaviourally relevant components. A control distribution or reference of some type would possibly help here.”
We agree that including reference signals could provide more context. The Churchland paper said stimulus onset can lead to a reduction in neural variability. However, our experiment focuses specifically on the reaching process, and thus, we don't have comparative experiments involving different types of signals.
Thank you for your valuable feedback.
Q8: “The authors compare the method to LFADS. While this is a reasonable benchmark as a prominent method in the field, LFADS does not attempt to solve the same problem as d-VAE. A better and much more fair comparison would be TNDM [4], an extension of LFADS which is designed to identify behaviourally relevant dimensions.”
We have added the comparison experiments with TNDM in the revised manuscript (see Fig. 2 and Fig. S2). The details of model hyperparameters and training settings can be found in the Methods section in the revised manuscripts.
Thank you for your valuable feedback.
Reviewer #3
Q1.1: “TNDM: LFADS is not the best baseline for comparison. The authors should have compared with TNDM (Hurwitz et al. 2021), which is an extension of LFADS that (unlike LFADS) actually attempts to extract behaviorally relevant factors by adding a behavior term to the loss. The code for TNDM is also available on Github. LFADS is not even supervised by behavior and does not aim to address the problem that d-VAE aims to address, so it is not the most appropriate comparison. ”
We have added the comparison experiments with TNDM in the revised manuscript (see Fig. 2 and Fig. S2). The details of model hyperparameters and training settings can be found in the Methods section in the revised manuscripts.
Thank you for your valuable feedback.
Q1.2: “LFADS: LFADS is a sequential autoencoder that processes sections of data (e.g. trials). No explanation is given in Methods for how the data was passed to LFADS. Was the moving averaged smoothed data passed to LFADS or the raw spiking data (at what bin size)? Was a gaussian loss used or a poisson loss? What are the trial lengths used in each dataset, from which part of trials? For dataset C that has back-to-back reaches, was data chopped into segments? How long were these segments? Were the edges of segments overlapped and averaged as in (Keshtkaran et al. 2022) to avoid noisy segment edges or not? These are all critical details that are not explained. The same details would also be needed for a TNDM comparison (comment 1.1) since it has largely the same architecture as LFADS.
It is also critical to briefly discuss these fundamental differences between the inputs of methods in the main text. LFADS uses a segment of data whereas VAE methods just use one sample at a time. What does this imply in the results? I guess as long as VAEs outperform LFADS it is ok, but if LFADS outperforms VAEs in a given metric, could it be because it received more data as input (a whole segment)? Why was the factor dimension set to 50? I presume it was to match the latent dimension of the VAE methods, but is the LFADS factor dimension the correct match for that to make things comparable?
I am also surprised by the results. How do the authors justify LFADS having lower neural similarity (fig 2d) than VAE methods that operate on single time steps? LFADS is not supervised by behavior, so of course I don't expect it to necessarily outperform methods on behavior decoding. But all LFADS aims to do is to reconstruct the neural data so at least in this metric it should be able to outperform VAEs that just operate on single time steps? Is it because LFADS smooths the data too much? This is important to discuss and show examples of. These are all critical nuances that need to be discussed to validate the results and interpret them.”
Regarding “Was the moving averaged smoothed data passed to LFADS or the raw spiking data (at what bin size)? Was a gaussian loss used or a poisson loss?”: The data used by all models was applied to the same preprocessing procedure. That is, using moving averaged smoothed data with three bins, where the bin size is 100ms. For all models except PSID, we used a Poisson loss.
Regrading “What are the trial lengths used in each dataset, from which part of trials? For dataset C that has back-to-back reaches, was data chopped into segments? How long were these segments? Were the edges of segments overlapped and averaged as in (Keshtkaran et al. 2022) to avoid noisy segment edges or not?”:
For datasets A and B, a trial length of eighteen is set. Trials with lengths below the threshold are zero-padded, while trials exceeding the threshold are truncated to the threshold length from their starting point. In dataset A, there are several trials with lengths considerably longer than that of most trials. We found that padding all trials with zeros to reach the maximum length (32) led to poor performance. Consequently, we chose a trial length of eighteen, effectively encompassing the durations of most trials and leading to the removal of approximately 9% of samples. For dataset B (center-out), the trial lengths are relatively consistent with small variation, and the maximum length across all trials is eighteen. For dataset C, we set the trial length as ten because we observed the video of this paradigm and found that the time for completing a single trial was approximately one second. The segments are not overlapped.
Regarding “Why was the factor dimension set to 50? I presume it was to match the latent dimension of the VAE methods, but is the LFADS factor dimension the correct match for that to make things comparable?”: We performed a grid search for latent dimensions in {10,20,50} and found 50 is the best.
Regarding “I am also surprised by the results. How do the authors justify LFADS having lower neural similarity (fig 2d) than VAE methods that operate on single time steps? LFADS is not supervised by behavior, so of course I don't expect it to necessarily outperform methods on behavior decoding. But all LFADS aims to do is to reconstruct the neural data so at least in this metric it should be able to outperform VAEs that just operate on single time steps? Is it because LFADS smooths the data too much?”: As you pointed out, we found that LFADS tends to produce excessively smooth and consistent data, which can lead to a reduction in neural similarity.
Thank you for your valuable feedback.
Q1.3: “PSID: PSID is linear and uses past input samples to predict the next sample in the output. Again, some setup choices are not well justified, and some details are left out in the 1-line explanation given in Methods.
Why was a latent dimension of 6 chosen? Is this the behaviorally relevant latent dimension or the total latent dimension (for the use case here it would make sense to set all latent states to be behaviorally relevant)? Why was a horizon hyperparameter of 3 chosen? First, it is important to mention fundamental parameters such as latent dimension for each method in the main text (not just in methods) to make the results interpretable. Second, these hyperparameters should be chosen with a grid search in each dataset (within the training data, based on performance on the validation part of the training data), just as the authors do for their method (line 779). Given that PSID isn't a deep learning method, doing a thorough grid search in each fold should be quite feasible. It is important that high values for latent dimension and a wider range of other hyperparmeters are included in the search, because based on how well the residuals (x_i) for this method are shown predict behavior in Fig 2, the method seems to not have been used appropriately. I would expect ANN to improve decoding for PSID versus its KF decoding since PSID is fully linear, but I don't expect KF to be able to decode so well using the residuals of PSID if the method is used correctly to extract all behaviorally relevant information from neural data. The low neural reconstruction in Fid 2d could also partly be due to using too small of a latent dimension.
Again, another import nuance is the input to this method and how differs with the input to VAE methods. The learned PSID model is a filter that operates on all past samples of input to predict the output in the "next" time step. To enable a fair comparison with VAE methods, the authors should make sure that the last sample "seen" by PSID is the same as then input sample seen by VAE methods. This is absolutely critical given how large the time steps are, otherwise PSID might underperform simply because it stopped receiving input 300ms earlier than the input received by VAE methods. To fix this, I think the authors can just shift the training and testing neural time series of PSID by 1 sample into the past (relative to the behavior), so that PSID's input would include the input of VAE methods. Otherwise, VAEs outperforming PSID is confounded by PSID's input not including the time step that was provided to VAE.”
Thanks for your suggestions for letting PSID see the current neural observations. We did it per your suggestions and then performed a grid search for the hyperparameters for PSID. Specifically, we performed a grid search for the horizon hyperparameter in {2,3,4,5,6,7}. Since the relevant latent dimension should be lower than the horizon times the dimension of behavior variables (two-dimensional velocity in this paper) and increasing the dimension will reach performance saturation, we directly set the relevant latent dimensions as the maximum. The horizon number of datasets A, B, C, and synthetic datasets is 7, 6, 6 and 5, respectively.
And thus the latent dimension of datasets A, B, and C and the synthetic dataset is 14, 12, 12 and 10, respectively.
Our experiments show that KF can decode information from irrelevant signals obtained by PSID. Although PSID extracts the linear part of raw signals, KF can still use the linear part of the residuals for decoding. The low reconstruction performance of PSID may be because the relationship between latent variables and neural signals is linear, and the relationship between latent variables and behaviors is also linear; this is equivalent to the linear relationship between behaviors and neural signals, and linear models can only explain a small fraction of neural signals.
Thank you for your valuable feedback.
Q1.4: “CEBRA: results for CEBRA are incomplete. Similarity to raw signals is not shown. Decoding of behaviorally irrelevant residuals for CEBRA is not shown. Per Fig. S2, CEBRA does better or similar ANN decoding in datasets A and C, is only slightly worse in Dataset B, so it is important to show the other key metrics otherwise it is unclear whether d-VAE has some tangible advantage over CEBRA in those 2 datasets or if they are similar in every metric. Finally, it would be better if the authors show the results for CEBRA on Fig. 2, just as is done for other methods because otherwise it is hard to compare all methods.”
CEBRA is a non-generative model, this model cannot generate behaviorally-relevant signals. Therefore, we only compared the decoding performance of latent embeddings of CEBRA and signals of d-VAE.
Thank you for your valuable feedback.
Q2: “Given the fact that d-VAE infers the latent (z) based on the population activity (x), claims about properties of the inferred behaviorally relevant signals (x_r) that attribute properties to individual neurons are confounded.
The authors contrast their approach to population level approaches in that it infers behaviorally relevant signals for individual neurons. However, d-VAE is also a population method as it aggregates population information to infer the latent (z), from which behaviorally relevant part of the activity of each neuron (x_r) is inferred. The authors note this population level aggregation of information as a benefit of d-VAE, but only acknowledge it as a confound briefly in the context of one of their analyses (line 340): "The first is that the larger R2 neurons leak their information to the smaller R2 neurons, causing them contain too much behavioral information". They go on to dismiss this confounding possibility by showing that the inferred behaviorally relevant signal of each neuron is often most similar to its own raw signals (line 348-352) compared with all other neurons. They also provide another argument specific to that result section (i.e., residuals are not very behavior predictive), which is not general so I won't discuss it in depth here. These arguments however do not change the basic fact that d-VAE aggregates information from other neurons when extracting the behaviorally relevant activity of any given neuron, something that the authors note as a benefit of d-VAE in many instances. The fact that d-VAE aggregates population level info to give the inferred behaviorally relevant signal for each neuron confounds several key conclusions. For example, because information is aggregated across neurons, when trial to trial variability looks smoother after applying d-VAE (Fig 3i), or reveals better cosine tuning (Fig 3b), or when neurons that were not very predictive of behavior become more predictive of behavior (Fig 5), one cannot really attribute the new smoother single trial activity or the improved decoding to the same single neurons; rather these new signals/performances include information from other neurons. Unless the connections of the encoder network (z=f(x)) is zero for all other neurons, one cannot claim that the inferred rates for the neuron are truly solely associated with that neuron. I believe this a fundamental property of a population level VAE, and simply makes the architecture unsuitable for claims regarding inherent properties of single neurons. This confound is partly why the first claim in the abstract are not supported by data: observing that neurons that don't predict behavior very well would predict it much better after applying d-VAE does not prove that these neurons themselves "encode rich[er] behavioral information in complex nonlinear ways" (i.e., the first conclusion highlighted in the abstract) because information was also aggregated from other neurons. The other reason why this claim is not supported by data is the characterization of the encoding for smaller R2 neurons as "complex nonlinear", which the method is not well equipped to tease apart from linear mappings as I explain in my comment 3.”
We acknowledge that we cannot obtain the exact single neuronal activity that does not contain any information from other neurons. However, we believe our model can extract accurate approximation signals of the ground truth relevant signals. These signals preserve the inherent properties of single neuronal activity to some extent and can be used for analysis at the single-neuron level.
We believe d-VAE is a reasonable approach to extract effective relevant signals that preserve inherent properties of single neuronal activity for four key reasons:
d-VAE is a latent variable model that adheres to the neural population doctrine. The neural population doctrine posits that information is encoded within interconnected groups of neurons, with the existence of latent variables (neural modes) responsible for generating observable neuronal activity [1, 2]. If we can perfectly obtain the true generative model from latent variables to neuronal activity, then we can generate the activity of each neuron from hidden variables without containing any information from other neurons. However, without a complete understanding of the brain’s encoding strategies (or generative model), we can only get the approximation signals of the ground truth signals.
After the generative model is established, we need to infer the parameters of the generative model and the distribution of latent variables. During the inference process, inference algorithms such as variational inference or EM algorithms will be used. Generally, the obtained latent variables are also approximations of the real latent variables. When inferring the latent variables, it is inevitable to aggregation the information of the neural population, and latent variables are derived through weighted combinations of neuronal populations [3].
This inference process is consistent with that of d-VAE (or VAE-based models).
- Latent variables are derived from raw neural signals and used to explain raw neural signals. Considering the unknown ground truth of latent variables and behaviorally-relevant signals, it becomes evident that the only reliable reference at the signal level is the raw signals. A crucial criterion for evaluating the reliability of latent variable models (including latent variables and generated relevant signals) is their capability to effectively explain the raw signals [3]. Consequently, we firmly maintain the belief that if the generated signals closely resemble the raw signals to the greatest extent possible, in accordance with an equivalence principle, we can claim that these obtained signals faithfully retain the inherent properties of single neurons. d-VAE explicitly constrains the generated signal to closely resemble the raw signals. These results demonstrate that d-VAE can extract effective relevant signals that preserve inherent properties of single neuronal activity.
Based on the above reasons, we hold that generating single neuronal activities with the VAE framework is a reasonable approach. The remaining question is whether our model can obtain accurate relevant signals in the absence of ground truth. To our knowledge, in cases where the ground truth of relevant signals is unknown, there are typically two approaches to verifying the reliability of extracted signals:
Conducting synthetic experiments where the ground truth is known.
Validation based on expert knowledge (Three criteria were proposed in this paper). Both our extracted signals and key conclusions have been validated using these two approaches.
Next, we will provide a detailed response to the concerns regarding our first key conclusion that smaller R2 neurons encode rich information.
We acknowledge that larger R2 neurons play a role in aiding the reconstruction of signals in smaller R2 neurons through their neural activity. However, considering that neurons are correlated rather than independent entities, we maintain the belief that larger R2 neurons assist damaged smaller R2 neurons in restoring their original appearance. Taking image denoising as an example, when restoring noisy pixels to their original appearance, relying solely on the noisy pixels themselves is often impractical. Assistance from their correlated, clean neighboring pixels becomes necessary.
The case we need to be cautious of is that the larger R2 neurons introduce additional signals (m) that contain substantial information to smaller R2 neurons, which they do not inherently possess. We believe this case does not hold for two reasons. Firstly, logically, adding extra signals decreases the reconstruction performance, and the information carried by these additional signals is redundant for larger R2 neurons, thus they do not introduce new information that can enhance the decoding performance of the neural population. Therefore, it seems unlikely and unnecessary for neural networks to engage in such counterproductive actions. Secondly, even if this occurs, our second criterion can effectively exclude the selection of these signals. To clarify, if we assume that x, y, and z denote the raw, relevant, and irrelevant signals of smaller R2 neurons, with x=y+z, and the extracted relevant signals become y+m, the irrelevant signals become z-m in this case. Consequently, the irrelevant signals contain a significant amount of information. It's essential to emphasize that this criterion holds significant importance in excluding undesirable signals.
Furthermore, we conducted a synthetic experiment to show that d-VAE can indeed restore the damaged information of smaller R2 neurons with the help of larger R2 neurons, and the restored neuronal activities are more similar to ground truth compared to damaged raw signals. Please see Fig. S11a,b for details.
Thank you for your valuable feedback.
[1] Saxena, S. and Cunningham, J.P., 2019. Towards the neural population doctrine. Current opinion in neurobiology, 55, pp.103-111.
[2] Gallego, J.A., Perich, M.G., Miller, L.E. and Solla, S.A., 2017. Neural manifolds for the control of movement. Neuron, 94(5), pp.978-984.
[3] Cunningham, J.P. and Yu, B.M., 2014. Dimensionality reduction for large-scale neural recordings. Nature neuroscience, 17(11), pp.1500-1509.
Q3: “Given the nonlinear architecture of the VAE, claims about the linearity or nonlinearity of cortical readout are confounded and not supported by the results.
The inference of behaviorally relevant signals from raw signals is a nonlinear operation, that is x_r=g(f(x)) is nonlinear function of x. So even when a linear KF is used to decode behavior from the inferred behaviorally relevant signals, the overall decoding from raw signals to predicted behavior (i.e., KF applied to g(f(x))) is nonlinear. Thus, the result that decoding of behavior from inferred behaviorally relevant signals (x_r) using a linear KF and a nonlinear ANN reaches similar accuracy (Fig 2), does not suggest that a "linear readout is performed in the motor cortex", as the authors claim (line 471). The authors acknowledge this confound (line 472) but fail to address it adequately. They perform a simulation analysis where the decoding gap between KF and ANN remains unchanged even when d-VAE is used to infer behaviorally relevant signals in the simulation. However, this analysis is not enough for "eliminating the doubt" regarding the confound. I'm sure the authors can also design simulations where the opposite happens and just like in the data, d-VAE can improve linear decoding to match ANN decoding. An adequate way to address this concern would be to use a fully linear version of the autoencoder where the f(.) and g(.) mappings are fully linear. They can simply replace these two networks in their model with affine mappings, redo the modeling and see if the model still helps the KF decoding accuracy reach that of the ANN decoding. In such a scenario, because the overall KF decoding from original raw signals to predicted behavior (linear d-VAE + KF) is linear, then they could move toward the claim that the readout is linear. Even though such a conclusion would still be impaired by the nonlinear reference (d-VAE + ANN decoding) because the achieved nonlinear decoding performance could always be limited by network design and fitting issues. Overall, the third conclusion highlighted in the abstract is a very difficult claim to prove and is unfortunately not supported by the results.”
We aim to explore the readout mechanism of behaviorally-relevant signals, rather than raw signals. Theoretically, the process of removing irrelevant signals should not be considered part of the inherent decoding mechanisms of the relevant signals. Assuming that the relevant signals we extracted are accurate, the conclusion of linear readout is established. On the synthetic data where the ground truth is known, our distilled signals show a significant improvement in neural similarity to the ground truth when compared to raw signals (refer to Fig. S2l). This observation demonstrates that our distilled signals are accurate approximations of the ground truth. Furthermore, on the three widely-used real datasets, our distilled signals meet the stringent criteria we have proposed (see Fig. 2), also providing strong evidence for their accuracy.
Regarding the assertion that we could create simulations in which d-VAE can make signals that are inherently nonlinearly decodable into linearly decodable ones: In reality, we cannot achieve this, as the second criterion can rule out the selection of such signals. Specifically,z=x+y=n^2+y, where z, x, y, and n denote raw signals, relevant signals, irrelevant signals and latent variables. If the relevant signals obtained by d-VAE are n, then these signals can be linear decoded accurately. However, the corresponding irrelevant signals are n^2-n+z; thus, irrelevant signals will have much information, and these extracted relevant signals will not be selected. Furthermore, our synthetic experiments offer additional evidence supporting the conclusion that d-VAE does not make inherently nonlinearly decodable signals become linearly decodable ones. As depicted in Fig. S11c, there exists a significant performance gap between KF and ANN when decoding the ground truth signals of smaller R2 neurons. KF exhibits notably low performance, leaving substantial room for compensation by d-VAE. However, following processing by d-VAE, KF's performance of distilled signals fails to surpass its already low ground truth performance and remains significantly inferior to ANN's performance. These results collectively confirm that our approach does not convert signals that are inherently nonlinearly decodable into linearly decodable ones, and the conclusion of linear readout is not a by-product by d-VAE.
Regarding the suggestion of using linear d-VAE + KF, as discussed in the Discussion section, removing the irrelevant signals requires a nonlinear operation, and linear d-VAE can not effectively separate relevant and irrelevant signals.
Thank you for your valuable feedback.
Q4: “The authors interpret several results as indications that "behavioral information is distributed in a higher-dimensional subspace than expected from raw signals", which is the second main conclusion highlighted in the abstract. However, several of these arguments do not convincingly support that conclusion.
4.1) The authors observe that behaviorally relevant signals for neurons with small principal components (referred to as secondary) have worse decoding with KF but better decoding with ANN (Fig. 6b,e), which also outperforms ANN decoding from raw signals. This observation is taken to suggest that these secondary behaviorally relevant signals encode behavior information in highly nonlinear ways and in a higher dimensions neural space than expected (lines 424 and 428). These conclusions however are confounded by the fact that A) d-VAE uses nonlinear encoding, so one cannot conclude from ANN outperforming KF that behavior is encoded nonlinearly in the motor cortex (see comment 3 above), and B) d-VAE aggregates information across the population so one cannot conclude that these secondary neurons themselves had as much behavior information (see comment 2 above).
4.2) The authors observe that the addition of the inferred behaviorally relevant signals for neurons with small principal components (referred to as secondary) improves the decoding of KF more than it improves the decoding of ANN (red curves in Fig 6c,f). This again is interpreted similarly as in 4.1, and is confounded for similar reasons (line 439): "These results demonstrate that irrelevant signals conceal the smaller variance PC signals, making their encoded information difficult to be linearly decoded, suggesting that behavioral information exists in a higher-dimensional subspace than anticipated from raw signals". This is confounded by because of the two reasons explained in 4.1. To conclude nonlinear encoding based on the difference in KF and ANN decoding, the authors would need to make the encoding/decoding in their VAE linear to have a fully linear decoder on one hand (with linear d-VAE + KF) and a nonlinear decoder on the other hand (with linear d-VAE + ANN), as explained in comment 3.
4.3) From S Fig 8, where the authors compare cumulative variance of PCs for raw and inferred behaviorally relevant signals, the authors conclude that (line 554): "behaviorally-irrelevant signals can cause an overestimation of the neural dimensionality of behaviorally-relevant responses (Supplementary Fig. S8)." However, this analysis does not really say anything about overestimation of "behaviorally relevant" neural dimensionality since the comparison is done with the dimensionality of "raw" signals. The next sentence is ok though: "These findings highlight the need to filter out relevant signals when estimating the neural dimensionality.", because they use the phrase "neural dimensionality" not "neural dimensionality of behaviorally-relevant responses".”
Questions 4.1 and 4.2 are a combination of Q2 and Q3. Please refer to our responses to Q2 and Q3.
Regarding question 4.3 about “behaviorally-irrelevant signals can cause an overestimation of the neural dimensionality of behaviorally-relevant responses”: Previous studies usually used raw signals to estimate the neural dimensionality of specific behaviors. We mean that using raw signals, which include many irrelevant signals, will cause an overestimation of the neural dimensionality. We have modified this sentence in the revised manuscripts.
Thank you for your valuable feedback.
Q5: “Imprecise use of language in many places leads to inaccurate statements. I will list some of these statements”
5.1) In the abstract: "One solution is to accurately separate behaviorally-relevant and irrelevant signals, but this approach remains elusive due to the unknown ground truth of behaviorally-relevant signals". This statement is not accurate because it implies no prior work does this. The authors should make their statement more specific and also refer to some goal that existing linear (e.g., PSID) and nonlinear (e.g., TNDM) methods for extracting behaviorally relevant signals fail to achieve.
5.2) In the abstract: "we found neural responses previously considered useless encode rich behavioral information" => what does "useless" mean operationally? Low behavior tuning? More precise use of language would be better.
5.3) "... recent studies (Glaser 58 et al., 2020; Willsey et al., 2022) demonstrate nonlinear readout outperforms linear readout." => do these studies show that nonlinear "readout" outperforms linear "readout", or just that nonlinear models outperform linear models?
5.4) Line 144: "The first criterion is that the decoding performance of the behaviorally-relevant signals (red bar, Fig.1) should surpass that of raw signals (the red dotted line, Fig.1).". Do the authors mean linear decoding here or decoding in general? If the latter, how can something extracted from neural surpass decoding of neural data, when the extraction itself can be thought of as part of decoding? The operational definition for this "decoding performance" should be clarified.
5.5) Line 311: "we found that the dimensionality of primary subspace of raw signals (26, 64, and 45 for datasets A, B, and C) is significantly higher than that of behaviorally-relevant signals (7, 13, and 9), indicating that behaviorally-irrelevant signals lead to an overestimation of the neural dimensionality of behaviorally-relevant signals." => here the dimensionality of the total PC space (i.e., primary subspace of raw signals) is being compared with that of inferred behaviorally-relevant signals, so the former being higher does not indicate that neural dimensionality of behaviorally-relevant signals was overestimated. The former is simply not behavioral so this conclusion is not accurate.
5.6) Section "Distilled behaviorally-relevant signals uncover that smaller R2 neurons encode rich behavioral information in complex nonlinear ways". Based on what kind of R2 are the neurons grouped? Behavior decoding R2 from raw signals? Using what mapping? Using KF? If KF is used, the result that small R2 neurons benefit a lot from d-VAE could be somewhat expected, given the nonlinearity of d-VAE: because only ANN would have the capacity to unwrap the nonlinear encoding of d-VAE as needed. If decoding performance that is used to group neurons is based on data, regression to the mean could also partially explain the result: the neurons with worst raw decoding are most likely to benefit from a change in decoder, than neurons that already had good decoding. In any case, the R2 used to partition and sort neurons should be more clearly stated and reminded throughout the text and I Fig 3.
5.7) Line 346 "...it is impossible for our model to add the activity of larger R2 neurons to that of smaller R2 neurons" => Is it really impossible? The optimization can definitely add small-scale copies of behaviorally relevant information to all neurons with minimal increase in the overall optimization loss, so this statement seems inaccurate.
5.8) Line 490: "we found that linear decoders can achieve comparable performance to that of nonlinear decoders, providing compelling evidence for the presence of linear readout in the motor cortex." => inaccurate because no d-VAE decoding is really linear, as explained in comment 3 above.
5.9) Line 578: ". However, our results challenge this idea by showing that signals composed of smaller variance PCs nonlinearly encode a significant amount of behavioral information." => inaccurate as results are confounded by nonlinearity of d-VAE as explained in comment 3 above.
5.10) Line 592: "By filtering out behaviorally-irrelevant signals, our study found that accurate decoding performance can be achieved through linear readout, suggesting that the motor cortex may perform linear readout to generate movement behaviors." => inaccurate because it us confounded by the nonlinearity of d-VAE as explained in comment 3 above.”
Regarding “5.1) In the abstract: "One solution is to accurately separate behaviorally-relevant and irrelevant signals, but this approach remains elusive due to the unknown ground truth of behaviorally-relevant signals". This statement is not accurate because it implies no prior work does this. The authors should make their statement more specific and also refer to some goal that existing linear (e.g., PSID) and nonlinear (e.g., TNDM) methods for extracting behaviorally relevant signals fail to achieve”:
We believe our statement is accurate. Our primary objective is to extract accurate behaviorally-relevant signals that closely approximate the ground truth relevant signals. To achieve this, we strike a balance between the reconstruction and decoding performance of the generated signals, aiming to effectively capture the relevant signals. This crucial aspect of our approach sets it apart from other methods. In contrast, other methods tend to emphasize the extraction of valuable latent neural dynamics. We have provided elaboration on the distinctions between d-VAE and other approaches in the Introduction and Discussion sections.
Thank you for your valuable feedback.
Regarding “5.2) In the abstract: "we found neural responses previously considered useless encode rich behavioral information" => what does "useless" mean operationally? Low behavior tuning? More precise use of language would be better.”:
In the analysis of neural signals, smaller variance PC signals are typically seen as noise and are often discarded. Similarly, smaller R2 neurons are commonly thought to be dominated by noise and are not further analyzed. Given these considerations, we believe that the term "considered useless" is appropriate in this context. Thank you for your valuable feedback.
Regarding “5.3) "... recent studies (Glaser 58 et al., 2020; Willsey et al., 2022) demonstrate nonlinear readout outperforms linear readout." => do these studies show that nonlinear "readout" outperforms linear "readout", or just that nonlinear models outperform linear models?”:
In this paper, we consider the two statements to be equivalent. Thank you for your valuable feedback.
Regarding “5.4) Line 144: "The first criterion is that the decoding performance of the behaviorally-relevant signals (red bar, Fig.1) should surpass that of raw signals (the red dotted line, Fig.1).". Do the authors mean linear decoding here or decoding in general? If the latter, how can something extracted from neural surpass decoding of neural data, when the extraction itself can be thought of as part of decoding? The operational definition for this "decoding performance" should be clarified.”:
We mean the latter, as we said in the section “Framework for defining, extracting, and separating behaviorally-relevant signals”, since raw signals contain too many behaviorally-irrelevant signals, deep neural networks are more prone to overfit raw signals than relevant signals. Therefore the decoding performance of relevant signals should surpass that of raw signals. Thank you for your valuable feedback.
Regarding “5.5) Line 311: "we found that the dimensionality of primary subspace of raw signals (26, 64, and 45 for datasets A, B, and C) is significantly higher than that of behaviorally-relevant signals (7, 13, and 9), indicating that behaviorally-irrelevant signals lead to an overestimation of the neural dimensionality of behaviorally-relevant signals." => here the dimensionality of the total PC space (i.e., primary subspace of raw signals) is being compared with that of inferred behaviorally-relevant signals, so the former being higher does not indicate that neural dimensionality of behaviorally-relevant signals was overestimated. The former is simply not behavioral so this conclusion is not accurate.”:
In practice, researchers usually used raw signals to estimate the neural dimensionality. We mean that using raw signals to do this would overestimate the neural dimensionality. Thank you for your valuable feedback.
Regarding “5.6) Section "Distilled behaviorally-relevant signals uncover that smaller R2 neurons encode rich behavioral information in complex nonlinear ways". Based on what kind of R2 are the neurons grouped? Behavior decoding R2 from raw signals? Using what mapping? Using KF? If KF is used, the result that small R2 neurons benefit a lot from d-VAE could be somewhat expected, given the nonlinearity of d-VAE: because only ANN would have the capacity to unwrap the nonlinear encoding of d-VAE as needed. If decoding performance that is used to group neurons is based on data, regression to the mean could also partially explain the result: the neurons with worst raw decoding are most likely to benefit from a change in decoder, than neurons that already had good decoding. In any case, the R2 used to partition and sort neurons should be more clearly stated and reminded throughout the text and I Fig 3.”:
When employing R2 to characterize neurons, it indicates the extent to which neuronal activity is explained by the linear encoding model [1-3]. Smaller R2 neurons have a lower capacity for linearly tuning (encoding) behaviors, while larger R2 neurons have a higher capacity for linearly tuning (encoding) behaviors. Specifically, the approach involves first establishing an encoding relationship from velocity to neural signal using a linear model, i.e., y=f(x), where f represents a linear regression model, x denotes velocity, and y denotes the neural signal. Subsequently, R2 is utilized to quantify the effectiveness of the linear encoding model in explaining neural activity. We have provided a comprehensive explanation in the revised manuscript. Thank you for your valuable feedback.
[1] Collinger, J.L., Wodlinger, B., Downey, J.E., Wang, W., Tyler-Kabara, E.C., Weber, D.J., McMorland, A.J., Velliste, M., Boninger, M.L. and Schwartz, A.B., 2013. High-performance neuroprosthetic control by an individual with tetraplegia. The Lancet, 381(9866), pp.557-564.
[2] Wodlinger, B., et al. "Ten-dimensional anthropomorphic arm control in a human brain− machine interface: difficulties, solutions, and limitations." Journal of neural engineering 12.1 (2014): 016011.
[3] Inoue, Y., Mao, H., Suway, S.B., Orellana, J. and Schwartz, A.B., 2018. Decoding arm speed during reaching. Nature communications, 9(1), p.5243.
Regarding Questions 5.7, 5.8, 5.9, and 5.10:
We believe our conclusions are solid. The reasons can be found in our replies in Q2 and
Q3. Thank you for your valuable feedback.
Q6: “Imprecise use of language also sometimes is not inaccurate but just makes the text hard to follow.
6.1) Line 41: "about neural encoding and decoding mechanisms" => what is the definition of encoding/decoding and how do these differ? The definitions given much later in line 77-79 is also not clear.
6.2) Line 323: remind the reader about what R2 is being discussed, e.g., R2 of decoding behavior using KF. It is critical to know if linear or nonlinear decoding is being discussed.
6.3) Line 488: "we found that neural responses previously considered trivial encode rich behavioral information in complex nonlinear ways" => "trivial" in what sense? These phrases would benefit from more precision, for example: "neurons that may seem to have little or no behavior information encoded". The same imprecise word ("trivial") is also used in many other places, for example in the caption of Fig S9.
6.4) Line 611: "The same should be true for the brain." => Too strong of a statement for an unsupported claim suggesting the brain does something along the lines of nonlin VAE + linear readout.
6.5) In Fig 1, legend: what is the operational definition of "generating performance"? Generating what? Neural reconstruction?”
Regarding “6.1) Line 41: "about neural encoding and decoding mechanisms" => what is the definition of encoding/decoding and how do these differ? The definitions given much later in line 77-79 is also not clear.”:
We would like to provide a detailed explanation of neural encoding and decoding. Neural encoding means how neuronal activity encodes the behaviors, that is, y=f(x), where y denotes neural activity and, x denotes behaviors, f is the encoding model. Neural decoding means how the brain decodes behaviors from neural activity, that is, x=g(y), where g is the decoding model. For further elaboration, please refer to [1]. We have included references that discuss the concepts of encoding and decoding in the revised manuscript. Thank you for your valuable feedback.
[1] Kriegeskorte, Nikolaus, and Pamela K. Douglas. "Interpreting encoding and decoding models." Current opinion in neurobiology 55 (2019): 167-179.
Regarding “6.2) Line 323: remind the reader about what R2 is being discussed, e.g., R2 of decoding behavior using KF. It is critical to know if linear or nonlinear decoding is being discussed.”:
This question is the same as Q5.6. Please refer to the response to Q5.6. Thank you for your valuable feedback.
Regarding “6.3) Line 488: "we found that neural responses previously considered trivial encode rich behavioral information in complex nonlinear ways" => "trivial" in what sense? These phrases would benefit from more precision, for example: "neurons that may seem to have little or no behavior information encoded". The same imprecise word ("trivial") is also used in many other places, for example in the caption of Fig S9.”:
We have revised this statement in the revised manuscript. Thanks for your recommendation.
Regarding “6.4) Line 611: "The same should be true for the brain." => Too strong of a statement for an unsupported claim suggesting the brain does something along the lines of nonlin VAE + linear readout.”
We mean that removing the interference of irrelevant signals and decoding the relevant signals should logically be two stages. We have revised this statement in the revised manuscript. Thank you for your valuable feedback.
Regarding “6.5) In Fig 1, legend: what is the operational definition of "generating performance"? Generating what? Neural reconstruction?””:
We have replaced “generating performance” with “reconstruction performance” in the revised manuscript. Thanks for your recommendation.
Q7: “In the analysis presented starting in line 449, the authors compare improvement gained for decoding various speed ranges by adding secondary (small PC) neurons to the KF decoder (Fig S11). Why is this done using the KF decoder, when earlier results suggest an ANN decoder is needed for accurate decoding from these small PC neurons? It makes sense to use the more accurate nonlinear ANN decoder to support the fundamental claim made here, that smaller variance PCs are involved in regulating precise control”
Because when the secondary signal is superimposed on the primary signal, the enhancement in KF performance is substantial. We wanted to explore in which aspect of the behavior the KF performance improvement is mainly reflected. In comparison, the improvement of ANN by the secondary signal is very small, rendering the exploration of the aforementioned questions inconsequential. Thank you for your valuable feedback.
Q8: “A key limitation of the VAE architecture is that it doesn't aggregate information over multiple time samples. This may be why the authors decided to use a very large bin size of 100ms and beyond that smooth the data with a moving average. This limitation should be clearly stated somewhere in contrast with methods that can aggregate information over time (e.g., TNDM, LFADS, PSID) ”
We have added this limitation in the Discussion in the revised manuscript. Thanks for your recommendation.
Q9: “Fig 5c and parts of the text explore the decoding when some neurons are dropped. These results should come with a reminder that dropping neurons from behaviorally relevant signals is not technically possible since the extraction of behaviorally relevant signals with d-VAE is a population level aggregation that requires the raw signal from all neurons as an input. This is also important to remind in some places in the text for example:
- Line 498: "...when one of the neurons is destroyed."
- Line 572: "In contrast, our results show that decoders maintain high performance on distilled signals even when many neurons drop out."”
We want to explore the robustness of real relevant signals in the face of neuron drop-out. The signals our model extracted are an approximation of the ground truth relevant signals and thus serve as a substitute for ground truth to study this problem. Thank you for your valuable feedback.
Q10: “Besides the confounded conclusions regarding the readout being linear (see comment 3 and items related to it in comment 5), the authors also don't adequately discuss prior works that suggest nonlinearity helps decoding of behavior from the motor cortex. Around line 594, a few works are discussed as support for the idea of a linear readout. This should be accompanied by a discussion of works that support a nonlinear encoding of behavior in the motor cortex, for example (Naufel et al. 2019; Glaser et al. 2020), some of which the authors cite elsewhere but don't discuss here.”
We have added this discussion in the revised manuscript. Thanks for your recommendation.
Q11: “Selection of hyperparameters is not clearly explained. Starting line 791, the authors give some explanation for one hyperparameter, but not others. How are the other hyperparameters determined? What is the search space for the grid search of each hyperparameter? Importantly, if hyperparameters are determined only based on the training data of each fold, why is only one value given for the hyperparameter selected in each dataset (line 814)? Did all 5 folds for each dataset happen to select exactly the same hyperparameter based on their 5 different training/validation data splits? That seems unlikely.”
We perform a grid search in {0.001, 0.01,0.1,1} for hyperparameter beta. And we found that 0.001 is the best for all datasets. As for the model parameters, such as hidden neuron numbers, this model capacity has reached saturation decoding performance and does not influence the results.
Regarding “Importantly, if hyperparameters are determined only based on the training data of each fold, why is only one value given for the hyperparameter selected in each dataset (line 814)? Did all 5 folds for each dataset happen to select exactly the same hyperparameter based on their 5 different training/validation data splits”: We selected the hyperparameter based on the average performance of 5 folds data on validation sets. The selected value denotes the one that yields the highest average performance across the 5 folds data.
Thank you for your valuable feedback.
Q12: “d-VAE itself should also be explained more clearly in the main text. Currently, only the high-level idea of the objective is explained. The explanation should be more precise and include the idea of encoding to latent state, explain the relation to pip-VAE, explain inputs and outputs, linearity/nonlinearity of various mappings, etc. Also see comment 1 above, where I suggest adding more details about other methods in the main text.”
Our primary objective is to delve into the encoding and decoding mechanisms using the separated relevant signals. Therefore, providing an excessive amount of model details could potentially distract from the main focus of the paper. In response to your suggestion, we have included a visual representation of d-VAE's structure, input, and output (see Fig. S1) in the revised manuscript, which offers a comprehensive and intuitive overview. Additionally, we have expanded on the details of d-VAE and other methods in the Methods section.
Thank you for your valuable feedback.
Q13: “In Fig 1f and g, shouldn't the performance plots be swapped? The current plots seem counterintuitive. If there is bias toward decoding (panel g), why is the irrelevant residual so good at decoding?”
The placement of the performance plots in Fig. 1f and 1g is accurate. When the model exhibits a bias toward decoding, it prioritizes extracting the most relevant features (latent variables) for decoding purposes. As a consequence, the model predominantly generates signals that are closely associated with these extracted features. This selective signal extraction and generation process may result in the exclusion of other potentially useful information, which will be left in the residuals. To illustrate this concept, consider the example of face recognition: if a model can accurately identify an individual using only the person's eyes (assuming these are the most useful features), other valuable information, such as details of the nose or mouth, will be left in the residuals, which could also be used to identify the individual.
Thank you for your valuable feedback.