A novel method for estimating properties of attentional oscillators reveals an age-related decline in flexibility

Reviewer #1 (Public Review):

Summary:

This study assumes but also demonstrates that auditory rhythm processing is produced by internal oscillating systems and evaluates the properties of internal oscillators across individuals. The authors designed an experiment and performed analyses that address individuals' preferred rate and flexibility, with a special focus on how much past rhythms influence subsequent trials. They find evidence for such historical dependence and show that we adapt less well to new rhythms as we age. While I have some doubts about the entrainment-based interpretation of the results, this work offers a useful contribution to our understanding of individual differences in rhythm processing regardless.

Strengths:

The inclusion of two tasks -- a tapping and a listening task -- complement each other methodologically. By analysing both the production and tracking of rhythms, the authors emphasize the importance of the characteristics of the receiver, the external world, and their interplay. The relationship between the two tasks and components within tasks are explored using a range of analyses. The visual presentation of the results is very clear. The age-related changes in flexibility are useful and compelling.

The paper includes a discussion of the study assumptions, and it contextualizes itself more explicitly as taking entrainment frameworks as a starting point. As such, even if the entrainment of oscillators cannot be decisively shown, it is now clear that this is nevertheless adopted as a useful theoretical lens.

Weaknesses:

The newly included analyses that justify an entrainment or oscillator-based interpretation of the result could be presented in a clearer manner so that readers can parse their validity better. For example, in line with an entrainment interpretation, the regression lines in Figure 2B show accuracy increases as the IOI moves towards the preferred rate -- but then beyond the preferred rate, accuracy appears to increase further still. Furthermore, the additional analyses on harmonic relationships could be enriched with justification and explanation of each of its steps.

Reviewer #2 (Public Review):

Summary:

The current work describes a set of behavioral tasks to explore individual differences in the preferred perceptual and motor rhythms. Results show a consistent individual preference for a given perceptual and motor frequency across tasks and, while these were correlated, the latter is slower than the former one. Additionally, the adaptation accuracy to rate changes is proportional to the amount of rate variation and, crucially, the amount of adaptation decreases with age.

Strengths:

Experiments are carefully designed to measure individual preferred motor and perceptual tempo. Furthermore, the experimental design is validated by testing the consistency across tasks and test-retest, what makes the introduced paradigm a useful tool for future research.
The obtained data is rigorously analyzed using a diverse set of tools, each adapted to the specificities across the different research questions and tasks.
This study identifies several relevant behavioral features: (i) each individual shows a preferred and reliable motor and perceptual tempo and, while both are related, the motor is consistently slower than the pure perceptual one; (ii) the presence of hysteresis in the adaptation to rate variations; and (iii) the decrement of this adaptation with age. All these observations are valuable for the auditory-motor integration field of research, and they could potentially inform existing biophysical models to increase their descriptive power.

Weaknesses:

To get a better understanding of the mechanisms underlying the behavioral observations, it would have been useful to compare the observed pattern of results with simulations done with existing biophysical models. However, this point is addressed if the current study is read along with this other publication of the same research group: Kaya, E., & Henry, M. J. (2024, February 5). Modeling rhythm perception and temporal adaptation: top-down influences on a gradually decaying oscillator. https://doi.org/10.31234/osf.io/q9uvr

Author Response

The following is the authors’ response to the original reviews.

General response:

We thank the reviewers for their thorough evaluation of our manuscript. Working on the raised concerns has improved the manuscript greatly. Specifically, the recommendations to clarify the adopted assumptions in the study strengthened the motivation for the study; further, following up some of the reviewers’ concerns with additional analyses validated our chosen measures and strengthened the compatibility of the findings with the predictions of the dynamic attending framework. Below, you will find our detailed point-by-point responses, along with information on specific revisions.

The reviewers pointed out that study assumptions were unclear, some of the measures we chose were not well motivated, and the findings were not well enough explained considering possible alternatives. As suggested, we reformulated the introduction, explained the common assumptions of entrainment models that we adopted in the study, and further clarified how our chosen measures for the properties of the internal oscillators relate to these assumptions.

We realized that the initial emphasis on the compatibility of the current findings with predictions of entrainment models might have led to the wrong impression that the current study aimed to test whether auditory rhythmic processing is governed by timekeeper or oscillatory mechanisms. However, testing these theoretical models to explain human behavior necessitates specific paradigms designed to compare the contrasting predictions of the models. A number of studies do so by manipulating regularity in a stimulus sequence or expectancy of stimulus onsets, or assessing the perceived timing of targets that follow a stimulus rhythm. Such paradigms allow testing the prediction that an oscillator, underlying perceptual timing, would entrain to a regular but not an irregular sequence. This would further lead to stronger expectancies at the peak of the oscillation, where 'attentional energy' is the highest. These studies report 'rhythmic facilitation', where targets that align with the peaks of the oscillation are better detected than those that do not (see Henry and Herrmann (2014) and Haegens and Zion Golumbic (2018) for reviews). Additionally, unexpected endings of standard intervals, preceded by a regular entraining sequence, lead to a biased estimation of subsequent comparison intervals, due to the contrast between the attentional oscillator's phase and a deviating stimulus onset (Barnes & Jones, 2000; Large & Jones, 1999; McAuley & Jones, 2003). Even a sequence rate that is the multiple of the to-be-judged standard and comparison intervals give rise to rhythmic facilitation (McAuley & Jones, 2003), and the expectancy of a stimulus onset modulates duration judgments. These findings are not compatible with predictions of timekeeper models as time intervals in these models are represented arbitrarily and are not affected by expectancy violations.

In the current study, we adopted an entrainment approach to timing, rather than testing predictions of competing models. This choice was motivated by several aspects of entrainment models that align better with the aims of the current study. First, our focus was on understanding perception and production of rhythms, for which perception is better explained by entrainment models than by timekeeper models, which excel at explaining perception of isolated time intervals (McAuley, 2010). Moreover, we wanted to leverage the fact that entrainment models elegantly include parameters that can explain different aspects of timing abilities, and these parameters can be estimated in an individualized manner. For instance, the flexibility property of oscillators can be linked to the ability to adapt to changes in external context, while timekeeper or Bayesian timing approaches lack a specific mechanism to quantify temporal adaptation across perceptual and motor domains. Finally, that entrainment is observed across theoretical, behavioral, and neural levels renders entrainment models useful in explaining and generalizing behavior across different domains. Nevertheless, some results showed partial compatibility with predictions of the timekeeper models, such as the modulation of 'bestperformance rates' by the temporal context, observed in Experiment 1’ random-order sessions, where stimulus rates maximally differed across consecutive trials. However, given that the mean, standard deviation, and range of stimulus rates were identical across sessions, and timekeeper models assume no temporal adaptation in duration perception, we should have observed similar results across these sessions. Conversely, we found significant accuracy differences, biased duration judgments, and harmonic relationships between the best-performance rates. We elaborate more on these results with respect to their compatibility with the contrasting models of human temporal perception in the revised discussion.

Responses to specific comments:

(1.1) At times, I found it challenging to evaluate the scientific merit of this study from what was provided in the introduction and methods. It is not clear what the experiment assumes, what it evaluates, and which competing accounts or predictions are at play. While some of these questions are answered, clear ordering and argumentative flow is lacking. With that said, I found the Abstract and General Discussion much clearer, and I would recommend reformulating the early part of the manuscript based on the structure of those segments.

Second, in my reading, it is not clear to what extent the study assumes versus demonstrates the entrainment of internal oscillators. I find the writing somewhat ambiguous on this count: on the one hand, an entrainment approach is assumed a priori to design the experiment ("an entrainment approach is adopted") yet a primary result of the study is that entrainment is how we perceive and produce rhythms ("Overall, the findings support the hypothesis that an oscillatory system with a stable preferred rate underlies perception and production of rhythm..."). While one could design an experiment assuming X and find evidence for X, this requires testing competing accounts with competing hypotheses -- and this was not done.

We appreciate the reviewer’s concerns and suggestion to clarify the assumptions of the study and how the current findings relate to the predictions of competing accounts. To address these concerns:

• We added the assumptions of the entrainment models that we adopted in the Introduction section and reformulated the motivation to choose them accordingly.

• We clarified in the Introduction that the study’s aim was not to test the entrainment models against alternative theories of rhythm perception.

• We added a paragraph in the General Discussion to further distinguish predictions from the competing accounts. Here we discussed the compatibility of the findings with predictions of both entrainment and timekeeper models.

• We rephrased reasoning in the Abstract, Introduction, and General Discussion to further clarify the aims of the study, and how the findings support the hypotheses of the current study versus those of the dynamic attending theory.

(1.2) In my view, more evidence is required to bolster the findings as entrainment-based regardless of whether that is an assumption or a result. Indeed, while the effect of previous trials into the behaviour of the current trial is compatible with entrainment hypotheses, it may well be compatible with competing accounts as well. And that would call into question the interpretation of results as uncovering the properties of oscillating systems and age-related differences in such systems. Thus, I believe more evidence is needed to bolster the entrainment hypothesis.

For example, a key prediction of the entrainment model -- which assumes internal oscillators as the mechanism of action -- is that behaviour in the SMT and PTT tasks follows the principles of Arnold's Tongue. Specifically, tapping and listening performance should worsen systematically as a function of the distance between the presented and preferred rate. On a participant-by-participant, does performance scale monotonically with the distance between the presented and preferred rate? Some of the analyses hint at this question, such as the effect of 𝚫IOI on accuracy, but a recontextualization, further analyses, or additional visualizations would be helpful to demonstrate evidence of a tongue-like pattern in the behavioural data. Presumably, non-oscillating models do not follow a tongue-like pattern, but again, it would be very instructive to explicitly discuss that.

We thank the reviewer for the excellent suggestion of assessing 'Arnold's tongue' principles in timing performance. We agree that testing whether timing performance forms a pattern compatible with an Arnold tongue would further support our assumption that the findings related to preferred rate stem from an entrainment-based mechanism. We rather refer to the ‘entrainment region’, (McAuley et al., 2006) that corresponds to a slice in the Arnold tongue at a fixed stimulus intensity that entrains the internal oscillator. In both representations of oscillator behavior across a range of stimulus rates, performance should systematically increase as the difference between the stimulus rate and the oscillator's preferred rate, namely, 'detuning' decreases. In response to the reviewer’s comment, we ran further analyses to test this key prediction of entrainment models. We assessed performance at stimulus rates that were faster and slower than an individual's preferred rate estimates from in Experiment 1. To do so, we ran logistic regression models on aggregated datasets from all participants and sessions, where normalized IOI, in trials where the stimulus rate was faster than the preferred rate estimate, and in those where it was slower, predicted accuracy. Stimulus IOIs were normalized within each direction (faster- versus slower-than-preferred rate) using z-score transformation, and the direction was coded as categorical in the model. We reasoned that a positive slope for conditions with stimulus rates faster than IOI, and a negative slope from conditions with slower rates, should indicate a systematic accuracy increase toward the preferred rate estimate. This is exactly what we found. These results revealed significant main effect for the IOI and a significant interaction between IOI and direction, indicating that accuracy increased towards the preferred rate at fast rates and decreased as the stimulus rate diverged from the preferred rate at slow rates. We added these results to the respective subsections of Experiment 1 Methods and Results, added a plot showing the slices of the regression surfaces to Figure 2B and elaborated on the results in Experiment 1 Discussion. As the number of trials in Experiment 2 was much lower (N = 81), we only ran these additional analyses in Experiment 1.

(1.3) Fourth, harmonic structure in behaviour across tasks is a creative and useful metric for bolstering the entrainment hypothesis specifically because internal oscillators should display a preference across their own harmonics. However, I have some doubts that the analyses as currently implemented indicate such a relationship. Specifically, the main analysis to this end involves summing the residuals of the data closest to y=x, y=2*x and y=x/2 lines and evaluating whether this sum is significantly lower than for shuffled data. Out of these three dimensions, y=x does not comprise a harmonic, and this is an issue because it could by itself drive the difference of summed residuals with the shuffled data. I am uncertain whether rerunning the same analysis with the x=y dimension excluded constitutes a simple resolution because presumably there are baseline differences in the empirical and shuffled data that do not have to do with harmonics that would leak into the analysis. To address this, a simulation with ground truths could be helpful to justify analyses, or a different analysis that evaluates harmonic structure could be thought of.

We thank the reviewer for pointing out the weakness of the permutation test we developed to assess the harmonic relationship between Experiment 1’s preferred rate estimates. Datapoints that fall on the y=x line indeed do not represent harmonic relationships. They rather indicate one-to-one correspondence between the axes, which is a stronger indicator of compatibility between the estimates. Maybe speaking to the reviewer’s point, standard correlation analyses were not significant, which would have been expected if the permutation results were being driven by the y=x relationship. This was the reason we developed the permutation test to include integer-ratio datapoints could also contribute.

Based on reviewer’s comment, we ran additional analyses to assess the harmonic relationships between the estimates. The first analysis involved a circular approach. We first normalized each participant’s estimates by rescaling the slower estimate with respect to the faster one by division; and converted the values to radians, since a pair of values with an integer-ratio relationship should correspond to the same phase on a unit circle. Then, we assessed whether the resulting distribution of normalized values differed from a uniform distribution, using Rayleigh’s test, which was significant (p = .004). The circular mean of the distribution was 44 (SD = 53) degrees (M = 0.764, SD = 0.932 radians), indicating that the slower estimates were slightly slower than the fast estimate or its duplicates. As this distribution was skewed toward positive values due to the normalization procedure, we did not compare it against zero angle. Instead, we ran a second test, which was a modular approach. We first calculated how much the slower estimate deviated proportionally from the faster estimate or its multiples (i.e., subharmonics) by normalizing the estimates from both sessions by the faster estimate. The outcome measure was the modulus of the slower, relative to the faster estimate, divided by the faster estimate. Then, we ran a permutation test, shuffling the linear-order session estimates over 1000 iterations and taking the median percent deviation values for each iteration. The test statistic was significant (p = .004), indicating that the harmonic relationships we observed in the estimates were not due to chance or dependent on the assessment method. We added these details of additional analyses to assess harmonic relationships between the Experiment 1 preferred rate estimates in the Supplementary Information.

(2.1) The current study is presented in the framework of the ongoing debate of oscillator vs. timekeeper mechanisms underlying perceptual and motor timing, and authors claim that the observed results support the former mechanism. In this line, every obtained result is related by the authors to a specific ambiguous (i.e., not clearly related to a biophysical parameter) feature of an internal oscillator. As pointed out by an essay on the topic (Doelling & Assaneo, 2021), claiming that a pattern of results is compatible with an "oscillator" could be misleading, since some features typically used to validate or refute such mechanisms are not well grounded on real biophysical models. Relatedly, a recent study (Doelling et al., 2022) shows that two quantitatively different computational algorithms (i.e., absolute vs relative timing) can be explained by the same biophysical model. This demonstrates that what could be interpreted as a timekeeper, or an oscillator can represent the same biophysical model working under different conditions. For this reason, if authors would like to argue for a given mechanism underlying their observations, they should include a specific biophysical model, and test its predictions against the observed behavior. For example, it's not clear why authors interpret the observation of the trial's response being modulated by the rate of the previous one, as an oscillator-like mechanism underlying behavior. As shown in (Doelling & Assaneo, 2021) a simple oscillator returns to its natural frequency as soon as the stimulus disappears, which will not predict the long-lasting effect of the previous trial. Furthermore, a timekeeper-like mechanism with a long enough integration window is compatible with this observation.

Still, authors can choose to disregard this suggestion, and not testing a specific model, but if so, they should restrict this paper to a descriptive study of the timing phenomena.

We thank the reviewer for their valuable suggestion of to include a biophysical model to further demonstrate the compatibility of the current findings with certain predictions of the model. While we acknowledge the potential benefits of implementing a biophysical model to understand the relationships between model parameters and observed behavior, this goes beyond the scope of the current study.

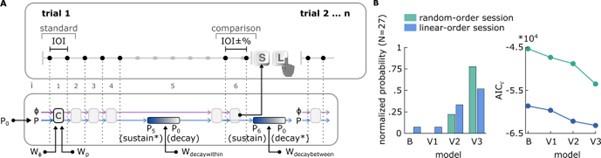
We note that we have employed a modeling approach in a subsequent study to further explore how the properties and the resulting behavior of an oscillator map onto the patterns of human behavior we observed in the current study (Kaya & Henry, 2024, February 5). In that study, we fitted a canonical oscillator model, and several variants thereof, separately to datasets obtained from random-order and linear-order sessions of Experiment 1 of the current submission. The base model, adapted from McAuley and Jones (2003), assumed sustained oscillations within the trials of the experiment, and complete decay towards the preferred rate between the trials. We introduced a gradual decay parameter (Author response image 1A) that weighted between the oscillator's concurrent period value at the time of decay and its initial period (i.e., preferred rate). This parameter was implemented only within trials, between the standard stimulus sequence and comparison interval in Variant 1, between consecutive trials in Variant 2, and at both temporal locations in Variant 3. Model comparisons (Author response image 1B) showed that Variant 3 was the best-fitting model for both random- and linear-order datasets. Crucially, estimates for within- and between-trial decay parameters, obtained from Variant 3, were positively correlated, suggesting that oscillators gradually decayed towards their preferred rate at similar timescales after cessation of a stimulus.

Author response image 1.

(A) Illustration of the model fitted to Experiment 1 datasets and (B) model comparison results. In each trial, the model is initialized with a phase (ɸ) and period (P) value. A At the offset of each stimulus interval i, the model updates its phase (pink arrows) and period (blue arrows) depending on the temporal contrast (C) between the model state and stimulus onset and phase and period correction weights, Wɸ and Wp. Wdecaywithin updates the model period as a weighted average between the period calculated for the 5th interval, P5, and model’s preferred rate, P0. C, calculated at the offset of the comparison interval. Wdecaybetween parameter initializes the model period at the beginning of a new trial as a weighted average between the last period from the previous trial and P0. The base model’s assumptions are marked by asterisks, namely sustained oscillation during the silence (i=5), and complete decay between trials. B Left: The normalized probability of each model having the minimum BIC value across all models and across participants. Right: AICc, calculated from each model’s fit to participants’ single-session datasets. In both panels, random-order and linear-order sessions were marked in green and blue, respectively. B denotes the base model, and V1, V2 and V3 denote variants 1, 2 and 3, respectively.

Although our behavioral results and modeling thereof must necessarily be interpreted as reflecting the mechanics of an attentional, but not a neural oscillator, these findings might shed light on the controversy in neuroscience research regarding the timeline of entrainment decay. While multiple studies show that neural oscillations can continue at the entrained rate for a number of cycles following entrainment (Bouwer et al., 2023; Helfrich et al., 2017; Lakatos et al., 2013; van Bree et al., 2021), different modeling approaches reveal mixed results on this phenomenon. Whereas Doelling and Assaneo (2021) show that a Stuart-Landau oscillator returns immediately back to its preferred rate after synchronizing to an external stimulus, simulations of other oscillator types suggest gradual decay toward the preferred rate (Large, 1994; McAuley, 1995; Obleser et al., 2017) or self-sustained oscillation at the external stimulus rate (Nachstedt et al., 2017).

While the Doelling & Assaneo study (2021) provides insights on entrainment and behavior of the Stuart-Landau oscillator under certain conditions, the internal oscillators hypothesized by the dynamic attending theory might have different forms, therefore may not adhere to the behavior of a specific implementation of an oscillator model. Moreover, that a phase-coupled oscillator does not show gradual decay does not preclude that models with period tracking behave similarly. Adaptive frequency oscillators, for instance, are able to sustain the oscillation after the stimulus ceases (Nachstedt et al., 2017). Alongside with models that use Hebbian learning (Roman et al., 2023), the main implementations of the dynamic attending theory have parameters for period tracking and decay towards the preferred rate (Large, 1994; McAuley, 1995). In fact, the u-shaped pattern of duration discrimination sensitivity across a range of stimulus rates (Drake & Botte, 1993) is better explained by a decaying than a non-decaying oscillator (McAuley, 1995). To conclude, the literature suggests that the emergence of decay versus sustain behavior of the oscillators and the timeline of decay depend on the particular model used as well as its parameters and does therefore not offer a one-for-all solution.

Reviewer #2 (Recommendations For The Authors):

• Are the range, SD and mean of the random-order and linear-order sessions different? If so, why?

Information regarding the SD and mean of the random-order and linear-order sessions was added to Experiment 1 Methods section.

“While the mean (M = 599 ms), standard deviation (SD = 231 ms) and range (200, 998 ms) of the presented stimulus IOIs were identical between the sessions, the way IOI changed from trial to trial was different.“ (p. 5)

• Perhaps the title could mention the age-related flexibility effect you demonstrate, which is an important contribution that without inclusion in the title could be missed in literature searches.

We have changed the title to include age-related changes in oscillator flexibility. Thanks for the great suggestion.

• Is the statistical analysis in Figure 4A between subjects? Shouldn't the analyses be within subjects?

We have now better specified that the statistical analyses of Experiment 2’s preferred rate estimates were across the tasks, in Figure 4 caption.

"Vertical lines above the box plots represent within-participants pairwise comparisons." (p. 17)

• It says participants' hearing thresholds were measured using standard puretone audiometry. What threshold warranted participant exclusion and how many participants were excluded on the basis of hearing skills?

We have now clarified that hearing threshold was not an exclusion criterion.

"Participants were not excluded based on hearing threshold." (p. 11)

• "Tapping rates from 'fastest' and 'slowest' FMT trials showed no difference between pre- and postsession measurements, and were additionally correlated across repeated measurements" - could you point to the statistics for this comparison?

Table 2 includes the results from both experiments’ analyses on unpaced tapping. (p. 10)

“The results of the pairwise comparisons between tapping rates from all unpaced tapping tasks across measurements are provided in Table 2.” (p. 15)

• How was the loudness (dB) of the woodblock stimuli determined on a participant-by-participant basis? Please ignore if I missed this.

Participants were allowed to set the volume to a comfortable level.

"Participants then set the sound volume to a level that they found comfortable for completing the task." (p. 4)

• Please spell out IOI, DEV, and other terms in full the first time they are mentioned in the manuscript.

We added the descriptions of abbreviations before their initial mention.

"In each experimental session, 400 unique trials of this task were presented, each consisting of a combination of the three main independent variables: the inter-onset interval, IOI; amount of deviation of the comparison interval from the standard, DEV, and the amount of change in stimulus IOI between consecutive trials, 𝚫IOI. We explain each of these variables in detail in the next paragraphs." (p. 4)

• Small point: In Fig 1 sub-text, random order and linear order are explained in reverse order from how they are presented in the figure.

We fixed the incompatibility between of Figure 1 content and caption.

• Small point: I found the elaborate technical explanation of windowing methods, including alternatives that were not used, unnecessary.

We moved the details of the smoothing analysis to the Supplementary Information.

• With regard to the smoothing explanation, what is an "element"? Is this a sample? If so, what was the sampling rate?

We reworded ‘element’ as ‘sample’. In the smoothing analyses, the sampling rate was the size of the convolution window, which was set to 26 for random-order, 48 for linear-order sessions.

• Spelling/language error: "The pared-down", "close each other", "always small (+4 ms), than".

We fixed the spelling errors.

Reviewer #3 (Recommendations For The Authors):

• My main concern is the one detailed as a weakness in the public review. In that direction, if authors decide to keep the mechanistic interpretation of the outcomes (which I believe is a valuable one) here I suggest a couple of models that they can try to adapt to explain the pattern of results:

a. Roman, Iran R., et al. "Hebbian learning with elasticity explains how the spontaneous motor tempo affects music performance synchronization." PLOS Computational Biology 19.6 (2023): e1011154.

b. Bose, Amitabha, Áine Byrne, and John Rinzel. "A neuromechanistic model for rhythmic beat generation." PLoS Computational Biology 15.5 (2019): e1006450.

c. Egger, Seth W., Nhat M. Le, and Mehrdad Jazayeri. "A neural circuit model for human sensorimotor timing." Nature Communications 11.1 (2020): 3933.

d. Doelling, K. B., Arnal, L. H., & Assaneo, M. F. (2022). Adaptive oscillators provide a hard-coded Bayesian mechanism for rhythmic inference. bioRxiv, 2022-06

Thanks for the suggestion! Please refer to our response (2.1.) above. To summarize, although we considered a full, well-fleshed-out modeling approach to be beyond the scope of the current work, we are excited about and actively working on exactly this. Our modeling take is available as a preprint (Kaya & Henry, 2024, February 5).

• Since the authors were concerned with the preferred rate they circumscribed the analysis to extract the IOI with better performance. Would it be plausible to explore how is the functional form between accuracy and IOI? This could shed some light on the underlying mechanism.

Unfortunately, we were unsure about what the reviewer meant by the functional form between accuracy and IOI. We interpret it to mean a function that takes IOI as input and outputs an accuracy value. In that case, while we agree that estimating this function might indeed shed light on the underlying mechanisms, this type of analysis is beyond the scope of the current study. Instead, we refer the reviewer and reader to our modeling study (please see our response (2.1.) above) that includes a model which takes the stimulus conditions, including IOI, and model parameters for preferred rate, phase and period correction and within- and between-trial decay and outputs predicted accuracy for each trial. We believe that such modeling approach, as compared to a simple function, gives more insights regarding the relationship between oscillator properties and duration perception.

• Is the effect caused by the dIOI modulated by the distance to the preferred frequency?

We thank the reviewer for the recommendation. We measured flexibility by the oscillator's ability to adapt to on-line changes in the temporal context (i.e., effect of 𝚫IOI on accuracy), rather than by quantifying the range of rates with improved accuracy. Nevertheless, we acknowledge that distance to the preferred rate should decrease accuracy, as this is a key prediction of entrainment models. In fact, testing this prediction was recommended also by the other reviewer, in response to which we ran additional analyses. These analyses involved assessment of the relationship between accuracy and detuning. Specifically, we assessed accuracy at stimulus rates that were faster and slower than an individual's preferred rate estimates from in Experiment 1. We ran logistic regression models on aggregated datasets from all participants and sessions, where accuracy was predicted by z-scored IOI, from trials where the stimulus rate was faster than the preferred rate estimate, and in those where it was slower. The model had a significant main effect of IOI and an interaction between IOI and direction (i.e., whether stimulus rate was faster or slower than the preferred rate estimate), indicating that accuracy increased towards the preferred rate at fast rates and decreased as the stimulus rate diverged from the preferred rate at slow rates. We added information regarding this analysis to the respective subsections of Experiment 1 Methods and Results, added a plot showing the slices of the regression surfaces to Figure 2B and elaborated on the results in Experiment 1 Discussion. As the number of trials in Experiment 2 was insufficient, we only ran these additional analyses in Experiment 1. We agree that a range-based measure of oscillator flexibility would also index the oscillators’ adaptive abilities. However, the current paradigms were designed for assessment of temporal adaptation. Thus, comparison of the two approaches to measuring oscillator flexibility, which can be addressed in future studies, is beyond the scope of the current study.

• Did the authors explore if the "motor component" (the difference between the motor and perceptual rates) is modulated by the participants age?

In response to the reviewer’s comment, we correlated the difference between the motor and perceptual rates with age, which was nonsignificant.

• Please describe better the slider and the keypress tasks. For example, what are the instructions given to the participant on each task, and how they differ from each other?

We added the Experiment 2 instructions in Appendix A.

• Typos: The caption in figure one reads 2 ms, while I believe it should say 200. Page 4 mentions that there are 400 trials and page 5 says 407.

We fixed the typos.

References

Barnes, R., & Jones, M. R. (2000). Expectancy, attention, and time. Cogn Psychol, 41(3), 254-311. https://doi.org/10.1006/cogp.2000.0738

Bouwer, F. L., Fahrenfort, J. J., Millard, S. K., Kloosterman, N. A., & Slagter, H. A. (2023). A Silent Disco: Differential Effects of Beat-based and Pattern-based Temporal Expectations on Persistent Entrainment of Low-frequency Neural Oscillations. J Cogn Neurosci, 35(6), 9901020. https://doi.org/10.1162/jocn_a_01985

Doelling, K. B., Arnal, L. H., & Assaneo, M. F. (2022). Adaptive oscillators provide a hard-coded Bayesian mechanism for rhythmic inference. bioRxiv. https://doi.org/10.1101/2022.06.18.496664

Doelling, K. B., & Assaneo, M. F. (2021). Neural oscillations are a start toward understanding brain activity rather than the end. PLoS Biol, 19(5), e3001234. https://doi.org/10.1371/journal.pbio.3001234

Drake, C., & Botte, M. C. (1993). Tempo sensitivity in auditory sequences: evidence for a multiplelook model. Percept Psychophys, 54(3), 277-286. https://doi.org/10.3758/bf03205262

Haegens, S., & Zion Golumbic, E. (2018). Rhythmic facilitation of sensory processing: A critical review. Neurosci Biobehav Rev, 86, 150-165. https://doi.org/10.1016/j.neubiorev.2017.12.002

Helfrich, R. F., Huang, M., Wilson, G., & Knight, R. T. (2017). Prefrontal cortex modulates posterior alpha oscillations during top-down guided visual perception. Proc Natl Acad Sci U S A, 114(35), 9457-9462. https://doi.org/10.1073/pnas.1705965114

Henry, M. J., & Herrmann, B. (2014). Low-Frequency Neural Oscillations Support Dynamic Attending in Temporal Context. Timing & Time Perception, 2(1), 62-86. https://doi.org/10.1163/22134468-00002011

Kaya, E., & Henry, M. J. (2024, February 5). Modeling rhythm perception and temporal adaptation: top-down influences on a gradually decaying oscillator. https://doi.org/10.31234/osf.io/q9uvr

Lakatos, P., Musacchia, G., O'Connel, M. N., Falchier, A. Y., Javitt, D. C., & Schroeder, C. E. (2013). The spectrotemporal filter mechanism of auditory selective attention. Neuron, 77(4), 750-761. https://doi.org/10.1016/j.neuron.2012.11.034

Large, E. W. (1994). Dynamic representation of musical structure. The Ohio State University.

Large, E. W., & Jones, M. R. (1999). The dynamics of attending: How people track time-varying events. Psychological Review, 106(1), 119-159. https://doi.org/Doi 10.1037/0033295x.106.1.119

McAuley, J. D. (1995). Perception of time as phase: Toward an adaptive-oscillator model of rhythmic pattern processing Indiana University Bloomington].

McAuley, J. D. (2010). Tempo and Rhythm. In Music Perception (pp. 165-199). https://doi.org/10.1007/978-1-4419-6114-3_6

McAuley, J. D., & Jones, M. R. (2003). Modeling effects of rhythmic context on perceived duration: a comparison of interval and entrainment approaches to short-interval timing. J Exp Psychol Hum Percept Perform, 29(6), 1102-1125. https://doi.org/10.1037/0096-1523.29.6.1102

McAuley, J. D., Jones, M. R., Holub, S., Johnston, H. M., & Miller, N. S. (2006). The time of our lives: life span development of timing and event tracking. J Exp Psychol Gen, 135(3), 348-367. https://doi.org/10.1037/0096-3445.135.3.348

Nachstedt, T., Tetzlaff, C., & Manoonpong, P. (2017). Fast Dynamical Coupling Enhances Frequency Adaptation of Oscillators for Robotic Locomotion Control. Front Neurorobot, 11, 14. https://doi.org/10.3389/fnbot.2017.00014

Obleser, J., Henry, M. J., & Lakatos, P. (2017). What do we talk about when we talk about rhythm? PLoS Biol, 15(9), e2002794. https://doi.org/10.1371/journal.pbio.2002794

Roman, I. R., Roman, A. S., Kim, J. C., & Large, E. W. (2023). Hebbian learning with elasticity explains how the spontaneous motor tempo affects music performance synchronization. PLoS Comput Biol, 19(6), e1011154. https://doi.org/10.1371/journal.pcbi.1011154
van Bree, S., Sohoglu, E., Davis, M. H., & Zoefel, B. (2021). Sustained neural rhythms reveal endogenous oscillations supporting speech perception. PLoS Biol, 19(2), e3001142. https://doi.org/10.1371/journal.pbio.3001142