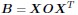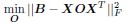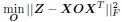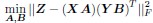Deciphering the Genetic Code of Neuronal Type Connectivity: A Bilinear Modeling Approach

Reviewer #1 (Public Review):

Summary of what the author was trying to achieve:
In this study, the author aimed to develop a method for estimating neuronal-type connectivity from transcriptomic gene expression data, specifically from mouse retinal neurons. They sought to develop an interpretable model that could be used to characterize the underlying genetic mechanisms of circuit assembly and connectivity.

Strengths:
The proposed bilinear model draws inspiration from commonly implemented recommendation systems in the field of machine learning. The author presents the model clearly and addresses critical statistical limitations that may weaken the validity of the model such as multicollinearity and outliers. The author presents two formulations of the model for separate scenarios in which varying levels of data resolution are available. The author effectively references key work in the field when establishing assumptions that affect the underlying model and subsequent results. For example, correspondence between gene expression cell types and connectivity cell types from different references are clearly outlined in Tables 1-3. The model training and validation are sufficient and yield a relatively high correlation with the ground truth connectivity matrix. Seemingly valid biological assumptions are made throughout, however, some assumptions may reduce resolution (such as averaging over cell types), thus missing potentially important single-cell gene expression interactions.

Weaknesses:
The main results of the study could benefit from replication in another dataset beyond mouse retinal neurons, to validate the proposed method. Dimensionality reduction significantly reduces the resolution of the model and the PCA methodology employed is largely non-deterministic. This may reduce the resolution and reproducibility of the model. It may be worth exploring how the PCA methodology of the model may affect results when replicating. Figure 5, 'Gene signatures associated with the two latent dimensions', lacks some readability and related results could be outlined more clearly in the results section. There should be more discussion on weaknesses of the results e.g. quantification of what connectivity motifs were not captured and what gene signatures might have been missed.

The main weakness is the lack of comparison against other similar methods, e.g. methods presented in
Barabási, Dániel L., and Albert-László Barabási. "A genetic model of the connectome." Neuron 105.3 (2020): 435-445.
Kovács, István A., Dániel L. Barabási, and Albert-László Barabási. "Uncovering the genetic blueprint of the C. elegans nervous system." Proceedings of the National Academy of Sciences 117.52 (2020): 33570-33577.
Taylor, Seth R., et al. "Molecular topography of an entire nervous system." Cell 184.16 (2021): 4329-4347.

Appraisal of whether the author achieved their aims, and whether results support their conclusions:
The author achieved their aims by recapitulating key connectivity motifs from single-cell gene expression data in the mouse retina. Furthermore, the model setup allowed for insight into gene signatures and interactions, however could have benefited from a deeper evaluation of the accuracy of these signatures. The author claims the method sets a new benchmark for single-cell transcriptomic analysis of synaptic connections. This should be more rigorously proven. (I'm not sure I can speak on the novelty of the method)

Discussion of the likely impact of the work on the field, and the utility of methods and data to the community :
This study provides an understandable bilinear model for decoding the genetic programming of neuronal type connectivity. The proposed model leaves the door open for further testing and comparison with alternative linear and/or non-linear models, such as neural network-based models. In addition to more complex models, this model can be built on to include higher resolution data such as more gene expression dimensions, different types of connectivity measures, and additional omics data.

Reviewer #2 (Public Review):

Summary:
In this study, Mu Qiao employs a bilinear modeling approach, commonly utilized in recommendation systems, to explore the intricate neural connections between different pre- and post-synaptic neuronal types. This approach involves projecting single-cell transcriptomic datasets of pre- and post-synaptic neuronal types into a latent space through transformation matrices. Subsequently, the cross-correlation between these projected latent spaces is employed to estimate neuronal connectivity. To facilitate the model training, connectomic data is used to estimate the ground-truth connectivity map. This work introduces a promising model for the exploration of neuronal connectivity and its associated molecular determinants. However, it is important to note that the current model has only been tested with Bipolar Cell and Retinal Ganglion Cell data, and its applicability in more general neuronal connectivity scenarios remains to be demonstrated.

Strengths:
This study introduces a succinct yet promising computational model for investigating connections between neuronal types. The model, while straightforward, effectively integrates single-cell transcriptomic and connectomic data to produce a reasonably accurate connectivity map, particularly within the context of retinal connectivity. Furthermore, it successfully recapitulates connectivity patterns and helps uncover the genetic factors that underlie these connections.

Weaknesses:
1. The study lacks experimental validation of the model's prediction results.
2. The model's applicability in other neuronal connectivity settings has not been thoroughly explored.
3. The proposed method relies on the availability of neuronal connectomic data for model training, which may be limited or absent in certain brain connectivity settings.

Author Response

Response to Reviewer 1:

Summary of what the author was trying to achieve: In this study, the author aimed to develop a method for estimating neuronal-type connectivity from transcriptomic gene expression data, specifically from mouse retinal neurons. They sought to develop an interpretable model that could be used to characterize the underlying genetic mechanisms of circuit assembly and connectivity.

Strengths: The proposed bilinear model draws inspiration from commonly implemented recommendation systems in the field of machine learning. The author presents the model clearly and addresses critical statistical limitations that may weaken the validity of the model such as multicollinearity and outliers. The author presents two formulations of the model for separate scenarios in which varying levels of data resolution are available. The author effectively references key work in the field when establishing assumptions that affect the underlying model and subsequent results. For example, correspondence between gene expression cell types and connectivity cell types from different references are clearly outlined in Tables 1-3. The model training and validation are sufficient and yield a relatively high correlation with the ground truth connectivity matrix. Seemingly valid biological assumptions are made throughout, however, some assumptions may reduce resolution (such as averaging over cell types), thus missing potentially important single-cell gene expression interactions.

Thank you for acknowledging the strengths of this work. The assumption to average gene expression data across individual cells within a given cell type was made in response to the inherent limitations of, for example, the mouse retina dataset, where individual cell-level connectivity and gene expression data are not profiled jointly (the second scenario in our paper). This approach was a necessary compromise to facilitate the analysis at the cell type level. However, in datasets where individual cell-level connectivity and gene expression data are matched, such as the C.elegans dataset referenced below, our model can be applied to achieve single-cell resolution (the first scenario in our paper), offering a more detailed understanding of genetic underpinnings in neuronal connectivity.

Weaknesses: The main results of the study could benefit from replication in another dataset beyond mouse retinal neurons, to validate the proposed method. Dimensionality reduction significantly reduces the resolution of the model and the PCA methodology employed is largely non-deterministic. This may reduce the resolution and reproducibility of the model. It may be worth exploring how the PCA methodology of the model may affect results when replicating. Figure 5, ’Gene signatures associated with the two latent dimensions’, lacks some readability and related results could be outlined more clearly in the results section. There should be more discussion on weaknesses of the results e.g. quantification of what connectivity motifs were not captured and what gene signatures might have been missed.

I value the suggestion of validating the propose method in another dataset. In response, I found the C.elegans dataset in the references the reviewer suggested below a good candidate for this purpose, and I plan to explore this dataset and incorporate findings in the revised manuscript. I understand the concerns regarding the PCA methodology and its potential impact on the model’s resolution and reproducibility. In response, alternative methods, such as regularization techniques, will be explored to address these issues. Additionally, I agree that enhancing the clarity and readability of Figure 5, as well as including a more comprehensive discussion of the model’s limitations, would significantly strengthen the manuscript.

The main weakness is the lack of comparison against other similar methods, e.g. methods presented in Barabási, Dániel L., and Albert-László Barabási. "A genetic model of the connectome." Neuron 105.3 (2020): 435-445. Kovács, István A., Dániel L. Barabási, and Albert-László Barabási. "Uncovering the genetic blueprint of the C. elegans nervous system." Proceedings of the National Academy of Sciences 117.52 (2020): 33570-33577. Taylor, Seth R., et al. "Molecular topography of an entire nervous system." Cell 184.16 (2021): 4329-4347.

Thank you for highlighting the importance of comparing our model with others, particularly those mentioned in your comments. After reviewing these papers, I find that our bilinear model aligns closely with the methods described, especially in [1, 2]. To see this, let’s start with Equation 1 in Kovács et al. [2]:

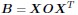
In this equation, B represents the connectivity matrix, while X denotes the gene expression patterns of individual neurons in C.elegans. The operator O is the genetic rule operator governing synapse formation, linking connectivity with individual neuronal expression patterns. It’s noteworthy that the work of Barabási and Barabási [1] explores a specific application of this framework, focusing on O for B that represents biclique motifs in the C.elegans neural network.

To identify the the operator O, the authors sought to minimize the squared residual error:

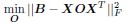
with regularization on O.

Adopting the notation from our bilinear model paper and using Z to represent the connectivity matrix, the above becomes

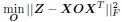
Coming back to the bilinear model formulation, the optimization problem, as formulated for the C.elegans dataset where individual neuron connectivity and gene expression are accessible, takes the form:

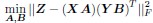
where we consider each neuron as a distinct neuronal type. In addition, we extend the dimensions of X and Y to encompass the entire set of neurons in C.elegans, with X = Y ∈ Rn×p, where n signifies the total number of neurons and p the number of genes. Accordingly, our optimization challenge evolves into:

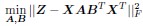
Upon comparison with the earlier stated equation, it becomes clear that our approach aligns consistently with the notion of O = ABT. This effectively results in a decomposition of the genetic rule operator O. This decomposition extends beyond mere mathematical convenience, offering several substantial benefits reminiscent of those seen in the collaborative filtering of recommendation systems:

• Computational Efficiency: The primary advantage of this approach is its improvement in computational efficiency. For instance, solving for O ∈ Rp×p necessitates determining p2 entries. In contrast, solving for A ∈ Rp×d and B ∈ Rp×d involves determining only 2pd entries, where p is the number of genes, and d is the number of latent dimensions. Assuming the existence of a lower-dimensional latent space (d << p) that captures the essential variability in connectivity, resolving A and B becomes markedly more efficient than resolving O. Additionally, from a computational system design perspective, inferring the connectivity of a neuron allows for caching the latent embeddings of presynaptic neurons XA or postsynaptic neurons XB with a space complexity of O(nd). This is significantly more space-efficient than caching XO or OXT, which has a space complexity of O(np). This difference is particularly notable when dealing with large numbers of neurons, such as those in the entire mouse brain. The bilinear modeling approach thus enables effective handling of large datasets, simplifying the optimization problem and reducing computational load, thereby making the model more scalable and faster to execute.

• Interpretability: The separation into A for presynaptic features and B for postsynaptic features provides a clearer understanding of the distinct roles of pre- and post- synaptic neurons in forming the connection. By projecting the pre- and post- synaptic neurons into a shared latent space through XA and YB, one can identify meaningful representations within each axis, as exemplified in different motifs from the mouse retina dataset. The linear characteristics of A and B facilitate direct evaluation of each gene’s contribution to a latent dimension. This interpretability, offering insights into the genetic factors influencing synaptic connections, is beyond what O could provide itself.

• Flexibility and Adaptability: The bilinear model’s adaptability is another strength. Much like collaborative filtering, which can manage very different user and item features, our bilinear model can be tailored to synaptic partners with genetic data from varied sources. A potential application of this model is in deciphering the genetic correlates of long-range projectomic rules, where pre- and post-synaptic neurons are processed and sequenced separately, or even involving post-synaptic targets being brain regions with genetic information acquired through bulk sequencing. This level of flexibility also allows for model adjustments or extensions to incorporate other biological factors, such as proteomics, thereby broadening its utility across various research inquiries into the determinants of neuronal connectivity.

In the study by Taylor et al. [3], the authors introduced a generalization of differential gene expressions (DGE) analysis called network DGE (nDGE) to identify genetic determinants of synaptic connections. It focuses on genes co-expressed across pairs of neurons connected, compared with pairs without connection.

As the authors acknowledged in the method part of the paper, nDGE can only examine single genes co-expressed at synaptic terminals: "While the nDGE technique introduced here is a generalization of standard DGE, interrogating the contribution of pairs of genes in the formation and maintenance of synapses between pairs of neurons, nDGE can only account for a single co-expressed gene in either of the two synaptic terminals (pre/post)."

In contrast, the bilinear model offers a more comprehensive analysis by seeking a linear combination of gene expressions in both pre- and post-synaptic neurons. This model goes beyond the scope of examining individual co-expressed genes, as it incorporates different weights for the gene expressions of pre- and post-synaptic neurons. This feature of the bilinear model enables it to capture not only homogeneous but also complex and heterogeneous genetic interactions that are pivotal in synaptic connectivity. This highlights the bilinear model’s capability to delve into the intricate interactions of synaptic gene expression.

Appraisal of whether the author achieved their aims, and whether results support their conclusions: The author achieved their aims by recapitulating key connectivity motifs from single-cell gene expression data in the mouse retina. Furthermore, the model setup allowed for insight into gene signatures and interactions, however could have benefited from a deeper evaluation of the accuracy of these signatures. The author claims the method sets a new benchmark for single-cell transcriptomic analysis of synaptic connections. This should be more rigorously proven. (I’m not sure I can speak on the novelty of the method)

I value your appraisal. In response, additional validation of the bilinear model on a second dataset will be undertaken.

Discussion of the likely impact of the work on the field, and the utility of methods and data to the community : This study provides an understandable bilinear model for decoding the genetic programming of neuronal type connectivity. The proposed model leaves the door open for further testing and comparison with alternative linear and/or non-linear models, such as neural networkbased models. In addition to more complex models, this model can be built on to include higher resolution data such as more gene expression dimensions, different types of connectivity measures, and additional omics data.

Thank you for your positive assessment of the potential impact of the study.

Response to Reviewer 2:

Summary: In this study, Mu Qiao employs a bilinear modeling approach, commonly utilized in recommendation systems, to explore the intricate neural connections between different pre- and post-synaptic neuronal types. This approach involves projecting single-cell transcriptomic datasets of pre- and post-synaptic neuronal types into a latent space through transformation matrices. Subsequently, the cross-correlation between these projected latent spaces is employed to estimate neuronal connectivity. To facilitate the model training, connectomic data is used to estimate the ground-truth connectivity map. This work introduces a promising model for the exploration of neuronal connectivity and its associated molecular determinants. However, it is important to note that the current model has only been tested with Bipolar Cell and Retinal Ganglion Cell data, and its applicability in more general neuronal connectivity scenarios remains to be demonstrated.

Strengths: This study introduces a succinct yet promising computational model for investigating connections between neuronal types. The model, while straightforward, effectively integrates singlecell transcriptomic and connectomic data to produce a reasonably accurate connectivity map, particularly within the context of retinal connectivity. Furthermore, it successfully recapitulates connectivity patterns and helps uncover the genetic factors that underlie these connections.

Thank you for your positive assessment of the paper.

Weaknesses:

1. The study lacks experimental validation of the model’s prediction results.

Thank you for pointing out the importance of experimental validation. I acknowledge that the current version of the study is focused on the development and validation of the computational model, using the datasets presently available to us. Moving forward, I plan to collaborate with experimental neurobiologists. These collaborations are aimed at validating our model’s predictions, including the delta-protocadherins mentioned in the paper. However, considering the extensive time and resources required for conducting and interpreting experimental results, I believe it is more pragmatic to present a comprehensive experimental study, including the design and execution of experiments informed by the model’s predictions, in a separate follow-up paper. I intend to include a paragraph in the discussion of this paper outlining the future direction for experimental validation.

1. The model’s applicability in other neuronal connectivity settings has not been thoroughly explored.

I recognize the importance of assessing the model across different neuronal systems. In response to similar feedback from Reviewer 1, I am keen to extend the study to include the C.elegans dataset mentioned earlier. The results from applying our bilinear model to the second dataset will be incorporated into the revised manuscript.

1. The proposed method relies on the availability of neuronal connectomic data for model training, which may be limited or absent in certain brain connectivity settings.

The concern regarding the dependency of our model on the availability of connectomic data is valid. While complete connectomes are available for organisms like C.elegans and Drosophila, and efforts are underway to map the connectome of the entire mouse brain, such data may not always be accessible for all research contexts. Recognizing this limitation, part of the ongoing research is to explore ways to adapt our model to the available data, such as projectomic data. Furthermore, our bilinear model is compatible with trans-synaptic virus-based sequencing techniques [4, 5], allowing us to leverage data from these experimental approaches to uncover the genetic underpinnings of neuronal connectivity. These initiatives are crucial steps towards broadening the applicability of our model, ensuring its relevance and usefulness in diverse brain connectivity studies where detailed connectomic data may not be readily available.

References

[1] Dániel L. Barabási and Albert-László Barabási. A genetic model of the connectome. Neuron, 105(3):435–445, 2020.

[2] István A. Kovács, Dániel L. Barabási, and Albert-László Barabási. Uncovering the genetic blueprint of the c. elegans nervous system. Proceedings of the National Academy of Sciences, 117(52):33570–33577, 2020.

[3] Seth R. Taylor, Gabriel Santpere, Alexis Weinreb, Alec Barrett, Molly B. Reilly, Chuan Xu, Erdem Varol, Panos Oikonomou, Lori Glenwinkel, Rebecca McWhirter, Abigail Poff, Manasa Basavaraju, Ibnul Rafi, Eviatar Yemini, Steven J. Cook, Alexander Abrams, Berta Vidal, Cyril Cros, Saeed Tavazoie, Nenad Sestan, Marc Hammarlund, Oliver Hobert, and David M. 3rd Miller. Molecular topography of an entire nervous system. Cell, 184(16):4329–4347, 2021.

[4] Nicole Y. Tsai, Fei Wang, Kenichi Toma, Chen Yin, Jun Takatoh, Emily L. Pai, Kongyan Wu, Angela C. Matcham, Luping Yin, Eric J. Dang, Denise K. Marciano, John L. Rubenstein, Fan Wang, Erik M. Ullian, and Xin Duan. Trans-seq maps a selective mammalian retinotectal synapse instructed by nephronectin. Nat Neurosci, 25(5):659–674, May 2022.

[5] Aixin Zhang, Lei Jin, Shenqin Yao, Makoto Matsuyama, Cindy van Velthoven, Heather Sullivan, Na Sun, Manolis Kellis, Bosiljka Tasic, Ian R. Wickersham, and Xiaoyin Chen. Rabies virusbased barcoded neuroanatomy resolved by single-cell rna and in situ sequencing. bioRxiv, 2023.