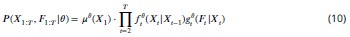High frequency spike inference with particle Gibbs sampling

Reviewer #1 (Public review):

Summary:

In this study, Diana et al. present a Monte Carlo-based method to perform spike inference from calcium imaging data. A particular strength of their approach is that they can estimate not only averages but also uncertainties of the modeled process. The authors focus on the quantification of spike time uncertainties in simulated data and in data recorded with high sampling rate in cebellar slices with GCaMP8f, and they demonstrate the high temporal precision that can be achieved with their method to estimate spike timing.

Strengths:

- The author provide a solid ground work for sequential Monte Carlo-based spike inference, which extends previous work of Pnevmatikakis et al., Greenberg et al. and others.

- The integration of two states (silence vs. burst firing) seems to improve the performance of the model.

- The acquisition of a GCaMP8f dataset in cerebellum is useful and helps make the point that high spike time inference precision is possible under certain conditions.

Weaknesses:

- Although the algorithm is compared (in the revised manuscript) to other models to infer individual spikes (e.g., MLSpike), these comparisons could be more comprehensive. Future work that benchmarks this and other algorithms under varying conditions (e.g., noise levels, temporal resolution, calcium indicators) would help assess and confirm robustness and useability of this algorithm.

- The mathematical complexity underlying the method may pose challenges for experimentalist who may want to use the methods for their analyses. While this is not a weakness of the approach itself, this highlights the need for further validation and benchmarking in future work, to build user confidence.

Reviewer #2 (Public review):

Summary:

Methods to infer action potentials from fluorescence-based measurements of intracellular calcium dynamics are important for optical measurements of activity across large populations of neurons. The variety of existing methods can be separated into two broad classes: a) model-independent approaches that are trained on ground truth datasets (e.g., deep networks), and b) approaches based on a model of the processes that link action potentials to calcium signals. Models usually contains parameters describing biophysical variables, such as rate constants of the calcium dynamics and features of the calcium indicator. The method presented here, PGBAR, is model-based and uses a Bayesian approach. A novelty of PGBAR is that static parameters and state variables are jointly estimated using particle Gibbs sampling, a sequential Monte Carlo technique that can efficiently sample the latent embedding space.

Strengths:

A main strength of PGBAR is that it provides probability distributions rather than point estimates of spike times. This is different from most other methods and may be an important feature in cases when estimates of uncertainty are desired. Another important feature of PGBAR is that it estimates not only the state variable representing spiking activity, but also other variables such as baseline fluctuations and stationary model variables, in a joint process. PGBAR can therefore provide more information than various other methods. The information in the github repository is well-organized.

Weaknesses:

On the other hand, the accuracy of spike train reconstructions is not higher than that of other model-based approaches, and clearly lower than the accuracy of a model-independent approach based on a deep network. The authors demonstrate convincingly that PGBAR can resolve inter-spike intervals in the range of 5 ms using fluorescence data obtained with a very fast genetically encoded calcium indicator at very high sampling rates (line scans at >= 1 kHz).

Author response:

The following is the authors’ response to the previous reviews

We thank the Reviewers and the Editor for their thoughtful and constructive feedback. In the revised manuscript, we have addressed all comments thoroughly and made several substantial improvements:

● Benchmarking against state-of-the-art methods: We now provide a detailed comparison of our method, PGBAR, with MLspike and CASCADE using our cerebellar dataset recorded at high sampling rates. This comparison demonstrates that PGBAR offers more reliable spike time estimates with significantly lower variability in temporal accuracy (Figure 9).

● Quantitative analyses: We replaced qualitative statements with quantitative metrics. For example, we now report Pearson’s correlation (>0.95) of spike probabilities across trials and 100% of posterior samples with correct spike number detection during low SNR conditions (Figures 7 and 8).

● Clarified modeling rationale: We elaborated on the motivation behind modeling bursting dynamics using a hidden two-state process, which helps mitigate bias in spike detection under non-stationary firing conditions.

● Model identifiability and robustness: We demonstrate that our approach avoids parameter degeneracy through careful model design and parameter reparameterization. Sensitivity analyses (Figure 10) show that PGBAR is more robust to hyperparameter variation than MLspike.

● Improved clarity and accessibility: We revised the Introduction and Results sections to better explain the context, goals, and implications of our method, and clarified the advantages of joint parameter and state inference within our Bayesian framework.

We believe that these additions significantly strengthen our manuscript and demonstrate the utility of PGBAR for high-temporal-precision spike inference. Please find below our detailed responses to both Public Reviews and Recommendations for the authors.

Public Reviews

Reviewer #1 (Public Review):

Summary:

In this study, Diana et al. present a Monte Carlo-based method to perform spike inference from calcium imaging data. A particular strength of their approach is that they can estimate not only averages but also uncertainties of the modelled process. The authors then focus on the quantification of spike time uncertainties in simulated data and in data recorded with a high sampling rate in cerebellar slices with GCaMP8f.

Strengths:

- The authors provide a solid groundwork for sequential Monte Carlo-based spike inference, which extends previous work of Pnevmatikakis et al., Greenberg et al., and others.

- The integration of two states (silence vs. burst firing) seems to improve the performance of the model.

- The acquisition of a GCaMP8f dataset in the cerebellum is useful and helps make the point that high spike time inference precision is possible under certain conditions.

Weaknesses:

- The algorithm is designed to predict single spike times. Currently, it is not benchmarked against other algorithms in terms of single spike precision and spike time errors. A benchmarking with the most recent other SMC model and another good model focused on single spike outputs (e.g., MLSpike) would be useful to have.

We thank the reviewer for the observation. In our revised manuscript, we have included a detailed comparison of spike time accuracy between our method, MLspike, and the supervised method, CASCADE, now summarized in Figure 9. In this analysis, we used our in vitro dataset to estimate the average temporal accuracy of spike detection across the three methods. As discussed in the main text, the average temporal accuracy was defined as the time difference between ground truth and the nearest detected spikes averaged across the ground truth. The distributions of temporal accuracies across our experiments obtained from MLspike, Cascade, and PGBAR differ in their spread, with 10th-to-90th percentile ranges of 14 ms, 8 ms, and 3 ms, respectively. This result demonstrates that PGBAR spike time estimates are more reliable than MLspike and CASCADE across trials, with a narrower unbiased distribution of temporal accuracy.

A direct comparison of PGBAR with the Sequential Binding Model (SBM) developed by Greenberg et al. was not possible since the biophysical model is designed around early GCaMP variants and thus not suitable for inference with our GCaMP8f dataset. We generally agree that employing realistic models of the calcium indicator can improve inference, however, PGBAR responds to a different question, namely how to simultaneously infer spike times and model parameters, which was still an issue with the SBM approach.

Some of the analyses and benchmarks seem too cursory, and the reporting simply consists of a visual impression of results instead of proper analysis and quantification. For example, the authors write "The spike patterns obtained using our method are very similar across trials, showing that PGBAR can reliably detect single-trial action potential-evoked GCaMP8f fluorescence transients." This is a highly qualitative statement, just based on the (subjective) visual impression of a plot. Similarly, the authors write "we could reliably identify the two spikes in each trial", but this claim is not supported by quantification or a figure, as far as I can see.

We thank the reviewer for this remark. We have now justified quantitatively our statement regarding the similarity across trials. In the revised preprint, we explain that in the specific experiment illustrated in Figure 7, Pearson’s pairwise correlation between spike probabilities (Gaussian filtered with 20 ms bandwidth) across trials is always larger than 0.95. The statement quoted by the reviewer, "we could reliably identify the two spikes in each trial" refers to the fact that in 100% of the posterior samples, generated from the analysis of each trial, we detected 2 spikes in the time window considered. The temporal accuracy of our detection was then illustrated for all trials in Figure 7H, where we compared the posterior distribution of the inter-spike interval between the first two spikes across trials.

The statement referred by the Reviewer has been revised to read

(line 319) “The Pearson’s pairwise correlation between spike probabilities (Gaussian filtered with 20 ms bandwidth) across trials is always larger than 0.95, which demonstrates that PGBAR provides robust predictions across trials and it can reliably detect single-trial action potential-evoked GCaMP8f fluorescence transients.”

We revised the second statement as:

(line 324) “Despite the relatively low SNR, 100% of the posterior samples contained two spikes in the considered time interval.”

The authors write "but the trade-off between temporal accuracy, SNR and sampling frequency must be considered", but they don't discuss these trade-offs systematically.

We thank the reviewer for the comment. We have now removed the quoted sentence in the updated preprint. We revised this statement to read:

(line 302) “Based on this analysis we expect PGBAR to provide accurate estimates of inter-spike intervals down to 5 ms.”

It has been shown several times from experimental data that spike inference with single spike resolution does not work well (Huang et al. eLife, 2021; Rupprecht et al., Nature Neuroscience, 2021) in general. This limitation should be discussed with respect to the applicability of the proposed algorithm for standard population calcium imaging data.

We thank the reviewer for this comment. Detecting single spike times is indeed a difficult task. Compared to previous methods for single spike estimation, the advantage of our statistical approach is the rigorous analysis of uncertainties propagated by unknown model parameters and noisy recordings. This is an important aspect that was missing in previous approaches and that we were able to address thanks to our fully probabilistic approach.

Several analyses are based on artificial, simulated data with simplifying assumptions. Ever since Theis et al., Neuron, 2016, it has been known that artificially generated ground truth data should not be used as the primary means to evaluate spike inference algorithms. It would have been informative if the authors had used either the CASCADE dataset or their cerebellum dataset for more detailed analyses, in particular of single spike time precision.

We thank the reviewer for this comment.

To address the reviewer’s concern about single spike time precision, we have added to our revised preprint a further comparison between the temporal accuracy of PGBAR, CASCADE, and MLspike for our cerebellar dataset (Fig. 9, already discussed above).

Nevertheless, as pointed out by the reviewer, simulated data should not be used as the primary means to evaluate the performance of an inference algorithm. However, it is standard practice in the field of model-based inference to validate the approach first with data generated by the same model used for inference. This step is usually done for two main reasons: first, for internal consistency of the method, and second, to explore the regimes where inference is achievable. We made use of simulated data to address specific questions. Specifically, in Figure 2, we illustrate the analysis of data simulated using the same model for inference. In Figure 3, we used simulated data to highlight the importance of modeling bursting activity to avoid biases induced by non-homogeneous firing rates. In Figure 6, we used simulated data to explore the theoretical accuracy of PGBAR under different conditions of signal-to-noise ratio and acquisition frequencies.

In its current state, the sum of the current weaknesses makes the suggested method, while interesting for experts, rather unattractive for experimentalists who want to perform spike inference on their recorded calcium imaging data.

In our preprint, we illustrated the application of PGBAR to benchmark data and our cerebellar recordings. Therefore, our approach can be part of the calcium imaging data analysis pipeline. The advantage of estimating statistical uncertainties and model parameters makes PGBAR an attractive tool for the wide neuroscience community interested in spike inference and statistical accuracy. In addition, as noted by Reviewer 2, our code is well documented. User-friendliness and integrating our method within GUI analysis software might be the next step if there is increasing interest in using this method.

Other comments:

One of the key features of the SMC model is the assumption of two states (bursting vs. non-bursting). However, while it seems clear that this approach is helpful, it is not clear where this idea comes from, from an observation of the data or another concept.

We thank the reviewer for this comment. As the reviewer pointed out, accounting for two firing regimes is helpful as it prevents biases in estimating the number of spikes when the firing rate is non-stationary and does not follow single-frequency Poisson statistics (as shown in Figure 3 of our preprint), as expected during in vivo recordings. Animals can alter their behavioral state and be exposed to different sensory stimulations, which condition the activity of neurons. A first step beyond the assumption of a steady firing rate is indeed to introduce a hidden two-state process to separate periods of high and low firing rates. In our revised text, we explicitly discuss the rationale behind this choice. We want to emphasize that PGBAR is the only model-based approach that accounts for nonhomogeneous firing rates. In addition, due to the binary character of the underlying bursting state and the high dimensionality of the problem, traditional optimization methods would not be applicable. We solved this problem by applying modern sequential Monte Carlo algorithms (PGAS, Lindsten 2014, for joint estimation for time-varying signals and model parameters) for the first time in the context of spike inference. In summary, the novelty of our work is both in modeling the firing statistics and the inference strategy used.

Another SMC algorithm (Greenberg et al., 2018) stated that the fitted parameters showed some degeneracy, resulting in ambiguous fitting parameters. It would be good to know if this problem was avoided by the authors.

As the reviewer pointed out, one of the weaknesses of the SBM approach is the optimization of the model parameters. This is expected, as SBM uses a biophysical model of the calcium indicator, and a general issue of dynamical models is the presence of so-called sloppy directions in the parameter space, which leads to ambiguous estimations. This is an intrinsic problem due to the model complexity also associated with poorly known parameters such as kinetic constants, which are hard to constrain experimentally. PGBAR uses a much simpler model to describe calcium transients (a second-order autoregressive process) precisely to avoid the non-identifiability of model parameters. Furthermore, we employed a parameterization of the autoregressive model (discussed in the Reparameterization section of Materials and Methods) regarding peak response to a single action potential, decay constant, and rise time (i.e., time to peak). These phenomenological parameters are well documented for different calcium indicators, which enables us to design appropriate prior distributions that significantly facilitate the identifiability of parameters.

Reviewer #2 (Public Review):

Summary:

Methods to infer action potentials from fluorescence-based measurements of intracellular calcium dynamics are important for optical measurements of activity across large populations of neurons. The variety of existing methods can be separated into two broad classes: a) model-independent approaches that are trained on ground truth datasets (e.g., deep networks), and b) approaches based on a model of the processes that link action potentials to calcium signals. Models usually contain parameters describing biophysical variables, such as rate constants of the calcium dynamics and features of the calcium indicator. The method presented here, PGBAR, is model-based and uses a Bayesian approach. A novelty of PGBAR is that static parameters and state variables are jointly estimated using particle Gibbs sampling, a sequential Monte Carlo technique that can efficiently sample the latent embedding space.

Strengths:

A main strength of PGBAR is that it provides probability distributions rather than point estimates of spike times. This is different from most other methods and may be an important feature in cases when estimates of uncertainty are desired. Another important feature of PGBAR is that it estimates not only the state variable representing spiking activity but also other variables such as baseline fluctuations and stationary model variables, in a joint process. PGBAR can therefore provide more information than various other methods. The information in the GitHub repository is well-organised.

Weaknesses:

On the other hand, the accuracy of spike train reconstructions is not higher than that of other model-based approaches, and clearly lower than the accuracy of a model-independent approach based on a deep network. The authors demonstrate convincingly that PGBAR can resolve inter-spike intervals in the range of 5 ms using fluorescence data obtained with a very fast genetically encoded calcium indicator at very high sampling rates (line scans at >= 1 kHz). It would be interesting to more systematically compare the performance of PGBAR to other methods in this regime of high temporal resolution, which has not been explored much.

We appreciate the Reviewer’s comment. In response to this observation, we have now included a thorough comparison of PGBAR, MLspike, and CASCADE in addition to the analysis of our cerebellar dataset acquired with a high sampling rate (Figure 9 in the revised preprint). PGBAR and CASCADE predictions are comparable in terms of correlation with the ground truth spikes, and both outperform MLspike. We have also quantified the spike time accuracy as the average distance between ground-truth spikes and the nearest prediction for all the methods. Among the three, PGBAR has the lowest variability of spike time accuracy across our experimental trials. We concluded that while PGBAR and CASCADE show comparable correlations with ground truth, our method provides more reliable spike time estimates.

Recommendations for the authors

Reviewing Editor (Recommendations For The Authors):

In the discussion with reviewers, it was also suggested that while the manuscript emphasized the high temporal resolution of the method (5 ms), this was achieved under favorable conditions (very high sampling rate, fast indicator). Results cannot be compared easily to alternative methods based on published data because these conditions are unusual. Do other methods (at least some of which are presumably easier to use) achieve similar temporal resolution when applied to the same dataset? I feel this could be addressed easily and add valuable information.

We thank the Reviewing Editor for the suggestion. In our revised preprint, we have now added a full comparison between the performance of PGBAR, MLspike (as an alternative Bayesian approach), and CASCADE (as a state-of-the-art supervised method) tested on our cerebellar dataset. This analysis highlights the improved reliability of our method in terms of temporal accuracy and trial-to-trial variability.

Reviewer #1 (Recommendations For The Authors):

- It is in several places difficult to understand the bigger context of some details. For example, the authors write "In this work, we use Monte Carlo methods to approximate the posterior distribution in Eq. (13)." It would be helpful to state what the bigger goal behind this procedure is, here and at other places. Please go through the Introduction and the Results, there is some room for improvement in terms of accessibility.

We thank the Reviewer for the comment. Monte Carlo methods are generally used when dealing with intractable (non-analytical) probability distributions, which is the case for the models used for spike inference. The “bigger goal behind this procedure” is just the numerical approximation of posterior probabilities, which simply formalizes the question of estimating unknowns from data given a statistical model according to the Bayesian theorem. The advantage of Monte Carlo methods, compared to other techniques (e.g., variational methods), is to be statistically unbiased, which is one of the main reasons why we developed this approach. We clarified the goal of the Monte Carlo inference In the introduction, by adding the following text:

(line 79) “In this work we employ the particle Gibbs (PG) sampler on a bursting autoregressive (BAR) model of time series calcium-dependent fluorescence to provide not only point estimates of spike times but also quantify the statistical uncertainty of each estimate. This is important for downstream analyses such as comparing activity across neurons or conditions.”

We introduce the Results/Model section with the sentence:

(line 91) “To infer spike times and their uncertainty from noisy fluorescence traces, we first build a probabilistic generative model that captures the main dynamics underlying the fluorescence signal.”

And later on in the Results/Sequential Monte Carlo section, we added:

(line 156) “The model described in the previous section is analytically intractable, therefore we employ Monte Carlo methods to sample from the posterior distribution in Eq. (13) of spike times and model parameters, allowing us to make probabilistic inferences rather than relying on point estimates alone.”

In the Abstract: "it provides a flexible statistical framework to test more specific models of calcium indicators". What is meant by this sentence? I was unable to find any results related to this statement.

In our work, we propose a statistical model (depicted in Figure 1A) that accounts for a binary model for non-homogeneous firing, a Gaussian random walk to describe the modulation of the baseline fluorescence coupled to an autoregressive process to link spikes to fluorescence. The phrase quoted by the Reviewer refers to the possibility of replacing the autoregressive model with more specific models of calcium indicators in the future. For instance, employing the biophysical models of calcium indicators to refine the link between spikes and calcium fluorescence. The inference algorithm does not depend on the specific spike-to-fluorescence model. In this sense, our framework is flexible as it offers the opportunity to analyze data acquired using other calcium indicators.

The authors write "One of the key advantages of our sampling algorithm is the joint estimation of latent states and time-independent model parameters." Why is this an advantage? Advantage compared to which alternative algorithm?

We thank the reviewer for this comment. All existing spike inference algorithms use ad-hoc techniques to choose or calibrate the hyperparameters introduced. The estimation of spike times is in general highly sensitive to parameters such as the peak fluorescence in response to single action potentials, kinetic constants, noise levels, baseline, or any regularization or model parameter. These parameters are usually unknown, and all available inference methods provide additional prescriptions to calibrate them. This problem can lead to the propagation of errors and systematic biases. Modern Monte Carlo algorithms, such as the ones employed in our work, address specifically this problem by targeting the joint posterior distribution of all time-dependent variables and the model parameters. Compared to previous approaches, our method offers a statistically rigorous algorithm to identify the parameters. Furthermore, this approach enables us to use Bayesian priors to constrain their ranges without introducing ad-hoc biases and reducing the sensitivity to inaccurate choices of hyperparameters compared to other methods (MLspike), as shown in our new Figure 10 (following a suggestion from Reviewer 2), where we illustrate a parameter sensitivity analysis across MLspike and PGBAR (see responses to Reviewer 2 for further details). We clarified this in the Introduction by adding the sentence:

(line 60) “[...] Moreover, current Bayesian methods do not treat time-independent model parameters (e.g. rate constants) and dynamic variables equally. Instead, they require additional optimization procedures to calibrate model parameters, typically relying on ad-hoc tuning or grid search. This separation can lead to biased inference and poorly calibrated uncertainty estimates, particularly when parameters such as calcium decay time or spike amplitude are inaccurately specified. In contrast, our approach jointly infers both spike times and model parameters within a unified Bayesian framework, enabling uncertainty-aware estimation and avoiding separate, error-prone calibration steps.”

and In the section “Validation and performance of PGBAR” we added the text:

(line 201) “One of the key advantages of our sampling algorithm is the joint estimation of latent states and time-independent model parameters, such as spike amplitude, decay time, noise level, and baseline variance. This stands in contrast to most existing spike inference algorithms, which rely on fixed or externally calibrated parameters. Such fixed-parameter methods are vulnerable to systematic errors when parameter values are uncertain or misestimated. By jointly sampling from the posterior of all variables and parameters, our method propagates uncertainty correctly and mitigates bias due to manual tuning or poor initialization.”

We also added the following text in the discussion:

(line 411) “The estimation of time-independent model parameters is a well-known issue in spike detection algorithms, typically requiring ad-hoc calibration procedures, grid search, or manual settings. Because spike inference is sensitive to parameters such as the calcium response amplitude, rise and decay kinetics, and noise level, errors in these parameters can substantially affect the accuracy of spike time estimates. By jointly sampling model parameters and latent variables, PGBAR eliminates the need for separate calibration and ensures that uncertainty in parameters is propagated to spike time estimates in a principled way. As illustrated in Figure 10, this leads to a more robust inference compared to existing methods like MLSpike, which show greater sensitivity to parameter variation. In addition, PGBAR enables the users to calibrate the inference of action potentials by setting prior mean and variance of phenomenological parameters (e.g. rise and decay constants, firing rates, bursting frequencies).”

The authors write "We tested our approach on the fast calcium indicator GCaMP8f (...)". Be more precise. Why exactly were these experiments done, what aspects of the algorithm were supposed to be tested? It is left to the reader to make sense out of these experiments. Please provide the logic of this experiment.

We thank the reviewer for the comment. We developed our method specifically for regimes of high firing rates. For this reason, in addition to the CASCADE benchmark dataset, we have tested our approach on recordings of cerebellar granule cells due to their fast spiking patterns. For this purpose, we have employed the ultrafast state-of-the-art calcium indicator GCaMP8f combined with linescan imaging techniques to enable fast acquisition rates. We added the following text in the manuscript to clarify:

(line 306) “We tested our approach on the fast calcium indicator GCaMP8f by performing high-speed (2.8 kHz) two-photon linescan calcium imaging of cerebellar granule cells in vitro. GCaMP8f was expressed in the Crus I region of the cerebellum using adeno-associated virus (AAV) injection (Fig. 7A). Compared to GCaMP6f, GCaMP8f exhibits a rise time that is nearly an order of magnitude faster, which we expected to translate into substantially improved temporal accuracy in spike time detection.”

The authors write "If we consider as reference correlation the average across the CASCADE dataset (0.75) (...)". Why would this threshold be appropriate? This sounds arbitrary; this experiment was conducted with 2.8 kHz line scan imaging of GCaMP8, while the reference stems from low-rate imaging of older indicators.

We thank the reviewer for the remark. In the sentence quoted, we have used 0.75 as a reference for the state-of-the-art correlation between ground truth and predicted spikes and indicated the lowest temporal resolution (10 ms) where the PGBAR correlation is larger than the reference value. As the Reviewer correctly pointed out, the reference 0.75 refers to datasets with much lower acquisition frequency; therefore, in our revised preprint, we have added a comparison of the correlations obtained from PGBAR, CASCADE, and MLspike using high-speed recordings of cerebellar GCs (Figure 9), showing the increased performance of our method at high temporal resolution.

How was PGBAR evaluated using a given dataset in Figure 4c or in Figure 7? It is unclear to the reviewer whether the priors were automatically/manually adjusted for each data set.

We thank the Reviewer for this comment. Briefly, for the CASCADE dataset, we have designed the priors for all parameters according to the existing characterization of the calcium indicator used in each experiment (Chen et al. 2013). For our cerebellar data, we have performed single stimulation trials for each recording, which we used to design priors on peak fluorescence response, decay constant, and time to peak fluorescence. In the Results section of the revised preprint, we clarified more specifically how priors were designed for the CASCADE and our cerebellar datasets. We have added the following statements:

(line 239) “Bayesian priors for all PGBAR parameters were adapted to each experiment according to the existing characterization of the different calcium indicators used (Chen et al., 2013).”

(line 314) “For each recorded soma and bouton we applied two types of stimulations. Single time point stimulation and a fixed stimulation pattern generated from a 20 Hz Poisson process with 29 stimulation time points. First, we used the single-stimulation trials to design prior distributions of amplitudes, rise and decay constants (Fig. 7C). Next, we used PGBAR to analyze independently each Poisson stimulation trial in Figure 7E. By generating thousands of posterior samples of spike time patterns, we obtained the spike probability for all time frames and trials (Fig. 7F).”

The authors write "This analysis illustrates the variability expected when analyzing multiple trials of the same neuron." Variability across trials of neuronal activity? Or variability of spike inference?

We thank the reviewer for the comment. In the revised text, we clarify that we refer to the variability of spike inference across trials.

The original statement has been revised to read:

(line 301) “This analysis illustrates the expected variability of spike inference when analyzing multiple trials of the same neuron.”

Technical question: How can the authors be sure that glass electrode stimulation only elicits a single AP per stimulation? This was not clear to me from the manuscript alone.

We thank the reviewer for the question. Our experimental protocol is designed in a way that in each trial we make sure a single electrical stimulation elicits a single AP. We adjust our stimulation strength until we see an all-or-none calcium transient in response to a single AP. Given the fast temporal properties of GCaMP8f, we could distinguish a single AP response from multiple APs during a single electrical stimulation. We then introduced a single stim trial ahead of each Poisson-train trial to see whether our stimulation strength could elicit a single AP response reliably and consistently. In this way, we ensured that every single stim was producing a single AP.

Figure 8: Please explain what you mean by "bouton". What is the dashed line in (A)? Why is it interesting to look at the differences between bouton and soma?

We thank the Reviewer for the comment. In the updated text we clarified that we refer to synaptic boutons along the parallel fiber (line 311) and that the dashed line in Figure 8 refers to the ground-truth number of spikes (29). We also pointed out that the estimated delay between somas and boutons is compatible with the proximity of synaptic boutons to the stimulation site along the parallel fiber by adding the following text:

(line 340) “This result is compatible with the proximity of synaptic boutons to the electrical stimulation along the parallel fiber. We analyzed both signals from somata and synaptic boutons because in vivo two-photon imaging can be made from both parts of the cell. Here we showed that our method performs reliably on both, demonstrating its robustness across recording sites.”

Reviewer #2 (Recommendations For The Authors):

The authors emphasised the result that PGBAR can resolve spike timing differences of 5 ms. However, this result was obtained based on fluorescence data measured with a very fast calcium indicator at very high sampling rates. It remains unclear how the performance of PGBAR compares to other methods in this regime of high temporal resolution, which has not been explored much in previous comparisons of methods. Potential users interested in this regime would benefit from a direct comparison to other approaches.

We thank the Reviewer for this suggestion. In our revised manuscript, we have included a detailed comparison of spike time accuracy between our method, MLspike, and Cascade, summarized in Figure 9. In this analysis, we used our in vitro dataset to estimate the average temporal accuracy of spike detection across the three methods. As discussed in the main text, the average temporal accuracy was defined as the temporal offset between the ground truth and the nearest detected spikes averaged across the ground truth. The distributions of temporal accuracies across our experiments obtained from MLspike, Cascade, and PGBAR differ in their spread, with 10th-to-90th percentile ranges of 14 ms, 8 ms, and 3 ms, respectively. This result demonstrates that PGBAR estimates are more reliable than MLspike and CASCADE across trials, with a narrower unbiased distribution of temporal accuracy.

In practice, approaches are more appealing to users when they do not require dedicated measurements to estimate parameters such as rise/decay time constants of calcium fluorescence signals within cells. Users may therefore be interested to know how results would be affected if these parameters are estimated only crudely. It would thus be useful to know how spike probability estimates vary as a function of these parameters, which should be easy to test systematically, and whether the sensitivity of PGBAR to inaccurate initial parameter estimates is lower or higher than that of other methods, which should also be easy to test. As PGBAR jointly estimates spike probabilities and model parameters, it may have an advantage here over other methods.

We thank the Reviewer for this suggestion. In the new Figure 10, we show a parametric sensitivity analysis for both PGBAR and MLspike. For PGBAR, we considered the hyperparameters of the Bayesian priors associated with the peak response to a single spike and the baseline variance, which influences how much of the fluorescence can be attributed to baseline modulation. For MLspike, we considered the transient amplitude and the decay time constant. For both methods, we varied the parameters between -50% and +50% of their optimal value and estimated the correlation between predictions and ground truth as well as the number of spikes (Figure 10A). Next, we calculated the coefficient of variation across all parameter configurations for each trial (Figure 10B). Our analysis shows that, compared to previous methods, PGBAR has a much lower sensitivity to the initial choices of the hyperparameters, confirming the intuition of the Reviewer thanks to the simultaneous inference of spike times and model parameters. This result provides an important addition to our work.

Equation 10: -1 should be in subscript (t-1). Remark: I have not fully verified the mathematical parts because some of it is beyond my expertise.

We thank the Reviewer for pointing out the typo. This has been corrected in the revised preprint.