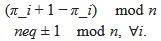Peer review process
Not revised: This Reviewed Preprint includes the authors’ original preprint (without revision), an eLife assessment, and public reviews.
Read more about eLife’s peer review process.Editors
- Reviewing EditorAdrien PeyracheMcGill University, Montreal, Canada
- Senior EditorLaura ColginUniversity of Texas at Austin, Austin, United States of America
Reviewer #1 (Public Review):
Rebecca R.G. et al. set to determine the function of grid cells. They present an interesting case claiming that the spatial periodicity seen in the grid pattern provides a parsimonious solution to the task of coding 2D trajectories using sequential cell activation. Thus, this work defines a probable function grid cells may serve (here, the function is coding 2D trajectories), and proves that the grid pattern is a solution to that function. This approach is somewhat reminiscent in concept to previous works that defined a probable function of grid cells (e.g., path integration) and constructed normative models for that function that yield a grid pattern. However, the model presented here gives clear geometric reasoning to its case.
Stemming from 4 axioms, the authors present a concise demonstration of the mathematical reasoning underlying their case. The argument is interesting and the reasoning is valid, and this work is a valuable addition to the ongoing body of work discussing the function of grid cells.
However, the case uses several assumptions that need to be clearly stated as assumptions, clarified, and elaborated on: Most importantly, the choice of grid function is grounded in two assumptions:
(1) that the grid function relies on the activation of cell sequences, and
(2) that the grid function is related to the coding of trajectories. While these are interesting and valid suggestions, since they are used as the basis of the argument, the current justification could be strengthened (references 28-30 deal with the hippocampus, reference 31 is interesting but cannot hold the whole case).
The work further leans on the assumption that sequences in the same direction should be similar regardless of their position in space, it is not clear why that should necessarily be the case, and how the position is extracted for similar sequences in different positions. The authors also strengthen their model with the requirement that grid cells should code for infinite space. However, the grid pattern anchors to borders and might be used to code navigated areas locally. Finally, referencing ref. 14, the authors claim that no existing theory for the emergence of grid cell firing that unifies the experimental observations on periodic firing patterns and their distortions under a single framework. However, that same reference presents exactly that - a mathematical model of pairwise interactions that unifies experimental observations. The authors should clarify this point.
Reviewer #2 (Public Review):
Summary:
In this work, the authors consider why grid cells might exhibit hexagonal symmetry - i.e., for what behavioral function might this hexagonal pattern be uniquely suited? The authors propose that this function is the encoding of spatial trajectories in 2D space. To support their argument, the authors first introduce a set of definitions and axioms, which then lead to their conclusion that a hexagonal pattern is the most efficient or parsimonious pattern one could use to uniquely label different 2D trajectories using sequences of cells. The authors then go through a set of classic experimental results in the grid cell literature - e.g. that the grid modules exhibit a multiplicative scaling, that the grid pattern expands with novelty or is warped by reward, etc. - and describe how these results are either consistent with or predicted by their theory. Overall, this paper asks a very interesting question and provides an intriguing answer. However, the theory appears to be extremely flexible and very similar to ideas that have been previously proposed regarding grid cell function.
Major strengths:
The general idea behind the paper is very interesting - why *does* the grid pattern take the form of a hexagonal grid? This is a question that has been raised many times; finding a truly satisfying answer is difficult but of great interest to many in the field. The authors' main assertion that the answer to this question has to do with the ability of a hexagonal arrangement of neurons to uniquely encode 2D trajectories is an intriguing suggestion. It is also impressive that the authors considered such a wide range of experimental results in relation to their theory.
Major weaknesses:
One major weakness I perceive is that the paper overstates what it delivers, to an extent that I think it can be a bit confusing to determine what the contributions of the paper are. In the introduction, the authors claim to provide "mathematical proof that ... the nature of the problem being solved by grid cells is coding of trajectories in 2-D space using cell sequences. By doing so, we offer a specific answer to the question of why grid cell firing patterns are observed in the mammalian brain." This paper does not provide proof of what grid cells are doing to support behavior or provide the true answer as to why grid patterns are found in the brain. The authors offer some intriguing suggestions or proposals as to why this might be based on what hexagonal patterns could be good for, but I believe that the language should be clarified to be more in line with what the authors present and what the strength of their evidence is.
Relatedly, the authors claim that they find a teleological reason for the existence of grid cells - that is, discover the function that they are used for. However, in the paper, they seem to instead assume a function based on what is known and generally predicted for grid cells (encode position), and then show that for this specific function, grid cells have several attractive properties.
There is also some other work that seems very relevant, as it discusses specific computational advantages of a grid cell code but was not cited here: https://www.nature.com/articles/nn.2901.
A second major weakness was that some of the claims in the section in which they compared their theory to data seemed either confusing or a bit weak. I am not a mathematician, so I was not able to follow all of the logic of the various axioms, remarks, or definitions to understand how the authors got to their final conclusion, so perhaps that is part of the problem. But below I list some specific examples where I could not follow why their theory predicted the experimental result, or how their theory ultimately operated any differently from the conventional understanding of grid cell coding. In some cases, it also seemed that the general idea was so flexible that it perhaps didn't hold much predictive power, as extra details seemed to be added as necessary to make the theory fit with the data.
I don't quite follow how, for at least some of their model predictions, the 'sequence code of trajectories' theory differs from the general attractor network theory. It seems from the introduction that these theories are meant to serve different purposes, but the section of the paper in which the authors claim that various experimental results are predicted by their theory makes this comparison difficult for me to understand. For example, in the section describing the effect of environmental manipulations in a familiar environment, the authors state that the experimental results make sense if one assumes that sequences are anchored to landmarks. But this sounds just like the classic attractor-network interpretation of grid cell activity - that it's a spatial metric that becomes anchored to landmarks.
It was not clear to me why their theory predicted the field size/spacing ratio or the orientation of the grid pattern to the wall.
I don't understand how repeated advancement of one unit to the next, as shown in Figure 4E, would cause the change in grid spacing near a reward.
I don't follow how this theory predicts the finding that the grid pattern expands with novelty. The authors propose that this occurs because the animals are not paying attention to fine spatial details, and thus only need a low-resolution spatial map that eventually turns into a higher-resolution one. But it's not clear to me why one needs to invoke the sequence coding hypothesis to make this point.
The last section, which describes that the grid spacing of different modules is scaled by the square root of 2, says that this is predicted if the resolution is doubled or halved. I am not sure if this is specifically a prediction of the sequence coding theory the authors put forth though since it's unclear why the resolution should be doubled or halved across modules (as opposed to changed by another factor).
Reviewer #3 (Public Review):
The manuscript presents an intriguing explanation for why grid cell firing fields do {\em not} lie on a lattice whose axes aligned to the walls of a square arena. This observation, by itself, merits the manuscript's dissemination to the journals audience.
The presentation is quirky (but keep the quirkiness!).
But let me recast the problem presented by the authors as one of combinatorics. Given repeating, spatially separated firing fields across cells, one obtains temporal sequences of grid cells firing. Label these cells by integers from $[n]$. Any two cells firing in succession should uniquely identify one of six directions (from the hexagonal lattice) in which the agent is currently moving.
Now, take the symmetric group $\Sigma$ of cyclic permutations on $n$ elements.
We ask whether there are cyclic permutations of $[n]$ such that
So, for instance, $(4,2,3,1)$ would not be counted as a valid permutation of $(1,2,3,4)$, as $(2,3)$ and $(1,4)$ are adjacent.
Furthermore, given $[n]$, are there two distinct cyclic permutations such that {\em no} adjacencies are preserved when considering any pair of permutations (among the triple of the original ordered sequence and the two permutations)? In other words, if we consider the permutation required to take the first permutation into the second, that permutation should not preserve any adjacencies.
{\bf Key question}: is there any difference between the solution to the combinatorics problem sketched above and the result in the manuscript? Specifically, the text argues that for $n=7$ there is only {\em one} solution.
Ideally, one would strive to obtain a closed-form solution for the number of such permutations as a function of $n$.