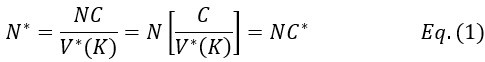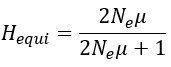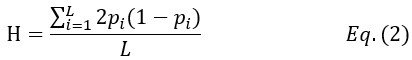The paradox of extremely fast evolution driven by genetic drift in multi-copy gene systems

Reviewer #1 (Public review):

The revision by Wang et al is a much more clear and readable manuscript than the original version, which I think was a bit too terse and hard to parse. In this version, I think I basically understand all the analyses that the authors undertake and how they argue that those analyses support their conclusions.

The fundamental claim of the manuscript is that rRNA genes experience substitutions much too quickly, given that they are a multi-copy gene system. As clarified by the authors in their response, and as I think is relatively clear in the manuscript, they are collapsing all copies of the rRNA array down. They first quantify polymorphism (in this expanded definition, where polymorphism means variable at a given site across any copy). The authors find elevated levels of heterozygosity in rRNA genes compared to single copy genes, which isn't surprising, given that there is a substantially higher target size; that being said, the increase in polymorphism is smaller than the increase in target size. They then look at substitutions between mouse species and also between human and chimp, and argue that the substitution rate is too fast compared to single copy genes in many cases.

I think that this is an interesting problem and one that obviously occupies some space in the literature. As the authors point out, one possibility for explaining the elevated fixation rate is that there is some kind of positive selection in these putatively non-functional regions. The authors, instead, argue that the elevated rate of evolution is due to neutral homogenizing processes. I'm sympathetic to this argument, I'm a neutralist myself :)

That being said, I find the whole analysis and the connection with the WFH model very strange. As I stated in my previous review, it feels very odd to chalk everything up to variance in reproductive success, rather than explicitly modeling the molecular processes that may lead to the homogenization. For example, the authors bring up gene conversion, and even do a small test of gene conversion. But a force like biased gene conversion is perhaps better modeled as a deterministic force, rather than a stochastic force. Indeed, I think that explicit modeling of mutation dynamics has been very helpful in understanding the role of replicative vs damage-related mutation in humans, as seen in Gao et al (2016) and Spisak et al (2024). I realize, as the authors say in their cover letter, that this is hard! But a major concern with this manuscript is that it's about whether drift can plausibly explain the pattern, but then it's basically impossible to know if it really can, because we have no way to compare the estimated parameters with biophysical or biochemical measurements of the rates of homogenizing forces, because the homogenizing forces are just wrapped up under "variance in reproductive success". I think a much more interesting manuscript would have a more explicit model of homogenizing forces.

I also have some concerns about the data analysis, echoing some concerns of the other reviewer. The biggest issue is that traditional read mapping and SNP calling pipelines for highly duplicated loci don't really make sense. I don't fully understand the variant calling pipeline. The authors state that "All mapping and analysis are performed among individual copies of rRNA genes." which makes it sound like the reads mapping to different copies were somehow deconvolved, which is what you'd need to do to use "normal" variant calling approaches that call look for homozygotes and heterozygotes. But I don't know enough about this literature to understand how they did that and if it makes any sense. If, instead, they called variants against collapsed rRNA copies, then using a standard variant calling approach does not make sense. If you have a variant in 2 out of 100 copies, a standard variant calling algorithm would very likely call that a homozygous ancestral site. Conditional on the variant calls being reasonable, however, I'm basically okay with their use of read counts to estimate "allele frequencies" within individuals.

I have some more minor comments:

(1) In the paragraph starting line 61, the authors say that WF models are unable to handle things like viral epidemics and transposons. I don't think that's really fair: the issue here isn't WF dynamics or not, it's that there is fundamentally evolution on two levels (which is also the case in the rRNA case considered in this manuscript). I certainly agree with the authors that you can't just naively apply standard pop gen theory in these systems, but I think the arrow at the WF model is misaimed, as the real issue is drift and selection on multiple levels.

(2) Line 268-269: The authors argue that the long term rate of evolution in rRNA genes is roughly similar to single copy genes, suggesting not a big influence of increased mutation rate. I'm not sure I understand where this number comes from, as opposed to the divergence numbers they look at in Table 3. These seem to be two different conclusions from roughly the same measurement? Surely I am misunderstanding something.

References:

Gao, Z., Wyman, M. J., Sella, G., & Przeworski, M. (2016). Interpreting the dependence of mutation rates on age and time. PLoS biology, 14(1), e1002355.

Spisak, N., de Manuel, M., Milligan, W., Sella, G., & Przeworski, M. (2024). The clock-like accumulation of germline and somatic mutations can arise from the interplay of DNA damage and repair. PLoS biology, 22(6), e3002678.

Reviewer #2 (Public review):

I appreciate the authors' efforts in addressing previous feedback by correcting typos, clarifying terms, and expanding the methodological descriptions. The revisions have notably improved the manuscript's clarity and readability. However, despite these positive changes, I still have several significant concerns, both conceptual and technical, that need to be addressed to strengthen the conclusions of the paper.

The key idea of this paper is the treatment of rDNA copies in an individual as a pseudo-population and model their sequence evolution with the WFH framework by introducing the parameter V*(K). With this modeling framework, the authors claim that the molecular evolution rate of rDNA relative to that of single-copy genes can be expressed as a simple function V*(K) and C (the copy number per individual). Moreover, when V*(K) is sufficiently large, the neutral molecular evolution of rDNA can be faster than expected under a naïve model without considering horizontal, homogenizing processes and thus be potentially compatible with empirical data. However, several issues persist in the definition, assumptions, and derivation of the model:

(1) Several terms in the model remain undefined. While Ne is clearly defined in the standard single-copy gene model as the reciprocal of genetic drift (i.e., the decay in heterozygosity), its meaning for multiple-copy genes is unclear. Based on the context, it appears that the authors define Ne as the parameter that fits the population polymorphism level (Hs) using the equation in line 165. This definition is reasonable, but it should be explicitly clarified in the text."
(2) Another key parameter V*(K) was still not defined within the paper. In response 9, the authors explained that V*(K) refers to "the number of progeny to whom the gene copy of interest is transmitted (K) over a specific time interval". However, the meaning of "progeny" remains unclear. Are the authors referring to the descendent copies of a gene copy, or the offspring individuals (i.e., the living organisms)? For example, if a variant spreads horizontally through homogenizing processes and transmits vertically to multiple offspring individuals, the number of descent gene copies could differ substantially from the number of descendent individuals to whom a gene copy is transmitted to. This distinction needs to be clarified and clearly stated in the paper.
(3) The authors state that V*(K)>=1 for rDNA genes because of the homogenizing processes (lines 139-141) without providing justification. It is unclear, at least to me, whether homogenizing processes are expected increase or decrease the variance in "reproductive success" across gene copies. Moreover, the authors claim that V*(K) "can potentially reach values in the hundreds and may even exceed C, resulting in C*=C/V*(K)<1" (Response 7). This claim is unlikely to be true, as the minimum value of K is bounded by zero and E(K) is assumed to be 1. Even in the extreme case that 1% gene copies leave large numbers of descends while the others leave none, V*(K) would still be less than 100. Such extreme case seems highly improbable, given realistic rates of the homogenizing processes.
(4) Regardless of how the authors define V*(K), it is not immediately clear why Equation 1 (N*=NC/V*(K)) holds. Both sides of the equation have their independent meanings, so the authors need to provide a step-by-step derivation demonstrating that they are equal. Only by doing this will the implicit underlying assumptions become clearer. I also strongly recommend that the authors conduct forward-in-time simulations with fixed N, C, V*(K) (however they define it) and μ to confirm that the right side of Equation 1 actually predicts the N* as calculated from the polymorphism level using the equation in line 165.
(5) Without providing justification, the authors assumed that a certain number N* exists for rRNA such that it fits both the polymorphism level (line 156) in recent timescales and divergence level in longer timescales (i.e., in the comparison between Tf and Td). However, if N, C or any other relevant parameters have varied substantially throughout evolution, N* is expected to vary with time, and the same value may not fit both polymorphism and divergence data simultaneously.

The authors also provided more detailed description of their data analysis methods, but some of my major concerns remain:
(1) A significant issue with aligning reads to a single reference genome is reference bias, referring to the phenomenon that reads carrying the reference alleles tend to align more easily than those with one or more non-reference alleles, thus creating a bias in genotype calling or variant allele frequency quantification. As a result, there may be an underrepresentation of non-reference alleles in called variants or an underestimate of non-reference allele frequency, particularly in regions with high genetic diversity. Simply focusing on bi-allelic SNVs is insufficient to minimize reference bias. Given the fourfold increase in diversity within rDNA, the authors must either provide evidence that reference bias is not a significant concern or adopt graph-based reference genomes or more sophisticated alignment algorithms to address this issue.
(2) The potential for reference bias also renders the analysis of divergence sites unreliable, as aligning reads from one species (e.g. chimpanzee) to the reference of another species (e.g., human) is likely to introduce biases in variant calling between the two. One commonly adopted approach to address this imbalance is to align reads from both species to a third reference genome that is expected to be equidistantly related to both.
(3) Although it is somewhat reassuring that the estimated divergence rate of rDNA between human and macaque is comparable to that of the rest of the genome, there still remains concern of a under-estimation of divergence in rDNA regions due to reference bias issue. Note that while the "third genome" approach reduces imbalance between two genomes in comparison, it may still under-estimate overall divergence level due to under-calling of non-reference variants.
(4) In response to my question about the similarity in rDNA substitution rates estimated with or without CpG sites, the authors suggest that this "may be due to strong homogenizing forces, which can rapidly fix or eliminate variants" (response17). However, this explanation is insufficient, because the observed substitution rate depends on the mutation rate multiplied by the fixation probability, and accelerated fixation or loss does not alter either. Unless the authors can provide more convincing explanation, technical errors in calling of fixed sites still remain a concern.

Minor points
Line 157: The statement "where μ is the mutation rate of the entire gene" must be wrong, as the heterozygosity calculated with such μ would correspond to the chance of seeing two different haplotypes at gene level, which is incompatible with the empirical calculation specified in Equation 2. Instead, μ must represent the mutation rate per site averaged over the entire gene.

In response 22, the authors explained that the allele frequency spectrum shown in Fig 3 is folded, because the ancestral allele was not determined. However, this is inconsistent with x-axis Fig 3 ranging between 0 and 1. I suspect the x-axis represents the frequency of the alternative (i.e., non-reference) allele. If so, the reported correlation is inflated, as the reference allele is somewhat random, and a variant at joint ALT allele frequencies of (0.9, 0.9) is no different from a variant at (0.1, 0.1). The proper way of calculate this correlation is to first determine the minor allele frequency across individuals and then calculate the correlation between minor allele frequencies.

Similarly, in response 14, it is unclear what the x-axis represents. Is it the ALT allele frequency or derived allele frequency? If the former, why are only variants with AF>0.8 defined as fixed variants, while those with AF<0.2 excluded? If it is the latter, please describe how ancestral state is determined.

Author response:

The following is the authors’ response to the original reviews.

eLife Assessment

This study attempts to resolve an apparent paradox of rapid evolutionary rates of multi-copy gene systems by using a theoretical model that integrates two classic population models. While the conceptual framework is intuitive and thus useful, the specific model is perplexing and difficult to penetrate for non-specialists. The data analysis of rRNA genes provides inadequate support for the conclusions due to a lack of consideration of technical challenges, mutation rate variation, and the relationship between molecular processes and model parameters.

Overall Responses:

Since the eLife assessment succinctly captures the key points of the reviews, the reply here can be seen as the overall responses to the summed criticisms. We believe that the overview should be sufficient to address the main concerns, but further details can be found in the point-by-point responses below. The overview covers the same grounds as the provisional responses (see the end of this rebuttal) but is organized more systematically in response to the reviews. The criticisms together fall into four broad areas.

First, the lack of engagement with the literature, particularly concerning Cannings models and non-diffusive limits. This is the main rebuttal of the companion paper (eLife-RP-RA-2024-99990). The literature in question is all in the WF framework and with modifications, in particular, with the introduction of V(K). Nevertheless, all WF models are based on population sampling. The Haldane model is an entirely different model of genetic drift, based on gene transmission. Most importantly, the WF models and the Haldane model differ in the ability to handle the four paradoxes presented in the two papers. These paradoxes are all incompatible with the WF models.

Second, the poor presentation of the model that makes the analyses and results difficult to interpret. In retrospect, we fully agree and thank all the reviewers for pointing them out. Indeed, we have unnecessarily complicated the model. Even the key concept that defines the paradox, which is the effective copy number of rRNA genes, is difficult to comprehend. We have streamlined the presentation now. Briefly, the complexity arose from the general formulation permitting V(K) ≠ E(K) even for single copy genes. (It would serve the same purpose if we simply let V(K) = E(K) for single copy genes.) The sentences below, copied from the new abstract, should clarify the issue. The full text in the Results section has all the details.

“On average, rDNAs have C ~ 150 - 300 copies per haploid in humans. While a neutral mutation of a single-copy gene would take 4N generations (N being the population size of an ideal population) to become fixed, the time should be 4NC* generations for rRNA genes (C* being the effective copy number). Note that C* >> 1, but C* < (or >) C would depend on the drift strength. Surprisingly, the observed fixation time in mouse and human is < 4N, implying the paradox of C* < 1.”

Third, the confusion about which rRNA gene is being compared with which homology, as there are hundreds of them. We should note that the effective copy number C* indicates that the rRNA gene arrays do not correspond with the “gene locus” concept. This is at the heart of the confusion we failed to remove clearly. We now use the term “pseudo-population” to clarify the nature of rDNA variation and evolution. The relevant passage is reproduced from the main text shown below.

“The pseudo-population of ribosomal DNA copies within each individual

While a human haploid with 200 rRNA genes may appear to have 200 loci, the concept of "gene loci" cannot be applied to the rRNA gene clusters. This is because DNA sequences can spread from one copy to others on the same chromosome via replication slippage. They can also spread among copies on different chromosomes via gene conversion and unequal crossovers (Nagylaki 1983; Ohta and Dover 1983; Stults, et al. 2008; Smirnov, et al. 2021). Replication slippage and unequal crossovers would also alter the copy number of rRNA genes. These mechanisms will be referred to collectively as the homogenization process. Copies of the cluster on the same chromosome are known to be nearly identical in sequences (Hori, et al. 2021; Nurk, et al. 2022). Previous research has also provided extensive evidence for genetic exchanges between chromosomes (Krystal, et al. 1981; Arnheim, et al. 1982; van Sluis, et al. 2019).

In short, rRNA gene copies in an individual can be treated as a pseudo-population of gene copies. Such a pseudo-population is not Mendelian but its genetic drift can be analyzed using the branching process (see below). The pseudo-population corresponds to the "chromosome community" proposed recently (Guarracino, et al. 2023). As seen in Fig. 1C, the five short arms harbor a shared pool of rRNA genes that can be exchanged among them. Fig. 1D presents the possible molecular mechanisms of genetic drift within individuals whereby mutations may spread, segregate or disappear among copies. Hence, rRNA gene diversity or polymorphism refers to the variation across all rRNA copies, as these genes exist as paralogs rather than orthologs. This diversity can be assessed at both individual and population levels according to the multi-copy nature of rRNA genes.”

Fourth, the lack of consideration of many technical challenges. We have responded to the criticisms point-by-point below. One of the main criticisms is about mutation rate differences between single-copy and rRNA genes. We did in fact alluded to the parity in mutation rate between them in the original text but should have presented this property more prominently as is done now. Below is copied from the revised text:

“We now consider the evolution of rRNA genes between species by analyzing the rate of fixation (or near fixation) of mutations. Polymorphic variants are filtered out in the calculation. Note that Eq. (3) shows that the mutation rate, m, determines the long-term evolutionary rate, l. Since we will compare the l values between rRNA and single-copy genes, we have to compare their mutation rates first by analyzing their long-term evolution. As shown in Table S1, l falls in the range of 50-60 (differences per Kb) for single copy genes and 40 – 70 for the non-functional parts of rRNA genes. The data thus suggest that rRNA and single-copy genes are comparable in mutation rate. Differences between their l values will have to be explained by other means.”

While the overview should address the key issues, we now present the point-by-point response below.

Public Reviews:

Reviewer #1 (Public Review):

The manuscript by Wang et al is, like its companion paper, very unusual in the opinion of this reviewer. It builds off of the companion theory paper's exploration of the "Wright-Fisher Haldane" model but applies it to the specific problem of diversity in ribosomal RNA arrays.

The authors argue that polymorphism and divergence among rRNA arrays are inconsistent with neutral evolution, primarily stating that the amount of polymorphism suggests a high effective size and thus a slow fixation rate, while we, in fact, observe relatively fast fixation between species, even in putatively non-functional regions.

They frame this as a paradox in need of solving, and invoke the WFH model.

The same critiques apply to this paper as to the presentation of the WFH model and the lack of engagement with the literature, particularly concerning Cannings models and non-diffusive limits. However, I have additional concerns about this manuscript, which I found particularly difficult to follow.

Response 1: We would like to emphasize that, despite the many modified WF models, there has not been a model for quantifying genetic drift in multi-copy gene systems, due to the complexity of two levels of genetic drift – within individuals as well as between individuals of the population. We will address this question in the revised manuscript (Ruan, et al. 2024) and have included a mention of it in the text as follows:

“In the WF model, gene frequency is governed by 1/N (or 1/2_N_ in diploids) because K would follow the Poisson distribution whereby V(K) = E(K). As E(K) is generally ~1, V(K) would also be ~ 1. In this backdrop, many "modified WF" models have been developed(Der, et al. 2011), most of them permitting V(K) ≠ E(K) (Karlin and McGregor 1964; Chia and Watterson 1969; Cannings 1974). Nevertheless, paradoxes encountered by the standard WF model apply to these modified WF models as well because all WF models share the key feature of gene sampling (see below and (Ruan, et al. 2024)). ”

My first, and most major, concern is that I can never tell when the authors are referring to diversity in a single copy of an rRNA gene compared to when they are discussing diversity across the entire array of rRNA genes. I admit that I am not at all an expert in studies of rRNA diversity, so perhaps this is a standard understanding in the field, but in order for this manuscript to be read and understood by a larger number of people, these issues must be clarified.

Response 2: We appreciate the reviewer’s feedback and acknowledge that the distinction between the diversity of individual rRNA gene copies and the diversity across the entire array of rRNA genes may not have been clearly defined in the original manuscript. The diversity in our manuscript is referring to the genetic diversity of the population of rRNA genes in the cell. To address this concern, we have revised the relevant paragraph in the text:

“Hence, rRNA gene diversity or polymorphism refer to the variation across all rRNA copies, as these genes exist as paralogs rather than orthologs. This diversity can be assessed at both individual and population levels according to the multi-copy nature of rRNA genes.”

Additionally, we have updated the Methods section to include a detailed description of how diversity is measured as follows:

“All mapping and analysis are performed among individual copies of rRNA genes.

Each individual was considered as a psedo-population of rRNA genes and the diversity of rRNA genes was calculated using this psedo-population of rRNA genes.”

The authors frame the number of rRNA genes as roughly equivalent to expanding the population size, but this seems to be wrong: the way that a mutation can spread among rRNA gene copies is fundamentally different than how mutations spread within a single copy gene. In particular, a mutation in a single copy gene can spread through vertical transmission, but a mutation spreading from one copy to another is fundamentally horizontal: it has to occur because some molecular mechanism, such as slippage, gene conversion, or recombination resulted in its spread to another copy. Moreover, by collapsing diversity across genes in an rRNA array, the authors are massively increasing the mutational target size.

For example, it's difficult for me to tell if the discussion of heterozygosity at rRNA genes in mice starting on line 277 is collapsed or not. The authors point out that Hs per kb is ~5x larger in rRNA than the rest of the genome, but I can't tell based on the authors' description if this is diversity per single copy locus or after collapsing loci together. If it's the first one, I have concerns about diversity estimation in highly repetitive regions that would need to be addressed, and if it's the second one, an elevated rate of polymorphism is not surprising, because the mutational target size is in fact significantly larger.

Response 3: As addressed in previous Response2, the measurement of diversity or heterozygosity of rRNA genes is consistently done by combining copies, as there is no concept of single gene locus for rDNAs. We agree that by combining the diversity across multiple rRNA gene copies into one measurement, the mutational target size is effectively increased, leading to higher observed levels of diversity than one gene. This is in line with our text:

“If we use the polymorphism data, it is as if rDNA array has a population size 5.2 times larger than single-copy genes. Although the actual copy number on each haploid is ~ 110, these copies do not segregate like single-copy genes and we should not expect N* to be 100 times larger than N. The HS results confirm the prediction that rRNA genes should be more polymorphic than single-copy genes.”

Under this consensus, the reviewer points out that the having a large number of rRNA genes is not equivalent to having a larger population size, because the spreading of mutations among rDNA copies within a species involves two stages: within individual (horizontal transmission) and between individuals (vertical transmission). Let’s examine how the mutation spreading mechanisms influence the population size of rRNA genes.

First, an increase in the copy number of rRNA genes dose increase the actual population size (CN) of rRNA genes. If reviewer is referring to the effective population size of rRNA genes in the context of diversity (N* = CN/V*(K)), then an increase in C would also increase N*. In addition, the linkage among copies would reduce the drift effect, leading to increase diversity. Conversely, homogenization mechanism, like gene conversion and unequal crossing-over would reduce genetic variations between copies and increase V*(K), leading to lower diversity. Therefore, the C* =C/V*(K) in mice is about 5 times larger for rRNA genes than the rest of the genome (which mainly single-copy genes), even though the actual copy number is about 110, indicating a high homogenization rate.

Even if these issues were sorted out, I'm not sure that the authors framing, in terms of variance in reproductive success is a useful way to understand what is going on in rRNA arrays. The authors explicitly highlight homogenizing forces such as gene conversion and replication slippage but then seem to just want to incorporate those as accounting for variance in reproductive success. However, don't we usually want to dissect these things in terms of their underlying mechanism? Why build a model based on variance in reproductive success when you could instead explicitly model these homogenizing processes? That seems more informative about the mechanism, and it would also serve significantly better as a null model, since the parameters would be able to be related to in vitro or in vivo measurements of the rates of slippage, gene conversion, etc.

In the end, I find the paper in its current state somewhat difficult to review in more detail, because I have a hard time understanding some of the more technical aspects of the manuscript while so confused about high-level features of the manuscript. I think that a revision would need to be substantially clarified in the ways I highlighted above.

Response 4: We appreciate your perspective on modeling the homogenizing processes of rRNA gene arrays.

We employ the WFH model to track the drift effect of the multi-copy gene system. In the context of the Haldane model, the term K is often referred to as reproductive success, but it might be more accurate to interpret it as “transmission rate” in this study. As stated in the caption of Figure 1D, two new mutations can have very large differences in individual output (K) when transmitted to the next generation through homogenization process.

Regarding why we did not explicitly model different mechanisms of homogenization, previous elegant models of multigene families have involved mechanisms like unequal crossing over(Smith 1974a; Ohta 1976; Smith 1976) or gene conversion (Nagylaki 1983; Ohta 1985) for concerted evolution, or using conversion to approximate the joint effect of conversion and crossing over (Ohta and Dover 1984). However, even when simplifying the gene conversion mechanism, modeling remains challenging due to controversial assumptions, such as uniform homogenization rate across all gene members (Dover 1982; Ohta and Dover 1984). No models can fully capture the extreme complexity of factors, while these unbiased mechanisms are all genetic drift forces that contribute to changes in mutant transmission. Therefore, we opted for a more simplified and collective approach using V*(K) to see the overall strength of genetic drift.

We have discussed the reason for using V*(K) to collectively represent the homogenization effect in Discussion. As stated in our manuscript:

“There have been many rigorous analyses that confront the homogenizing mechanisms directly. These studies (Smith 1974b; Ohta 1976; Dover 1982; Nagylaki 1983; Ohta and Dover 1983) modeled gene conversion and unequal cross-over head on. Unfortunately, on top of the complexities of such models, the key parameter values are rarely obtainable. In the branching process, all these complexities are wrapped into V*(K) for formulating the evolutionary rate. In such a formulation, the collective strength of these various forces may indeed be measurable, as shown in this study.”

Reviewer #2 (Public Review):

Summary:

Multi-copy gene systems are expected to evolve slower than single-copy gene systems because it takes longer for genetic variants to fix in the large number of gene copies in the entire population. Paradoxically, their evolution is often observed to be surprisingly fast. To explain this paradox, the authors hypothesize that the rapid evolution of multi-copy gene systems arises from stronger genetic drift driven by homogenizing forces within individuals, such as gene conversion, unequal crossover, and replication slippage. They formulate this idea by combining the advantages of two classic population genetic models -- adding the V(k) term (which is the variance in reproductive success) in the Haldane model to the Wright-Fisher model. Using this model, the authors derived the strength of genetic drift (i.e., reciprocal of the effective population size, Ne) for the multi-copy gene system and compared it to that of the single-copy system. The theory was then applied to empirical genetic polymorphism and divergence data in rodents and great apes, relying on comparison between rRNA genes and genome-wide patterns (which mostly are single-copy genes). Based on this analysis, the authors concluded that neutral genetic drift could explain the rRNA diversity and evolution patterns in mice but not in humans and chimpanzees, pointing to a positive selection of rRNA variants in great apes.

Strengths:

Overall, the new WFH model is an interesting idea. It is intuitive, efficient, and versatile in various scenarios, including the multi-copy gene system and other cases discussed in the companion paper by Ruan et al.

Weaknesses:

Despite being intuitive at a high level, the model is a little unclear, as several terms in the main text were not clearly defined and connections between model parameters and biological mechanisms are missing. Most importantly, the data analysis of rRNA genes is extremely over-simplified and does not adequately consider biological and technical factors that are not discussed in the model. Even if these factors are ignored, the authors' interpretation of several observations is unconvincing, as alternative scenarios can lead to similar patterns. Consequently, the conclusions regarding rRNA genes are poorly supported. Overall, I think this paper shines more in the model than the data analysis, and the modeling part would be better presented as a section of the companion theory paper rather than a stand-alone paper. My specific concerns are outlined below.

Response 5: We appreciate the reviewer’s feedback and recognize the need for clearer definitions of key terms. We have made revisions to ensure that each term is properly defined upon its first use.

Regarding the model’s simplicity, as in the Response4, our intention was to create a framework that captures the essence of how mutant copies spread by chance within a population, relying on the variance in transmission rates for each copy (V(K)). By doing so, we aimed to incorporate the various homogenization mechanisms that do not affect single-copy genes, highlighting the substantially stronger genetic drift observed in multi-copy systems compared to single-copy genes. We believe that simplifying the model was necessary to make it more accessible and practical for real-world data analysis and provides a useful approximation that can be applied broadly. It is clearly an underestimate the actual rate as some forces with canceling effects might not have been accounted for.

(1) Unclear definition of terms

Many of the terms in the model or the main text were not clearly defined the first time they occurred, which hindered understanding of the model and observations reported. To name a few:

(i) In Eq(1), although C* is defined as the "effective copy number", it is unclear what it means in an empirical sense. For example, Ne could be interpreted as "an ideal WF population with this size would have the same level of genetic diversity as the population of interest" or "the reciprocal of strength of allele frequency change in a unit of time". A few factors were provided that could affect C*, but specifically, how do these factors impact C*? For example, does increased replication slippage increase or decrease C*? How about gene conversion or unequal cross-over? If we don't even have a qualitative understanding of how these processes influence C*, it is very hard to make interpretations based on inferred C*. How to interpret the claim on lines 240-241 (If the homogenization is powerful enough, rRNA genes would have C*<1)? Please also clarify what C* would be, in a single-copy gene system in diploid species.

Response 6: We apology for the confusion caused by the lack of clear definitions in the initial manuscript. We recognize that this has led to misunderstandings regarding the concept we presented. Our aim was to demonstrate the concerted evolution in multi-copy gene systems, involving two levels of “effective copy number” relative to single-copy genes: first, homogenization within populations then divergence between species. We used C* and Ne* to try to designated the two levels driven by the same homogenization force, which complicated the evolutionary pattern.

To address these issues, we have simplified the model and revised the abstract to prevent any misunderstandings:

“On average, rDNAs have C ~ 150 - 300 copies per haploid in humans. While a neutral mutation of a single-copy gene would take 4_N_ (N being the population size) generations to become fixed, the time should be 4_NC*_ generations for rRNA genes where 1<< C* (C* being the effective copy number; C* < C or C* > C would depend on the drift strength). However, the observed fixation time in mouse and human is < 4_N_, implying the paradox of C* < 1. Genetic drift that encompasses all random neutral evolutionary forces appears as much as 100 times stronger for rRNA genes as for single-copy genes, thus reducing C* to < 1.”

Thus, it should be clear that the fixation time as well as the level of polymorphism represent the empirical measures of C*.We have also revised the relevant paragraph in the text to define C* and V*(K) and removed Eq. 2 for clarity:

“Below, we compare the strength of genetic drift in rRNA genes vs. that of single-copy genes using the Haldane model (Ruan, et al. 2024). We shall use * to designate the equivalent symbols for rRNA genes; for example, E(K) vs. E*(K). Both are set to 1, such that the total number of copies in the long run remains constant.

For simplicity, we let V(K) = 1 for single-copy genes. (If we permit V(K) ≠ 1, the analyses will involve the ratio of V*(K) and V(K) to reach the same conclusion but with unnecessary complexities.) For rRNA genes, V*(K) ≥ 1 may generally be true because K for rDNA mutations are affected by a host of homogenization factors including replication slippage, unequal cross-over, gene conversion and other related mechanisms not operating on single copy genes. Hence,

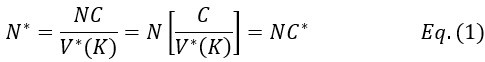
where C is the average number of rRNA genes in an individual and V*(K) reflects the homogenization process on rRNA genes (Fig. 1D). Thus,

C* = C/V*(K)

represents the effective copy number of rRNA genes in the population, determining the level of genetic diversity relative to single-copy genes. Since C is in the hundreds and V*(K) is expected to be > 1, the relationship of 1 << C* ≤ C is hypothesized. Fig. 1D is a simple illustration that the homogenizing process may enhance V*(K) substantially over the WF model.

In short, genetic drift of rRNA genes would be equivalent to single copy genes in a population of size NC* (or N*). Since C* >> 1 is hypothesized, genetic drift for rRNA genes is expected to be slower than for single copy genes.”

(ii) In Eq(1), what exactly is V*(K)? Variance in reproductive success across all gene copies in the population? What factors affect V*(K)? For the same population, what is the possible range of V*(K)/V(K)? Is it somewhat bounded because of biological constraints? Are V*(K) and C*(K) independent parameters, or does one affect the other, or are both affected by an overlapping set of factors?

Response 7: - In Eq(1), what exactly is V*(K)? In Eq(1), V*(K) refers to the variance in the number of progeny to whom the gene copy of interest is transmitted (K) over a specific time interval. When considering evolutionary divergence between species, V*(K) may correspond to the divergence time.

- What factors affect V*(K)? For the same population, what is the possible range of V*(K)/V(K)? Is it somewhat bounded because of biological constraints? “V*(K) for rRNA genes is likely to be much larger than V(K) for single-copy genes, because K for rRNA mutations may be affected by a host of homogenization factors including replication slippage, unequal cross-over, gene conversion and other related mechanisms not operating on single-copy genes. For simplicity, we let V(K) = 1 (as in a WF population) and V*(K) ≥ 1.” Thus, the V*(K)/V(K) = V*(K) can potentially reach values in the hundreds, and may even exceed C, resulting in C*(= C/V*(K)) values less than 1. Biological constraints that could limit this variance include the minimum copy number within individuals, sequence constraints in functional regions, and the susceptibility of chromosomes with large arrays to intrachromosomal crossover (which may lead to a reduction in copy number)(Eickbush and Eickbush 2007), potentially reducing the variability of K.

- Are V*(K) and C*(K) independent parameters, or does one affect the other, or are both affected by an overlapping set of factors? There is no C*(K), the C* is defined as follows in the text:

“C* = C/V*(K) represents the effective copy number of rRNA genes, reflecting the level of genetic diversity relative to single-copy genes. Since C is in the hundreds and V*(K) is expected to be > 1, the relationship of 1 << C* ≤ C is hypothesized.” The factors influencing V*(K) directly affect C* due to this relationship.

(iii) In the multi-copy gene system, how is fixation defined? A variant found at the same position in all copies of the rRNA genes in the entire population?

Response 8: We appreciate the reviewer's suggestion and have now provided a clear definition of fixation in the context of multi-copy genes within the manuscript.

“For rDNA mutations, fixation must occur in two stages – fixation within individuals and among individuals in the population. (Note that a new mutation can be fixed via homogenization, thus making rRNA gene copies in an individual a pseudo-population.)”

The evolutionary dynamics of multi-copy genes differ from those of single-copy (Mendelian) genes, which mutate, segregate and evolve independently in the population. Fixation in multi-copy genes, such as rRNA genes, is influenced by their ability to transfer genetic information among their copies through nonreciprocal exchange mechanisms, like gene conversion and unequal crossover (Ohta and Dover 1984). These processes can cause fluctuations in the number of mutant copies within an individual's lifetime and facilitate the spread of a mutant allele across all copies even in non-homologous chromosomes. Over time, this can result in the mutant allele replacing all preexisting alleles throughout the population, leading to fixation (Ohta 1976) meaning that the same variant will eventually be present at the corresponding position in all copies of the rRNA genes across the entire population. Without such homogenization processes, fixation would be unlikely to be obtained in multi-copy genes.

(iv) Lines 199-201, HI, Hs, and HT are not defined in the context of a multi-copy gene system. What are the empirical estimators?

Response 9: We appreciate the reviewer's comment and would like to clarify the definitions and empirical estimators for within the context of a multi-copy gene system in the text:

“A standard measure of genetic drift is the level of heterozygosity (H). At the mutation-selection equilibrium

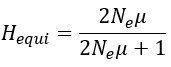
where μ is the mutation rate of the entire gene and Ne is the effective population size. In this study, Ne = N for single-copy gene and Ne = C*N for rRNA genes. The empirical measure of nucleotide diversity H is given by

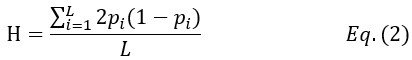
where L is the gene length (for each copy of rRNA gene, L ~ 43kb) and pi is the variant frequency at the i-th site.

We calculate H of rRNA genes at three levels – within-individual, within-species and then, within total samples (HI, HS and HT, respectively). HS and HT are standard population genetic measures (Hartl, et al. 1997; Crow and Kimura 2009). In calculating HS, all sequences in the species are used, regardless of the source individuals. A similar procedure is applied to HT. The HI statistic is adopted for multi-copy gene systems for measuring within-individual polymorphism. Note that copies within each individual are treated as a pseudo-population (see Fig. 1 and text above). With multiple individuals, HI is averaged over them.”

(v) Line 392-393, f and g are not clearly defined. What does "the proportion of AT-to-GC conversion" mean? What are the numerator and denominator of the fraction, respectively?

Response 10: We appreciate the reviewer's comment and have revised the relevant text for clarity as well as improved the specific calculation methods for f and g in the Methods section.

“We first designate the proportion of AT-to-GC conversion as f and the reciprocal, GC-to-AT, as g. Specifically, f represents the proportion of fixed mutations where an A or T nucleotide has been converted to a G or C nucleotide (see Methods). Given f ≠ g, this bias is true at the site level.”

Methods:

“Specifically, f represents the proportion of fixed mutations where an A or T nucleotide has been converted to a G or C nucleotide. The numerator for f is the number of fixed mutations from A-to-G, T-to-C, T-to-G, or A-to-C. The denominator is the total number of A or T sites in the rDNA sequence of the specie lineage.

Similarly, g is defined as the proportion of fixed mutations where a G or C nucleotide has been converted to an A or T nucleotide. The numerator for g is the number of fixed mutations from G-to-A, C-to-T, C-to-A, or G-to-T. The denominator is the total number of G or C sites in the rDNA sequence of the specie lineage.

The consensus rDNA sequences for the species lineage were generated by Samtools consensus (Danecek, et al. 2021) from the bam file after alignment. The following command was used:

‘samtools consensus -@ 20 -a -d 10 --show-ins no --show-del yes input_sorted.bam output.fa’.”

(2) Technical concerns with rRNA gene data quality

Given the highly repetitive nature and rapid evolution of rRNA genes, myriads of things could go wrong with read alignment and variant calling, raising great concerns regarding the data quality. The data source and methods used for calling variants were insufficiently described at places, further exacerbating the concern.

(i) What are the accession numbers or sample IDs of the high-coverage WGS data of humans, chimpanzees, and gorillas from NCBI? How many individuals are in each species? These details are necessary to ensure reproducibility and correct interpretation of the results.

Response 11: We apologize for not including the specific details of the sample information in the main text. All accession numbers and sample IDs for the WGS data used in this study, including mice, humans, chimpanzee, and gorilla, are already listed in Supplementary Tables S4-S5. We have revised the table captions and referenced them at the appropriate points in the Methods to ensure clarity.

“The genome sequences of human (n = 8), chimpanzee (n = 1) and gorilla (n = 1) were sourced from National Center for Biotechnology Information (NCBI) (Supplementary Table 4). … Genomic sequences of mice (n = 13) were sourced from the Wellcome Sanger Institute’s Mouse Genome Project (MGP) (Keane, et al. 2011).

The concern regarding the number of individuals needed to support the results will be addressed in Response 13.

(ii) Sequencing reads from great apes and mice were mapped against the human and mouse rDNA reference sequences, respectively (lines 485-486). Given the rapid evolution of rRNA genes, even individuals within the same species differ in copy number and sequences of these genes. Alignment to a single reference genome would likely lead to incorrect and even failed alignment for some reads, resulting in genotyping errors. Differences in rDNA sequence, copy number, and structure are even greater between species, potentially leading to higher error rates in the called variants. Yet the authors provided no justification for the practice of aligning reads from multiple species to a single reference genome nor evidence that misalignment and incorrect variant calling are not major concerns for the downstream analysis.

Response 12: While the copy number of rDNA varies in each individuals, the sequence identity among copies is typically very high (median identity of 98.7% (Nurk, et al. 2022)). Therefore, all rRNA genes were aligned against to the species-specific reference sequences, where the consensus nucleotide nearly accounts for >90% of the gene copies in the population. In minimize genotyping errors, our analysis focused exclusively on single nucleotide variants (SNVs) with only two alleles, discarding other mutation types.

Regarding sequence divergence between species, which may have greater sequence variations, we excluded unmapped regions with high-quality reads coverage below 10. In calculation of substitution rate, we accounted for the mapping length (L), as shown in the column 3 in Table 3-5.

We appreciate the reviewer’s comments and have provide details in the Methods.

(vi) It is unclear how variant frequency within an individual was defined conceptually or computed from data (lines 499-501). The population-level variant frequency was calculated by averaging across individuals, but why was the averaging not weighted by the copy number of rRNA genes each individual carries? How many individuals are sampled for each species? Are the sample sizes sufficient to provide an accurate estimate of population frequencies?

Response 13: Each individual was considered as a psedo-population of rRNA genes, varaint frequency within an individual was the proportions of mutant allele in this psedo-population. The calculation of varaint frequency is based on the number of supported reads of each individual.

The reason for calculating population-level variant frequency by averaging across individuals is relevant in the calculation of FIS and FST. In calculating FST, the standard practice is to weigh each population equally. So, when we show FST in humans, we do not consider whether there are more Africans, Caucasians or Asians. There is a reason for not weighing them even though the population sizes could be orders of magnitude different, say, in the comparison between an ethnic minority and the main population. In the case of FIS, the issue is moot. Although copy number may range from 150 to 400 per haploid, most people have 300 – 500 copies with two haploids.

As for the concern regarding the number the individuals needed to support of the results:

Considering the nature of multi-copy genes, where gene members undergo continuous exchanges at a much slower rate compared to the rapid rate of random distribution of chromosomes at each generation of sexual reproduction, even a few variant copies that arise during an individual's lifetime would disperse into the gene pool in the next generation (Ohta and Dover 1984). Thus, there is minimal difference between individuals. Our analysis is also aligns with this theory, particularly in human population (FIS = 0.059), where each individual carries the majority of the population's genetic diversity. Therefore, even a single chimpanzee or gorilla individual caries sufficient diversity with its hundreds of gene copies to calculate divergence with humans.

(vii) Fixed variants are operationally defined as those with a frequency>0.8 in one species. What is the justification for this choice of threshold? Without knowing the exact sample size of the various species, it's difficult to assess whether this threshold is appropriate.

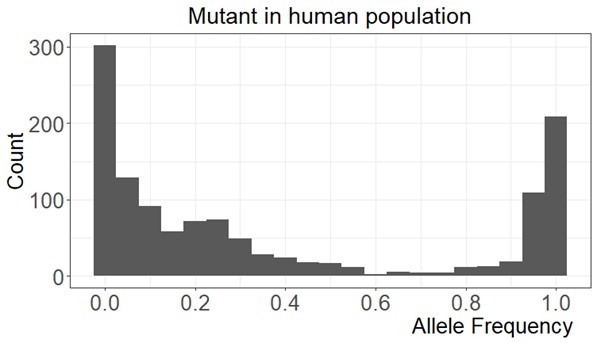
Response 14: First, the mutation frequency distribution is strongly bimodal (see Figure below) with a peak at zero and the other at 1. This high frequency peak starts to rise slowly at 0.8, similar to FST distribution in Figure 4C. That is why we use it as the cutoff although we would get similar results at the cutoff of 0.90 (see Table below). Second, the sample size for the calculation of mutant frequency is based on the number of reads which is usually in the tens of thousands. Third, it does not matter if the mutation frequency calculation is based on one individuals or multiple individuals because 95% of the genetic diversity of the population is captured by the gene pool within each individual.

Author response image 1.

Author response table 1.

The A/T to G/C and G/C to A/T changes in apes and mouse.

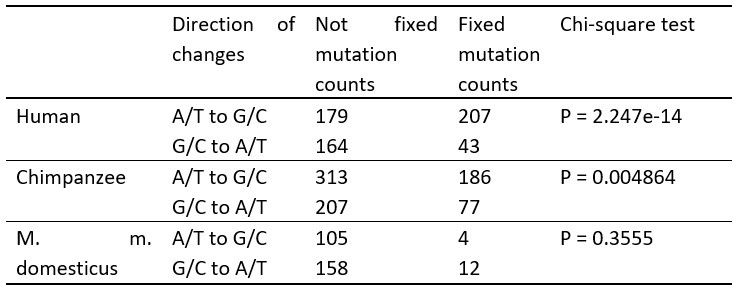
New mutants with a frequency >0.9 within an individual are considered as (nearly) fixed, except for humans, where the frequency was averaged over 8 individuals in the Table 2.

The X-squared values for each species are as follows: 58.303 for human, 7.9292 for chimpanzee, and 0.85385 for M. m. domesticus.

(viii) It is not explained exactly how FIS, FST, and divergence levels of rRNA genes were calculated from variant frequency at individual and species levels. Formulae need to be provided to explain the computation.

Response 15: After we clearly defined the HI, HS, and HT in Response9, understanding FIS and F_ST_ becomes straightforward.

“Given the three levels of heterozygosity, there are two levels of differentiation. First, FIS is the differentiation among individuals within the species, defined by

FIS = [HS - HI]/HS

FIS is hence the proportion of genetic diversity in the species that is found only between individuals. We will later show FIS ~ 0.05 in human rDNA (Table 2), meaning 95% of rDNA diversity is found within individuals.

Second, FST is the differentiation between species within the total species complex, defined as

FST = [HT – HS]/HT

FST is the proportion of genetic diversity in the total data that is found only between species.”

(3) Complete ignorance of the difference in mutation rate difference between rRNA genes and genome-wide average

Nearly all data analysis in this paper relied on comparison between rRNA genes with the rest (presumably single-copy part) of the genome. However, mutation rate, a key parameter determining the diversity and divergence levels, was completely ignored in the comparison. It is well known that mutation rate differs tremendously along the genome, with both fine and large-scale variation. If the mutation rate of rRNA genes differs substantially from the genome average, it would invalidate almost all of the analysis results. Yet no discussion or justification was provided.

Response 16: We appreciate the reviewer's observation regarding the potential impact of varying mutation rates across the genome. To address this concern, we compared the long-term substitution rates on rDNA and single-copy genes between human and rhesus macaque, which diverged approximately 25 million years ago. Our analysis (see Table S1 below) indicates that the substitution rate in rDNA is actually slower than the genome-wide average. This finding suggests that rRNA genes do not experience a higher mutation rate compared to single-copy genes, as stated in the text:

“Note that Eq. (3) shows that the mutation rate, m, determines the long-term evolutionary rate, l. Since we will compare the l values between rRNA and single-copy genes, we have to compare their mutation rates first by analyzing their long-term evolution. As shown in Table S1, l falls in the range of 50-60 (differences per Kb) for single copy genes and 40 – 70 for the non-functional parts of rRNA genes. The data thus suggest that rRNA and single-copy genes are comparable in mutation rate. Differences between their l values will have to be explained by other means.”

However, given the divergence time (Td) being equal to or smaller than Tf, even if the mutation rate per nucleotide is substantially higher in rRNA genes, these variants would not become fixed after the divergence of humans and chimpanzees without the help of strong homogenization forces. Thus, the presence of divergence sites (Table 5) still supports the conclusion that rRNA genes undergo much stronger genetic drift compared to single-copy genes.

Related to mutation rate: given the hypermutability of CpG sites, it is surprising that the evolution/fixation rate of rRNA estimated with or without CpG sites is so close (2.24% vs 2.27%). Given the 10 - 20-fold higher mutation rate at CpG sites in the human genome, and 2% CpG density (which is probably an under-estimate for rDNA), we expect the former to be at least 20% higher than the latter.

Response 17: While it is true that CpG sites exhibit a 10-20-fold higher mutation rate, the close evolution/fixation rates of rDNA with and without CpG sites (2.24% vs 2.27%) may be attributed to the fact that fixation rates during short-term evolutionary processes are less influenced by mutation rates alone. As observed in the Human-Macaque comparison in the table above, the substitution rate of rDNA in non-functional regions with CpG sites is 4.18%, while it is 3.35% without CpG sites, aligning with your expectation of 25% higher rates where CpG sites are involved.

This discrepancy between the expected and observed fixation rates may be due to strong homogenization forces, which can rapidly fix or eliminate variants, thereby reducing the overall impact of higher mutation rates at CpG sites on the observed fixation rate. This suggests that the homogenization mechanisms play a more dominant role in the fixation process over short evolutionary timescales, mitigating the expected increase in fixation rates due to CpG hypermutability.

Among the weaknesses above, concern (1) can be addressed with clarification, but concerns (2) and (3) invalidate almost all findings from the data analysis and cannot be easily alleviated with a complete revamp work.

Recommendations for the authors:

Reviewing Editor Comments:

Both reviewers found the manuscript confusing and raised serious concerns. They pointed out a lack of engagement with previous literature on modeling and the presence of ill-defined terms within the model, which obscure understanding. They also noted a significant disconnection between the modeling approach and the biological processes involved. Additionally, the data analysis was deemed problematic due to the failure to consider essential biological and technical factors. One reviewer suggested that the modeling component would be more suitable as a section of the companion theory paper rather than a standalone paper. Please see their individual reviews for their overall assessment.

Reviewer #2 (Recommendations For The Authors):

Beyond my major concerns, I have numerous questions about the interpretation of various findings:

Lines 62-63: Please explain under what circumstance Ne=N/V(K) is biologically nonsensical and why.

Response 18: “Biologically non-sensical” is the term used in (Chen, et al. 2017). We now used the term “biologically untenable” but the message is the same. How does one get V(K) ≠ E(K) in the WF sampling? It is untenable under the WF structure. Kimura may be the first one to introduce V(K) ≠ E(K) into the WF model and subsequent papers use the same sort of modifications that are mathematically valid but biologically dubious. As explained extensively in the companion paper, the modifications add complexities but do not give the WF models powers to explain the paradoxes.

Lines 231-234: The claim about a lower molecular evolution rate (lambda) is inaccurate - under neutrality, the molecular evolution rate is always the same as the mutation rate. It is true that when the species divergence Td is not much greater than fixation time Tf, the observed number of fixed differences would be substantially smaller than 2*mu*Td, but the lower divergence level does not mean that the molecular evolution is slower. In other words, in calculating the divergence level, it is the time term that needs to be adjusted rather than the molecular evolution rate.

Response 19: Thanks, we agree that the original wording was not accurate. It is indeed the substitution rate rather than the molecular evolution rate that is affected when species divergence time Td is not much greater than the fixation time Tf. We have revised the relevant text in the manuscript to correct this and ensure clarity.

Lines 277-279: Hs for rRNA is 5.2x fold than the genome average. This could be roughly translated as Ne*/Ne=5.2. According to Eq 2: (1/Ne*)/(1/Ne)= Vh/C*, it can be drived that mean Ne*/Ne=C*/Vh. Then why do the authors conclude "C*=N*/N~5.2" in line 278? Wouldn't it mean that C*/Vh is roughly 5.2?

Response 20: We apologize for the confusion. To prevent misunderstandings, we have revised Equation 1 and deleted Equation 2 from the manuscript. Please refer to the Response6 for further details.

Lines 291-292: What does "a major role of stage I evolution" mean? How does it lead to lower FIS?

Response 21: We apologize for the lack of clarity in our original description, and we have revised the relevant content to make them more directly.

“In this study, we focus on multi-copy gene systems, where the evolution takes place in two stages: both within (stage I) and between individuals (stage II).”

“FIS for rDNA among 8 human individuals is 0.059 (Table 2), much smaller than 0.142 in M. m. domesticus mice, indicating minimal genetic differences across human individuals and high level of genetic identity in rDNAs between homologous chromosomes among human population. … Correlation of polymorphic sites in IGS region is shown in Supplementary Fig. 1. The results suggest that the genetic drift due to the sampling of chromosomes during sexual reproduction (e.g., segregation and assortment) is augmented substantially by the effects of homogenization process within individual. Like those in mice, the pattern indicates that intra-species polymorphism is mainly preserved within individuals.”

Line 297-300: why does the concentration at very allele frequency indicate rapid homogenization across copies? Suppose there is no inter-copy homogenization, and each copy evolves independently, wouldn't we still expect the SFS to be strongly skewed towards rare variants? It is completely unclear how homogenization processes are expected to affect the SFS.

Response 22: We appreciate the reviewer’s insightful comments and apologize for any confusion in our original explanation. To clarify:

If there is no inter-copy homogenization and each copy evolves independently, it would effectively result in an equivalent population size that is C times larger than that of single-copy genes. However, given the copies are distributed on five chromosomes, if the copies within a chromosome were fully linked, there would be no fixation at any sites. Considering the data presented in Table 4, where the substitution rate in rDNA is higher than in single-copy genes, this suggests that additional forces must be acting to homogenize the copies, even across non-homologous chromosomes.

Regarding the specific data presented in the Figure 3, the allele frequency spectrum is based on human polymorphism sites and is a folded spectrum, as the ancestral state of the alleles was not determined. High levels of homogenization would typically push variant mutations toward the extremes of the SFS, leading to fewer intermediate-frequency alleles and reduced heterozygosity. The statement that "allele frequency spectrum is highly concentrated at very low frequency within individuals" was intended to emphasize the localized distribution of variants and the high identity at each site. However, we recognize that it does not accurately reflect the role of homogenization and this conclusion cannot be directly inferred from the figure as presented. Therefore, we have removed the sentence in the text.

The evidence of gBGC in rRNA genes in great apes does not help explain the observed accelerated evolution of rDNA relative to the rest of the genome. Evidence of gBGC has been clearly demonstrated in a variety of species, including mice. It affects not only rRNA genes but also most parts of the genome, particularly regions with high recombination rates. In addition, gBGC increases the fixation probability of W>S mutations but suppresses the fixation of S>W mutations, so it is not obvious how gBGC will increase or decrease the molecular evolution rate overall.

Response 23: We have thoroughly rewritten the last section of Results. The earlier writing has misplaced the emphasis, raising many questions (as stated above). To answer them, we would have to present a new set of equations thus adding unnecessary complexities to the paper. Here is the streamlined and more logical flow of the new section.

First, Tables 4 and 5 have shown the accelerated evolution of the rRNA genes. We have now shown that rRNA genes do not have higher mutation rates. Below is copied from the revised text:

“We now consider the evolution of rRNA genes between species by analyzing the rate of fixation (or near fixation) of mutations. Polymorphic variants are filtered out in the calculation. Note that Eq. (3) shows that the mutation rate, m, determines the long-term evolutionary rate, l. Since we will compare the l values between rRNA and single-copy genes, we have to compare their mutation rates first by analyzing their long-term evolution. As shown in Table S1 l falls in the range of 50-60 (differences per Kb) for single copy genes and 40 – 70 for the non-functional parts of rRNA genes. The data thus suggest that rRNA and single-copy genes are comparable in mutation rate. Differences between their l values will have to be explained by other means.”

Second, we have shown that the accelerated evolution in mice is likely due to genetic drift, resulting in faster fixation of neutral variants. We also show that this is unlikely to be true in humans and chimpanzees; hence selection is the only possible explanation. The section below is copied from the revised text. It shows the different patterns of gene conversions between mice and apes, in agreement with the results of Tables 4 and 5. In essence, it shows that the GC ratio in apes is shifting to a new equilibrium, which is equivalent to a new adaptive peak. Selection is driving the rDNA genes to move to the new adaptive peak.

Revision - “Thus, the much accelerated evolution of rRNA genes between humans and chimpanzees cannot be entirely attributed to genetic drift. In the next and last section, we will test if selection is operating on rRNA genes by examining the pattern of gene conversion.

1. Positive selection for rRNA mutations in apes, but not in mice – Evidence from gene conversion patterns

For gene conversion, we examine the patterns of AT-to-GC vs. GC-to-AT changes. While it has been reported that gene conversion would favor AT-to-GC over GC-to-AT conversion (Jeffreys and Neumann 2002; Meunier and Duret 2004) at the site level, we are interested at the gene level by summing up all conversions across sites. We designate the proportion of AT-to-GC conversion as f and the reciprocal, GC-to-AT, as g. Both f and g represent the proportion of fixed mutations between species (see Methods). So defined, f and g are influenced by the molecular mechanisms as well as natural selection. The latter may favor a higher or lower GC ratio at the genic level between species. As the selective pressure is distributed over the length of the gene, each site may experience rather weak pressure.

Let p be the proportion of AT sites and q be the proportion of GC sites in the gene. The flux of AT-to-GC would be pf and the flux in reverse, GC-to-AT, would be qg. At equilibrium, pf = qg. Given f and g, the ratio of p and q would eventually reach p/q = g/f. We now determine if the fluxes are in equilibrium (pf =qg). If they are not, the genic GC ratio is likely under selection and is moving to a different equilibrium.

In these genic analyses, we first analyze the human lineage (Brown and Jiricny 1989; Galtier and Duret 2007). Using chimpanzees and gorillas as the outgroups, we identified the derived variants that became nearly fixed in humans with frequency > 0.8 (Table 6). The chi-square test shows that the GC variants had a significantly higher fixation probability compared to AT. In addition, this pattern is also found in chimpanzees (p < 0.001). In M. m. domesticus (Table 6), the chi-square test reveals no difference in the fixation probability between GC and AT (p = 0.957). Further details can be found in Supplementary Figure 2. Overall, a higher fixation probability of the GC variants is found in human and chimpanzee, whereas this bias is not observed in mice.

Tables 6-7 here

Based on Table 6, we could calculate the value of p, q, f and g (see Table 7). Shown in the last row of Table 7, the (pf)/(qg) ratio is much larger than 1 in both the human and chimpanzee lineages. Notably, the ratio in mouse is not significantly different from 1. Combining Tables 4 and 7, we conclude that the slight acceleration of fixation in mice can be accounted for by genetic drift, due to gene conversion among rRNA gene copies. In contrast, the different fluxes corroborate the interpretations of Table 5 that selection is operating in both humans and chimpanzees.”

References

Arnheim N, Treco D, Taylor B, Eicher EM. 1982. Distribution of ribosomal gene length variants among mouse chromosomes. Proc Natl Acad Sci U S A 79:4677-4680.

Brown T, Jiricny J. 1989. Repair of base-base mismatches in simian and human cells. Genome / National Research Council Canada = Génome / Conseil national de recherches Canada 31:578-583.

Cannings C. 1974. The latent roots of certain Markov chains arising in genetics: A new approach, I. Haploid models. Advances in Applied Probability 6:260-290.

Chen Y, Tong D, Wu CI. 2017. A New Formulation of Random Genetic Drift and Its Application to the Evolution of Cell Populations. Mol Biol Evol 34:2057-2064.

Chia AB, Watterson GA. 1969. Demographic effects on the rate of genetic evolution I. constant size populations with two genotypes. Journal of Applied Probability 6:231-248.

Crow JF, Kimura M. 2009. An Introduction to Population Genetics Theory: Blackburn Press.

Danecek P, Bonfield JK, Liddle J, Marshall J, Ohan V, Pollard MO, Whitwham A, Keane T, McCarthy SA, Davies RM, et al. 2021. Twelve years of SAMtools and BCFtools. Gigascience 10.

Datson NA, Morsink MC, Atanasova S, Armstrong VW, Zischler H, Schlumbohm C, Dutilh BE, Huynen MA, Waegele B, Ruepp A, et al. 2007. Development of the first marmoset-specific DNA microarray (EUMAMA): a new genetic tool for large-scale expression profiling in a non-human primate. Bmc Genomics 8:190.

Der R, Epstein CL, Plotkin JB. 2011. Generalized population models and the nature of genetic drift. Theoretical Population Biology 80:80-99.

Dover G. 1982. Molecular drive: a cohesive mode of species evolution. Nature 299:111-117.

Eickbush TH, Eickbush DG. 2007. Finely orchestrated movements: evolution of the ribosomal RNA genes. Genetics 175:477-485.

Galtier N, Duret L. 2007. Adaptation or biased gene conversion? Extending the null hypothesis of molecular evolution. Trends in Genetics 23:273-277.

Gibbs RA, Rogers J, Katze MG, Bumgarner R, Weinstock GM, Mardis ER, Remington KA, Strausberg RL, Venter JC, Wilson RK, et al. 2007. Evolutionary and Biomedical Insights from the Rhesus Macaque Genome. Science 316:222-234.

Guarracino A, Buonaiuto S, de Lima LG, Potapova T, Rhie A, Koren S, Rubinstein B, Fischer C, Abel HJ, Antonacci-Fulton LL, et al. 2023. Recombination between heterologous human acrocentric chromosomes. Nature 617:335-343.

Hartl DL, Clark AG, Clark AG. 1997. Principles of population genetics: Sinauer associates Sunderland.

Hori Y, Shimamoto A, Kobayashi T. 2021. The human ribosomal DNA array is composed of highly homogenized tandem clusters. Genome Res 31:1971-1982.

Jeffreys AJ, Neumann R. 2002. Reciprocal crossover asymmetry and meiotic drive in a human recombination hot spot. Nat Genet 31:267-271.

Karlin S, McGregor J. 1964. Direct Product Branching Processes and Related Markov Chains. Proceedings of the National Academy of Sciences 51:598-602.

Keane TM, Goodstadt L, Danecek P, White MA, Wong K, Yalcin B, Heger A, Agam A, Slater G, Goodson M, et al. 2011. Mouse genomic variation and its effect on phenotypes and gene regulation. Nature 477:289-294.

Krystal M, D'Eustachio P, Ruddle FH, Arnheim N. 1981. Human nucleolus organizers on nonhomologous chromosomes can share the same ribosomal gene variants. Proceedings of the National Academy of Sciences of the United States of America 78:5744-5748.

Meunier J, Duret L. 2004. Recombination drives the evolution of GC-content in the human genome. Molecular Biology and Evolution 21:984-990.

Nagylaki T. 1983. Evolution of a large population under gene conversion. Proc Natl Acad Sci U S A 80:5941-5945.

Nurk S, Koren S, Rhie A, Rautiainen M, Bzikadze AV, Mikheenko A, Vollger MR, Altemose N, Uralsky L, Gershman A, et al. 2022. The complete sequence of a human genome. Science 376:44-53.

Ohta T. 1985. A model of duplicative transposition and gene conversion for repetitive DNA families. Genetics 110:513-524.

Ohta T. 1976. Simple model for treating evolution of multigene families. Nature 263:74-76.

Ohta T, Dover GA. 1984. The Cohesive Population Genetics of Molecular Drive. Genetics 108:501-521.

Ohta T, Dover GA. 1983. Population genetics of multigene families that are dispersed into two or more chromosomes. Proc Natl Acad Sci U S A 80:4079-4083.

Ruan Y, Wang X, Hou M, Diao W, Xu S, Wen H, Wu C-I. 2024. Resolving Paradoxes in Molecular Evolution: The Integrated WF-Haldane (WFH) Model of Genetic Drift. bioRxiv:2024.2002.2019.581083.

Smirnov E, Chmúrčiaková N, Liška F, Bažantová P, Cmarko D. 2021. Variability of Human rDNA. Cells 10.

Smith GP. 1976. Evolution of Repeated DNA Sequences by Unequal Crossover. Science 191:528-535.

Smith GP. 1974a. Unequal crossover and the evolution of multigene families. Cold Spring Harbor symposia on quantitative biology 38:507-513.

Smith GP. 1974b. Unequal Crossover and the Evolution of Multigene Families. 38:507-513.

Stults DM, Killen MW, Pierce HH, Pierce AJ. 2008. Genomic architecture and inheritance of human ribosomal RNA gene clusters. Genome Res 18:13-18.

van Sluis M, Gailín M, McCarter JGW, Mangan H, Grob A, McStay B. 2019. Human NORs, comprising rDNA arrays and functionally conserved distal elements, are located within dynamic chromosomal regions. Genes Dev 33:1688-1701.

Wall JD, Frisse LA, Hudson RR, Di Rienzo A. 2003. Comparative linkage-disequilibrium analysis of the beta-globin hotspot in primates. Am J Hum Genet 73:1330-1340.