The structure of the COPII transport-vesicle coat assembled on membranes
- University of California, Berkeley, United States
- European Molecular Biology Laboratory, Germany
- Martin Luther University of Halle-Wittenberg, Germany
- Howard Hughes Medical Institute, University of California, Berkeley, United States
Figures
Figure 1
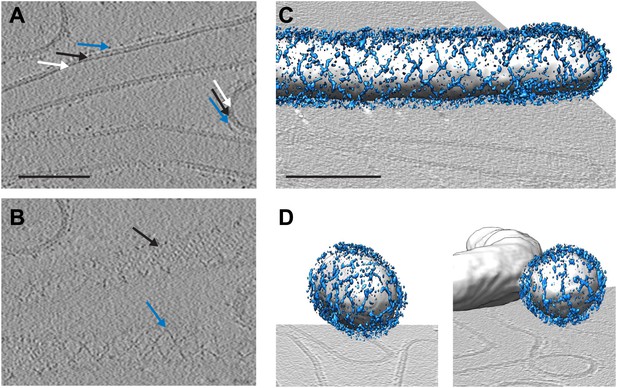
Cryo-electron tomograms of a reconstituted COPII budding reaction. Scale bars = 100 nm.
(A) A slice through a tomogram showing two coat layers arranged around tubular and spherical membranes. White, black and blue arrows point to the membrane, inner, and outer coat layers respectively. (B) A slice through the top of the tubes in panel A, showing repeating features in the coat layers. (C) A surface rendering of a COPII-coated tube. The membrane and inner coat are in grey, the outer coat in blue. (D) Surface renderings of spherically curved regions of membrane, coloured as in panel C.
Figure 2 with 2 supplements
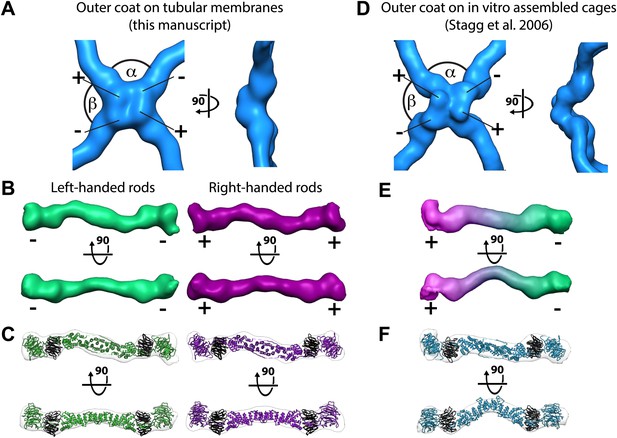
Structure of the outer COPII coat.
(A) Isosurface representation of the outer coat vertex solved by sub-tomogram averaging of tubular membranes. ‘+’ and ‘−’ ends of Sec13/31 and alpha and beta angles are as defined by (Stagg et al., 2008) (Figure 2—figure supplement 2 and panel D). (B) Structures of the rods that interconnect neighbouring vertices in left-handed (green) and right-handed (purple) helical directions, viewed from the top (upper panels), and the side (lower panels). Left-handed rods have two ‘−’ ends, whereas right-handed rods have two ‘+’ ends. (C) Atomic model of the Sec13/31 complex (Fath et al., 2007) (PDB 2PM9 and 2PM6) fitted as a rigid body into left- and right-handed rods. (D) Isosurface representation of the Sec13/31 vertex structure from cryo-electron microscopy of in vitro assembled cuboctahedral cages (Stagg et al., 2006) (EMDB ID 1232). (E) Structure of the rods segmented from in vitro assembled cuboctahedral cages (Stagg et al., 2006) (EMDB ID 1232) for comparison. ‘+’ and ‘−’ ends are coloured purple and green respectively. (F) The Sec13/31 complex fitted into a rod from the cuboctahedral cage. To adapt to the 45° bend in the rod two equivalent heterodimers were fitted independently.
Figure 2—figure supplement 1
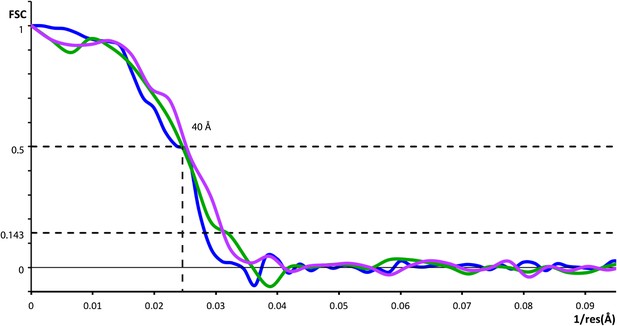
Resolution of outer coat structures.
The resolution of the sub-tomogram averaged structures of outer coat (blue = vertices, purple = right-handed rods, green = left-handed rods) were estimated by Fourier Shell Correlation (see ‘Materials and methods’ for details). Resolution at the 0.5 threshold criterion is indicated.
Figure 2—figure supplement 2
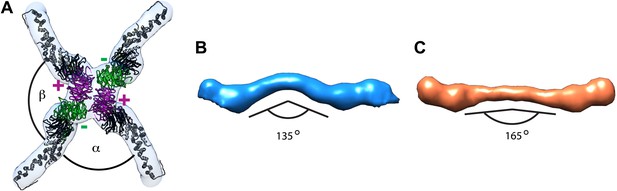
Previously published outer coat structures.
(A) A close up view of the vertex in the cuboctahedral cage (Stagg et al., 2006), with the X-ray model for Sec13/31 dimers fitted into the half-rods. The vertex forms upon interaction of four N-terminal Sec31 β-propellers. The β-propellers on two heterotetramer rods (purple) face each other at the center of the vertex and are referred to as the ‘plus’ ends of the rods, while the β-propellers on the other two rods (green) are further away from the center, and are referred to as the ‘minus’ ends. In the cuboctahedral and icosidodecahedral cage geometries, each rod has a plus and a minus end. When viewing the vertex from outside the cage, alpha is defined as the clockwise angle from ‘+’ to ‘−’, and beta the clockwise angle from ‘−’ to ‘+’. These interactions allow assembly of a coat that curves in two directions, appropriate for coating spherical membranes. (B) A close up view of the rod segmented from the edge of the cuboctahedral cage. The rod is bent in the middle at the Sec31 dimerisation interface by an angle of 135°. (C) A surface representation of the atomic structure of the Sec13/31 heterodimer as solved by X-ray crystallography (Fath et al., 2007), filtered to a resolution of 40 Å. The structure is overall very similar to the cuboctahedral cage edge, but the bend in the middle of the rod is less accentuated, with an angle of 165°.
Figure 3 with 3 supplements
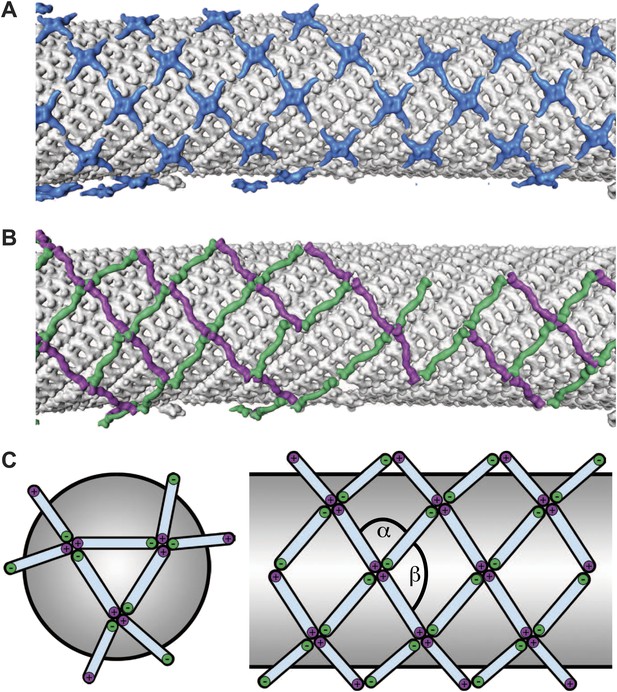
Arrangement of the outer COPII coat.
(A) Visualization of the positions and orientations at which vertices were identified for a representative tube. They are arranged to form a rhomboidal lattice. The positions of inner coat subunits are shown in grey (Figure 4). (B) Visualization of the positions of aligned rods, as in panel A. Right- and left-handed rods in purple and green respectively. (C) Schematic depiction of how ‘+/−’ rods can coat regions of spherical curvature by arranging to form orthogonal vertices (left panel). Tubular surfaces (right panel) are coated with +/+ and −/− rods that form parallel vertices (alpha and beta are always in the same direction with respect to the tube axis).
Figure 3—figure supplement 1
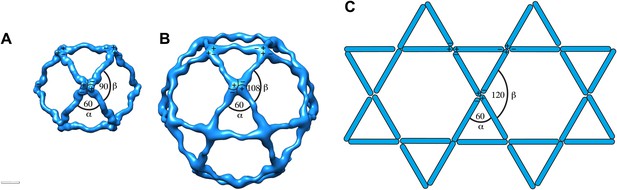
Current models for assembly and size variation of outer COPII coat cages.
(A) The 60 nm cuboctahedral cage is formed by twofold symmetrical vertices linked by rods. The angle alpha is 60°, the angle beta is 90° (see Figure 2—figure supplement 2A for definition of alpha and beta) (Stagg et al., 2006). (B) In the 90 nm icosidodecahedral cage (Stagg et al., 2008), alpha is 60°, but beta is 108°, leading to formation of pentagonal faces. (C) If beta was sufficiently flexible to form 120° angles, hexagonal faces could form, leading to assembly of a flat coat, as hypothesized by Stagg et al. (2008). Combinations of square, pentagonal and hexagonal faces into the same cage could potentially increase the extent of size variations allowed for the COPII coat.
Figure 3—figure supplement 2
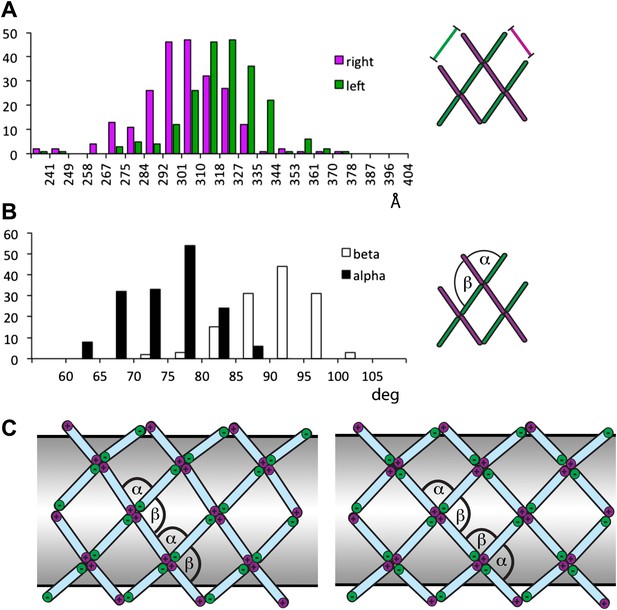
Variability and flexibility in the outer coat calculated from the coordinates of aligned subtomograms.
Note that the variability around the mean values may result from alignment errors from the subtomogram averaging. (A) The distances between neighbouring vertices measured along right-handed +/+ rods (purple), and along left-handed (−/−) rods (green). (B) Alpha and beta angles measured based on the coordinates of each vertex and the two corresponding neighbouring vertices. (C) A rhomboidal lattice could take two forms. In the first, each vertex would have the same orientation relative to the tube (left-hand panel). In this case the alpha and beta angles would always have the same orientation relative to the direction of the tube, and alpha could be smaller than beta. In the second, each vertex would be rotated by approximately 90° in the plane of the membrane relative to the adjacent vertices (right-hand panel). In this second form, alpha and beta would both be close to 90°. Assembling the second form would therefore require more substantial deformation of the vertex structure seen in in vitro assembled cages, in which alpha is smaller than beta.
Figure 3—figure supplement 3
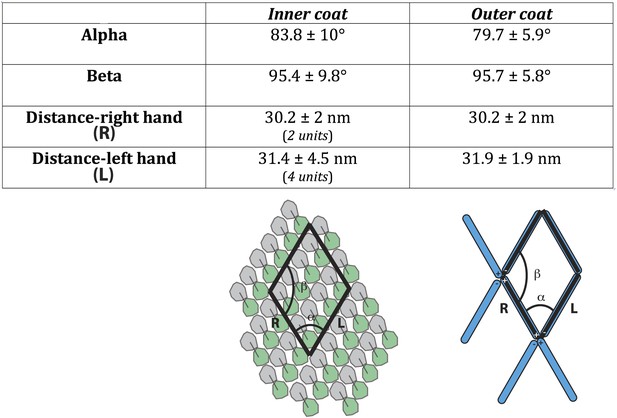
The unit cell dimensions for the inner and outer coat lattices.
The unit cell angles for the inner coat lattice are 83.8° ± 10° and 95.4° ± 9.8°, very close to the angles of 79.7° ± 5.9° (alpha) and 95.7° ± 5.8° (beta) measured for the outer coat. The distance between neighbouring outer coat vertices in the right-handed direction (30.2 ± 2 nm) is similar to the distance between two rows of inner coat subunits (30.2 ± 2 nm), while the distance between outer coat vertices in the left-handed direction (31.9 ± 1.9 nm) is similar to the distance between 4 inner coat subunits (31.4 ± 4.5 nm). The two lattices are therefore very closely matched.
Figure 4 with 1 supplement
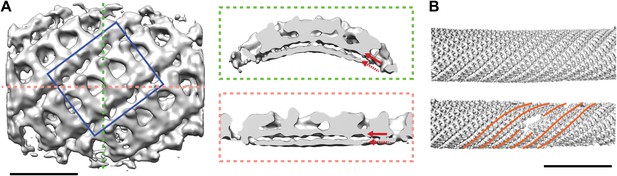
Structure and arrangement of the inner COPII coat.
(A) Isosurface representation of the inner coat on tubular membranes solved by sub-tomogram averaging. Top view and perpendicular slices cut along the dotted lines (green and pink boxes) are shown. Inner and outer leaflets of the lipid bilayer are indicated by dotted and continuous red arrows, respectively. Scale bar 20 nm. (B) Inner coat subunits placed in their aligned positions and orientations on two representative tubes. At positions where tube diameter changes, the helical symmetry changes (orange lines). Scale bar 100 nm.
Figure 4—figure supplement 1
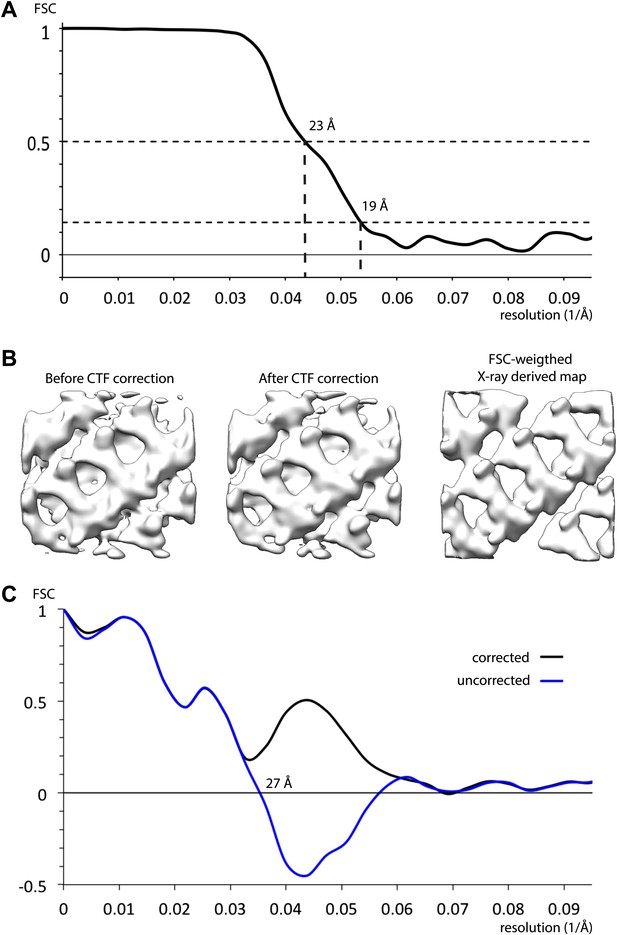
Resolution of inner coat structure.
(A) The resolution of the sub-tomogram averaged structures of inner coat was estimated by Fourier shell correlation (see ‘Materials and methods’ for details). Resolutions at the 0.5 and the 0.143 threshold criteria are indicated. (B) A visual comparison of maps obtained by averaging subtomograms extracted before and after CTF correction, with a map generated from the Sec23/24/Sar1 X-ray structures fitted into the inner coat array. To generate a map from the X-ray structures with a comparable resolution to the EM structures, the simulated electron density was multiplied by the Fourier shell correlation in panel A, and all frequencies where the correlation was lower than 0.143 were set to zero. (C) Fourier shell correlation between the map generated from the atomic model (panel B, right) and the CTF corrected (panel B, center), and uncorrected (panel B, left) subtomogram averages. A spherical mask with 5 pixel dropoff was applied, in addition to a soft (5 pixel dropoff) mask to exclude the membrane. When the uncorrected map was used, correlations beyond the position of the mean first node in the CTF are negative.
Figure 5 with 1 supplement
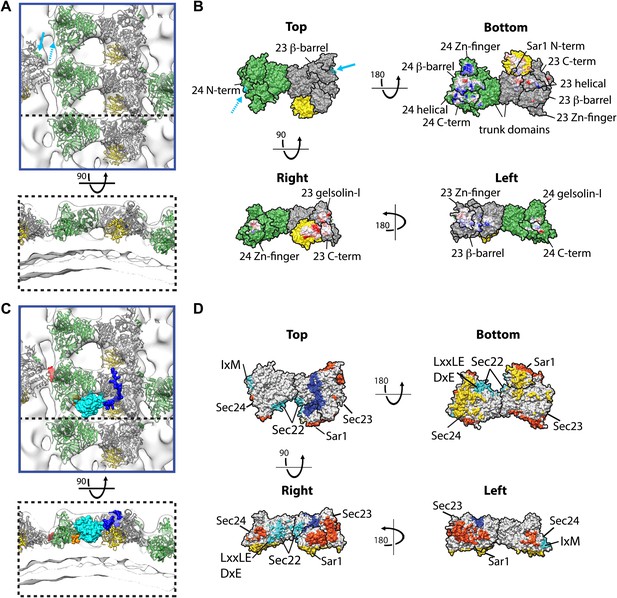
Interactions within inner coat lattice and membrane.
(A) Magnified view of the blue-outlined region in Figure 4A, viewed from top (upper panel) and side (lower panel). Atomic model of the inner coat (PDB 1M2V and 2QTV) is fitted into the reconstruction (Sec24 green, Sec23 grey, Sar1 yellow). Helix 61–73 of Sec24 (solid cyan arrow) is shown in the position where it binds Sec23 in the Sec23-24 co-crystal structure. Residue 133 of Sec24 is marked (dotted cyan arrow) (‘Materials and methods’). (B) Surface representations of the fitted atomic model with boundaries between domains marked. Cyan arrows as in A. Residues interacting with the membrane (‘bottom view’) or mediating protein-protein interactions (‘right’ and ‘left’ views) are coloured based on coulombic potential (red: negative, blue: positive). (C) Atomic models of Sec23/24 co-crystallised with cargo or Sec31 active fragment superimposed to the fitted model: the IxM containing peptide from syntaxin 5 (PDB 3EFO) (red), the Sec22 cytosolic domain (PDB 3EGD) (cyan), a DxE containing peptide derived from VSV-G (PDB 3EGD) (orange), and the Sec31 active peptide (PDB 2QTV) (blue). (D) As in B, with surfaces coloured by interaction partner: membrane (yellow), cargo (cyan), Sec31 (blue), and neighbouring Sar1/Sec23/24 heterotrimers in the lattice (orange).
Figure 5—figure supplement 1
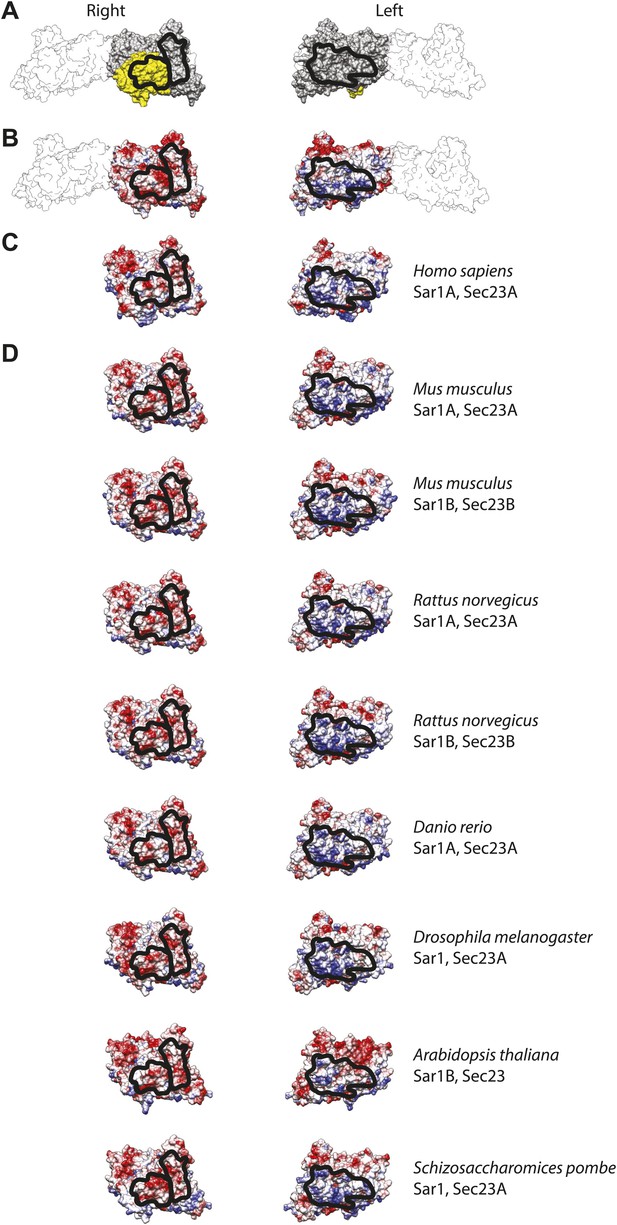
Interactions between inner coat subunits are mediated by surfaces with conserved electrostatic properties.
(A) Atomic model of the inner coat from yeast protein structures (PDB 2QTV and 1M2V), shown from the right and from the left as in Figure 5B,D. Sec23 is grey, Sar1 yellow, and Sec24 white. The regions that interact with each other at the interface between rows of inner coat subunits are in outlined in black. (B) The same model coloured by coulombic potential to illustrate basic and acidic surfaces in blue and red, respectively. (C) Human Sec23 and Sar1 (PDB 3EFO and 3GA0) superimposed to the fitted model and coloured according to surface coulombic potential. The black line shows the regions expected to interact. (D) Gallery of structures of several model organisms, obtained by homology modeling on the yeast structure templates using swissmodel.expasy.org.
Figure 6
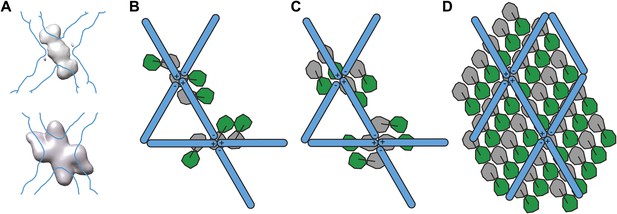
Models for the spatial relationship between inner and outer coat.
(A) Cryo-electron microscopy reconstructions of COPII cages assembled in vitro in the presence of inner coat subunits, but in the absence of a membrane, showed additional density below that of the outer coat. The top panel shows the density for the inner coat obtained in cages formed in the presence of Sec23 alone (Bhattacharya et al., 2012). The bottom panel shows the density for the inner layer in cages formed in the presence of Sec23/24 (Stagg et al., 2008). The position of the outer coat is marked as a blue outline. Note that in both studies, the twofold symmetry of the outer coat vertex was imposed on the inner coat. (B) Based on the comparison between the structures in panel A, Stagg et al. proposed that Sec23 binds at two positions: one copy below each vertex and two copies at its side. Sec24 would be located under the holes in the cage (Bhattacharya et al., 2012). According to this model, the inner coat arrangement does not conform to the twofold symmetry applied during the reconstruction procedure, explaining why it is poorly resolved in the cage reconstruction. (C) A previous model was proposed based on the reconstruction of icosidodecahedral cages (bottom panel in A). In this model, Sec23/24 subunits are oriented with their long axes in the direction of the +/+ connection of the outer coat vertex. Two arrangements consistent with this model are shown: in the first (top) the subunits all have the same orientation, in the second (bottom), subunits have opposite orientations, following the twofold symmetry of the outer coat. (D) A schematic representation of the relationship between inner and outer coat as identifed in this study. This arrangement is similar to the model suggested in C (top). The stoichiometry of the two coat layers is 1:2 outer:inner in coated tubes, meaning that only half of the inner coat subunits are bound by the known Sec31 interface. The percentage of bound inner coat subunits would be higher on spherical vesicles. The difficulty in resolving the position of the inner coat in the studies of cages assembled in the absence of a membrane can be explained by our observation that the relative positions of outer and inner coats are constrained but not fixed, and that the two layers do not follow the same symmetry.
Figure 7
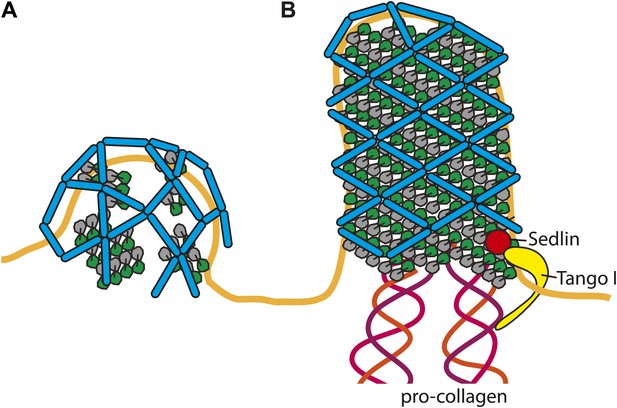
Cartoon depiction of a model for two COPII assembly modes.
(A) On a spherically curved membrane the bow-tie shaped inner coat subunits assemble in small patches that may be randomly oriented with respect to each other. Outer coat rods bind to the inner coat patches in a preferred orientation. The outer coat can assemble to form triangles, squares, or pentamers. (B) If the inner coat forms large arrays instead of small patches, then the outer coat, interacting with the inner coat in its preferred orientation, will tend to arrange to form a lozenge pattern. This arrangement of inner and outer coats results in coated tubular membranes. This arrangement could simply be promoted by packaging of elongated cargoes. It could also be favoured when external factors intervene to either delay outer coat recruitment, and/or stabilise larger inner coat patches. Tango I and Sedlin (Saito et al., 2009; Venditti et al., 2012) have been proposed to facilitate formation of large COPII carriers that are capable of incorporating 300 nm-long procollagen molecules, and to achieve this by stabilizing the inner coat on the membrane.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The structure of the COPII transport-vesicle coat assembled on membranes
eLife 2:e00951.
https://doi.org/10.7554/eLife.00951
