Dynamical feature extraction at the sensory periphery guides chemotaxis
- Centre for Genomic Regulation, Spain
- Universitat Pompeu Fabra, Spain
- Janelia Research Campus, Howard Hughes Medical Institute, United States
- Institucio Catalana de Recerca i Estudis Avancats, Spain
- Yale University, United States
- Tata Institute of Fundamental Research, India
Figures
Figure 1
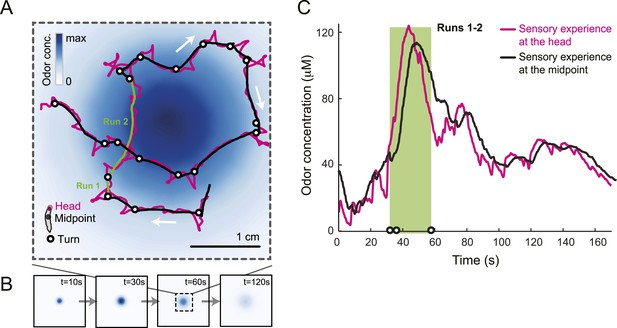
Sensory experience corresponding to unconstrained chemotactic behavior.
(A) Illustrative trajectory of a larva freely moving in an attractive odor gradient (isoamyl acetate, source concentration: 0.25 M). Position of the midpoint shown in black; position of the head shown in magenta. Two run segments, R1 and R2, are underlined in green. Turns are depicted as white disks. White arrows indicate the direction of motion. (B) Reconstruction of the odor gradient based on numerical simulations of the odor diffusion process modeled by a partial differential equation (PDE) system with realistic boundary conditions (‘Materials and methods’). The gradient shown in panel A corresponds to a snapshot obtained 60 s after onset of the odor diffusion. (C) Time course of the odor concentration experienced at the head (magenta) and midpoint (black) of the larva during the trajectory shown in panel A. The sensory experiences are reconstructed based on mapping the positions of interest on the dynamic odor gradient computed upon integration of the PDE system for the entire duration of the trajectory. The green box outlines the sensory experience corresponding to run segments R1 and R2. Small disks on the abscissa indicate the turns comprised in this behavioral sequence.
Figure 2
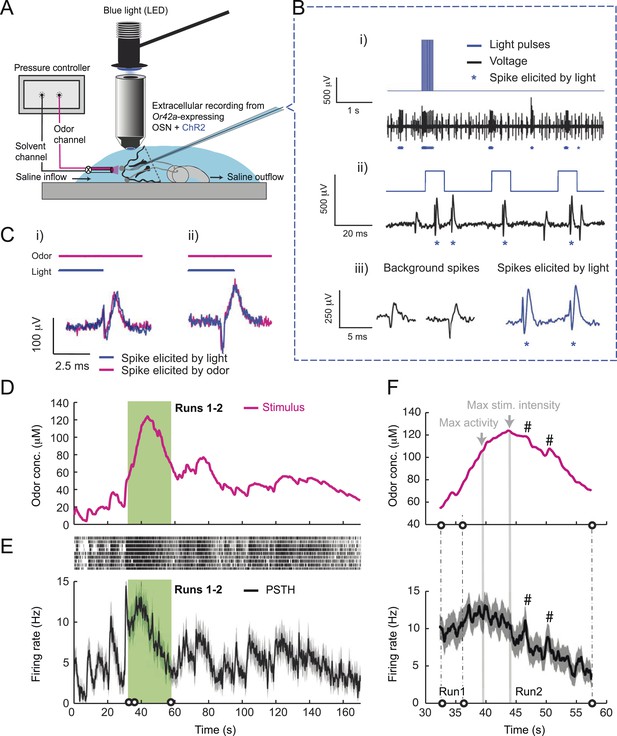
Response of a single larval olfactory sensory neuron (OSN) to naturalistic odor stimulation.
(A) Illustration of preparation for suction electrode recordings of single functional OSNs expressing channelrhodopsin (ChR2). The preparation is bathed in saline to prevent the dehydration of the dorsal organ ganglion to which the recording electrode is attached. Controlled odor stimulations are achieved in liquid phase with a customized mass flow controller system. (B) Recording from the dorsal organ stimulated by a series of 10-ms light pulses. (i–ii) The voltage trace shows spikes with different amplitudes. (iii) Close-up view of the voltage trace corresponding to three consecutive light pulses. Action potentials with a stereotyped waveform are observed at a short-latency after the onset of the light pulse (spikes denoted by a blue star *). These spikes are associated with the activity of the Or42a OSN expressing ChR2. Each light pulse yielded an average of 1.8 light-evoked spikes. (C) Superimposition of light- and odor-evoked spike waveforms observed for the same OSN. The results of two different recordings are shown in (i) and (ii). Spike waveforms associated with the light stimulation (blue spikes) are superimposed on spike waveforms collected during an episode of odor stimulation (magenta spikes). The high similarity between the light- and odor-evoked spikes serves as a basis to spike sort the recordings arising from the dorsal organ ganglion (‘Materials and methods’). (D) Dynamic reconstruction of the concentration time course corresponding to the trajectory of the head position depicted in Figure 1. (E) Results of 9 suction electrode recordings for the Or42a>ChR2 OSN stimulated by the concentration shown in panel D (5 preparations). (Top) Raster plot. (Bottom) PSTH of the OSN response to the concentration time course shown in panel D with shade representing the standard deviation. (F) Close-up view of the sensory experience (top) and OSN response (bottom) corresponding to the illustrative runs R1 and R2 shown in panel D (green box). Since the maximum firing rate is attained earlier than the stimulus intensity reaches its maximum, the input–output relationship driving the dynamics of the OSN activity is more complex than a proportional detector. Short increases in odor concentration lead to transient bursts in spiking activity (bursts indicated by sharp # signs). Small disks on the abscissa denote turns in the original trajectory presented in Figure 1.
Figure 3 with 1 supplement
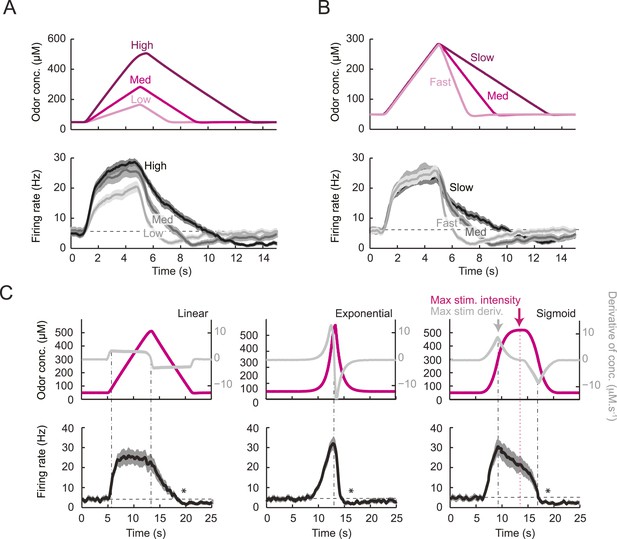
Characterization of the dynamical features extracted by the Or42a-expressing olfactory sensory neuron.
(A) Response to three linear ramps with variable slopes during the rising phase and equal slope during the falling phase. The ‘low’ (‘high’) ramps have a positive slope that is twice slower (faster) than the medium ramp. PSTH computed on a pool of minimum 24 recordings obtained from minimum 8 preparations. During the rising phase of the ramp, the activity of the OSN reaches a peak value that scales with the slope of the ramp. (B) Response to three linear ramps with variable slopes during the falling phase and equal slope during the rising phase. The ‘slow’ (‘fast’) ramp has a negative slope that is twice slower (faster) than the medium ramp. During the rising phase of the ramp, the plateau reached by the OSN activity grows with the slope of the ramp. During the falling phase of the ramp, the activity of the OSN is more directly driven by the stimulus intensity. For the three ramps, the OSN activity becomes inhibited when the ramp terminates. PSTH computed on a pool of minimum 24 recordings obtained from minimum 8 preparations. (B) Response to nonlinear ramps featuring a symmetrical 8 s-rise and 8 s–fall profiles. From left to right, the ramps tested have the following characteristics: linear (∝ t), exponential (∝ e−8(et −1)), and sigmoid (∝ t3/(t3+43)) with the time given in s. PSTH computed on a pool of minimum 16 recordings obtained from minimum 9 preparations. For panels C, the odor concentration (magenta) is computed from the flow ratio measured experimentally based on the flow controller outputs (‘Materials and methods’). The time derivative of the concentration time course is represented according to the y-scale on the right of the graph (gray). The derivative was computed after mild smoothening of the stimulus input. Asterisks denote inhibitory phases of the OSN response where the activity decreases below its basal level (horizontal dashed line).
Figure 3—figure supplement 1
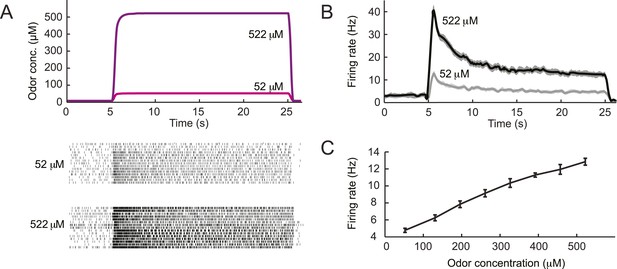
Dose-response of the Or42a-expressing olfactory sensory neuron stimulated by prolonged odor pulses.
(A) Response to odor step stimulations of low and high concentrations: 52 μM and 522 μM. (Bottom) Raster plot of the OSN activity in response to low- and high-concentration odor steps (light and dark gray, respectively). 15 recordings conducted on 5 different preparations. (B) PSTH of the OSN activity in response to the low- and high-concentration odor steps (light and dark gray, respectively) shown in panel A. Shades represent standard deviations. The response dynamics of the Or42a OSN to static odor pulses is similar to that observed in adult-fly OSNs (de Bruyne et al., 1999, Nagel and Wilson, 2011, Martelli et al., 2013). (C) Dose-response curve observed for the activity of the OSN after it has relaxed to a steady state value (mean firing rate computed during the time interval 20–24 s). Error bars represent standard deviations.
Figure 4 with 2 supplements
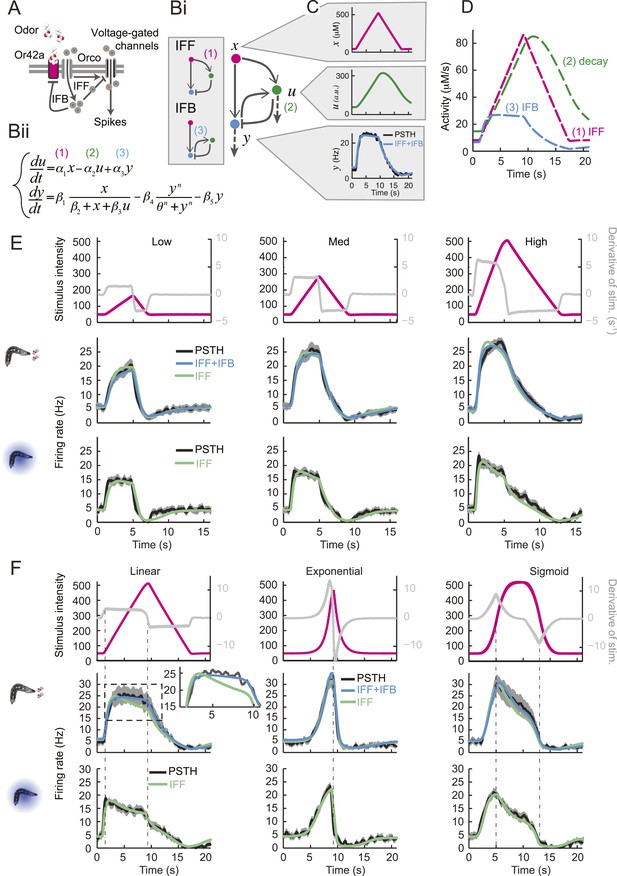
Quantitative model for signal processing achieved by a single olfactory sensory neuron.
(A) Hypothetical physiological processes underlying the olfactory transduction pathway and spike generation. The integral feedback (IFB) motif is built on the assumption that inhibitory feedback modulates the activity of the odorant receptor, as was proposed in the adult fly (Nagel and Wilson, 2011). This motif appears to be essential to olfactory transduction in vertebrates (De Palo et al., 2013). The incoherent feed-forward (IFF motif) relies on the hypothetical existence of a delayed inhibitory effect, as was proposed for the transduction cascade of C. elegans (Kato et al., 2014). (B) Biophysical model of the olfactory transduction pathway. (Bi) Circuit elements combining the IFF and IFB motifs described in panel A. Variable x represents the stimulus intensity, u, the activity or concentration of the intermediate variable and y, the firing rate of the OSN. Pathway (3) is specific to the IFB motif (light blue). (Bii) ODE system providing a phenomenological description of the reaction scheme outlined in panel A for the combination of the IFF and IFB regulatory motifs. The three pathways regulating the activity of u are outlined by numbers (1)–(3). Reaction (1) corresponds to a ‘production’ of u through the IFF branch; (2) corresponds to a first-order ‘decay’ of u; (3) corresponds to a ‘production’ of u through the IFB branch. (C) Simulated activity of u (green, middle) and firing rate y (blue, bottom) in response to an 8-s linear odor ramp (magenta, top). Numerical simulations were achieved by integrating the ODE system described in panel Bii with the parameter values listed in Table 1. (D) Decomposition of the predicted activity of individual pathways contributing to the regulation of u for the linear odor ramp displayed in panel C. Activity computed from the terms (1)–(3) outlined in panel B for the feed-forward activation by the stimulus (IFF, 1), first-order decay (2) and coupling of the firing rate with the intermediate variable through the negative feedback (IFB, 3). Notably, the contribution of the reaction specific to the IFB motif (3) is dominated by the reaction specific to the IFF motif (1). (E) Fit of the solution of the ODE model for three linear stimulation ramps introduced in Figure 3A,B and produced with odor (middle) and light (bottom). (Top) Stimulus intensity given as odor concentration (μM). The time derivative of the concentration profile (gray lines) is given according to the y-axis shown on the right side of the graph. The derivative was computed after mild smoothening of the stimulus time course. The same (idealized) profile was used for the light stimulation with an intensity ranging between 15 W/m2 and 207 W/m2. (Middle) Comparison of the outcome of the model featuring a pure IFF motif (green) and a combination of the IFF and IFB motifs (blue). The parameters of both models were obtained independently through a Simplex optimization procedure (‘Materials and methods’). For the pure IFF model, parameter α3 was artificially set to 0. (Bottom) Comparison of the outcome of the experimental PSTH and the model's predictions based on a pure IFF motif (green) for light stimulation. Parameter optimization shows that the IFB motif does not contribute to the light-evoked OSN dynamics. (F) Fit of the solution of the ODE model for three nonlinear stimulation ramps generated with odor and light. (Middle) Results of the model compared to the odor-evoked OSN activity. Close-up view of the 8-s linear ramp highlighting the differences between the behavior of the pure IFF (green) and combined IFF+IFB (blue) circuit motifs for odor stimulation. (Bottom) Comparison of the outcome of the experimental PSTH and model based on a pure IFF motif (green) for light stimulation. For all conditions shown in the figure, PSTHs were computed on a pool of a minimum of 10 recordings obtained from a minimum of 10 preparations.
Figure 4—figure supplement 1
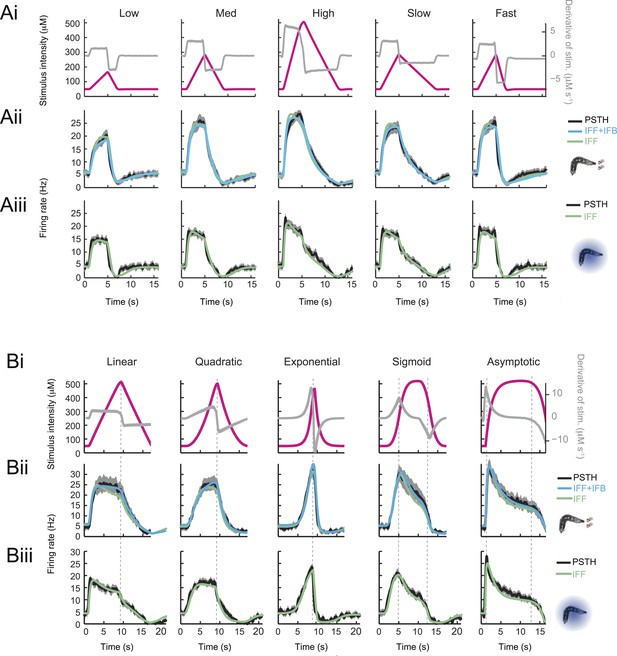
Response dynamics of the Or42a>ChR2 OSN to linear and nonlinear stimulation ramps induced with odor and light, and fits of the stimulus-to-neural (ODE) models.
(A) Set of 4-s linear ramps with different rising and falling slopes. (Ai) Five ramps with a rising phase that lasts 4 s. Stimulus intensity given as odor concentration (μM, magenta). Upon mild smoothening of the stimulus time course trajectories with a Savitzky-Golay filter, the time derivative (gray) of the concentration profile is represented according to the y-axis on the right of the graph. The same (idealized) profile was used for the light stimulation with an intensity ranging between 15 W/m2 and 207 W/m2. (Aii) Fit of the solution of the ODE model for the linear stimulation ramps generated with odor. Comparison of the experimental PSTH (black) with the outcome of the model featuring a pure IFF motif (green), and a combination of the IFF and IFB motifs (blue). (Aiii) Modeling of the OSN activity elicited by the linear light ramps. Comparison of the experimental PSTH with the outcome of the model based on a pure IFF motif (green). (B) Set of 8-s linear and nonlinear ramps. (Bi) Stimulus intensity given as odor concentration (μM, magenta). Same conditions as panel A. (Bii) Modeling of the OSN activity elicited by odor ramps. Comparison of the experimental PSTH (black) with the outcome of the model featuring a pure IFF motif (green), and a combination of the IFF and IFB motifs (blue). (Biii) Same as Bi for the light ramps. Comparison of the experimental PSTH with the outcome of the model based on a pure IFF motif (green). For all conditions shown in this figure, the PSTHs were computed on a pool of a minimum of 10 recordings obtained from a minimum of 10 preparations.
Figure 4—figure supplement 2
Validation of the stimulus-to-neural (ODE) model for the olfactory transduction cascade upon training on partial datasets.
(A) Training of the ODE model described in Figure 4B on a set of 5 linear ramps with rising phase lasting 4 s. (B) The ODE model trained on the 4-s linear ramps alone (panel A) is validated on 8-s stimulus ramps: a linear ramp (left), an exponential ramp (middle), and a sigmoid ramp (right). The model is trained independently for odor (middle row) and light stimulations (bottom row). The predictions of the model are shown as a dashed line. The PSTH experimentally observed is shown in black (shades denote standard deviation). The output of the model trained on the entire set of ramps (plain line, parameter set listed in Table 1) shows nearly no improvement compared to the model trained on the subset of linear ramps. For both the odor-evoked and light-evoked OSN dynamics, the correlation coefficients (ρ) and coefficients of variation of the RMSE (Table 1) corresponding to the model trained on the linear ramps and that trained on all ramps differ by less than 1% and 5%, respectively. (C) Validation of the ODE model obtained in panel A on naturalistic stimulation with odor (middle row) and light (bottom row). Stimulus time course represented in magenta. The experimental PSTH is shown in black (shades denote standard deviation). The predictions of the model trained on the linear ramps alone (dashed line) show nearly no difference with the output of the model trained on the entire set of ramps (plain line). The naturalistic odor stimulus corresponds to the trajectory presented in Figure 2D. The naturalistic light stimulus corresponds to the trajectory presented in Figure 6B. For both the light and the odor-evoked spiking activity, the correlation coefficients (ρ) and coefficients of variation of the root-mean-square error (RMSE) corresponding to the model trained on the linear ramps alone and that trained on all ramps differ by less than 1% and 7%, respectively.
Figure 5 with 3 supplements
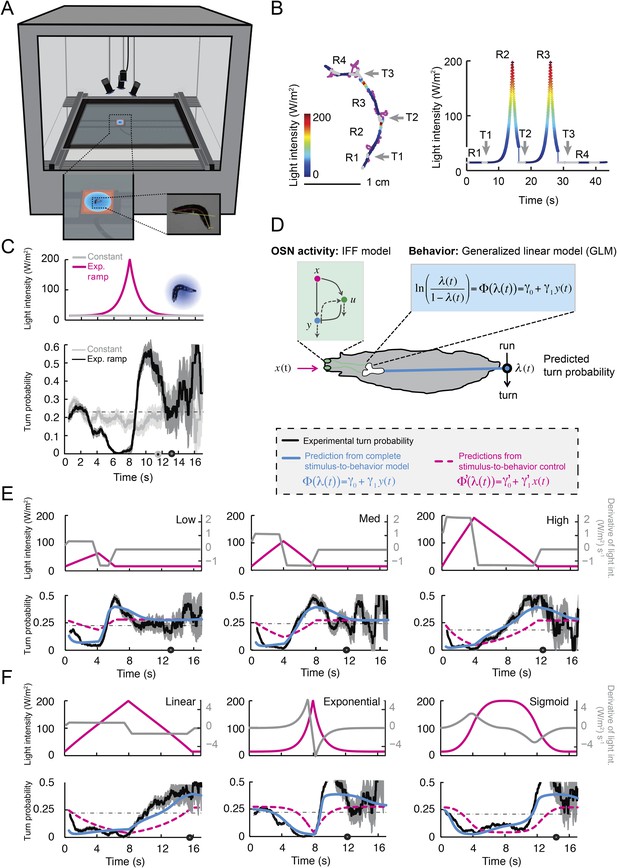
Modulation of run-to-turn transitions by light-evoked activity in the Or42a-expressing OSN.
(A) Illustration of the closed-loop tracker used to synthesize virtual olfactory realities with light stimulation coupled to optogenetics. Close-up view of the larva illuminated by a red light pad fixed to a moving stage below the agarose slab. The camera and LEDs are mounted on a second moving stage whose position is updated synchronously with the bottom stage to remain locked on the position of the larva. The platform on which the larva behaves is fixed. (B) Presentation of the run-based light stimulation paradigm where runs are randomly assigned to constant stimulation (control) or to a test ramp with an exponential profile similar to that introduced in Figure 3C. (Right) Midpoint position of the larva during a trajectory with the light intensity color-coded in accordance with the color bar on the left. Illustrative runs denoted as R1-4 are interspaced by turns T1-3 denoted by arrows. (C) Turn probability estimated from a set of runs associated with constant stimulation (light gray) or stimulation by an exponential light ramp (black). The turn probabilities are reported as the fraction of turns occurring during a 1-s window centered on the time point of interest (‘Materials and methods’). Error bars are estimated from resampled sets of runs (shaded areas denote standard deviation, see ‘Materials and methods’). The dashed line depicts the mean turning rate computed for constant light stimulation. The turning rate is in first approximation independent of the run duration. Small disks on the x-axis indicate time points after which fewer than 10% of the total number of runs are left for the constant stimulation (light gray) and exponential ramp (dark gray). Beyond these time points, the estimates of the turn probability should be considered as unreliable. (D) Generalized linear model (GLM) for the modulation of turn probability as a function of the sensory experience (integrated stimulus-to-behavior model). The turn probability is predicted from a linear combination of the predicted neural activity (γ1 y (t)) and a constant term (γ0). This linear combination is then fed into a logit transformation to convert the domain of definition of the neural activity into a probability. The two parameters of the model, γ0 and γ1, are determined from a linear regression on the experimental profiles of turn probability. The OSN activity driven by light, y, is predicted from the pure IFF (ODE) model described in Figure 4B. As a control, we consider the same model where the input is the stimulus intensity. The parameters of this control model are denoted as γ′0 and γ′1. Upon training of the test and control models on the full set of linear and nonlinear ramps (Figure 5—figure supplement 1), we derived the parameter values reported in Table 3. (E) Predictions of the integrated stimulus-to-behavior GLM for linear ramps of different rising and falling slopes. (Top) For the individual ramps, the time course of light intensity is shown in magenta. The time derivative of the light ramp (gray line) is computed after mild smoothening of the stimulus input. (Bottom) Behavioral predictions based on the neural activity predicted by the IFF (plain blue line) and the control model that is purely based on the stimulus (dashed magenta line). The integrated stimulus-to-behavior model clearly outperforms the predictions of the control model, which highlights the importance of the signal processing achieved by the OSN. (F) Predictions of the integrated stimulus-to-behavior model for 8-s light ramps. For all conditions tested, the experimental turn probability was estimated on a sample of 490–970 runs. Quantification of the goodness of fit is reported in Table 4 for the test and control models.
Figure 5—figure supplement 1
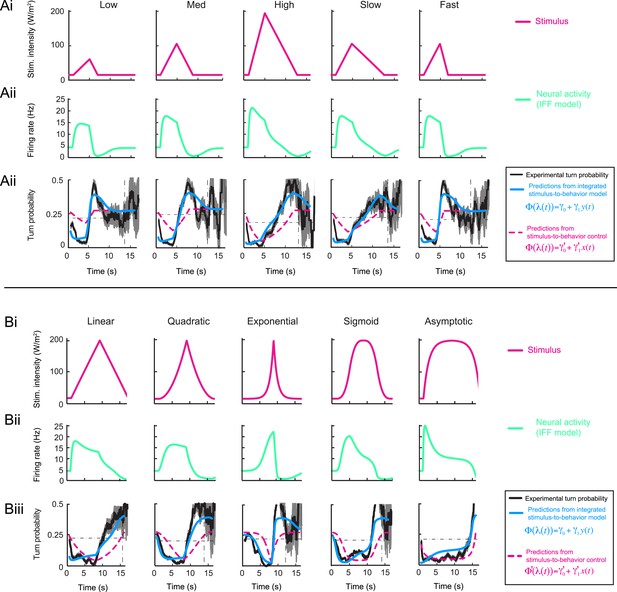
Fit of the integrated stimulus-to-behavior generalized linear model (GLM) for the linear and nonlinear light ramps.
(A) Set of 4-s linear ramps. (Ai) Light intensity profile (W/m2). (Aii) Application of pure IFF motif to model the OSN activity elicited by the light ramps (green line). (Aiii) Application of the integrated stimulus-to-behavior GLM to predict behavior in response to stereotyped light ramps. The test model (blue line) is based on the neural activity modeled by the IFF motif. The turn probability estimated experimentally is shown in black (shades denote standard deviation as described in ‘Materials and methods’). As indicated in the textbox on the right, the control model is based on the stimulus without any processing of the OSN (dashed magenta line). The black dashed line in the background represents the average turn probability observed upon stimulation at constant light intensity. The integrated stimulus-to-behavior model clearly outperforms the predictions of the control model. (B) Set of 8-s linear and nonlinear ramps. (Bi–Biii) Same as panels Ai–Aiii for the behavior elicited by 8-s light ramps. For all test conditions, the experimental turn probability was estimated on a sample of 490–970 runs. The outputs of the test and control models are obtained based on the parameter sets listed in Table 1 (ODE model) and Table 3 (GLM).
Figure 5—figure supplement 2
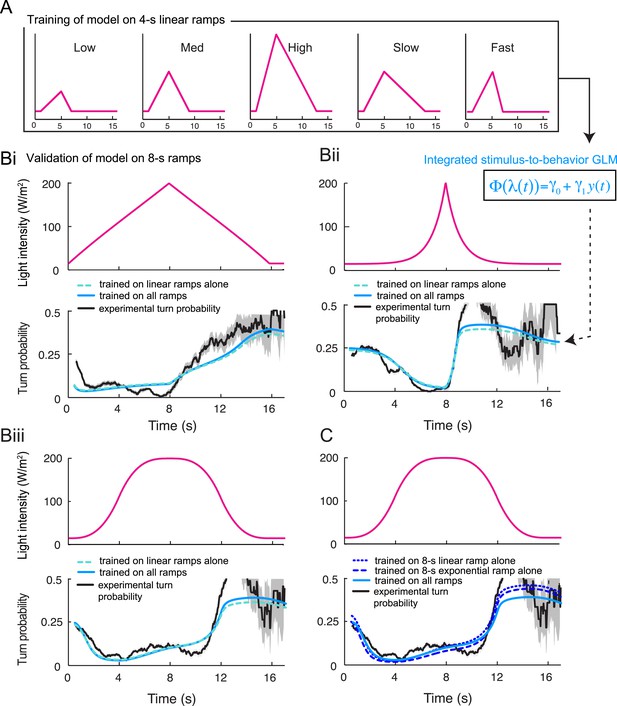
Validation of the integrated stimulus-to-behavior generalized linear model (GLM) upon training on a partial set of light ramps.
(A) Training of the GLM described in Figure 5D restricted to the set of 4-s linear light ramps. (B) Validation of the GLM model trained on the set of 4-s linear ramps (panel A) on 8-s ramps (dashed green line). Comparison with the output of the model trained on the entire set of ramps (plain blue line, parameter set presented in Table 3) shows nearly no difference with the model trained on a subset of linear ramps. The turn probability estimated experimentally is shown in black (shades denote standard deviation as described in ‘Materials and methods’). (Bi) Validation of the model on the 8-s linear ramp. (Bii) Validation of the model on the 8-s exponential ramp. (Biii) Validation of model on the 8-s sigmoid ramp. The correlation coefficients and coefficients of variation of the RMSE corresponding to the model trained on the linear ramps and the model trained on all ramps differ by less than 1% and 9%, respectively. (C) Training of the GLM on a single light ramp and validation on the 8-s sigmoid ramp: training on the 8-s linear ramp (short dashed line); training on the 8-s exponential ramp (long dashed line). The output of the model trained on the complete set of ramps is shown as plain line. The correlation coefficients and coefficients of variation of the RMSE corresponding to the model trained on a single ramp and the model trained on all ramps differ by less than 1% and 10%, respectively.
Figure 5—figure supplement 3
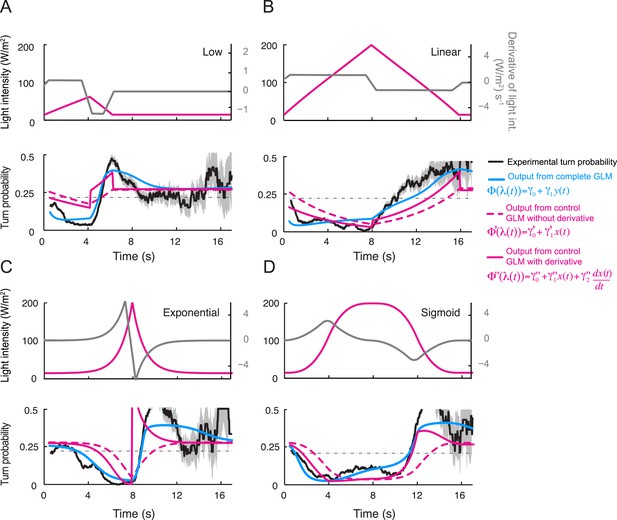
Comparison of the predictions of the integrated and control generalized linear model (GLM) with and without the contribution of the first derivative of the stimulus intensity.
(A) Predictions for the linear low (4-s) ramp. (Top) Time courses of the stimulus intensity (magenta line) and its time derivative (gray line). (Bottom) The turn probability estimated experimentally is shown in black (shades denote standard deviation as described in ‘Materials and methods’). The predictions of the integrated stimulus-to-behavior GLM are shown in blue. The performance of the stimulus-to-behavior control model, based on the stimulus intensity alone (dashed magenta line), improves by combining the light intensity with its first derivative. We note that the integrated stimulus-to-behavior GLM outperforms the two control GLMs. The discrepancies between the controls and the test model are particularly pronounced during the beginning of the rising phase of the ramp. The goodness of fit is quantified in Table 4. (B) Same as panel A for the 8-s linear ramp. (C) Same as panel A for the 8-s exponential ramp. (D) Same as panel A for the 8-s sigmoid ramp.
Figure 6
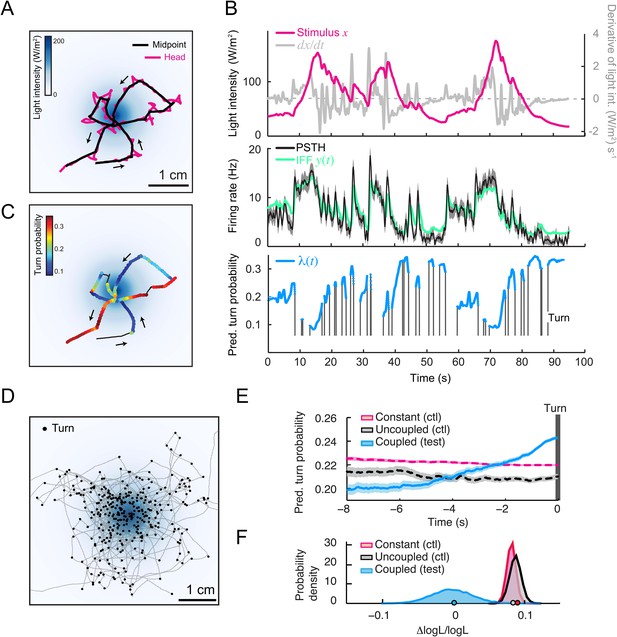
Predictions of the integrated stimulus-to-behavior generalized linear model (GLM) for run-to-turn transitions observed in a virtual olfactory gradient.
(A) Synthetic chemotaxis in a virtual odor gradient produced by light stimulation. The larva experiences a light intensity determined by a predefined stimulus landscape. The landscape displayed in the background of panel A is an exponential gradient centered on a point ‘source’. Larvae responding to this light gradient accumulate at the gradient's peak as observed for odor gradients. Illustrative trajectory of the midpoint (black) and head (magenta). Black arrows indicate the direction of motion. (B) Sensorimotor analysis of a representative trajectory. (Top) Time course of the light intensity associated with the trajectory displayed in panel A. (Middle) PSTH of the OSN activity measured experimentally upon a replay of the intensity time course at the electrophysiology rig (black line). Numerical simulations of the neural activity carried out by the IFF motif (green line) presented in Figure 4B. (Bottom) Turn probability (blue line) predicted from the integrated stimulus-to-behavior GLM presented in Figure 5D (parameter set listed in Table 3). The neural activity simulated in the middle panel is fed into the GLM to predict the turn probability shown in the bottom panel. Behavioral predictions are only shown for the sequences associated with runs. (C) Overlay of the trajectory of the midpoint with the predicted turn probability color-coded in accordance with the color bar on the left. We observe that the turn probability tends to increase (red color range) when the larva is moving away from the gradient's peak, whereas it decreases (blue color range) when the larva is moving toward the peak. (D) Overlay of 10 trajectories recorded in the exponential light gradient shown in panel A. For each trajectory, the position of the midpoint is shown in gray. Turns are indicated as small black circles. (E) Turn-triggered average of the predicted turn probability for the exponential light gradient. A comparison is made between predictions based on the simulated OSN activity driven by the stimulus intensity (test model, blue line), predictions based on the simulated OSN activity driven by the time-reversed stimulus time course (uncoupled control, black line), and predictions based on the assumption that the neural activity stays constant over the course of each trajectory (constant control, magenta line). The parameters of the stimulus-to-behavior GLM are listed in Table 3. We observe that the turn probability steeply increases 4 s before the turn, which coincides with the median duration (3.8 s) of the entire set of runs. Analysis conduced over 750 runs with a duration of minimum 1 s. Shaded areas represent SEM. (F) Log-likelihood of the predictions of the stimulus-to-behavior test GLM compared to the controls. Bootstrap analysis of the difference in log-likelihood (logL) between the test model and the controls normalized by the log-likelihood of the test model (ΔlogL/logLtest). Distribution of the relative difference in logL is shown for the test model against the constant neural activity control (red), and the uncoupled stimulus control (black). The median of the distribution is equal to the value obtained from the original full set of runs; the median of the entire distribution is indicated by a dot in the x-axis. As an internal control, the test model was compared to itself (blue). Out of 10,000 resampled subsets of runs, none of the controls was found to be more likely than the test model (p < 0.0001). The analysis included all observed runs with a duration of minimum 1 s (750 runs originating from 25 trajectories).
Figure 7
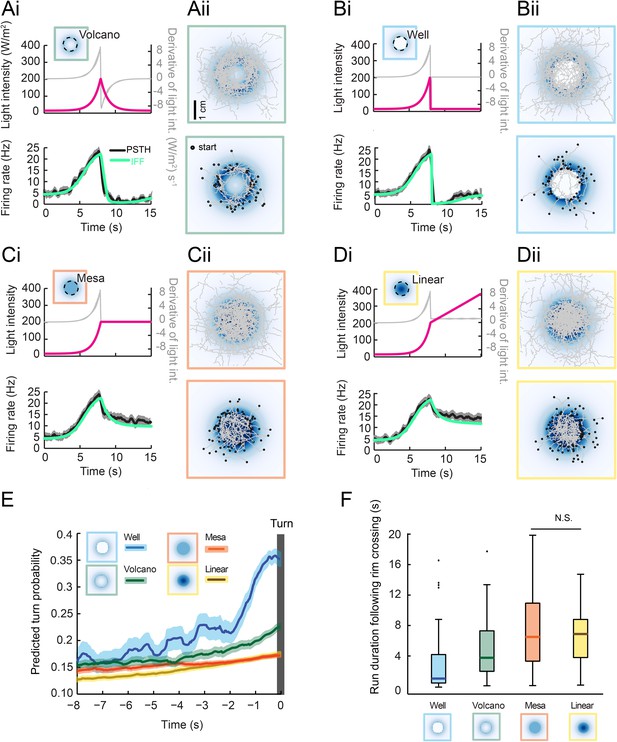
Predictions of run-to-turn transitions elicited by a family of radially symmetrical light landscapes.
(Ai–Di) Stereotyped OSN responses to light ramps starting with a common 8-s exponential rise: ramp with a smooth exponential fall (‘volcano’, see panel A), ramp with an abrupt fall to basal intensity (‘well’, see panel B), ramp with a prolongation of the maximum intensity (‘mesa’, see panel C), and ramp with a linear increase (‘linear’, see panel D). The spiking activity of the OSN is computed from the pure IFF (ODE) model presented in Figure 4B (parameter set listed in Table 1). Time course of the light intensity shown in magenta; first derivative of the light intensity shown in gray; simulated OSN activity shown in green. (Ai) Experimental and predicted OSN activity elicited by an exponential rise followed by an exponential fall. (Aii) Symmetrical two-dimensional light landscapes corresponding to the exponential ‘volcano’ profile described in panel Ai. (Top) Set of 54 trajectories superimposed onto the stimulus landscape. (Bottom) Set of 48 runs starting from the external edge of the ‘volcano’ and heading toward its center (minimum run duration: 1 s). (Bi) Same as Ai for the ‘well’ profile. Strong inhibition of the OSN activity follows the abrupt fall in light intensity. (Bii) Crossing of the rim leads to an aversive response. As a consequence, larvae avoid the well at the center of the landscape. Set of 42 trajectories represented in the diagram at the top; set of 63 entering runs represented in the diagram at the bottom. (Ci) Same as Ai for the ‘mesa’ profile. The transition from an exponential rise in light intensity to constant intensity leads to a transient drop in neural activity before a steady state value is reached. (Cii) For the mesa landscape, crossing of the rim does not lead to an aversive response: larvae tend to maintain their ongoing run. The center of the landscape is therefore visited. Set of 36 trajectories represented in the diagram at the top; set of 79 entering runs represented in the diagram at the bottom. (Di) Same as Ai for a ‘linear’ hat profile. The deceleration in stimulus from an exponential rise to a linear rise leads to a transient drop in neural activity before a steady state value is reached. The corresponding OSN dynamics is similar to that elicited by the mesa (panel Ci). (Dii) Upon crossing of the rim of the linear hat landscape, larvae undergo a deceleration in light intensity that is expected to modulate behavior in a way similar to the mesa landscape. Set of 47 trajectories represented in the diagram at the top; set of 72 entering runs represented in the diagram at the top. (E) Turn-triggered averages of the predicted turn probability for the subset of runs entering the landscape's central area (bottom graphs of Aii–Dii). Each run included in the analysis crosses the rim of the landscape (minimum run duration: 1 s). Shaded areas represent SEM. (F) Distribution of run durations following the crossing of the landscape's rim. Analysis restricted to the subset of runs described in the diagram at the tops of panels Aii–Dii (runs entering the central area of the landscape). The experience of an abrupt fall in light intensity promotes rapid turning (‘well’ condition), whereas runs are elongated by constant light stimulation or by a linear rise in light intensity (‘mesa’ and ‘linear’ landscapes). Differences between the median of the run durations associated with each of the four landscapes is assessed through a Kruskal–Wallis test (p < 10−10) followed by pair-wise Wilcoxon tests with a Bonferroni correction (for the non-significant difference p > 0.05/6; for all other pairwise comparisons p < 0.05/6). The behavior predicted from turn probability (panel E) is in good agreement with the shortening or elongation of the runs observed for each of the four landscapes.
Figure 8 with 1 supplement
Predictions of the integrated stimulus-to-behavior model for run-to-turn transitions observed in a real odor gradient.
(A) Superimposition of 10 consecutive trajectories observed in an odor gradient of isoamyl acetate (same experimental conditions as Figure 1). For every trajectory, the position of the midpoint is shown in gray. Small black circles indicate turns. The head position of the trajectory presented in Figure 1A is highlighted in magenta. Arrows indicate the direction of motion. The odor gradient shown in the background corresponds to the reconstructed snapshot 60 s after the onset of the diffusion process (‘Materials and methods’). (B) Sensorimotor analysis of a representative trajectory. (Top) Time course of the reconstructed odor concentration associated with the trajectory displayed in panel A. (Center) PSTH of the OSN measured experimentally in response to a replay of the odor concentration course (black line). Neural activity simulated by the composite IFF+IFB ODE model (blue line) presented in Figure 4B (parameter set listed in Table 1). (Bottom) Turn probability (blue line) predicted by the stimulus-to-behavior GLM trained on the light-evoked open-loop behavior reported in Figure 5—figure supplement 1 (parameter set listed in Table 3). The neural activity simulated in the middle panel is fed into the GLM to predict the turn probability shown in the bottom panel. Behavioral predictions are only shown for the sequences associated with runs. The predicted turn probability is only shown for the behavioral sequences associated with runs. (C) Turn-triggered average of the predicted probability of turning for behavior observed in the odor gradient. A comparison is made between predictions based on the simulated OSN activity driven by the stimulus intensity (coupled test, blue), predictions based on the simulated OSN activity driven by the time-reversed stimulus time courses (uncoupled control, black), and predictions based on the assumption that the neural activity stays constant over the course of each trajectory (constant control, red). As for the light gradient, we observe that the predicted turn probability increases 5 s before the turn, which coincides with the median duration (5.4 s) of the entire set of runs. Since the geometry of the odor gradient is shallower than the light gradient (Figure 8—figure supplement 1), the increase in turn probability has a reduced amplitude compared to the behavior elicited by the light gradient (Figure 6E). Shaded areas denote SEM. (D) Log-likelihood of the predictions of the integrated stimulus-to-behavior GLM compared to the controls. Bootstrap analysis of the difference in log-likelihood (logL) of the test model and the controls normalized by the log-likelihood of the test model (ΔlogL/logLtest). Distribution of the relative difference in logL computed for the test model against itself (blue), against the constant neural activity control (red), and against the uncoupled stimulus control (gray). The median of the distribution is equal to the value obtained from the original full set of runs; the median of the entire distribution is indicated by a dot in the x-axis. Based on 10,000 resampled subsets of runs, we conclude that the test model is significantly larger than both controls (p = 0.0001 for the constant neural activity control and the uncoupled stimulus control). For panels C and D, the analysis includes all runs with a duration of minimum 1 s (304 runs originating from 20 trajectories).
Figure 8—figure supplement 1
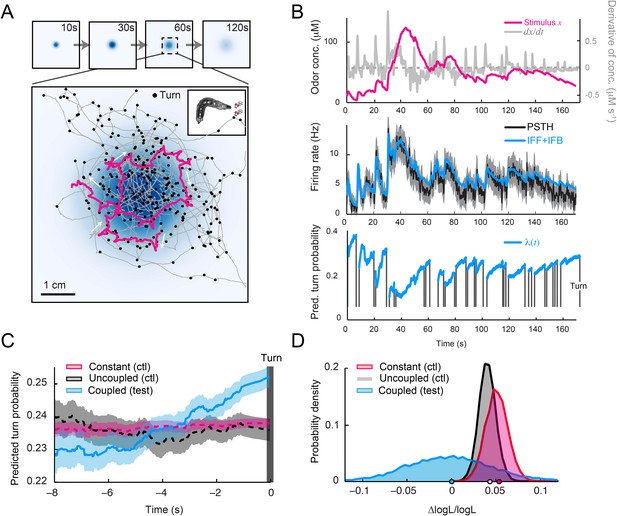
Comparison of the geometry of the exponential light gradient and the odor gradient.
(A) Reconstruction of the odor gradient displayed in Figures 1, 8 with color-coding in accordance with the scale on the right. Snapshot corresponding to the odor landscape 60 s after the initiation of the diffusion process. Cross-section intersecting the gradient's peak: f(5, y). (B) Same as panel A for the light gradient presented in Figure 6. Cross-section along gradient: g(5, y). (C) Comparison of the cross-sections f and g of the odor and light gradients, respectively. Each profile was normalized by its maximum value reached under the gradient's peak. (D) Comparison of the derivative of the cross-sections of the odor and light gradients: df/dy and dg/dy where y represents the variable associated with the vertical axis. From this analysis, we observe that the slope of the light gradient is considerably steeper than the slope of the odor gradient, which is expected to facilitate chemotaxis.
Figure 9
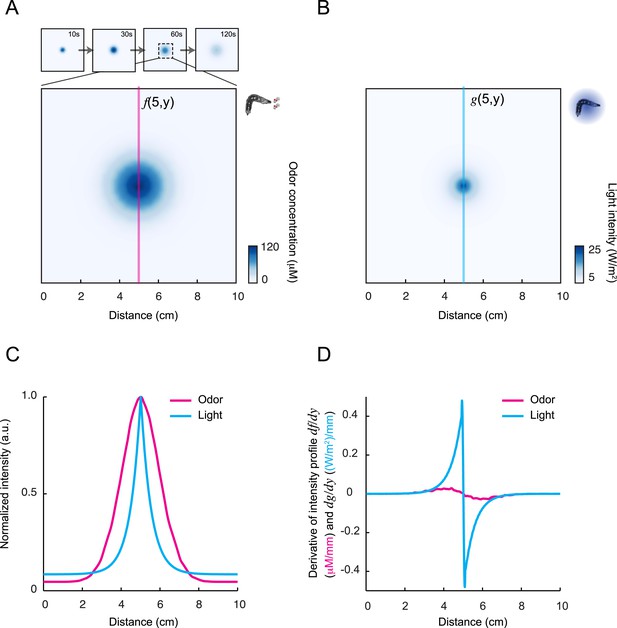
Physical model of odor diffusion in behavioral arena.
(A) Configuration of behavioral arena on which the PDE model is based. The arena consists of a square shaped transparent plastic box with a side length of 120 mm and a height of 12 mm. The lid is inverted on a surface of agarose. The odor source consists of a solution of isoamyl acetate mixed with paraffin oil. A droplet of 3 μl of odor is placed inside a transparent reinforcement ring of a radius rring. This volume fills the ring evenly and, upon inversion of the lid on an agarose slab, the droplet remains suspended due to surface tension. The droplet shape is modeled as a spherical cap. The flat face of the droplet is in contact with the top plastic lid. The volume vdrop of the droplet is related to the radius of the flat face rring and the droplet height hdrop according to the formula of a sphere. The agarose layer at the bottom of the chamber is modeled as a two-dimensional sheet with an independent diffusion constant. The top flat face of the droplet that contacts the plastic cap is treated as a no-flux boundary, and flux continuity is imposed on the spherical interface with air. The remaining boundaries, air-agarose and air-plastic, are modeled as Robin boundary conditions to accommodate the possibility of adsorption-desorption at these boundaries. The establishment of the odor gradient in the arena is modeled by two simultaneous diffusion processes, both of which are described by partial differential equation (PDE): ∂x(r⃑, t)/∂t = D ∇2x(r⃑, t) where x(r⃑, t) denotes the odor concentration at position r⃑ and time t. The diffusion constant D depends on whether the medium is air or the odor droplet. We used a flux continuity condition at the droplet-air boundary. For additional details about the model, see ‘Materials and methods’. (B) As described in Louis et al. (2008), infrared spectroscopy was used to estimate the absorbance and thereby the average concentration along sections of the arena (IR beam depicted in panel A). The time course of the cumulated concentration was determined for 7 sections at a distance from the source ranging from 0 to 45 mm (only first 6 are shown in the graph). Each concentration profile results from an average over 2 to 4 independent measurements. The absorbance was measured for a source concentration of 1.0 M. As discussed in ‘Materials and methods’, the parameters of the model are estimated by optimizing the fit of the model with the average concentration profiles along the 7 sections of the arena. The parameters of the model are reported in Table 5. The PDE model leads to a good fit of the temporal profiles of the average concentrations after an initial transient phase of 30 s. (C) Assessment of variability in the concentration estimates at a fixed position of the center of the 1.0 M odor source (7.5 mm). Mean concentration obtained from four independent infrared measurements. Error bars denote standard deviation. The time course of the simulated concentration is shown as a dashed line. (D) Assessment of variability in the concentration estimates at a fixed position of the center of the 1.0 M odor source (15 mm). Mean concentration obtained from three independent infrared measurements. Error bars denote standard deviation. The time course of the simulated concentration is shown as a dashed line.
Figure 10
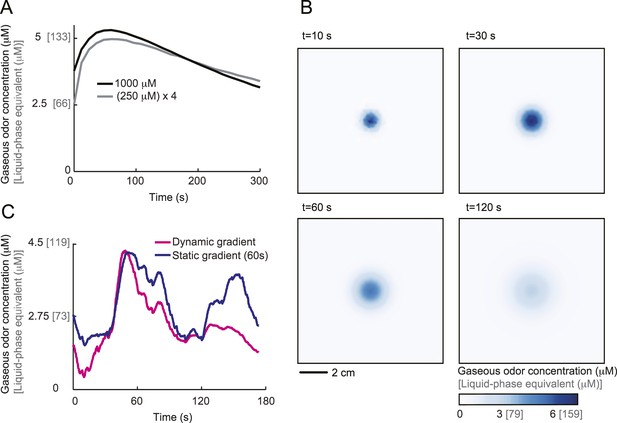
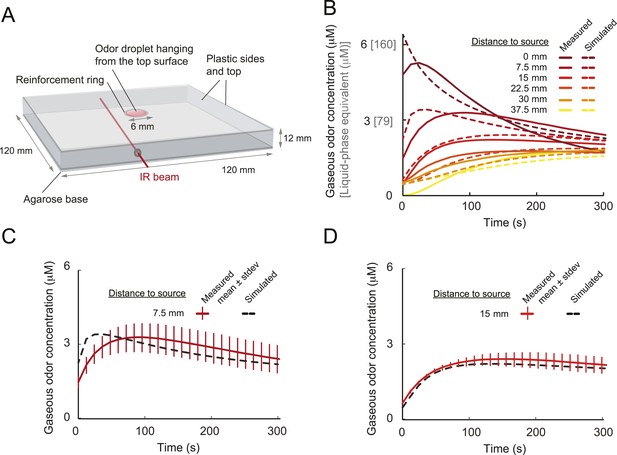
Dynamical reconstruction of the odor gradient experienced by the larva during free behavior.
(A) Behavioral experiments were conducted with a 3-μl odor droplet at a concentration of 0.25 M. At this low concentration and due to the small volume of the source, accurate temporal profiles of the average odor concentration could not be obtained through infrared spectroscopy for all sections of the plate. Under the source, we find that the average concentration of the odor scales as a function of the source concentration. We therefore assume that the gradient obtained for a 0.25 M source can be approximated by the gradient reconstructed at 1.0 M scaled by a factor 0.25. (B) Numerical integration of the PDE model (parameter set listed in Table 5) permits us to reconstruct the temporal evolution of the odor gradient experienced by the larva at arbitrary spatiotemporal precision. Due to practical considerations, the reconstruction was saved at time steps of 1 s. As on the time scale of 1 s the geometry of the gradient does not evolve considerably, a linear interpolation is applied between defined sections of the gradient. Over time, the gradient tends to flatten out. This effect is due to the gradual depletion of the source. It is worth noting that in previous studies (Louis et al., 2008; Asahina et al., 2009; Gomez-Marin et al., 2011), the gradients generated by a single odor source could be approximated as roughly constant. In these configurations, the enhanced stability of the gradient was due to the larger volume of the odor source (10 μl) and the reduced dimension of the behavioral arenas. (C) Reconstruction of the concentration time course experienced during the trajectory displayed in Figure 1A. The magenta trace was obtained after mapping the behavior onto the dynamical reconstruction of the gradient shown in panel B. In contrast, the blue trace was obtained after mapping the behavior onto a static gradient computed 60 s after the onset of the odor diffusion. The differences between the two temporal profiles highlight the importance of the dynamical reconstruction for the experimental conditions in the present study.
Figure 11
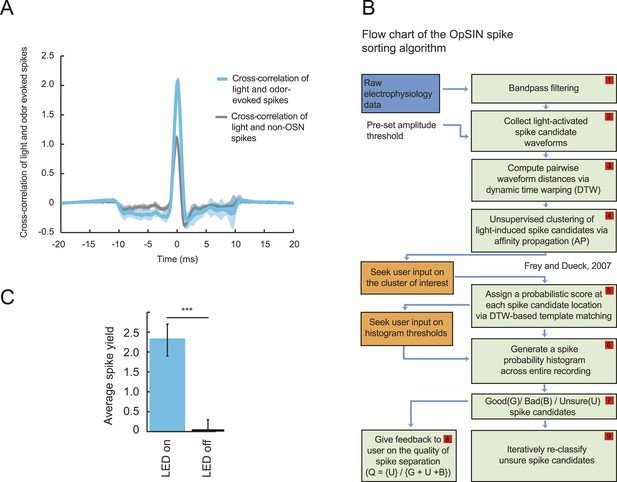
Semi-automated channelrhodopsin assisted spike sorting (OpSIN).
(A) Cross-correlation of light- and odor-evoked spikes (blue) recorded from the Or42a>ChR2 OSN, and cross-correlation of light-evoked and spontaneous background spikes (gray). The similarity in the shape of the waveform is larger between the light- and odor-evoked spikes compared to light-evoked and background spikes. Light-evoked spikes were collected from time windows during a light stimulation interval; odor-evoked spikes were collected during the odor stimulation interval; background spikes were collected from intervals devoid of light and odor stimulations. Although light- and odor-evoked spike waveforms are very similar to each other during the same recording, the overall shape of the spike waveforms can vary across recordings. (B) Flow chart of the functions underlying the spike-sorting algorithm (OpSIN). Spike candidates were selected during light-activation episodes based on simple amplitude thresholding and local non-maximum suppression. Spike selection was accomplished by comparing candidate waveforms identified throughout the recording to the ChR2-derived waveform template by transforming candidate waveforms to appear as similar as possible to the template via dynamic time warping. Orange boxes denote steps where inputs are sought from the user. For more details, see ‘Materials and methods’. (C) Average spike yield of the Or42a>ChR2 OSN measured in a 58-ms time window with and without light stimulation. The data were obtained by analyzing 35 recordings. The spike yield during the light stimulation is 2.30 ± 0.40 spikes. The corresponding spike latency is 6.96 ± 1.02 ms (t-test, p < 0.001).
Figure 12
Phase conversion of air and liquid phase odor stimulation.
(A) Schematic illustration of the single-OSN imaging setup: liquid phase odor stimulation of the larval dorsal organ with a pressure controller connected to a two-barrel pipette. The odor solution is placed in one channel of a two-barrel pipette while the other channel contains pure saline. The fixed larval head is perfused by a constant flow of extracellular saline while the odorous solution is delivered via the glass pipette. As for the olfactometer in gaseous phase (panel B), rapid changes in concentration of the odorous stream are achieved by varying the flow of the empty channel and the odorous channel while keeping the overall flow constant. As described in ‘Materials and methods’, the flow rates of individual channels are controlled by a system of mass flow controllers. (B) Air-phase odor stimulation of the larval dorsal organ with a custom-built olfactometer. A continuous stream of air (510 ml/min) is regulated by combining the outputs of two mass flow controllers. The air stream is humidified, and subsequently passed through the odor solution after which the odorous air stream is delivered to the larval dorsal organ. Rapid concentration changes of the odorous stream are achieved by varying the flow between the empty channel and the odor channel while keeping the overall flow constant. As described in the ‘Materials and methods’, individual flow rates are controlled in real-time. The OSN activity was recorded by imaging the GCaMP activity elicited in the axon terminal of the Or42a OSN. (C) Schematic illustration of the site of imaging of single OSN glomeruli at the level of the antennal lobe (inset: false-color-coded activity in the axon terminal of the Or42a OSN). (D) Odor response profile (ΔF/F) of the Or42a OSN in response to an exponential odor stimulation in the air-phase (left) and liquid-phase (right). The response amplitude and overall dynamics are conserved between the liquid and gaseous phases. Shades denote standard deviation. Recordings were made on a total of six experiments conducted on three different preparations. (E) Calibration of fluorescein in liquid phase showing a linear relationship of the fluorescein concentration and the measured change in fluorescence (left panel). Linear relationship between the observed change in fluorescence and the output pressure of the odorous stream (right panel). (F) Calibration of the photoionization detector (PID) with airborne odorant stimuli showing a linear relationship between the odor concentration and the measured voltage change. Error bars denote standard deviation.
Figure 13
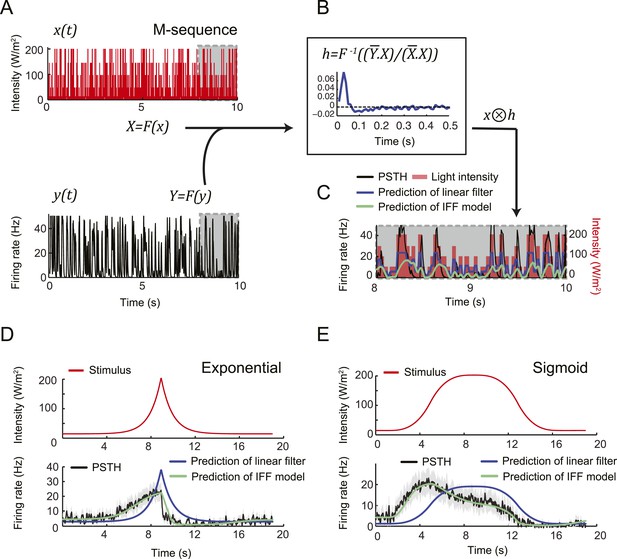
A linear filter alone is insufficient to account for the transfer function of the Or42a>ChR2 OSN.
(A) Stimulation of the Or42a>ChR2 OSN by a maximum-length (M) sequence generated with light. The M-sequence was based on a discretization of the light intensity range 15–207 W/m2 into the following 5 values: 15, 50, 100, 150, and 207 W/m2. The M-sequence featured all possible 4-element combinations of these 5 intensities. In the experiments, changes in light intensity occurred with time steps of 33 ms. (Bottom, left) PSTH of the neural response computed over 10 trials (10 preparations) and for a bin size of 10 ms. The gray boxes outline a 2-s time window over which the predictions of the linear filter are reported in panel C. (B) Computation of the linear filter, h, through the operations described in panel B (Chichilnisky, 2001; Nagel and Wilson, 2011). Function F represents the Fourier transform from the time domain to the frequency domain; F−1 represents the inverse transformation from the frequency domain to the time domain. The bar above the variables in frequency space denotes the complex conjugate transformation. To cancel any DC drifts in the OSN response, the filter was computed on windows of 5-s slid over the entire duration of stimulus (20 s). An average filter was computed from this series (dark blue line). The linear filter was used to make predictions about particular stimulus time courses. (C) Neural activity predicted from the linear filter in response to the M-sequence. The prediction was obtained by convolving the filter with the time course of the stimulus. The resulting activity was normalized to have the same mean as the experimental activity. The result of the prediction is shown for a 2-s window of the complete stimulus (dashed gray box in panel A). The activity predicted from the linear filter (dark blue line) is compared to the output of the IFF (ODE) model introduced in Figure 4B (green line). Pearson's correlation coefficient (ρ) of the predicted and the experimental activities is 0.37 for the linear filter reconstruction compared to 0.57 for the IFF model. (D) Application of the linear filter derived in panel C for the M-sequence to stimulation by an exponential ramp (red line). The linear filter (dark blue line) fails to predict the PSTH that was observed experimentally (black line; gray error bars represent the standard deviation) (ρ = 0.56). Prediction of the IFF model shown in green (ρ = 0.93). (E) Application of the linear filter derived in panel C to a sigmoid ramp (red line). As in panel D, the linear filter (dark blue line) fails to reproduce the experimental PSTH (ρ = 0.54) while the IFF model leads to a good fit (green line, ρ = 0.98).
Figure 14
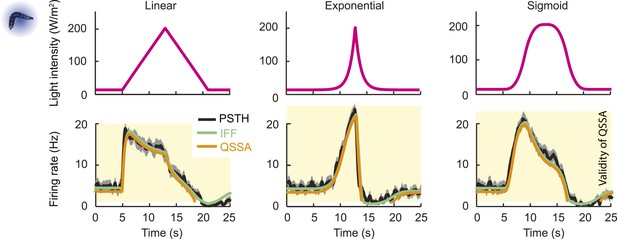
Quasi-steady state approximation of the IFF model describing the spiking dynamics of a single OSN stimulated by light ramps.
Comparisons of the analytical solution of the OSN activity upon numerical integration of the full ODE system (green line) with the solution obtained under the quasi-steady state approximation (QSSA, orange line) and the experimental PSTH (black line, shades denote standard deviation). The goodness of fit of the QSSA is remarkable for the linear and nonlinear ramps. As discussed in the ‘Materials and methods’, the QSSA holds for values of y such that the Hill term can be linearized (y >1.3 Hz). This domain of validity is depicted by the orange background.
Figure 15
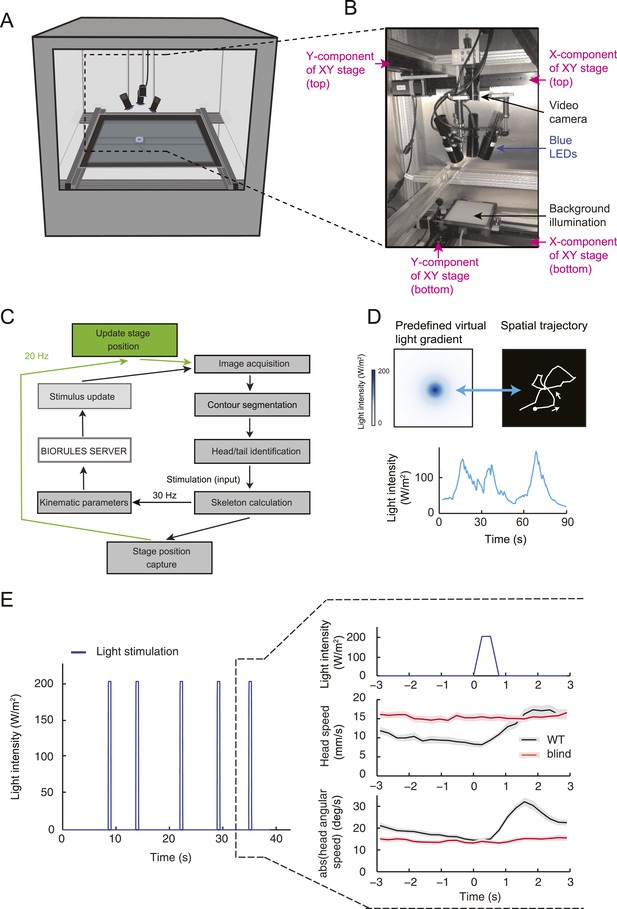
Technical description of the closed-loop tracker for virtual olfactory realities.
(A) Schematic drawing of the closed-loop tracker. The blue LEDs and the camera are mounted on a moving stage that follows the larva while it crawls on an agarose slab (40 × 40 cm or approximately 120 × 120 body lengths of the larva). (B) Depiction and description of the moving camera stage equipped with three LEDs. (C) Flow chart outlining the interaction of the core modules of the tracking software (‘Materials and methods’). (D) Illustration of the spatial trajectory generated by an Or42a>ChR2 larva undergoing closed-loop light stimulation in a virtual odor gradient. (Top-left) Predefined light landscape with a geometry approximating the odor distribution produced by a point source. During the behavioral tests, the full gradient is not projected onto the arena: the larva is illuminated by the LEDs at an intensity determined by its position in the virtual light gradient. (Bottom) The light intensity is updated based on the motion of the larva, which forms the temporal evolution shown in the graph. (Top-right) The spatial trajectory described by an Or42a>ChR2 larva in the virtual light gradient. The orientation response faithfully reproduces chemotactic behavior. In closed-loop experiments, the LED intensity was updated according to the position of the head with respect to a predefined spatial landscape. In open-loop experiments, the LED intensity was determined by a predefined temporal profile implemented only when a larva was in a run mode (Figure 5B). During a run, the motion of the larva had no influence on the intensity of the stimulus. As soon as the larva interrupted a run, the light intensity returned to a baseline value (15 W/m2). (E) Abolishment of photophobic behavior in blind larvae. Stimulation of larvae with light flashes of 0.5 s (intensity: 207 W/m2). The flashes were interspaced by a time interval picked from a Poisson distribution with mean 7.7 s. To ensure that a larva had sufficient time to react to individual light pulses, the minimum inter-flash interval was set to 5 s. The behavior resulting from the flash was characterized by computing the flash-triggered averages of the amplitude of the absolute head angle and its time derivative. Wild-type larvae (black trace) display an increase in head motion following the flash (release of head cast). Blind GMR-hid;dTrpA11 larvae (red trace) were not affected by the light flashes. The graph represents the means of the kinematic variables computed across trajectories; error bars denote SEM.
Figure 16
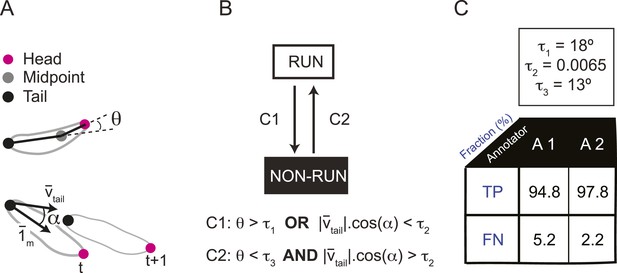
Real-time classification of the locomotor behavior of the larva.
(A) In the present study, the locomotor behavior of the larva is classified into two basic types of action: forward runs and non-runs. Non-run is a meta-state that includes stops, turns, casts, and backward runs. No distinction is made between non-run behaviors. To distinguish runs from non-runs, we defined empirical filters based on the following three sensorimotor features: (1) the head angle between the direction of the body axis (tail-midpoint) and the neck axis (head-midpoint); (2) the instantaneous velocity vector measured at the tail position (vector vtail) and (3) the angle α formed by tail velocity vector and the direction of the body axis (unitary vector 1m). (B) Transitions from a run to a non-run state take place as soon as (i) the head angle is larger than a threshold τ1 or (ii) the dot product of the tail velocity vector and unitary vector corresponding to the direction of the body axis is smaller than τ2 (condition C1). The first condition on the head angle identifies head casts while the second condition on the dot product identifies sequences of behavior associated with a stop or a backward run. Transitions from a non-run to a run take place when the following two conditions are verified: (iii) the head angle must be lower than the threshold value τ3 and (iv) the dot product of the tail velocity and unitary vector along the body axis must be larger than τ2 (condition C2). (C) The thresholds of conditions (i–iv) were set at a value that maximizes the difference in the cumulative distribution of the run and non-run states along the relevant sensorimotor feature (head angle or dot product) for the two possible types of behavioral state transitions (run → non-run or non-run → run). Distributions of the frame-by-frame sensorimotor features were constructed by pooling the annotated frames from four representative trajectories. Manual annotation was achieved by two trained experimenters. (Top) The values of the thresholds used in the analysis were: τ1 = 18°, τ2 = 0.0065, and τ3 = 13°. (Bottom) Comparison of frame-by-frame manual classification of run/non-run behavior achieved by the two trained annotators (A1 and A2) vs the computational classification obtained by filters described in panel B. The table reports the percentage of true positives (frames classified as a run by both the annotator and the algorithm) and false negatives (frames classified as a run by the annotator and a non-run by the algorithm). This good match validates the use of the computational classifiers in real-time experiments.
Figure 17
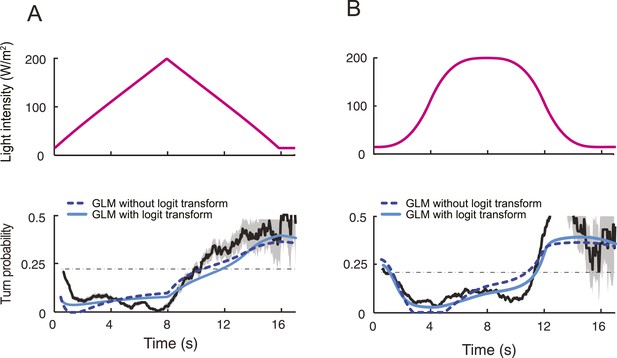
Contribution of the logit transform to the predictions of the integrated stimulus-to-behavior generalized linear model (GLM).
(A) Comparison of the behavioral outputs of the GLM with and without logit transformation for the run-to-turn transitions elicited by a 8-s linear light ramp. In the absence of logit transformation, the GLM is based on a linear combination λ(t) = γ0 + γ1y(t). Negative values of the linear combination were rectified to be equal to 0. The parameters of the model were trained on the full set of ramps presented in Figure 5—figure supplement 1 (derived parameter set: γ0 = 0.3762, γ1 = −0.0198 Hz−1). The result of the GLM without logit transformation is represented by a dashed line. The GLM model that includes the logit transformation is represented by a plain line (parameter set listed in Table 3). The correlation coefficients (ρ) and coefficients of variation of the RMSE computed on the outputs of the GLM with and without logit transformation differ by 12% and 10%, respectively. (B) Same as panel A for a sigmoid light ramp. The correlation coefficients and coefficients of variation of the RMSE computed on the outputs of the GLM with and without logit transformation differ by 5% and 22%, respectively.
Figure 18
Behavior of single functional Or42a>ChR2 OSN in the background of a silenced and an intact peripheral olfactory system (1 vs 21 functional OSNs).
(A) Open-loop stimulation protocol with a 8-s linear light ramp (magenta line). Comparison of the behavior elicited by ChR2 in the Or42a OSN in the background of 20 silenced OSNs (1 functional OSN, black line) and 21 functional OSNs (green line). The genotype of larvae with only one functional OSN is: w;Or42a-Gal4,GMR-hid;Orco2,dTrpA11 × w;UAS-Orco,UAS-ChR2-H134R;Orco2,dTrpA11. This genotype is used throughout the study. The genotype of control larvae with 21 functional OSNs is: UAS-ChR2-H134R/Or42a-Gal4;gl60j,dTrpA11. This genotype is only used in the present control. The modulation of the turn probability elicited by the stimulus is similar for both genotypes. Plain lines indicate the mean of the turn probability; shaded areas denote standard deviation (see ‘Materials and methods’). (B) Closed-loop behavior in an exponential light gradient. The stimulus landscape is the same as that used in Figure 6A. Side-by-side comparison of 10 light-driven trajectories superimposed onto the gradient. The overall patterns of the trajectories indicate that light-driven chemotaxis can be mediated by a single OSN in the background of 21 functional OSNs.
Videos
Video 1
Illustrative trajectory sequence in an exponential light gradient with predicted turn probability colored in red.
The scale bar at the bottom left of the Video represents 1 cm. The green trace displays a 20 s segment of the past positions of the centroid. White spots represent the position of the head every 20 frames (or 0.66 s). The behavioral sequence is accelerated by a factor 3.
Video 2
Illustrative trajectory sequence in ‘volcano’ light gradient with predicted turn probability colored in red.
The scale bar at the bottom left of the Video represents 1 cm. The green trace displays a 20 s segment of the past positions of the centroid. White spots represent the position of the head every 20 frames (or 0.66 s). The behavioral sequence is accelerated by a factor 3.
Video 3
Illustrative trajectory sequence in the ‘well’ light gradient with predicted turn probability colored in red.
The scale bar at the bottom left of the Video represents 1 cm. The green trace displays a 20 s segment of the past positions of the centroid. White spots represent the position of the head every 20 frames (or 0.66 s). The behavioral sequence is accelerated by a factor 3.
Video 4
Illustrative trajectory sequence in the plateau light gradient with predicted turn probability colored in red.
The scale bar at the bottom left of the Video represents 1 cm. The green trace displays a 20 s segment of the past positions of the centroid. White spots represent the position of the head every 20 frames (or 0.66 s). The behavioral sequence is accelerated by a factor 3.
Video 5
Illustrative trajectory sequence in the linear ‘hat’ light gradient with predicted turn probability colored in red.
The scale bar at the bottom left of the Video represents 1 cm. The green trace displays a 20 s segment of the past positions of the centroid. White spots represent the position of the head every 20 frames (or 0.66 s). The behavioral sequence is accelerated by a factor 3.
Video 6
Illustrative trajectory sequence in odor gradient with turn probability colored in red. Same trajectory as that shown in Figure 8A.
Superimposition of the behavior on the dynamical reconstruction of the odor gradient based on the PDE simulations. The scale bar at the bottom left of the Video represents 5 mm. The green trace displays a 20 s segment of the past positions of the centroid. White spots represent the position of the head every 20 frames (or 0.66 s).
Tables
Table 1
Parameters of ODE model derived from the Simplex optimization procedure (‘Materials and methods’) applied on the OSN spiking activity elicited by light stimulation (pure IFF model—left column) and odor stimulation (pure IFF model—middle column; combined IFF+IFB model—right column)
| Light: IFF motif | Odor: pure IFF motif | Odor: IFF+IFB motifs | |
|---|---|---|---|
| α1 | 0.1 (W m−2)−1 s−1 | 0.1 μM−1 s−1 | 0.13 μM−1 s−1 |
| α2 | 0.88 s−1 | 0.6 s−1 | 0.26 s−1 |
| α3 | 10−6 Hz−1 s−1 | 0* Hz−1 s−1 | 1.1 Hz−1 s−1 |
| β1 | 1731.41 Hz s−1 | 1002.25 μM s−1 | 2903.36 μM s−1 |
| β2 | 1.27 W m−2 | 8.63 μM | 0.01 μM |
| β3 | 2.48 W m−2 | 2.39 μM | 2.65 μM |
| β4 | 1214.08 Hz s−1 | 624.69 μM s−1 | 795.62 μM s−1 |
| β5 | 13.03 s−1 | 6.44 s−1 | 23.79 s−1 |
| θ | 0.3 Hz | 1.01 Hz | 1.88 Hz |
| n | 2 | 2 | 2 |
-
Parameters were obtained upon training of the model on 10 stereotyped stimulus ramps (see Figure 4—figure supplement 1) together with the naturalistic stimulation patterns shown in Figure 2D (odor) or Figure 6B (light). For light stimulation, the parameter of the IFB pathway (α3) was negligible and considered equal to 0 in the rest of the study. For odor stimulation, parameter α3 was artificially set to 0 in the case of the pure IFF motif. Note that the units of the intermediate variable u are undefined. We empirically found that the goodness of fit improved when the value of the offset β4 undergoes a small correction over time. In all numerical simulations of this study, we used β4(t) = (1.023 t4/(t4 + 304)) × β4. The Hill coefficient n was set equal to 2. In this table, all concentrations are given for odor stimulation in liquid phase. As described in the ‘Materials and methods’ section, the concentration equivalence in gaseous phase can be approximated by multiplying the liquid phase concentration by a factor ρliquid → gas = 26.73. The parameters listed in this table are used in all numerical simulations of the study, except the validation controls described in Figure 4—figure supplement 2.
-
*
parameter set artificially to 0.
Table 2
Quantification of the goodness of fit between the stimulus-to-neural (ODE) models and the experimental firing dynamics of the OSN stimulated by the linear and nonlinear ramps
| Odor, IFF | Odor, IFF+IFB | Light, IFF | |
|---|---|---|---|
| A Correlation coefficient (ρ) | |||
| Linear (4 s), low | 0.982 | 0.985 | 0.954 |
| Linear (4 s), med | 0.994 | 0.994 | 0.980 |
| Linear (4 s), high | 0.986 | 0.995 | 0.983 |
| Linear (4 s), slow | 0.993 | 0.994 | 0.980 |
| Linear (4 s), fast | 0.983 | 0.979 | 0.970 |
| Linear (8 s) | 0.983 | 0.994 | 0.982 |
| Quadratic | 0.993 | 0.993 | 0.988 |
| Exponential | 0.990 | 0.984 | 0.965 |
| Sigmoid | 0.985 | 0.994 | 0.990 |
| Asymptotic | 0.990 | 0.994 | 0.972 |
| B CV(RMSE) | |||
| Linear (4 s), low | 0.143 | 0.121 | 0.225 |
| Linear (4 s), med | 0.112 | 0.097 | 0.174 |
| Linear (4 s), high | 0.159 | 0.093 | 0.184 |
| Linear (4 s), slow | 0.111 | 0.091 | 0.167 |
| Linear (4 s), fast | 0.173 | 0.179 | 0.229 |
| Linear (8 s) | 0.185 | 0.106 | 0.153 |
| Quadratic | 0.131 | 0.111 | 0.150 |
| Exponential | 0.155 | 0.226 | 0.237 |
| Sigmoid | 0.175 | 0.102 | 0.131 |
| Asymptotic | 0.124 | 0.080 | 0.193 |
-
(A) Pearson's correlation coefficient (ρ) computed for stimulus ramps listed in Figure 4—figure supplement 1. (B) Coefficient of variation (CV) of the root-mean-square error (RMSE).
Table 3
Parameters of the stimulus-to-behavior generalized linear model (GLM) obtained upon training of model on the stimulation ramps listed in Figure 5—figure supplement 1
| γ0 (constant) | −0.8156 | −0.8200 | −0.3534 |
| γ1 (input variable) | −0.0114 (W/m2)−1 | −0.0013 (W/m2)−1 | −0.1523 Hz−1 |
| γ2 (derivative of input variable) | – | −0.0214 (W/m2)−1 s | – |
-
The first two columns of the table report the value of the stimulus-to-behavior control model without (left) and with (center) the contribution of the first derivative of the stimulus. The last column reports the value of the integrated stimulus-to-behavior model fed with the predicted firing rate of the OSN. The parameters listed in this table are used in all numerical simulations of the study, except for the validation controls described in Figure 5—figure supplement 2.
Table 4
Quantification of the goodness of fit of the control and the test generalized linear model (GLM)
| A Correlation coefficient (ρ) | |||
| Linear (4 s), low | 0.69 | 0.75 | 0.89 |
| Linear (4 s), med | 0.62 | 0.90 | 0.90 |
| Linear (4 s), high | 0.67 | 0.96 | 0.95 |
| Linear (4 s), slow | 0.54 | 0.92 | 0.91 |
| Linear (4 s), fast | 0.65 | 0.76 | 0.90 |
| Linear (8 s) | −0.05 | 0.66 | 0.78 |
| Quadratic | 0.11 | 0.70 | 0.88 |
| Exponential | 0.29 | 0.43 | 0.92 |
| Sigmoid | 0.13 | 0.61 | 0.60 |
| Asymptotic | −0.10 | 0.25 | 0.03 |
| All conditions (all time points included) | 0.53 | 0.74 | 0.86 |
| B CV(RMSE) | |||
| Linear (4 s), low | 0.59 | 0.54 | 0.33 |
| Linear (4 s), med | 0.60 | 0.41 | 0.32 |
| Linear (4 s), high | 0.75 | 0.41 | 0.33 |
| Linear (4 s), slow | 0.56 | 0.34 | 0.27 |
| Linear (4 s), fast | 0.53 | 0.45 | 0.31 |
| Linear (8 s) | 1.06 | 0.71 | 0.59 |
| Quadratic | 1.06 | 0.73 | 0.55 |
| Exponential | 0.84 | 0.85 | 0.39 |
| Sigmoid | 0.95 | 0.65 | 0.58 |
| Asymptotic | 0.85 | 0.52 | 0.97 |
| All conditions (all time points included) | 0.65 | 0.51 | 0.39 |
-
Comparison of the performances of the integrated stimulus-to-behavior GLM and the control model bypassing the OSN processing. The outputs of the test and control GLMs are obtained based on the parameter sets listed in Table 3. (A) Application of Pearson's correlation coefficient (ρ) on the time course of the experimental turn probability and the simulated turn probability. Restriction of the quantification to the first 12 s of the ramp where the experimental estimate of the turn probability is reliable. (B) Same as panel A for the coefficient of variation of the RMSE. The goodness of fit computed for the entire set of ramps is reported at the bottom of the table for both metrics.
Table 5
Parameters of PDE model for odor diffusion
| Parameter | Physical description | Converged value |
|---|---|---|
| Dair | Diffusion constant in air | 8.9377 × 10−7 m2s−1 |
| Ddrop | Diffusion constant in droplet | 8.7859 × 10−11 m2s−1 |
| c0,air | Initial odorant concentration in air | 4.0492 × 10−7 mol l−1 |
| c0,drop | Initial odorant concentration in droplet | 0.0450 mol l−1 |
| kagar | Robin rate for air-agar boundary | 1.5762 × 10−6 ms−1 |
| kplastic | Robin rate for air-plastic boundary | 5.8025 × 10−5 ms−1 |
| c0,agar | Saturation concentration of agar | 3.6817 × 10−5 mol l−1 |
| c0,plastic | Saturation concentration of plastic | 5.7921 × 10−7 mol l−1 |
-
The parameters are optimized for an odor gradient of isoamyl acetate under the experimental condition outlined in Figure 9.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Dynamical feature extraction at the sensory periphery guides chemotaxis
eLife 4:e06694.
https://doi.org/10.7554/eLife.06694
