Unipolar distributions of junctional Myosin II identify cell stripe boundaries that drive cell intercalation throughout Drosophila axis extension
- University of Cambridge, United Kingdom
- University of Sheffield, United Kingdom
Figures
Figure 1 with 3 supplements
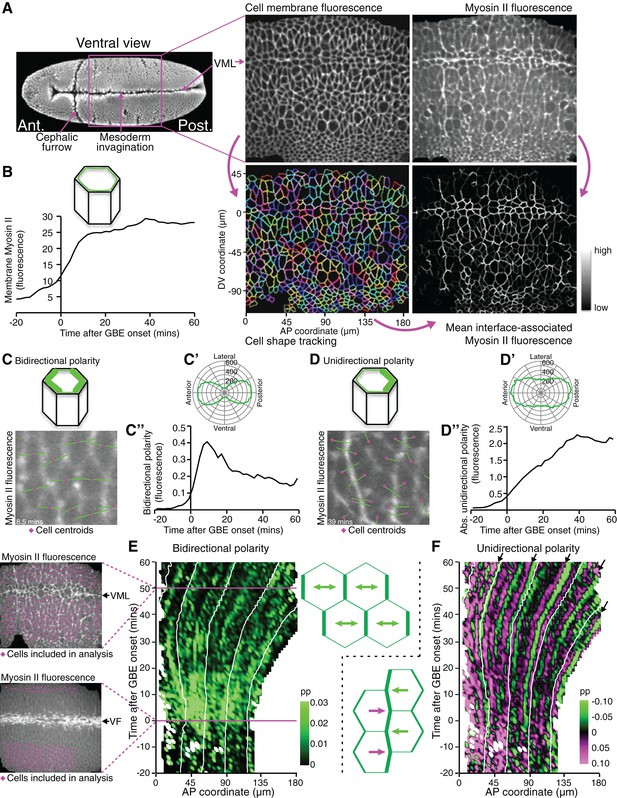
Quantifying Myosin II polarisation over time during Drosophila axis extension.
(A) sqhAX3; sqh-GFP; GAP43-mCherry embryos are imaged ventrally by confocal microscopy with a 196 x 173 μm field of view, with cell membranes visualised in the red channel and Myosin II in the green channel. Apical cell-cell interfaces are tracked over time based on the cell membrane signal. Next, Myosin II fluorescence intensities associated with the tracked cell-cell interfaces are quantified. Six movies were collected. VML: ventral midline. SEM image on the left from Flybase (dos Santos et al., 2015). (B) Total fluorescence intensities for Myosin II at apical cell-cell interfaces over time. Data shown in B, C’, C”, D’ and D” is averaged for the 6 movies. (C–C”) Quantification of Myosin II bidirectional polarity. (C) Fourier quantification of Myosin II bipolarity, depicted here on a movie frame 8.5 min after GBE onset. The length of the bipolar green vector represents the amplitude of polarity and its angle, the orientation of the polarity relative to the AP embryonic axis. Because the polarity is essentially aligned along the AP embryonic axis (rosette in C’), the polarity amplitude can be projected onto the AP axis and quantified using a Gaussian fit which allows a better separation between bidirectional and unidirectional polarity signals, compared to the Fourier method (Figure 1—figure supplement 2). (C”) Amplitude of Myosin II bidirectional polarity along the AP axis and over time, calculated using the Gaussian method. (D) Fourier quantification of Myosin II unidirectional polarity, shown on a movie frame 39 min after GBE onset. The length of the unipolar green vector represents the amplitude of polarity and its slope, the orientation of the polarity relative to the AP embryonic axis (see corresponding rosette in D’). The vector either points towards the anterior or the posterior, depending which side of a given cell is enriched in Myosin II. (D”) Absolute amplitude of Myosin II unidirectional polarity along the AP axis and over time, calculated using the Gaussian method (Figure 1—figure supplement 2). (E) Spatio-temporal map showing Myosin II bidirectional polarity for one representative movie (SG_4, Figure 1—figure supplement 1 and 3), as a function of the AP position in the field of view (x-axis, in µm) and time relative to the start of GBE (y-axis, in min). Movie frames corresponding to 0 and 50 min are shown on the left. At time 0, the mesoderm is invaginating through the ventral furrow (VF, white streak in the middle of the image). Mesoderm and mesectoderm cells on either side of the VF are not included in the analysis, nor are the germband cells at the posterior, because these move out of the field of view with the convergence extension of the tissue. Germband cells included in the analysis are labelled in magenta on both frames. At 50 min, most of the cells in the field of view are included in the analysis, except the mesectoderm cells at the midline (VML) and very dorsal germband cells coming in the field of view (bottom). The amplitude of Myosin II bipolarity is expressed as a proportion (Abbreviated as pp in all figures) of the mean Myosin II intensity around the perimeter of each cell. Scale shows highest bidirectional polarity in bright green and no polarity in black. White lines on the plot follow the displacement of AP coordinates over time, which move posteriorly as the tissue undergoes extension. (F) Spatio-temporal map showing Myosin II unidirectional polarity for the same representative movie. The amplitude of unipolarity is expressed as a proportion (pp) of mean Myosin II intensities at cell-cell interfaces. Scale shows enrichment towards anterior cell-cell interfaces as green (negative values) and towards posterior as magenta (positive values). Input data and statistics are in Figure 1—source data 1.
-
Figure 1—source data 1
Source data for Figure 1, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.004
-
Figure 1—source data 2
Source data for Figure 1—figure supplement 1, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.005
Figure 1—figure supplement 1
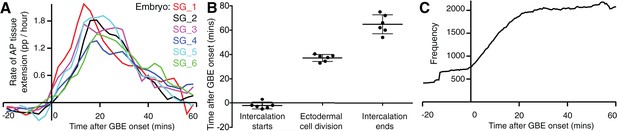
Synchronisation of sqhAX3; sqh-GFP; GAP43-mCherry movies.
(A) Rates of tissue strain in the AP direction (in proportion per hour) comparing axis extension for the 6 movies sqhAX3; sqh-GFP; GAP43-mCherry (named SG_1 to 6). The movies have been synchronised to the start of GBE (time zero) (B) To check that the 6 movies are appropriately synchronised, we plotted when polarised cell intercalation starts and ends (determined by our calculated intercalation strain rate, see Materials and methods) and when the first ectodermal cell divisions occur (determined by eye). (C) Frequency in the y-axis gives the number of tracked germband cells used in subsequent polarity analyses, per 30 s time bins from the start of GBE (x-axis), pooled from the 6 movies. Input data and statistics are in Figure 1—source data 2.
Figure 1—figure supplement 2
Methods for calculating bidirectional and unidirectional Myosin II polarity.
(A, A’) To quantify bi- and uni- directional polarisation of Myosin II, we aim at identifying either two peaks (A) or one peak (A’) around the perimeter of a given cell. Myosin II fluorescence intensities (f.i., y-axis) are plotted along the unwrapped cell perimeter from 0 to 360 degrees (x-axis), starting from the East side of the cell and going anti-clockwise. (B-D’) We used two different methods, 'Fourier' and 'Gaussian', to identify one (unidirectional polarity) or two (bidirectional polarity) peaks in the Myosin II fluorescence signal around the perimeter of each cell. Graphs B-D’ show simulated data for a cell with either bidirectional polarity in Myosin II (B,B’) or unidirectional polarity (C,C’) or a mixture of the two (D,D’). In the first method (B, C, D), Fourier decomposition gave period 1 (unidirectional polarity) and period 2 (bidirectional polarity) amplitude estimates. In the second method (B’, C’, D’), two Gaussians curves with their means 180 degrees apart were fitted to Myosin II fluorescence intensities through minimisation, varying the amplitude of each Gaussian curve and a standard deviation common to both. (B, B’) Example cell with bidirectional polarity. Both Fourier (B) and Gaussian (B’) methods succeed well at fitting the two peaks of Myosin II intensities (fluorescence intensities, f. i., represented as a black castellated curve as in A,A’). (C, C’) Example cell with unidirectional polarity. The Fourier method fits a unidirectional peak at the correct position, but because the Myosin II signal is discrete, or castellated, there is also a strong period 2 harmonic in phase with the unidirectional signal. Thus with the Fourier method, the quantification of uni- and bi- directional polarities is not completely independent: specifically the period 2 estimate used for estimating bidirectional polarity will also describe some of the unidirectional polarity signal (C). Gaussian fitting finds the correct unidirectional peak (C’). (D, D’) Example cell with a combination of uni- and bidirectional polarity. Similar to (C), the period 2 amplitude is augmented by the castellated signal in the Fourier method (D), whereas the Gaussian fitting correctly identifies two independent peaks of different amplitude: the smallest amplitude identified by the West peak (blue) corresponds to the bidirectional polarity, whereas the higher East peak correspond to the unidirectional polarity (D’).
Figure 1—figure supplement 3
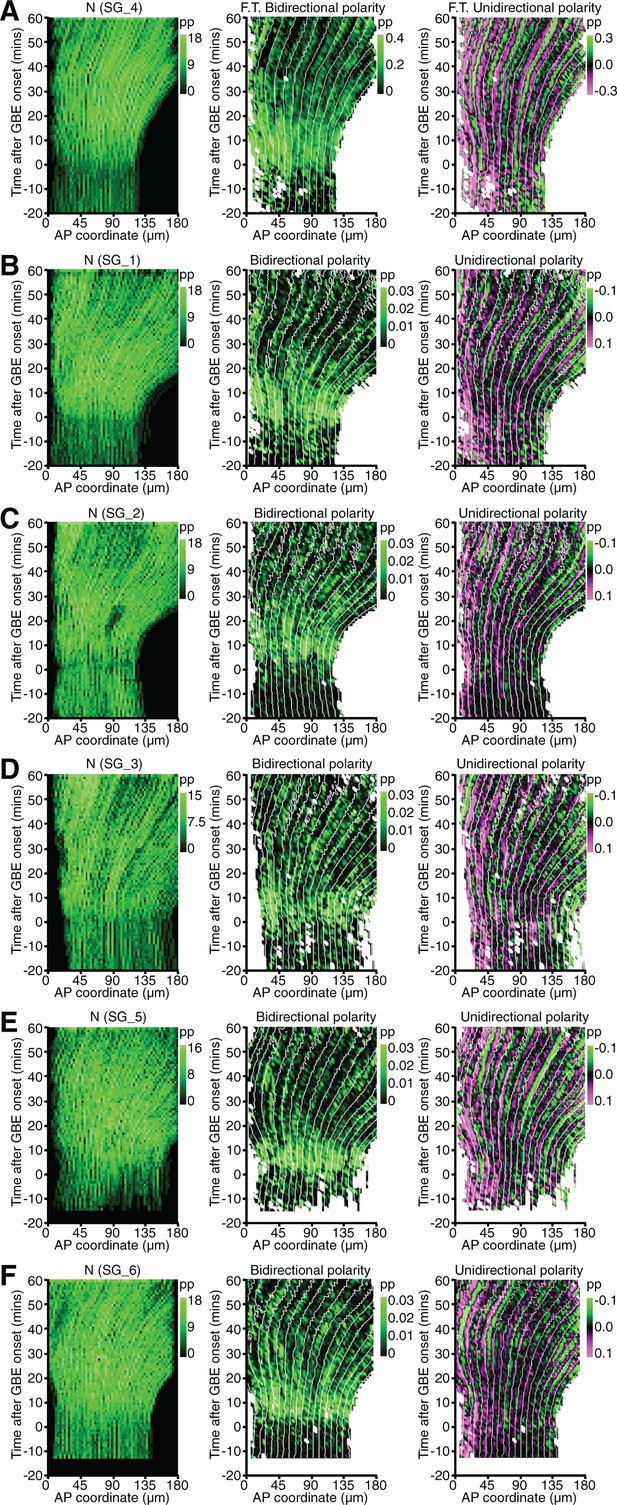
Spatiotemporal maps for all sqhAX3; sqh-GFP; GAP43-mCherry movies.
(A) Spatiotemporal maps for the representative sqhAX3; sqh-GFP; GAP43-mCherry movie SG_4 shown in Figure 1E,F. Cell number (left panel), bidirectional (middle) and unidirectional (right) polarity contour maps calculated using the Fourier component method. Note the more persistent bidirectional polarity signal from 20 min onwards compared to Figure 1F (which shows the Gaussian quantification), due to contamination from the unidirectional signal. (B-F) Cell number (left panel), bidirectional (middle) and unidirectional (right) polarity contour maps for the 5 other movies, using the Gaussian fitting method as in Figure 1E,F.
Figure 2 with 1 supplement
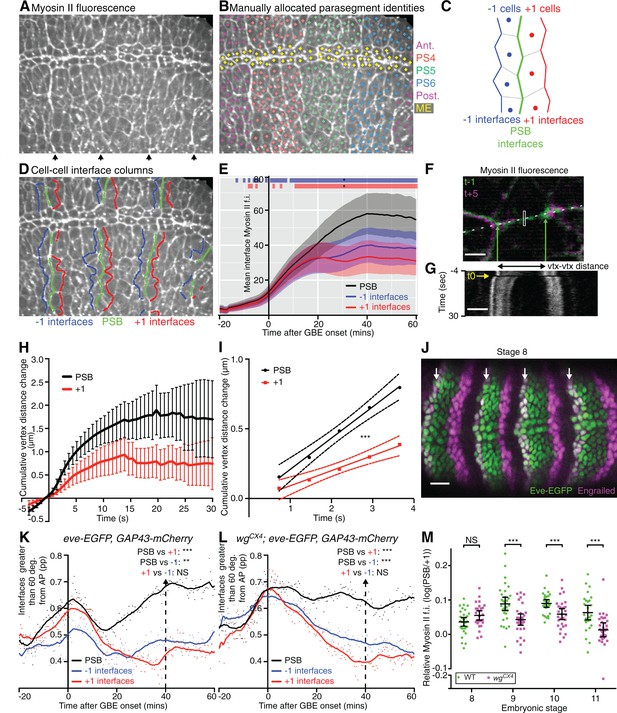
Parasegmental boundaries become mechanically active early during axis extension.
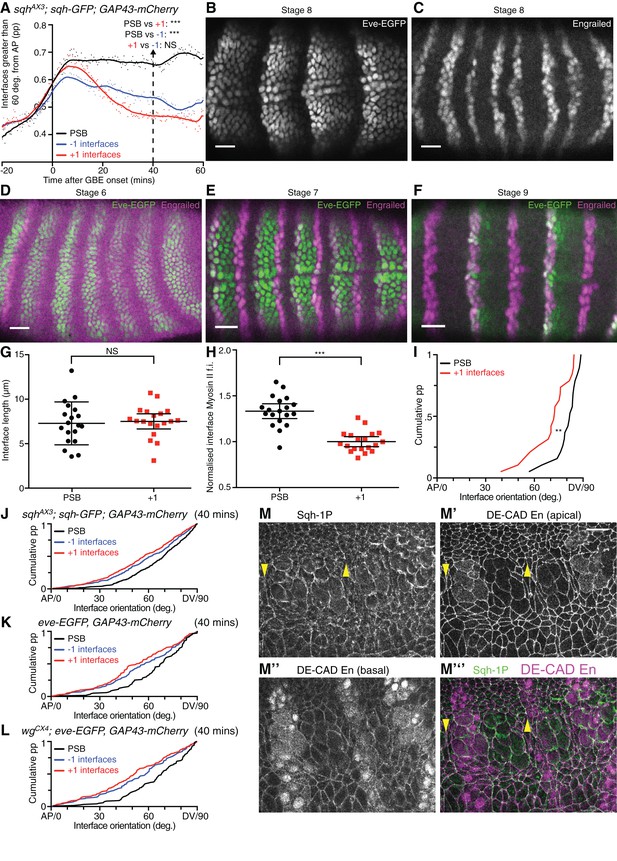
(A, B, D) Frames of a representative sqhAX3; sqh-GFP; GAP43-mCherry movie (SG_6) at 60 min after the start of GBE. (A) PSBs are identified at the end of the movie by strong enrichments in actomyosin (arrows). (B) These are used to manually identify each parasegment (differently coloured cell centroids). Note that the mesectodermal cells (ME, highlighted in yellow) present at the midline are not included in our analyses. (C,D) Using parasegment identification, we define 3 classes of linked columns of interfaces, the PSB interfaces (green) and those one cell anterior (named ‘-1’, in blue) and posterior (named ‘+1’, in red) to the PSB, shown in a schematic (C) and on the representative movie frame (D). (E) Myosin II fluorescence intensities (y-axis) found at the three different classes of interfaces over time (x-axis) for the six sqhAX3; sqh-GFP; GAP43-mCherry embryos. Solid lines represent means. Ribbons (error bands) show an indicative confidence interval of the mean, calculated as a sum of the variance of the embryo means and the mean of the within-embryo variances. Blue and red bars at the top of the panel show time intervals over which -1 and +1 interfaces, respectively, differ from the PSB. Significance is calculated for each one-minute bin using a mixed model (‘lmer4’ package in ‘R’) using variation between embryos as the random effect. We use p<0.0005 as the significance threshold, which corresponds to a 0.05 threshold (*) modified by a Bonferroni correction to take into account the 81 one-minutes bins. The same conventions for displaying confidence intervals and statistical significance are used in all subsequent ribbon plots. (F-I) Comparison of junctional tension at PSB and +1 cell-cell interfaces using laser ablation. (F) Overlay of a PSB junction immediately prior to (-1 time point, green) and after ablation (+5 time point, magenta). The rectangle shows the ablated region. Green arrows show the position of the vertices flanking the junction just prior to ablation. White dashes indicate the line used to produce the kymograph in (G). Scale bar, 3μm. The kymograph shows the vertices recoil after ablation (black frame indicated by yellow arrow at time zero). Time corresponds to -3.65 to 29.95 s relative to ablation. The changes in distance between vertices as measured on similar kymographs for each ablation are plotted in (H). The graph shows the mean change in vertex distance over time for ablations at PSB (black) and +1 (red) interfaces (N=19 ablated junctions for each). Error bars represent the 95% confidence interval of the mean. (I) Graph showing linear regression (solid lines) for the first 5 time points after ablation. The 95% confidence interval of the regressed line is also shown (dotted lines). The data did not significantly deviate from linearity. Slopes were significantly different, with gradients of 0.2245 (+-0.02665) for PSBs and 0.1084 (+-0.0201) for +1s, so a ratio of 2.07 between the two. (J) Immunostaining of an eve-EGFP embryo at stage 8 using α-GFP and α-Engrailed antibodies, showing that the odd-numbered stripes of Engrailed-expressing cells are faithfully labelled by Eve-EGFP. Scale bar=25 μm. (K) -1, PSB and +1 interfaces were identified in the three eve-EGFP, GAP43-mCherry movies and their orientation relative to the AP embryonic axis measured. The graph shows the proportion (pp) of interfaces oriented between 60 and 90 degrees relative to the AP axis, as a function of time. A LOWESS curve with a smoothing window of 10 points has been fitted to the data, for this graph and all other interface alignment graphs. Statistical comparisons are shown for the time point 40 min (Cumulative interface orientation distribution for all interfaces at 40 min are shown in Figure 2—figure supplement 1K). The convention for P values for this graph and all subsequent similar graphs are: NS: p>0.05; *p<0.05; **p<0.01; ***p<0.001. (L) Same analysis for 3 wgCX4; eve-EGFP, GAP43-mCherry movies (See also Figure 2–supplement 1L). This shows that in wingless mutants, PSB interfaces are more DV-oriented than -1 or +1, as in wildtype (K). (M) Graph comparing Myosin II enrichment at PSBs relative to +1 interfaces in fixed embryos labelled with α-Sqh1P antibodies, during GBE (stage 8) and at later stages (stage 9, 10, 11), in wildtype and wingless mutants. Input data and statistics are in Figure 2—source data 1.
-
Figure 2—source data 1
Source data for Figure 2, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.011
-
Figure 2—source data 2
Source data for Figure 2—figure supplement 1, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.012
Figure 2—figure supplement 1
Identification and characterisation of parasegmental boundaries properties during axis extension.
(A) -1, PSB and +1 interfaces were identified in 6 sqhAX3; sqh-GFP; GAP43-mCherry movies, and their orientations relative to the AP axis measured. The graph shows the proportion (pp) of interfaces between 60 and 90 degrees (y-axis), as a function of time (x-axis). Statistical comparisons are shown for the 40 min timepoint (see also the cumulative distribution of all interface orientations for this timepoint in J). (B,C), Separate Engrailed and GFP channel images for the stage 8 embryo shown in Figure 2J. Scale bars = 25 μm. (D-F) Immunostainings of stage 6, 7 and 9 eve-EGFP, GAP43-mCherry embryos using anti-GFP and anti-En antibodies. The Eve-EGFP reporter labels the anterior edge of odd-numbered engrailed-expressing stripes faithfully, therefore marking the PSBs in every other parasegment. Scale bars = 25 μm. (G-I) Further analyses for the ablations shown in Figure 2 F-I. For all graphs N=19 for both PSB and +1 interfaces. (G) Graph comparing lengths of ablated PSB and +1 interfaces (95% confidence interval of the mean is shown). Interface lengths were not significantly different. (H) Graph comparing Sqh-GFP fluorescence intensities at ablated PSB and +1 interfaces (95% confidence interval of the mean in shown). Myosin II intensities were significantly higher in PSB junctions. (I) Cumulative distribution of the orientation of ablated PSB and +1 interfaces relative to the AP axis. AP=0 degrees; DV=90 degrees; pp= proportion. PSB interfaces were significantly more aligned to the DV axis than +1 interfaces. (J-L) Cumulative distributions of all interface orientations at the 40 min timepoint for the 3 types of movies analysed. (M-M”’) Example of images used for the quantification of Myosin II in fixed embryos (Figure 2M), here in a WT stage 9 embryo. Embryos are triple stained with Sqh-1P, DE-CAD and Engrailed antibodies. The En and DE-CAD channel is used to identify PSB interfaces (arrowheads) and +1 interfaces. The Sqh-1P channel is used for Myosin II quantification at the corresponding interfaces. Scale bar = 20 μm. Input data and statistics are in Figure 2—source data 2.
Figure 3 with 1 supplement
Within-parasegmental patterns reveal two further myosin-enriched boundaries at stereotypical AP locations.
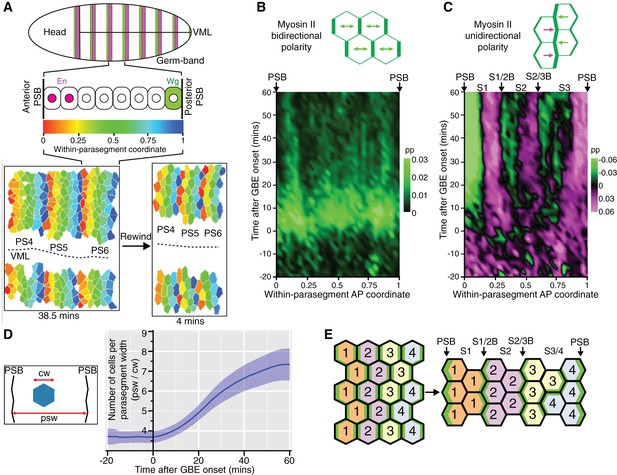
(A) Schematic of Drosophila embryo showing the parasegment domains along AP (VML: ventral midline). Cells expressing Engrailed (En) and Wingless (Wg) abut the posterior and anterior edge, respectively, of each parasegmental boundary (PSB). The identification of PSBs in movies (Figure 2) was used to allocate an AP coordinate to each cell within each parasegment domain. The anterior-most position is recorded as 0 (red in the heat scale) and the posterior-most position is recorded as 1 (blue). This coordinate system is used to pool cell information from all the different parasegments present throughout each movie, in order to look for stereotypical within-parasegment patterns. AP coordinates for a representative movie are shown at a late (38.5 min) and an early (4 min) timepoint, for 3 parasegments tracked (PS4, PS5 and PS6). (B) Spatio-temporal map showing Myosin II bidirectional polarity for all averaged PS domains, as a function of the within-parasegmental AP coordinate (x-axis) and time relative to the start of GBE (y-axis, in min). Heat scale shows highest bidirectional polarity in bright green and no polarity in black (See statistics in Figure 3—figure supplement 1A,B). (C) Spatio-temporal map showing Myosin II unidirectional polarity for all averaged PS domains, as a function of the within-parasegmental AP coordinate (x-axis) and time relative to the start of GBE (y-axis, in min). Heat scale shows enrichment of posterior cell-cell interfaces as magenta (positive values) and of anterior ones as green (negative values) (See statistics in Figure 3—figure supplement 1A,C). (D) Quantification of average cell number per parasegment domain as a function of time relative to the start of GBE (y-axis, in min). Cell numbers are obtained by dividing the average parasegment width (psw) by the average cell width (cw). (E) Diagram showing the proposed model: at the start of GBE, 3 to 4 cells of distinct identity per parasegment enrich Myosin II at their shared interfaces. After cell rearrangement, stripes of cells of the same identity become adjacent. Myosin II is enriched preferentially at interfaces shared between cells of different identity (PSBs, S1/2Bs and S2/3Bs, also marked on panel (C). There is more Myosin II enrichment at PSBs compared to other boundaries, indicated as thicker green lines. We postulate that the third stripe, S3 as defined by unidirectional polarity data above (panel C), is composed of a mixture of two identities, named 3 and 4 here, whose boundary is more variable. In support of this, S3 is wider than S1 and S2, but not wide enough for 4 cells across (2+2) (see also cell numbers per stripe in Figure 4D). Input data and statistics are in Figure 3—source data 1.
-
Figure 3—source data 1
Source data for Figure 3, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.016
-
Figure 3—source data 2
Source data for Figure 3—figure supplement 1, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.017
Figure 3—figure supplement 1
Within-parasegmental patterns of Myosin II cell polarity.
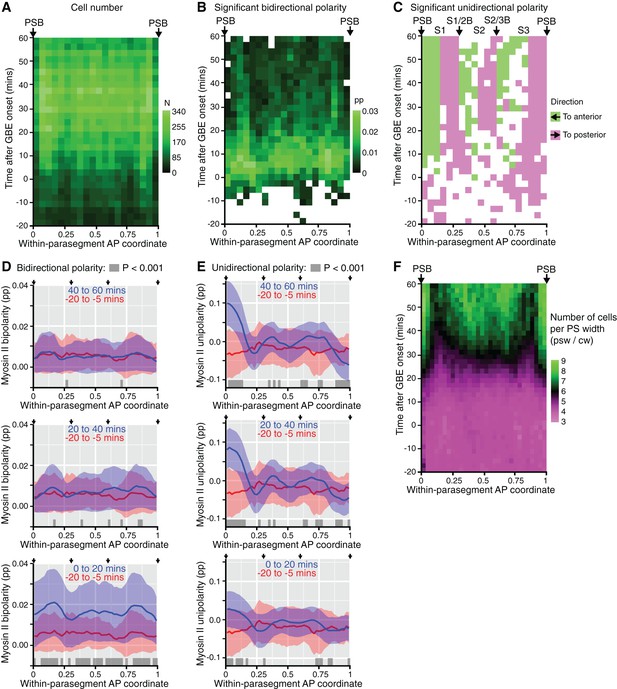
(A) Number of cells (N) per grid square for panels B,C in this figure and for the spatiotemporal maps in Figure 3B,C. Data pooled from 6 sqhAX3; sqh-GFP; GAP43-mCherry embryos. The total number of cell instances sampled was 124,241. (B,C) Statistical information for spatiotemporal maps in Figure 3B,C. White squares indicate where Myosin II polarity is not significantly different from zero. Embryo variances are assumed to be equal. (B) Data significance for bidirectional Myosin II polarity. Coloured grid squares show where the data is significant, defined as where the mean value for each spatio-temporal grid square is greater than the 99.9% confidence interval of its distribution. Bipolarity strength is shown with the same scale as in Figure 3B. (C) Data significance for unidirectional Myosin II polarity. Coloured grid squares show where the data is significant, defined as where the absolute mean value per grid square is greater than the 95% confidence interval of its distribution. Unipolarity is colour-coded by the direction of polarity (anterior or posterior), without the strength of polarity shown in Figure 3C. (D, E) Comparison of within-parasegment bidirectional (D) and unidirectional (E) polarity patterns prior to GBE (-20 to -5 min) and at three time periods during GBE; 0 to 20 min, 20 to 40 min and 40 to 60 min, from bottom to top panels. Y-axes show the strength of either bidirectional (D) or unidirectional (E) polarity. X-axes show the within-parasegment coordinates, 0 anterior-most, and 1, posterior-most (See Figure 3). Grey ribbons close to the x-axes show where along AP the data is significantly different. (F) Expected number of cells as a function of within-parasegment AP coordinates (x-axis) versus time (y-axis), averaged for all 6 sqhAX3; sqh-GFP; GAP43-mCherry movies. The number of cells per parasegment increases from 3.6 at the onset of GBE, to 7.3 on average at 60 , as shown in Figure 3D. The total number of cell instances sampled was 124,886. Input data and statistics are in Figure 3—source data 2.
Figure 4
Behaviour of S1/2 and S2/3 boundaries.
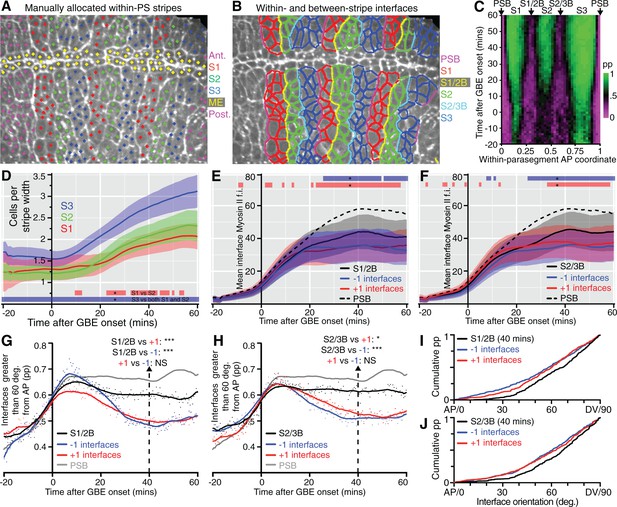
(A) The image is taken from a sqhAX3; sqh-GFP; GAP43-mCherry movie 60 min after the start of GBE, where cells have been manually allocated to putative within-parasegment stripes S1 (red centroids), S2 (green centroids) and S3 (blue centroids), based on Myosin II enrichment and position along AP. In this movie, allocation was done for 3 parasegments (magenta centroids highlight cells belonging to other parasegments and yellow centroids belong to midline cells, ME). (B) Same movie frame where interfaces are classified as belonging to boundaries between stripes (PSB interfaces in magenta, S1/2B interfaces in yellow, S2/3B interfaces in cyan) or not belonging to any boundaries (red interfaces in S1, green interfaces in S2 and blue interfaces in S3). (C) Spatiotemporal plot (time in y-axis and within-parasegment coordinates in x-axis) to check that the locations of manually identified within-parasegment boundaries correspond to the location of the S1/2B and S2/3B given by the unidirectional polarity map (arrows, see Figure 3C). The proportion (pp) of non-boundary interfaces is colour-coded so that 1 is green (only non-boundary interfaces) and 0 is magenta (only boundary interfaces). There is high concordance between the locations of S1/2B and S2/3B interfaces in both plots (compare with Figure 3C). (D-J) Once stripe and interface identities are allocated, analyses can be performed on all tracked parasegments throughout GBE. (D) Average cell number per stripe in AP (y-axis) as a function of time from the start of GBE (x-axis). At the bottom of the panel, red bar indicates the time intervals where S1 differs from S2, and blue bar where S1 and S2 differ from S3. (E) Average Myosin II intensity at boundary interfaces between stripe 1 and 2 (S1/2B) compared to interfaces immediately anterior (-1) or immediately posterior (+1). Mean for PSB interfaces is shown for reference (dashed line). Blue and red bars at the top of the panel show time intervals where -1 and +1 interfaces, respectively, differ from S1/2B interfaces. (F) Same quantifications as in E but for S2/3B. (G) Proportion of interfaces with orientation between 60 and 90 degrees relative to the AP axis (y-axis), as a function of time (x-axis), for S1/2B interfaces compared to -1 or +1 interfaces. The same measure for PSB interfaces is shown for reference (grey curve). A statistical comparison is shown at 40 min (see also I). (H) Same quantifications as in G, but for S2/3B. (I, J) show the cumulative distributions of interface orientation for S1/2B and S2/3B and control interfaces at 40 min. Input data and statistics are in Figure 4—source data 1.
-
Figure 4—source data 1
Source data for Figure 4, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.021
Figure 5 with 1 supplement
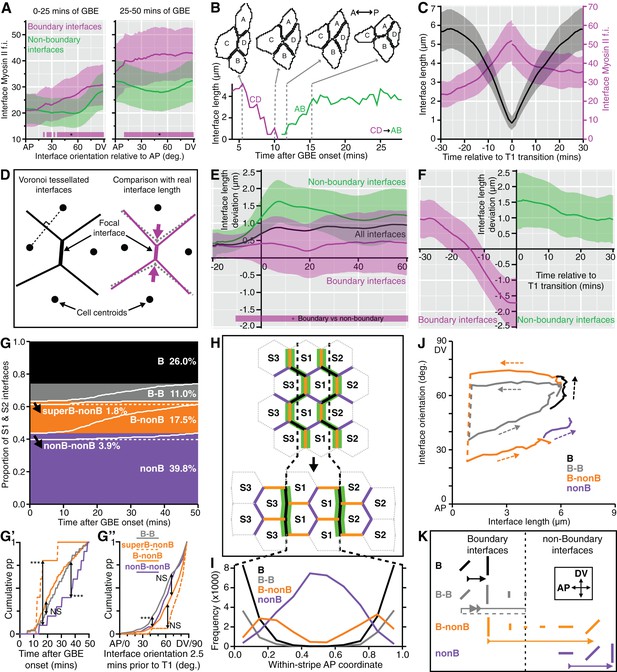
Characterisation of the behaviours of boundary and non-boundary interfaces.
(A) Average Myosin II intensity in boundary versus non-boundary interfaces for two time periods of GBE (0–25 and 25–50 min), as a function of their orientation relative to the AP embryonic axis. 0 degrees is parallel to AP, 90 degrees parallel to DV. (B, C) Analysis of cell neighbour exchanges. (B) Example of a T1 transition where the interface between cells C and D shortens to a single vertex, followed by the growth of a new interface between cells A and B. The graph gives the interface length (y-axis) as a function of time after the start of GBE (x-axis). In this particular example, the T1 transition starts at 5 min and finishes at 15 min after the start of GBE. (C) Aligning all interfaces in time so that the T1 transitions are at zero min, this plot shows how the shortening of interfaces (black curves) correlates with the increase in Myosin II fluorescence intensity (magenta curves) during neighbour exchange. (D-F) Analysis of cell geometries. (D) We compared interface lengths predicted by a Voronoi tessellation (black on the left, dotted grey on the right) with real interface lengths (magenta) to extract a length deviation from the Voronoi tessellation, a geometric proxy for local stress. (E) Graph showing the average deviation in length from a Voronoi prediction (y-axis), for all interfaces (black line), for boundary interfaces (magenta curve) and for non-boundary interfaces (green curve), as a function of GBE time (x-axis). Non-boundary interfaces are on average longer and boundary interfaces shorter than the average length deviation for all interfaces. (F) On average, boundary interfaces become increasingly geometrically stressed (shorter than Voronoi prediction) over a period of 15 min just prior to T1 transitions. (G-K) Fate of boundary (abbreviated to B) and non-boundary (abbreviated to nonB) interfaces during GBE, for stripes S1 and S2 (Data pooled from 6 embryos, N=96,343 interface instances). (G) S1 and S2 interfaces behaviours fall into four main types: interfaces that remain boundary throughout GBE and do not go through a T1 transition (black); interfaces that remain boundary throughout but go through a T1 transition (grey); boundary interfaces that go through a T1 transition and become non-boundary (orange); interfaces that remain non-boundary interfaces throughout (purple). The percentage of each interface type is shown. Within each type, interfaces are sorted according to the time of T1 transition (white lines). Black arrows indicate two infrequent subtypes. In the orange class, a subtype of boundary interfaces corresponds to interfaces between either cell identities 1 and 3 (cell identity 2 is missing) or 3 and 2 (cell identity 1 is missing). We call these interfaces 'super-boundaries' (abbreviated to superB) (see main text). We have inferred that identity 1 or 2 are skipped because for this subtype the tracking data shows that either stripe S1 or stripe S2 has a local width of zero. The other subtype is in the purple class (arrow) and corresponds to rare non-boundary interfaces that do go through a T1 transition. (G’) Comparison of the timings of T1 transitions in the different interface types. The two infrequent subtypes have opposite behaviours: the super-boundary T1 transitions (dashed orange curve) are earliest, while non-boundary T1 transitions are latest (purple curve) compared to boundary T1 transitions (orange and grey). (G’’) Comparison of the distributions of the orientations of interfaces 2.5 min prior to T1 transition for the different types of interface. 'Super-boundary' interfaces are the most DV-oriented (dashed orange). (H) Cartoon showing the expected location of the four types of interfaces relative to the position of the stripe boundaries (dashed black lines). Green shows Myosin II enrichment. (I) Graph giving the frequency (y-axis) of each type of interface as a function of the AP position within a S1 or S2 stripe (x-axis). Each AP location (bin) within a stripe is attributed a within-stripe coordinate from 0 (anterior-most) to 1 (posterior-most). (J) Plot showing the fates of each type of interface during GBE. The mean interface orientation (y-axis) and length (x-axis) is plotted for each type over time. Dashed arrows show the direction of time. Dashed lines connect interfaces before and after T1 transitions. See Figure 5—figure supplement 1E for individual curves for each sqhAX3; sqh-GFP; GAP43-mCherry movie. (K) Cartoon summarising the behaviour of each type of interface during GBE. Changes in length and orientation of interfaces are depicted as well as the transition between boundary and non-boundary class. Direction of time is indicated by arrows. The dashed part of the grey arrow depicts the situation where a boundary interface remains a boundary after a T1 swap. Input data and statistics are in Figure 5—source data 1.
-
Figure 5—source data 1
Source data for Figure 5, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.024
-
Figure 5—source data 2
Source data for Figure 5—figure supplement 1, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.025
Figure 5—figure supplement 1
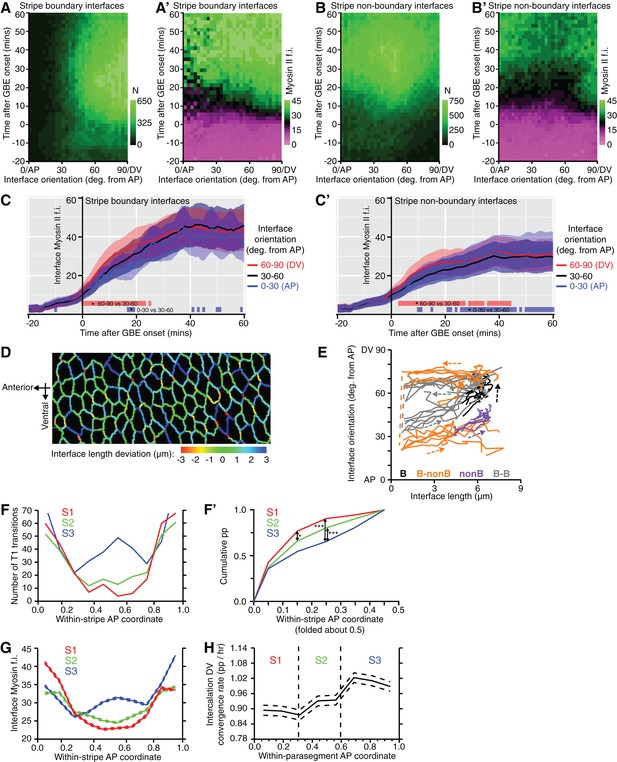
Analysis of cell-cell interface behaviour.
(A-B’) Relationship between interface orientation and Myosin II fluorescence over time. Spatiotemporal plots show interface orientation relative to the AP axis (x-axis; deg., degree) as a function of time during GBE (y-axis). Plots A and B show the number of cells sampled per square grid, for boundary (A) and non-boundary interfaces (B). Plots A’ and B’ show Myosin II fluorescence intensities associated with boundary (A’) and non-boundary (B’) interfaces. Boundary interfaces (A’) have higher levels of Myosin II fluorescence (green) compared to non-boundary interfaces (B’) throughout GBE, irrespective of interface orientation. (C,C’) Comparisons of Myosin II fluorescence intensities (f.i.) over time at boundary (C) and non-boundary (C’) interfaces for three groups of interface orientations; 0–30˚ (parallel to AP), 30–60˚ and 60–90˚ (parallel to DV). Blue and red bars show time intervals in which DV and AP-oriented interfaces, respectively, differ from 30–60 degree interfaces. Although there are subtle differences in Myosin II enrichment depending on interface orientations, the main difference in Myosin II is between boundary and non-boundary interfaces (Compare graphs C and C’). (D) Interface length deviation from topologies predicted from a Voronoi tessellation. Interfaces shorter than expected from a Voronoi topology (negative values; yellow to red) are strongly DV-oriented and heading towards T1 transitions. (E) Fate of each interface type as a function of time in the course of GBE, with a curve for each movie (legend in Figure 5J). (F-H) Evidence for an additional boundary within stripe S3. (F) Number of T1 transitions (y-axis) as a function of AP position, attributing coordinates 0 (anterior-most) to 1 (posterior-most) for each stripe S1, S2 and S3 (x-axis). The number of T1 transitions is highest close to 0 and 1, corresponding to the PSB, S1/2B and S2/3B boundaries. Another boundary is suggested by a peak in the middle of S3, which according to our model would arise between cell identities 3 and 4 (Figure 3E). (F’) Cumulative frequency distributions of the number of T1 transitions (y-axis) as a function of the distance from the stripe boundaries (x-axis). S3 has significantly more T1 transitions away from the flanking boundaries, as expected from an additional peak within S3. (G) Comparison of interface Myosin II fluorescence across the three stripes. Dashed lines show confidence intervals of data pooled from the 6 sqhAX3; sqh-GFP; GAP43-mCherry movies. Stripe 3 has a noticeable peak mid-stripe that is missing in stripes S1 and S2. (H) Rate of intercalation convergence in the DV-axis for the first 25 min of germband extension (y-axis) as a function of within-parasegment coordinates (x-axis). The rate of intercalation increase from anterior to posterior, being highest in S3. 95% confidence intervals are shown for data pooled as in G. Input data and statistics are in Figure 5—source data 2.
Figure 6 with 1 supplement
Finding the smallest number of receptors explaining Myosin II planar polarization during axis extension.
(A) Expression patterns of two putative receptors A and B repeated every double parasegment (corresponding to the expression patterns of, respectively, Toll-2 and Toll-8 as described in Figure 1p in Paré et al., 2014). PSBs are shown as solid black lines. Summing the number of receptor differences at each boundary, this combination lacks a difference at the PSBs. For cell pairs brought together when single cells are missing (second line), the number of cell receptor differences increases only when cell identity 2 or cell identity 3 is missing (grey boxes highlight an increase in receptor differences). There is no increase in receptor differences, hence no robustness, built in if two contiguous cells are missing at any location (third line). We calculate a 'robustness' score by adding the number of instances, for two parasegments, where there is an increase in receptor differences in the event of 1 or 2 cells missing: the score for this scenario is 10 (number of grey boxes for a double parasegment unit) (see Figure 6—figure supplement 1C). (B) When considering 0, 1 or 2 missing cells, the most robust solution with three receptors is achieved with an additional receptor C spanning one parasegment out of two (either odd or even). This provides a receptor difference at the PSBs (grey boxes in first line) and systematically increases receptor differences when one cell is missing at a given location (grey boxes in second line). When 2 cells are missing, the number of receptor differences increases at a subset of locations, notably in the case where cell identities 3 and 4 are missing (grey boxes in third line). The robustness score for this solution is 20 (arrow in Figure 6—figure supplement 1C). Code for receptor permutations is in Source code 1.
-
Figure 6—source data 1
Source data for Figure 6—figure supplement 1, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.028
Figure 6—figure supplement 1
Combinatorial receptor patterns.
(A,B) Receptor differences when cells are missing. Permutations of receptors and receptor differences when S3 (A) or both S3 and S4 cells (B) are missing, for the scenario in Figure 6B. In locations where S3 cells are missing alone (A), receptor differences increase to 2. In locations where both S3 and S4 cells are missing (B), receptor differences increase to 3. (C) Scoring robustness with a three-receptor combination. We randomised the location of three receptors, each expressed in 4 cells per double parasegment, one million times. Each permutation was scored as the sum of i) the number of receptor differences between neighbouring cells (grey boxes in first line of example in Figure 6B), ii) the increase in number of receptor differences when one cell is missing at a given location (grey boxes in second line in Figure 6B) and iii) the increase in number of receptor differences when two cells are missing (grey boxes in third line in Figure 6B). The total score for the solution in Figure 6B is 20, shown by the red arrow on the frequency histogram. Note that receptor C can be expressed in either even or odd parasegments, making no difference to the robustness score. (D) We also randomized the locations of four receptors, each expressed in 4 stripes per double-parasegment. Considering again events where 0, 1 or 2 cells are missing, the only permutation of 4 receptors that has a higher robustness score, 24, than the solution shown in Figure 6B, 20, is shown in (D). Remarkably, the number of receptor differences increases progressively when 1 or 2 cells are missing at any given location (grey boxes). Note that this is a very similar permutation to the solution in Figure 6B, but the expression pattern for previously named receptor A is split into two pair-rule domains, now named receptors A and B, which confer additional robustness when 2 cell identities are missing. (E) Frequency histogram of the robustness score of one million randomisations for the expression of 4 receptors. The best score, 24 (red arrow), corresponds to the solution shown in (D). Input data and statistics are in Figure 6—source data 1.
Figure 7 with 1 supplement
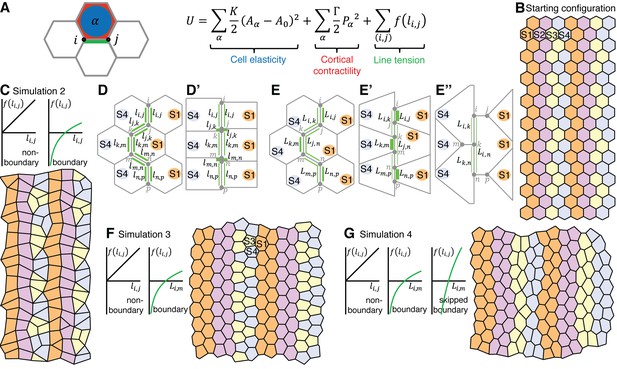
A vertex model based on cell-cell interactions replicates the interface behaviours during axis extension.
(A) Summary of vertex model of germband extension. Cells are considered as two-dimensional polygons representing cell-cell interfaces, with vertices forming where three polygons meet. An ‘energy function’ is calculated and used to update the position of every vertex i over time. This energy function encodes mechanical contributions associated with cell elasticity, cortical contractility and interfacial ‘line tension energy’. We consider a number of simulations (see main text), which differ in the hypothesised dependence of the line tension f on interface lengths. (B) The initial configuration for each simulation comprises regular hexagonal cells organised into parasegments, each comprising cells of 4 stripe identities (S1-S4). Note that the initial configuration starts with 14x20 cells (Video 5) and smaller snapshots are shown in this Figure and Figure 7—figure supplement 1. (C) In simulation 2, the line tension energy f varies linearly with interface length for non-boundary interfaces, but we specify a nonlinear dependence for boundary interfaces to represent a positive feedback between interface shortening and Myosin II enrichment. In this simulation, cells undergo neighbour exchanges but become stuck locally in four-cell junctions and hence convergent extension cannot proceed (D, D’). In Simulation 3, we apply our non-linear dependence of line tension to the total length of contiguous boundary interfaces for a given cell (length ) (E), rather than to individual boundary interfaces (length ) (D, D’). This allows vertices to slide independently on either side of a column of interfaces that makes a boundary (E’, E”) and the simulated tissue now undergoes convergent extension (F), but identities S3 and S4 clump together. (G) Simulation 4 resolves this issue by incorporating ‘supercontractility’, where boundary interfaces between cells of non-adjacent identities (‘skipped boundary’) are more contractile. Code for vertex model is in Source code 1.
-
Figure 7—source data 1
Source data for Figure 7—figure supplement 1, including statistical analysis.
- https://doi.org/10.7554/eLife.12094.032
Figure 7—figure supplement 1
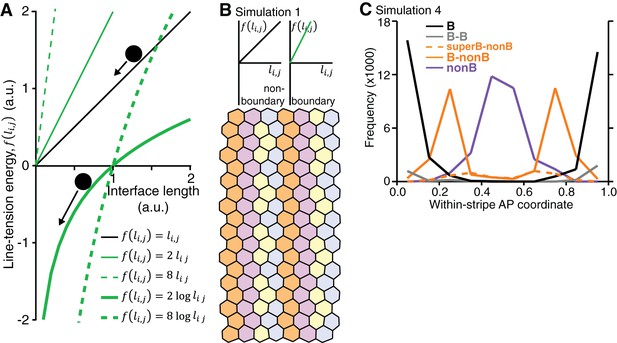
Further details of vertex model simulations for interface behaviours during axis extension.
(A) The model simulations 1–4 that we consider (see main text) differ in their hypothesised dependence of the ‘line tension’ energy term f (see Figure 7A) on interface lengths. (B) In simulation 1, the line tension energy associated with each cell-cell interface varies linearly with its length, but with a higher constant of proportionality for boundary interfaces than for non-boundary interfaces. In this simulation, cells fail to undergo neighbour exchange. (C) Analysis of the interface behaviours in simulation 4 as in real data in Figure 5I (legends therein). Input data and statistics are in Figure 7—source data 1.
Figure 8
Methodology for quantifying tissue strain rates.
https://doi.org/10.7554/eLife.12094.035Videos
Video 1
Representative sqhAX3; sqh-GFP; gap43-Cherry movie (SG_4), showing the red (top left) and green (top right) fluorescence channels as well as the tracked cell shapes (bottom left) and the quantification of Myosin II fluorescence at tracked interfaces (bottom right).
See also Figure 1A.
Video 2
Representative sqhAX3; sqh-GFP; gap43-Cherry movie (SG_4) showing the green channel (sqh-GFP) with identification of the different parasegments and the parasegmental boundary interfaces.
See also Figure 2A,B,D.
Video 3
Representative sqhAX3; sqh-GFP; gap43-Cherry movie (SG_4) showing the tracked cell contours with within-parasegment coordinate colour-coded as shown in Figure 3A.
https://doi.org/10.7554/eLife.12094.019
Video 4
Representative sqhAX3; sqh-GFP; gap43-Cherry movie (SG_4) showing the within-parasegment stripes colour-coded as in Figure 4A.
https://doi.org/10.7554/eLife.12094.022
Video 5
Movie of simulation 4 shown in Figure 7G.
https://doi.org/10.7554/eLife.12094.030Tables
Table 1
Summary of embryos analysed per genotype.
| Embryo Genotype | # Movies analysed | Mode of Tracking |
|---|---|---|
| sqhAX3; sqh-GFP; GAP43-mCherry | 6 | Automated |
| eve-EGFP, GAP43-mCherry | 3 | Automated, manual correction |
| wgCX4; eve-EGFP, GAP43-mCherry | 3 | Automated, manual correction |
Table 2
Summary of parasegments analysed for each sqhAX3; sqh-GFP; GAP43-mCherry movie.
| Movie Identifier | PS4 | PS5 | PS6 | PS7 |
|---|---|---|---|---|
| SG_1 | ✗ | ✔ | ✔ | ✔ |
| SG_2 | ✗ | ✔ | ✔ | ✔ |
| SG_3 | ✔ | ✔ | ✔ | ✗ |
| SG_4 | ✔ | ✔ | ✔ | ✗ |
| SG_5 | ✔ | ✔ | ✔ | ✗ |
| SG_6 | ✔ | ✔ | ✔ | ✔ |
Table 3
List of parameters and their values used in simulations.
| Parameter | Description | Value | Simulations |
|---|---|---|---|
| Drag coefficient | 1.0 | All | |
| Simulation end time | 500 | All | |
| Time step | 0.001 | All | |
| T1 swap threshold | 0.01 | All | |
| T1 swap distance multiplier | 1.5 | All | |
| Elastic coefficient | 1 | All | |
| Cell target area | 1 | All | |
| Contractility coefficient | 0.04 | All | |
| Line-tension coefficient for non-boundary (or tissue-boundary) interfaces | 0.05 | 1-3 | |
| Line-tension coefficient for (stripe-) boundary interfaces | 2 | 2-3 | |
| Line-tension coefficient for super-contractile (stripe-) boundary interfaces | 8 | 4 |
Additional files
-
Source code 1
Code for receptor permutations (Figure 6) and vertex model (Figure 7), as cited in the Materials and methods.
- https://doi.org/10.7554/eLife.12094.038
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Unipolar distributions of junctional Myosin II identify cell stripe boundaries that drive cell intercalation throughout Drosophila axis extension
eLife 5:e12094.
https://doi.org/10.7554/eLife.12094
