Active sensing in the categorization of visual patterns

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record updated: February 6, 2017 (This version)
Version of Record updated: December 13, 2016 (Go to version)
Version of Record published: February 10, 2016 (Go to version)
Accepted: December 6, 2015
Received: October 10, 2015

1. Of interest
ACC neural ensemble dynamics are structured by strategy prevalence

Mikhail Proskurin, Maxim Manakov, Alla Karpova

Research Article Dec 7, 2023
Further reading

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Interpreting visual scenes typically requires us to accumulate information from multiple locations in a scene. Using a novel gaze-contingent paradigm in a visual categorization task, we show that participants' scan paths follow an active sensing strategy that incorporates information already acquired about the scene and knowledge of the statistical structure of patterns. Intriguingly, categorization performance was markedly improved when locations were revealed to participants by an optimal Bayesian active sensor algorithm. By using a combination of a Bayesian ideal observer and the active sensor algorithm, we estimate that a major portion of this apparent suboptimality of fixation locations arises from prior biases, perceptual noise and inaccuracies in eye movements, and the central process of selecting fixation locations is around 70% efficient in our task. Our results suggest that participants select eye movements with the goal of maximizing information about abstract categories that require the integration of information from multiple locations.

https://doi.org/10.7554/eLife.12215.001

eLife digest

To interact with the world around us, we need to decide how best to direct our eyes and other senses to extract relevant information. When viewing a scene, people fixate on a sequence of locations by making fast eye movements to shift their gaze between locations. Previous studies have shown that these fixations are not random, but are actively chosen so that they depend on both the scene and the task. For example, in order to determine the gender or emotion from a face, we fixate around the eyes or the nose, respectively.

Previous studies have only analyzed whether humans choose the optimal fixation locations in very simple situations, such as searching for a square among a set of circles. Therefore, it is not known how efficient we are at optimizing our rapid eye movements to extract high-level information from visual scenes, such as determining whether an image of fur belongs to a cheetah or a zebra.

Yang, Lengyel and Wolpert developed a mathematical model that determines the amount of information that can be extracted from an image by any set of fixation locations. The model could also work out the next best fixation location that would maximize the amount of information that could be collected. This model shows that humans are about 70% efficient in planning each eye movement. Furthermore, it suggests that the inefficiencies are largely caused by imperfect vision and inaccurate eye movements.

Yang, Lengyel and Wolpert’s findings indicate that we combine information from multiple locations to direct our eye movements so that we can maximize the information we collect from our surroundings. The next challenge is to extend this mathematical model and experimental approach to even more complex visual tasks, such as judging an individual’s intentions, or working out the relationships between people in real-life settings.

https://doi.org/10.7554/eLife.12215.002

Introduction

Several lines of evidence suggest that humans and other animals direct their sensors (e.g. their eyes, whiskers, or hands) so as to extract task-relevant information efficiently (Yarbus, 1967; Kleinfeld et al., 2006; Lederman and Klatzky, 1987). Indeed, in vision, the pattern of eye movements used to scan a scene depends on the type of information sought (Hayhoe and Ballard, 2005; Rothkopf et al., 2007), and has been implied to follow from an active strategy (Najemnik and Geisler, 2005; Renninger et al., 2007; Navalpakkam et al., 2010; Nelson and Cottrell, 2007; Toscani et al., 2013; Chukoskie et al., 2013) in which each saccade depends on the information gathered about the current visual scene and prior knowledge about scene statistics. However, until now, studies of such active sensing have either been limited to search tasks or to qualitative descriptions of the active sensing process. In particular, no studies have shown whether the information acquired by each individual fixation is being optimized. Rather, the fixation patterns have either been described without a tight link to optimality (Ballard et al., 1995; Epelboim and Suppes, 2001) or compared to an optimal strategy only through summary statistics such as the total number of eye movements and the distribution of saccade vectors (Najemnik and Geisler, 2005; 2008) that could have arisen through a heuristic. Therefore, these studies leave open the question as to what extent eye movements truly follow an active optimal strategy. In order to study eye movements in a more principled quantitative manner, we estimated the efficiency of eye movements in a high-level task on a fixation-by-fixation basis.

Here, we focus on a pattern categorization task that is fundamentally different from visual search, in which often there is a single location in the scene that has all the necessary information (the target), and eye movements are well described by the simple mechanism of inhibition of return (Klein, 2000). In contrast, in many other tasks, such as constructing the meaning of a sentence of written text, or judging from a picture how long a visitor has been away from a family (Yarbus, 1967), no single visual location has the necessary information in it and thus such tasks require more complex eye movement patterns. While some basic-level categorization tasks can be solved in a single fixation (Thorpe et al., 1996; Li et al., 2002), many situations require multiple fixations to extract several details at different locations to make a decision. Therefore, when people have to extract abstract information (eg., how long the visitor has been away) they need to integrate a series of detailed observations (such as facial expression, postures and gestures of the people) across the scene, relying heavily on foveal vision information with peripheral vision playing a more minor role (Levi, 2008).

We illustrate the key features of active sensing in visual categorization by a situation that requires the categorization of an animal based on its fur that is partially obscured by foliage (Figure 1). As each individual patch of fur can be consistent with different animals, such as a zebra or a cheetah, and the foliage prevents the usage of gist information (Oliva and Torralba, 2006), multiple locations have to be fixated individually, and the information accumulated across these locations, until a decision can be made with high confidence. For maximal efficiency, this requires a closed loop interaction between perception, which integrates information from the locations already fixated with prior knowledge about the prevalence of different animals and their fur patterns, and thus maintains beliefs about which animal might be present in the image, and the planning of eye movement, which should direct the next fixation at a location which has potentially the most information relevant for the categorization (Figure 1). Inspired by this example, and to allow a mathematically tractable quantification of the information at any fixation location, we designed an experiment with visual patterns that were statistically well-controlled and relatively simple, while ensuring that foveal vision would dominate by using a gaze-contingent categorization task in which we tracked the eye and successively revealed small apertures of the image at each fixation location. In contrast to previous studies (Najemnik and Geisler, 2005; Renninger et al., 2007; Peterson and Eckstein, 2012; Morvan and Maloney, 2012), our task required multiple locations to be visited to extract information about abstract pattern categories.

Figure 1

Download asset Open asset

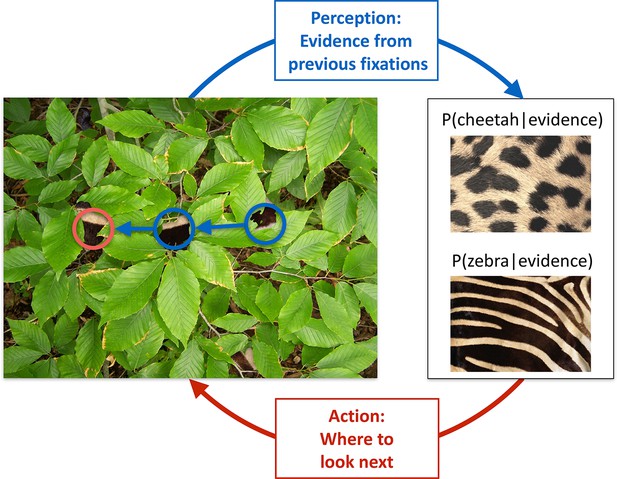
Active sensing involves an interplay between perception and action.

When trying to categorize whether a fur hidden behind foliage (left) belongs to a zebra or a cheetah, evidence from multiple fixations (blue, the visible patches of the fur, and their location in the image) needs to be integrated to generate beliefs about fur category (right, here represented probabilistically, as the posterior probability of the particular animal given the evidence). Given current beliefs, different potential locations in the scene will be expected to have different amounts of informativeness with regard to further distinguishing between the categories, and optimal sensing involves choosing the maximally informative location (red). In the example shown, after the first two fixations (blue) it is ambiguous whether the fur belongs to a zebra or a cheetah, but active sensing chooses a collinearly located revealing position (red) which should be informative and indeed reveals a zebra with high certainty. Note that this is just an illustrative example.

https://doi.org/10.7554/eLife.12215.003

Results

Categorization performance and eye movement patterns

We generated images of three types: patchy, horizontal stripy, and vertical stripy (Figure 2A). Participants had to categorize each image pattern as patchy or stripy (disregarding whether a stripy image was horizontal or vertical—the inclusion of two different stripy image types prevented participants from solving the task based on one image axis alone). The images were generated by a flexible statistical model that could generate many examples from each of the three image types, so that the individual pixel values varied widely even within a type and only higher order statistical information (ie. the length scale of spatial correlations) could be used for categorization. We first presented the participants with examples of full images to familiarize them with the statistics of the image types and to ensure their categorization with full images was perfect. We then switched to an active gaze-contingent mode in which the entire pattern was initially occluded by a black mask and the underlying image was revealed with a small aperture at each fixation location (Figure 2B; for visibility, the black mask is shown as white). As a control, we also used a number of passive revealing conditions in which the revealing locations were chosen by the computer rather than in a gaze-contingent manner. In all conditions, we controlled the number of revealings on each trial before requiring the participants to categorize the image (Figure 2B). To ensure that participants had equal chance to extract information from all revealing locations in the passive as well as the active conditions we allowed the participants to rescan the revealed locations after the final revealing (see also Materials and methods for full rationale). Importantly, in the active revealing condition, even though rescanning was allowed after the final revealing, participants had to select all revealing locations in real time without knowing how many revealings they would be allowed on a given trial. Therefore, although rescanning could improve categorization it was unlikely to influence participants’ active revealing strategy. To confirm this we also performed a control in which rescanning was not allowed (see below).

Figure 2 with 1 supplement see all

Download asset Open asset

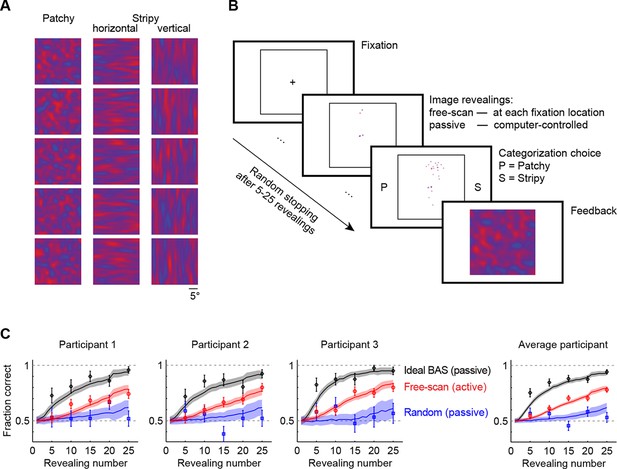
Image categorization task and participants’ performance.

(A) Example stimuli for each of the three image types sampled from two-dimensional Gaussian processes. (B) Experimental design. Participants started each trial by fixating the center cross. In the free-scan condition, an aperture of the underlying image was revealed at each fixation location. In the passive condition, revealing locations were chosen by the computer. In both conditions, after a random number of revealings, participants were required to make a category choice (patchy, P, versus stripy, S) and were given feedback. (C) Categorization performance as a function of revealing number for each of the three participants (symbols and error bars: mean $\pm$ SEM across trials), and their average, under the free-scan and passive conditions corresponding to different revealing strategies. Lines and shaded areas show across-trial mean $\pm$ SEM for the ideal observer model. Figure 2—figure supplement 1 shows categorization performance in a control experiment in which no rescanning was allowed.

https://doi.org/10.7554/eLife.12215.004

In the free-scan (active) condition, categorization performance improved with the number of revealings for each participant (Figure 2C, red points), indicating the successful integration of information across a large number of fixations. Although we used a gaze-contingent display, the task still allowed participants to employ natural every-day eye movement strategies, consistent with the inter-saccadic intervals (mean 408 ms) and relative saccade size (0.75–3.9 normalized by the three different relevant length scales of the stimuli) that were similar though somewhat shorter than those recorded for everyday activities (e.g. tea making; mean inter-saccadic interval 497 ms, and 0.95–19 relative saccade size normalized by the size of different fixated objects; Hayhoe et al., 2003; Land and Tatler, 2009).

To examine whether fixation locations depended on the underlying image patterns, we constructed revealing density maps for each image type. To account for the translation-invariant statistics of the underlying images of a type, we used the relative location of revealings obtained by subtracting from the absolute location of each revealing (measured in screen-centered coordinates) the center of mass of the absolute locations within each trial (Materials and methods). In order to compare eye movement patterns across conditions and participants, we subtracted the mean density map across all images for each participant. Importantly, we found that the pattern of revealings strongly depended on image type (Figure 3A, first four rows). The pattern of eye movements for images of the same type were positively correlated for each participant (Figure 3B, left, orange bars; p<0.001 in all cases), whereas eye movements for images of different types were negatively correlated (Figure 3B, left, purple bars; p<0.001 in all cases). We also found that eye movement patterns became increasingly differentiated over the course of the trial as progressively more of the image was revealed (Figure 3B, left, curves). The dependence of the eye movement patterns on the underlying image type shows that participants employed an active sensing strategy.

Figure 3 with 3 supplements see all

Download asset Open asset

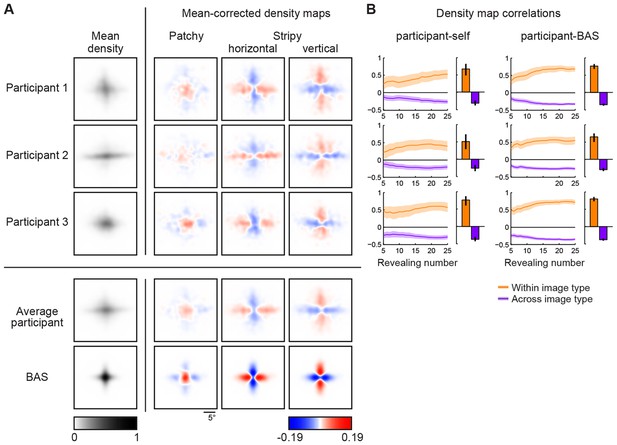
Density maps of relative revealing locations and their correlations.

(A) Revealing density maps for participants and BAS. Last three columns show mean-corrected revealing densities for each of the three underlying image types (removing the mean density across image types, first column). Bottom: color scales used for all mean densities (left), and for all mean-corrected densities (right). All density maps use the same scale, such that a density of 1 corresponds to the peak mean density across all maps. Figure 3—figure supplement 1 shows revealing density maps obtained for participants in a control experiment in which no rescanning was allowed. Figure 3—figure supplement 2 shows the measured saccadic noise that was incorporated into the BAS simulations. Figure 3—figure supplement 3 shows density maps separately for correct and incorrect trials. (B) The curves are correlations for individual participants as a function of revealing number with their own maps (left) and the maps generated by BAS (right). The bars are correlations at 25 revealing (see Materials and methods). Orange shows within image type correlation, ie. correlation between revealing densities obtained for images of the same type, and purple shows across image type correlation. Data are represented as mean $\pm$ SD for the curves and mean $\pm$ 95% confidence intervals for the bars.

https://doi.org/10.7554/eLife.12215.006

To assess whether this active strategy used by our participants contributed to performance improvement, we examined the same participants in a passive revealing condition. When the revealings were drawn randomly from an isotropic Gaussian centered on the image, performance was substantially impaired (Figure 2C, blue points), indicating that participants’ decision performance benefited from their active sensing strategy. After the final revealing, participants rescanned only briefly, on average for 5.0 s in the active condition, 6.4 s in the passive random condition before making a decision. Moreover, their performance did not improve with increased rescanning time, instead it correlated negatively with rescanning time for 2 out of 3 participants, such that the probability of a correct decision for rescanning times at the 25th and 75th percentiles of the rescanning time distribution fell from 0.77 to 0.54 (p<0.001) and from 0.77 to 0.66 (p<0.03), respectively. This suggests that longer rescanning times indicate when participants are uncertain rather than providing the main source of information for their decisions. This is in contrast to additional revealings during the original scanning period which clearly benefit performance when chosen appropriately (Figure 2C).

To further examine whether the rescanning period after the final revealing affected the participants scanning strategy, we examined additional participants in a free-scan condition in which no rescanning was allowed after the final revealing (the display blanked). The revealing density maps for these participants were very similar to the maps of participants who were allowed to rescan (average within-type vs. across-type correlation across the two groups of participants: 0.63 vs. −0.30) and performance was also similar (Figure 2—figure supplement 1 and Figure 3—figure supplement 1), although as expected slightly worse without rescanning. The proportion correct across all trials for the participants who were allowed to rescan was 0.65, 0.66 and 0.69 (average 0.66) and for those not allowed to rescan was 0.64, 0.58 and 0.66 (average 0.63). This confirms that allowing rescanning did not substantially change participants’ revealing strategy.

Bayesian ideal observer

We constructed an ideal observer (Geisler, 2011) which computed a posterior distribution, $ℙ (c | D)$ , over image category $c$ given the observations D (collection of previous revealing locations and revealed pixel values in the trial) and made a choice such that the category with higher posterior probability was more likely to be selected (see Materials and methods). To construct this model, we considered three sources of suboptimality: prior biases implying imperfect knowledge of the precise correlation length scales of each pattern category, perception noise that distorts the displayed pixel values, and decision noise which occasionally results in selecting the category with the lower posterior probability (Houlsby et al., 2013). We fitted six models to the individual choices of each participant. These models differed in the kind of prior bias and decision noise they included, and we selected the model with the strongest statistical evidence, as quantified by the Bayesian information criterion (Tables 1–2). The best model (4 parameters in total) provided a close match to the participants’ performance both in the active and passive random-revealing conditions (Figure 2C, red and blue lines). Crucially, this model also allowed us to estimate the beliefs that participants held about image categories at any point in a trial, which was necessary for determining the optimal next eye movement that could maximally disambiguate between the categories.

Table 1

Maximum likelihood parameters of the model (see Materials and methods for details) with the best BIC score (see Table 2).

https://doi.org/10.7554/eLife.12215.010

Participant	Perception noise, σ_p	Prior bias, Δ	Decision noise
Participant	Perception noise, σ_p	Prior bias, Δ	Stimulus-dependent, β	Stimulus-independent, κ
1	0.5	0.58°	1.4	0.044
2	0.5	0.61°	1.9	0.12
3	0.3	0.54°	1.5	0.10

Table 2

Model comparison results using Bayesian information criterion (BIC, lower is better). Each row is a different model using a different combination of included (+) and excluded (–) parameters (columns, see Materials and methods for details). Last column shows BIC score relative to the BIC of the best model (number 4).

https://doi.org/10.7554/eLife.12215.011

Model	Perception noise, σ_p	Prior bias		Decision noise		BIC
Model	Perception noise, σ_p	Scale, α	Offset, Δ	Stimulus-dependent, β	Stimulus-independent, κ	BIC
1	+	–	–	+	–	160
2	+	–	–	+	+	139
3	+	–	+	+	–	58
4	+	–	+	+	+	0
5	+	+	–	+	–	105
6	+	+	–	+	+	102

Predicting eye movement patterns by a Bayesian active sensor algorithm

To be able to rigorously assess how close our participants were to optimal sensing, we developed a Bayesian active sensor (BAS) algorithm which is optimal in minimizing categorization error with every single revealing. That is, for our task, the aim of BAS is to choose the next fixation location, $x^{*}$ , so as to maximally reduce uncertainty in the category (MacKay, 1992). This objective is formalized by the BAS score function which expresses the expected information gain when choosing $x^{*}$ , and which can be conveniently computed as:

Score (x^{*} | D) = H [z^{*} | x^{*}, D] - {⟨ H [z^{*} | x^{*}, c, D] ⟩}_{ℙ (c | D)}

where $H$ denotes entropy (a measure of uncertainty), $z^{*}$ is the possible pixel value at $x^{*}$ , $D$ is the collection of revealing locations and revealed pixel values that have been observed in the trial as above, $c$ is image category, and $⟨ \cdot ⟩$ denotes averaging over the two categories weighted by their posterior probabilities, as computed by the ideal observer (for more details, see Materials and methods). This expresses a trade-off between two terms. The first term encourages the selection of locations, $x^{*}$ , where we have the most overall uncertainty about the pixel value, $z^{*}$ , while the second term prefers locations for which our expected pixel value for each category is highly certain.

Figure 4A shows a sequence of fixations on a representative trial. On each fixation, the BAS score is computed for all possible positions (grayscale map) based on all previous fixation locations (green dots) and the pixel values revealed there. While the BAS algorithm would choose the position with the highest BAS score as the next fixation location (blue crosses), the participant might choose a different, suboptimal, fixation location (yellow circles). Nevertheless, the informativeness of most of the participant’s fixation locations were very high as expressed by their information-percentile values (the percentage of putative fixation locations with lower BAS scores than the one chosen by the participant).

Figure 4 with 1 supplement see all

Download asset Open asset

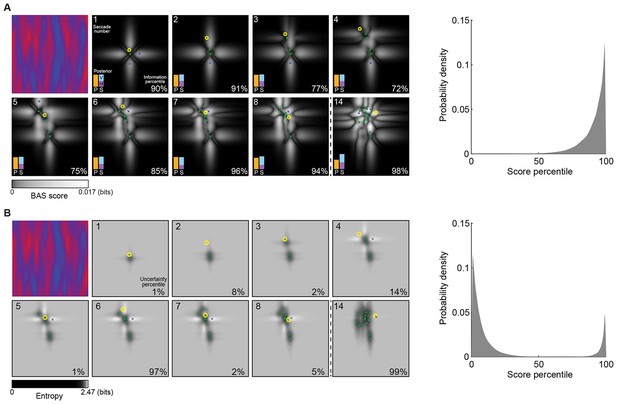
Example trial of the Bayesian active sensor (BAS) and its maximum entropy variant.

(A) The operation of BAS in a representative trial for saccades 1–8 and 14 (underlying image shown top left). For each fixation (left, panels), BAS computes a score across the image (gray scale, Equation 1). This indicates the expected informativeness of each putative fixation location based on its current belief about the image type, expressed as a posterior distribution (inset, lower left), which in turn is updated at each fixation by incorporating the new observation of the pixel value at that fixated location. Crosses show the fixation locations with maximal score for each saccade, green dots show past fixation locations chosen by the participant and yellow circle shows current fixation location. Percentage values (bottom right) show their information percentile values (the percentage of putative fixation locations with lower BAS scores than the one chosen by the participant). Histogram on the right shows distribution of percentile values across all participants, trials and fixations. (B) Predictions of the maximum entropy variant (the first term in Equation 1) as in (A). For saccades 1–3, the fixation locations with maximal score (crosses) are not shown because the maxima comprise a continuous region near the edge of the image instead of discrete points. Note that entropy can be maximal further (eg. fixation 4) or nearer the edges of the image (eg. fixation 1), depending on the tradeoff between the two additive components defining it: the BAS score, which tends to be higher near revealing locations (panel A), and uncertainty due to the stochasticity of the stimulus and perception noise, which tends to be greater away from revealing locations. Figure 4—figure supplement 1 shows two illustrative examples for this trade-off.

https://doi.org/10.7554/eLife.12215.012

We simulated eye movement patterns derived by BAS for the same images shown to our participants. In order to take into account basic biological constraints on the accuracy of eye movements, we included saccadic variability and bias in the model based on measurements made independently in a group of participants which took into account both the standard deviation and bias of saccades both along and orthogonal (standard deviation only) to the desired saccade direction as a function of desired amplitude (Figure 3—figure supplement 2). The predicted (mean-corrected) pattern of eye movements closely matched those observed (Figure 3A, last two rows): they were positively correlated with participants’ eye movements for the same image type (Figure 3B, right, orange bars; p $<$ 0.001 in all cases), but negatively correlated with those for different image types (Figure 3B, right, purple bars; p<0.001 in all cases). These differences increased as a function of revealing number (Figure 3B, right, curves). Moreover, when we split participants’ trials into those in which they made a correct or incorrect decision, the pattern of eye movements derived from the correct trials correlated better with the BAS pattern than that derived from incorrect trials (Figure 3—figure supplement 3, $ρ_{correct} = 0.74$ , $ρ_{incorrect} = 0.20$ , p<0.001 for the average participant), further suggesting that following a BAS-like strategy was beneficial for performance.

For comparison, we also analyzed how well participants’ fixations could be accounted for by a strategy using a variant of the score that only included the first term in Equation 1 and thus selected locations with maximal entropy rather than maximal information gain. We found that this strategy provided a substantially poorer fit to our eye movement data than the full BAS algorithm, as measured by the distribution of the scores corresponding to actual fixation locations (Figure 4B) and the anti-correlations between predicted and actual revealing maps at 25 revealings ( $ρ$ = $-$ 0.62, $-$ 0.51, $-$ 0.43; all p<0.001).

Fixation informativeness

In order to obtain a fixation-by-fixation measure of the informativeness of participants’ individual eye movements, we used the ideal observer model to quantify the amount of information accumulated about image category over subsequent revealings in a trial for different revealing strategies (Figure 5A). This information-based measure is more robust than directly measuring distances between optimal and actual scan paths because multiple locations are often (nearly) equally informative when planning the next saccade. For example, in the trial shown in Figure 4A, the BAS score map was clearly multimodal for several fixations, and some of the participant’s fixation locations were indeed distant from the corresponding locations that BAS would have chosen, yet their informativeness was generally very high. Therefore, categorization performance is better understood in terms of information measures on the revealed locations rather than by the geometry of individual scan paths, which has traditionally been used in previous studies (Najemnik and Geisler, 2005; Renninger et al., 2007).

Figure 5 with 1 supplement see all

Download asset Open asset

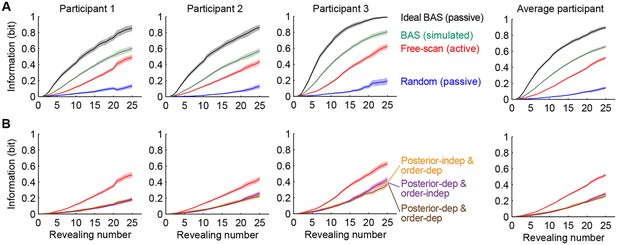
Information gain as a function of revealing number for different strategies.

(A) Cumulative information gain of an ideal observer (matched to participants’ prior bias and perceptual noise) with different revealing strategies (black, green, and blue) and participants’ own revealings (red). Data are represented as mean $\pm$ SEM across trials. Figure 5—figure supplement 1 shows a measure of efficiency extracted from these information curves across sessions. (B) Information gains for three heuristic strategies (See text for details, and Materials and methods): posterior-independent & order-dependent fixations (orange), posterior-dependent & order-independent fixations (purple), and posterior- & order-dependent fixations (brown). The information gain curves for the three heuristics overlap in all cases. Participants’ active revealings (red lines, as in A) were 1.81 (95% CI, 1.68–1.94), 1.85 (95% CI, 1.72–1.99), and 1.92 (95% CI, 1.74–2.04) times more efficient in gathering information than these heuristics, respectively. Data are represented as mean $\pm$ SEM across trials.

https://doi.org/10.7554/eLife.12215.014

We compared the information efficiency of different revealing strategies by measuring the relative number of revealings required by them to gain the same amount of information. Participants’ active revealings (Figure 5A–B, red lines) were 2.93 (95% confidence interval [CI], 2.60–3.32) times more efficient than random revealings (Figure 5A, blue lines). As a more stringent control than a random strategy, we also simulated eye movement patterns for three heuristic strategies that reproduced different aspects of the statistics of participants’ actual eye movement patterns but lacked the full closed-loop Bayesian interaction between belief updating and eye-movement selection (see Materials and methods for details). We first used a feed-forward strategy, which retained order-dependence, i.e. the way the statistics of revealing locations chosen by the participants depended on revealing number, but ignored participants’ inferences about the category (Figure 5B, orange). The second heuristic took into account the participant’s belief about the underlying image, but not the revealing number (Figure 5B, purple). The third heuristic was a partial closed-loop strategy, that thus respected both the belief- and order-dependence of revealings, but not the details of previous revealings (Figure 5B, brown line). Notably, this strategy would be optimal for simpler stimuli and tasks, such as visual search for a target, but not for our spatially correlated stimuli and task requiring information integration across multiple locations. Participants’ revealings were 1.81–1.92 times more efficient than these three heuristic strategies.

However, participants’ active revealings were less efficient by a factor of 2.48 (95% CI, 2.33–2.62) than the information provided by revealings generated by the BAS algorithm with ‘idealized’ parameters: minimal perception noise (2–3 times lower than our participants’; see Materials and methods) and no prior biases or saccadic inaccuracies (Figure 5A, black lines). Indeed, this efficiency in information gathering was also reflected in our participants’ performance when they viewed revealings generated by this ideal BAS (Figure 2C, black points). In this condition, participants only rescanned the revealed locations for a short amount of time after the final revealing (average of 4.4 s), less than in the active and passive random conditions, thus their increased efficiency could not be attributed to longer rescanning times. The discrepancies between participants’ and BAS’s revealings may be caused by participants employing an inefficient strategy to select their fixation locations, or, alternatively, they may be due to more trivial factors upstream or downstream of the process responsible for selecting the next fixation, such as noise and variability in perception or execution, respectively. Importantly, when we computed the information gain provided by BAS when operating with participants’ prior biases, perceptual noise and the typical saccadic inaccuracies as described above, the discrepancy between the informativeness of BAS-generated revealings compared to that of participants’ revealings was markedly reduced (Figure 5A, green lines, BAS/free-scan efficiency = 1.45, 95% CI, 1.37–1.53). This suggests that the central component of choosing where to fixate was around 70% efficient in our participants, and a large component of suboptimality arose due to other processes. To examine the role of learning in participants’ active sensing strategy, we computed the relative efficiency of each of the free-scan sessions of our experiment, spanning multiple days, compared to the final session (Figure 5—figure supplement 1). We found that efficiency remained stable over the whole course of the experiment, suggesting there was minimal, if any, learning required in the free-scan task.

Discussion

Our results show that humans employ an active sensing strategy in deciding where to look in a high-level pattern categorization task. In our task, participants’ patterns of eye movements were well predicted by a Bayes-optimal algorithm seeking to maximize information gain relevant to the task with each individual eye movement. This Bayes optimal strategy involved finding the location in the scene which when fixated was most likely to lead to the greatest reduction in categorization error, rather than simply the location associated with the most uncertainty about pixel value.

The efficiency of active sensing in human vision

Although our participants performed better when revealings were chosen by the BAS algorithm than with their own scan paths, our results suggest that this suboptimality in participants’ performance was to a large part due to prior biases, perception noise, and saccadic inaccuracies constraining the selection of fixation locations rather than an inefficient active sensing strategy. In particular, our participants’ eye movements were substantially more efficient than heuristic strategies that only employed a subset of the elements of a fully closed-loop active sensing strategy, and were about 70% as efficient as the optimal active sensor that operated with the participants’ own prior bias, perception noise, and saccadic inaccuracies. Importantly, this estimate does not conflate the inference process with the selection process in that even if the participant’s inference is biased or inconsistent, we can measure, given those beliefs, the extent to which they select fixation locations optimally. The 30% inefficiency we found may be due to unmodeled constraints in human eye movement strategies, such as the biases for cardinal directions or fixating the centre of an image that were apparent in our data (Figure 3A) and that may also be beneficial in natural environments (Tatler and Vincent, 2008; 2009). Such suboptimalities are conceptually different from those that we factored out using the specific biases and noise included in the BAS model. The latter are suboptimalities that arise in the execution of a planned saccade (as in Figure 3—figure supplement 2), while the former could be suboptimalities of the planning itself. Therefore, as we were interested in the degree of (sub)optimality of the planning component, we chose not to factor out potential biases for cardinal directions or locations. Should such suboptimalities turn out to be part of the execution process, then our estimate of 70% would become a lower bound on the efficiency of the planning process.

Our results contrast with recent studies suggesting that the pattern of eye movements do not follow an active sensing strategy. In one study, using a simple object localization task, it was found that the choice of fixation locations was close to random despite obvious learning of the underlying stimulus statistics (Holm et al., 2012). In another study, using a simplified visual search task, participants’ eye movements were virtually unaffected by the configuration of the visual stimuli presented in the trial (Morvan and Maloney, 2012). In contrast, we found that participants used both their prior knowledge of stimulus statistics as well as evidence accumulated about the current visual scene to guide their eye movements. We speculate that better performance in our case may be due to our more naturalistic task, which involves the extraction of abstract latent features, revealing more typical processing of the sensorimotor system.

Relevance for natural vision

Although our task was designed to emulate many features of natural vision, there remain several differences. First, our gaze-contingent display involved exposing small patches of the image at each fixation whereas in natural vision information is available from the full visual field, albeit with decreasing acuity away from the fovea. If participants’ selection process was aware of and actively optimized for the changed field of vision in our task, the resulting eye movement patterns could be different from those in natural vision. Nevertheless, the basic summary statistics of (macro-)saccades in our task (average size and inter-saccadic intervals) were similar to those found in natural vision (Hayhoe et al., 2003; Land and Tatler, 2009), and there was a lack of adaptation to the task over the course of several days of free-scan sessions (Figure 5—figure supplement 1). These seem to suggest, at least indirectly, that participants did not depart dramatically from their natural eye movement strategies.

Second, our task focuses on the voluntary component of eye movements, that is the scan paths of fixations, rather than the more involuntary processes of micro-saccades and drift (Rolfs, 2009; Ko et al., 2010; Rucci et al., 2007; Poletti et al., 2013; Kuang et al., 2012), which did not trigger new revealings. Importantly, in our task these involuntary processes are likely to be used for extracting information within each revealed patch, whereas high-level categorization required macro-saccades. This is because these involuntary processes cover an area with a standard deviation (SD) on the order of 0.22° (over the course of each fixation; Rolfs, 2009), which is similar to our Gaussian apertures (SD of 0.18°), whereas the smallest length scale of our stimuli (0.91°) is 4 times larger. However, it is possible that in natural scenes with finer structure, micro-saccades and drift may contribute more to abstract feature extraction.

Third, our stimuli set had strictly stationary statistics. This is an approximation to natural image statistics that are often assumed to be spatially stationary on average (eg. Field, 1987) but usually include local non-stationarities (eg. different objects with different characteristic spatial frequencies). Nevertheless, our stimuli were more naturalistic than many of the stimuli used in active sensing studies of visual search (eg. simple 1/f noise) while still allowing a rigorous control and measurement of the amount of high-level category information available at any potential revealing location which would not have been possible with natural scenes.

Finally, natural vision works under time constraints. Our task limited the number of revealings in each trial rather than the time, although the temporal aspects of the eye movements (inter-saccadic intervals) were similar to eye movements with natural scenes. We also showed in a control experiment that the additional time allowed for rescanning the revealed locations did not affect the initial scanning strategy.

A challenge for future studies will be to employ visual tasks that are more naturalistic in these respects while still retaining our ability to quantify the task-relevant information available to participants at any point in a trial. It may well be that participants are more efficient in such naturalistic settings than the 70% we found in our task.

Relation to earlier work

Our approach makes several important contributions. First, by using a gaze-contingent display we were able to isolate the top-down strategies of eye movement selection, thereby complementing studies which examined the influence of low-level visual features and salience (Itti and Koch, 2000; Wismeijer and Gegenfurtner, 2012) on eye movement selection. In addition, our task focuses on integrating low-level visual information into an abstract category thus complementing studies that examine the effect of target value (Navalpakkam et al., 2010; Krajbich et al., 2010; Markowitz et al., 2011; Schutz et al., 2012) or more cognitive tasks that use eye movement (Nelson and Cottrell, 2007) or button-pressing for information search (Castro et al., 2009; Gureckis and Markant, 2009; Borji and Itti, 2013). Some of these studies used a similar Bayesian formalism to obtain the active learning strategies specific to their tasks and showed that humans perform active learning when given the opportunity to consciously deliberate from which location in a scene they should gather information next. In contrast, our work shows that high-efficiency active sensing is a natural strategy for eye movements that humans adopt without overt deliberation, as evidenced by the inter-saccadic intervals matching naturalistic tasks and the fact that our participants reached near-asymptotic efficiency already in the first session of our task.

Second, by using a pattern categorization task we could ensure that no single location was especially informative but that the task required an integration of information from multiple locations both to select the next eye movement and to solve the task, and specifically that a closed-loop strategy was necessary for solving the task efficiently. This is in contrast with studies that attempted to quantify the general informativeness of single locations in a scene (Gosselin and Schyns, 2001), and showed that they are the target of fixations humans tend to choose in general (Peterson and Eckstein, 2012; Toscani et al., 2013; Chukoskie et al., 2013), or visual search in which, by the nature of the task, the target location is fully informative by itself (Najemnik and Geisler, 2005). As such, most previous studies have not addressed the important interplay between information gathering and fixation selection characteristic of naturalistic active sensing: that, in general, the most informative location is ever-changing, dependent on the history of fixations one has already performed.

Third, in contrast to active sensing for simple visual search (Najemnik and Geisler, 2005; Navalpakkam et al., 2010; Morvan and Maloney, 2012), our formalism extends the range of active sensing to tasks which have arbitrary, not necessarily spatial, latent features (such as categories). In particular, it provides the first fixation-by-fixation analysis of information gathering under active eye movements by carefully matching our observer model to participants’ performance. As a result, for the first time, we were able to dissociate the contributions of the eye-movement selection process from those of perceptual, motor, and decision processes, identify predominant sources of apparent sub-optimality in active sensing, and quantify the efficiency of choosing each individual fixation throughout scanning a whole scene. Taken together, these features make our approach amenable to multiple tasks in different perceptual domains (Kleinfeld et al., 2006), as well as high-level cognitive tasks such as estimating the age or socio-economic status of people in a scene (Yarbus, 1967).

Materials and methods

Participants

Three naive participants (aged 25–35 years, none of them were authors or neuroscientists) took part in the experiment. All participants were neurologically healthy, had normal or corrected to normal vision and gave their informed consent before participating. The study was approved by the institutional ethics committee. Each experiment took approximately 12 hr across 6 days (2 hr per day). As this experiment was particularly laborious we focus on within-participant analysis.

Experimental apparatus and setup

Request a detailed protocol

Participants sat 42 cm in front of a 17” Sony Multiscan G200 FD Trinitron CRT monitor (32-bit color, 1024x768 resolution, 100 Hz refresh rate). An EyeLink 1000 eye tracker was used to track the participant’s right eye position at 1000 Hz. A chin and forehead rest was used to stabilize the head.

Stimuli

Request a detailed protocol

Stimuli were generated such that the value of a pixel, $z$ , depended on its two-dimensional location, $x$ , through a function $z = f (x)$ sampled from a two-dimensional Gaussian process (Rasmussen and Williams, 2006) with zero mean and covariance function $K_{θ} (\cdot, \cdot)$ . The covariance function was squared-exponential and it was parameterized by $θ = {λ_{h}, λ_{v}}$ setting the image pattern’s horizontal and vertical correlation length scales, with the variance set to unity, such that the covariance of the pixel values at two positions, $x$ and $x^{'}$ (each two-dimensional), was:

K_{θ} (x, x') = e^{- \frac{1}{2} {(x - x^{'})}^{T} {[\begin{matrix} λ_{h}^{2} & 0 \\ 0 & λ_{v}^{2} \end{matrix}]}^{^{- 1}} (x - x^{'})}

For the patchy ( $PA$ ), stripy horizontal ( $SH$ ), and stripy vertical ( $SV$ ) pattern types the hyperparameters were $θ_{PA} = {{1.39}^{\circ}, {1.39}^{\circ}}$ , $θ_{SH} = {{4.63}^{\circ}, {0.91}^{\circ}}$ , and $θ_{SV} = {{0.91}^{\circ}, {4.63}^{\circ}}$ , respectively. Function values ( $z$ ) in the range $- 4$ to $4$ were mapped to image pixel colors so that the extremes corresponded to pure red (RGB value [1, 0, 0]) and blue ([0, 0, 1]), with intermediate values being linearly interpolated in RGB space. Functions which had values outside [ $- 4$ , $4$ ] were discarded and a new function was generated. The images were sampled over a grid of 77 $\times$ 77 locations subtending ${27.8}^{\circ}$ at the eye in the horizontal and vertical dimensions and then supersampled, using 2D splines, up to a resolution of 770 $\times$ 770 pixels (this allowed images to be generated rapidly without compromising visual appearance). On each trial, a pattern category $c$ , that was patchy ( $P$ ) or stripy ( $S$ ), was chosen with equal probability and if the stripy category was chosen then a horizontal or vertical pattern type was chosen with equal probability. Having two different types within the stripy pattern category ensured that the optimal scan path depended on the image (otherwise, always scanning in one direction where the length scales were different would be optimal).

Task

The task on each trial was for participants to determine whether a pattern displayed on the monitor was patchy or stripy (irrespective of whether it was vertical or horizontal) under different experimental conditions. The experiment consisted of four conditions: training, free-scan familiarization, free-scan, and passive revealing.

Training (8 sessions $\times$ 40 trials)

Request a detailed protocol

Participants triggered the start of each trial by fixating (within 1.5° for 500 ms) a cross centered on the screen, at which point the cross disappeared. An image was displayed centered on the location of the fixation cross, and participants had to decide whether the image was patchy or stripy. They were allowed to scan the image freely for up to 10 s and make their decision by fixating (within 2.8° for 800 ms) on one of the two choice letters, P or S, which were displayed to the left and right of the displayed image, respectively. Participants received audio feedback as to the correctness of their choice. Twenty images from each category were presented in a randomized order. The training sessions ensured that participants could learn the statistics of the image patterns. Categorization performance was perfect in training sessions for all participants.

Free-scan familiarization (5 sessions $\times$ 40 trials)

Request a detailed protocol

Each trial started with participants fixating a center cross. A randomly generated image from one of the categories was then displayed but initially completely obscured by a black mask. Participants could freely scan the display, and wherever they fixated, the underlying image was revealed by unmasking a small aperture at the fixation location. This was achieved by revealing an isotropic Gaussian region with standard deviation 0.18° at the fixation location, with the values of the Gaussian used to interpolate linearly between complete transparency (alpha=0) at the maximum of the Gaussian and black (alpha=1) where the value of the Gaussian is 0. A new fixation was detected, and hence a new revealing triggered, when the following three criteria were met: 1) a saccade had occurred since the last fixation as determined by eye speed greater than 59° s $^{- 1}$ ; 2) the displacement from the previous fixation was greater than 0.59°; and 3) the standard deviation of the eye position was less than 0.28° for the last 100 ms. These parameters were based on pilot experiments with the aim of making the revealings in the free-scan session feel natural so that each location viewed was revealed and spurious locations were not revealed. Participants were required to make 25 fixations before making their decision. After the 25 revealings, the category choices appeared (P vs. S) and participants had 60 s to choose a category with the revealed locations remaining on the display. Upon answering, participants were shown the full image with audio feedback. All participants achieved an average performance of 70% accuracy or higher.

Free-scan (6 sessions $\times$ 100 trials)

Request a detailed protocol

Free-scan trials were exactly the same as free-scan familiarization trials except that the number of revealings across trials was chosen randomly on each trial from 5 to 25 in steps of 5 (balanced) and was a priori unknown to the participants. The choice letters, P and S, appeared after the given number of revealings and no new revealings occurred after this point. The unknown, random stopping number of revealings served to encourage participants to be greedy in their information seeking.

Passive revealing (8 sessions $\times$ 100 trials)

Request a detailed protocol

This session was the same as the free-scan session except that the revealing locations were pre-determined by an algorithm independent of participant’s eye movements and sequentially appeared at intervals of 400 ms (which was about the average interval between consecutive fixations in the free scan experiment: 408 ms, which in turn was very similar to the inter-saccadic intervals measured under natural viewing conditions in everyday tasks; Hayhoe et al., 2003; Land and Tatler, 2009). Participants were instructed to follow the revealings as much as possible and were allowed to scan the scene after all revealings had appeared until they made their category decision. The algorithm followed one of three strategies randomly chosen:

Random: revealing locations were drawn from a scene-centered isotropic Gaussian with standard deviation 9.27°. For comparison, participants’ revealing locations in the free-scan condition had an average location that was 0.05° from the center of the scene and had a standard deviation 4.50°. Revealing locations that fell outside the image were resampled;
Ideal BAS: revealing locations were generated by the BAS algorithm (see below). For establishing an upper bound on the informativeness of the optimal revealing locations, the algorithm was allowed to access the displayed, as opposed to perception noise-corrupted pixel values, and did not include prior biases and saccadic inaccuracies (see below).
Anti-BAS: revealing locations were generated by the BAS algorithm as above but as if it was observing a different image than the real one, which belonged to a wrong type. For example, if the real image belonged to type $SH$ , the revealing locations were generated based on an image from type $PA$ or $SV$ (randomly chosen).

We mixed the BAS and anti-BAS trials to ensure participants could not use the pattern of revealing locations (independent of pixel values) to infer the category of the underlying image. The experiment included 8 passive revealing sessions with a total of 200, 200, and 400 trials from strategy 1, 2, and 3, respectively. The trials were first randomly mixed then divided into 8 sessions.

The eye tracker was calibrated before each session (25-point calibration for the free-scan condition and 9-point calibration for the passive-revealing conditions). Drift correction was performed at the start of each trial after fixation on the center cross was achieved. Re-calibration was performed whenever participants reported that the revealing locations did not match where they fixated, whenever they could not trigger the start of a trial, or make their category choice by fixating.

Participants ran using the following schedule: day one, 3 training sessions intermixed with 5 free-scan familiarization sessions; day two and three, 1 training session and 3 free-scan sessions each; day four to six, 1 training session and 2 or 3 passive revealing sessions each. All the free-scan sessions came before any passive revealing sessions so as to avoid influencing participants’ choice of eye movements by our choice of passive revealing strategies.

As we wished to compare the active strategy with passive revealing we allowed participants to rescan the revealed locations after the final revealing but before making a decision. This was critical as in the passive revealing conditions, although participants may detect and follow the revealings, because they are small and dispersed, they need to scan the scene to find and view them all. Therefore, the reason for allowing additional time after the final revealing was so as to make sure they had a chance to extract as much information as they liked from the revealed locations (locations and pixel values). In order to make the conditions directly comparable, we followed the same procedure in the active condition. Thus, allowing a rescanning period was the only way we could make a fair comparison across conditions using our gaze contingent design, which in turn allowed fine control over the information participants could obtain by eye movements.

Crucially, our key interest was in where participants chose to fixate during the initial revealing period and not in the perception model. During the active condition, all the selection happened prior to the rescanning phase and participants did not know how many saccades they would be allowed so they still needed to be efficient in choosing revealing locations even if they could rescan them later. Therefore, as we were analyzing the initial scanning, the final rescanning simply equalized the information that could be extracted from each revealing for all conditions but it was unlikely to influence the initial selection. Although, it is theoretically possible that participants adopted a different eye movement strategy knowing they could freely re-visit already revealed locations, the rescanning control (described below) suggests that this was not the case (Figure 3—figure supplement 1).

To examine whether rescanning time had an effect on performance, we fit each participants choice accuracy as a logistic function (bounded between 0.5 and 1) of rescanning time. We allowed different shifts per condition (active, passive random, passive BAS) but the same slope parameter across conditions.

No-rescanning control

Request a detailed protocol

To directly examine whether the rescanning period allowed after the final revealing affected participants scanning strategy, we performed a control experiment with three additional naive participants. These participants performed the training, free-scan familiarization, and free-scan sessions as in the original experiment except that no rescanning after the final revealing was allowed. That is all revealings disappeared (i.e. display returned to a black screen) 350 ms after the saccade away from the final revealing and participants were required to indicate their choice.

The ideal observer model of the task

Request a detailed protocol

The ideal observer maintains and continually (after each observation) updates a posterior distribution over categories, $c \in {P,S}$ , given knowledge of the parameters defining each image type, $θ \in {θ_{PA}, θ_{SV}, θ_{SH}}$ , and data, $D = {z, x}$ , which is the set of perceived pixel values $z = {z_{1}, z_{2} \dots z_{L}}$ at the $L$ locations $x = {x_{1}, x_{2} \dots x_{L}}$ revealed in the trial so far:

ℙ (c = P | D) = \frac{ℙ (D | θ_{P A})}{ℙ (D | θ_{P A}) + \frac{1}{2} ℙ (D | θ_{S H}) + \frac{1}{2} ℙ (D | θ_{S V})}

ℙ (c = S | D) = 1 - ℙ (c = P | D)

ℙ (D | θ) = 𝒩 ⁢ (z; 0, K_{θ} (x, x) + σ_{p}^{2} I)

where $σ_{p}^{2}$ is the variance of the participant’s (Gaussian) perceptual noise on the pixel value, and $K_{θ} (x, x^{'})$ is a matrix with element $(i, j)$ being $K_{θ} (x_{i}, x_{j}^{'})$ (Equation 2). Note that the length scales of the three pattern types as assumed by the observer, $θ$ , need not necessarily be the same as those actually used to generate the images, and indeed we explore below variants of the model that differ in their assumptions about these length scales. For simplicity, the ideal observer model assumes a fixed extraction of information from each revealing and therefore does not include temporal factors such as fixation durations (i.e. perception noise in Equation 5 is constant).

The Bayesian active sensor model of eye movements

Request a detailed protocol

The Bayesian active sensor (BAS) algorithm computes a score, the expected reduction in entropy of the distribution over categories as a function of a possible next revealing location, $x^{*}$ , and chooses the next fixation to be at the location with the highest score. The score is defined as

Score (x^{*} | D) = H [c | D] - {⟨ H [c | z^{*}, x^{*}, D] ⟩}_{ℙ (z^{*} | x^{*}, D)}

where $z^{*}$ is a possible (and as yet, unobserved) pixel value at $x^{*}$ , and $H [\cdot]$ denotes entropy in bits. Using the insight that the BAS score formally expresses the mutual information between $c$ and $z^{*}$ (for the given $x^{*}$ ), Equation 6 can be rewritten in a different form that is computationally far more convenient, as it does not require expensive posterior updates for a continuum of imaginary data, $z^{*}$ , to compute $ℙ (c | z^{*}, x^{*}, D)$ for the second term (Houlsby et al., 2011):

Score (x^{*} | D) = H [z^{*} | x^{*}, D] - {⟨ H [z^{*} | x^{*}, c, D] ⟩}_{ℙ (c | D)}

This form (equivalent to Equation 1) is also more plausible psychologically as it is easily approximated by simple mental simulation for a few hypotheses sampled from the current posterior. Note that maximizing just the first term would be equivalent to “maximum entropy sampling” (Sebastiani and Wynn, 2000) which is suboptimal in general, and in the context of our task would be similar to simple “inhibition of return” which does not account well for participants’ fixations (Figure 4B). The two distributions needed for evaluating Equation 7 are the current posterior over categories, $ℙ (c | D)$ , and the predictive distribution of the pixel value at a location for a category, $ℙ (z^{*} | x^{*}, c, D)$ . (Note that the predictive distribution in the first term can also be computed using these two distributions: $ℙ (z^{*} | x^{*}, D) = {⟨ ℙ (z^{*} | x^{*}, c, D) ⟩}_{ℙ (c | D)}$ .) The category posterior is given by Equation 3-5 and the category-specific predictive distribution is (Rasmussen and Williams, 2006):

ℙ (z^{*} | x^{*}, c = P, D) = ℙ (z^{*} | x^{*}, θ_{PA}, D)

P (z^{*} | x^{*}, c = S, D) = \frac{P (D | θ_{SV})}{P (D | θ_{SV}) + P (D | θ_{SH})} P (z^{*} | x^{*}, θ_{SV}, D) + \frac{P (D | θ_{SH})}{P (D | θ_{SV}) + P (D | θ_{SH})} P (z^{*} | x^{*}, θ_{SH}, D)

with

ℙ (z^{*} | x^{*}, θ, D) = 𝒩 (z^{*}; K_{θ} (x^{*}, x) {[K_{θ} (x, x) + σ_{p}^{2} I]}^{- 1} z, K_{θ} (x^{*}, x^{*}) - K_{θ} (x^{*}, x) {[K_{θ} (x, x) + σ_{p}^{2} I]}^{- 1} K_{θ} (x, x^{*}) + σ_{p}^{2})

For all simulations, we computed the BAS score on a 110 $\times$ 110 grid of $x^{*}$ that covered the image. The entropies of the predictive distributions (which are mixtures of Gaussians) in Equation 7 were approximated by their Jensen lower bound for efficiency (Huber et al., 2008).

Importantly, at least in principle, the ideal observer and BAS algorithms can be generalised to more complex stimuli as long as their statistics are known and can be expressed as $ℙ (z_{1}, \dots, z_{n} | x_{1}, \dots, x_{n}, c)$ .

Saccadic variability and bias

Request a detailed protocol

Due to the gaze-contingent design of our experiment, most saccades were made towards locations without any visible target. Saccades are known to be variable and biased, and to incorporate this variability and bias into our model we measured saccadic variability and bias in an independent experiment with 6 participants (including two from the main experiment) under similar conditions to those in the free-scan session of the main experiment. Although in the main experiment participants chose the location they wished to saccade to, to reliably measure saccadic variability and bias we needed to know the target of the saccade but not display it. Therefore we first trained participants on the locations of two saccadic targets and that on each trial the color of a stimulus shown at the fixation point indicated to which of these they needed to saccade. The two targets were at equal eccentricity from the fixation point, one to the right and one above it. On each training trial, participants first fixated a central fixation cross. Then two isotropic Gaussian patches (SD 0.18° as in the main experiment) appeared, one at the fixation location and one at one of the two target locations. The color of the fixation patch determined where the eccentric target was, either to the right (red) or above (blue), and participants were informed that the relation between the fixation color and the target direction was fixed throughout the experiment. To ensure that participants paid attention to the target, they were asked to report the color of the eccentric target which could either be red or blue. Note that this task by itself did not necessarily require them to saccade to the target, to avoid overtraining on particular saccades, but ensured that they developed a strong association between the color of the central fixation stimulus and the location of the target on that trial, such that in the next phase we could instruct them to saccade to a particular target without showing it. A training session of 40 trials was performed for each target eccentricity tested (1.39, 2.78, 5.56 and 8.34° in this order) with each session followed by a test session of 100 trials with the same eccentricity.

In the test sessions, only the fixation patch appeared and its color determined which target the participant should make an eye movement to. As in the free-scan sessions, a patch was revealed wherever the participant fixated, and their task was to report the target’s color. However, as this first eye movement was often inaccurate (see below) it did not necessarily reveal the target which needed to be reported. Thus, to motivate participants by making the task feasible, they were allowed to make four additional eye movements, leading to more revealings, before reporting the color of the target. (Although they were allowed 5 revealings, they were instructed to be as accurate as possible with their first eye movement.) The entire image was then shown as feedback.

To estimate saccadic variability and bias we used only the first saccade after fixation. We removed trials in which participants did not accurately maintain fixation (drift of >0.56°) or where they clearly mis-directed their saccade (saccade was closer to the non-cued target). We calculated the bias and standard deviation (robust estimate from the median absolute deviation) both along (tangential) and orthogonal (SD only) to the direction of the target. We fit the bias and SD as a linear function of target distance for both the tangential and orthogonal components for each participant (Figure 3—figure supplement 2). We averaged the model parameters across the participants and used these values to corrupt the desired saccade locations in the BAS simulations (unless otherwise noted).

Model parameters and data fitting

Request a detailed protocol

To match empirical data collected from our participants, we included perception noise, decision noise, and potential prior biases in the ideal observer model.

To model perception noise, we added Gaussian noise (SD $σ_{p}$ ) to the displayed pixel values to obtain z, which was either fit to individual participants’ categorization data (see below), or set at $σ_{p} = 0.17$ for computing the BAS score (in Equations 5 and 10) when determining ideal BAS revealings in passive revealing sessions. The ideal observer model then received these noisy pixel values as input instead of the pixel values actually shown to the participants.

To incorporate decision noise, the category posterior of Equation 3-4 was transformed by a softmax function to obtain the probability of choosing the patchy category:
$\hat{ℙ} (c = P | D) = (1 - κ) \frac{1}{1 + e^{- β LPR (D)}} + \frac{κ}{2}$
where $κ$ describes the stimulus-independent decision noise and can be interpreted as the lapse rate, $β$ is the stimulus-dependent decision noise (larger values of $β$ result in more deterministic behavior and lower values in more random behavior), and $LPR (D) = \log \frac{ℙ (c = P | D)}{ℙ (c = S | D)}$ is the log posterior ratio under the ideal observer model (Equation 3–4).

To model prior biases, i.e. imperfect knowledge of the stimulus statistics, we considered three qualitatively different ways in which participants could misrepresent the length scales used to generate the stimuli (6 length scales for three types of stimulus and 2 directions):
1. no prior biases, i.e. the length scales used by the model were identical to those actually used to generate the stimuli;
2. a uniform scaling of all length scales relative to their true values, $α$ ;
3. a fixed offset of all length scales from their true values, $Δ$ ;Thus, the last two models has a single parameter controlling the relation between the extent of misrepresentation.

For a systematic model comparison, we constructed a set of models which all included perception noise ( $σ_{p}$ ) and stimulus-dependent decision noise ( $β$ ) and differed in whether they also included stimulus-independent decision noise ( $κ$ ) and which of the three prior biases they had (none, $α$ , or $Δ$ ). This gave six models and for each we fit all the free parameters on the combined category choice data (from both the free-scan and passive revealing conditions) of each participant using maximum likelihood.

In order to fit the models to empirical data, we needed to take into account that the ideal observer was conditioned on the perceived pixel values, which were noisy versions of the pixel values actually displayed (corrupted by perception noise) and were thus unknown to us. Thus, we integrated out the unknown perceived pixel values in order to compute the actual choice probabilities predicted by the model (Houlsby et al., 2013). This was approximated by a Monte Carlo integral, by simulating each trial 500 times, drawing random samples of the perceived pixel values given the displayed pixel values from the perceptual noise distribution for each revealing. In each simulated trial, we then computed the probability of a participant’s choice according to Equation 11, and finally averaged over simulations to obtain the expected probability of each response category in that trial. For optimizing the values of $σ_{p}$ and the parameters for prior bias, $α$ and $Δ$ , we conducted a grid search with a resolution $0.1$ , $0.1$ , and ${0.01}^{\circ}$ , respectively. For each setting of these parameters, we optimized $β$ and $κ$ (when used) using gradient-based search so that all the parameters were jointly optimized. Table 1 shows the best fit parameters. We used the Bayesian information criterion (computed across all participants) to compare the models by controlling for their differing number of free parameters and chose the best one (Table 2).

We used the BAS algorithm to predict the pattern of eye movements for each participant individually given the values of $σ_{p}$ and $Δ$ fitted to their categorization choices and the measured saccadic inaccuracies. This meant that once we fitted categorization choices, eye movements were predicted without any further tuning of parameters. Note that $β$ and $κ$ affected only choice probabilities in the categorization decision process, not the eye-movement selection process described by Equation 1.

Revealing densities

Request a detailed protocol

As the statistics of stimuli were translationally invariant, the critical features of the optimal solution was the relative locations of the revealing to each other. Therefore, for each trial we first shifted all the revealing locations in that trial equally so that their mean (centre of mass) was located at the centre of the image, thereby removing the variability caused by which part of the image the participants explored in that trial, which was irrelevant to optimality. We then computed the mean density maps by assigning the revealing locations to centers of a 770 $\times$ 770 grid of bins (the resolution of the images), normalizing the counts, and smoothing the distribution with an isotropic Gaussian filter (std. of 20 bins, ie. $\sim {0.73}^{\circ}$ ). For a balanced comparison, we computed densities as if each trial had 25 revealings and the three underlying patterns were chosen with equal probability. To achieve this we multiplied the count for the n^th revealings by both the relative frequency of first revealings to n^th revealings and by the inverse of the frequency of the image type. For each participant, we computed the mean density map across all trials (Figure 3A first column) and the mean-corrected density map for each underlying image type (Figure 3A last three columns) by removing the mean from those averaged for each image type. The density maps for BAS were generated with simulations that used the same trials (image and number of revealings) that the participants performed. We repeated the simulation of each trial 10 times to obtain a reliable Monte Carlo estimate of the BAS revealing density maps marginalized over the unknown perceived pixel values.

Correlation analysis

Request a detailed protocol

To examine whether the participants’ pattern of eye movements depended on the underlying image, and hence what they saw at the revealing locations, we compared correlations between mean-corrected density maps within and across image types for each participant. In computing the correlation as a function of revealing number, we kept the number of samples used to construct the maps constant. This number of samples was chosen to be the maximum number that still allowed the image type and revealing number to be sampled with equal probability without replacement. To increase the sample size for all revealings we only examined revealings from 5 onwards. For the bar plots, we used about 3 times the number of samples, but weighted each revealing so that the maps were still effectively constructed with an equal number of samples from each revealing number.

To obtain statistics of the correlations, we split the revealing locations for an image type randomly into two data sets of equal size. This produced 6 different data sets (two for each image type). For within-type correlations, we computed the three correlations (using a Gaussian smoothing kernel with ${1.5}^{\circ}$ SD) between the mean-corrected maps of the same image types, and averaged these three correlations across the three image types to obtain a single within-type correlation value. Similarly, for across-type correlations, we computed the six correlations between the mean-corrected maps of different image types (across the two different halves of the split), and averaged these six correlations to obtain a single across-type correlation value. We repeated this procedure 1000 times, using a different random split of the data each time, to obtain the means, SD, and 95% confidence intervals (Figure 3B).

We also performed the same analysis on the three participants’ pooled data, treating the ensemble as data from an 'average' participant. Here the data sets used to calculate the density maps were thus three times larger than those for the individuals. These results together are shown as participant-self correlations (Figure 3B, left). We applied the same approach to compute participant-BAS correlations. For this, participant- as well as BAS-generated revealing location data were each randomly split in half (as above), and correlations were always computed between a participant- and a BAS-generated data set (Figure 3B, right).

The correlation between the eye movement patterns derived from correct / incorrect trials and that from BAS was calculated in the same way described above, but only for the 'average' participant as the number of incorrect trials was limited. The p-value reported is the fraction of bootstrapped samples that satisfied the condition $ρ_{correct} \leq ρ_{incorrect}$ .

Information gain and efficiency

Request a detailed protocol

According to the ideal observer, at any point in a trial, the information gain associated with the set of revealings made thus far is defined as $1 - H [c | D]$ . As described above (Model parameters and data fitting), since we only knew the displayed but not the perceived pixel values, we used Monte Carlo integration to marginalize out the unknown perceived pixel values. To do this, we simulated each experiment 200 times using the parameters of the best fit model, drawing new samples of perceived values for the chosen revealing locations given the displayed pixel values, and then averaged the information gains across runs and trials. Figure 5A shows the average information gain as a function of revealing number across the 200 simulations with the average across-trial SEM for each revealing strategy. To characterize the efficiency of each strategy, $s$ , we fit the information vs. revealing number curves from each simulation obtained with the above analysis using a cumulative Weibull distribution: $I_{s} (n) = 1 - \exp (- {(\frac{n}{a_{s}})}^{b})$ , where $n$ is the revealing number, $b$ is a shape parameter shared across strategies (free-scan, passive random, passive ideal BAS, and simulated BAS), and $a_{s}$ is a strategy-specific scale parameter, which captures the overall efficiency of the strategy. As a relative measure of efficiency for comparing any two strategies, we computed the ratio of their $a_{s}$ , and obtained 95% confidence intervals by using the 200 simulations as bootstrap samples.

Heuristics

Request a detailed protocol

To address whether a heuristic algorithm could account for participants’ eye movement patterns, we computed the information gains achieved using several heuristics.

Posterior-independent & order-dependent fixations (Figure 5B, orange). For each participant, the fixation location on the i^th revealing was obtained by sampling (with replacement) from fixation locations pooled across their i^th revealing of all free-scan trials, regardless of the underlying image pattern and the ensuing posterior. This feed-forward strategy respects the participant’s average order-dependent fixation map, but is otherwise based on a set of pre-determined fixation locations rather than on what was observed about the actual scene.
Posterior-dependent & order-independent fixations (Figure 5B, purple). For each participant, the fixation location on the i^th revealing was obtained by first computing the likelihood $ℙ (D | θ)$ , where $D$ included the i revealing locations and pixel values observed up to this revealing, finding the type that had the maximum posterior probability, and then sampling from the fixation locations pooled across trials with that image type as the underlying image pattern. This strategy uses the observations only indirectly, through the posterior, but does not otherwise take into account previous fixation locations and the corresponding pixel values for evaluating the informativeness of potential new revealing locations.
Posterior- & order-dependent fixations (Figure 5B, brown). This combined order-dependence, as in the 1st heuristic, with posterior-dependence, as in the 2nd, but still did not take into account previous fixation locations and the corresponding pixel values. While this strategy would be optimal for simpler stimuli, in which pixels are independent for each image category, or simpler tasks, such as visual search, in which knowledge of the task-relevant posterior (eg. target location) is sufficient for optimal action, it is suboptimal with the kind of naturalistic stimuli and task we used.

References

(1995) Memory representations in natural tasks
Journal of Cognitive Neuroscience 7:66–80.
https://doi.org/10.1162/jocn.1995.7.1.66
- PubMed
- Google Scholar
1. Borji A
2. Itti L
(2013)
Advances in Neural Information Processing Systems 26

55–63, Bayesian optimization explains human active search, Advances in Neural Information Processing Systems 26, NIPS.
- Google Scholar
1. Castro RM
2. Kalish C
3. Nowak R
4. Qian R
5. Rogers T
6. Zhu X
(2009)
Advances in Neural Information Processing Systems 21

241–248, Human active learning, Advances in Neural Information Processing Systems 21, NIPS.
- Google Scholar
(2013) Learning where to look for a hidden target
Proceedings of the National Academy of Sciences of the United States of America 110:10438–10445.
https://doi.org/10.1073/pnas.1301216110
- Google Scholar
1. Epelboim J
2. Suppes P
(2001) A model of eye movements and visual working memory during problem solving in geometry
Vision Research 41:1561–1574.
https://doi.org/10.1016/S0042-6989(00)00256-X
- PubMed
- Google Scholar
1. Field DJ
(1987) Relations between the statistics of natural images and the response properties of cortical cells
Journal of the Optical Society of America A 4:2379–2394.
https://doi.org/10.1364/JOSAA.4.002379
- PubMed
- Google Scholar
1. Geisler WS
(2011) Contributions of ideal observer theory to vision research
Vision Research 51:771–781.
https://doi.org/10.1016/j.visres.2010.09.027
- PubMed
- Google Scholar
1. Gosselin F
2. Schyns PG
(2001) Bubbles: a technique to reveal the use of information in recognition tasks
Vision Research 41:2261–2271.
https://doi.org/10.1016/S0042-6989(01)00097-9
- PubMed
- Google Scholar
Book
1. Gureckis TM
2. Markant D
(2009)
Active learning strategies in a spatial concept learning game

In: TaatgenN, van Rijn H, Schomaker L, Nerbonne J, editors. Proceedings of the 31st Annual Conference of the Cognitive Science Society. Austin, TX: Cognitive Science Society. pp. 3145–3150.
- Google Scholar
1. Hayhoe M
2. Ballard D
(2005) Eye movements in natural behavior
Trends in Cognitive Sciences 9:188–194.
https://doi.org/10.1016/j.tics.2005.02.009
- PubMed
- Google Scholar
(2003) Visual memory and motor planning in a natural task
Journal of Vision 3:6–63.
https://doi.org/10.1167/3.1.6
- PubMed
- Google Scholar
(2012) Object learning improves feature extraction but does not improve feature selection
PloS One 7:e51325.
https://doi.org/10.1371/journal.pone.0051325
- PubMed
- Google Scholar
(2011)
arXiv

p. 1112.5745, Bayesian active learning for classification and preference learning, arXiv.
- Google Scholar
(2013) Cognitive tomography reveals complex, task-independent mental representations
Current Biology 23:2169–2175.
https://doi.org/10.1016/j.cub.2013.09.012
- PubMed
- Google Scholar
(2008)
IEEE International Conference on Multisensor Fusion and Integration forIntell. Syst

181–188, On entropy approximation for Gaussian mixture random vectors., IEEE International Conference on Multisensor Fusion and Integration forIntell. Syst, IEEE MFI.
- Google Scholar
1. Itti L
2. Koch C
(2000) A saliency-based search mechanism for overt and covert shifts of visual attention
Vision Research 40:1489–1506.
https://doi.org/10.1016/S0042-6989(99)00163-7
- PubMed
- Google Scholar
1. Klein RM
(2000) Inhibition of return
Trends in Cognitive Sciences 4:138–147.
https://doi.org/10.1016/S1364-6613(00)01452-2
- PubMed
- Google Scholar
(2006) Active sensation: insights from the rodent vibrissa sensorimotor system
Current Opinion in Neurobiology 16:435–444.
https://doi.org/10.1016/j.conb.2006.06.009
- PubMed
- Google Scholar
1. Ko HK
2. Poletti M
3. Rucci M
(2010) Microsaccades precisely relocate gaze in a high visual acuity task
Nature Neuroscience 13:1549–1553.
https://doi.org/10.1038/nn.2663
- PubMed
- Google Scholar
(2010) Visual fixations and the computation and comparison of value in simple choice
Nature Neuroscience 13:1292–1298.
https://doi.org/10.1038/nn.2635
- PubMed
- Google Scholar
1. Kuang X
2. Poletti M
3. Victor JD
4. Rucci M
(2012) Temporal encoding of spatial information during active visual fixation
Current Biology 22:510–514.
https://doi.org/10.1016/j.cub.2012.01.050
- PubMed
- Google Scholar
Book
1. Land M
2. Tatler B
(2009) Looking and Acting: Vision and Eye Movements in Natural Behaviour
Oxford University Press.
https://doi.org/10.1093/acprof:oso/9780198570943.001.0001
- Google Scholar
1. Lederman SJ
2. Klatzky RL
(1987) Hand movements: a window into haptic object recognition
Cognitive Psychology 19:342–368.
https://doi.org/10.1016/0010-0285(87)90008-9
- PubMed
- Google Scholar
1. Levi DM
(2008) Crowding–an essential bottleneck for object recognition: a mini-review
Vision Research 48:635–654.
https://doi.org/10.1016/j.visres.2007.12.009
- PubMed
- Google Scholar
1. Li FF
2. VanRullen R
3. Koch C
4. Perona P
(2002) Rapid natural scene categorization in the near absence of attention
Proceedings of the National Academy of Sciences of the United States of America 99:9596–9601.
https://doi.org/10.1073/pnas.092277599
- Google Scholar
1. MacKay DJC
(1992) Information-based objective functions for active data selection
Neural Computation 4:590–604.
https://doi.org/10.1162/neco.1992.4.4.590
- Google Scholar
(2011) Competition for visual selection in the oculomotor system
Journal of Neuroscience 31:9298–9306.
https://doi.org/10.1523/JNEUROSCI.0908-11.2011
- PubMed
- Google Scholar
(2012) Human visual search does not maximize the post-saccadic probability of identifying targets
PLoS Computational Biology 8:e1002342.
https://doi.org/10.1371/journal.pcbi.1002342
- PubMed
- Google Scholar
1. Najemnik J
2. Geisler WS
(2005) Optimal eye movement strategies in visual search
Nature 434:387–391.
https://doi.org/10.1038/nature03390
- PubMed
- Google Scholar
1. Najemnik J
2. Geisler WS
(2008) Eye movement statistics in humans are consistent with an optimal search strategy
Journal of Vision 8:4–14.
https://doi.org/10.1167/8.3.4
- PubMed
- Google Scholar
(2010) Optimal reward harvesting in complex perceptual environments
Proceedings of the National Academy of Sciences of the United States of America 107:5232–5237.
https://doi.org/10.1073/pnas.0911972107
- Google Scholar
1. Nelson JD
2. Cottrell GW
(2007) A probabilistic model of eye movements in concept formation
Neurocomputing 70:2256–2272.
https://doi.org/10.1016/j.neucom.2006.02.026
- PubMed
- Google Scholar
1. Oliva A
2. Torralba A
(2006) Building the gist of a scene: the role of global image features in recognition
Progress in Brain Research 155:23–36.
https://doi.org/10.1016/S0079-6123(06)55002-2
- PubMed
- Google Scholar
1. Peterson MF
2. Eckstein MP
(2012) Looking just below the eyes is optimal across face recognition tasks
Proceedings of the National Academy of Sciences of the United States of America 109:E3314–E3323.
https://doi.org/10.1073/pnas.1214269109
- Google Scholar
(2013) Microscopic eye movements compensate for nonhomogeneous vision within the fovea
Current Biology 23:1691–1695.
https://doi.org/10.1016/j.cub.2013.07.007
- PubMed
- Google Scholar
Book
1. Rasmussen CE
2. Williams CKI
(2006)
Gaussian Processes for Machine Learning

Cambridge, MA: MIT Press.
- Google Scholar
(2007) Where to look next? Eye movements reduce local uncertainty
Journal of Vision 7:6–17.
https://doi.org/10.1167/7.3.6
- PubMed
- Google Scholar
1. Rolfs M
(2009) Microsaccades: small steps on a long way
Vision Research 49:2415–2441.
https://doi.org/10.1016/j.visres.2009.08.010
- PubMed
- Google Scholar
(2007) Task and context determine where you look
Journal of Vision 7:16–20.
https://doi.org/10.1167/7.14.16
- PubMed
- Google Scholar
1. Rucci M
2. Iovin R
3. Poletti M
4. Santini F
(2007) Miniature eye movements enhance fine spatial detail
Nature 447:852–855.
https://doi.org/10.1038/nature05866
- PubMed
- Google Scholar
(2012) Dynamic integration of information about salience and value for saccadic eye movements
Proceedings of the National Academy of Sciences of the United States of America 109:7547–7552.
https://doi.org/10.1073/pnas.1115638109
- Google Scholar
1. Sebastiani P
2. Wynn HP
(2000) Maximum entropy sampling and optimal Bayesian experimental design
Journal of the Royal Statistical Society: Series B 62:145–157.
https://doi.org/10.1111/1467-9868.00225
- Google Scholar
1. Tatler BW
2. Vincent BT
(2008)
Systematic tendencies in scene viewing

Journal of Eye Movement Research 2(2):5.
- Google Scholar
1. Tatler BW
2. Vincent BT
(2009) The prominence of behavioural biases in eye guidance
Visual Cognition 17:1029–1054.
https://doi.org/10.1080/13506280902764539
- Google Scholar
1. Thorpe S
2. Fize D
3. Marlot C
(1996) Speed of processing in the human visual system
Nature 381:520–522.
https://doi.org/10.1038/381520a0
- PubMed
- Google Scholar
(2013) Optimal sampling of visual information for lightness judgments
Proceedings of the National Academy of Sciences of the United States of America 110:11163–11168.
https://doi.org/10.1073/pnas.1216954110
- Google Scholar
1. Wismeijer DA
2. Gegenfurtner KR
(2012) Orientation of noisy texture affects saccade direction during free viewing
Vision Research 58:19–26.
https://doi.org/10.1016/j.visres.2012.02.003
- PubMed
- Google Scholar
Book
1. Yarbus AL
(1967) Eye Movements and Vision
Boston, MA: Springer US.
https://doi.org/10.1007/978-1-4899-5379-7
- Google Scholar

Decision letter

Doris Y Tsao

Reviewing Editor; California Institute of Technology, United States

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your work entitled "Active sensing in the categorization of visual patterns" for consideration by eLife. Your article has been favourably reviewed by three peer reviewers, one of whom is a member of our Board of Reviewing Editors. The evaluation has been overseen by this Reviewing Editor and Eve Marder as the Senior Editor.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Having conferred about this paper, we agree that it is acceptable for publication pending revision. However, there was an extended discussion among the reviewers about the extent to which the current results apply to natural vision. The reviewers agree that the authors need to qualify their conclusions to clearly state that while they were trying to emulate natural vision, their task was unnatural in several important ways (e.g. very small exposures, uniform statistics, small saccades not allowed, and reviewing for up to 60s after presentation in the passive conditions), all of which may have changed the participants' strategy from that used in natural vision. Natural vision works under entirely different constrains – larger exposures, natural scene statistics, all saccades allowed, and limited time. Under these constrains the selection of targets may (or may not) be completely different. These differences between the paradigm used in the study and natural vision should be carefully discussed, and relevant parts of the Abstract and Discussion should be modified accordingly.

[Editors’ note: a previous version of this study was rejected after peer review, but the authors submitted for reconsideration. The previous decision letter after peer review is shown below.]

Thank you for choosing to send your work entitled "Active sensing in the categorization of visual patterns" for consideration at eLife. Your full submission has been evaluated by Eve Marder (Senior editor) and three peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the decision was reached after discussions between the reviewers. Based on our discussions and the individual reviews below, we regret to inform you that your work will not be considered further for publication in eLife.

While all of the reviewers appreciated the significance of the work, they were very concerned about potential confounds due to letting subjects continue viewing the display for 60s after the last revealing. Given this confound, the reviewers were not certain that a revision would adequately deal with this problem, which led to the decision to reject the paper at this time. If you feel you can adequately answer the concerns of this review, the reviewers were sufficiently potentially positive about your manuscript that eLife would allow a submission of a new manuscript that addresses these concerns.

Reviewer #1:

Summary

The present work utilizes an innovative gaze-contingent paradigm where subjects have to identify the category of a texture and can actively reveal locations based on where they saccade to. The authors compare the fixation density maps for the three different stimulus categories and find that they are consistent and category-specific across participants, i.e. each stimulus category evokes a specific pattern of fixations. When revealing locations randomly controlled by the computer the categorization performance decreases indicating that active sensing does increase the information yield for the participants. Next, they construct an ideal observer model that computes the posterior probability of each category given the revealed pixel values, and fit the parameters prior bias, perception noise and decision noise to predict the subject's choice of category. Based on these parameters fitted to the subject's category choice the authors try to predict saccade choices using a Bayesian active sensor algorithm which chooses the saccade location which maximizes the expected information gain, taking into account saccade inaccuracies. They claim that the subject's saccades are predicted well by their Bayesian active sensor algorithm, as the predicted category-specific fixation density maps are significantly correlated with the actual density maps. As a better measure of the goodness of their model they compare the information (in the ideal observer sense) gained by the subject's saccades to the information gained by their simulated saccades, random saccades and saccades based on other strategies. They find that the information gained by the subject's saccades is higher than random saccades and saccades based on three heuristic strategies but lower than the information of the saccades simulated by the Bayesian active sensor, even if prior bias, perception noise and category decision noise are taken into account. They call the latter discrepancy a 30% inefficiency of saccade choice. To show that the saccade choices made by the subject are indeed not optimal in efficiency of making the category choice, they reveal the fixation locations computer-controlled based on the optimal locations predicted by the active Bayesian sensor model without biases and low noise. Thereby, the subject's categorization performance is increased. The efficiency of saccade choice does not vary over time, so there does not appear to be any learning.

Remarks

1) In Figure 1, it is not clear to me, why the patch surrounded by the red circle should have more information about zebra vs. cheetah than other blue patches, so maybe use a better example.

2) In Figure 2C, the blue condition titled Random should be called passive or computer-controlled random locations to avoid confusion. Also, please clarify the term "gaze-contingent".

3) In Formula 1, D is not defined.

4) Regarding Figure 4B, I don't understand why the first term of the formula isn't maximal at locations as far as possible from previous locations (i.e. on the borders of the image). Given that spatial correlations of the stimulus decrease with distance, the uncertainty about pixel values at a far distance from known pixel values should be highest.

5) The correlation analysis done in Figure 3 should be repeated with simulated entropy-maximizing saccades, to show that the correlation analysis is meaningful. Just correlating the fixation density maps might not be the best measure to evaluate fit of the simulation, since it does not consider each fixation on a case-by-case basis given the prior information from previous saccades.

6) In addition to the BIC it would be nice to know the cross-validated prediction accuracy of category choice on a testing set.

7) Also, when showing the performance decrease when revealing at random locations, I would have matched the inter-saccadic distribution (including the variance) and the saccadic distance distribution, to ensure the performance decline is not due to the variance in fixation duration or the subject needing to recover from longer saccades.

Reviewer #2 (General assessment and major comments (Required)):

The paper addresses the strategy underlying the selection of gaze targets along the scanpath of fixations. Specifically, the paper compares human selections and performances with those of an optimal Bayesian algorithm. The authors conclude that while humans employ an information-based strategy, this strategy is sub-optimal. They also identify the sources of this sub-optimality and suggest that "participants select eye movements with the goal of maximizing information about abstract categories that require the integration of information from multiple locations".

This is potentially an important paper, which can contribute significantly to the understanding of perceptual processes. The topic is important, the work is, for the most part, elegant and the paper is in general well written. However, there are several crucial points that question the conclusions reached by the authors – these and other comments are listed below.

1) The authors employ a reductionist method, which is indeed necessary if one wants to reveal underlying mechanisms. However, some of the reductionist choices made in this work fuel the questioning of several of its conclusions. The most concerning reductionist steps are:

A) Small saccades (< 1 deg) were not allowed. The use of small ("micro") saccades is task dependent and it may be the case, for example, that with images like those used here a possible strategy is scanning a continuous region. This possibility was "reduced-out" here.

B) The exposed area was effectively < 0.5 deg and was scaled down in transparency from the center out – this reduced-out a meaningful drift-based scanning of the fixational region.

C) The images had uniform statistics, which preclude generalization to natural images.

The authors mention that "the task still allowed them to employ natural every-day eye movement strategies as evidenced by the inter-saccadic intervals (mean 408 ms) that were similar to those recorded for everyday activities […]" – evidently, normal ISIs do not indicate a natural strategy – a) there is much more into an active strategy and b) ISIs seems to be determined by hard-wired circuits that are only slightly modulated in different contexts – see a variety of tests of ISIs in the last decade.

2) The "last 60s" problem. Natural viewing involves a scanpath of fixations. However, natural viewing does not allow a re-scanning of the collection of previous fixation locations. The design of the trial is thus odd– why were the subjects given those extra 60s at the end of the trial to rescan their revealings? This is not justified in the paper and it is actually hidden, in a way, in the Materials and methods section – it took me some time to understand that this was the case. The implications of this design are significant:

A) How can the authors relate performance to either of the two different phases of the trial (the "acquiring" and the "rescanning")?

B) Even in the "acquiring" phase, how can the authors rule out brief rescanning of exposed revealings for periods shorter than the threshold period?

C) If performance depended on the perception during these 60s, then what was the underlying strategy while rescanning?

The authors must describe the procedure clearly at the outset, relate to all these issues explicitly, and explain how they affect (or not) their conclusions.

3) As indicated by the above, the primary characterization of the active strategy here is about which revealing were or should be selected, and less about when or in what order. True, order was a factor during the acquiring phase, but not during the rescanning phase. Order seems to play a role in the correlations in Figure 3B but it is not clear by how much. The collection of revealing locations may indeed be the most relevant factor when trying to categorize an image out of several known images with known structures. This is, however, not the case in most natural cases, in which real-time information is essential.

4) From the above and from further analysis it appears that the strong statements of the Abstract are not supported by the data in the paper.

A) "Categorization performance was markedly improved when participants were guided to fixate locations selected by an optimal Bayesian active sensor algorithm […]" – this statement sounds as if guiding the next saccade improves performance. This cannot be concluded here because of the "60 s problem" – during rescanning subjects could select any pattern they wanted. Moreover, performance may even depend on the rescanning period only.

B) "By using […] we show that a major portion of this apparent suboptimality of fixation locations arises from prior biases, perceptual noise and inaccuracies in eye movements[…]" – you do not really show this. You show that if you add these imperfections to your model you get performance level that resembles that of the subjects. However, there are so many ways to impair the performance of your model – where do you show that these are the crucial factors?

C) "The central process of selecting fixation locations is around 70% efficient" – this is correct only for the specific task and context of your experiment. The statement sounds much more general than that.

D) "Participants select eye movements with the goal of maximizing information about abstract categories that require the integration of information from multiple locations" – again, a statement with a general flavor without such justification – the statement should be toned and tuned down to reflect the narrow context of the findings.

5) Audience and style. As written now the paper seems to address experts in Bayesian models of perception. Given that it is submitted to eLife I assume that the paper should address primarily, or at least to the same degree, biologists who are interested in understanding perception. And indeed, papers like this form a wonderful opportunity to create a productive dialogue between biologists and theoreticians. For this end, the style of writing must change. The amount of statistical details should be reduced, the biological meaning of the various strategies discussed should be provided, the rational for selecting the BAS algorithm as the optimal strategy should be explained, the meaning of each strategy in terms of actual eye movements in natural scenes should be explained. At the end, the reader should understand the biological meaning of each strategy (that is, a biologically-plausible description of the strategy employed by their subjects in this task, and a strategy they would employ in a natural task), the rational of why one strategy is better than the other, and in what sense humans are sub-optimal.

6) The discussions about active-sensing in the paper are written as if they come from a sort of a theoretical vacuum. Active sensing has been introduced, studied and discussed at various levels for various species and modalities for years, and intensively so for the last decade or two. Nevertheless, the paper sounds as if these concepts are only beginning to be addressed, and as if active vision is mostly covered by addressing saccades scanpath selections. This introduces a huge distortion of the concepts of active sensing and active vision. Active vision is much more than scanpath selections. Eye movements include saccades and drifts, and as far as we know today vision does not occur without the drift movements. Saccades include large and small ("micro") saccades, making a continuous spectrum of saccade amplitudes. In this study only large (> 1 deg) saccades were allowed. Thus, this study ignores a substantial portion of visually-crucial eye movements. While this is ok as a reductionist method, it is not ok to ignore the reduced-away components in the discussion and interpretation of the results. Thus:

A) There is no justification to use the term "eye movements" in this paper – the components of eye movements studied here should be termed properly (perhaps use terms like "fixation scanpath" or "saccadic order" or anything else that is appropriate).

B) Previous results and hypotheses about active sensing/active vision that refer to all kinds of movements must be discussed and referred to when interpreting the current results.

C) The results of the current study should be put in the context of this general active sensing context, and the generality of the conclusions should be phrased accordingly – mostly, they should be toned down and related to the specific reduced context of this study.

Minor comments:

1) Arbitrary selection of parameters – please explain the choice of every parameter you use (e.g., the criteria for saccades and fixations).

2) Figure 3B – please run a shuffling control analysis to show how much of the correlation is order-dependent.

Reviewer #3:

The authors investigated the control of eye movements in a visual categorization task. By using a gaze-contingent paradigm, they could show that eye movement patterns became more specific to the underlying image structure with increasing fixation number. A comparison with a Bayesian active sensor (BAS) model showed that humans were quite efficient, given certain biases and inaccuracies of eye movements.

The study should be interesting to a broad audience and is well conducted. A few further analyses could strengthen the message.

2) Since there were a lot of incorrect judgments overall, it would be interesting to compare the density maps for correct and incorrect judgments. If eye movements are indeed controlled by an active strategy, the differences and correlations should be more pronounced for correct judgments.

3) The example trial in Figure 4 provides a good illustration of BAS and the maximum entropy variant but it does not allow a quantitative comparison. It would be helpful to show the full distributions of percentile values with respect to BAS and entropy scores.

4) As I understand the task, the revealings stayed on screen after the last revealing for 60 s or an unlimited duration, depending on the condition. The behavior of the subjects after the last revealing should be reported because it could have influenced their perceptual judgment.

https://doi.org/10.7554/eLife.12215.018

Author response

Thank you for the reviewers’ comments on our revised manuscript. We have now added in a whole section in the Discussion on the relation of our task and results to natural vision and discuss in detail the four issues raised by the reviewers. Some of these issues were discussed already in other parts of the paper such as the Methods but have now been put together in this section headed “Relevance for natural vision”.

[Editors’ note: the author responses to the previous round of peer review follow.]

All three reviewers were concerned that allowing additional time after the last revealing (rescanning period) was a confound in the experiment and undermined our conclusions. In fact the additional time is essential for the interpretation of the experimental results and does not affect our conclusions. We realise we did not highlight this sufficiently and have now done so in the revised manuscript.

1) As we wished to compare the active strategy with passive revealing we allowed participants to rescan the revealed locations after the final revealing but before making a decision. This was critical as in the passive revealing conditions, although participants may detect and follow the revealings, because they are small and dispersed, the participants need to scan the scene to find and view them all. Therefore, the reason for allowing additional time after the final revealing was so as to make sure they had a chance to extract as much information as they like from the revealed locations (locations and pixel values). In order to make the conditions directly comparable, we followed the same procedure in the active condition. Thus, allowing a rescanning period was the only way we could make a fair comparison across conditions using our gaze contingent design, which in turn allowed us fine control over the information participants could obtain by eye movements.

2) Critically, our key interest is in where participants choose to fixate during the initial revealing period and not in the perception model. During the active condition all the selection happens prior to the rescanning phase and participants do not know how many saccades they will be allowed so they still need to be efficient in revealing locations even if they can rescan them later. Therefore, as we are analyzing the initial selection, the final rescanning simply equalizes the information that can be extracted from each revealing for all conditions but it is unlikely to influence the initial selection. Although, it is theoretically possible that participants adopted a different eye movement strategy knowing they could freely re-visit already revealed locations, given the little improvement they showed across sessions in our task (Figure 7), this remains a highly unlikely possibility.

3) Although we allowed up to 60 s after the final revealing (we wished participants to feel that they had as long as they wanted), participants took on average only 5.0 s to make a decision in the active condition, 6.4 s in the passive random and 4.4 s in the passive BAS. We expected that participants would use rescanning time so that information extracted from the revealings would have saturated by the time of choice. To examine whether rescanning time had an effect on performance, we fit each participant’s choice accuracy as a logistic function (bounded between 0.5 and 1) of rescanning time. We allowed different shifts per condition (active, passive random, passive BAS) but the same slope parameter across conditions. This showed that for two participants there was a significant effect of rescanning time on performance (i.e. slope significantly different from zero) but with a decrement in performance for longer rescanning times. The probability of a correct decision for rescanning times at the 25th and 75th percentiles of the rescanning time distribution falls from 0.77 to 0.54 (p<0.001) and from 0.77 to 0.66 (p <0.03) for these two participants. We have included this information in the revision. Therefore, if anything, participants did not use longer rescanning times to improve performance but may have taken a little extra time when they were uncertain. In contrast, their performance correlated quite strongly with the number of revealings (Figure 2C). This indicates that the main determinant of their performance was how well they chose the revealing locations in the first place, rather than how long they rescanned the location, as our original results already showed.

4. To fully assuage the reviewers’ concerns we have now run a control experiment on 3 new participants in the active revealing condition except that no rescanning after the final revealing was allowed (all revealings returned to a black screen 350 ms after the saccade away from the final revealing). The results from this show that the revealing density maps are very similar to those from the original experiment (average within-type vs. across-type correlation across the two groups of participants: 0.63 vs. 0.30) and performance is also similar (although not surprisingly slightly worse). The proportion correct across all active revealing trials for the original participants was 0.65, 0.66 & 0.69 (average 0.66) and for the new controls 0.64, 0.58 & 0.66 (average 0.63). We include these new results in the paper and in a supplementary figure (Figure 2—figure supplement 1) and take them to indicate that allowing rescanning in our original design did not change participants’ revealing strategy.

In addition, we realized we could further improve our analysis of the revealing density maps. In particular, in our original analysis these maps were constructed using the absolute positions of revealings. However, the statistics of our stimuli are translationally invariant and therefore the critical features of the optimal solution are the relative locations of the revealing to each other. Therefore, for each trial we first shifted all the revealing locations in that trial equally so that their mean (centre of mass) was located at the centre of the image, thereby removing the variability caused by which part of the image the participants explored in that trial, which is irrelevant to optimality (due to the translationally invariant nature of the statistics of our images, see above). This analysis leads to much cleaner and more compelling maps and we have redone all analyses (correlations of revealing densities) based on these new densities. We checked that all conclusions (including those reported in the response to reviewers below) remained the same (although quantitatively stronger) compared to the original absolute location method.

Reviewer #1:

Remarks

1) In Figure 1, it is not clear to me, why the patch surrounded by the red circle should have more information about zebra vs. cheetah than other blue patches, so maybe use a better example.

We have modified this figure and legend to make the example more intuitive.

2) In Figure 2C, the blue condition titled Random should be called passive or computer-controlled random locations to avoid confusion. Also, please clarify the term "gaze-contingent".

We have relabelled Figure 2C and Figure 5A to explicitly show the passive and active conditions and modified the text to use consistent terminology where necessary. We have also added a phrase to clarify the term “gaze-contingent.”

3) In Formula 1, D is not defined.

D was actually defined in the previous section “Bayesian ideal observer” already, but we now define it again right after Eq. 1.

We understand that this seems counter-intuitive, but it is correct. We try here to give an intuition. However, as the maximum entropy model is not the focus of the paper we would prefer to omit the lengthy description and figure but will be happy to include them in the paper if the Reviewer deems it necessary.

We have added a short note to the caption of Figure 4 to alert the reader to the non-intuitive nature of the MaxEnt model, and also included a new Figure 4—figure supplement 1.

In more detail, the total uncertainty (equivalent to the first term on the right hand side of Eq. 1) about pixel value can be decomposed into two parts (this can be most easily understood formally if entropy is substituted by variance, by the law of total variance, Figure 4—figure supplement 1.). The first part is “unexplained variance” (equivalent to the second term on the right hand side of Eq. 1): even if we knew what the image type was, there is still uncertainty due to the stochastic nature of the stimulus and perception noise. Unexplained variance increases with distance from revealings. Because the stimulus is spatially correlated, i.e. it is not white noise, knowing about the pixel value at a particular revealing location provides some information about nearby pixel values but not about distant pixel values. The second part is “explained variance” (equivalent to our BAS score, Eq. 1) and it is due to uncertainty about image type and the fact that each type predicts different pixel values at the characteristic length scale of stimulus spatial correlations. At very short length scales, each image type is bound to predict the same pixel values as that at the revealing location (as they are constrained by this observation), and so the explained variance is diminishingly small, and beyond the stimulus correlation length scale the differences again become small as the average predictions are the same (zero) due to stochasticity. Thus, explained variance peaks around the stimulus correlation length scales (which in our case are small relative to the total image size) and fall off from there, resulting in a contribution that predominantly decreases with distance from revealings. Therefore, the total uncertainty determined as a combination of these two sources of uncertainty can peak at the borders or at intermediate distances, close to the autocorrelation length scale of the stimulus, depending on the balance of these two sources, which in turn depends on the revealed pixel values (and locations)

We repeated the correlation analysis simulating the maximum entropy strategy. The results show no significant correlation between the revealing locations chosen by MaxEnt and those chosen by the participants (Author response table 1). This suggests that the correlation shown in the original Figure 3 is meaningful and that MaxEnt does not describe our participants’ behaviour well. We now present this analysis in the results but would prefer not to overload the paper with this additional Table.

	within-type correlation; p-value for correlation (ρ)	across-type correlation; p-value for correlation (ρ)
participant 1	ρ=-0.121; p=0.13	ρ=0.060; p=0.13
participant 2	ρ=-0.117; p=0.12	ρ=0.056; p=0.13
participant 3	ρ=-0.024; p=0.43	ρ=0.017; p=0.38

Author response table 1. Correlation between participant’s eye movement and those derived from the MaxEnt algorithm at 25 revealing.

We also agree that the correlation is not the best way to evaluate the model but they are intuitive to understand. Critically, this is why we also analyzed the information curves which are a more principled measure that includes prior information from previous saccades.

6) In addition to the BIC it would be nice to know the cross-validated prediction accuracy of category choice on a testing set.

We have now performed this analysis and the results are in Author response table 2. We computed 10-fold cross validated prediction errors by 10 times holding out a different random 10% of the data, fitting parameters to the remaining 90% and measuring prediction performance on the held out 10%. As one can see, cross validation errors show the same trend as BIC values, and thus we decided not to include this in the manuscript as the BIC is more informative for model comparison.

BIC difference from Table 2:	Average prediction error per trial (arithmetic mean; geometric mean):
160	0.4294; 0.4262
139	0.3958; 0.4246
58	0.3671; 0.4194
0	0.3658; 0.4179
105	0.3731; 0.4237
102	0.3729; 0.4228

Author response table 2. BIC values and cross-validated prediction errors.

As discussed above in the response to the editors, in both the passive and active conditions, participants could rescan the revealed locations after the final revealing before making a decision. Therefore, these concerns are not relevant as the participants can fixate as long as they like each of the revealed locations. Please also see the response to the editors above for the rationale for the time that participants are allowed to rescan the scene after the last revealing.

Reviewer #2:

1) The authors employ a reductionist method, which is indeed necessary if one wants to reveal underlying mechanisms. However, some the reductionist choices made in this work fuel the questioning of several of its conclusions. The most concerning reductionist steps are:

B) The exposed area was effectively < 0.5 deg and was scaled down in transparency from the center out – this reduced-out a meaningful drift-based scanning of the fixational region.

The reviewer is concerned that micro-saccades and drift could play an important role in our task but that we do not account for them in our experimental protocol. As we now clarify in the revised manuscript, the key aim of the experiment was to look at a more voluntary component of movement, that is, the scan paths of fixations, rather than the more involuntary process of

micro-saccades and drift (Rolfs, 2009). Over the course of each fixation in our experiment (~350 ms), based on the work of Rolfs (2009) who systematically studied fixation variability (ibid Figure 4), the SD of eye position is on the order of 0.22 deg. As each of our Gaussian revealing aperture had a SD of 0.18 degree, drifts and microsaccades were in fact likely to be used for extracting information within each revealed patch. Critically, if we allowed revealings on this length scale, the revealed locations would be too close together to be informative, as the smallest length scale of the our patterns (stripy) is 0.91 deg and is more than 4 times larger than the typical distance covered by microsaccades and drift (0.22 deg, see above).

Finally, if participants are limited in the number of saccades they are allowed to make (micro or otherwise) then our model makes it very clear that micro- (or small) saccades are highly sub-optimal for the high-level category judgments we study, and in agreement with this our participants’ selection of revealing locations were on average 3.51 deg apart. Therefore, we feel that the existence of drift and micro-saccades does not undermine the main message of our paper and include a discussion of these issues, in particular, that they may play a complementary role in increasing information about low-level visual features.

C) The images had uniform statistics, which preclude generalization to natural images.

Natural image statistics are often assumed to be spatially stationary (e.g. Field, 1987), although this is undoubtedly an approximation. Our stimulus was more naturalistic than many of the stimuli used in active sensing studies of visual search (e.g. 1/f noise) while still allowing a rigorous control and measurement of the amount of high-level category information available at any potential revealing location which would have not been possible with real natural scenes. Thus, we felt our stimuli strike the right balance on the eternally debated natural-vs.-artificial stimulus scale. We agree that ISIs by themselves are only necessary but not sufficient to prove that natural eye movement strategies are at play, but – as we also mention in the manuscript – we also found little to no learning across several sessions which we take as further (albeit still only circumstantial) evidence. Importantly, at least in principle, our mathematical approach generalises to more complex stimuli as long as their statistics are known and can be expressed as P(z₁ z_n x₁ x_n, c) (with the notation used in the manuscript). We have included these points in the Methods to more clearly express the strengths and limitations of our stimuli and approach.

2) The "last 60s" problem. Natural viewing involves a scanpath of fixations. However, natural viewing does not allow a re-scanning of the collection of previous fixation locations. The design of the trial is thus odd– why were the subjects given those extra 60s at the end of the trial to rescan their revealings? This is not justified in the paper and it is actually hidden, in a way, in the Methods section – it took me some time to understand that this was the case. The implications of this design are significant:

A) How can the authors relate performance to either of the two different phases of the trial (the "acquiring" and the "rescanning")?

As this point was raised by all three reviewers and highlighted as the key reason the paper was rejected, we have provided a full response to editors above (that includes an analysis of performance as a function of rescanning time as well as a new control experiment without rescanning).

B) Even in the "acquiring" phase, how can the authors rule out brief rescanning of exposed revealings for periods shorter than the threshold period?

The revealed locations are generally far apart so it is not possible to return to a revealing without triggering an additional revealing. Even if participants could rescan during the revealing stage this still does not undermine the analysis of whether they are efficient in the selection of N discrete revealings.

C) If performance depended on the perception during these 60s, then what was the underlying strategy while rescanning?

Please see point 3 and 4 in the response to the editors for this point.

The authors must describe the procedure clearly at the outset, relate to all these issues explicitly, and explain how they affect (or not) their conclusions.

We have now clarified all the issues relating to rescanning in the revision.

3) As indicated by the above, the primary characterization of the active strategy here is about which revealing were or should be selected, and less about when or in what order. True, order was a factor during the acquiring phase, but not during the rescanning phase. Order seems to play a role in the correlations in Figure 3B but it is not clear by how much (see below). The collection of revealing locations may indeed be the most relevant factor when trying to categorize an image out of several known images with known structures. This is, however, not the case in most natural cases, in which real-time information is essential.

This is really the rescanning issue again. As the participant does not know how many saccades they will be allowed on each trial, they have to select them in an order that will be informative at the time they choose them and several of our analyses examine order effects. Therefore the selection process operates in real time. Please see the full response to the editors. We agree that we are not studying the “when” question (i.e. how long each fixation should be hold for) and we mention this in the Materials and methods.

4) From the above and from further analysis it appears that the strong statements of the Abstract are not supported by the data in the paper.

Please see the response to the editors. We do not claim the participant has to see the revealings in a specific order in the passive condition and our perceptual model does not take order into account (and the reason for this is that we allow rescanning). To reiterate, in order to equate the information on location and pixel color in the passive and active conditions we allow the rescanning period. The performance may well depend on only the rescanning period in both conditions but critically the selection in the active condition has to be done in real time. We have revised the phrasing of this sentence to: “categorization performance was markedly improved when locations were revealed to participants by an optimal Bayesian active sensor algorithm.”

B) "By using […] we show that a major portion of this apparent suboptimality of fixation locations arises from prior biases, perceptual noise and inaccuracies in eye movements […]" – you do not really show this. You show that if you add these imperfections to your model you get performance level that resembles that of the subjects. However, there are so many ways to impair the performance of your model – where do you show that these are the crucial factors?

We chose to start with what we (and we expect most readers) would regard as the most natural sources and forms of sub-optimality – sensory and motor noise and biases. Clearly, the number of potential models is unbounded but in any given scientific study one has to consider a finite set of possible alternative models. We did do formal comparison of a set of models, so we emphasize that it is not as though we hand-picked one. Our aim was to explain the data parsimoniously and we are happy to consider alternative models if the reviewer has something particular in mind but do feel the set of models we examined forms a reasonable set for our study. We have removed the word “show” and now use “estimate” instead.

C) "The central process of selecting fixation locations is around 70% efficient" – this is correct only for the specific task and context of your experiment. The statement sounds much more general than that.

We clarify that this is for our task. However, note that no paper can ever make a claim of anything apart from what particular task was studied in the experiment. We feel it reasonable that an Abstract then tries to abstract a message for the reader. To take just one example, Najemnik and Geisler in the Abstract of their 2005 Nature paper say “We find that humans achieve nearly optimal search performance” whereas clearly that can’t be stated unless they have examined every search task and stimuli that humans have ever used. But most readers understand what they and others mean by the statement.

We do use the word “estimate” earlier in the Abstract, so again we find this criticism rather unfair as it would apply to almost all papers on this topic.

5) Audience and style. As written now the paper seems to address experts in Bayesian models of perception. Given that it is submitted to eLife I assume that the paper should address primarily, or at least to the same degree, biologists who are interested in understanding perception. And indeed, papers like this form a wonderful opportunity to create a productive dialogue between biologists and theoreticians. For this end, the style of writing must change. The amount of statistical details should be reduced,

We feel it is very important to back up our results with statistical rigor so would not be keen to remove statistical tests from the results. Indeed other reviewers have asked for more statistical tests which we have included where necessary. If the reviewer means the equations for the BAS, this is the single equation we have in the main text which is so central to the paper we would be reluctant to remove it.

the biological meaning of the various strategies discussed should be provided, the rational for selecting the BAS algorithm as the optimal strategy should be explained, the meaning of each strategy in terms of actual eye movements in natural scenes should be explained. At the end, the reader should understand the biological meaning of each strategy (that is, a biologically-plausible description of the strategy employed by their subjects in this task, and a strategy they would employ in a natural task), the rational of why one strategy is better than the other, and in what sense humans are sub-optimal.

We have explained the rationale for selecting the BAS algorithm in the section “Predicting eye movement patterns by a Bayesian active sensor algorithm”. In terms of giving a “biologically-plausible description of the strategy employed by their subjects in this task,” we are a little unsure what the reviewer wants – the detailed description of BAS is the strategy that we propose participants are using, which is to find the location in the scene that when fixated is most likely to lead to the greatest reduction in the categorization error. We now highlight this in words in the Discussion and hope this addresses the reviewer’s comment.

We felt it would be very awkward to replace all mention of “eye movement” in the paper and as suggested we clarify now that we only studied fixation scanpaths and not microsaccades or drift. Again there are many examples in the literature where it is common practice to refer to the kind of study we did as being about “eye movements”. If the reviewer and editors insist, we can replace all mention of eye movements but feel it would make the paper far less accessible.

B) Previous results and hypotheses about active sensing/active vision that refer to all kinds of movements must be discussed and referred to when interpreting the current results.

We now reference several papers on microsaccades and drift.

We have clarified that we study fixation scanpaths.

Minor comments:

1) Arbitrary selection of parameters – please explain the choice of every parameter you use (e.g., the criteria for saccades and fixations).

The parameters were based on pilot experiments on the authors with the aim of making the revealings in the free-scan session feel natural so that each location viewed was revealed and spurious locations were not revealed. We have now explained this in the Methods.

2) Figure 3B – please run a shuffling control analysis to show how much of the correlation is order-dependent.

We have performed the shuffling control and in doing this, we realized that the magnitude of correlation depends on the number of samples used to construct the density maps. When we calculated the correlation in our original analysis, the number of samples increased with the number of revealing on the x-axis. This means that the increasing separation could have arisen from the increasing sample size. We have therefore modified the way we calculate the correlation and ensured that the number of samples used to construct the density maps remains the same as the number of revealing increases. The new results are in the updated Figure 3B. As one can see, the trend of the correlation curves is the same: the within- and across- type correlations increasingly separate as a function of revealing, with the within-type correlation increasing and the across-type correlation decreasing. In contrast, the shuffling analysis shows that the correlation curves remain constant as a function of revealing number. This is expected for the shuffling case because the density maps are now constructed with random subsamples of the same pool of data regardless of revealing number. The shuffled results are shown in Author response image 1 but we don’t think they need to be included in the paper as they have to be flat by construction now that we have ensured that the sample size is independent of revealing number. We thank the reviewer for suggesting the shuffling control as it led to us improving the analysis.

Author response image 1

Download asset Open asset

Correlation as a function of revealing number with the revealing number shuffled.

Orange denotes within-type correlation; purple denotes across-type (cf. Figure 3B in the manuscript). Line and shaded area represent mean and SD, respectively.

https://doi.org/10.7554/eLife.12215.016

Reviewer #3:

1) The authors corrected for errors in saccade targeting tangential and orthogonal to saccade direction. However, as they correctly stated in the Discussion, there are also other potential sources of errors due to biases along cardinal directions or the bias to fixate the center of an image. It would be very interesting to see how much of the performance reduction is caused by these biases. It should be possible to assess these biases directly from the existing data. It is important to clarify that the suboptimalities the Reviewer asks us to identify are conceptually different from those that we factored out using the specific biases and noise included in the (non-ideal) BAS model. The ones we considered are suboptimalities that arise in the execution of a planned saccade (as in Figure 3—figure supplement 2), while the ones that the reviewer refers to could be suboptimalities of the planning itself. As we are interested in the degree of (sub)optimality of the planning component, we thought it would be misleading to factor out the biases the Reviewer is considering. We realise that our discussion of this issue was confusing in the original manuscript so we have now rewritten it.

The Reviewer asks us to assess possible fixation bias towards the center of the image and saccade directional bias towards cardinal directions. With the old analysis of the density maps that uses the absolute revealing locations (see point 4 in response to the editor), we see that the participants actually tend to fixate away from the center compared to BAS. Similarly, with the new analysis that uses relative locations, we see that the participants actually tend to have a more diffuse distribution of fixation compared to BAS (see mean revealing density maps in Figure 3A). The fact that the revealings chosen by BAS are more efficient and more concentrated at the center of the field of view (both in absolute and shifted position) suggests that this type of fixation bias will actually improve the performance rather than reduce it and therefore would not account for any sub-optimality.

Comparing the saccades made by the participants and the BAS algorithm, we see that our participants tend to make more horizontal saccades and fewer vertical saccades (Author response image 2). The deviations from BAS may well reduce performance, but it is not obvious how to formalize or determine if this is a true bias on top of planning or part of planning itself. In particular, it is not clear to us how we can measure bias directly from the existing data (as the reviewer suggests) separate from any active strategy as we do not know where subjects are aiming. We would prefer not to add the plot below to the paper as there is no really strong message we can make about it, but are happy to add it if the reviewer wishes.

Author response image 2

Download asset Open asset

Probability density of saccade angles.
https://doi.org/10.7554/eLife.12215.017

Thank you for this great suggestion. We have now performed this analysis and below are the density maps for correct and incorrect trials (averaged across participants, new Figure 3—figure supplement 3). We chose to analyze only for the “average” participant as the number of incorrect trials is limited for each participant. The correlation with BAS is higher for correct compared to incorrect trials (average of 0.35 vs 0.01; p<0.05). We have added this into the revised manuscript.

We have computed the distribution of score percentiles across revealings for the two sensing algorithms. The result makes it clear that the BAS algorithm is a much better description for human eye movement than the MaxEnt algorithm. We have added this graph as a subpanel of Figure 4 in the revision and mentioned this in the text.

As this point was raised by all three reviewers and highlighted as the key reason the paper was rejected, we have provided a full response to this issue in the response to the editors above.

https://doi.org/10.7554/eLife.12215.019

Article and author information

Author details

Scott Cheng-Hsin Yang

Computational and Biological Learning Lab, Department of Engineering, University of Cambridge, Cambridge, United Kingdom

Contribution
SC-HY, Conception and design, Acquisition of data, Analysis and interpretation of data, Drafting or revising the article

For correspondence
schy2@eng.cam.ac.uk

Competing interests
The authors declare that no competing interests exist.
Máté Lengyel
1. Computational and Biological Learning Lab, Department of Engineering, University of Cambridge, Cambridge, United Kingdom
2. Department of Cognitive Science, Central European University, Budapest, Hungary
Contribution
ML, Conception and design, Analysis and interpretation of data, Drafting or revising the article

Contributed equally with
Daniel M Wolpert

Competing interests
The authors declare that no competing interests exist.

"This ORCID iD identifies the author of this article:" 0000-0001-7266-0049
Daniel M Wolpert

Computational and Biological Learning Lab, Department of Engineering, University of Cambridge, Cambridge, United Kingdom

Contribution
DMW, Conception and design, Analysis and interpretation of data, Drafting or revising the article

Contributed equally with
Máté Lengyel

Competing interests
The authors declare that no competing interests exist.

"This ORCID iD identifies the author of this article:" 0000-0003-2011-2790

Funding

Wellcome Trust

Scott Cheng-Hsin Yang
Máté Lengyel
Daniel M Wolpert

Human Frontier Science Program

Daniel M Wolpert

Royal Society

Daniel M Wolpert

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank C Rothkopf for useful comments on the manuscript, N Houlsby and F Huszár for their contributions to the theory underlying BAS, and J Ingram for technical support. This work was supported by the Wellcome Trust (SC-HY, ML, DMW), the Human Frontier Science Program (DMW), and the Royal Society Noreen Murray Professorship in Neurobiology (to DMW).

Ethics

Human subjects: The study was approved by the Cambridge Psychology Research Ethics Committee. All participants gave written informed consent prior to the experiment.

Reviewing Editor

Doris Y Tsao, California Institute of Technology, United States

Version history

Received: October 10, 2015
Accepted: December 6, 2015
Version of Record published: February 10, 2016 (version 1)
Version of Record updated: December 13, 2016 (version 2)
Version of Record updated: February 6, 2017 (version 3)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.