DYT1 dystonia increases risk taking in humans
- Hadassah Medical Center and the Hebrew University, Israel
- Princeton University, United States
- Beth Israel Medical Center, United States
- Columbia University, United States
Figures
Figure 1
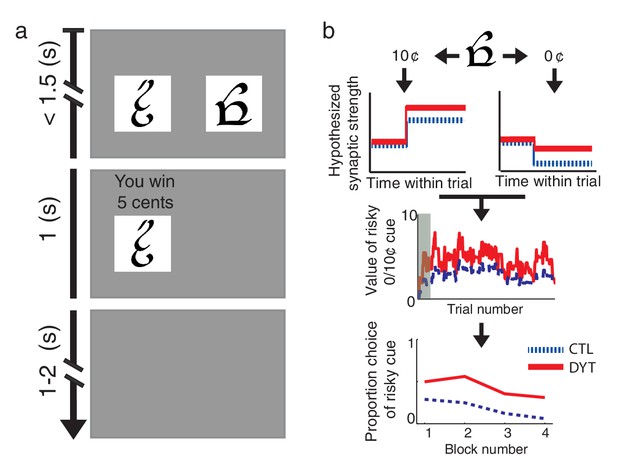
Behavioral task and hypothesis.
(a) In ‘choice trials’ two visual cues were simultaneously presented on a computer screen. The participant was required to make a choice within 1.5 s. The chosen option and the outcome then appeared for 1 s, followed by a variable inter-trial interval. (b) Theoretical framework. Top: trials in which the risky cue is chosen and the obtained outcome is larger than expected (trials with a 10¢ outcome) should result in strengthening of corticostriatal connections (LTP), thereby increasing the expected value of the cue and the tendency to choose it in the future. Conversely, outcomes that are smaller than expected (0¢) should cause synaptic weakening (LTD) and a resulting decrease in choice probability. Middle: In DYT1 dystonia patients (red solid), increased LTP combined with decreased LTD are expected to result in an overall higher learned value for the risky cue, as compared to controls (blue dashed). In the model, this is reflected in higher probability of choosing the risky cue when presented together with sure 5¢ cue (Bottom). Simulations (1000 runs) used the actual order of trials and mean model parameters of each group as fit to participants’ behavior. Gray shadow in the middle plot denotes trials in the initial training phase.
Figure 2
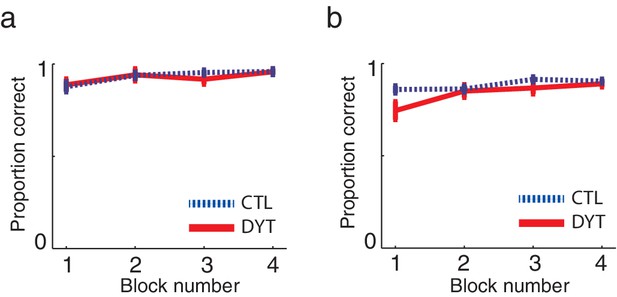
Learning curves did not differ between the groups.
Mean probabilities (± s.e.m) of choosing the cue associated with the higher outcome, on average, (a) among pairs of two sure cues (15 trials per ‘block’) or (b) when the risky 0/10¢ cue was paired with a sure cue of 0¢ or 10¢ value (20 trials per ‘block’) confirmed that both groups quickly learned to choose the best cue in trials in which one cue was explicitly better than the other. These results verify that both groups understood the task instructions and could perform the task similarly well (in terms of choosing and executing their responses fast enough, etc.). Participants evidenced learning of values for deterministically-rewarded cues even in the first choice trials despite the fact that they were never informed verbally or otherwise of the monetary outcomes associated with each of the cues, and thus could only learn these from experience. However, for cues leading to deterministic outcomes, a little experience can go a long way (Shteingart et al., 2013), and participants received 16 training trials prior to the test phase. Our data suggest that learning in this phase did not differ between the groups: in the first 5 choice trials in the test phase that involved a pair of sure cues, the probability of a correct response was 0.78 ± 0.18 in the DYT group and 0.81 ± 0.07 in the CTL group (Mann-Whitney U test, df = 24, P = 0.59). We verified that that this level of performance could result from trial-and-error learning by simulating the behaviors of individuals using the best-fit learning rates (see Materials and methods). The simulation confirmed that both groups should show similar rates of success on the first 5 choice trials (DYT 0.81 ± 0.17 probability for correct choice, CTL 0.87 ± 0.13, Mann-Whitney U test z = 0.88, df = 24, P = 0.38) despite differences in learning rates from positive and negative prediction errors (see Results). Indeed the model, which started from initial values of 0 and learned only via reinforcement learning, performed on average better than participants.
Figure 3 with 4 supplements
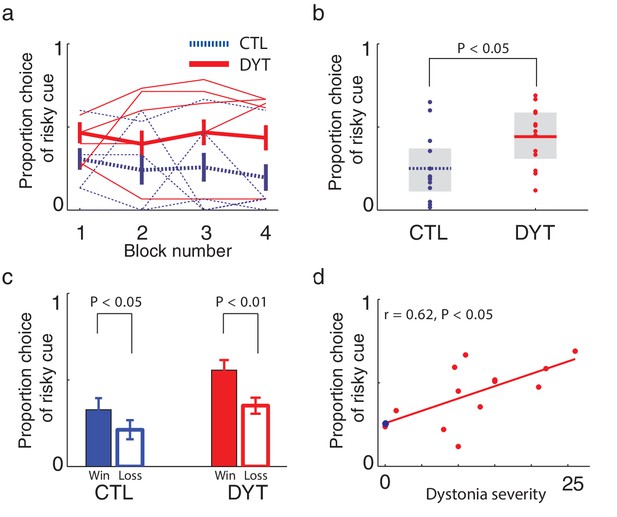
Risk taking in DYT1 dystonia patients as compared to healthy sex- and age-matched controls.
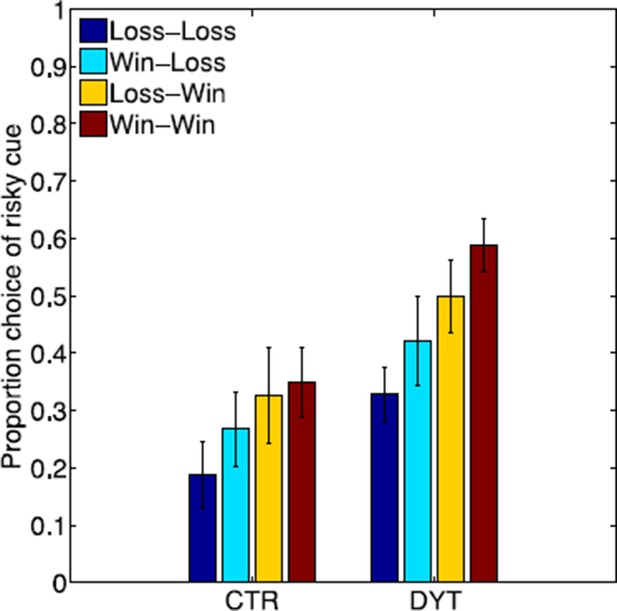
(a) Mean proportion (± s.e.m) of choosing the risky 0/10¢ cue over the sure 5¢ cue (15 trials per block) in each of the groups. DYT1 dystonia patients (red solid) were less risk-averse than controls (blue dashed). Results from several randomly-selected participants are plotted in the background to illustrate within-participant fluctuations in risk preference over the course of the experiment, presumably driven by ongoing trial-and-error learning. (b) Overall percentage of choosing the risky 0/10¢ cue throughout the experiment. Horizontal lines denote group means; grey boxes contain the 25th to 75th percentiles. DYT1 dystonia patients showed significantly more risk-taking behavior than healthy controls. (c) Proportion of choices of the risky 0/10¢ cue over the sure 5¢ cue, divided according to the outcome of the previous instance in which the risky cue was selected. Both controls and DYT1 dystonia patients chose the risky 0/10¢ cue significantly more often after a 10¢ ‘win’ than after a 0¢ ‘loss’ outcome, demonstrating the effect of previous outcomes on the current value of the risky 0/10¢ cue due to ongoing reinforcement learning. Error bars: s.e.m. The effect of recent outcomes on the propensity to choose the risky option was evident throughout the task, especially in the DYT group, and was seen after both free choice and forced trials (Figure 3—figure supplement 1), suggesting that participants continuously updated the value of the risky cue based on feedback, and used this learned value to determine their choices. (d) Risk taking was correlated with clinical severity of dystonia (Fahn-Marsden dystonia rating scale). The mean of the control group is denoted in blue for illustration purposes only. Interestingly, the regression line for DYT1 dystonia patients’ risk preference intersected the ordinate (0 severity of symptoms) close to the mean risk preference of healthy controls.
Figure 3—figure supplement 1
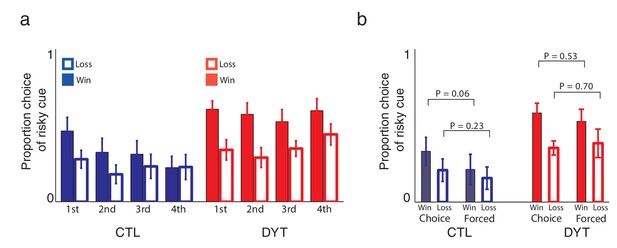
Learning about the risky cue continued throughout the task.
(a) Our experimental design was aimed explicitly at focusing on learning about the risky cue so that we could analyze learning from positive and negative prediction errors decoupled from initial learning about deterministic cues. As shown in Figure 3c, participants’ tendency to choose the risky 0/10 cue over the same-mean 5¢ cue was dynamically adjusted according to experience: if the previous choice of the risky cue was rewarded with 10¢, participants were significantly more likely to choose the risky cue again on the next time it was available, as compared to the case in which the previous choice of the risky cue resulted in 0¢. To verify that the value of the risky cue was continuously updated, we calculated the proportion of choices of the risky cue over the sure 5¢ cue after different outcomes of the previous instance in which the risky cue was selected, for different time bins throughout the task (15 risky trials in each). A three way ANOVA (group X outcome X time-bin) revealed a significant effect for group (P < 0.001), outcome (win or loss; P < 0.001) and no effect of time-bin or interactions. Post-hoc comparisons revealed that the differences between win and loss conditions were significant in all bins for the DYT group only (all Ps < 0.05, two tailed). The first two bins for the CTL group approached significance (P = 0.054, two-tailed). This analysis showed that DYT patients changed their behavior based on outcomes of the risky cue throughout training. Control participants, on the other hand, evidenced somewhat less learning as the task continued, with their behavior in the last quarter of training settling on a risk-averse policy that was not sensitive to local outcomes. In reinforcement learning, this could result from a gradual decrease of learning rates, which is optimal in a stationary environment. Indeed, the final risk-averse policy was predicted by our model, based on the ratio of positive and negative learning rates. In any case, these results suggest that participants learned to evaluate the risky cue based on experienced rewards, and that the locally fluctuating value of the risky cue affected choice behavior, at least in the first half of the experiment, and for the DYT group, throughout the experiment. (b) Recent work on similar reinforcement learning tasks has shown that choice trials and forced trials may exert different effects on learning (Cockburn et al., 2014). To test for this effect in our data, we examined separately the probability of choosing the risky cue over the sure cue following wins or losses, after either forced or choice trials. Our analysis revealed that choices were significantly dependent upon the previous outcome of the risky cue (P < 0.01, F = 7.45, df = 1 for main effect of win versus loss; 3-way ANOVA with factors outcome, choice and group) but not upon its context (P = 0.38, F = 0.93, df = 1 for main effect of forced vs. choice trials). Similar to Cockburn et al. (2014), we did observe a numerically smaller effect of the outcome of forced trials (as compared to choice trials) on future choices, however this was not significant (interaction between outcome and choice P = 0.46, F = 0.56, df = 1). P values in the figure reflect paired t-tests.
Figure 3—figure supplement 2
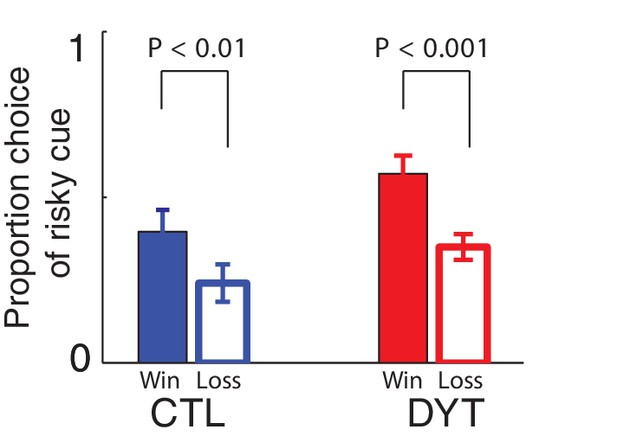
Effects of ongoing learning in the simulated data.
Proportion of choices of the risky 0/10¢ cue over the sure 5¢ cue, divided according to the outcome of the previous instance in which the risky cue was selected, according to the asymmetric learning model with parameters fit to each participant’s behavior. The model captures the behavioral findings faithfully.
Figure 3—figure supplement 3
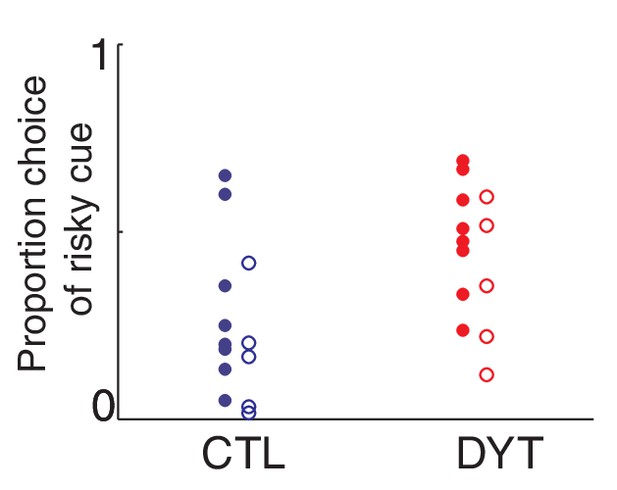
Sex of participants did not affect risk sensitivity in our task.
To avoid any possible sex-dependent bias, we matched the sex of both groups when comparing control participants to DYT1 dystonia patients. Similar to Figure 3b, plotted are overall percentage of choices of the risky 0/10¢ cue over sure 5¢ cue throughout the experiment, for different participants (Female N = 8 in each group, filled dots; Male, N = 5 in each group, open dots). A two-way ANOVA (CTL/DYT x Male/Female) did not reveal a significant main effect of sex (P = 0.08) although this analysis is obviously underpowered. The difference between CTL and DYT remained significant in this analysis (P = 0.01 for the main effect of group).
Figure 3—figure supplement 4
Medication did not affect risk-sensitivity.
To minimize the effect of medication on learning in our task, we tested patients before their scheduled dose of medication to the extent that this was possible. As in Figure 3b, plots show overall percentage of choices of the risky 0/10¢ cue over sure 5¢ cue throughout the experiment and its relation to medications and doses.(a) Similar risk-taking (choosing the risky 0/10¢ cue over the sure 5¢ cue) behavior among untreated patients and those taking trihexyphenidyl or baclofen, (b) lack of correlation between risk-taking behavior and the daily dose of trihexyphenidyl (Pearson’s r = 0.19, df = 11, P = 0.526) or (c) baclofen (Pearson’s r = −0.20, df = 11, P = 0.51) all suggested that medication did not contribute significantly to the observed results.
Figure 4
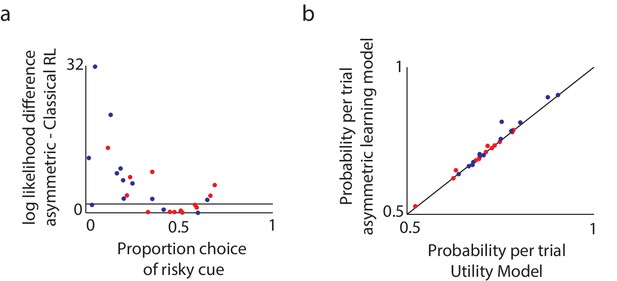
Model comparison supports the asymmetric learning model.
We compared three alternative models in terms of how well they fit the experimental data. (a) To compare the asymmetric learning model with the classical (symmetric) reinforcement learning (RL) model, we used the likelihood ratio test, which is valid for nested models. Plotted are the log likelihood differences between the asymmetric learning model and the classical RL model. Black line: the minimal difference above which there is a P < 0.05 chance that the additional parameter improves the behavioral fit, as tested via a likelihood ratio test for nested models (dots above this line support the asymmetric learning model). For the majority of participants (16 out of 26; DYT 6, CTL 10) the more complex asymmetric model was justified (chi square test with df = 1, P < 0.05). In particular, and as expected based on Niv et al. (2012), the asymmetric learning model was justified for participants who were either risk-averse or risk-taking, but not those who were risk-neutral. (b) The asymmetric learning model and the nonlinear utility model have the same number of free parameters and therefore could be compared directly using the likelihood of the data under each model. Plotted is the average probability per trial for the asymmetric learning model as compared to the nonlinear utility model, for healthy controls (blue dots) and patients with dystonia (red). Dots above the black line support the asymmetric learning model. The asymmetric learning model fit the majority of participants better than the utility model (15 out of 26; DYT 6, CTL 9) with large differences in likelihoods always in favor of the asymmetric model, and over the entire population the asymmetric learning model performed significantly better (paired one-tailed t-test on the difference in model likelihoods, t = 1.92, df = 25, P < 0.05).
Author response image 1
Learning rate similarity by participant.
https://doi.org/10.7554/eLife.14155.011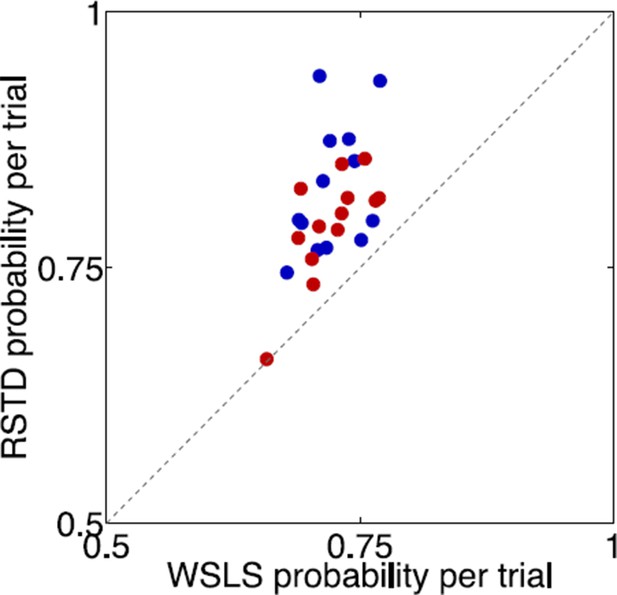
Author response image 2
Comparison of risk sensitive (learning asymmetry) model and win-stay-lose-shift model.
https://doi.org/10.7554/eLife.14155.012
Author response image 3
Effect of outcomes of the past two trials on choices of the risky cue.
https://doi.org/10.7554/eLife.14155.013Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
DYT1 dystonia increases risk taking in humans
eLife 5:e14155.
https://doi.org/10.7554/eLife.14155
