Direction-dependent arm kinematics reveal optimal integration of gravity cues
- Université Bourgogne Franche-Comté, INSERM CAPS UMR 1093, France
- CIAMS, Université Paris-Sud, Université Paris Saclay, France
- CIAMS, Université d'Orléans, France
- Baylor College of Medicine, United States
Figures
Figure 1 with 3 supplements
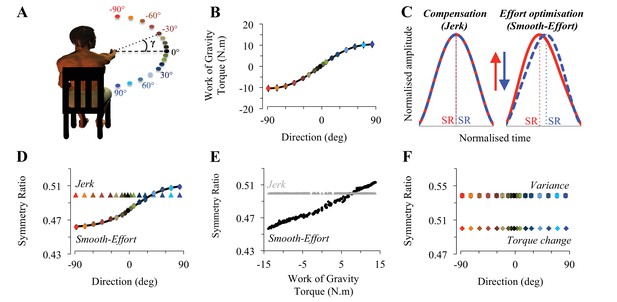
Task design and theoretical prediction.
(A) Participants’ initial position and projection of the 17 targets onto the frontal plane. The angle γ, representing the target inclination with respect to horizontal, was used to calculate the gravity torque projecting onto the plane of motion (see also Figure 1—figure supplement 1). (B) The Work of Gravity Torque (WGT), projected onto the plane of motion and integrated over the whole movement, is plotted as a function of movement direction (same color code as in A). This non-linear (cosine-tuned) dependence is well fitted by a sigmoidal function (black curve, average RMSE = 0.12; [min: 0.09, max: 0.15], see Materials and methods). Positive/negative values indicate that WGT has the same/opposite direction as the arm movement. (C) Mean velocity profiles (for the average subject), normalized in both amplitude and duration, illustrate the predictions of the compensation hypothesis (Jerk) and the effort optimization hypothesis (Smooth-Effort) in the vertical plane (upwards, −90; downwards, 90°; see arrows and color-coded direction definition in panel A). SR up (red) and SR down (blue) illustrate the calculation of a symmetry ratio (acceleration time / movement time) allowing quantification of kinematic differences/similarities. (D) Simulated symmetry ratio predicted by the compensation hypothesis: Minimum Jerk (triangles, Flash and Hogan, 1985); and the effort optimization hypothesis: Minimum Smooth-Effort model (dots, Gaveau et al., 2014); as a function of movement direction (−90°, upwards and 90°, downwards). Similarly to WGT (see panels B), simulated symmetry ratio obtained from the Smooth-Effort model is well fitted by a sigmoidal function (black curve). (E) Simulated symmetry ratio as a function of WGT (grey triangles, Jerk and black dots, Smooth-Effort). Each data point represents the prediction for one subject moving in one direction (n = 255 in each plot). It is noticeable that according to the effort optimization hypothesis, arm kinematics (symmetry ratio) should not be invariant but instead linearly correlate with WGT. (F) Simulated symmetry ratio predicted by two other well-known models minimizing dynamic cost functions: the Minimum Variance (Harris and Wolpert, 1998) and the Minimum Torque Change (Uno et al., 1989). It can be observed that the modulation of kinematics with movement direction is a specific feature of the effort-related optimization only.
Figure 1—figure supplement 1
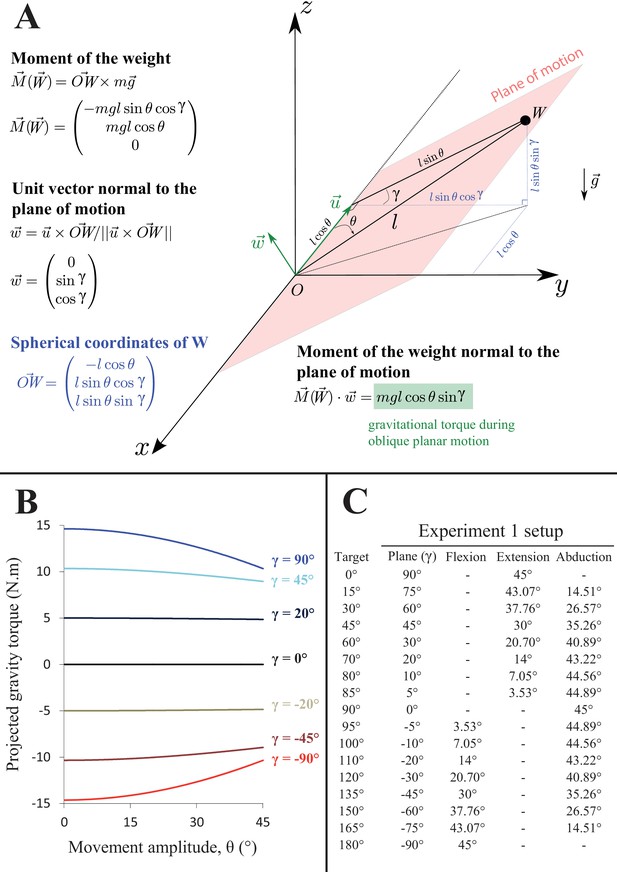
Gravity torque projection in Experiment 1.
(A) Geometrical representation of the task and equations for computing gravity torque, projecting onto the plane of motion, from endpoint kinematics. Subjects were asked to perform single degree of freedom reaching movements, from a horizontal initial position, to a target requiring a θ = 45° shoulder rotation with an orientation relative to horizontal defined by an angle γ. is the lever arm length. (B) Gravity torque projected onto the plane of motion for 7 exemplary plane orientations (γ angle) throughout the θ = 45° required movement amplitude. The gravity torque projecting onto the plane of motion was calculated using Equation 1 for all γ values presented panel C. The Work of Gravity Torque was then calculated using Equation 2. (C) The convention on plane of motion angle values () used to compute the Work of Gravity Torque in Experiment 1 is provided along with the exact positioning of each target defined as shoulder angular coordinates.
Figure 1—figure supplement 2
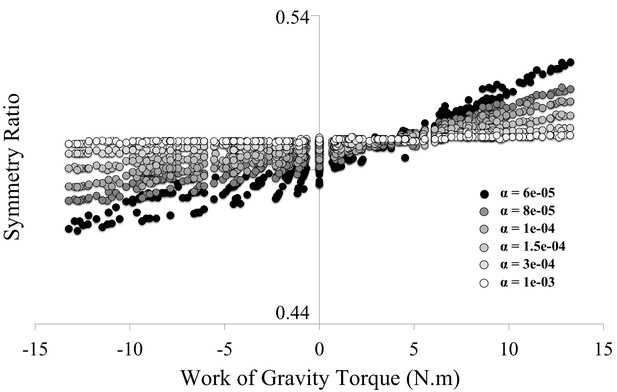
Clarification on the hybrid cost used in the Smooth-Effort model.
Because the Smooth-Effort model minimizes a combination of the Absolute Work of force and Jerk, one may wonder whether the predicted linear correlation of symmetry ratio with the Work of Gravity Torque (WGT, see Figure 1E) emerges from the effort-related cost (absolute work of force) or from the kinematic cost (Jerk). This figure presents the results of 1530 simulations performed for the 15 subjects * 17 targets * 6 different values of α (the weighting factor for the Jerk cost in the Smooth-Effort model, see Methods). For larger values of α, the symmetry ratio saturates at SR = 0.5. As illustrated, the higher the weight of the jerk, the flatter the correlation between symmetry ratio (SR) and WGT. This undeniably confirms the effort-related origin of the experimental findings presented in Figure 2.
Figure 1—figure supplement 3
Supplemental minimum Variance simulations including muscle dynamics.
Similarly to results presented in the main text (Figure 1F), including muscle dynamics into the minimization of end-point variance predicts constant symmetry ratios for all movement directions.
Figure 2 with 1 supplement
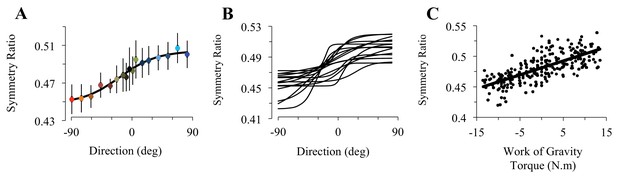
Experimental findings.
(A) Experimentally recorded symmetry ratio, averaged across all subjects, is plotted as a function of movement direction. Similarly to the effort optimization hypothesis prediction (see panels D in Figure 1), experimental symmetry ratio is well fitted by a sigmoidal function (black curve). Error bars illustrate SD. (B) Fits of a sigmoid function to symmetry ratio as a function of movement direction for data from individual subjects. (C) Symmetry ratio as a function of Work of Gravity Torque (WGT). Each data point represents the mean of 12 trials for one subject moving in one direction (n = 255; 3060 trials total). It is noticeable that, similarly to the effort optimization hypothesis prediction (Figure 1E), arm kinematics (symmetry ratio) linearly correlates with gravity torque.
Figure 2—figure supplement 1
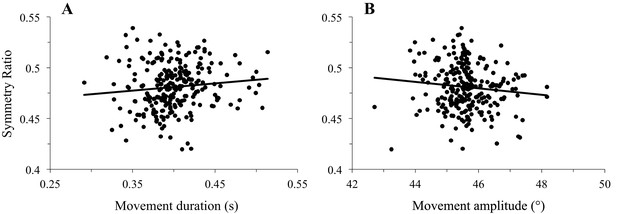
Supplemental analyses testing the effect of movement duration and amplitude on experimental findings.
Each data point represents the mean of 12 trials for one subject in one direction (n = 255 in each plot; 3060 trials total). (A) Symmetry ratio as a function of movement duration. (B) Symmetry ratio as a function of movement amplitude. These two plots reveal that the symmetry ratio was independent of movement duration (individual correlation coefficients averaged R = 0.22 [min: 0.04, max: 0.57], p=0.41) and amplitude (on average R = 0.29 [min: 0.02, max: 0.69], p=0.26); therefore ensuring that the modulation of arm kinematics observed in Figure 2 truly reflects gravity torque effects.
Figure 3 with 1 supplement
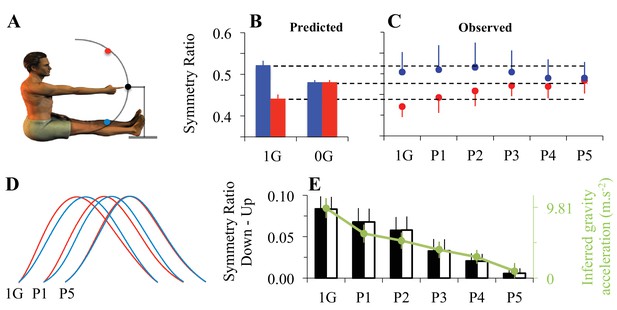
Adaptation to microgravity.
(A) Participants’ initial position and positioning of the 3 targets in the sagittal plane. Eleven participants performed fast and visually guided mono-articular arm movements (shoulder rotations) in the sagittal plane under normal gravity (one-G) and micro-gravity conditions (zero-G) during a parabolic flight (parabola 1, P1 to parabola 5, P5). (B) Symmetry ratios (acceleration time / movement time) predicted by the Minimum Smooth-Effort model in one-G and in zero-G conditions. (C) Symmetry ratios experimentally recorded before (1g) and during adaptation to zero-G (P1 to P5). (D) Mean velocity profiles, normalized in amplitude and duration. Qualitative comparisons between upward and downward arm movements illustrate the progressive decrease of directional asymmetries when subjects adapted to the new microgravity environment. (E) Vertical bars represent the average symmetry ratio (black vertical axis, left) for the recorded (black filled bars) and simulated (black open bars) data in one-G and during zero-G (P1 to P5) environments. For simulated data, the g value was fitted (−2*G<g<2*G) in order to best predict the measured symmetry ratios. These fitted g values, represented by the green dots (green vertical axis, right), reveal a progressive decrease of the g internal model value during zero-G exposure. Error bars illustrate SD and color-coded arrows denote movement direction (red = up; blue = down). See also Figure 3—figure supplement 1.
Figure 3—figure supplement 1
Supplemental analysis on the effect of subject order during the microgravity experiment.
Because two subjects were successively tested during each parabolic flight, the second subject to be tested had therefore already been submitted to microgravity during the test period of the first subject. To reduce sensorimotor adaptation before the experiment was performed for the second subject, we restrained this subject on the ground and prevented him from moving his body limbs. Our rationale was that preventing motor interaction with the various unwanted gravito-inertial force fields would reduce sensorimotor adaptation. Vertical bars represent the directional difference (Down-Up) between average symmetry ratios for subjects who performed the experiment first (black filled bars) and those who performed the experiment second (black open bars) in one-G and during zero-G (P1 to P5) environments. Subjects in both groups exhibited similar behavior (Kruskal-Wallis ANOVA: H1,11<2.13 and p>0.14 in all cases); i.e. directional asymmetry was present during the first parabola and then progressively disappeared.
Author response image 1
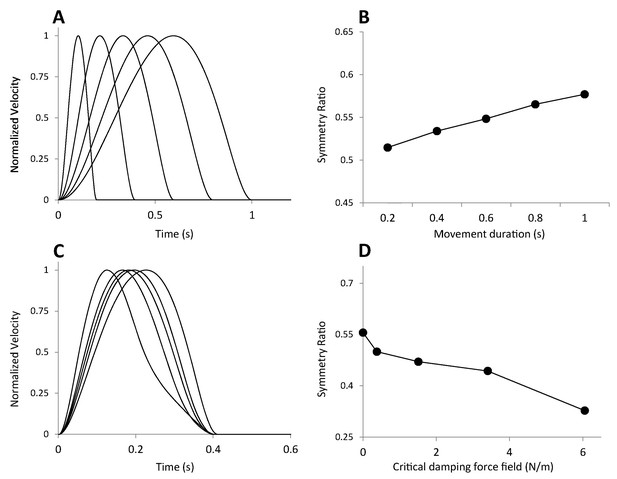
Additional simulations testing the validity of our minimum Variance simulations by comparison to previously published results from Tanaka et al. 2004.
(A) Normalized velocity profiles obtained for various movement durations. (B) Symmetry Ratio was shown to increase with movement duration (C) Normalized velocity profiles obtained for various degrees of system’s stability. The right-most curve corresponds to the case of no external force. The other four curves, from right to left, are for critical damping system with increased stability via external viscous and elastic forces (see Tanaka et al. 2004). (D) Symmetry Ratio was shown to decrease when the force field level increased.
Author response image 2
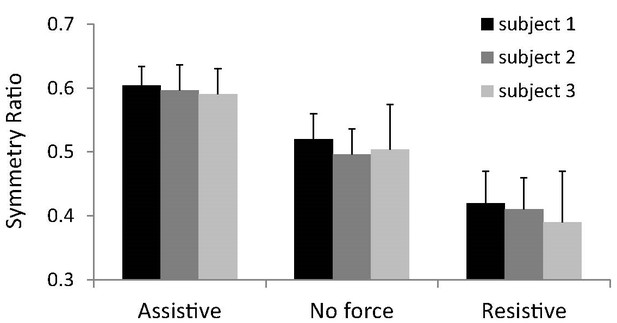
Symmetry ratios (average of 30 trials, +SD) obtained for three subjects performing fast arm reaching movements in the horizontal plane under three conditions of external force.
Assistive: the manipulandum pushes the arm toward the final target. No force: the manipulandum does not exert any force. Resistive: the manipulandum pushes the arm toward the starting target. Movement amplitude was 30 cm and duration 300ms.
Author response image 3
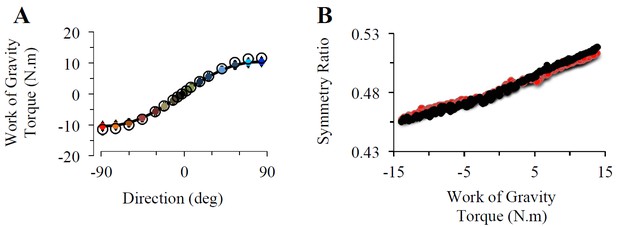
(A) Effect of Equation 10 approximation on the work of gravity torque. Empty black circles depict the work of gravity torque (as a function of movement direction; i.e., plane angle 𝛾) computed with the same approximation as Equation 10; i.e., when assuming that gravity torque is constant throughout movement amplitude. Colored circles depict the work of gravity torque without any approximation (same data as in Figure 1B). (B) Effect of Equation 10 approximation on Smooth-Effort simulated symmetry ratios as a function of WGT. Black dots depict simulated data with the same approximation as Equation 10; i.e., when assuming that gravity torque is constant throughout movement amplitude. Red dots depict simulated data without approximation (same data as in Figure 1E). Each data point represents one subject moving in one direction (n=255 in each plot).
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Direction-dependent arm kinematics reveal optimal integration of gravity cues
eLife 5:e16394.
https://doi.org/10.7554/eLife.16394
