Structure in the variability of the basic reproductive number (R0) for Zika epidemics in the Pacific islands
Figures

Graphical representation of compartmental models.
Squared boxes and circles correspond respectively to human and vector compartments. Plain arrows represent transitions from one state to the next. Dashed arrows indicate interactions between humans and vectors. (a) Pandey model (Pandey et al., 2013). susceptible individuals; infected (not yet infectious) individuals; infectious individuals; recovered individuals; is the rate at which -individuals move to infectious class ; infectious individuals () then recover at rate ; susceptible vectors; infected (not yet infectious) vectors; infectious vectors; constant size of total mosquito population; is the rate at which -vectors move to infectious class ; vectors die at rate . (b) Laneri model (Laneri et al., 2010). susceptible individuals; infected (not yet infectious) individuals; infectious individuals; recovered individuals; is the rate at which -individuals move to infectious class ; infectious individuals () then recover at rate ; implicit vector-borne transmission is modeled with the compartments and ; current force of infection; latent force of infection reflecting the exposed state for mosquitoes during the extrinsic incubation period; is the transition rate associated to the extrinsic incubation period.

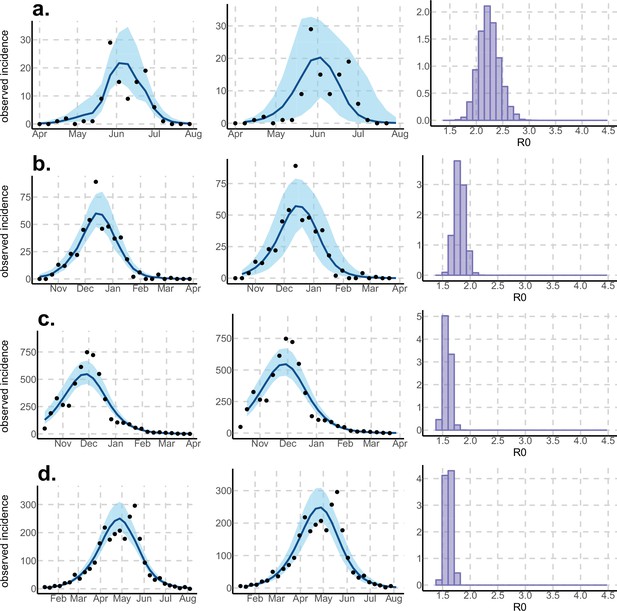
Results using the Pandey model.
Posterior median number of observed Zika cases (solid line), 95% credible intervals (shaded blue area) and data points (black dots). First column: particle filter fit. Second column: Simulations from the posterior density. Third column: posterior distribution. (a) Yap. (b) Moorea. (c) Tahiti. (d) New Caledonia. The estimated seroprevalences at the end of the epidemic (with 95% credibility intervals) are: (a) 73% (CI95: 68–77, observed 73%); (b) 49% (CI95: 45–53, observed 49%); (c) 49% (CI95: 45–53, observed 49%); (d) 39% (CI95: 8–92). See Figure 4.
Results using the Laneri model.
Posterior median number of observed Zika cases (solid line), 95% credible intervals (shaded blue area) and data points (black dots). First column: particle filter fit. Second column: Simulations from the posterior density. Third column: posterior distribution. (a) Yap. (b) Moorea. (c) Tahiti. (d) New Caledonia. The estimated seroprevalences at the end of the epidemic (with 95% credibility intervals) are: (a) 72% (CI95: 68–77, observed 73%); (b) 49% (CI95: 45–53, observed 49%); c) 49% (CI95: 45–53, observed 49%); d) 65% (CI95: 24–91). See Figure 5.
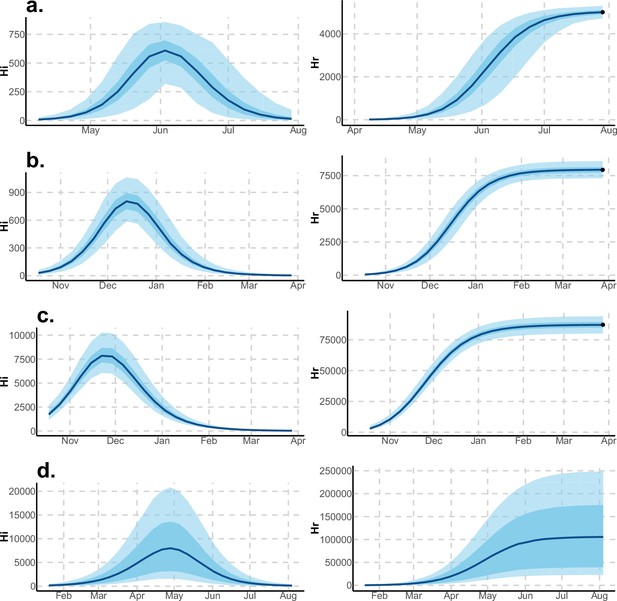
Infected and recovered humans evolution during the outbreak with Pandey model.
Simulations from the posterior density: posterior median (solid line), 95% and 50% credible intervals (shaded blue areas) and observed seroprevalence (black dots). First column: Infected humans (). Second column: Recovered humans (). (a) Yap. (b) Moorea. (c) Tahiti. (d) New Caledonia.
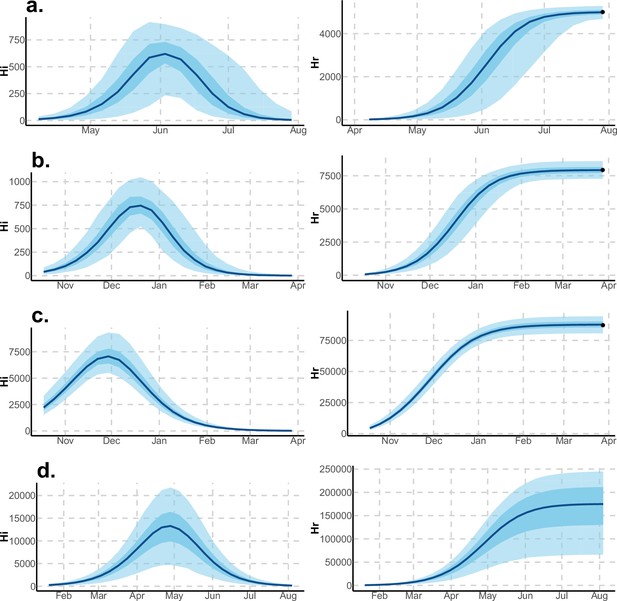
Infected and recovered humans evolution during the outbreak with Laneri model.
Simulations from the posterior density: posterior median (solid line), 95% and 50% credible intervals (shaded blue areas) and observed seroprevalence (black dots). First column: Infected humans (). Second column: Recovered humans (). (a) Yap. (b) Moorea. (c) Tahiti. (d) New Caledonia.

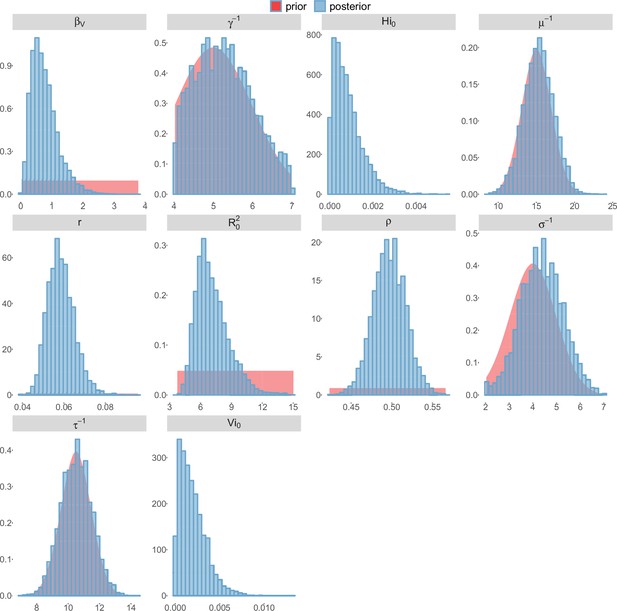
Posterior distributions.
Pandey model, Yap island.
Posterior distributions.
Pandey model, Moorea island.
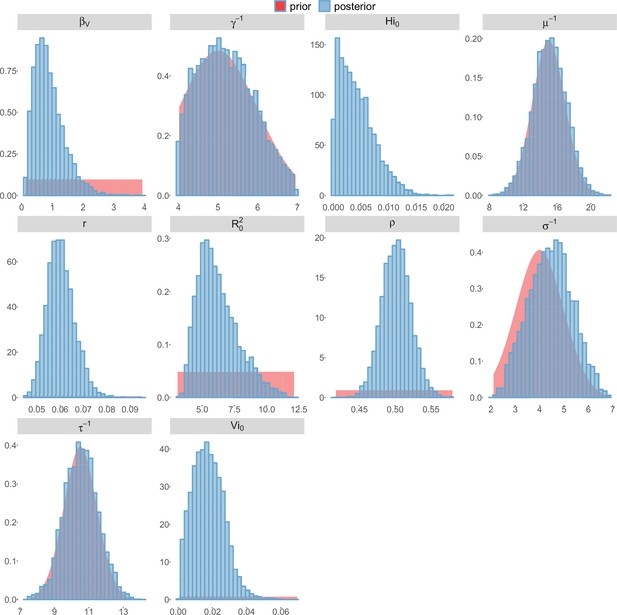
Posterior distributions.
Pandey model, Tahiti island.
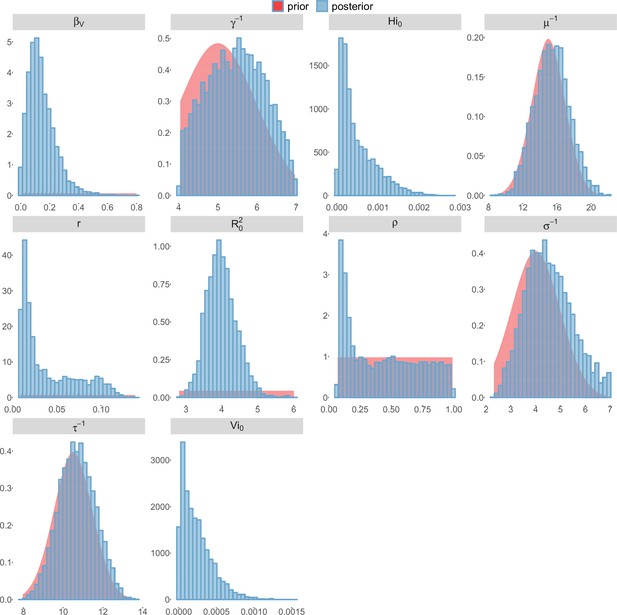
Posterior distributions.
Pandey model, New Caledonia.
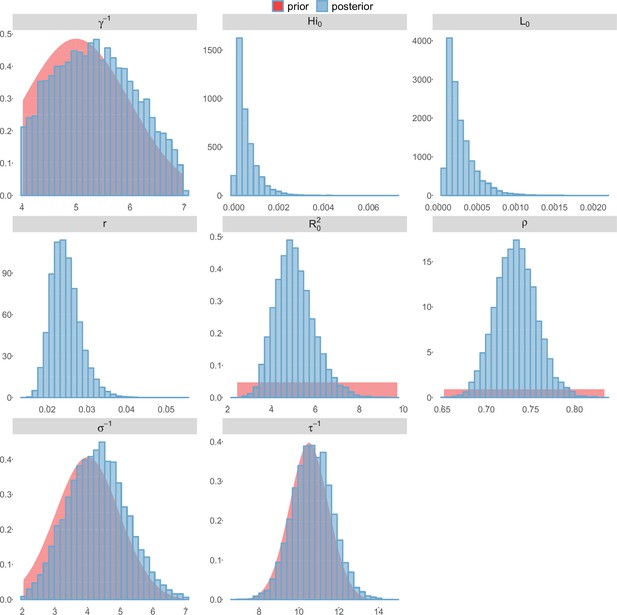
Posterior distributions.
Laneri model, Yap island.
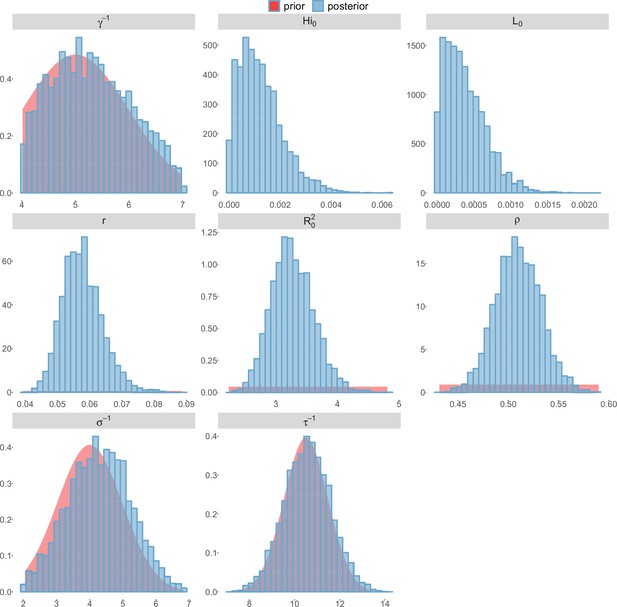
Posterior distributions.
Laneri model, Moorea island.
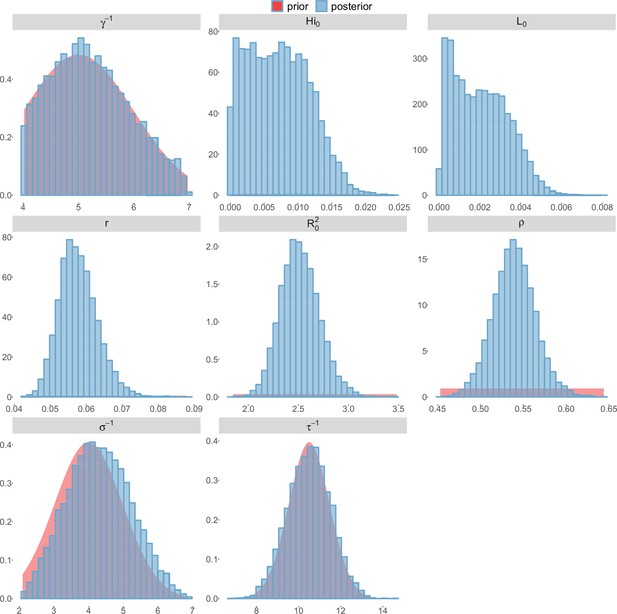
Posterior distributions.
Laneri model, Tahiti island.
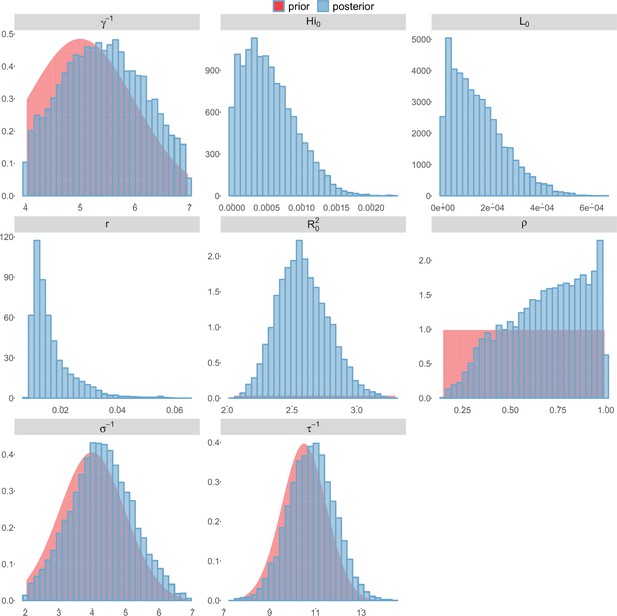
Posterior distributions.
Laneri model, New Caledonia.
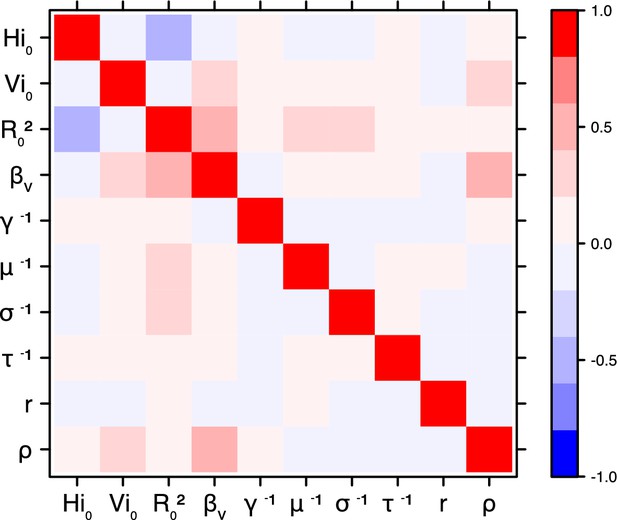
Correlation plot of MCMC output.
Pandey model, Yap island.
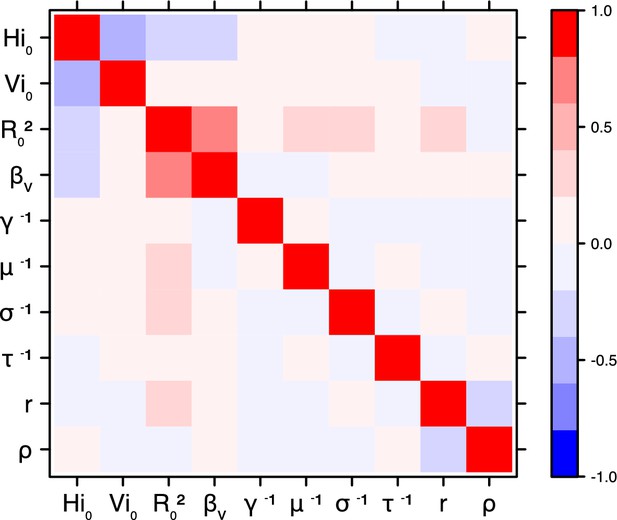
Correlation plot of MCMC output.
Pandey model, Moorea island.
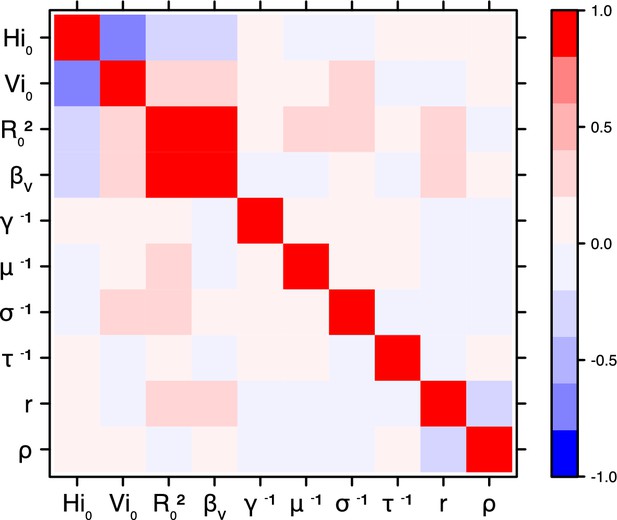
Correlation plot of MCMC output.
Pandey model, Tahiti island.
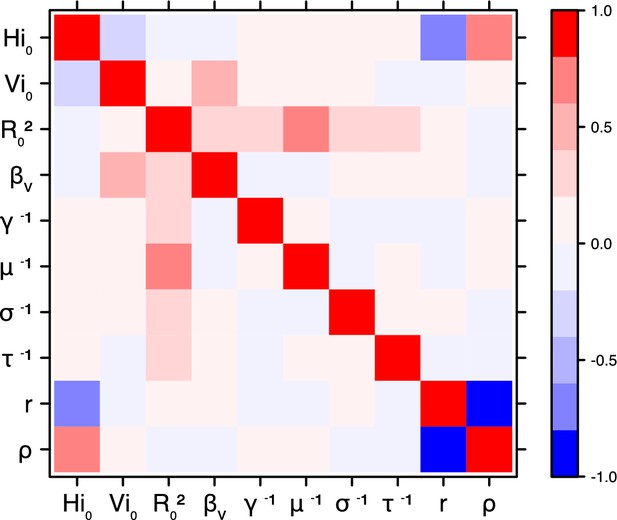
Correlation plot of MCMC output.
Pandey model, New Caledonia.
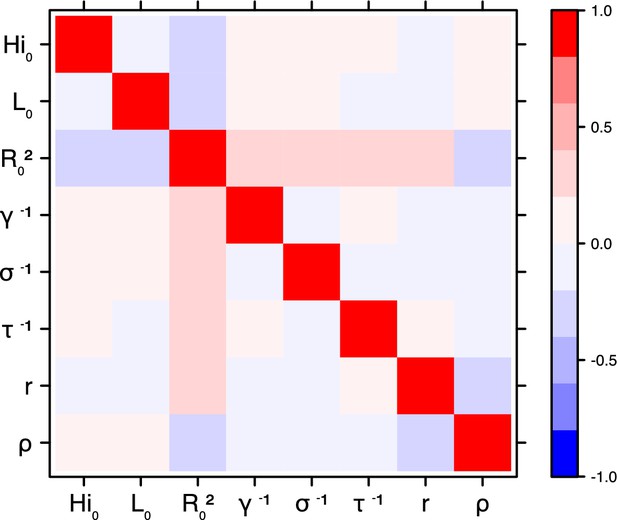
Correlation plot of MCMC output.
Laneri model, Yap island.
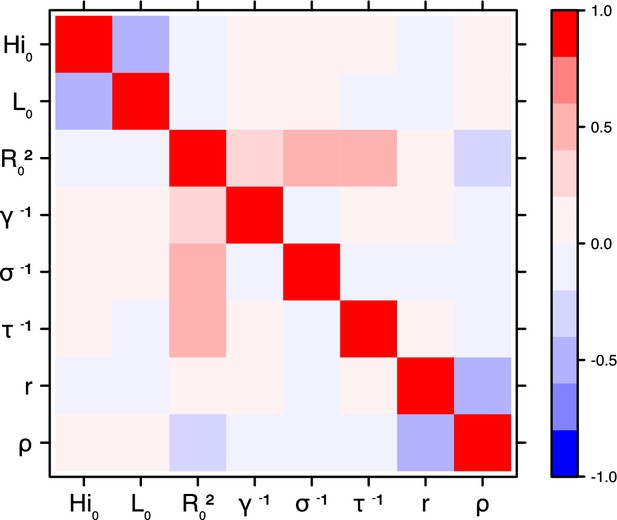
Correlation plot of MCMC output.
Laneri model, Moorea island.

Correlation plot of MCMC output.
Laneri model, Tahiti island.
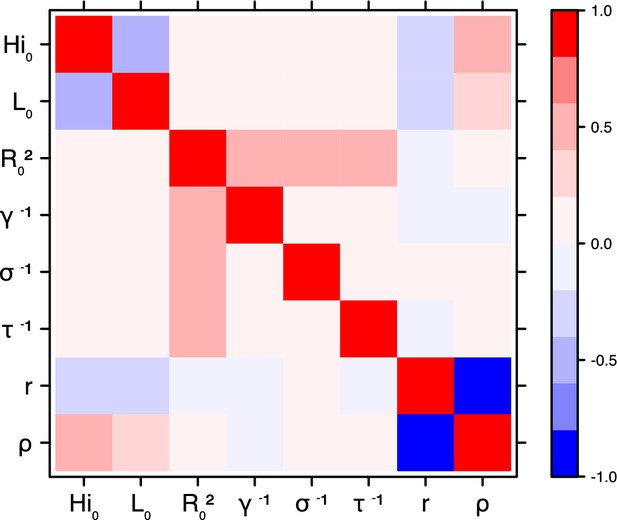
Correlation plot of MCMC output.
Laneri model, New Caledonia.
Tables
Parameter estimations for the Pandey model. Posterior median (95% credible intervals). All the posterior parameter distributions are presented in Figures 6–9 .
| Pandey model | Yap | Moorea | Tahiti | New Caledonia | |
|---|---|---|---|---|---|
| Population size | H | 6892 | 16,200 | 178,100 | 268,767 |
| Basic reproduction number | 3.2 (2.4–4.1) | 2.6 (2.2–3.3) | 2.4 (2.0–3.2) | 2.0 (1.8–2.2) | |
| Observation rate | 0.024 (0.019-0.032) | 0.058 (0.048-0.073) | 0.060 (0.050-0.073) | 0.024 (0.010-0.111) | |
| Fraction of population involved | 74% (69–81) | 50% (48–54) | 50% (46–54) | 40% (9–96) | |
| Initial number of infected individuals | 2 (1–8) | 5 (0–21) | 329 (16–1047) | 37 (1–386) | |
| Infectious period in human (days) | 5.2 (4.1–6.7) | 5.2 (4.1–6.8) | 5.2 (4.1–6.7) | 5.5 (4.2–6.8) | |
| Extrinsic incubation period in mosquito (days) | 10.6 (8.7–12.5) | 10.5 (8.6–12.4) | 10.5 (8.6–12.6) | 10.7 (8.9–12.5) | |
| Mosquito lifespan (days) | 15.6 (11.7–19.3) | 15.3 (11.4–19.1) | 15.1 (11.2–19.0) | 15.4 (11.6–19.4) |
Parameter estimations for the Laneri model. Posterior median (95% credible intervals). All the posterior parameter distributions are presented in Figures 10–13.
| Laneri model | Yap | Moorea | Tahiti | New Caledonia | |
|---|---|---|---|---|---|
| Population size | H | 6892 | 16,200 | 178,100 | 268,767 |
| Basic reproduction number | 2.2 (1.9–2.6) | 1.8 (1.6–2.0) | 1.6 (1.5–1.7) | 1.6 (1.5–1.7) | |
| Observation rate | 0.024 (0.019–0.033) | 0.057 (0.047–0.07) | 0.057 (0.049–0.069) | 0.014 (0.010–0.037) | |
| Fraction of population involved | 73% (69–78) | 51% (47–55) | 54% (49–59) | 71% (27–98) | |
| Initial number of infected individuals | 2 (1–10) | 9 (1–28) | 667 (22–1570) | 82 (2–336) | |
| Infectious period in human (days) | 5.3 (4.1–6.6) | 5.3 (4.1–6.7) | 5.2 (4.1–6.7) | 5.4 (4.1–6.8) | |
| Extrinsic incubation period in mosquito (days) | 10.7 (8.8–12.7) | 10.6 (8.6–12.6) | 10.5 (8.5–12.5) | 10.8 (8.9–12.8) |
Details of the observation models for seroprevalence
| Island | Date | Standard deviation | Observed seroprevalence |
|---|---|---|---|
| Yap | 2007-07-29 | 150 | 5005 (Duffy et al., 2009) |
| Moorea | 2014-03-28 | 325 | 0.49 × 16200 = 7938 (Aubry et al., 2015b) |
| Tahiti | 2014-03-28 | 3562 | 0.49 × 178100 = 87269 (Aubry et al., 2015b) |
Prior distributions of parameters. 'Uniform[0,20]' indicates a uniform distribution in the range [0,20]. 'Normal(5,1) in [4,7]' indicates a normal distribution with mean five and standard deviation 1, restricted to the range [4,7].
| Parameters | Pandey model | Laneri model | References | |||
|---|---|---|---|---|---|---|
| squared basic reproduction number | Uniform[0, 20] | Uniform[0, 20] | assumed | |||
| transmission from human to mosquito | Uniform[0,10] | . | assumed | |||
| infectious period (days) | Normal(5,1) in [4,7] | Normal(5,1) in [4,7] | (Mallet et al., 2015) | |||
| intrinsic incubation period (days) | Normal(4,1) in [2,7] | Normal(4,1) in [2,7] | (Nishiura et al., 2016b; Bearcroft, 1956; Lessler et al., 2016) | |||
| extrinsic incubation period (days) | Normal(10.5,1) in [4,20] | Normal(10.5,1) in [4,20] | (Hayes, 2009; Chouin-Carneiro et al., 2016) | |||
| mosquito lifespan (days) | Normal(15,2) in [4,30] | . | (Brady et al., 2013; Liu-Helmersson et al., 2014) | |||
| fraction of population involved | Uniform[0,1] | Uniform[0,1] | ||||
| Initial conditions (t=0) | Pandey model | Laneri model | ||||
|---|---|---|---|---|---|---|
| HI(0) | infected humans | Uniform[10-6,1]N | Uniform[10-6,1]N | |||
| HE(0) | exposed humans | HI(0) | HI(0) | |||
| HR(0) | recovered humans | 0 | 0 | |||
| infected vectors | VI(0)=Uniform[10-6,1]H | L(0)=Uniform[10-6,1]N | ||||
| exposed vectors | VE(0) = VI(0) | K(0)=L(0) | ||||
| Local conditions | Yap | Moorea | Tahiti | New Caledonia | References | |
|---|---|---|---|---|---|---|
| r | observation rate | Uniform[0,1] | Uniform[0,1] | Uniform[0,0.3] | Uniform[0,0.23] | (Mallet et al., 2015; DASS, 2014) |
| H | population size | 6,892 | 16,200 | 178,100 | 268,767 | (Duffy et al., 2009; Insee, 2012, 2014) |
Square root of the number of secondary cases after the introduction of a single infected individual in a naive population. Median and 95% credible intervals of 1000 deterministic simulations using parameters from the posterior distribution.
| Pandey model | Laneri model | |
|---|---|---|
| Yap | 3.1 (2.5–4.3) | 2.2 (1.9–2.6) |
| Moorea | 2.6 (2.2–3.3) | 1.8 (1.6–2.0) |
| Tahiti | 2.4 (2.0–3.2) | 1.6 (1.5–1.7) |
| New Caledonia | 2.0 (1.8–2.2) | 1.6 (1.5–1.7) |
Sensitivity analysis in Pandey model. Tahiti island. 1000 parameter sets were sampled with latin hypercube sampling (LHS), using 'lhs' R package (Carnell, 2016). On each parameter set, the model was simulated deterministically in order to explore variability in parameters without interference with variations due to stochasticity. PRCC were computed using the 'sensitivity' R package (Pujol et al., 2016).
| Parameters | Distribution | Seroprevalence | Peak intensity | Peak date |
|---|---|---|---|---|
| Model parameters | ||||
| Uniform[0,20] | 0.87 | 0.90 | −0.55 | |
| Uniform[0,10] | −0.66 | −0.73 | 0.35 | |
| Uniform[4,7] | −0.25 | 0.10 | 0.20 | |
| Uniform[2,7] | −0.03 | −0.10 | 0.15 | |
| Uniform[4,20] | −0.05 | −0.07 | 0.06 | |
| Uniform[4,30] | −0.56 | −0.70 | 0.49 | |
| Initial conditions | ||||
| HI(0) | Uniform[2.10-5,0.011] | 0.05 | −0.02 | 0.02 |
| VI(0) | Uniform[10-4,0.034] | 0.11 | −0.00 | −0.26 |
| Fraction involved and observation model | ||||
| Uniform[0.46,0.54] | 0.47 | 0.15 | −0.03 | |
| Uniform[0.048,0.072] | −0.04 | 0.03 | 0.05 |
Sensitivity analysis in Laneri model. Tahiti island. 1000 parameter sets were sampled with latin hypercube sampling (LHS), using 'lhs' R package (Carnell, 2016). On each parameter set, the model was simulated deterministically in order to explore variability in parameters without interference with variations due to stochasticity. PRCC were computed using the 'sensitivity' R package (Pujol et al., 2016).
| Parameters | Distribution | Seroprevalence | Peak intensity | Peak date |
|---|---|---|---|---|
| Model parameters | ||||
| Uniform[0,20] | 0.62 | 0.93 | −0.50 | |
| Uniform[4,7] | 0.01 | 0.62 | 0.15 | |
| Uniform[2,7] | −0.03 | −0.54 | 0.21 | |
| Uniform[4,20] | −0.03 | −0.70 | 0.47 | |
| Initial conditions | ||||
| HI(0) | Uniform[10-5,0.015] | 0.05 | 0.02 | −0.32 |
| L(0) | Uniform[2.10-5,0.004] | 0.05 | 0.00 | −0.16 |
| Fraction involved and observation model | ||||
| Uniform[0.49,0.59] | 0.80 | 0.34 | 0.02 | |
| Uniform[0.048,0.068] | −0.01 | 0.01 | −0.02 |
Additional files
-
Supplementary file 1
Codes for the implementation of each model.
- https://doi.org/10.7554/eLife.19874.031
-
Supplementary file 2
Data file, Yap island.
Number of cases per week and number of immune individuals at the end of the epidemic (Duffy et al., 2009).
- https://doi.org/10.7554/eLife.19874.032
-
Supplementary file 3
Data file, Moorea island.
Number of cases per week and number of immune individuals at the end of the epidemic (Mallet et al., 2015; Aubry et al., 2015b).
- https://doi.org/10.7554/eLife.19874.033
-
Supplementary file 4
Data file, Tahiti island.
Number of cases per week and number of immune individuals at the end of the epidemic (Mallet et al., 2015; Aubry et al., 2015b).
- https://doi.org/10.7554/eLife.19874.034
-
Supplementary file 5
Data file, New Caledonia.
Number of cases per week (DASS, 2014).
- https://doi.org/10.7554/eLife.19874.035





