Flexible theta sequence compression mediated via phase precessing interneurons
- University of Edinburgh, United Kingdom
Figures
Figure 1
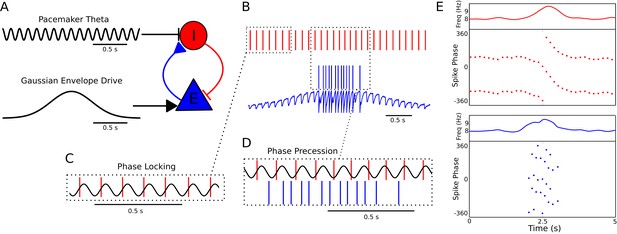
A minimal CA1 circuit model for theta phase precession.
(A) An interneuron (red) is driven by a pacemaker theta oscillation from the medial septum. The interneuron synapses reciprocally onto a pyramidal cell (blue). The pyramidal cell is driven by slower external inputs occurring over behavioral timescales. (B–E) A simulation of this network as the animal crosses the place field of the pyramidal cell. (B) Interneuron spiking activity (red lines) and pyramidal cell spikes (blue lines) and membrane potential (blue trace). (C) A sample of the interneuron spike train when the pyramidal cell is inactive (i.e., outside of the place field), with the pacemaker rhythm overlaid for reference. In this case, the interneuron locks to the pacemaker input. (D) A sample of the interneuron and pyramidal cell spike trains inside the place field. In this case, the interneuron precesses in phase against the pacemaker input and the pyramidal cell fires in bursts which also precess in phase. (E) The membrane frequency in the theta band and the spike phases of the interneuron (red) and pyramidal cell (blue) corresponding to the data shown in parts (A)-(D). Phases are replicated over two cycles for clarity. Note that the pyramidal cell fires up to two spikes per theta cycle in this simulation.
-
Figure 1—source data 1
Table comparing the proposed model to previous models of phase precession.
Our model is the first to successfully explain speed-modulation of precession frequency, two-dimensional phase precession and 360 degrees of phase precession without introducing unobserved circuit components, directionally modulated external inputs or inputs with speed-modulated oscillation frequencies.
- https://doi.org/10.7554/eLife.20349.004
Figure 2 with 1 supplement
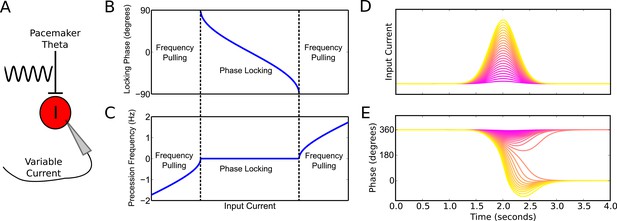
Phase precession and phase locking in a reduced model of an interneuron driven by depolarizing current and weak pacemaker drive.
(A) Schematic of the model. (B–C) Steady state dynamics for a constant depolarizing drive, assuming a linear f-I curve. (B) Phase locking as a function of input current. (C) Precession frequency as a function of input current. For sufficiently strong currents, the interneuron oscillates with a frequency above that of the pacemaker (phase precession). For sufficiently weak currents, the interneuron oscillates more slowly than the pacemaker (phase regression). Note that for more biophysical f-I curves the phase regression regime may be absent. (D–E) Evolution of interneuron phase during a transient, slowly varying current injection. (D) Input currents with Gaussian profiles and a range of amplitudes. (E) Interneuron phase as a function of time, for each current profile shown in (D), showing a total of one cycle of phase precession for stronger drives and only transient phase precession before reversing in phase for weaker drives (purple).
Figure 2—figure supplement 1
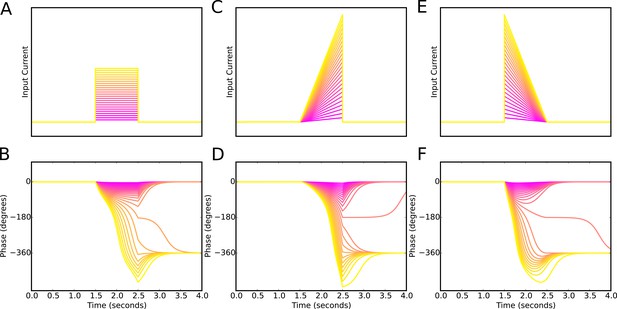
Phase precession is robust to the temporal profile of excitatory drive.
Square pulse excitatory currents (A), upward-going asymmetric ramps (C) and downward-going asymmetric ramps (E) are each able to drive 360 degrees of phase precession (B, D and E). Continuous phase precession through the firing field requires sufficiently strong excitatory drive, but is independent of the shape of the drive. This is in contrast to models that integrate an asymmetric input with a dendritic oscillation.
Figure 3
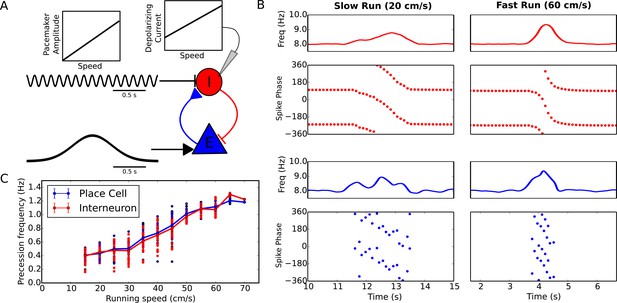
Running speed dependence of phase precession.
(A) Illustration of the model circuit. To account for running speed dependence, pacemaker amplitude and depolarizing current amplitude are increased linearly with running speed. (B) Examples of phase precession at a slow and fast running speed, where the pacemaker amplitude and depolarizing current to interneurons are varied. (C) Phase precession frequency as a function of running speed. Individual dots illustrate the estimated precession frequency on a single lap.
Figure 4
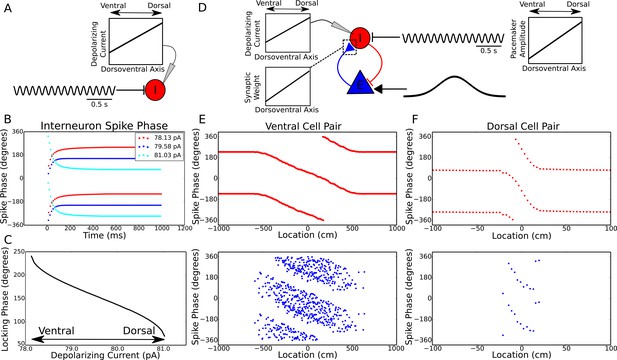
Theta dynamics across the dorsoventral axis.
(A) Inputs to interneurons across the dorsoventral axis hypothesized to produce a gradient in theta phase. (B) Interneuron spike phases for three simulations with different depolarizing currents. (C) Interneuron locking phase vs depolarizing current (cf. Figure 2B). (D) A circuit model, and its dependence on dorsoventral location, which could produce simultaneous traveling theta waves and gradients in precession slope. (E) Phase precession in a ventral place cell/interneuron pair (place field size 10 meters). (F) Phase precession in a dorsal place cell/interneuron pair (place field size 0.3 meters). Note the change in both locking phase and precession slope from dorsal to ventral.
Figure 5 with 2 supplements
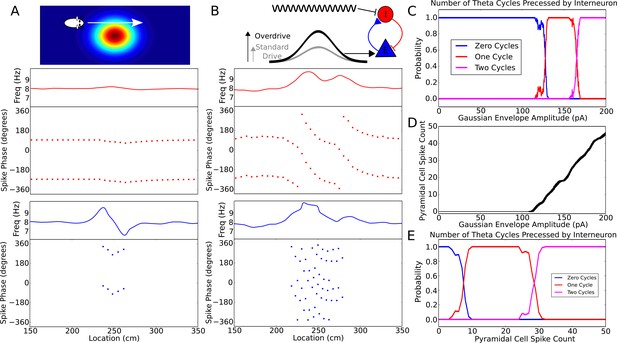
Robustness of phase precession to changes in the strength of place field drive.
(A) Failure to precess through one full cycle. In this case, the external inputs were not strong enough to drive the interneuron past the threshold to be pulled into the next theta cycle, and instead it is pulled back towards the phase it started at. This is also seen in an initial increase followed by a decrease in frequency as the cell advances before reversing in phase against the pacemaker. (B) Precession through two full cycles. In this simulation, the amplitude of the slow envelope current was increased. This results in an increased firing rate of the pyramidal cell and hence an increased excitatory input to the interneuron. As a result, the interneuron received enough drive to pass through two cycles of pacemaker input. (C) The probability of an interneuron precessing through one, two, or three cycles of pacemaker theta phase as a function of the amplitude of the depolarizing envelope current onto the place cell. (D) The number of spikes fired by the place cell (with standard deviation shown as error bars) as a function of the amplitude of depolarizing envelope current. (E) The probability of the interneuron precessing through one, two, or three cycles of pacemaker theta phase replotted as a function of the number of spikes fired by the place cell.
Figure 5—figure supplement 1
Phase precession is robust to transient intrahippocampal perturbation.
Zugaro et al. (2005) demonstrated that spike phase precession persists after transient inactivation of the hippocampus. To address whether our model can account for these observations, we simulated transient silencing of interneurons and pyramidal cells and simultaneous reset of the external pacemaker. Three representative example simulations are shown. In each case, phase precession resumes following the transient perturbation (cf. Figure 3of Zugaro et al., 2005). Left column: The theta phase (black trace), interneuron membrane potential and spikes (red) and pyramidal cell membrane potential and spikes (blue). Right column: The interneuron and pyramidal cell spike phases relative to the pacemaker theta rhythm. Black bars show periods of silencing.
Figure 5—figure supplement 2
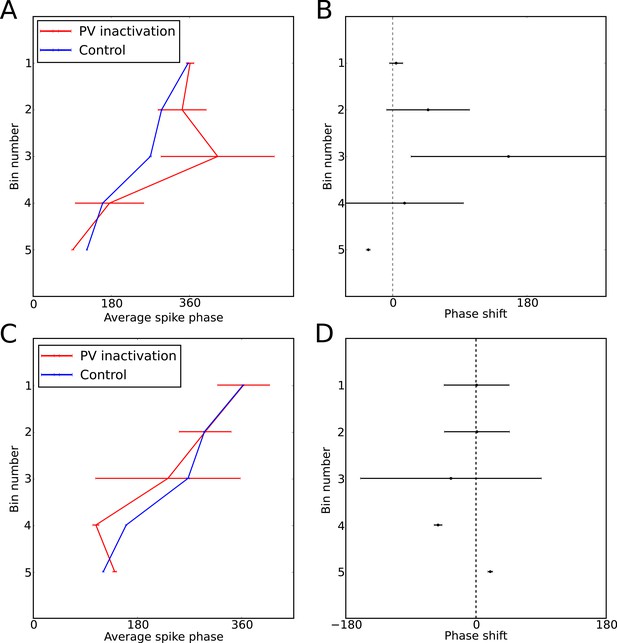
Perturbation of spike phase during interneuron silencing.
(Royer et al., 2012) showed that phase precession by pyramidal cells is maintained following transient silencing of PV neurons, while the phase can appear to shift. To examine whether our model can account for these observations we simulated transient inhibition of interneurons. (A–B) When interneurons were silenced for 1 s, centered on the place cell’s firing field, phase precession was maintained and on average spike phase appears to advance. (A) Average spike phase (circular standard error) across five bins spanning the length of the place field, for the control simulation and for simulations in which interneurons are silenced (cf. Figure 7c in Royer et al., 2012). (B) The mean shift in spike phase in each bin (cf. Figure 7b in Royer et al., 2012). The relatively minor effects of interneuron silencing in our simulations is a result of the phase locking of cells outside of the place field (before interneuron silencing begins), which ensures that pyramidal cells begin spiking at the correct phase upon place field entry. Despite the lack of any theta coordination via interneuron input inside the place field, their tonic spiking over the place field combined with the correct phase alignment at place field entry is sufficient to generate results similar to those of Royer et al. in the averaged data. (C–D) Simulations as for (A–B), but with silencing of interneurons centered on a random location within 20 cm of the place field center, which may better approximate the conditions in Royer et al. (2012). In these simulations phase precession is again maintained, while the phase change is reduced. Thus, when optogenetic silencing only covers part of the place field, interneuron inputs in the unsilenced portion of the place field further reduce the amount of disruption in the averaged data.
Figure 6
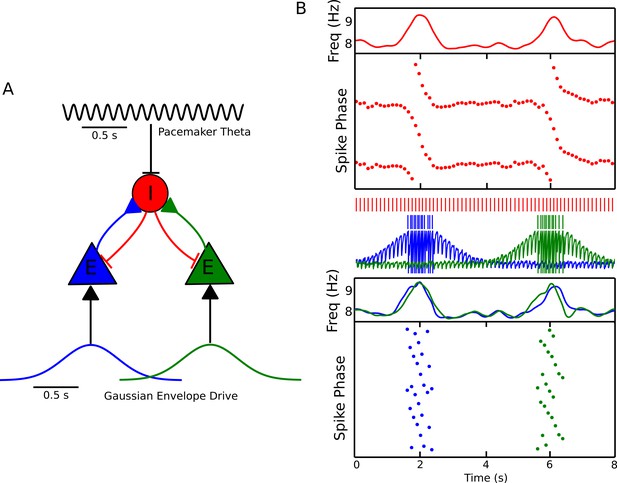
Recruitment of an interneuron for phase precession by multiple pyramidal cells.
(A) Circuit diagram showing two pyramidal cells connected to the same interneuron and receiving slow envelope currents at different points in time. (B) Simulation of this circuit showing the intrinsic theta frequency, spike phases and membrane potentials. When the blue cell recruits the interneuron for phase precession as the animal crosses its place field, this is also reflected in phase precession of the membrane potential oscillation of the green cell while the animal is outside of its firing field (and vice versa).
Figure 7 with 4 supplements
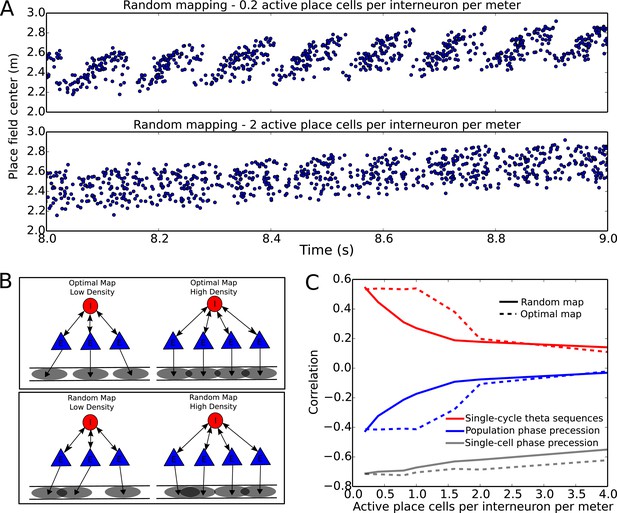
Compression of slow input sequences in CA1 networks.
(A) Network simulations at low and high mapping densities. For sparse, random place field maps, input sequences are compressed into robust theta sequences. For dense, random place field maps, no such sequence compression is observed. (B) Top: Examples of optimal maps given two different place field densities. A set of place cells attached to the same interneuron are mapped onto a linear track. In an optimal map, their place field centers are organized such that their overlap is minimized. For a certain number of place cells per interneuron (here, four) overlap occurs even for an optimal map. Bottom: Example of random maps. The location of each place field on the track is drawn from a uniform probability distribution. In this case, a larger number of place cells per interneuron causes an increase in the probability that place fields will overlap. (C) Network performance vs number of active place cells per interneuron. As more place cells become active (or the number of interneurons is decreased), the compression of inputs into theta sequences is degraded (red and blue traces). This is caused by a drop in the coherence of phase precession in the population, despite a relatively constant phase-position correlation in individual place cells on single laps (blue trace vs gray trace).
Figure 7—figure supplement 1
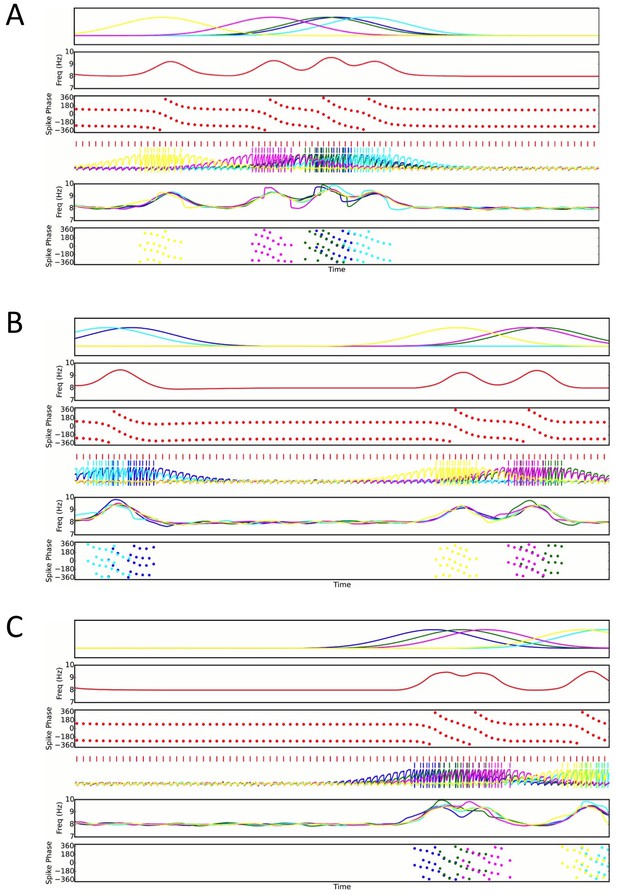
Three examples of random place field maps with a density of one active place cell per interneuron per meter, for which disruption of sequence compression occurs (Figure 7C).
A single interneuron is shown, as well as the active place cells which couple to that interneuron. Top panels: Place field inputs to the five pyramidal cells active on the track and coupled to the single interneuron. Second panels: Interneuron theta frequency over time for a single lap as the animal moves along the track. Third panels: Interneuron spike phases over time. Note that the interneuron precesses over multiple cycles when it receives sufficient pyramidal cell input, but that place field overlap does not always lead to multiple cycles of phase precession. Fourth panels: Interneuron spiking (red ticks), pyramidal cell spiking (colored ticks) and pyramidal cell membrane potential (colored traces) over time. Fifth panels: Pyramidal cell membrane potential theta frequencies over time. Bottom Panels: Pyramidal cell spike phases over time. Note that pyramidal cell spiking is highly synchronous within a theta cycle when multiple pyramidal cells are coactive. This synchrony, as well as the multiple cycles of interneuron phase precession, underlies the disruption of sequence compression observed in Figure 7.
Figure 7—figure supplement 2
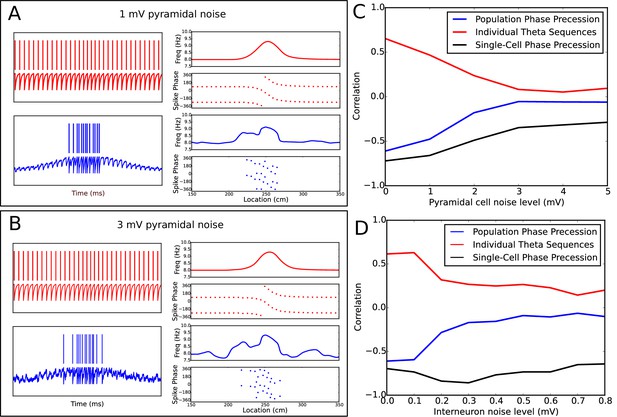
Robustness of phase precession under extraneous noise.
(A−B) Examples of phase precession in simulations with low (A) and moderate (B) levels of noise injected into the pyramidal cell. (C−D) Dependence of phase precession and population sequence compression on the level of injected pyramidal cell (C) and interneuron (D) noise (for an explanation of these metrics, see Figure 7 and its description in both the main text and the Materials and methods section). Note that, for a given amplitude in mV, the noise level also depends on the simulation timestep and membrane time constant (see Equation 14). Note also that, although interneurons and pyramidal cells appear to differ in their sensitivity to noise in these simulations, this is consistent with the amplitudes of other currents injected into the two cell types in the model, which are an order of magnitude smaller for interneurons than pyramidal cells (e.g., the pacemaker and velocity-dependent current to interneurons vs the place field drive and velocity-dependent current to pyramidal cells). As the overall scale of inputs depend strongly on the neuron model and biophysical parameters such as membrane resistance, they cannot be interpreted quantitatively in the present model due to a lack of biophysical detail.
Figure 7—figure supplement 3
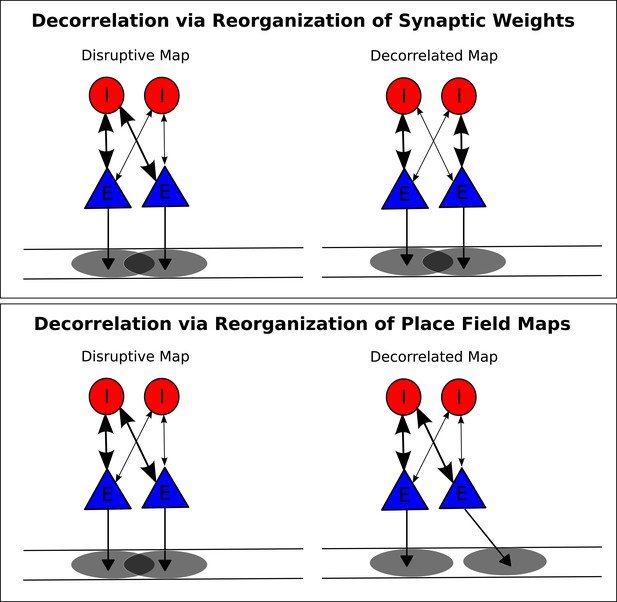
Putative mechanisms for removing disruption from network theta sequences.
(A) In one possible mechanism, synaptic weights between pyramidal cells and interneurons are altered so that pyramidal cell pairs with overlapping place fields no longer functionally couple to the same interneuron. (B) In a second mechanism, the place fields themselves undergo changes to remove overlap for pyramidal cells coupled to the same interneuron.
Figure 7—figure supplement 4
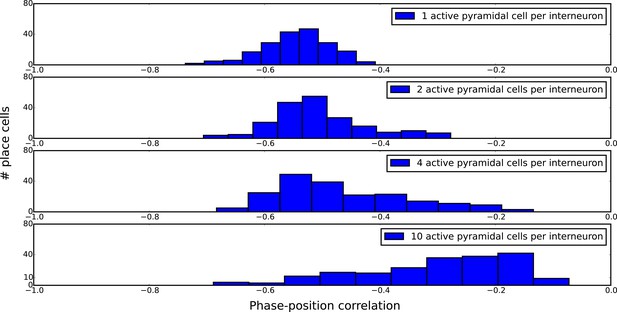
Distributions of single-cell phase precession strengths in random maps with varying degrees of disruptive place field overlap.
Phase-position correlation is measured for each cell using its pooled spiking activity over 30 laps. Each map consisted of 200 pyramidal cells with place fields randomly organized under a uniform distribution over a five meter track. When there is just one active pyramidal cell per interneuron on the track (top panel), the distribution of phase-position correlations simply reflects limited sample size effects, so that increasing the number of laps would yield a narrower distribution. As the number of active pyramidal cells per interneuron is increased, the mean phase-position correlation decreases due to disruptive place field overlap in the network. Nevertheless, strong phase precession continues to be generated in a fraction of pyramidal cells even for very dense maps (bottom panel).
Figure 8
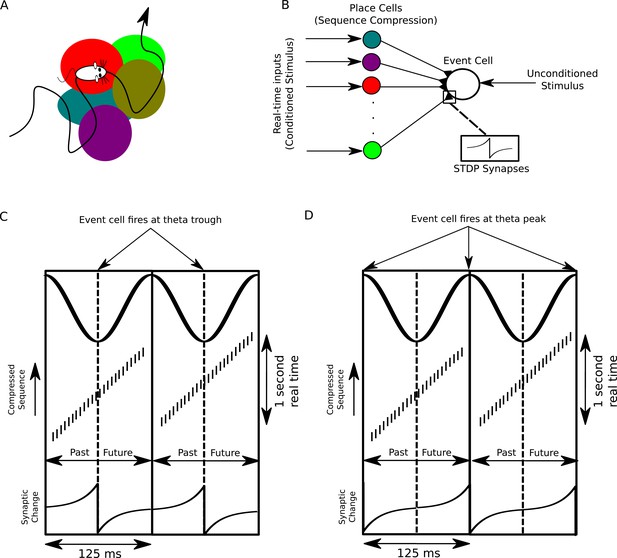
A proposed function of sequence compression for associative learning.
(A) The animal explores an environment, activating different cells in CA1 in a particular temporal order on a behavioral timescale. (B) A population of CA1 place cells performs sequence compression on the slow Gaussian envelope inputs. These cells project onto a downstream neuron which signals some event of interest (the unconditioned stimulus). When this event occurs, this cell fires tonically at the trough of the theta cycle. Synapses from CA1 place cells to the event cell are modifiable via STDP. (C) During each cycle of the theta rhythm, CA1 cell assemblies representing past, present and future events in behavioral time are activated sequentially. At the trough of the theta cycle, place cells representing the animal’s current location are active, whereas during the descending and ascending phases cells representing past and future locations respectively are active. If the downstream cell signaling the unconditioned stimulus fires an action potential at the trough of the theta cycle, STDP between pre- and post-synaptic spikes establishes an association between cells representing recently visited locations and the event. (D) If instead the downstream cell encoding spikes at the peak of the theta rhythm, an association between cells representing upcoming locations and this cell is formed, whereas cells representing recently visited locations and these cells have their synapses weakened (i.e., the temporal associations are reversed relative to those in C).
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Flexible theta sequence compression mediated via phase precessing interneurons
eLife 5:e20349.
https://doi.org/10.7554/eLife.20349
