Figures and data in The cyanobacterial circadian clock follows midday in vivo and in vitro

Figures
Tables

8 figures and 1 table

Figures

Figure 1 with 3 supplements

Download asset Open asset

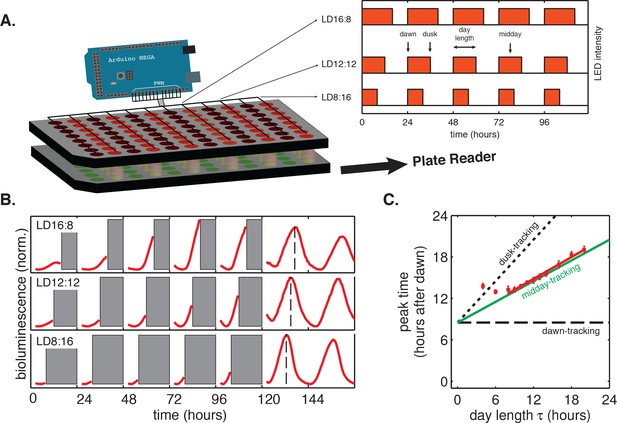
Phase of the cyanobacterial circadian rhythm scales linearly with day length.

(A) LED array device used to grow *S. elongatus* in programmable light-dark cycles. Cells grown in a 96-well plate on solid media (lower plate, *green circles*) are illuminated from above by LEDs (*red circles*). An Arduino microcontroller is used to dynamically change LED intensity in different columns of the plate (*inset*). Luminescence from the bottom plate is read out every 30 min on a plate reader. Drawing not to scale. (B) Drive-and-release strategy to measure phase of the circadian clock under light-dark (LD) cycling. Cells were exposed to five entraining LD cycles and then released into constant light. Bioluminescence signals (P_kaiBC::luxAB) from each well were separated into individual ‘day’ and ‘night’ windows. Data from night portions of the experiment were omitted from analysis (*gray bars*), and data from the day portions of the experiment were aligned to zero baseline and normalized to unit variance. Dashed lines indicate time of peak reporter signal calculated by parabolic fitting. See Computational methods for details. (C) Peak time of bioluminescence (P_kaiBC::luxAB) in light-dark cycles of different day length (*red squares*) was quantified by local parabolic fitting around the first maximum of the oscillation after release into constant light. Error bars represent standard deviations of peak time estimates from technical replicates (n = 4–8). Slope of the linear fit (*red line*, m = 0.53 ± 0.01) was determined by linear regression. *Dashed and dotted black lines* indicate scaling of phase with day length for dawn- and dusk-tracking oscillators; *green line* indicates midday-tracking behavior.

https://doi.org/10.7554/eLife.23539.003

Figure 1—source data 1 Source data for Figure 1B.: https://doi.org/10.7554/eLife.23539.004
Download elife-23539-fig1-data1-v2.xlsx
Figure 1—source data 2 Source data for Figure 1C.: https://doi.org/10.7554/eLife.23539.005
Download elife-23539-fig1-data2-v2.csv
Figure 1—source data 3 Source data for bioluminescence trajectories in Figure 1—figure supplement 1.: https://doi.org/10.7554/eLife.23539.006
Download elife-23539-fig1-data3-v2.csv
Figure 1—source data 4 Source data for Kendall’s τ correlations in Figure 1—figure supplement 1.: https://doi.org/10.7554/eLife.23539.007
Download elife-23539-fig1-data4-v2.csv
Figure 1—source data 5 Source data for Figure 1—figure supplement 2A–E.: https://doi.org/10.7554/eLife.23539.008
Download elife-23539-fig1-data5-v2.xlsx
Figure 1—source data 6 Source data for Figure 1—figure supplement 3A, showing bioluminescence output from the purF repoter.: https://doi.org/10.7554/eLife.23539.009
Download elife-23539-fig1-data6-v2.xlsx
Figure 1—source data 7 Source data for Figure 1—figure supplement 3B.: https://doi.org/10.7554/eLife.23539.010
Download elife-23539-fig1-data7-v2.xlsx

Figure 1—figure supplement 1

Download asset Open asset

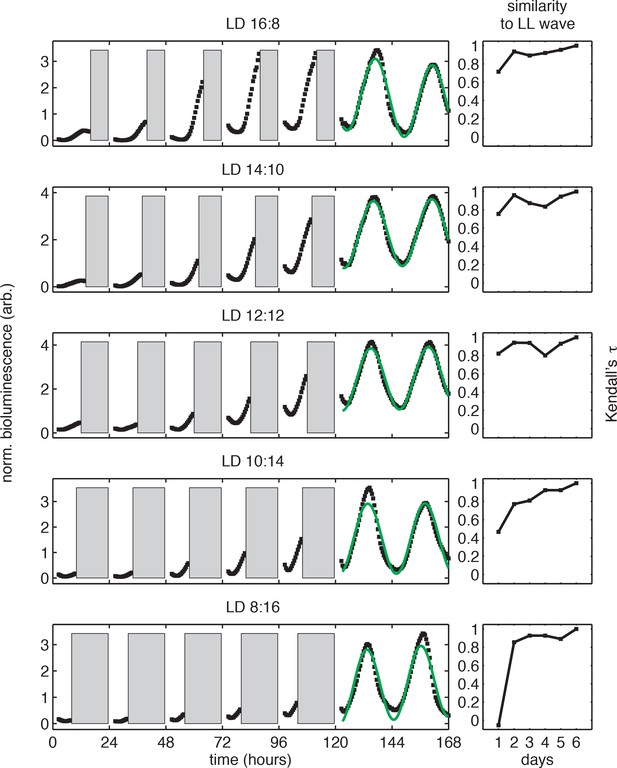
Bioluminescence recordings from *P_kaiBC::luxAB* reporter in light-dark cycles.

(*left*) Selected bioluminescence traces (*P_kaiBC::luxAB, black*) recorded from individual wells of the 96-well LED array device in conditions simulating day-night cycles of different day length (same dataset as in Figure 1B–C). Data recorded in the dark (*gray bars*) and in the first two hours after lights-on were omitted from analysis. Each trajectory was normalized to the mean and variance of the bioluminescence signal recorded after the release into constant light, and trajectories recorded after release into constant light were fit to sinusoids (*green*). For illustration purposes here, trajectories were aligned to zero baseline. See Computational methods for fitting details. (*right*) Similarity between the bioluminescence rhythms (*P_kaiBC::luxAB)* recorded during light-dark entrainment and after release into free running conditions. Nonparametric correlation coefficient (Kendall’s τ) between bioluminescence trajectories recorded in the light during entrainment (days 1–5) and the corresponding time period after release into constant light (e.g. a 16-hr window in LL for LD 16:8). See Computational methods for details.

https://doi.org/10.7554/eLife.23539.011

Figure 1—figure supplement 2

Download asset Open asset

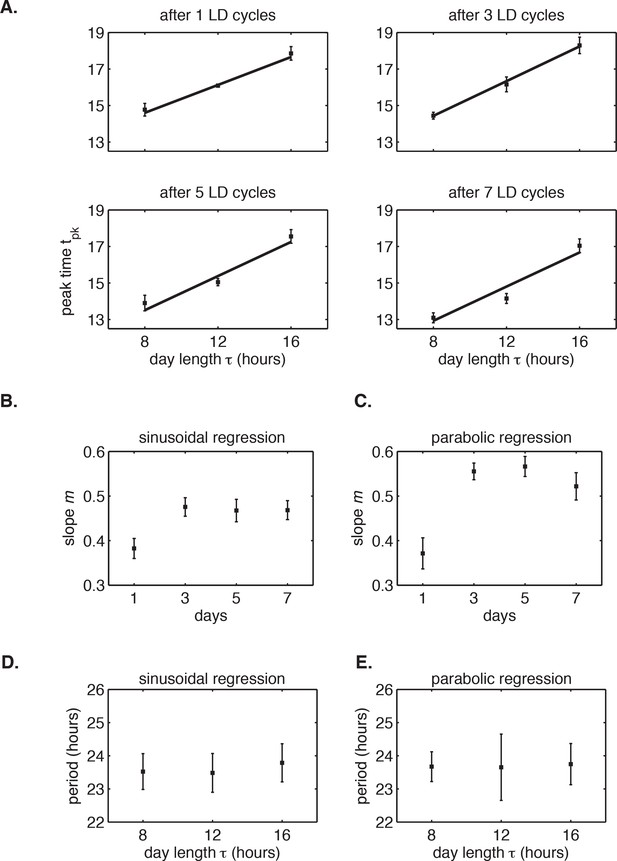
The circadian rhythm of *S. elongatus* rapidly entrains to 24 hr diurnal cycles with 8–16 hr of daylight.

(A) Peak times of *P_kaiBC::luxAB* reporter after release into LL from 1 to 7 LD cycles of different day length (LD 8:16, LD 12:12 or LD 16:8), as estimated by sinusoidal regression. Error bars represent the standard deviation (σ) of technical replicates (n = 6–8 replicates per condition). Lines mark linear fits to the data. (B) Slope m of clock phase scaling with day length stabilizes after three light-dark cycles. Slope of linear fits in (A) plotted against day length in diurnal cycles. Error bars mark uncertainty in fit slope (±σ). (C) Slope m of clock phase scaling with day length, as estimated by parabolic regression (see Computational methods). (**D and E**) Free-running period of *P_kaiBC::luxAB* reporter rhythms, as estimated from sinusoidal fits (D) or local parabolic fits (E), recorded in continuous light after entrainment to 24 hr cycles with 8, 12, or 16 hr of daylight.

https://doi.org/10.7554/eLife.23539.012

Figure 1—figure supplement 3

Download asset Open asset

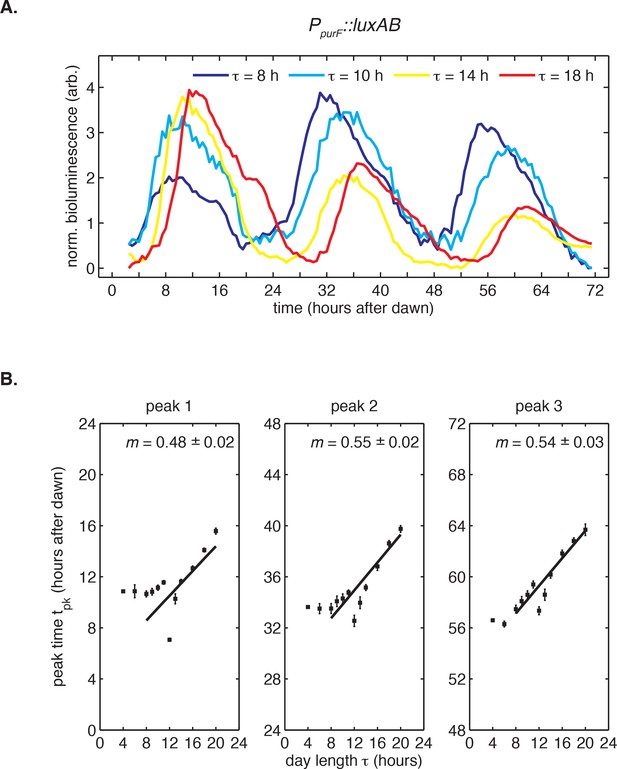
Bioluminescence recordings from *P_purF::luxAB* reporter in light-dark cycles.

(A) Rhythms in bioluminescence in continuous light recorded from a dawn gene reporter (*PpurF::luxAB)* after entrainment to 24 hr light-dark cycles of different day length τ (LD 8:16, LD 10:14, LD 14:10, LD 18:6). Following the protocol in Figure 1, cells received five light-dark cycles and were then placed under continuous illumination. Bioluminescence trajectories from first 72 hr after release into constant conditions were aligned to zero baseline and normalized to unit variance. (B) Peak times of the *PpurF::luxAB* reporter in constant light after entrainment with five LD cycles of different day length (LD 4:20 to LD 20:4). Peak times were determined by local parabolic regression (see Computational methods). Error bars represent standard errors of technical replicates (n = 4–8). Straight lines represent linear fits to data from wells entrained to day lengths at least 8 hr long.

https://doi.org/10.7554/eLife.23539.013

Figure 2 with 1 supplement

Download asset Open asset

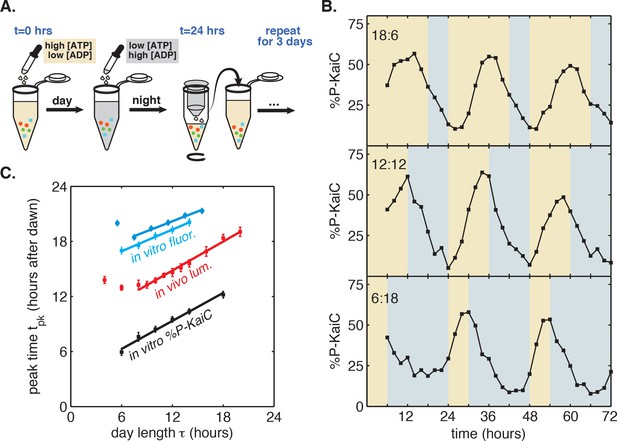
Reconstitution of the seasonal clock response in vitro.

(A) Buffer exchange protocol to simulate metabolic driving of the clock. To mimic daytime in vitro, purified Kai proteins (*green, blue and red symbols*) were incubated in ‘day’ reaction buffer containing ATP. ADP was added to mimic nightfall ([ATP]/([ATP]+[ADP]) ≈ 25%). At simulated dawn, reactions were returned to ‘day’ buffer via buffer exchange. (B) Example traces of KaiC phosphorylation rhythm from in vitro reactions mimicking LD 18:6 (*top*), LD 12:12 (*middle*), and LD 6:18 (*bottom*). (C) Phase of KaiABC oscillation scales linearly with simulated day length (time spent in ‘day’ buffer), as assessed by the peak time of KaiC phosphorylation (*black squares*) or peak time of fluorescence polarization (*cyan squares* and *circles*, for two replicates) of fluorescently labeled KaiB. Peak times of fluorescence polarization were estimated from sinusoidal fits to oscillations recorded in free-running conditions after entraining the oscillator with three metabolic cycles. Peak time of %P-KaiC was estimated by fitting sinusoids to KaiC phosphorylation time series from the third day of reactions. Error bars represent uncertainty of fit phase from sinusoidal regression. Lines of best fit were determined by linear regression (*cyan squares: m* = 0.39 ± 0.06, *cyan circles: m* = 0.36 ± 0.04, *black: m* = 0.51 ± 0.04). In vivo data (from Figure 1C) is plotted in *red*. Scaling of entrained phase was measured once via KaiC phosphorylation analysis (*black*) and twice using the fluorescence polarization probe (*cyan squares* and *circles*) with an independent preparation of proteins.

https://doi.org/10.7554/eLife.23539.015

Figure 2—source data 1 Source data for Figure 2B.: https://doi.org/10.7554/eLife.23539.016
Download elife-23539-fig2-data1-v2.csv
Figure 2—source data 2 Source data for Figure 2C.: https://doi.org/10.7554/eLife.23539.017
Download elife-23539-fig2-data2-v2.xlsx
Figure 2—source data 3 Source data for Figure 2—figure supplement 1.: https://doi.org/10.7554/eLife.23539.018
Download elife-23539-fig2-data3-v2.xlsx

Figure 2—figure supplement 1

Download asset Open asset

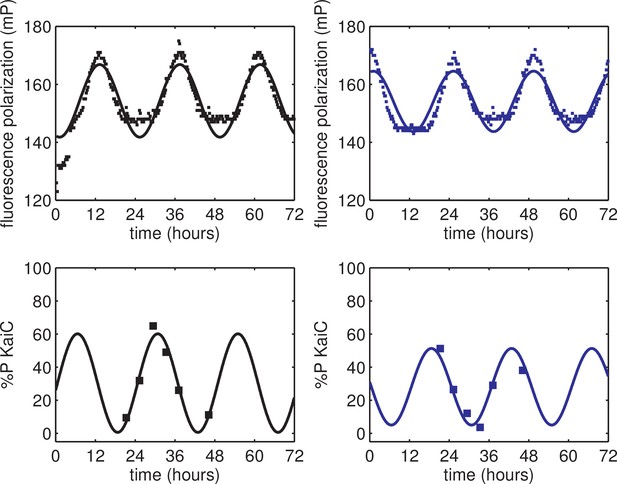
Validation of KaiB fluorescence polarization reporter against KaiC phosphorylation rhythm.

(*top*) Fluorescence polarization of KaiABC mixture probed with fluorescently labeled KaiB exhibits ≈24 hr rhythms (*black and blue squares*). (*bottom*) KaiC phosphorylation rhythm of the same reaction mixtures as in the top panel (*black and blue squares*). *Black vs blue markers* show data from two identical reactions started at different times. Curves show best-fit sinusoids, where all fits share a common period; the phase offset between out-of-phase reactions was also a shared parameter across fits to polarization and phosphorylation datasets. This experiment was performed once.

https://doi.org/10.7554/eLife.23539.019

Figure 3 with 2 supplements

Download asset Open asset

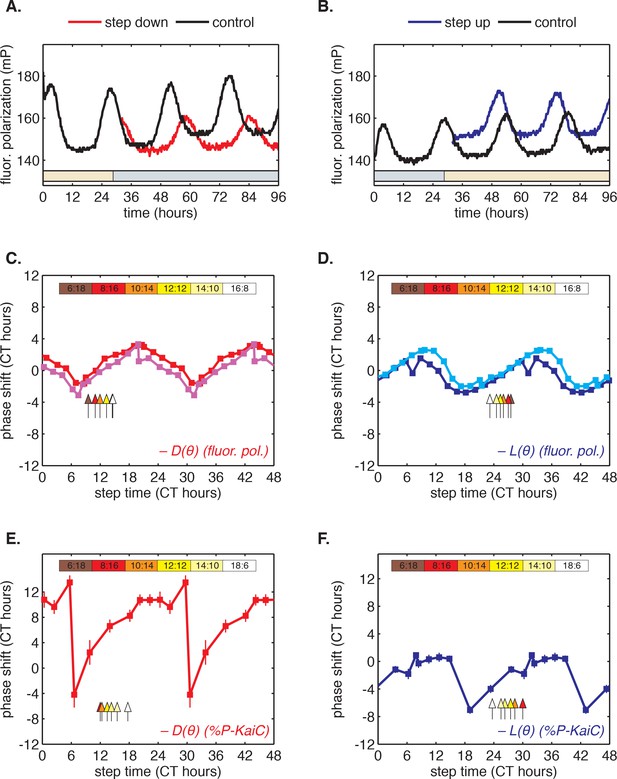
Clock responses to metabolic steps mimicking dawn (step up) and dusk (step down).

(A) Phase shift in fluorescence polarization (*red curve*) caused by a shift to a buffer that mimics the nucleotide pool at night ([ATP]/([ATP]+[ADP]) ≈ 25%, *gray bar*). The control reaction remained in the original buffer (*black curve*). (B) Phase shift in fluorescence polarization (*blue curve*) caused by a shift from night buffer back to day buffer ([ATP]/([ATP]+[ADP]) ≈ 100%, *beige bar*). (**C, D**) Summary of phase shifts caused by metabolic step-down (C) or step-up (D) perturbations throughout the clock cycle. Simulated day-night or night-day steps were administered as in (A) and (B). Different colors represent independent measurements. To estimate the phase of each reaction, trajectories were fit to sinusoids. Phase shifts were determined relative to the respective control reactions. The times at which buffer steps were administered were converted to circadian time (CT 0 corresponds to the estimated trough of KaiC phosphorylation based on Figure 2—figure supplement 1). Colored arrows indicate clock phases when metabolic shifts occur in entrained conditions. (**E, F**) Analogs of (**C, D**) for the gel-based phosphorylation measurements on an independent preparation of Kai proteins. Error bars represent standard deviations calculated by bootstrapping (see Computational methods). Horizontal error bars are smaller than marker widths.

https://doi.org/10.7554/eLife.23539.020

Figure 3—source data 1 Source data for Figure 3A–B.: https://doi.org/10.7554/eLife.23539.021
Download elife-23539-fig3-data1-v2.csv
Figure 3—source data 2 Source data for Figure 3C–D.: https://doi.org/10.7554/eLife.23539.022
Download elife-23539-fig3-data2-v2.xlsx
Figure 3—source data 3 Source data for Figure 3E–F.: https://doi.org/10.7554/eLife.23539.023
Download elife-23539-fig3-data3-v2.xlsx

Figure 3—figure supplement 1

Download asset Open asset

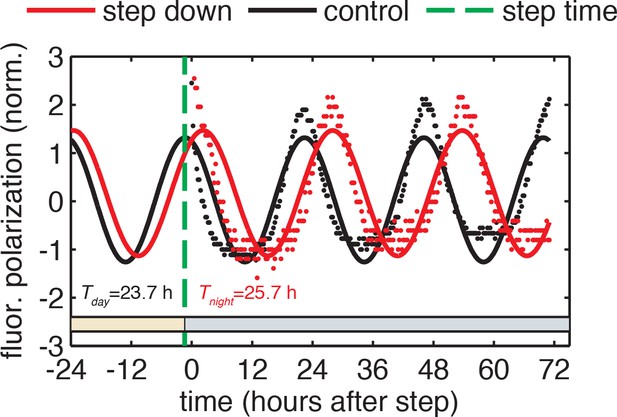
Example calculation of phase shifts in response to metabolic step transitions.

Phase shifts are computed from the difference in phase of the control reaction and the perturbed reaction evaluated at the time of the step. Phase of each reaction at the time of the step (*green dashed line*) is calculated based on the sinusoidal fit to the normalized fluorescence polarization trajectory for that reaction. Periods of the oscillator in day and night conditions were fit globally to all reactions measured in one experiment. See Computational methods for fitting details.

https://doi.org/10.7554/eLife.23539.024

Figure 3—figure supplement 2

Download asset Open asset

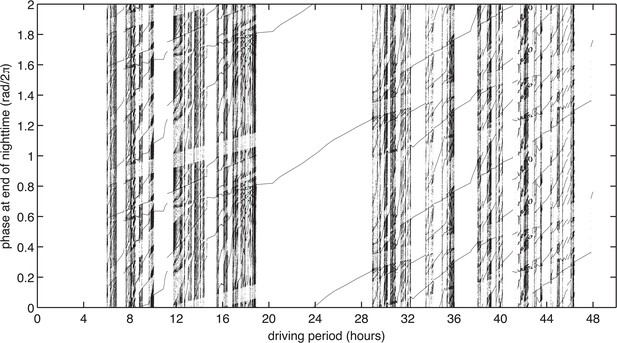
Experimentally measured step-response functions predict entrainment to driving periods near 24 hr.

(A) Entrainment simulations with driving periods 4–48 hr were performed for 1000 cycles, and phases at the end of nighttime (immediately before the action of $L$ ) of the last 920 cycles were plotted. Simulation results are double-plotted along the vertical axis for clarity. In each simulation, the oscillator runs at constant angular speed in the light and dark, and experiences instantaneous phase shifts at dawn and dusk, according to the values of $L$ and $D$ . Refer to Figure 4A for an illustration of a single entrainment simulation.

https://doi.org/10.7554/eLife.23539.025

Figure 4 with 3 supplements

Download asset Open asset

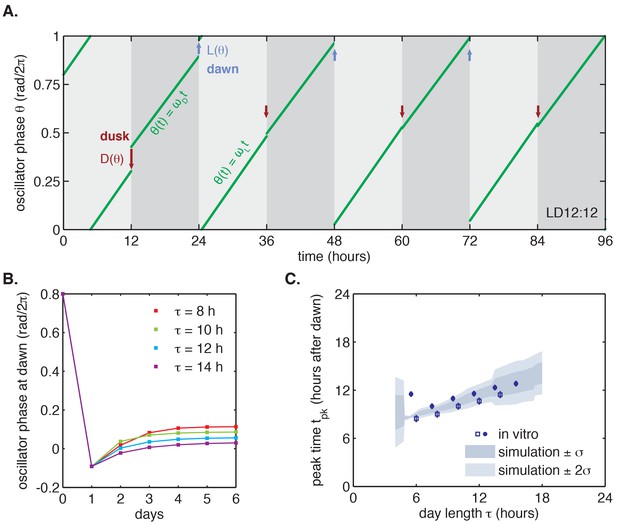
Entrainment of the phase oscillator model to a driving cycle.

(A) Schematic of a phase-only oscillator that responds to dawn and dusk with instantaneous phase shifts. The oscillator runs at constant velocities $ω_{L}$ during the day and $ω_{D}$ at night (*green lines*), except for dawn and dusk where sudden shifts occur (*red and blue arrows*). This simulation illustrates entrainment to a LD 12:12 cycle for an oscillator with $ω_{L}$ (1/23.7 hr), $ω_{D}$ (1/25.7 hr), and $L (θ)$ and $D (θ)$ as experimentally measured for the KaiABC oscillator (see main text, Computational Methods). Refer to Figure 4—figure supplement 1B for illustrations of $L (θ)$ and $D (θ)$ used in this simulation. (B) Simulated approach to stable entrainment in the model (as in Figure 4A) for light-dark cycles of different day length (τ = 8–14 hr). (C) Simulated seasonal response of an oscillator that responds rapidly to light-dark cues according to the phase shift functions in Figure 3C (see text). In simulations, $t_{p k}$ is defined as the time when oscillator phase $θ$ equals π rad (0.5 cycles), corresponding to the peak of KaiC phosphorylation. Shaded areas correspond to standard deviations of entrainment simulations using the four possible combinations of $L$ and $D$ functions shown in Figure 3(C–D). *Blue squares and circles* indicate experimentally determined entrained phases measured using the fluorescence polarization reporter in Figure 2C. Peak times in polarization data were converted to equivalent peak KaiC phosphorylation times using the measured phase offset for the polarization reporter (Figure 2—figure supplement 1). Error bars on in vitro data show uncertainty of fit phase.

https://doi.org/10.7554/eLife.23539.026

Figure 4—source data 1 Source data for Figure 4C. This file contains data from in vitro entrainment measurements shown as blue circles and squares.: https://doi.org/10.7554/eLife.23539.027
Download elife-23539-fig4-data1-v2.csv
Figure 4—source data 2 Source data for Figure 4—figure supplement 2. This file contains in vitro entrainment measurements shown as blue squares in Figure 4—figure supplement 2B.: https://doi.org/10.7554/eLife.23539.028
Download elife-23539-fig4-data2-v2.csv

Figure 4—figure supplement 1

Download asset Open asset

Example simulation of a phase oscillator governed by one set of experimentally determined $L (θ)$ and $D (θ)$ functions and subjected to a driving cycle.

(A) The phase oscillator reaches stable entrainment within 3–5 light-dark cycles (τ = 10–14 hr) for a wide range of starting phases. Simulation parameters same as in Figure 4B; $L (θ)$ and $D (θ)$ as shown in (B) below. (B) Example pair of step response functions, denoted $\hat{L} (\hat{θ})$ and $\hat{D} (\hat{θ})$ , measured using the fluorescence-polarization reporter of KaiB-KaiC binding (magenta and blue curves in Figure 3C–D). Colored circles mark phases corresponding to dawn (on $\hat{L} (\hat{θ})$ ) and dusk (on $\hat{D} (\hat{θ})$ ) in seasonal entrainment simulations of different day length τ (see color bar). $θ$ = 0 refers to the phase when the minimum of the KaiC phosphorylation rhythm occurs. See Computational methods for details.

https://doi.org/10.7554/eLife.23539.029

Figure 4—figure supplement 2

Download asset Open asset

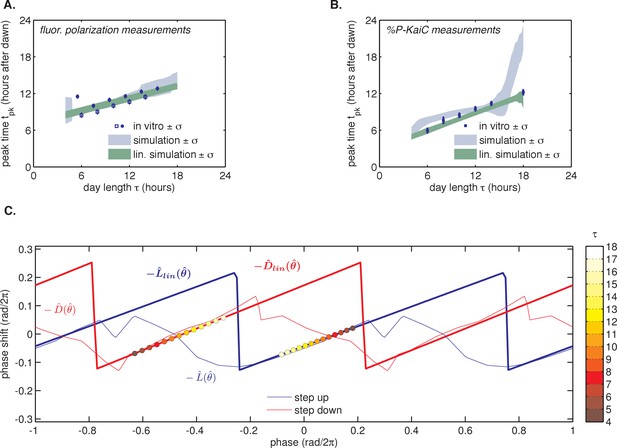
Simulations of seasonal entrainment for a phase oscillator driven by linearized step-response functions ( $L_{l i n}$ and $D_{l i n}$ ).

(A) Simulated seasonal response of phase oscillators governed by the four possible combinations of nonlinear $\hat{L} (\hat{θ})$ and $\hat{D} (\hat{θ})$ step-response functions in Figure 3(C–D) (*blue shaded areas*) and their linearized versions ${\hat{L}}_{l i n} (\hat{θ})$ and ${\hat{D}}_{l i n} (\hat{θ})$ (*shaded green areas*). In simulations, $t_{p k}$ is defined as the time when oscillator phase $θ$ equals π rad (0.5 cycles), corresponding to the peak of KaiC phosphorylation. In vitro measurements overlaid in blue as in Figure 4C. (B) Simulated seasonal response of phase oscillators governed by step-response functions measured for an independent preparation of clock proteins using SDS-PAGE analysis of KaiC phosphorylation Figure 3(E–F). Shaded areas correspond to standard deviations determined by bootstrapping (see Computational methods). *Blue squares* show seasonal response measured in the purified KaiABC oscillator using the same preparation of proteins and measured via SDS-PAGE (Figure 2C). $t_{p k}$ is defined as in (B) above. Error bars represent uncertainty of fit phase from sinusoidal regression. (C) Example pair of step-response functions $\hat{L} (\hat{θ})$ and $\hat{D} (\hat{θ})$ and their linearized versions, ${\hat{L}}_{l i n} (\hat{θ})$ and ${\hat{D}}_{l i n} (\hat{θ})$ , used in simulations in (A) above and measured using the fluorescence-polarization reporter of KaiB-KaiC binding (magenta and blue curves in Figure 3C–D). Colored circles mark stably entrained phases corresponding to dawn (for $\hat{L} (\hat{θ})$ ) and dusk (for $\hat{D} (\hat{θ})$ ) in simulations of different day length τ (see color bar). $θ$ = 0 refers to the minimum of the KaiC phosphorylation rhythm. See Computational methods for details.

https://doi.org/10.7554/eLife.23539.030

Figure 4—figure supplement 3

Download asset Open asset

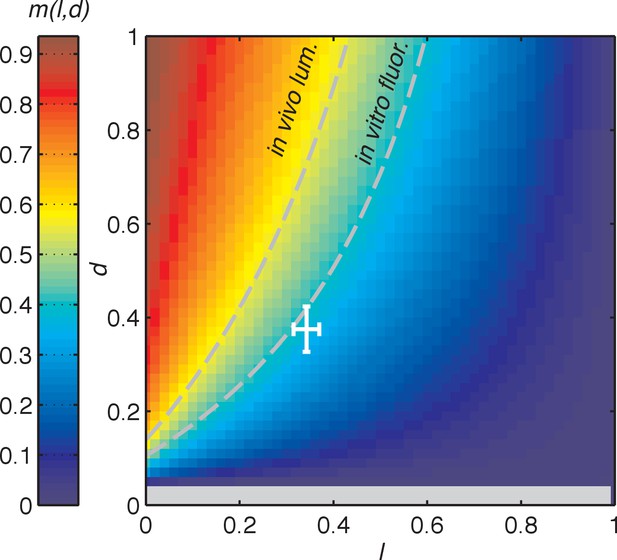
Dependence of the slope of entrained phase on the slopes of step response functions.

Heat map of slope m, describing the scaling of oscillator peak time with day length, as a function of the slopes l and d of linear $L (θ)$ and $D (θ)$ step response functions and oscillator frequencies in light and dark ( $ω_{D}$ and $ω_{L}$ ) (see main text and Appendix 1). This relationship is described by $m (l, d) = 1 - \frac{- (1 - l) \times (ω_{D} / ω_{L})}{d + l - l d} - \frac{1}{d + l - l d}$ . The ratio of oscillator frequencies in light and dark was estimated to be $ω_{D} / ω_{L} = 0.93$ based on the analysis of datasets in Figure 3(C–D). Dashed isolines connect all points with m = 0.53 (*left*) and m = 0.38 (*right*), corresponding to our estimates of scaling coefficients in vivo and in vitro in Figure 2(C). The approximate range of values of l and d estimated from experimental measurements in Figure 3(C–D) is indicated by the white crosshair. Crosshair lengths represent mean±standard deviation of estimates of l and d determined by bootstrapping, as described in Computational methods. Negative values of m are colored in grey.

https://doi.org/10.7554/eLife.23539.031

Figure 7

Download asset Open asset

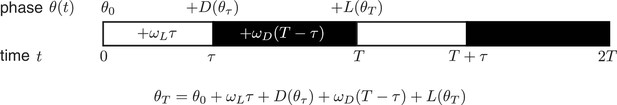
Phase oscillator entrainment.
https://doi.org/10.7554/eLife.23539.032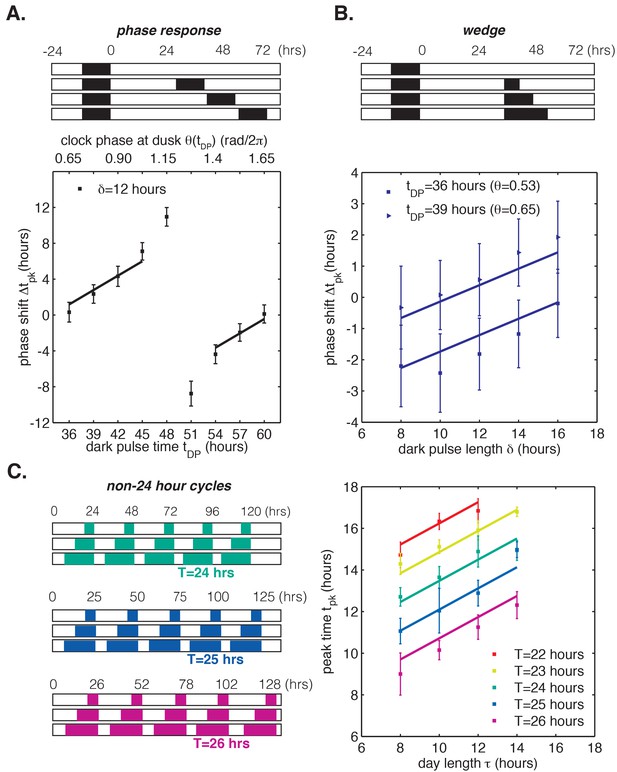

Figure 5 with 1 supplement

Download asset Open asset

Phase oscillator model with linear phase shift functions predicts entrainment of the cyanobacterial clock to different light-dark (LD) patterns.

In all panels, error bars represent standard deviations (n = 4–8 technical replicates per point). Lines are fit globally to all three datasets in (A)-(C). See Computational methods for details. (A) Phase resetting analysis. Phase shifts of bioluminescence rhythm (P_kaiBC::luxAB) due to 12 hr dark pulses (δ = 12 hr) administered throughout the circadian cycle. The experimental protocol is represented schematically above the graph. Cells were exposed to one 12 hr dark pulse and released into constant light; 12 hr dark pulses were administered at the indicated times. *θ(t_DP)* is the clock phase at beginning of the dark pulse, with $θ$ = 0 defined as clock phase at the trough of the bioluminescence rhythm. (B) Wedge analysis. Phase shifts of bioluminescence rhythm (P_kaiBC::luxAB) due to dark pulses of varied length (δ = 8–16 hr) administered near subjective dusk (36 or 39 hr after an initial 12 hr dark pulse). Clock phases at the beginning of the dark pulse are listed in parentheses; $θ$ = 0 is defined as clock phase at the trough of the bioluminescence rhythm. The experimental protocol is represented schematically above the graph. (C) Seasonal response in non-24 hour environmental cycles. Cells were grown in LD cycles with period T = 22–26 hr and day length τ = 8–14 hr (see schematic on left). After five entraining cycles, cells were released into LL and the phase of the circadian rhythm was estimated by sinusoidal regression.

https://doi.org/10.7554/eLife.23539.033

Figure 5—source data 1 Source data for Figure 5A–C.: https://doi.org/10.7554/eLife.23539.034
Download elife-23539-fig5-data1-v2.xlsx

Figure 5—figure supplement 1

Download asset Open asset

Simulation of a phase-resetting curve.

(*left*) Simulated phase-resetting curve due to a 12 hr dark pulse for a phase oscillator governed by linear step-response functions ${\hat{L}}_{l i n} (\hat{θ})$ and ${\hat{D}}_{l i n} (\hat{θ})$ (*right*), as in in Figure 4—figure supplement 2. Colored circles indicate phases at the beginning of the dark pulse (see color bar). $θ$ = 0 refers to the trough of the KaiC phosphorylation rhythm.

https://doi.org/10.7554/eLife.23539.035

Figure 6 with 3 supplements

Download asset Open asset

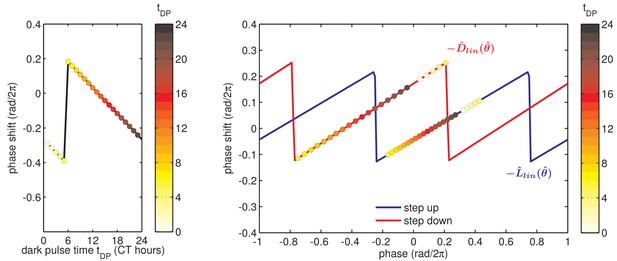
Nearly linear step response functions can arise from the relative geometry of day and night limit cycles.

(A) Geometric model of oscillator phase resetting. During the day, the oscillator runs with constant angular velocity along the daytime orbit (*yellow*), which has unit radius and is centered at the origin. At dusk, the oscillator transits to the nighttime orbit (*black*), which has radius R and is displaced from the daytime orbit by X units. In the limit where the nighttime orbit is strongly radially attracting, we can approximate oscillator response to the light-dark transition ( $D (θ_{τ})$ , *red arrow*) as an instantaneous jump from phase $θ_{τ}$ on the daytime orbit toward the center of the nighttime cycle, resulting in phase $θ_{τ} + D (θ_{τ})$ on the night orbit. (B) Simulation of oscillator phase shifts due to light-dark transitions at different phases on the day orbit (*red arrows*) for R = 2, X = 2. For geometries with X ≈ R, phase angles on the day orbit are compressed to an arc on the night limit cycle that subtends a smaller angle. See Computational methods for calculation details. (**C and D**) Simulations of $L (θ)$ and $D (θ)$ step response functions arising from the geometric arrangement of day and night cycles in (B). Linear regions of $L (θ)$ and $D (θ)$ are marked with black dashes. See Computational methods and Appendix 1 for calculation details. (E) Heat map of the slope m of the approximately linear relationship between entrained phase and day length, plotted as a function of X and R. In white regions, the oscillator does not entrain stably or the oscillator does not show linear scaling of phase with day length. Slope determined from simulations of oscillator entrainment to 24 hr driving cycles of day length τ = 6–18 hr. See Computational methods for details. (F) Limit cycles traversed by the KaiABC oscillator in vitro in metabolic conditions mimicking day (*yellow*, [ATP]/([ATP]+[ADP]) ≈ 100%) and night (*black*, [ATP]/([ATP]+[ADP]) ≈ 25%). Oscillations in KaiC phosphorylation on Ser431 and Thr432 are replotted from data in Phong et al. (2013).

https://doi.org/10.7554/eLife.23539.036

Figure 6—figure supplement 1

Download asset Open asset

Illustrations of limit cycle geometries that give rise to step-response functions $L (θ)$ and $D (θ)$ with different slopes, resulting in dusk-, dawn-, or midday-tracking entrainment.

In all schematics, the day orbit (*yellow*) is centered at the origin and has radius 1. The night orbit (*black*) has radius R and is displaced from the day orbit ( $\log X = 0.5)$ units). Light-dark ( $D (θ)$ ) and dark-light ( $L (θ)$ ) transitions are indicated by *red* and *blue arrows*, respectively. (A) When the night cycle is much smaller than the day cycle (R << 1), both dawn and dusk are strongly resetting (l≈1, d≈1). Because all phases on the night orbit are mapped to a small range of phases on the day orbit, oscillator phase at dawn is independent of day length during entrainment (m≈0, dawn-tracking). (B) When the sizes of day and night orbits are comparable (R ≈ 1), the slopes of $L (θ)$ and $D (θ)$ depend on the fine-tuned arrangement of the orbits. Generally, both $L (θ)$ and $D (θ)$ exert entraining effects in this regime (l > 0, *d >* 0). The slope of entrained phase with day length depends on both l and d, according to $m (l, d) = d (1 - l) / (d + l - l d)$ (see Figure 4—figure supplement 3 and Appendix 1). (C) When the night cycle is much bigger than the day cycle (R >> 1), dusk is strongly resetting, but dawn transitions have little effect on clock phase (l≈0, d≈1). Entrainment to repeated light-dark cycles maps clock phases on the night orbit to a shrinking range of angles, leading to dusk-tracking entrainment (m≈1).

https://doi.org/10.7554/eLife.23539.037

Figure 6—figure supplement 2

Download asset Open asset

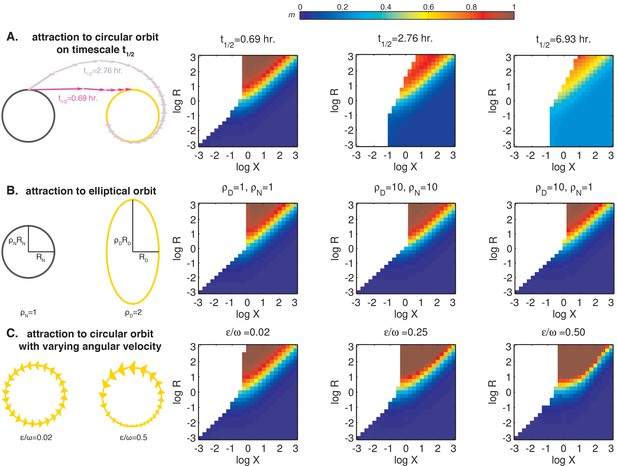
The relative size (R) and center-to-center distance (X) of day and night limit cycles are major determinants of entrained behavior.

Heat maps of m, the slope of the approximately linear relationship between entrained phase and day length, are plotted as a function of X and R on the same color scale as in Figure 6E. See Computational methods for simulation details. (A) Entrainment simulations with non-instantaneous jumps between day and night limit cycles. The half-times $t_{1 / 2}$ for transition between the circular orbits are indicated above the heat maps. Schematic on the left illustrates the evolution of the oscillator from a point on the night limit cycle to the day limit cycle in two scenarios with different relaxation times. Each arrow represents the displacement of the oscillator in 1 hr. (B) Entrainment simulations for day and night limit cycles of varying ellipticity. The ratios of the major axis length to the minor axis length of the day and night orbits (ρ_D and ρ_N) are indicated above the heatmaps. In these simulations, we considered strongly attracting orbits ( $t_{1 / 2} = 0.069$ hr) oriented with their major axes perpendicular to the separation between their centers. (C) Entrainment simulations for day and night limit cycles with non-constant angular velocities. In these simulations, we considered circular orbits for both day and night limit cycles. Orbit attraction timescale was set to $t_{1 / 2} = 0.69$ hours. The variability in angular speed $\dot{θ}$ throughout the cycle is given by $\dot{θ} = ω (1 + \frac{ε}{ω} \sin ω t)$ . Schematic on the left illustrates the evolution of the oscillator along day limit cycle in two scenarios with different values of $\frac{ε}{ω}$ . Each arrow represents the displacement of the oscillator in 1 hr; size of the arrowheads illustrates changes in angular velocity throughout the cycle (not to scale).

https://doi.org/10.7554/eLife.23539.038

Figure 6—figure supplement 3

Download asset Open asset

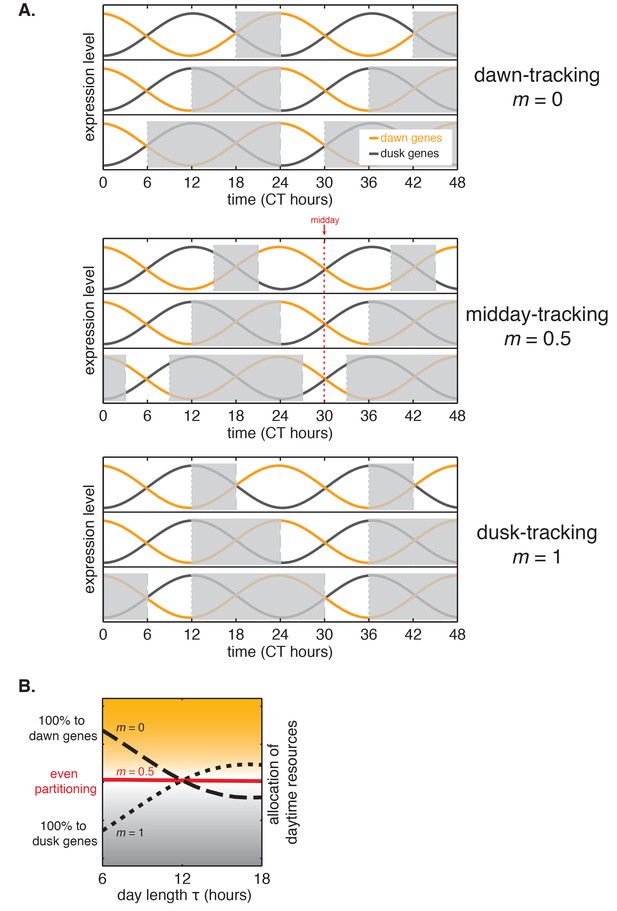
Interpretation of m, the slope of the approximately linear relationship between entrained phase and day length.

(A) The value of m dictates whether the circadian rhythm aligns to dawn (m = 0), dusk (m = 1), or an intermediate point of the day-night cycle (e.g. midday for m = 0.5). Orange and gray curves show sinusoidal fits to average transcriptional profiles of dawn and dusk genes in *S. elongatus* based on data from Vijayan et al. (2009). Gray bars indicate night in light-dark cycles for m = 0, 0.5, and 1. (B) Tracking midday as the day length varies may be a strategy to balance biosynthetic resources between dawn and dusk transcriptional programs. For each value of m, the corresponding curve shows a numerical estimate of the relative fraction of dusk and dawn gene expression that occurs during the day in *S. elongatus* (arbitrary units, see Computational methods).

https://doi.org/10.7554/eLife.23539.039

Appendix 1—figure 1

Download asset Open asset

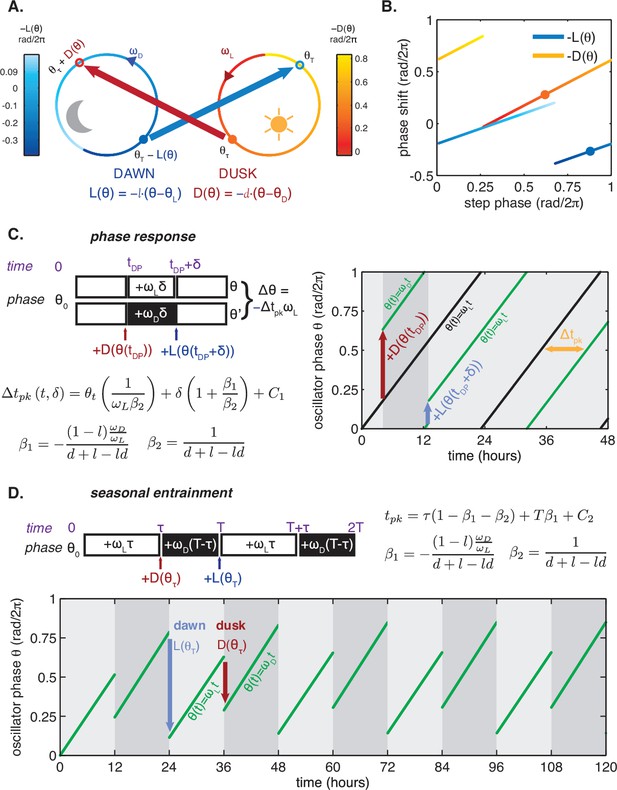
Phase oscillator with step response framework.

(A) Schematic of the framework. In the light portion of the day, the oscillator runs along the ‘light’ limit cycle (*orange*) and accumulates phase $θ$ at constant rate $ω_{L}$ ; in the dark, the oscillator runs along the ‘dark’ limit cycle (*blue*) with frequency $ω_{D}$ . At dawn (*solid blue circle*) and dusk (*solid orange circle*), the oscillator transitions between the light and dark limit cycles (*blue and orange arrows*) and incurs instantaneous phase shifts given by $L (θ)$ at dawn and $D (θ)$ at dusk. $L (θ)$ and $D (θ)$ can be approximated by linear functions of phase, such that $L (θ) = - l (θ - θ_{L})$ and $D (θ) = - d (θ - θ_{D})$ . Colors along the ‘light’ and ‘dark’ limit cycles indicate the magnitude of phase shifts due to light-to-dark ( $D (θ)$ ) and dark-to-light ( $L (θ)$ ) responses throughout the cycle for a single set of linearized $L (θ)$ and $D (θ)$ , shown in (B), generated by bootstrapping the measurements in Figure 3E–F. $θ = 0$ refers to the minimum of the KaiC phosphorylation rhythm. (B) One set of linearized step response functions ${\hat{L}}_{l i n} (\hat{θ})$ and ${\hat{D}}_{l i n} (\hat{θ})$ for the KaiABC oscillator determined by SDS-PAGE analysis of KaiC phosphorylation rhythms (see Figure 3E–F). The functions plotted represent one pair of ${\hat{L}}_{l i n} (\hat{θ})$ and ${\hat{D}}_{l i n} (\hat{θ})$ generated by bootstrapping (see Computational Methods). Colors denote phase shift magnitude as in (A). Solid circular markers correspond to dawn and dusk transitions in (A). (C) (*left*) Schematic of phase response analysis in the phase oscillator framework. The phase shift is a linear function of the dark pulse time (*t_DP*) and duration (δ) if $L (θ)$ and the $D (θ)$ are linear functions. Slopes of linear dependencies on *t_DP* and duration δ can be computed based on clock frequencies in light and dark ( $ω_{L}$ *, $ω_{D}$* ) and slopes of $L (θ)$ and $D (θ)$ functions. (*right*) Simulation of a phase response experiment for a phase oscillator with experimentally determined parameters ( $ω_{L}$ , $ω_{D}$ , l, and d from the same bootstrapped parameter set as in (B)). A 9 hr dark pulse applied 4 hr after the beginning of the simulation to an oscillator (*green*) results in a ≈8 hr phase delay relative to a control (*black*) that remains in light throughout the simulation. (D) (*top*) Schematic of analysis of seasonal entrainment in the phase oscillator framework. Entrained phase is a linear function of day length (τ) and driving period (T) if $L (θ)$ and the $D (θ)$ are linear functions. Slopes of linear dependencies on τ and T can be computed based on four parameters ( $ω_{L}$ , $ω_{D}$ , l, and d). (*bottom*) Simulation of entrainment to a LD 12:12 cycle for a phase oscillator with experimentally determined parameters ( $ω_{L}$ *, $ω_{D}$* , l, and d from the same bootstrapped parameter set as in (B)).

https://doi.org/10.7554/eLife.23539.040

Tables

Table 1

Summary of biologically independent in vivo experiments measuring entrainment to 24 hr light-dark cycles of varying day length and corresponding estimates of m, the proportionality coefficient between the peak time of P_kaiBC::luxAB reporter and day length during light-dark entrainment.

https://doi.org/10.7554/eLife.23539.014

Figure	Driving period T (hr)	Day length τ (hr)	Slope m ± SD of estimate
Figure 1C	24	4, 6, 8, 9, 10, 11, 12, 13, 14, 16, 18, 20	0.55 ± 0.02 (sinusoidal fitting) 0.53 ± 0.01 (parabolic fitting)
Figure 1—figure supplement 2	24	8, 12, 16	0.47 ± 0.03 (sinusoidal fitting) 0.57 ± 0.02 (parabolic fitting)
Figure 5C	22, 23, 24, 25, 26	8, 10, 12, 14	0.51 ± 0.11 (sinusoidal fitting)

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Eugene Leypunskiy
Jenny Lin
Haneul Yoo
UnJin Lee
Aaron R Dinner
Michael J Rust

(2017)

The cyanobacterial circadian clock follows midday in vivo and in vitro

eLife 6:e23539.

https://doi.org/10.7554/eLife.23539

Share this article

Cite this article

Phase of the cyanobacterial circadian rhythm scales linearly with day length.

Figure 1—source data 1

Figure 1—source data 2

Figure 1—source data 3

Figure 1—source data 4

Figure 1—source data 5

Figure 1—source data 6

Figure 1—source data 7

Bioluminescence recordings from PkaiBC::luxAB reporter in light-dark cycles.

The circadian rhythm of S. elongatus rapidly entrains to 24 hr diurnal cycles with 8–16 hr of daylight.

Bioluminescence recordings from PpurF::luxAB reporter in light-dark cycles.

Reconstitution of the seasonal clock response in vitro.

Figure 2—source data 1

Figure 2—source data 2

Figure 2—source data 3

Validation of KaiB fluorescence polarization reporter against KaiC phosphorylation rhythm.

Clock responses to metabolic steps mimicking dawn (step up) and dusk (step down).

Figure 3—source data 1

Figure 3—source data 2

Figure 3—source data 3

Example calculation of phase shifts in response to metabolic step transitions.

Experimentally measured step-response functions predict entrainment to driving periods near 24 hr.

Entrainment of the phase oscillator model to a driving cycle.

Figure 4—source data 1

Figure 4—source data 2

Example simulation of a phase oscillator governed by one set of experimentally determined L(θ) and D(θ) functions and subjected to a driving cycle.

Simulations of seasonal entrainment for a phase oscillator driven by linearized step-response functions (Llin and Dlin).

Dependence of the slope of entrained phase on the slopes of step response functions.

Phase oscillator entrainment.

Phase oscillator model with linear phase shift functions predicts entrainment of the cyanobacterial clock to different light-dark (LD) patterns.

Figure 5—source data 1

Simulation of a phase-resetting curve.

Nearly linear step response functions can arise from the relative geometry of day and night limit cycles.

Illustrations of limit cycle geometries that give rise to step-response functions L(θ) and D(θ) with different slopes, resulting in dusk-, dawn-, or midday-tracking entrainment.

The relative size (R) and center-to-center distance (X) of day and night limit cycles are major determinants of entrained behavior.

Interpretation of m, the slope of the approximately linear relationship between entrained phase and day length.

Phase oscillator with step response framework.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Bioluminescence recordings from P_kaiBC::luxAB reporter in light-dark cycles.

Bioluminescence recordings from P_purF::luxAB reporter in light-dark cycles.

Example simulation of a phase oscillator governed by one set of experimentally determined $L (θ)$ and $D (θ)$ functions and subjected to a driving cycle.

Simulations of seasonal entrainment for a phase oscillator driven by linearized step-response functions ( $L_{l i n}$ and $D_{l i n}$ ).

Illustrations of limit cycle geometries that give rise to step-response functions $L (θ)$ and $D (θ)$ with different slopes, resulting in dusk-, dawn-, or midday-tracking entrainment.