Tools and Resources

Neuroscience

Efficient and accurate extraction of in vivo calcium signals from microendoscopic video data

Carnegie Mellon University, United States
Columbia University, United States
University of North Carolina at Chapel Hill, United States
New York State Psychiatric Institute, United States
Harvard Medical School, Howard Hughes Medical Institute, United States
Flatiron Institute, Simons Foundation, United States
University of California, San Francisco, United States
University of California, United States

Feb 22, 2018

Open access
Copyright information

Abstract
Introduction
Results
Materials and methods
Data availability
References
Article and author information
Metrics

Abstract

In vivo calcium imaging through microendoscopic lenses enables imaging of previously inaccessible neuronal populations deep within the brains of freely moving animals. However, it is computationally challenging to extract single-neuronal activity from microendoscopic data, because of the very large background fluctuations and high spatial overlaps intrinsic to this recording modality. Here, we describe a new constrained matrix factorization approach to accurately separate the background and then demix and denoise the neuronal signals of interest. We compared the proposed method against previous independent components analysis and constrained nonnegative matrix factorization approaches. On both simulated and experimental data recorded from mice, our method substantially improved the quality of extracted cellular signals and detected more well-isolated neural signals, especially in noisy data regimes. These advances can in turn significantly enhance the statistical power of downstream analyses, and ultimately improve scientific conclusions derived from microendoscopic data.

https://doi.org/10.7554/eLife.28728.001

Introduction

Monitoring the activity of large-scale neuronal ensembles during complex behavioral states is fundamental to neuroscience research. Continued advances in optical imaging technology are greatly expanding the size and depth of neuronal populations that can be visualized. Specifically, in vivo calcium imaging through microendoscopic lenses and the development of miniaturized microscopes have enabled deep brain imaging of previously inaccessible neuronal populations of freely moving mice (Flusberg et al., 2008; Ghosh et al., 2011; Ziv and Ghosh, 2015). This technique has been widely used to study the neural circuits in cortical, subcortical, and deep brain areas, such as hippocampus (Cai et al., 2016; Ziv et al., 2013; Jimenez et al., 2018; Rubin et al., 2015), entorhinal cortex (Kitamura et al., 2015; Sun et al., 2015), hypothalamus (Jennings et al., 2015), prefrontal cortex (PFC) (Pinto and Dan, 2015), premotor cortex (Markowitz et al., 2015), dorsal pons (Cox et al., 2016), basal forebrain (Harrison et al., 2016), striatum (Barbera et al., 2016; Carvalho Poyraz et al., 2016; Klaus et al., 2017), amygdala (Yu et al., 2017), and other brain regions.

Although microendoscopy has potential applications across numerous neuroscience fields (Ziv and Ghosh, 2015), methods for extracting cellular signals from this data are currently limited and suboptimal. Most existing methods are specialized for two-photon or light-sheet microscopy. However, these methods are not suitable for analyzing single-photon microendoscopic data because of its distinct features: specifically, this data typically displays large, blurry background fluctuations due to fluorescence contributions from neurons outside the focal plane. In Figure 1, we use a typical microendoscopic dataset to illustrate these effects (see Video 1 for raw video). Figure 1A shows an example frame of the selected data, which contains large signals additional to the neurons visible in the focal plane. These extra fluorescence signals contribute as background that contaminates the single-neuronal signals of interest. In turn, standard methods based on local correlations for visualizing cell outlines (Smith and Häusser, 2010) are not effective here, because the correlations in the fluorescence of nearby pixels are dominated by background signals (Figure 1B). For some neurons with strong visible signals, we can manually draw regions-of-interest (ROI) (Figure 1C). Following (Barbera et al., 2016; Pinto and Dan, 2015), we used the mean fluorescence trace of the surrounding pixels (blue, Figure 1D) to roughly estimate this background fluctuation; subtracting it from the raw trace in the neuron ROI yields a relatively good estimation of neuron signal (red, Figure 1D). Figure 1D shows that the background (blue) has much larger variance than the relatively sparse neural signal (red); moreover, the background signal fluctuates on similar timescales as the single-neuronal signal, so we can not simply temporally filter the background away after extraction of the mean signal within the ROI. This large background signal is likely due to a combination of local fluctuations resulting from out-of-focus fluorescence or neuropil activity, hemodynamics of blood vessels, and global fluctuations shared more broadly across the field of view (photo-bleaching effects, drifts in $z$ of the focal plane, etc.), as illustrated schematically in Figure 1E.

Figure 1

Download asset Open asset

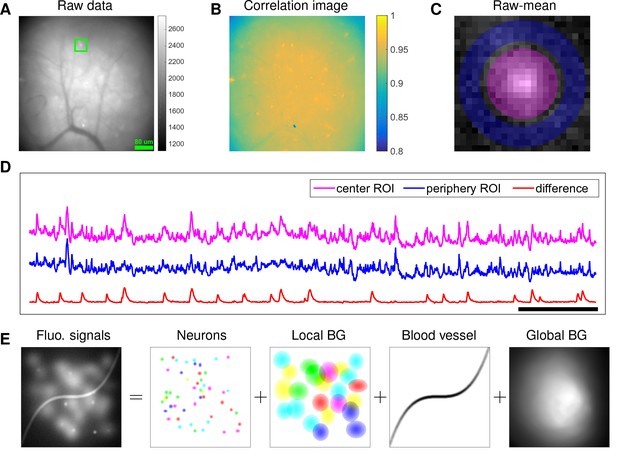
Microendoscopic data contain large background signals with rapid fluctuations due to multiple sources.

(A) An example frame of microendoscopic data recorded in dorsal striatum (see Materials and methods section for experimental details). (B) The local ‘correlation image’ (Smith and Häusser, 2010) computed from the raw video data. Note that it is difficult to discern neuronal shapes in this image due to the high background spatial correlation level. (C) The mean-subtracted data within the cropped area (green) in (A). Two ROIs were selected and coded with different colors. (D) The mean fluorescence traces of pixels within the two selected ROIs (magenta and blue) shown in (C) and the difference between the two traces. (E) Cartoon illustration of various sources of fluorescence signals in microendoscopic data. ‘BG’ abbreviates ‘background’.

https://doi.org/10.7554/eLife.28728.002

Video 1

Download asset

posterframe for video — An example of typical microendoscopic data.

The video was recorded in dorsal striatum; experimental details can be found above. MP4

https://doi.org/10.7554/eLife.28728.003

The existing methods for extracting individual neural activity from microendoscopic data can be divided into two classes: semi-manual ROI analysis (Barbera et al., 2016; Klaus et al., 2017; Pinto and Dan, 2015) and PCA/ICA analysis (Mukamel et al., 2009). Unfortunately, both approaches have well-known flaws (Resendez et al., 2016). For example, ROI analysis does not effectively demix signals of spatially overlapping neurons, and drawing ROIs is laborious for large population recordings. More importantly, in many cases, the background contaminations are not adequately corrected, and thus the extracted signals are not sufficiently clean enough for downstream analyses. As for PCA/ICA analysis, it is a linear demixing method and therefore typically fails when the neural components exhibit strong spatial overlaps (Pnevmatikakis et al., 2016), as is the case in the microendoscopic setting.

Recently, constrained nonnegative matrix factorization (CNMF) approaches were proposed to simultaneously denoise, deconvolve, and demix calcium imaging data (Pnevmatikakis et al., 2016). However, current implementations of the CNMF approach were optimized for $2$ -photon and light-sheet microscopy, where the background has a simpler spatiotemporal structure. When applied to microendoscopic data, CNMF often has poor performance because the background is not modeled sufficiently accurately (Barbera et al., 2016).

In this paper, we significantly extend the CNMF framework to obtain a robust approach for extracting single-neuronal signals from microendoscopic data. Specifically, our extended CNMF for microendoscopic data (CNMF-E) approach utilizes a more accurate and flexible spatiotemporal background model that is able to handle the properties of the strong background signal illustrated in Figure 1, along with new specialized algorithms to initialize and fit the model components. After a brief description of the model and algorithms, we first use simulated data to illustrate the power of the new approach. Next, we compare CNMF-E with PCA/ICA analysis comprehensively on both simulated data and four experimental datasets recorded in different brain areas. The results show that CNMF-E outperforms PCA/ICA in terms of detecting more well-isolated neural signals, extracting higher signal-to-noise ratio (SNR) cellular signals, and obtaining more robust results in low SNR regimes. Finally, we show that downstream analyses of calcium imaging data can substantially benefit from these improvements.

Model and model fitting

CNMF for microendoscope data (CNMF-E)

The recorded video data can be represented by a matrix $Y \in ℝ_{+}^{d \times T}$ , where $d$ is the number of pixels in the field of view and $T$ is the number of frames observed. In our model, each neuron $i$ is characterized by its spatial ‘footprint’ vector $𝒂_{i} \in ℝ_{+}^{d}$ characterizing the cell’s shape and location, and ‘calcium activity’ timeseries $𝒄_{i} \in ℝ_{+}^{T}$ , modeling (up to a multiplicative and additive constant) cell $i$ ’s mean fluorescence signal at each frame. Here, both $𝒂_{i}$ and $𝒄_{i}$ are constrained to be nonnegative because of their physical interpretations. The background fluctuation is represented by a matrix $B \in ℝ_{+}^{d \times T}$ . If the field of view contains a total number of $K$ neurons, then the observed movie data is modeled as a superposition of all neurons’ spatiotemporal activity, plus time-varying background and additive noise:

Y = \sum_{i = 1}^{K} 𝒂_{i} \cdot 𝒄_{i}^{T} + B + E = A C + B + E,

where $A = [𝒂_{1}, \dots, 𝒂_{K}]$ and $C = {[𝒄_{1}, \dots, 𝒄_{K}]}^{T}$ . The noise term $E \in ℝ^{d \times T}$ is modeled as Gaussian, $E (t) \sim 𝒩 (0, Σ)$ is a diagonal matrix, indicating that the noise is spatially and temporally uncorrelated.

Estimating the model parameters $A, C$ in model (1) gives us all neurons’ spatial footprints and their denoised temporal activity. This can be achieved by minimizing the residual sum of squares (RSS), aka the Frobenius norm of the matrix $Y - (A C + B)$ ,

{∥ Y - (A C + B) ∥}_{F}^{2},

while requiring the model variables $A, C$ and $B$ to follow the desired constraints, discussed below.

Constraints on neuronal spatial footprints $A$ and neural temporal traces $C$

Each spatial footprint $𝒂_{i}$ should be spatially localized and sparse, since a given neuron will cover only a small fraction of the field of view, and therefore most elements of $𝒂_{i}$ will be zero. Thus, we need to incorporate spatial locality and sparsity constraints on $A$ (Pnevmatikakis et al., 2016). We discuss details further below.

Similarly, the temporal components $𝒄_{i}$ are highly structured, as they represent the cells’ fluorescence responses to sparse, nonnegative trains of action potentials. Following (Vogelstein et al., 2010; Pnevmatikakis et al., 2016), we model the calcium dynamics of each neuron $𝒄_{i}$ with a stable autoregressive (AR) process of order $p$ ,

c_{i} (t) = \sum_{j = 1}^{p} γ_{j}^{(i)} c_{i} (t - j) + s_{i} (t),

where $s_{i} (t) \geq 0$ is the number of spikes that neuron fired at the $t$ -th frame. (Note that there is no further noise input into $c_{i} (t)$ beyond the spike signal $s_{i} (t)$ .) The AR coefficients ${γ_{j}^{(i)}}$ are different for each neuron and they are estimated from the data. In practice, we usually pick $p = 2$ , thus incorporating both a nonzero rise and decay time of calcium transients in response to a spike; then Equation (3) can be expressed in matrix form as

G_{i} \cdot c_{i} = s_{i}, with G_{i} = [\begin{matrix} 1 & 0 & 0 & \dots & 0 \\ - γ_{1}^{(i)} & 1 & 0 & \dots & 0 \\ - γ_{2}^{(i)} & - γ_{1}^{(i)} & 1 & \dots & 0 \\ ⋮ & ⋱ & ⋱ & ⋱ & ⋮ \\ 0 & \dots & - γ_{2}^{(i)} & - γ_{1}^{(i)} & 1 \end{matrix}] .

The neural activity $𝒔_{i}$ is nonnegative and typically sparse; to enforce sparsity, we can penalize the $ℓ_{0}$ (Jewell and Witten, 2017) or $ℓ_{1}$ (Pnevmatikakis et al., 2016; Vogelstein et al., 2010) norm of $𝒔_{i}$ , or limit the minimum size of nonzero spike counts (Friedrich et al., 2017b). When the rise time constant is small compared to the timebin width (low imaging frame rate), we typically use a simpler AR(1) model (with an instantaneous rise following a spike) (Pnevmatikakis et al., 2016).

Constraints on background activity $B$

In the above we have largely followed previously described CNMF approaches (Pnevmatikakis et al., 2016) for modeling calcium imaging signals. However, to accurately model the background effects in microendoscopic data, we need to depart significantly from these previous approaches. Constraints on the background term $B$ in Equation (1) are essential to the success of CNMF-E, since clearly, if $B$ is completely unconstrained we could just absorb the observed data $Y$ entirely into $B$ , which would lead to recovery of no neural activity. At the same time, we need to prevent the residual of the background term (i.e. $B - \hat{B}$ , where $\hat{B}$ denotes the estimated spatiotemporal background) from corrupting the estimated neural signals $A C$ in model (1), since subsequently, the extracted neuronal activity would be mixed with background fluctuations, leading to artificially high correlations between nearby cells. This problem is even worse in the microendoscopic context because the background fluctuation usually has significantly larger variance than the isolated cellular signals of interest (Figure 1D), and therefore any small errors in the estimation of $B$ can severely corrupt the estimated neural signal $A C$ .

In (Pnevmatikakis et al., 2016), $B$ is modeled as a rank- $1$ nonnegative matrix $B = 𝒃 \cdot 𝒇^{T}$ , where $𝒃 \in ℝ_{+}^{d}$ and $𝒇 \in ℝ_{+}^{T}$ . This model mainly captures the global fluctuations within the field of view (FOV). In applications to two-photon or light-sheet data, this rank-1 model has been shown to be sufficient for relatively small spatial regions; the simple low-rank model does not hold for larger fields of view, and so we can simply divide large FOVs into smaller patches for largely parallel processing (Pnevmatikakis et al., 2016; Giovannucci et al., 2017b). (See [Pachitariu et al., 2016] for an alternative approach.) However, as we will see below, the local rank-1 model fails in many microendoscopic datasets, where multiple large overlapping background sources exist even within modestly sized FOVs.

Thus, we propose a new model to constrain the background term $B$ . We first decompose the background into two terms:

B = B^{f} + B^{c},

where $B^{f}$ represents fluctuating activity and $B^{c} = 𝒃_{0} \cdot 𝟏^{T}$ models constant baselines ( $𝟏 \in ℝ^{T}$ denotes a vector of $T$ ones). To model $B^{f}$ , we exploit the fact that background sources (largely due to blurred out-of-focus fluorescence) are empirically much coarser spatially than the average neuron soma size $l$ . Thus, we model $B^{f}$ at one pixel as a linear combination of the background fluorescence in pixels which are chosen to be nearby but not nearest neighbors:

B_{i t}^{f} = \sum_{j \in Ω_{i}} w_{i j} \cdot B_{j t}^{f}, \forall t = 1 \dots T,

where $Ω_{i} = {j | dist (x_{i}, x_{j}) \in [l_{n}, l_{n} + 1)}$ , with $dist (𝒙_{i}, 𝒙_{j})$ the Euclidean distance between pixel $i$ and $j$ . Thus, $Ω_{i}$ only selects the neighboring pixels with a distance of $l_{n}$ from the $i$ -th pixel (the green dot and black pixels in Figure 2B illustrate $i$ and $Ω_{i}$ , respectively); here $l_{n}$ is a parameter that we choose to be greater than $l$ (the size of the typical soma in the FOV), e.g., $l_{n} = 2 l$ . This choice of $l_{n}$ ensures that pixels $i$ and $j$ in Equation (6) share similar background fluctuations, but do not belong to the same soma.

Figure 2

Download asset Open asset

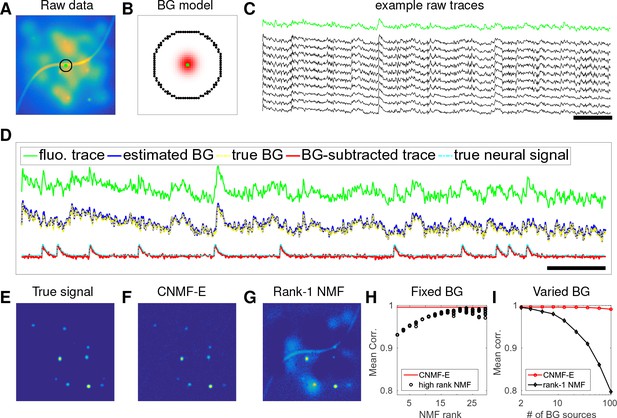
CNMF-E can accurately separate and recover the background fluctuations in simulated data.

(A) An example frame of simulated microendoscopic data formed by summing up the fluorescent signals from the multiple sources illustrated in Figure 1E. (B) A zoomed-in version of the circle in (A). The green dot indicates the pixel of interest. The surrounding black pixels are its neighbors with a distance of 15 pixels. The red area approximates the size of a typical neuron in the simulation. (C) Raw fluorescence traces of the selected pixel and some of its neighbors on the black ring. Note the high correlation. (D) Fluorescence traces (raw data; true and estimated background; true and initial estimate of neural signal) from the center pixel as selected in (B). Note that the background dominates the raw data in this pixel, but nonetheless we can accurately estimate the background and subtract it away here. Scalebars: $10$ seconds. Panels (**E–G**) show the cellular signals in the same frame as (A). (E) Ground truth neural activity. (F) The residual of the raw frame after subtracting the background estimated with CNMF-E; note the close correspondence with E. (G) Same as (F), but the background is estimated with rank-1 NMF. A video showing (**E–G**) for all frames can be found at Video 2. (H) The mean correlation coefficient (over all pixels) between the true background fluctuations and the estimated background fluctuations. The rank of NMF varies and we run randomly-initialized NMF for 10 times for each rank. The red line is the performance of CNMF-E, which requires no selection of the NMF rank. (I) The performance of CNMF-E and rank-1 NMF in recovering the background fluctuations from the data superimposed with an increasing number of background sources.

https://doi.org/10.7554/eLife.28728.004

Video 2

Download asset

We can rewrite Equation (6) in matrix form:

B^{f} = W B^{f},

where $W_{i j} = 0$ if $dist (𝒙_{i}, 𝒙_{j}) \notin [l_{n}, l_{n} + 1)$ . In practice, this hard constraint is difficult to enforce computationally and is overly stringent given the noisy observed data. We relax the model by replacing the right-hand side $B^{f}$ with the more convenient closed-form expression

B^{f} = W \cdot (Y - A C - 𝒃_{0} \cdot 𝟏^{T}) .

According to Equations (1) and (5), this change ignores the noise term $E$ ; since elements in $E$ are spatially uncorrelated, $W \cdot E$ contributes as a very small disturbance to ${\hat{B}}^{f}$ in the left-hand side. We found this substitution for ${\hat{B}}^{f}$ led to significantly faster and more robust model fitting.

Fitting the CNMF-E model

Table 1 lists the variables in the proposed CNMF-E model. Now we can formulate the estimation of all model variables as a single optimization meta-problem:

\begin{aligned} (P-All) & \overset{minimize}{A, C, S, B^{f}, W, b_{0}} & ‖ Y - A C - b_{0} \cdot 1^{T} - B^{f} ‖_{F}^{2} \\ s u b j e c t t o & A \geq 0, A i s s p a r s e a n d s p a t i a l l y l o c a l i z e d \\ c_{i} \geq 0, s_{i} \geq 0, G^{(i)} c_{i} = s_{i}, s_{i} is sparse \forall i = 1 \dots K \\ B^{f} \cdot 1 = 0 \\ B^{f} = W \cdot (Y - A C - b_{0} \cdot 1^{T}) \\ W_{i j} = 0 i f d i s t (x_{i}, x_{j}) \notin [l_{n}, l_{n} + 1) . \end{aligned}

Table 1

Variables used in the CNMF-E model and algorithm. $ℝ$ : real numbers; $ℝ_{+}$ : positive real numbers; $ℕ$ : natural numbers; $ℕ_{+}$ : positive integers.

https://doi.org/10.7554/eLife.28728.006

Name	Description	Domain
$d$	number of pixels	$ℕ_{+}$
$T$	number of frames	$ℕ_{+}$
$K$	number of neurons	$ℕ$
$Y$	motion corrected video data	$ℝ_{+}^{d \times T}$
$A$	spatial footprints of all neurons	$ℝ_{+}^{d \times K}$
$C$	temporal activities of all neurons	$ℝ_{+}^{K \times T}$
$B$	background activity	$ℝ_{+}^{d \times T}$
$E$	observation noise	$ℝ^{d \times T}$
$W$	weight matrix to reconstruct $B$ using neighboring pixels	$ℝ^{d \times d}$
$𝒃_{0}$	constant baseline for all pixels	$ℝ_{+}^{d}$
$𝒙_{i}$	spatial location of the $i$ th pixel	$ℕ^{2}$
$σ_{i}$	standard deviation of the noise at pixel $𝒙_{i}$	$ℝ_{+}$

We call this a ‘meta-problem’ because we have not yet explicitly defined the sparsity and spatial locality constraints on $A$ and $S = {[𝒔_{1}, \dots, 𝒔_{K}]}^{T}$ ; these can be customized by users under different assumptions (see details in Materials and methods). Also note that $𝒔_{i}$ is completely determined by $𝒄_{i}$ and $G^{(i)}$ , and $B^{f}$ is not optimized explicitly but (as discussed above) can be estimated as $W \cdot (Y - A C - 𝒃_{0} \cdot 𝟏^{T})$ , so we optimize with respect to $W$ instead.

The problem (P-All) optimizes all variables together and is non-convex but can be divided into three simpler subproblems that we solve iteratively:

Estimating $A, b_{0}$ given $\hat{C}, {\hat{B}}^{f}$

\begin{aligned} (P-S) & \overset{minimize}{A, b_{0}} & ‖ Y - A \cdot \hat{C} - b_{0} \cdot 1^{T} - {\hat{B}}^{f} ‖_{F}^{2} \\ s u b j e c t t o & A \geq 0, A i s s p a r s e a n d s p a t i a l l y l o c a l i z e d \end{aligned}

Estimating $C, b_{0}$ given $\hat{A}, {\hat{B}}^{f}$

\begin{aligned} (P-T) & \overset{minimize}{C, S, b_{0}} & ‖ Y - \hat{A} \cdot C - b_{0} \cdot 1^{T} - {\hat{B}}^{f} ‖_{F}^{2} \\ s u b j e c t t o & c_{i} \geq 0, s_{i} \geq 0 \\ G^{(i)} c_{i} = s_{i}, s_{i} i s s p a r s e \forall i = 1 \dots K \end{aligned}

Estimating $W, b_{0}$ given $\hat{A}, \hat{C}$

\begin{aligned} (P-B) & \overset{minimize}{W, B^{f}, b_{0}} & ‖ Y - \hat{A} \cdot \hat{C} - b_{0} \cdot 1^{T} - B^{f} ‖_{F}^{2} \\ s u b j e c t t o & B^{f} \cdot 1 = 0 \\ B^{f} = W \cdot (Y - \hat{A} \cdot \hat{C} - b_{0} \cdot 1^{T}) . \\ W_{i j} = 0 i f d i s t (x_{i}, x_{j}) \notin [l_{n}, l_{n} + 1) \end{aligned}

For each of these subproblems, we are able to use well-established algorithms (e.g. solutions for (P-S) and (P-T) are discussed in Friedrich et al., 2017a; Pnevmatikakis et al., 2016) or slight modifications thereof. By iteratively solving these three subproblems, we obtain tractable updates for all model variables in problem (P-All). Furthermore, this strategy gives us the flexibility of further potential interventions (either automatic or semi-manual) in the optimization procedure, for example, incorporating further prior information on neurons’ morphology, or merging/splitting/deleting spatial components and detecting missed neurons from the residuals. These steps can significantly improve the quality of the model fitting; this is an advantage compared with PCA/ICA, which offers no easy option for incorporation of stronger prior information or manually guided improvements on the estimates.

Full details on the algorithms for initializing and then solving these three subproblems are provided in the Materials and methods section.

Results

CNMF-E can reliably estimate large high-rank background fluctuations

We first use simulated data to illustrate the background model in CNMF-E and compare its performance against the low-rank NMF model used in the basic CNMF approach (Pnevmatikakis et al., 2016). We generated the observed fluorescence $Y$ by summing up simulated fluorescent signals of multiple sources as shown in Figure 1E plus additive Gaussian white noise (Figure 2A).

An example pixel (green dot, Figure 2A,B) was selected to illustrate the background model in CNMF-E (Equation (6)), which assumes that each pixel’s background activity can be reconstructed using its neighboring pixels’ activities. The selected neighbors form a ring and their distances to the center pixel are larger than a typical neuron size (Figure 2B). Figure 2C shows that the fluorescence traces of the center pixel and its neighbors are highly correlated due to the shared large background fluctuations. Here, for illustrative purposes, we fit the background by solving problem (P-B) directly while assuming $\hat{A} \hat{C} = 0$ . This mistaken assumption should make the background estimation more challenging (due to true neural components getting absorbed into the background), but nonetheless in Figure 2 we see that the background fluctuation was well recovered (Figure 2D). Subtracting this estimated background from the observed fluorescence in the center yields a good visualization of the cellular signal (Figure 2D). Thus, this example shows that we can reconstruct a complicated background trace while leaving the neural signal uncontaminated.

For the example frame in Figure 2A, the true cellular signals are sparse and weak (Figure 2E). When we subtract the estimated background using CNMF-E from the raw data, we obtain a good recovery of the true signal (Figure 2D,F). For comparison, we also estimate the background activity by applying a rank- $1$ NMF model as used in basic CNMF; the resulting background-subtracted image is still severely contaminated by the background (Figure 2G). This is easy to understand: the spatiotemporal background signal in microendoscopic data typically has a rank higher than one, due to the various signal sources indicated in Figure 1E), and therefore a rank- $1$ NMF background model is insufficient.

A naive approach would be to simply increase the rank of the NMF background model. Figure 2H demonstrates that this approach is ineffective: higher rank NMF does yield generally better reconstruction performance, but with high variability and low reliability (due to randomness in the initial conditions of NMF). Eventually as the NMF rank increases many single-neuronal signals of interest are swallowed up in the estimated background signal (data not shown). In contrast, CNMF-E recovers the background signal more accurately than any of the high-rank NMF models.

In real data analysis settings, the rank of NMF is an unknown and the selection of its value is a nontrivial problem. We simulated data sets with different numbers of local background sources and use a single parameter setting to run CNMF-E for reconstructing the background over multiple such simulations. Figure 2I shows that the performance of CNMF-E does not degrade quickly as we have more background sources, in contrast to rank- $1$ NMF. Therefore, CNMF-E can recover the background accurately across a diverse range of background sources, as desired.

CNMF-E accurately initializes single-neuronal spatial and temporal components

Next, we used simulated data to validate our proposed initialization procedure (Figure 3A). In this example, we simulated 200 neurons with strong spatial overlaps (Figure 3B). One of the first steps in our initialization procedure is to apply a Gaussian spatial filter to the images to reduce the (spatially coarser) background and boost the power of neuron-sized objects in the images. In Figure 3C, we see that the local correlation image (Smith and Häusser, 2010) computed on the spatially filtered data provides a good initial visualization of neuron locations; compare to Figure 1B, where the correlation image computed on the raw data was highly corrupted by background signals.

Figure 3

Download asset Open asset

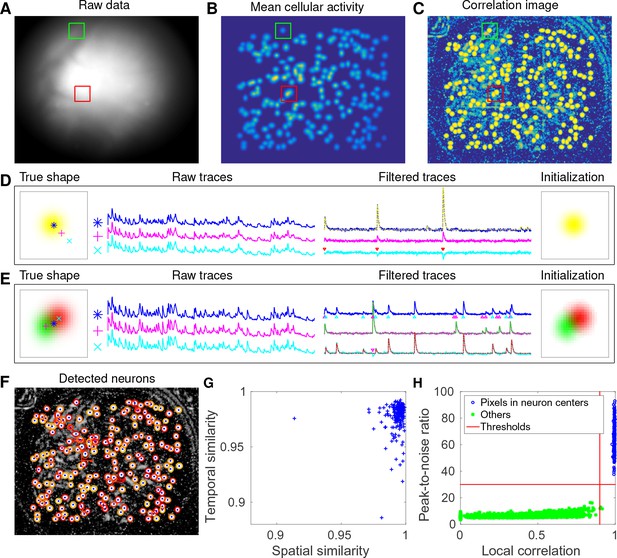
CNMF-E accurately initializes individual neurons’ spatial and temporal components in simulated data.

(A) An example frame of the simulated data. Green and red squares will correspond to panels (D) and (E) below, respectively. (B) The temporal mean of the cellular activity in the simulation. (C) The correlation image computed using the spatially filtered data. (D) An example of initializing an isolated neuron. Three selected pixels correspond to the center, the periphery, and the outside of a neuron. The raw traces and the filtered traces are shown as well. The yellow dashed line is the true neural signal of the selected neuron. Triangle markers highlight the spike times from the neuron. (E) Same as (D), but two neurons are spatially overlapping in this example. Note that in both cases neural activity is clearly visible in the filtered traces, and the initial estimates of the spatial footprints are already quite accurate (dashed lines are ground truth). (F) The contours of all initialized neurons on top of the correlation image as shown in (D). Contour colors represent the rank of neurons’ SNR (SNR decreases from red to yellow). The blue dots are centers of the true neurons. (G) The spatial and the temporal cosine similarities between each simulated neuron and its counterpart in the initialized neurons. (H) The local correlation and the peak-to-noise ratio for pixels located in the central area of each neuron (blue) and other areas (green). The red lines are the thresholding boundaries for screening seed pixels in our initialization step. A video showing the whole initialization step can be found at Video 3.

https://doi.org/10.7554/eLife.28728.007

Video 3

Download asset

We choose two example ROIs to illustrate how CNMF-E removes the background contamination and demixes nearby neural signals for accurate initialization of neurons’ shapes and activity. In the first example, we choose a well-isolated neuron (green box, Figure 3A+B). We select three pixels located in the center, the periphery, and the outside of the neuron and show the corresponding fluorescence traces in both the raw data and the spatially filtered data (Figure 3D). The raw traces are noisy and highly correlated, but the filtered traces show relatively clean neural signals. This is because spatial filtering reduces the shared background activity and the remaining neural signals dominate the filtered data. Similarly, Figure 3E is an example showing how CNMF-E demixes two overlapping neurons. The filtered traces in the centers of the two neurons still preserve their own temporal activity.

After initializing the neurons’ traces using the spatially filtered data, we initialize our estimate of their spatial footprints. Note that simply initializing these spatial footprints with the spatially filtered data does not work well (data not shown), since the resulting shapes are distorted by the spatial filtering process. We found that it was more effective to initialize each spatial footprint by regressing the initial neuron traces onto the raw movie data (see Materials and methods for details). The initial values already match the simulated ground truth with fairly high fidelity (Figure 3D+E). In this simulated data, CNMF-E successfully identified all 200 neurons and initialized their spatial and temporal components (Figure 3F). We then evaluate the quality of initialization using all neurons’ spatial and temporal similarities with their counterparts in the ground truth data. Figure 3G shows that all initialized neurons have high similarities with the truth, indicating a good recovery and demixing of all neuron sources.

Thresholds on the minimum local correlation and the minimum peak-to-noise ratio (PNR) for detecting seed pixels are necessary for defining the initial spatial components. To quantify the sensitivity of choosing these two thresholds, we plot the local correlations and the PNRs of all pixels chosen as the local maxima within an area of $\frac{l}{4} \times \frac{l}{4}$ , where $l$ is the diameter of a typical neuron, in the correlation image or the PNR image (Figure 3H). Pixels are classified into two classes according to their locations relative to the closest neurons: neurons’ central areas and outside areas (see Materials and methods for full details). It is clear that the two classes are linearly well separated and the thresholds can be chosen within a broad range of values (Figure 3H), indicating that the algorithm is robust with respect to these threshold parameters here. In lower SNR settings, these boundaries may be less clear, and an incremental approach (in which we choose the highest-SNR neurons first, then estimate the background and examine the residual to select the lowest-SNR cells) may be preferred; this incremental approach is discussed in more depth in the Materials and methods section.

CNMF-E recovers the true neural activity and is robust to noise contamination and neuronal correlations in simulated data

Using the same simulated dataset as in the previous section, we further refine the neuron shapes ( $A$ ) and the temporal traces ( $C$ ) by iteratively fitting the CNMF-E model. We compare the final results with PCA/ICA analysis (Mukamel et al., 2009) and the original CNMF method (Pnevmatikakis et al., 2016).

After choosing the thresholds for seed pixels (Figure 3H), we run CNMF-E in full automatic mode, without any manual interventions. Two open-source MATLAB packages, CellSort (https://github.com/mukamel-lab/CellSort; Mukamel, 2016) and ca_source_extraction (https://github.com/epnev/ca_source_extraction; Pnevmatikakis, 2016), were used to perform PCA/ICA (Mukamel et al., 2009) and basic CNMF (Pnevmatikakis et al., 2016), respectively. Since the initialization algorithm in CNMF fails due to the large contaminations from the background fluctuations in this setting (recall Figure 2), we use the ground truth as its initialization. As for the rank of the background model in CNMF, we tried all integer values between 1 and 16 and set it as 7 because it has the best performance in matching the ground truth. We emphasize that including the CNMF approach in this comparison is not fair for the other two approaches, because it uses the ground truth heavily, while PCA/ICA and CNMF-E are blind to the ground truth. The purpose here is to show the limitations of basic CNMF in modeling the background activity in microendoscopic data.

We first pick three closeby neurons from the ground truth (Figure 4A, top) and see how well these neurons’ activities are recovered. PCA/ICA fails to identify one neuron, and for the other two identified neurons, it recovers temporal traces that are sufficiently noisy that small calcium transients are submerged in the noise. As for CNMF, the neuron shapes remain more or less at the initial condition (i.e. the ground truth spatial footprints), but clear contaminations in the temporal traces are visible. This is because the pure NMF model in CNMF does not model the true background well and the residuals in the background are mistakenly captured by neural components. In contrast, on this example, CNMF-E recovers the true neural shapes and neural activity with high accuracy.

Figure 4

Download asset Open asset

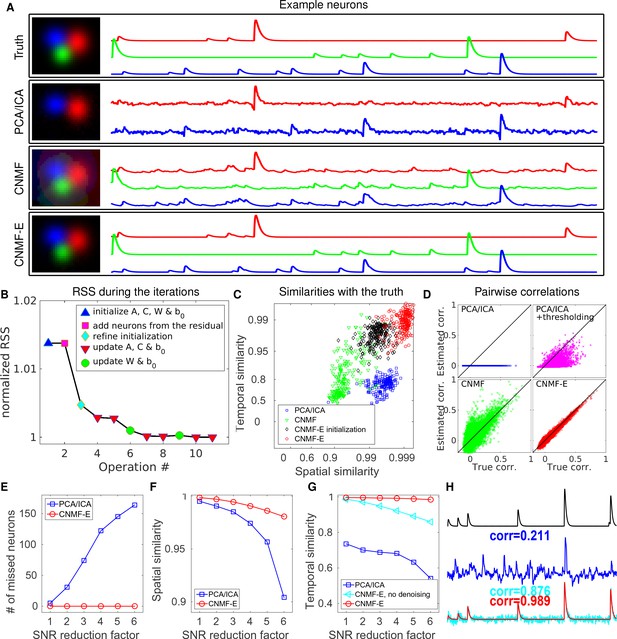
CNMF-E outperforms PCA/ICA analysis in extracting individual neurons’ activity from simulated data and is robust to low SNR.

(A) The results of PCA/ICA, CNMF, and CNMF-E in recovering the spatial footprints and temporal traces of three example neurons. The trace colors match the neuron colors shown in the left. (B) The intermediate residual sum of squares (RSS) values (normalized by the final RSS value), during the CNMF-E model fitting. The 'refine initialization’ step refers to the modification of the initialization results in the case of high temporal correlation (details in Materials and methods). (C) The spatial and the temporal cosine similarities between the ground truth and the neurons detected using different methods. (D) The pairwise correlations between the calcium activity traces extracted using different methods. (**E–G**) The performances of PCA/ICA and CNMF-E under different noise levels: the number of missed neurons (E), and the spatial (F) and temporal (G) cosine similarities between the extracted components and the ground truth. (H) The calcium traces of one example neuron: the ground truth (black), the PCA/ICA trace (blue), the CNMF-E trace (red) and the CNMF-E trace without being denoised (cyan). The similarity values shown in the figure are computed as the cosine similarity between each trace and the ground truth (black). Two videos showing the demixing results of the simulated data can be found in Video 4 (SNR reduction factor = 1) and Video 5 (SNR reduction factor = 6).

https://doi.org/10.7554/eLife.28728.009

Video 4

Download asset

Video 5

Download asset

We also compare the number of detected neurons: PCA/ICA detected 195 out of 200 neurons, while CNMF-E detected all 200 neurons. We also quantitatively evaluated the performance of source extraction by showing the spatial and temporal cosine similarities between detected neurons and ground truth (Figure 4C); we find that the neurons detected using PCA/ICA have much lower similarities with the ground truth (Figure 4C). We also note that the CNMF results are much worse than those of CNMF-E here, despite the fact that CNMF is initialized at the ground truth parameter values. This result clarifies an important point: the improvements from CNMF-E are not simply due to improvements in the initialization step. Furthermore, running the full iterative pipeline of CNMF-E leads to improvements in both spatial and temporal similarities, compared with the results in the initialization step.

In many downstream analyses of calcium imaging data, pairwise correlations provide an important metric to study coordinated network activity (Warp et al., 2012; Barbera et al., 2016; Dombeck et al., 2009; Klaus et al., 2017). Since PCA/ICA seeks statistically independent components, which forces the temporal traces to have near-zero correlation, the correlation structure is badly corrupted in the raw PCA/ICA outputs (Figure 4D). We observed that a large proportion of the independence comes from the noisy baselines in the extracted traces (data not shown), so we postprocessed the PCA/ICA output by thresholding at the 3 standard deviation level. This recovers some nonzero correlations, but the true correlation structure is not recovered accurately (Figure 4D). By contrast, the CNMF-E results matched the ground truth very well due to accurate extraction of individual neurons’ temporal activity (Figure 4D). As for CNMF, the estimated correlations are slightly elevated relative to the true correlations. This is due to the shared (highly correlated) background fluctuations that corrupt the recovered activity of nearby neurons.

Next, we compared the performance of the different methods under different SNR regimes. Because of the above inferior results we skip comparisons to the basic CNMF here. Based on the same simulation parameters as above, we vary the noise level $Σ$ by multiplying it with a SNR reduction factor. Figure 4E shows that CNMF-E detects all neurons over a wide SNR range, while PCA/ICA fails to detect the majority of neurons when the SNR drops to sufficiently low levels. Moreover, the detected neurons in CNMF-E preserve high spatial and temporal similarities with the ground truth (Figure 4F–G). This high accuracy of extracting neurons’ temporal activity benefits from the modeling of the calcium dynamics, which leads to significantly denoised neural activity. If we skip the temporal denoising step in the algorithm, CNMF-E is less robust to noise, but still outperforms PCA/ICA significantly (Figure 4G). When SNR is low, the improvements yielded by CNMF-E can be crucial for detecting weak neuron events, as shown in Figure 4H.

Finally, we examine the ability of CNMF-E to demix correlated and overlapping neurons. Using the two example neurons in Figure 3E, we ran multiple simulations at varying correlation levels and extracted neural components using the CNMF-E pipeline and PCA/ICA analysis. The spatial footprints in these simulations were fixed, but the temporal components were varied to have different correlation levels ( $γ$ ) between calcium traces by tuning their shared component with the common background fluctuations. For high correlation levels ( $γ > 0.7$ ), the initialization procedure tends to first initialize a component that explains the common activity between two neurons and then initialize another component to account for the residual of one neuron. After iteratively refining the model variables, CNMF-E successfully extracted the two neurons’ spatiotemporal activity even at very high correlation levels ( $γ = 0.95$ ; Figure 5A,B). PCA/ICA was also often able to separate two neurons for large correlation levels ( $γ = 0.9$ , Figure 5B), but the extracted traces have problematic negative spikes that serve to reduce their statistical dependences (Figure 4A).

Figure 5

Download asset Open asset

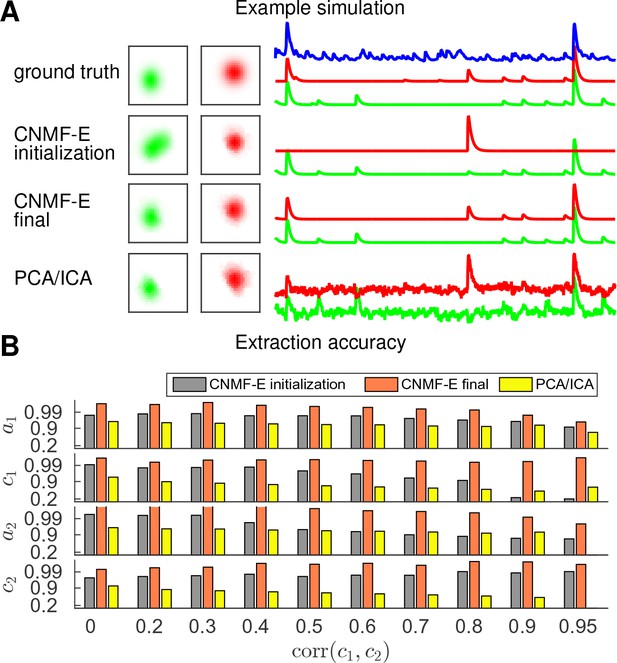
CNMF-E is able to demix neurons with high temporal correlations.

(A) An example simulation from the experiments summarized in panel (B), where $corr (𝒄_{1}, 𝒄_{2})$ is 0.9: green and red traces correspond to the corresponding neuronal shapes in the left panels. The blue trace is the mean background fluorescence fluctuation over the whole FOV. (B) The extraction accuracy of the spatial ( $𝒂_{1}$ and $𝒂_{2}$ ) and the temporal ( $𝒄_{1}$ and $𝒄_{2}$ ) components of two close-by neurons, computed via the cosine similarity between the ground truth and the extraction results.

https://doi.org/10.7554/eLife.28728.012

Application to dorsal striatum data

We now turn to the analysis of large-scale microendoscopic datasets recorded from freely behaving mice. We run both CNMF-E and PCA/ICA for all datasets and compare their performances in detail.

We begin by analyzing in vivo calcium imaging data of neurons expressing GCaMP6f in the mouse dorsal striatum. (Full experimental details and algorithm parameter settings for this and the following datasets appear in the Methods and Materials section.) CNMF-E extracted 692 putative neural components from this dataset; PCA/ICA extracted 547 components (starting from 700 initial components, and then automatically removing false positives using the same criterion as applied in CNMF-E). Figure 6A shows how CNMF-E decomposes an example frame into four components: the constant baselines that are invariant over time, the fluctuating background, the denoised neural signals, and the residuals. We highlight an example neuron by drawing its ROI to demonstrate the power of CNMF-E in isolating fluorescence signals of neurons from the background fluctuations. For the selected neuron, we plot the mean fluorescence trace of the raw data and the estimated background (Figure 6B). These two traces are very similar, indicating that the background fluctuation dominates the raw data. By subtracting this estimated background component from the raw data, we acquire a clean trace that represents the neural signal.

Figure 6

Download asset Open asset

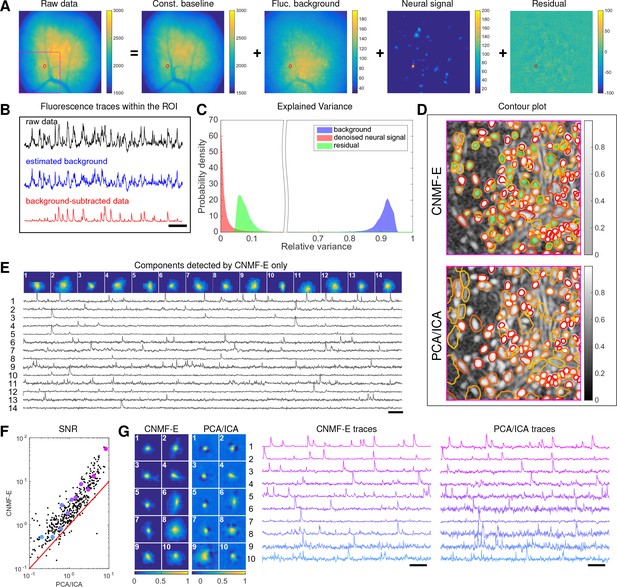
Neurons expressing GCaMP6f recorded in vivo in mouse dorsal striatum area.

(A) An example frame of the raw data and its four components decomposed by CNMF-E. (B) The mean fluorescence traces of the raw data (black), the estimated background activity (blue), and the background-subtracted data (red) within the segmented area (red) in (A). The variance of the black trace is about 2x the variance of the blue trace and 4x the variance of the red trace. (C) The distributions of the variance explained by different components over all pixels; note that estimated background signals dominate the total variance of the signal. (D) The contour plot of all neurons detected by CNMF-E and PCA/ICA superimposed on the correlation image. Green areas represent the components that are only detected by CNMF-E. The components are sorted in decreasing order based on their SNRs (from red to yellow). (E) The spatial and temporal components of 14 example neurons that are only detected by CNMF-E. These neurons all correspond to green areas in (D). (F) The signal-to-noise ratios (SNRs) of all neurons detected by both methods. Colors match the example traces shown in (G), which shows the spatial and temporal components of 10 example neurons detected by both methods. Scalebar: 10 s. See Video 6 for the demixing results.

https://doi.org/10.7554/eLife.28728.013

Video 6

Download asset

To quantify the background effects further, we compute the contribution of each signal component in explaining the variance in the raw data. For each pixel, we compute the variance of the raw data first and then compute the variance of the background-subtracted data. Then the reduced variance is divided by the variance of the raw data, giving the proportion of variance explained by the background. Figure 6C (blue) shows the distribution of the background-explained variance over all pixels. The background accounts for around 90% of the variance on average. We further remove the denoised neural signals and compute the variance reduction; Figure 6C shows that neural signals account for less than 10% of the raw signal variance. This analysis is consistent with our observations that background dominates the fluorescence signal and extracting high-quality neural signals requires careful background signal removal.

The contours of the spatial footprints inferred by the two approaches (PCA/ICA and CNMF-E) are depicted in Figure 6D, superimposed on the correlation image of the filtered raw data. The indicated area was cropped from Figure 6A (left). In this case, most neurons inferred by PCA/ICA were inferred by CNMF-E as well, with the exception of a few components that seemed to be false positives (judging by their spatial shapes and temporal traces and visual inspection of the raw data movie; detailed data not shown). However, many realistic components were only detected by CNMF-E (shown as the green areas in Figure 6D). In these plots, we rank the inferred components according to their SNRs; the color indicates the relative rank (decaying from red to yellow). We see that the components missed by PCA/ICA have low SNRs (green shaded areas with yellow contours).

Figure 6E shows the spatial and temporal components of 14 example neurons detected only by CNMF-E. Here (and in the following figures), for illustrative purposes, we show the calcium traces before the temporal denoising step. For neurons that are inferred by both methods, CNMF-E shows significant improvements in the SNR of the extracted cellular signals (Figure 6F), even before the temporal denoising step is applied. In panel G we randomly select 10 examples and examine their spatial and temporal components. Compared with the CNMF-E results, PCA/ICA components have much smaller size, often with negative dips surrounding the neuron (remember that ICA avoids spatial overlaps in order to reduce nearby neurons’ statistical dependences, leading to some loss of signal strength; see (Pnevmatikakis et al., 2016) for further discussion). The activity traces extracted by CNMF-E are visually cleaner than the PCA/ICA traces; this is important for reliable event detection, particularly in low SNR examples. See Klaus et al., 2017) for additional examples of CNMF-E applied to striatal data.

Application to data in prefrontal cortex

We repeat a similar analysis on GCaMP6s data recorded from prefrontal cortex (PFC, Figure 7), to quantify the performance of the algorithm in a different brain area with a different calcium indicator. Again we find that CNMF-E successfully extracts neural signals from a strong fluctuating background (Figure 7A), which contributes a large proportion of the variance in the raw data (Figure 7B). Similarly as with the striatum data, PCA/ICA analysis missed many components that have very weak signals (33 missed components here). For the matched neurons, CNMF-E shows strong improvements in the SNRs of the extracted traces (Figure 7D). Consistent with our observation in striatum (Figure 6G), the spatial footprints of PCA/ICA components are shrunk to promote statistical independence between neurons, while the neurons inferred by CNMF-E have visually reasonable morphologies (Figure 6E). As for calcium traces with high SNRs (Figure 7E, cell 1-6), CNMF-E traces have smaller noise values, which is important for detecting small calcium transients (Figure 7E, cell 4). For traces with low SNRs (Figure 7, cell 7-10), it is challenging to detect any calcium events from the PCA/ICA traces due to the large noise variance; CNMF-E is able to visually recover many of these weaker signals. For those cells missed by PCA/ICA, their traces extracted by CNMF-E have reasonable morphologies and visible calcium events (Figure 7F).

Figure 7

Download asset Open asset

Neurons expressing GCaMP6s recorded in vivo in mouse prefrontal cortex.

(**A–F**) follow similar conventions as in the corresponding panels of Figure 6. (G) Three example neurons that are close to each other and detected by both methods. Yellow shaded areas highlight the negative ‘spikes’ correlated with nearby activity, and the cyan shaded area highlights one crosstalk between nearby neurons. Scalebar: 20 s. See Video 7 for the demixing results and Video 8 for the comparision of CNMF-E and PCA/ICA in the zoomed-in area of (G).

https://doi.org/10.7554/eLife.28728.015

Video 7

Download asset

Video 8

Download asset

The demixing performance of PCA/ICA analysis can be relatively weak because it is inherently a linear demixing method (Pnevmatikakis et al., 2016). Since CNMF-E uses a more suitable nonlinear matrix factorization method, it has a better capability of demixing spatially overlapping neurons. As an example, Figure 7G shows three closeby neurons identified by both CNMF-E and PCA/ICA analysis. PCA/ICA forces its obtained filters to be spatially separated to reduce their dependence (thus reducing the effective signal strength), while CNMF-E allows inferred spatial components to have large overlaps (Figure 7G, left), retaining the full signal power. In the traces extracted by PCA/ICA, the component labeled in green contains many negative ‘spikes,’ which are highly correlated with the spiking activity of the blue neuron (Figure 7G, yellow). In addition, the green PCA/ICA neuron has significant crosstalk with the red neuron due to the failure of signal demixing (Figure 7G, cyan); the CNMF-E traces shows no comparable negative ‘spikes’ or crosstalk. See also Video 8 for further details.

Application to ventral hippocampus neurons

In the previous two examples, we analyzed data with densely packed neurons, in which the neuron sizes are all similar. In the next example, we apply CNMF-E to a dataset with much sparser and more heterogeneous neural signals. The data used here were recorded from amygdala-projecting neurons expressing GCaMP6f in ventral hippocampus. In this dataset, some neurons that are slightly above or below the focal plane were visible with prominent signals, though their spatial shapes are larger than neurons in the focal plane.

This example is somewhat more challenging due to the large diversity of neuron sizes. It is possible to set multiple parameters to detect neurons of different sizes (or to e.g. differentially detect somas versus smaller segments of axons or dendrites passing through the focal plane), but for illustrative purposes here we use a single neural size parameter to initialize all of the components. This in turn splits some large neurons into multiple components. Following this crude initialization step, we updated the background component and then picked the missing neurons from the residual using a second greedy component initialization step. Next, we ran CNMF-E for three iterations of updating the model variables $A, C$ , and $B$ . The first two iterations were performed automatically; we included manual interventions (e.g. merging/deleting components) before the last iteration, leading to improved source extraction results (see Video 10 for details on the manual merge and delete interventions performed here). In this example, we detected 24 CNMF-E components and 24 PCA/ICA components. The contours of these inferred neurons are shown in Figure 8A. In total we have 20 components detected by both methods (shown in the first three rows of Figure 8B+C); each method detected extra components that are not detected by the other (the last rows of Figure 8B+C). Once again, the PCA/ICA filters contain many negative pixels in an effort to reduce spatial overlaps; see components 3 and 5 in Figure 8A–C, for example. All traces of the inferred neurons are shown in Figure 8D+E. We can see that the CNMF-E traces have much lower noise level and cleaner neural signals in both high and low SNR settings. Conversely, the calcium traces of the three extra neurons identified by PCA/ICA show noisy signals that are unlikely to be neural responses.

Figure 8

Download asset Open asset

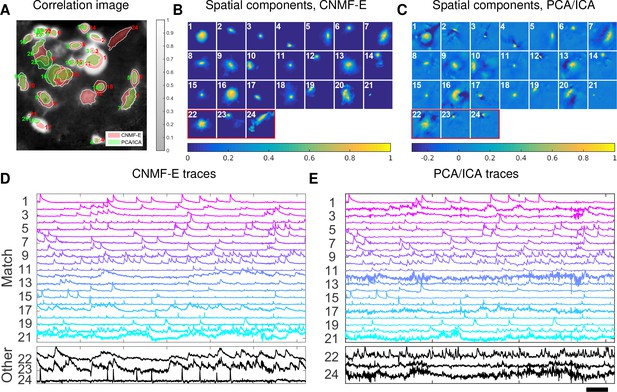
Neurons expressing GCaMP6f recorded in vivo in mouse ventral hippocampus.

(A) Contours of all neurons detected by CNMF-E (red) and PCA/ICA method (green). The grayscale image is the local correlation image of the background-subtracted video data, with background estimated using CNMF-E. (B) Spatial components of all neurons detected by CNMF-E. The neurons in the first three rows are also detected by PCA/ICA, while the neurons in the last row are only detected by CNMF-E. (C) Spatial components of all neurons detected by PCA/ICA; similar to (B), the neurons in the first three rows are also detected by CNMF-E and the neurons in the last row are only detected by PCA/ICA method. (D) Temporal traces of all detected components in (B). ‘Match’ indicates neurons in top three rows in panel (B); ‘Other’ indicates neurons in the fourth row. (E) Temporal traces of all components in (C). Scalebars: $20$ seconds. See Video 9 for demixing results.

https://doi.org/10.7554/eLife.28728.018

Video 9

Download asset

Video 10

Download asset

Application to footshock responses in the bed nucleus of the stria terminalis (BNST)

Identifying neurons and extracting their temporal activity is typically just the first step in the analysis of calcium imaging data; downstream analyses rely heavily on the quality of this initial source extraction. We showed above that, compared to PCA/ICA, CNMF-E is better at extracting activity dynamics, especially in regimes where neuronal activities are correlated (c.f. Figure 4D). Using in vivo electrophysiological recordings, we previously showed that neurons in the bed nucleus of the stria terminalis (BNST) show strong responses to unpredictable footshock stimuli (Jennings et al., 2013). We therefore measured calcium dynamics in CaMKII-expressing neurons that were transfected with the calcium indicator GCaMP6s in the BNST and analyzed the synchronous activity of multiple neurons in response to unpredictable footshock stimuli. We chose 12 example neurons that were detected by both CNMF-E and PCA/ICA methods and show their spatial and temporal components in Figure 9A–C. The activity around the onset of the repeated stimuli are aligned and shown as pseudo-colored images in panel D. The median responses of CNMF-E neurons display prominent responses to the footshock stimuli compared with the resting state before stimuli onset. In comparison, the activity dynamics extracted by PCA/ICA have relatively low SNR, making it more challenging to reliably extract footshock responses. Panel E summarizes the results of panel D; we see that CNMF-E outputs significantly more easily detectable responses than does PCA/ICA. This is an example in which downstream analyses of calcium imaging data can significantly benefit from the improvements in the accuracy of source extraction offered by CNMF-E. (sheintuch2017tracking recently presented another such example, showing that more neurons can be tracked across multiple days using CNMF-E outputs, compared to PCA/ICA.)

Figure 9

Download asset Open asset

Neurons extracted by CNMF-E show more reproducible responses to footshock stimuli, with larger signal sizes relative to the across-trial variability, compared to PCA/ICA.

(**A–C**) Spatial components (A), spatial locations (B) and temporal components (C) of 12 example neurons detected by both CNMF-E and PCA/ICA. (D) Calcium responses of all example neurons to footshock stimuli. Colormaps show trial-by-trial responses of each neuron, extracted by CNMF-E (top, red) and PCA/ICA (bottom, green), aligned to the footshock time. The solid lines are medians of neural responses over 11 trials and the shaded areas correpond to median $\pm 1$ median absolute deviation (MAD). Dashed lines indicate the shock timings. (E) Scatter plot of peak-to-MAD ratios for all response curves in (D). For each neuron, Peak is corrected by subtracting the mean activity within 4 s prior to stimulus onset and MAD is computed as the mean MAD values over all timebins shown in (D). The red line shows $y = x$ . Scalebars: 10 s. See Video 11 for demixing results.

https://doi.org/10.7554/eLife.28728.021

Video 11

Download asset

Conclusion

Microendoscopic calcium imaging offers unique advantages and has quickly become a critical method for recording large neural populations during unrestrained behavior. However, previous methods fail to adequately remove background contaminations when demixing single neuron activity from the raw data. Since strong background signals are largely inescapable in the context of one-photon imaging, insufficient removal of the background could yield problematic conclusions in downstream analysis. This has presented a severe and well-known bottleneck in the field. We have delivered a solution for this critical problem, building on the constrained nonnegative matrix factorization framework introduced in Pnevmatikakis et al., 2016 but significantly extending it in order to more accurately and robustly remove these contaminating background components.

The proposed CNMF-E algorithm can be used in either automatic or semi-automatic mode, and leads to significant improvements in the accuracy of source extraction compared with previous methods. In addition, CNMF-E requires very few parameters to be specified, and these parameters are easily interpretable and can be selected within a broad range. We demonstrated the power of CNMF-E using data from a wide diversity of brain areas (subcortical, cortical, and deep brain areas), SNR regimes, calcium indicators, neuron sizes and densities, and hardware setups. Among all these examples (and many others not shown here), CNMF-E performs well and improves significantly on the standard PCA/ICA approach. Considering that source extraction is typically just the first step in calcium imaging data analysis pipelines (Mohammed et al., 2016), these improvements should in turn lead to more stable and interpretable results from downstream analyses. Further applications of the CNMF-E approach appear in (Cameron et al., 2016; Donahue and Kreitzer, 2017; Jimenez et al., 2016; Jimenez et al., 2018; Klaus et al., 2017; Lin et al., 2017; Murugan et al., 2016; Murugan et al., 2017; Rodriguez-Romaguera et al., 2017; Tombaz et al., 2016; Ung et al., 2017; Yu et al., 2017; Mackevicius et al., 2017; Madangopal et al., 2017; Roberts et al., 2017; Ryan et al., 2017; Roberts et al., 2017; Sheintuch et al., 2017).

We have released our MATLAB implementation of CNMF-E as open-source software (https://github.com/zhoupc/CNMF_E (Zhou, 2017a)). A Python implementation has also been incorporated into the CaImAn toolbox (Giovannucci et al., 2017b). We welcome additions or suggestions for modifications of the code, and hope that the large and growing microendoscopic imaging community finds CNMF-E to be a helpful tool in furthering neuroscience research.

Dataset	Striatum	PFC	Hippocampus	BNST
Size (x × y × t)	256 × 256 × 6000	175 × 184 × 9000	175 × 184 × 9000	175 × 184 × 9000
(# PCs, # ICs)	(2000, 700)	(275, 250)	(100, 50)	(200, 150)
PFC/ICA	986	181	174	52
CNMF-E	726	221	225	435

Share this article

Cite this article

Microendoscopic data contain large background signals with rapid fluctuations due to multiple sources.

An example of typical microendoscopic data.

CNMF-E can accurately separate and recover the background fluctuations in simulated data.

Comparison of CNMF-E with rank-1 NMF in estimating background fluctuation in simulated data.

Variables used in the CNMF-E model and algorithm. ℝ: real numbers; ℝ+: positive real numbers; ℕ: natural numbers; ℕ+: positive integers.

CNMF-E accurately initializes individual neurons’ spatial and temporal components in simulated data.

Initialization procedure for the simulated data in Figure 3.

CNMF-E outperforms PCA/ICA analysis in extracting individual neurons’ activity from simulated data and is robust to low SNR.

The results of CNMF-E in demixing simulated data in Figure 4 (SNR reduction factor = 1).

The results of CNMF-E in demixing the simulated data in Figure 4 (SNR reduction factor = 6).

CNMF-E is able to demix neurons with high temporal correlations.

Neurons expressing GCaMP6f recorded in vivo in mouse dorsal striatum area.

The results of CNMF-E in demixing dorsal striatum data.

Neurons expressing GCaMP6s recorded in vivo in mouse prefrontal cortex.

The results of CNMF-E in demixing PFC data.

Comparison of CNMF-E with PCA/ICA in demixing overlapped neurons in Figure 7G.

Neurons expressing GCaMP6f recorded in vivo in mouse ventral hippocampus.

The results of CNMF-E in demixing ventral hippocampus data.

Extracted spatial and temporal components of CNMF-E at different stages (ventral hippocampal dataset).

Neurons extracted by CNMF-E show more reproducible responses to footshock stimuli, with larger signal sizes relative to the across-trial variability, compared to PCA/ICA.

The results of CNMF-E in demixing BNST data.

Illustration of the initialization procedure.

Optional user-specified parameters.

Running time (sec) for processing the 4 experimental datasets.

Author details

Pengcheng Zhou

Contribution

For correspondence

Competing interests

Shanna L Resendez

Contribution

Contributed equally with

Competing interests

Jose Rodriguez-Romaguera

Contribution

Contributed equally with

Competing interests

Jessica C Jimenez

Contribution

Contributed equally with

Competing interests

Shay Q Neufeld

Contribution

Contributed equally with

Competing interests

Andrea Giovannucci

Contribution

Competing interests

Johannes Friedrich

Contribution

Competing interests

Eftychios A Pnevmatikakis

Contribution

Competing interests

Garret D Stuber

Contribution

Competing interests

Rene Hen

Contribution

Competing interests

Mazen A Kheirbek

Contribution

Competing interests

Bernardo L Sabatini

Contribution

Competing interests

Robert E Kass

Contribution

Competing interests

Liam Paninski

Contribution

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Variables used in the CNMF-E model and algorithm. $ℝ$ : real numbers; $ℝ_{+}$ : positive real numbers; $ℕ$ : natural numbers; $ℕ_{+}$ : positive integers.