Inferring multi-scale neural mechanisms with brain network modelling
- Charité – Universitätsmedizin Berlin, corporate member of Freie Universität Berlin, Humboldt-Universität zu Berlin, and Berlin Institute of Health, Department of Neurology, Germany
- Berlin Institute of Health (BIH), Germany
- Bernstein Focus State Dependencies of Learning & Bernstein Center for Computational Neuroscience, Germany
- University of Toronto, Canada
- Institut de Neurosciences des Systèmes UMR INSERM 1106, Aix-Marseille Université Faculté de Médecine, France
- Universitat Pompeu Fabra, Spain
- Institució Catalana de la Recerca i Estudis Avançats (ICREA), Spain
- Max Planck Institute for Human Cognitive and Brain Sciences, Germany
- Monash University, Australia
- Humboldt University, Germany
Figures
Figure 1
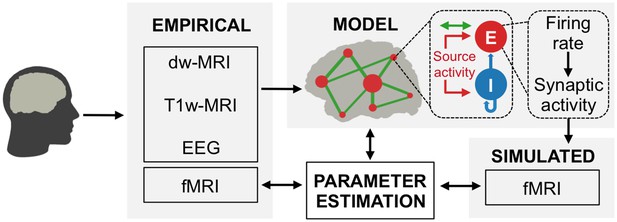
Hybrid modeling framework.
Hybrid brain network models are constructed from diffusion-weighted MRI tractography and region parcellations obtained from anatomical MRI. The nodes of the hybrid models are injected with subject-specific EEG source activity time series instead of noise. Predicted fMRI time series are fit to each subject’s empirical fMRI time series, which were simultaneously acquired with EEG. At each node (small red circles) of the long-range network (green lines) are local networks of excitatory (E) and inhibitory (I) neural population models that are driven by EEG source activity (red arrows). Nodes are globally coupled by structural connectomes (green arrows) that represent the heterogeneous white matter coupling strengths between different brain areas. Synaptic input currents (Equations 1 and 2), firing rates (Equations 3 and 4) and synaptic activity (Equations 5 and 6) underlying fMRI predictions are analysed to identify how neural population activity and network interactions relate to observable neuroimaging signals. See also Video 1 for a visualization of brain network model construction and exemplary results from hybrid model simulations.
Figure 2
Overview of six empirical phenomena on different temporal scales reproduced by the hybrid model.
(a) Neuron firing is inversely related to the phase of α-waves: during peaks of α-waves, neurons fire the least, while they fire maximally during troughs (adapted from Haegens et al., 2011). (b) Our simulations indicate that the inverse relationship between firing and α-phase is related to the ongoing balancing of neural excitation and inhibition (adapted from Atallah and Scanziani, 2009). Reprinted with permission of Elsevier.). (c) On a longer time scale (<0.25 Hz), oscillations of firing rates are inversely related to α-band power fluctuations (adapted from Haegens et al., 2011). (d) Model simulations suggest a mechanism that transforms α-band power oscillations into fMRI oscillations, predicting subject-specific resting-state fMRI time series, corresponding spatial network patterns and the inverse correlation between α-power and fMRI (adapted from de Munck et al., 2008. Reprinted with permission of Elsevier.). (e) Emergence of scale-free fMRI power spectra (adapted from He, 2011) resulted from long-range network input. (f) Individual functional connectivity matrices were predicted over long and short time windows (adapted from Allen et al., 2014).
Figure 3 with 1 supplement
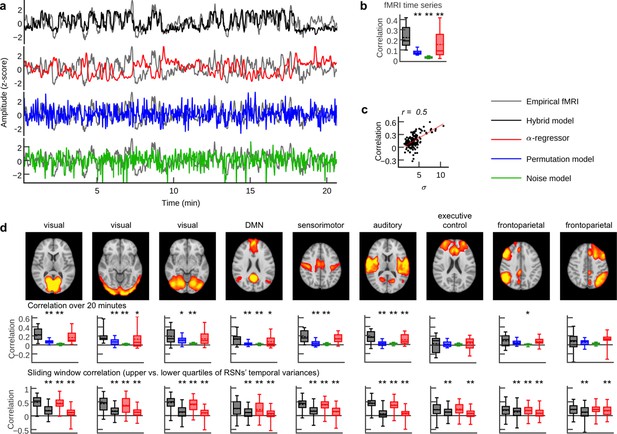
Person-specific fMRI time series prediction.
(a) Example time series of the hybrid model and the three control scenarios from one subject. (b) Box plots of average correlation coefficients between all simulated and empirical region time series (20.7 min) for each subject (n = 15; α-regressor values were inverted for illustration purposes). (c) Scatter plot of RSN time course standard deviation (s.d.) versus prediction quality. Dots depict data from the nine RSN time courses for each subject. (d) Comparison of prediction quality during upper versus lower quartile of epoch-wise RSN time course s.d.s. Upper row: spatial activation patterns of nine RSNs. Middle row: correlation coefficients between RSN temporal modes and hybrid model simulation results and the three control scenarios. Lower row: sliding window (length: 100 fMRI scans = 194 s; step width: one fMRI scan) correlations for the upper (first and third boxplot per panel) and lower quartiles (second and fourth boxplot per panel) of window-wise RSN temporal mode for the hybrid model and the α-regressor. Asterisks indicate significantly increased prediction quality of the hybrid model compared to control scenarios in one-tailed Wilcoxon rank sum test (*p<0.05, **p<0.01). Additionally, all hybrid model correlations in (b) and (d) were tested for the null hypothesis that they come from a distribution whose median is zero at the 5% significance level. All tests rejected the null hypothesis of zero medians except for RSN correlations over 20 min for the executive control and the frontoparietal networks (middle row).
Figure 3—figure supplement 1
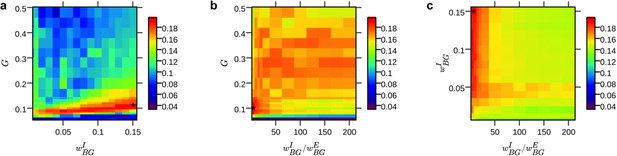
Parameter space exploration results.
(a–c) 2d parameter space heat maps show average time series correlation obtained from the hybrid model for different combinations of the three parameters G, ωBGE, ωBGI (the latter depicted as ratio ωBGI / ωBGE); results were averaged over all subjects and brain regions. Parameter values that yielded the highest average correlation were used for simulations with artificial α-input (marked with an asterisk). We confirmed identifiability of the model by showing that parameter space search converges toward a single optimal solution yielding best predictions.
Figure 4
Functional connectivity prediction.
(a, b) Box plots show correlation coefficients obtained from correlating all subdiagonal entries of empirical and simulated FC matrices. FC was computed for long epochs (static FC; computed over 20.7 min) and short epochs (dynamic FC; average sliding window correlation; 100 fMRI scans window length; one fMRI scan step width). Results were compared for (a) the parameter set that generated the best fMRI time series prediction and (b) the parameter set that yielded the best FC predictions for each subject. (c) Scatter plots compare empirical and simulated average FC for hybrid model simulations and the α-regressor. Dots depict all pair-wise region time series correlations averaged over all subjects. Asterisks in (a) and (b) indicate significantly increased prediction quality of the hybrid model compared to control conditions in one-tailed Wilcoxon rank sum test (*p<0.05, **p<0.01).
Figure 5
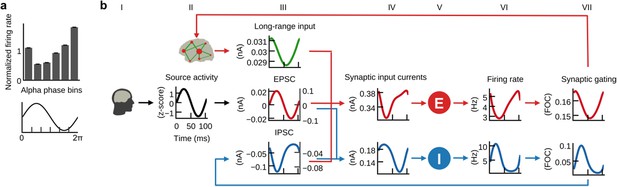
E/I balance generates the inverse relationship between α-phase and firing.
(a) Histogram of population firing rates divided into six bins according to α-cycle segments and normalized relative to the mean firing rate of each cycle. Population firing rates were highest during the trough and lowest during the peak of α-cycles. (b) Grand average waveforms of population inputs and outputs time locked to α-cycles of injected EEG source activity (black, column II). Left and right axes denote input currents to excitatory and inhibitory populations, respectively. Please refer to the main text for a description of the mechanism that explains the inverse relationship between α-cycles and firing rates.
Figure 6 with 1 supplement
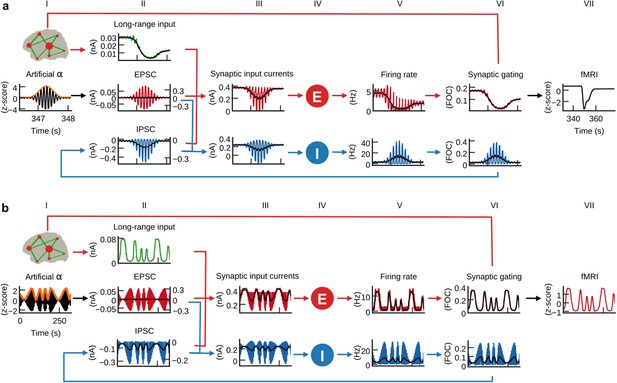
α-power fluctuations generate fMRI oscillations.
Grand average waveforms of population inputs and outputs on longer time scales. (a) Hybrid models were injected with artificial α-activity consisting of 10 Hz sine oscillations that contained a single brief high-power burst (black, column I; orange: signal envelope). While positive deflections of the α-wave generated positive deflections of inhibitory population firing rates, large negative deflections were bounded by the physiological constraint of 0 Hz (blue, fifth column; black: moving average). (b) Hybrid models were injected models with 10 Hz sine waves where ongoing power was modulated similar to empirical α-rhythms (0.01–0.03 Hz). Similarly to (a), but for a longer time frame, inhibitory populations rectified negative deflections, which introduced the α-power modulation as a new frequency component into firing rates and fMRI time series.
Figure 6—figure supplement 1
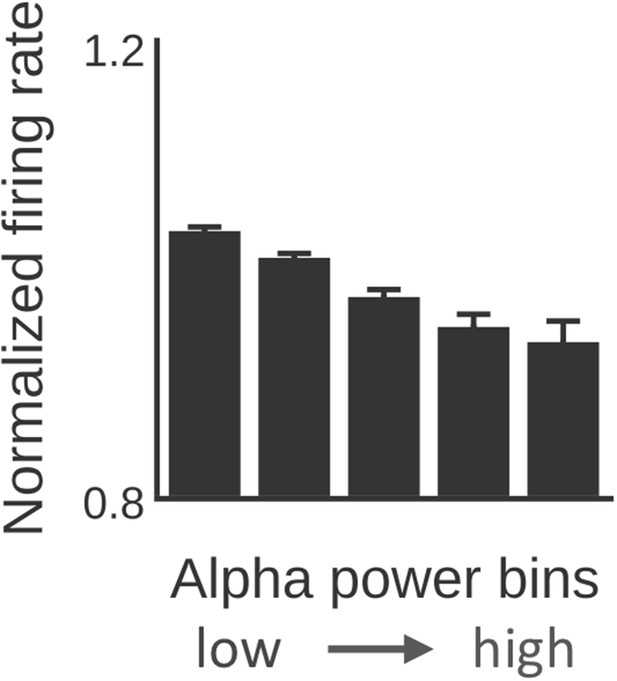
α-power predicts firing rate.
Similar to the electrophysiological results shown in Haegens et al. (2011), all time series for each subject and brain region were divided into five equal-sized bins on the basis of α-power level and average firing rate (normalized with average firing rate per brain region) was computed per bin. Firing rate decreased with increasing α-power (Kruskal-Wallis/Tukey’s post-hoc multiple comparison; p<0.001).
Figure 7 with 2 supplements
Long-range coupling controls fMRI power-law scaling.
(a) Power spectral densities of simulated and empirical fMRI and empirical α-band activity (straight-line fits of power spectra are for illustration purposes only; scale-invariance was determined in the time domain using rigorous model selection criteria, see Materials and methods). (b) As in Figure 6b, but with disabled long-range coupling. In contrast to Figure 6b, the amplitudes of firing rates, synaptic gating and fMRI are equally large, while in Figure 6b amplitudes were larger during slower α-band power modulations.
Figure 7—figure supplement 1
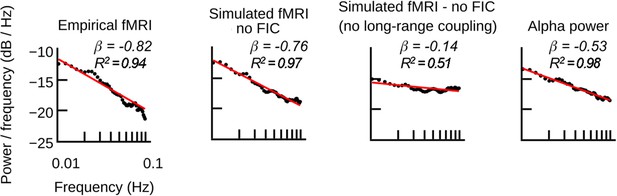
As in Figure 7a, but simulations were performed with the simplified hybrid model, that is, the models used no feedback inhibition control (FIC) and a single value for all local inhibitory connections Ji was used.
Empirical and simulated fMRI spectra have a large power-law exponent, that is a steeper slope, compared to ongoing α-power or wide-band power (βα-band = −0.53, βwide-band = −0.47). To analyze the effect of long-range network interaction, simulated fMRI was computed with and without long-range coupling. To exclude that power-law spectra emerge despite absent long-range coupling, local inhibition was tuned such that the model produced highest fMRI time series predictions. Without long-range coupling, simulated fMRI showed a similar exponent as injected EEG source activity. When long-range coupling was activated and global excitation was properly balanced with local inhibition, the exponent was closer to the exponent of empirical fMRI (Figure 7—figure supplement 2).
Figure 7—figure supplement 2
Fine-grained parameter space exploration of the simplified hybrid model for an exemplary subject.
Here, global coupling and a single value for all local inhibitory connection parameters Ji were tuned. Colors indicate the average correlations between simulated and empirical data (a–c) and the absolute difference between exponents of power-law fits with empirical and simulated power spectral densities (d, colormap was flipped to indicate highest fits in red to be consistently with the other subplots), averaged over all regions.
Videos
Video 1
Reverse-engineering neural information processing.
The video shows how computational brain network models are constructed from individual neuroimaging data, how these models can be used to simulate different types of neural activity of individual subjects on multiple temporal scales and how model activity can be used to derive mechanisms of brain function.
Tables
Table 1
State variables and parameters of the hybrid brain network model.
https://doi.org/10.7554/eLife.28927.015| Quantity | Value | Description |
|---|---|---|
| State variables | ||
| ri(E,I) | Population firing rate of the excitatory (E) or inhibitory (I) population in brain area i | |
| Si(E,I) | Average synaptic gating | |
| Ii(E,I) | Sums of all input currents | |
| IBG | EEG-derived input currents | |
| Parameters | ||
| w+ | 1.4 | Local excitatory recurrence |
| Cij | Obtained from diffusion tractography | Structural connectivity matrix |
| γE, γI | 6.41 × 10−4, 1.0 × 10−3 | Kinetic parameters |
| aE, bE, dE, τE, WE | 310 (nC−1), 125 (Hz), 0.16 (s), 100 (ms), 1 | Excitatory gating variables |
| aI, bI, dI, τI, WI | 615 (nC−1), 177 (Hz), 0.087 (s), 10 (ms), 0.7 | Inhibitory gating variables |
| JNMDA | 0.15 (nA) | Excitatory synaptic coupling |
| JI | Obtained by FIC heuristic (nA) | Feedback inhibitory synaptic coupling |
| I0 | 0.382 (nA) | overall effective external input |
| G | Obtained from model fitting | Global coupling scaling factor |
| , | Obtained from model fitting | Weights for scaling EEG-derived input currents |
Table 2
Parameters of the 15 hybrid brain network models obtained by parameter tuning.
https://doi.org/10.7554/eLife.28927.016| G | ||
|---|---|---|
| 0.12 | 0.13 | 5 |
| 0.1 | 0.03 | 5 |
| 0.14 | 0.08 | 50 |
| 0.09 | 0.03 | 10 |
| 0.13 | 0.15 | 5 |
| 0.44 | 0.03 | 25 |
| 0.15 | 0.05 | 20 |
| 0.09 | 0.12 | 5 |
| 0.48 | 0.04 | 125 |
| 0.2 | 0.15 | 10 |
| 0.11 | 0.12 | 10 |
| 0.12 | 0.02 | 5 |
| 0.25 | 0.04 | 5 |
| 0.44 | 0.07 | 200 |
| 0.09 | 0.04 | 5 |
Additional files
-
Supplementary file 1
Supplementary table to the eLife Transparent Reporting Form that summarizes the used statistical test, N, exact p-values and descriptive statistics for each hypothesis test.
- https://doi.org/10.7554/eLife.28927.017
-
Transparent reporting form
- https://doi.org/10.7554/eLife.28927.018
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Inferring multi-scale neural mechanisms with brain network modelling
eLife 7:e28927.
https://doi.org/10.7554/eLife.28927
