Computer assisted detection of axonal bouton structural plasticity in in vivo time-lapse images

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: November 7, 2017 (This version)
Accepted Manuscript published: October 23, 2017 (Go to version)
Accepted: October 22, 2017
Received: June 6, 2017

1. Of interest
Context-dependent requirement of G protein coupling for Latrophilin-2 in target selection of hippocampal axons

Daniel T Pederick, Nicole A Perry-Hauser ... Liqun Luo

Research Article Mar 20, 2023
Further reading

Article
Figures and data
Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

The ability to measure minute structural changes in neural circuits is essential for long-term in vivo imaging studies. Here, we propose a methodology for detection and measurement of structural changes in axonal boutons imaged with time-lapse two-photon laser scanning microscopy (2PLSM). Correlative 2PLSM and 3D electron microscopy (EM) analysis, performed in mouse barrel cortex, showed that the proposed method has low fractions of false positive/negative bouton detections (2/0 out of 18), and that 2PLSM-based bouton weights are correlated with their volumes measured in EM (r = 0.93). Next, the method was applied to a set of axons imaged in quick succession to characterize measurement uncertainty. The results were used to construct a statistical model in which bouton addition, elimination, and size changes are described probabilistically, rather than being treated as deterministic events. Finally, we demonstrate that the model can be used to quantify significant structural changes in boutons in long-term imaging experiments.

https://doi.org/10.7554/eLife.29315.001

Introduction

The repertoire of synaptic connectivity within neuronal networks is immensely increased through the continuous formation and elimination of synapses (Chklovskii et al., 2004; Stepanyants et al., 2002). Indeed, in vivo imaging studies over the last 15 years have shown that synaptic structures remain dynamic throughout adulthood (Holtmaat and Svoboda, 2009; Trachtenberg et al., 2002). This structural plasticity, i.e. the appearance, disappearance, and the morphological modifications of synapses in the adult brain has been established as a fundamental underpinning of learning and experience-dependent changes in neuronal circuits (Holtmaat and Caroni, 2016; Holtmaat and Svoboda, 2009; Stepanyants and Chklovskii, 2005).

Synapses in the central nervous system are morphologically distinct structures, visible only in electron microscopy (EM). In light microscopy (LM) a synapse can be detected based on the presence of a swelling on the axon, referred to as bouton, or a protrusion from the dendrite, known as spine. In the cerebral cortex, the majority of excitatory synapses and a minority of inhibitory synapses occur on dendritic spines (Gray, 1959). Spines can easily be detected, hence most studies of structural plasticity have used manual or semi-automated tracking of these structures in time-lapse images to infer circuit changes (Holtmaat and Svoboda, 2009). Yet, studies relying on tracking of dendritic spines may not reveal the full extent of synaptic plasticity because synapses can also occur on dendritic shafts. On the other hand, a dendrite’s presynaptic apposition can be detected as an irregularity or swelling on the axon. Similar to dendritic spines, such axonal boutons have long since been recognized as sites of functional connections between neurons (Van Gehuchten, 1904). Therefore, the detection of these structures would provide a powerful means to analyze synaptic connectivity (Markram et al., 2015; Meyer et al., 2010)

Many EM studies have revealed a variety of presynaptic morphologies and the arrangements of vesicles, endoplasmic reticulum, and mitochondria therein (Harris and Weinberg, 2012). This is the only method capable of verifying that LM observations of axonal boutons do indeed correspond to synaptic contacts, but applying such a method every time is difficult across large volumes and impossible at more than one time point. The few real-time imaging studies of presynaptic plasticity in vivo used semi-automatic detection methods to track individual axonal boutons in LM time-lapse images (Chen et al., 2015; De Paola et al., 2006; Grillo et al., 2013; Holtmaat et al., 2009; Johnson et al., 2016; Keck et al., 2011; Majewska et al., 2006; Mostany et al., 2013; Qiao et al., 2016; Stettler et al., 2006; Yang et al., 2016). Visually isolated axons were segmented, and axonal boutons, as presumed synaptic contacts, were scored by virtue of their integrated fluorescence (De Paola et al., 2006; Grillo et al., 2013). Based on arbitrarily defined thresholds, boutons are usually scored in a binary fashion, i.e. present or absent. However, due to jitter in fluorescence caused by fluctuations in imaging conditions, binary scoring of boutons may lead to high false positive/negative rates.

Several computer-assisted methods aid axon segmentation (Acciai et al., 2016; Parekh and Ascoli, 2013) and bouton detection (Song et al., 2016) in sparsely labeled tissue, but many challenges remain. The most difficult challenges to overcome are due to the limited resolution of two-photon microscopy (mainly along the optical axis, z). For example, due to the high density of boutons on cortical axons, boutons often lie in close proximity to one another and can appear fused in microscopy images (Figure 1). In densely labeled tissue bouton detection is further confounded by the fact that axons can also appear fused to one another which locally increases the integrated fluorescence. Furthermore, spatially and temporally non-uniform expression levels and the variability in axon caliber complicate the tracking of boutons over time. Such complications lead to inconsistencies and bias in LM-based bouton detection methods. The bias will affect bouton density estimates, while the inconsistencies, combined with binary scoring of boutons, will lead to an apparent increase in the bouton turnover rate.

Figure 1

Download asset Open asset

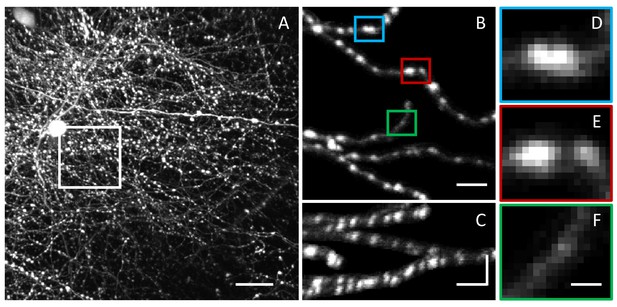
Challenges in LM-based bouton detection and measurement.

(A) Maximum intensity xy projection of an image stack showing axons of fluorescently labeled neurons in superficial layers of mouse barrel cortex. High density of labeled axons makes it difficult to automatically detect boutons and track their structural changes over time. Scale bar is 20 μm. (B) A subset of labeled axons from the region outlined in (A). To improve visibility, image intensity beyond five voxels from the axon centerlines was set to zero. Bouton detection and bouton size measurement are confounded by large variations in fluorescence levels across axons. (C) Axons from (B) shown on the zx maximum intensity projection. Horizontal scale bars in (B) and (C) are 5 μm. Vertical scale bar in (C) is 15 μm. Lower resolution in z compared to xy is yet another challenge in bouton analyses. (**D–F**) Magnified views of the highlighted boutons from (B). Close proximity of boutons on an axon (D), large range of bouton sizes (E), and large range of bouton fluorescence levels (**D–F**), present additional obstacles to accurate bouton detection and measurement. Scale bar in (**D–F**) is 1.25 μm.

https://doi.org/10.7554/eLife.29315.002

Here, we describe semi-automated methodology for bouton detection and tracking in images acquired by 2-photon laser scanning microscopy (2PLSM) in vivo. We validate the results of the method with correlative 3D EM of in vivo imaged axons, and by applying the detection method to images acquired under various conditions that mimic the variability in time-lapse imaging. We quantify variability in bouton detection and propose a statistical model to deal with the inherent uncertainties of this LM-based detection method.

Results

LM-based bouton detection and measurement of structural changes

Here, we describe and evaluate a heuristic strategy that utilizes axon traces to detect and quantify boutons in 2PLSM images taken through a cranial window in vivo. This procedure consists of the following major steps: (1) tracing axons in 3D, (2) optimization of traces, (3) generation of axon intensity profiles, (4) detection of putative boutons based on the profiles, (5) normalization of intensity profiles and calculation of bouton weights, and (6) matching putative boutons across time-lapse images.

Axons can be traced automatically or manually with various tools (Acciai et al., 2016; Parekh and Ascoli, 2013). In this study, high density of labeled axons (Figure 1A) precluded the possibility of automated tracing. Therefore, axons were traced manually by using NCTracer software (Chothani et al., 2011; Gala et al., 2014), and traces were optimized as described in Materials and methods. Following optimization, two intensity profiles were generated for each axon by convolving specifically designed filters with the image at all trace node positions and scaling the results to unit means. While various filters can be used to generate axon intensity profiles, in this study, we settled on the following two: (1) a modified, multi-scale Laplacian of Gaussian filter (LoG_xy) to detect putative boutons and (2) a fixed size Gaussian filter (G) to provide an estimate of axon intensity in the regions devoid of boutons (see Materials and methods for details). In the following we will refer to such inter-bouton regions as axon shaft.

\begin{array}{l} L o G_{x y} (x, y, z | R_{x y}, R_{z}) = \frac{4 e^{- (x^{2} + y^{2}) / R_{x y}^{2}}}{π R_{x y}^{4}} (1 - \frac{x^{2} + y^{2}}{R_{x y}^{2}}) \times \frac{e^{- z^{2} / R_{z}^{2}}}{\sqrt{π} R_{z}} \\ G (x, y, z | R) = \frac{e^{- (x^{2} + y^{2} + z^{2}) / R^{2}}}{{(π)}^{3 / 2} R^{3}} \end{array}

Figure 2A and B show that distinct putative boutons can be identified as peaks in the LoG_xy profile plotted against node positions along the trace, $I^{L o G_{x y}} (s_{i})$ . This is because the LoG_xy filter is designed to sharpen boundaries between boutons by suppressing intensity in the regions immediately adjacent to boutons. In contrast, the G filter yields a smoother profile, $I^{G} (s_{i})$ , which is not very useful for resolving putative boutons that are in close proximity (arrows in Figure 2C), but is well suited for estimating shaft intensity. For these reasons, LoG_xy profiles were used to identify putative boutons, while G profiles were used to determine intensities of axon shafts.

Figure 2 with 2 supplements see all

Download asset Open asset

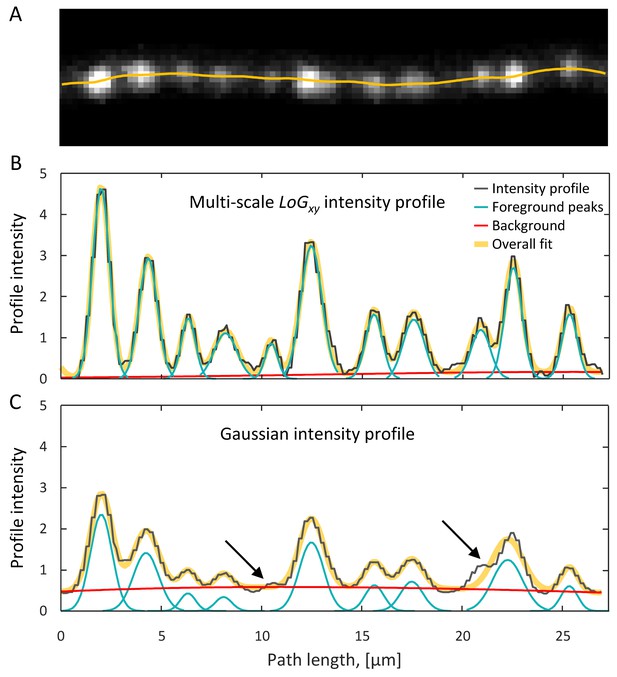
Detection of putative boutons as peaks on axon intensity profiles.

(A) Maximum intensity xy projection of an axon segment showing multiple putative boutons. Yellow line is the optimized trace of this axon. (B) Putative boutons visible in (A) correspond to peaks on the *LoG_xy* intensity profile (black line). Foreground peaks (cyan lines) and local background (red line) are fitted to the intensity profile as described in the text. The overall fit (thick yellow line), which is the sum of foreground peaks and background, closely matches the intensity profile. (C) G intensity profile is obtained by sliding a fixed size Gaussian filter along the optimized trace. Small or closely positioned peaks cannot be resolved on the G profile (arrows). Peak amplitudes from the *LoG_xy* profile and background from the G profile are used to define bouton weights.

https://doi.org/10.7554/eLife.29315.003

To automatically detect putative boutons in an LoG_xy profile we used an algorithm that is similar to the Backward-Stepwise Subset Selection method (Hastie et al., 2009). Here, a varying number of foreground peaks, $N_{f}$ , and a constant number of background peaks, $N_{b}$ , was fitted to $I^{L o G_{x y}} (s_{i})$ by minimizing the following objective function of peak positions, $μ_{j}^{f}$ and $μ_{k}^{b}$ , amplitudes, $a_{j}^{f}$ and $a_{k}^{b}$ , and widths, $σ_{j}^{f}$ and $σ_{k}^{b}$ (see Materials and methods for details):

\begin{array}{ll} min_{\binom{a_{j}^{f}, μ_{j}^{f}, σ_{j}^{f}}{a_{k}^{b}, μ_{k}^{b}, σ_{k}^{b}}} (\sum_{i} {(I^{L o G_{x y}} (s_{i}) - \sum_{j = 1}^{N_{f}} a_{j}^{f} e^{- \frac{{(s_{i} - μ_{j}^{f})}^{2}}{2 {(σ_{j}^{f})}^{2}}} - \sum_{k = 1}^{N_{b}} a_{k}^{b} e^{- \frac{{(s_{i} - μ_{k}^{b})}^{2}}{2 {(σ_{k}^{b})}^{2}}})}^{2}) \\ a_{j}^{f} \geq 0; 0.5 μ m \leq σ_{j}^{f} \leq 2.0 μ m \\ a_{k}^{b} \geq 0; σ_{k}^{b} \geq 20 μ m \end{array}

We note that, though profile background was fit with a sum of spatially distributed peak functions, constraints imposed on their widths ( $σ_{k}^{b} \geq$ 20 μm) ensure that the fit varies slowly along the axon (red line in Figure 2B).

Following the detection of putative boutons, intensity of bouton $j$ was defined as the sum of the $j$ -th foreground peak amplitude and background intensity at the peak location:

I_{j}^{B o u t o n} = a_{j}^{f} + \sum_{k = 1}^{N_{b}} a_{k}^{b} e^{- \frac{{(μ_{j}^{f} - μ_{k}^{b})}^{2}}{2 {(σ_{k}^{b})}^{2}}}

Shaft intensity was estimated from the G profile by incorporating information about the positions of detected putative boutons, Figure 2C. To that end, we initialized the above described peak detection algorithm with the foreground and background peaks detected on the LoG_xy profile, but ran the algorithm on the G intensity profile. Shaft intensity for a given axon was defined as the fitted background intensity on the G profile, averaged over trace nodes,

\begin{array}{l} I_{i}^{B a c k g r o u n d} = \sum_{k = 1}^{N_{b}} a_{k}^{b, G} e^{- \frac{{(s_{i} - μ_{k}^{b, G})}^{2}}{2 {(σ_{k}^{b, G})}^{2}}} \\ I^{S h a f t} = {⟨ I_{i}^{B a c k g r o u n d} ⟩}_{i} \end{array}

In this expression, index G in the superscripts of peak amplitudes, $a$ , positions, μ, and widths, σ, was added to emphasize that these quantities are calculated based on the G intensity profile. We note that background intensity, $I_{i}^{B a c k g r o u n d}$ , is designed to vary smoothly along the axon (red line in Figure 2C) and be independent of bouton density, providing a robust estimate of axon shaft intensity.

Our goal is to use intensity profiles to extract structural information related to the physical sizes of boutons. This task is hindered by the facts that axon intensity depends strongly on expression levels of fluorescent molecules (Figure 1A) and microscopy conditions. Therefore, to measure unbiased structural information, intensity profiles must be properly normalized. One may consider using median (or mean) profile intensity or local shaft intensity for normalization. However, these types of normalizations can lead to errors. For example, if density of boutons varies across axons, normalization with the median (or mean) may bias boutons on higher bouton density axons towards lower intensity values. Also, if density of boutons is sufficiently large, normalization with local shaft intensity can lead to variability as the latter cannot be measured reliably between closely positioned boutons.

Our heuristic normalization approach is based on the idea that by convolving the LoG_xy or G filter with the image at a trace node position $s_{i}$ along axon $a$ in imaging session $t$ , we obtain a quantity that is proportional to three factors: $M_{t}$ , a factor related to imaging conditions [e.g. laser power, photomultiplier tube (PMT) voltage, and cranial window quality], $ρ_{a, t}$ , volume density of fluorescent molecules, and $A_{a, t} (s_{i})$ , a structural factor which has been linked to axon cross-section area (drawn perpendicular to the xy projection of the axon centerline) convolved with the microscope point-spread function (Song et al., 2016) and profile filter:

{\tilde{I}}_{a, t}^{L o G_{x y}, G} (s_{i}) = M_{t} ρ_{a, t} A_{a, t}^{L o G_{x y}, G} (s_{i})

In creating the LoG_xy and G profiles (Figure 2) we rescale ${\tilde{I}}_{a, t}^{L o G_{x y}} (s_{i})$ and ${\tilde{I}}_{a, t}^{G} (s_{i})$ to unit means in order to minimize effects related to imaging conditions and expression levels, thus isolating structural information:

I_{a, t}^{L o G_{x y}, G} (s_{i}) = \frac{{\tilde{I}}_{a, t}^{L o G_{x y}, G} (s_{i})}{{⟨ {\tilde{I}}_{a, t}^{L o G_{x y}, G} (s_{i}) ⟩}_{i}} = \frac{A_{a, t}^{L o G_{x y}, G} (s_{i})}{{⟨ A_{a, t}^{L o G_{x y}, G} (s_{i}) ⟩}_{i}}

It may be tempting to use putative bouton intensity, $I_{j}^{B o u t o n}$ in Equation (3), which is detected based on $I_{a, t}^{L o G_{x y}} (s_{i})$ as proxy for bouton size. However, this may lead to bias as the denominators in Equation (6) depend strongly on bouton density. To address this issue, we use axon shaft intensity detected from G intensity profiles, $I^{S h a f t}$ in Equation (4), for normalization. The resulting quantity, referred to as bouton weight, $w_{j}^{B o u t o n}$ , conveys structural information, which is effectively independent of the above-mentioned bias,

w_{j}^{B o u t o n} = \frac{I_{j}^{B o u t o n}}{I^{S h a f t}}

Validation of LM-based bouton detection methodology with EM

Correlative light and electron microscopy (CLEM) was used to validate the described bouton detection procedure (Figure 3 and Figure 3—video 1). Four axon segments were selected for this analysis (Figure 3A). The axon segments were imaged in vivo with 2PLSM, the brain tissue was fixed shortly after, and subsequently imaged with EM (see Materials and methods for details). Putative boutons in the 2PLSM stack of images were detected and quantified as described above (Figure 3B). Axons in EM images were reconstructed in 3D (Figure 3C) and rendered in Blender software for further analysis.

Figure 3 with 1 supplement see all

Download asset Open asset

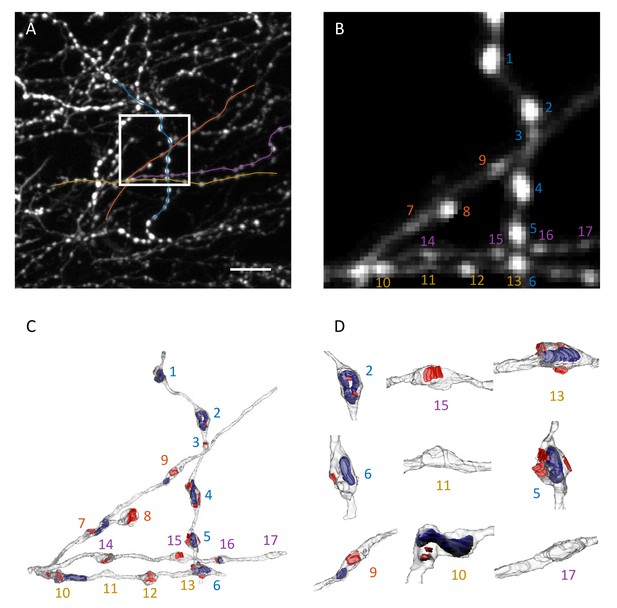
Correlative light and electron microscopy.

(A) Maximum intensity xy projection of an image stack used for CLEM analysis. White box demarcates the region imaged with EM. Colored lines are traces of four axon segments chosen for EM reconstruction. Scale bar is 10 μm. (B) Region outlined in (A) is shown at 4x magnification with background removed. (C) 3D EM reconstruction of the four axon segments shown in (B). Red areas mark PSDs, and blue volumes outline mitochondria. Most varicosities identified in EM are clearly visible in 2PLSM images (B). (D) Higher magnifications and different orientations of a subset of reconstructed varicosities shows that structural swellings on axons may or may not be associated with PSDs and/or contain mitochondria. Numbers in (**B–D**) enumerate distinct varicosities identified in EM.

https://doi.org/10.7554/eLife.29315.006

Putative boutons detected in 2PLSM images could be unambiguously matched with varicosities identified in EM (Figure 3—video 1, asterisks in Figure 4A–D, and Table 1). We used positions of the centers of matched boutons to register LM traces and EM centerlines with an optimal linear transformation (Hastie et al., 2009). Average distance between the registered traces (Gala et al., 2014) was small, 0.34 ± 0.17 μm (mean ± s.d.), confirming that the same set of axons was reconstructed in LM and EM. A small discrepancy between registered traces may be attributed to non-linear distortion of tissue in the EM experiment and the relatively low z-resolution of LM. Overall, 16 boutons en passant and one bouton terminaux could be identified in EM. The bouton terminaux was detected with our method, but was excluded from further analysis because it is not located on the axon centerline. With the omission of this bouton, the LM-based procedure detected 18 putative boutons with 0 false negatives and two false positives, both of which were small (1.1 and 2.2 in weight, #18 and #19 in Table 1).

Figure 4 with 1 supplement see all

Download asset Open asset

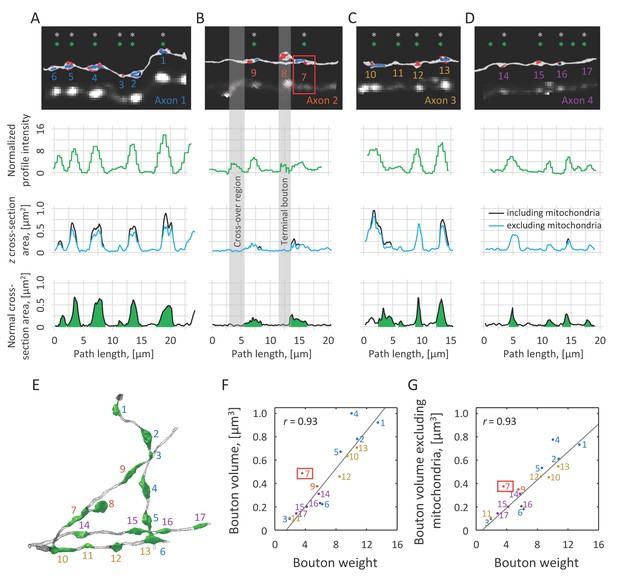
Normalized intensity profile is correlated with axon cross-section area, while bouton weight is indicative of bouton volume.

(**A–D**) Top row: EM reconstructions of axons are shown next to the corresponding 2PLSM maximum intensity projections. Varicosities identified in EM are marked with grey asterisks, and putative boutons automatically detected based on the intensity profiles are marked with green asterisks. Second row: Normalized intensity profiles of the same axons plotted as functions of position along axon centerlines obtained in EM. Third row: z cross-section areas of axons, including (black) and excluding (blue) mitochondria, are well correlated with intensity profiles. These cross-sections are drawn perpendicular to the 2PLSM xy projections of the axon centerlines. Fourth row: Normal cross-section areas showing the extents of boutons (green) based on criteria described in Materials and methods. (E) Demarcated boutons shown in 3D (green). Bouton weights are highly correlated with their EM-based volumes that include (F) or exclude (G) mitochondrial volumes. Grey regions in (B) highlight two spurious peaks in the normalized intensity profile, one resulting from a close apposition of two axons and another caused by the presence of a terminal bouton. Such regions were annotated in 2PLSM images and were excluded from all analyses. In addition, bouton #7 (red box in B, F, and G) was excluded from the correlation analysis because it is directly adjacent to a branch point, which biases weight calculation.

https://doi.org/10.7554/eLife.29315.008

Table 1

Comparison of LM-based and EM measurements.

Bouton IDs match those in Figures 3 and 4. The probability that a putative bouton belongs to the category of LM boutons, $P (b o u t o n | w)$ was calculated according to Equation (9) with $w_{t h r e s h o l d}$ = 2.0. Bouton #8 (grey) was excluded from the analyses as it is a terminal bouton. Hyphens indicate that boutons, mitochondria, or PSDs were not detected in EM.

https://doi.org/10.7554/eLife.29315.010

		2PLSM measurements		EM measurements
	Bouton ID	Putative bouton weight, w	P(bouton \| w)	Bouton volume [μm³]	Mitochondria volume [μm³]	PSD surface area [μm²]
Axon 1	1	13.5	1.00	0.919	0.189	0.666
	2	10.8	1.00	0.779	0.170	0.595
	3	1.98	0.48	0.093	-	0.371
	4	10.1	1.00	0.998	0.225	1.92
	5	8.65	1.00	0.669	0.139	1.83
	6	6.25	1.00	0.219	0.043	0.138
Axon 2	7	3.63	0.93	0.483	0.111	0.612
	8	N/A	N/A	0.574	-	2.75
	9	5.57	1.00	0.372	0.027	1.28
Axon 3	10	9.54	1.00	0.632	0.182	0.645
	11	1.99	0.49	0.102	-	-
	12	8.51	1.00	0.456	-	1.23
	13	10.8	1.00	0.704	0.161	1.49
Axon 4	14	5.80	1.00	0.308	-	0.867
	15	4.23	1.00	0.198	-	0.686
	16	5.96	1.00	0.229	0.027	0.402
	17	2.85	0.93	0.140	-	-
	18	1.14	0.01	-	-	-
	19	2.19	0.65	-	-	-

We tested the idea that 2PLSM intensity is correlated to the area of axon cross-section drawn perpendicular to the xy projection of axon centerline (Song et al., 2016). We refer to such cross-sections as z cross-sections (third row in Figure 4A–D) to distinguish them from normal cross-sections, which are drawn perpendicular to the axon centerline. For this, we calculated the normalized axon intensity profile, $I_{a, t}^{L o G_{x y}} (s_{i}) / I^{S h a f t}$ , and compared it to EM z cross-section areas including and excluding mitochondrial z cross-section areas. Both z cross-section areas appear to be well correlated with normalized intensity profiles. However, it is clear from visual inspection that the normalized intensity profiles do not resolve small changes in axon cross-section, which is the result of limited resolution of 2PLSM.

To examine the extent to which LM-based measurements provide information about bouton size, we plotted bouton weight against bouton volumes including (Figure 4F) and excluding (Figure 4G) mitochondrial volume. Normal axon cross-sections were used to identify bouton boundaries and calculate bouton volume as described in Materials and methods (fourth row in Figure 4A–D and Figure 4E). Bouton #7 (red box in Figure 4B) was excluded from these analyses, because it is bounded on one side by the terminal bouton branch which biases weight measurement. The results show high degree of correlation in both cases (Pearson’s r = 0.93), supporting the idea that LM-based measurements can be used to quantify volumes of even very small varicosities (#3, 0.093 μm³). The results also provide support for the choice of filters, Equation (1), and the normalization procedure, Equation (7), showing that the proposed method could overcome axon-specific differences in the expression levels and bouton density, capturing meaningful fine-scale structural information.

It is important to emphasize that we did not attempt to find the best procedure for fitting the EM data. It is possible that some other combinations of filter types, normalizations, and parameters would lead to marginally better correlations. However, due to the small sample size, this would likely be a case of over-fitting. The described procedure was designed based on theoretical considerations, and the parameters were chosen based on the observed range of bouton sizes (see Materials and methods). Nonetheless, we explored alternative filtering and normalization strategies. Figure 4—figure supplement 1 shows profiles derived from raw voxel intensities, and profiles obtained with mean, Gaussian, and median filters of different but fixed sizes. Each of these profiles was normalized by its median value. The figure makes it clear that some amount of filtering benefits bouton detection, as jagged unfiltered profiles can lead to false positives. Similarly, relatively large filters of fixed size (e.g. 5 × 5 × 5 and R = 2) are not well suited for bouton detection as they often suppress intensities of small boutons and merge closely positioned boutons. When the filter size is carefully tuned (3 × 3 × 3 and R = 1), resulting profiles can look similar to those of multi-scale LoG_xy, although higher baselines in these profiles can make peak detection more challenging. Furthermore, we examined the combined effect of filtering and normalization on bouton measurement by comparing the amplitudes of profile peaks to corresponding bouton volumes. Multi-scale LoG_xy profile normalized with shaft intensity as described above leads to the highest correlation compared to the best considered alternatives (Figure 4—figure supplement 1E).

Effects of imaging conditions on bouton analysis

Next, we sought to evaluate the effects of various imaging conditions on bouton detection and measurement. To that end, a set of fluorescently labeled axons was imaged seven times in a span of 80 min with different laser power (LP) and PMT voltage (see inset in Figure 5A). In addition, in condition E, a thin layer of agarose was applied to the cranial window to mimic deterioration of window quality which often accompanies long-term imaging experiments. In the following, we assume that there is negligible structural plasticity of boutons throughout the duration of this short-term imaging experiment, and therefore differences in bouton measurements can be attributed to the effects of imaging conditions and measurement uncertainties. The inset in Figure 5B shows the maximum intensity projections of an axon segment imaged in all seven conditions. This inset illustrates that increasing (decreasing) LP and/or PMT voltage results in an overall increase (decrease) in intensity, and therefore proper normalization procedure must be used to minimize the effects of such changes on bouton measurements.

Figure 5

Download asset Open asset

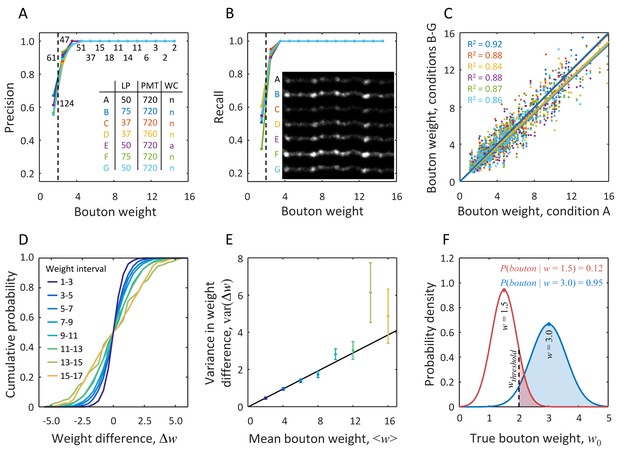
Probabilistic definition of an LM bouton based on measurement uncertainty derived from short-term imaging experiments.

The same set of axons was imaged 7 times within 80 min with various microscope settings and cranial window conditions (inset in A). Putative boutons detected based on the first imaging session (condition A) were chosen to be the gold standard. Precision (A) and recall (B) in bouton detection were measured under the remaining conditions, B-G. Both precision and recall increase with bouton weight. While for very small boutons ( $w$ < 2.0, dashed line) detection is unreliable, agreement with the gold standard is achieved across all imaging conditions in 95% of boutons with weights greater than 2.0. Numbers of boutons in the gold standard are indicated next to the data points in (A). Inset in (B) shows an example of one axon segment imaged in conditions A-G. (C) Bouton weights under different imaging conditions are plotted against the gold standard weight. Best fit lines show no significant bias for conditions B and C, however small, but significant reduction in mean bouton weight was observed in the remaining four conditions (all p < 0.03, two-sample t-test). Abbreviations used in the inset of A: LP is laser power in mW, PMT denotes photomultiplier tube voltage in Volts, and WC is cranial window condition, where ‘n’ stands for normal and ‘a’ indicates presence of a thin layer of agarose. Color code used in (**A–C**) is defined by the inset table in (A). (D) CDFs for differences in bouton weights across imaging conditions. Data from all conditions were pooled. Different lines show CDFs for various intervals of mean bouton weight. (E) Variance in bouton weight difference increases linearly with mean bouton weight (χ² linear regression with $var (Δ w) = α ⟨ w ⟩$ , p = 0.33, α = 0.24 ± 0.01, mean ± s.d.). Error-bars indicate standard deviations obtained with bootstrap sampling with replacement. (F) Red line shows the distribution of true bouton weight for a putative bouton of measured weight $w$ = 1.5. Area under the curve to the right of $w_{t h r e s h o l d}$ = 2.0 gives $P (b o u t o n | w)$ = 0.12. Large putative boutons (e.g. blue curve, $w$ = 3.0) have high probability of being LM boutons.

https://doi.org/10.7554/eLife.29315.011

Putative boutons on 16 axon segments were detected in all conditions independently (400 putative boutons per condition on average). Custom software was used to match the same putative boutons across conditions. Putative boutons detected in condition A were chosen to be the gold standard, and precision/recall in bouton detection in the remaining conditions B-G were evaluated as functions of bouton weight (Figure 5A and B). The results show that for 95% of putative boutons of weight $w$ > 2.0 both precision and recall equal one in all conditions. This number of unambiguously detected putative boutons goes up to 99% for $w$ > 2.5 and 100% for $w$ > 3.1. For reference, $w$ = 2.0 corresponds to the weights of the two smallest varicosities identified in EM (#3 and #11 in Table 1), and the weight of the next smallest bouton (#17) is $w$ = 2.8. Therefore, all but very small boutons can be detected with our method with high confidence.

To examine the effects of imaging conditions on bouton weight, we tested a subset of 290 putative boutons that were detected and matched across all seven experiments. Figure 5C shows bouton weights in conditions B-G plotted against the corresponding weights in condition A. Although axon intensities in conditions B and C are drastically different from A (see inset in Figure 5B), the normalization procedure could correct for these differences (blue and red lines in Figure 5C). However, small (≈ 7%) but significant bias was present in conditions D-G, which may have been caused by bleaching due to prolonged imaging. Figure 5C also reveals a considerable amount of variability in weight measurements. This variability, reflected in the R² coefficients, was similar across all comparisons, including the imaging experiments performed under the same conditions (e.g. A and G, cyan points). Therefore, bouton weight measurements are accompanied with uncertainty which is inherent to the LM-based methodology. This uncertainty cannot be eliminated entirely, and hence, it must be explicitly incorporated into models that derive biological information from bouton measurements.

Statistical framework for the analysis of structural plasticity of boutons

To model the variability observed in Figure 5C, we examined bouton weight differences for all pairs of imaging conditions, $Δ w = w_{1} - w_{2}$ . Because such changes clearly depend on bouton size, we looked at the statistics of $Δ w$ in various intervals of average bouton weight, $⟨ w ⟩ = (w_{1} + w_{2}) / 2$ . Figure 5D shows the cumulative distribution functions (CDFs) of bouton weight differences in eight intervals of $⟨ w ⟩$ . These distributions are not significantly different from Gaussian distributions, and their variances are roughly proportional to the mean bouton weights, $var (Δ w) = α ⟨ w ⟩$ , Figure 5E. Therefore, all CDFs shown in Figure 5D could be standardized by rescaling the weight differences as $Δ w / \sqrt{α ⟨ w ⟩}$ , leading to distributions that are statistically indistinguishable from the Standard Normal CDF (all p > 0.05, one-sample KS test).

Based on this result, we propose a statistical model in which measured bouton weight, $w$ , is the sum of the true weight, $w_{0}$ , and a noise term, δ. The latter is randomly drawn from a Gaussian distribution with variance proportional to the measured weight, $var (δ) = \frac{1}{2} α w$ :

w = w_{0} + δ; P (δ) = \frac{e^{- δ^{2} / α w}}{\sqrt{π α w}}

Equation (8) quantifies uncertainties in bouton weight measurements, making it possible to define bouton presence probabilistically. To that end, we impose a threshold on true bouton weight, $w_{t h r e s h o l d}$ , and refer to putative boutons with $w_{0}$ > $w_{t h r e s h o l d}$ , as LM (light microscopy) boutons. In the following we set $w_{t h r e s h o l d}$ = 2.0, which is motivated by several considerations. First, this value equals twice the average normalized axon shaft intensity. Therefore, by using $w_{t h r e s h o l d}$ = 2.0 we are only including peaks that are substantially larger than the axon shaft intensity. Second, $w$ = 2.0 corresponds to the weights of the two smallest varicosities detected in EM (#3 and #11 in Table 1). Finally, detection of putative boutons becomes unreliable for $w$ < 2.0 (Figure 5A and B). We note that as an alternative to choosing a single threshold value to define LM boutons, one could vary the threshold in a certain range (e.g. 1–3) and report results as functions of this parameter.

The probability that a putative bouton of measured weight $w$ belongs to the category of LM boutons, $P (b o u t o n | w)$ , can be calculated based on the noise model of Equation (8):

P (b o u t o n | w) = \frac{1}{2} (1 + e r f (\frac{w - w_{t h r e s h o l d}}{\sqrt{α w}}))

In this expression, $e r f$ denotes the error function. Shaded regions in Figure 5F illustrate these probabilities for two putative boutons of measured weights $w$ = 1.5 and $w$ = 3.0. Note that even when $w$ is less than $w_{t h r e s h o l d}$ , there is a non-zero probability that the detected peak is an LM bouton. For large $w$ (e.g. greater than 3), this probability approaches unity, and the LM bouton definition becomes virtually deterministic.

LM bouton definition can be used to calculate the probabilities of bouton addition, elimination, potentiation, and depression based on the measured weights in two imaging sessions (initial and final), $w_{i}$ and $w_{f}$ :

\begin{array}{ll} P (a d d e d | w_{i} \to w_{f}) = (1 - P (b o u t o n | w_{i})) \times P (b o u t o n | w_{f}) \\ P (e l i m i n a t e d | w_{i} \to w_{f}) = P (b o u t o n | w_{i}) \times (1 - P (b o u t o n | w_{f})) \\ P (p o t e n t i a t e d | w_{i} \to w_{f}) = P (b o u t o n | w_{i}) \times P (b o u t o n | w_{f}) \times \frac{1}{2} (1 + e r f (\frac{w_{f} - w_{i}}{\sqrt{α (w_{i} + w_{f})}})) \\ P (d e p r e s s e d | w_{i} \to w_{f}) = P (b o u t o n | w_{i}) \times P (b o u t o n | w_{f}) \times \frac{1}{2} (1 + e r f (\frac{w_{i} - w_{f}}{\sqrt{α (w_{i} + w_{f})}})) \end{array}

We would like to clarify that LM boutons may or may not correspond to varicosities seen in EM (Table 1), and the latter may not always be associated with postsynaptic densities (PSDs) and, thus, functional synapses (Shepherd and Harris, 1998). Therefore, the relationship between an LM bouton and a synapse is not deterministic and is likely to contain false-positives and false-negatives. However, the number of such errors is expected to decrease with increasing $w$ . For example, Table 1 shows that all LM boutons of $w$ > 2.2 correspond to EM varicosities, and all LM boutons of $w$ > 2.9 are varicosities associated with PSDs.

Bouton changes can be resolved despite the uncertainty in measurements

Next, we set out to determine if the above described bouton detection procedure can be used to identify significant structural changes in long-term, in vivo imaging experiments. To that end, axons of GFP labeled neurons were imaged in superficial layers of barrel cortex in five mice. Imaging was performed at 4 day intervals over a 24 day period (seven imaging sessions). On average, 968 bouton sites were detected on 20 axon segments in each animal and imaging session. These sites were tracked over the duration of the experiment (Figure 6—figure supplement 1) to quantify bouton addition, elimination, and weight changes as compared to the initial state of the circuit. The short-term imaging experiment of Figure 5 was used as control. Here, conditions B-G were compared to condition A, and the results were pooled.

Figure 6A shows the fraction of added LM boutons over time, as compared to the first imaging session. Specifically, we only consider significant bouton addition events, i.e. those for which the probability of addition according to Equation (10) is greater than 0.95. Analogous plots for the fractions of significant bouton eliminations and significant bouton weight changes (potentiation and depression combined) are shown in Figure 6B and C respectively. As was expected, the fractions of significant changes in the short-term imaging experiment (red points in Figure 6) are at the chance levels (dashed red lines). The latter was obtained with a bootstrap procedure in which the weights of individual boutons were independently shuffled across conditions. In contrast, in the long-term imaging experiment, the fractions of significant bouton additions, eliminations, and weight changes are significantly larger than chance already by the second imaging session (after 4 days), and these fractions continue to increase with time, consistent with the idea of gradual modification of the circuit. These results illustrate that the described methodology can be used to quantify circuit changes, despite the numerous challenges associated with long-term, in vivo imaging experiments.

Figure 6 with 1 supplement see all

Download asset Open asset

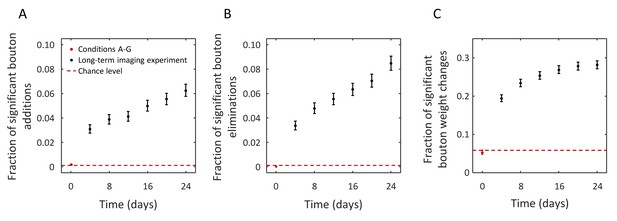
Structural change in boutons can be resolved in long-term in vivo imaging experiments despite measurement noise.

(A) Fraction of boutons that are absent on day 0 and are present at a later time with joint probability of 0.95 or greater (significant bouton addition). Red point (error-bars are too small to be visible) shows this fraction in images acquired within 80 min (conditions A-G). Black points show the results for a long-term imaging experiment. Statistically significant fraction of added boutons is detected after 4 days (interval between imaging sessions), and this fraction grows with time, consistent with the idea of gradual modification of the initial circuit. Similar trends were observed for the fractions of significant bouton eliminations (B) and significant bouton weight changes. Dashed red lines in (**A–C**) indicate baseline circuit changes expected from the statistical model. Error-bars indicate standard deviations based on Poisson statistics.

https://doi.org/10.7554/eLife.29315.012

Discussion

Detection of structural changes in boutons is hindered by various technical challenges and fundamental limitations of light microscopy. Unfortunately, any uncertainty that enters the analysis of long-term in vivo imaging data manifests itself as spurious structural plasticity. Therefore, it is important to account for all sources of errors, minimize their effect, and incorporate the residual uncertainty into the interpretation of results. Below, we describe various sources of errors affecting bouton measurements.

First, fluorescence based measurements provide only indirect evidence of bouton size. Therefore, such measurements need to be validated by showing that they are informative of bouton structures. In this study, we used CLEM to show that bouton weight, defined based on 2PLSM data, is well correlated with bouton volume (Figure 4F and G). Second, variability in expression levels of fluorescent proteins across axons and within axons over time makes it difficult to compare boutons on different axons and to identify true structural changes. Here, these problems were mitigated by a specifically designed normalization procedure (Figure 2), which was verified with CLEM (Figure 4) and was tested in the short-term imaging experiment (Figure 5A–C). Third, because the resolution of 2PLSM (≈ 0.3 µm in xy) is not much smaller than bouton size (≈ 1 µm for small boutons in Figure 3), there are inherent uncertainties in detection of small boutons, differentiation of closely positioned boutons, and measurement of bouton size changes. These uncertainties of the imaging method cannot be eliminated, and, therefore, they must be modeled to ensure that bouton measurements are interpreted correctly (Figure 5D–F).

Many other technical issues can add to the uncertainty and introduce bias in bouton measurements. For example, deterioration of cranial window quality with time, deformation of brain tissue, small changes in brain orientation relative to the microscope, and slight movement of boutons along axons can lead to the perception of increased plasticity. In contrast, limited temporal resolution of long-term imaging experiments, typically few days between imaging sessions, can lead to an underestimate of plasticity, as changes that occur between imaging sessions remain unaccounted. Finally, uncertainty can arise from the computational method used to detect boutons. Figure 2—figure supplement 2D shows that computational uncertainty of the method described in this study is small and can be ignored considering contributions from other sources (Figure 5C).

It is important to emphasize that not every putative bouton detected in LM will correspond to a varicosity if imaged with EM. This is particularly so for very small putative boutons ( $w$ < 2.0, bouton volume < 0.1 μm³) which can result from noise in fluorescence or inhomogeneity in labeling. In the absence of a reliable synaptic marker, the only reasonable way to eliminate such functionally irrelevant putative boutons is by imposing a threshold on bouton weight. In this study, we refer to putative boutons whose true weight exceeds the threshold as LM boutons and suggest setting this threshold at 2.0 based on CLEM and short-term imaging experiments. In practice, one may vary the threshold in a small range to ensure that specific conclusions are robust to the choice of this parameter.

Using a threshold to define an LM bouton as an all-or-none entity may impose a bias since the true bouton weight is unknown due to measurement uncertainty. The problem is exacerbated by the unimodal shape of bouton weight distributions (see Figure 2—figure supplement 2B), because of which a large fraction of weights will lie within the range of uncertainty around the threshold, regardless of its value. Such ambiguous boutons can either be discarded, which may bias biological interpretation, or, otherwise, they must be treated probabilistically. For example, probabilistic description is essential for calculation of the expected number of LM boutons. Simply counting the number of above threshold weights would result in an underestimate as bouton weight distribution is monotonically decreasing. Similar considerations apply to calculations of expected numbers of added, eliminated, potentiated, and depressed boutons. As most bouton structures are stable and do not change substantially over days-to-weeks, their weight changes often lie within the range of measurement uncertainty and must also be described probabilistically. Furthermore, probabilistic description is necessary for calculation of error-bars and for establishing statistical significance of results. To illustrate the feasibility of this approach, we applied it to a dataset of 4840 bouton sites tracked over 24 days. Figure 6 shows that statistically significant changes in LM boutons can be detected in long-term imaging experiments. It remains to be seen if the detected changes are informative of circuit alterations that subserve the many functions of the brain.

Materials and methods

In vivo imaging

Request a detailed protocol

All experiments were performed according to the guidelines of the Swiss Federal Act on Animal Protection and Swiss Animal Protection Ordinance. The ethics committee of the University of Geneva and the Cantonal Veterinary Office of Geneva, Switzerland (approval code GE/61/17) approved all experiments.

For development of the detection methodology we used data from mice that had been repeatedly imaged as part of a larger optical micro-stimulation and behavioral study (not yet published). Only the methodology that is relevant for the present study will be mentioned. Adeno-associated viral (AAV) vectors encoding floxed GFP (AAV2/9.CAG.flex.eGFP.WPRE.bGH2 [Upen]) were co-injected with an AAV vector encoding Cre (AAV2/9.hSynapsin.hGHintron.GFP-Cre.WPRE.SV40 [Upen]) at a ratio of 0.15 × 10⁹: 1 (genome copies: genome copies). This produced an average of about 150 GFP-expressing cells per animal, mostly in L2/3 and L5 of the barrel cortex. We exclusively imaged the processes of these neurons in the upper layers of the cortex. Hence, the source of the fluorescent signal in the green channel is dominated by cytosolic GFP.

Following the AAV injection, we implanted a 3 mm diameter glass window over the barrel cortex as previously described (Holtmaat et al., 2009). Imaging experiments were started 6 weeks after the virus injection. Imaging was performed under anaesthesia (0.5–1.5% isoflurane). A custom-built alignment system was used to ensure identical positioning of the mouse’s cranial window at different time points, and to avoid rotations relative to the axial dimension of the objective. The system was based on aligning a beam reflected by the cranial window through two apertures, which uniquely determines a line in three spatial dimensions. The apertures and the laser position were constant, and the only free variables were the cranial window position and rotation (i.e., the x, y, and z-positions, as well as the row and pitch needed to be identical between sessions to satisfy the passage of light through the two apertures). We used a custom built 2PLSM (Janelia Research Campus, model Non-MIMMS in vivo microscope) to acquire in vivo anatomical images of the anesthetized animals through the cranial window. We used the ScanImage software (Janelia Research Campus, Vidrio Technologies) (Pologruto et al., 2003) to record the 2PLSM images, and additional custom software to align anatomical structures present on the central image stack by using a red-green overlay between current and past images.

For imaging we used a 20x water immersion objective (NA 0.95, XLUMPlanFI, Olympus, Japan). Images were acquired at a voxel volume of ≈ 0.13 × 0.26 × 0.8 μm³ (x × y × z). We binned the data in the x dimension to generate isometric voxels in x and y for all analyses. The voxel dwell time was 0.8 μs for the full resolution images (and thus twice as high after 2x binning of the x dimension). Each ROI comprised an image stack of ≈ 270 × 270 × 250 μm³. As the imaging light source we used a Ti:sapphire femtosecond pulsed laser (Chameleon ultra II, Coherent) that was lasing at 1010 nm. Emitted fluorescence light was split into two channels using a dichroic mirror (Semrock, FF735-Di01−35.5 × 49.0) and two bandpass filters (red channel, Semrock FF01-607/70; green channel, Semrock FF01-530/70). Each channel was equipped with a PMT (red channel, Hamamatsu R3896; green channel, Hamamatsu H10770PA-40SEL). Images were analyzed only in the green channel.

Correlative 3D EM

Request a detailed protocol

Electron microscopy was carried out on the region outlined in Figure 3A using a previously described method (Maco et al., 2014; Maco et al., 2013). An image of the blood vessel pattern below the cranial window was taken immediately after the last 2PLSM imaging session. The anesthetized animal was then chemically fixed by perfusing, via the heart, 10 ml of isotonic PBS immediately followed by 200 ml of 2.5% glutaraldehyde and 2% paraformaldehyde in phosphate buffer (0.1 M, pH 7.4). Two hours later, the brain was removed and 60-μm-vibratome sections cut from the imaged region, tangential to the cortical surface. The region containing the imaged axons was located in these sections by matching the pattern of blood vessels seen in the first 2–3 sections with the image of the brain’s surface taken prior to the perfusion. The 2-photon laser was then used to burn lines into the fixed section around the region of interest. The laser was tuned to λ = 850 nm with a power of ~300 mW at the back focal plane of the objective. A rectangle of ~25 μm x 25 μm was burnt around the ROI using the line scan mode (2 ms/line). This shape acts as a fiducial mark that can be seen after the tissue has been stained, and resin embedded, ready for election microscopy. This section was then washed in sodium cacodylate buffer (0.1 M, pH 7.4) 5 × 3 min, postfixed and stained in reduced osmium (1.5% potassium ferrocyanide with 1% osmium tetroxide in 0.1 M sodium cacodylate buffer) for 40 min, followed by another 40 min incubation with 1% osmium tetroxide in the same buffer, and finally for 40 min with 1% aqueous uranyl acetate. Next, the section was dehydrated in a series of increasing concentrations of alcohol, then infiltrated in 100% Durcupan resin, and flat embedded between two glass slides and placed in a 60°C oven for 24 hr.

A small piece of the section (2 mm x 2 mm), containing the laser marked region, was trimmed from the rest of the section and glued onto a slab of blank resin, keeping the region of interest closest to the surface. This block was then trimmed in the ultramicrotome, using glass knives, so that the laser marks were within 5 μm of its surface, and less than 2 μm from one edge. The block was then mounted on a 45° aluminum stub, using conductive carbon paint, so that this edge was uppermost. It was then sputter coated with a 30 nm thick layer of gold. The sample was then placed in the focused ion beam scanning electron microscope chamber (FIBSEM; Zeiss NVision 40, Zeiss SMT, Germany) and orientated so that the ion beam could mill parallel to the laser marks, and therefore parallel to the 2PLSM plane of focus. The sample was imaged with an electron beam of 1.7 kV and a probe current of 1.1 nA using the back-scattered electron detector (ESB). Images with a pixel size of 6 nm were collected with a dwell time of 12 μs per pixel. The ion beam removed 12 nm of resin after each image, using a current of 700 pA, with an energy of 30 kV.

The serial electron micrographs were aligned in FIJI (http://fiji.sc; Schindelin et al., 2012) and the structures of interest segmented in the TrakEM2 part of the software (Cardona et al., 2012). Models were then exported to the Blender software (Blender Foundation, Amsterdam; http://www.blender.org), and the NeuroMorph toolset (http://neuromorph.epfl.ch; Jorstad et al., 2015) was used to measure axon cross-section areas, bouton and mitochondrial volumes, and PSD surface areas. The beginning and end of each bouton were defined, using the centerline processing tool, as the points along the axon where its normal cross-section area changed by more than 30% within a distance of 0.2 μm. The boutons were then delineated and their volumes calculated in the measurement tool (fourth row in Figure 4A–D and Figure 4E).

Trace optimization

Request a detailed protocol

Figure 2—figure supplement 1A shows three maximum intensity projection views of an axon segment, which was traced independently by five users. Inter-user trace variability, which is usually more pronounced along the z-dimension (optical axis), can hinder bouton detection and measurement. Therefore, it is essential to optimize the layout of manual traces, ensuring that they accurately follow axon centerlines in the underlying image.

In this study, we used the optimization algorithm described in (Chothani et al., 2011). In this version of the algorithm, positions of trace nodes $r_{k} = {(x_{k}, y_{k}, z_{k})}^{T}$ are updated to optimize a fitness function, which includes intensity integrated along the trace and a regularizing constraint on the positions of neighboring trace nodes:

ℱ ({r_{k}}) = \sum_{k} (\frac{1}{λ} \sum_{m} I (l_{m}) \frac{e^{\frac{- {‖ r_{k} - l_{m} ‖}^{2}}{2 R^{2}}}}{{(2 π)}^{3 / 2} R^{3}} (1 - \frac{2}{3} \frac{{‖ r_{k} ‖}^{2}}{R^{2}}) - \frac{α λ}{2} \sum_{k^{'}} {‖ r_{k} - r_{k^{'}} ‖}^{2})

Here, vectors $l_{m}$ denote the positions of voxel centers in the image stack, index $k^{'}$ enumerates the neighbors of node $k$ , parameter λ denotes the average density of nodes in the trace (number of nodes per voxel), and Lagrange multiplier α > 0 controls the stiffness of the trace. The first term in this expression represents convolution of the image with the Laplacian of Gaussian filter of size R, and due to the fast decay of the Gaussian factor, summation in this term can be restricted to a small number of voxels in the vicinity of the trace. The following parameter values were used to produce the results of this study. R was set to three voxels (roughly equal to axon diameter in the images), λ was set to 0.5, and α equaled 0.001. The fitness function was maximized with Newton’s method as previously described (Gala et al., 2014). Trace node positions were synchronously updated at every iteration step, and optimization terminated when the relative change in $ℱ$ fell below 10⁻⁶.

Results of this optimization procedure (Figure 2—figure supplement 1B) show marked improvement over manual traces. The optimized traces are smoother, closer to one another in z, and follow the underlying axon intensity in the image more accurately. Following optimization, all traces were subdivided to a higher density of nodes, λ = 4.

Generation of axon intensity profiles

Request a detailed protocol

Parameters of filters used to generate the axon intensity profiles, Equation (1), were chosen in the following way. The xy size of the multi-scale LoG_xy filter was chosen to span bouton sizes observed in 2PLSM images, R_xy∈ [1.5, 3.0] voxels (0.39 μm to 0.78 μm). Since the observed bouton size in the z dimension is dominated by the point spread function of the microscope, a single size was chosen for the z component of the filter, R_z = 2 voxels (1.6 μm). Upon convolution with the image, this multi-scale filter returns the maximum intensity calculated over the specified range of sizes. The Gaussian filter, G, was chosen to have a fixed size of R = 2 voxels in all three dimensions. This size was selected to be roughly equal to the typical axon shaft radius observed in the images (Figure 2—figure supplement 1A).

Figure 2—figure supplement 1C shows LoG_xy profiles for the five manual traces from Figure 2—figure supplement 1A. Small differences in the layout of manual traces can lead to significant variability in intensity profiles, which is undesirable. Trace optimization reduces this variability to an extent undetectable by visual inspection, Figure 2—figure supplement 1D.

Detection of putative boutons

Request a detailed protocol

Peak detection algorithm, Equation (2), was initialized with a number of foreground peaks, $N_{f} = ⌈ L / 0.5 μ m ⌉$ , which is much larger than the expected number of putative boutons. In this expression, $⌈ ⌉$ denotes the ceiling function and $L$ is the trace length in micrometers. The number of background peaks, $N_{b} = ⌈ L / 25 μ m ⌉$ , was determined based on the observed spatial scale of background variability. The peaks were initially distributed uniformly along the entire length of the trace. Both, Gaussian and Lorentzian peak functions were tested, but only the former was used in this study as it provided a better fit to intensity profiles as judged by the value of the objective function.

The objective function was minimized with the gradient descent method. Gradient steps were taken simultaneously along the $μ_{j}^{f}$ , $μ_{k}^{b}$ , $a_{j}^{f}$ , $a_{k}^{b}$ , $σ_{j}^{f}$ , and $σ_{k}^{b}$ dimensions. At every gradient step, parameters that moved outside the bounds specified in Equation (2) were set to these bounds. Upon convergence, that is, when the relative change in the value of the objective function became less than 10⁻⁶, one small foreground peak was eliminated or a pair of closely positioned foreground peaks was merged, and the resulting set of peaks was re-optimized. This procedure was continued until there were no peaks left that passed the following heuristic criteria: (1) a single foreground peak is marked for elimination if the peak amplitude is less than 0.3, and (2) a pair of overlapping foreground peaks is marked for merger if distance between the peaks is less than 1.0 μm or overlap area of the peaks exceeds 50% of either area. Here, the threshold of 0.3 was set to exclude small profile peaks that result from fluctuations of intensity along the axon. This threshold was chosen to be significantly lower than the mean profile intensity, which is one according to Equation (6). Distance threshold of 1.0 μm (size of a small bouton, see e.g. Figure 3) and threshold on inter-peak overlap were introduced to merge peaks corresponding to the same varicosity.

Matching putative boutons across imaging sessions

Request a detailed protocol

Custom software was used to match putative boutons over time. Because most large boutons remains stable over weeks to months, they can serve as fiducial points to match the remaining boutons. Here, piecewise linear registration of normalized intensity profiles was performed based on few fiducial boutons marked by users across imaging sessions (Figure 6—figure supplement 1). This was followed by matching the remaining putative boutons with a greedy, distance-based algorithm. All results were then validated with visual inspection. For putative boutons detected in some, but not all imaging sessions the missing bouton weights were filled in with the normalized intensity profile values at the corresponding registered positions. This procedure was performed for axons traced by different users (Figure 2—figure supplement 2), axons repeatedly imaged under different conditions (Figure 5), and axons monitored in the long-term imaging experiment (Figure 6).

Quantifying precision of bouton detection methodology

Request a detailed protocol

Small inaccuracies in layout of axon traces can introduce errors in bouton detection. Therefore, it is essential to verify that trace optimization can guarantee sufficiently high precision in bouton detection. For this test, putative boutons were detected automatically, both with and without trace optimization, on the same set of 16 axon segment traced manually by five users. In the absence of trace optimization, a total of 578 candidate bouton sites were identified and matched across all five user traces (Figure 2—figure supplement 2A). A candidate bouton site here is defined as a position on an axon where a putative bouton was detected based on at least one user trace. For the majority of candidate bouton sites, 348 (60%), a putative bouton was present in all five user traces, and thus, there was a full consensus in bouton detection. However, 141 (24%) candidate bouton sites had one conflict and 89 (16%) had two. A conflict is defined as a dissent from the majority, and given five traces, the maximum number of conflicts is two. In contrast, after trace optimization, 474 candidate bouton sites were detected, of which 409 (86%) had full consensus, 39 (8%) had one conflict, and 26 (6%) had two (Figure 2—figure supplement 2B). With trace optimization, it was possible to obtain complete agreement in all putative boutons of weights greater than 2.5. This is a marked improvement over bouton detection with no trace optimization where 17 putative boutons of weights greater than 2.5 had one or more conflicts.

Tracing inaccuracies also affect the weights of detected putative boutons. Figure 2—figure supplement 2C, shows that inaccurate manual traces can contribute to bias (slope difference from 1) and variance (deviation from the best fit line) in bouton weight, and that trace optimization significantly reduces such errors. To quantify the uncertainty in bouton weight we calculated root mean square (RMS) weight difference for putative boutons detected with no conflicts (Figure 2—figure supplement 2D). As was expected, trace optimization dramatically reduces this uncertainty in the entire range of bouton weights.

We would like to point out that some amount of uncertainty in bouton detection (Figure 2—figure supplement 2B) and measurement (Figure 2—figure supplement 2D) remains even after trace optimization. However, as shown in Figure 5A–C this uncertainty of the method is much smaller than variability originating from the experimental sources, and therefore, it is not a limiting factor in structural plasticity measurements.

Implementation

Request a detailed protocol

Axons of fluorescently labeled neurons were traced by using the manual tracing module of NCTracer software (http://www.neurogeometry.org). Custom software written in MATLAB, BoutonAnalyzer (Gala et al., 2017; copy archived at https://github.com/elifesciences-publications/BoutonAnalyzer), was used to optimize the traces, generate intensity profiles, detect putative boutons, and match these boutons across multiple user traces and imaging sessions. BoutonAnalyzer enables the user to visually inspect the results of bouton detection and matching and edit them if necessary. The NeuroMorph Centerline Processing and NeuroMorph Measurement tools were used to measure axon cross-section areas, bouton and mitochondrial volumes, and PSD surface areas (Jorstad and Knott, 2017). A copy is archived at https://github.com/elifesciences-publications/NeuroMorph.

Data availability

Request a detailed protocol

Data used in the CLEM experiment are available in the Dryad Digital Repository (https://dx.doi.org/10.5061/dryad.3q50t). This dataset includes a 2PLSM image stack in TIFF format (Figure 3A), optimized traces of four axon segments in SWC format (Figure 3A), and 3D EM reconstructions of these axons in Blender format (Figure 3C).

Data availability

The following data sets were generated

1. Gala R
2. Lebrecht D
3. Sahlender DA
4. Jorstad A
5. Knott G
6. Holtmaat A
7. Stepanyants A
(2017) Data from: Computer assisted detection of axonal bouton structural plasticity in in vivo time-lapse images
Available at Dryad Digital Repository under a CC0 Public Domain Dedication.

http://dx.doi.org/10.5061/dryad.3q50t

References

(2016) Automated neuron tracing methods: An updated account
Neuroinformatics 14:353–367.
https://doi.org/10.1007/s12021-016-9310-0
- PubMed
- Google Scholar
(2012) TrakEM2 software for neural circuit reconstruction
PLoS One 7:e38011.
https://doi.org/10.1371/journal.pone.0038011
- PubMed
- Google Scholar
1. Chen SX
2. Kim AN
3. Peters AJ
4. Komiyama T
(2015) Subtype-specific plasticity of inhibitory circuits in motor cortex during motor learning
Nature Neuroscience 18:1109–1115.
https://doi.org/10.1038/nn.4049
- PubMed
- Google Scholar
(2004) Cortical rewiring and information storage
Nature 431:782–788.
https://doi.org/10.1038/nature03012
- PubMed
- Google Scholar
(2011) Automated tracing of neurites from light microscopy stacks of images
Neuroinformatics 9:263–278.
https://doi.org/10.1007/s12021-011-9121-2
- PubMed
- Google Scholar
1. De Paola V
2. Holtmaat A
3. Knott G
4. Song S
5. Wilbrecht L
6. Caroni P
7. Svoboda K
(2006) Cell type-specific structural plasticity of axonal branches and boutons in the adult neocortex
Neuron 49:861–875.
https://doi.org/10.1016/j.neuron.2006.02.017
- PubMed
- Google Scholar
(2014) Active learning of neuron morphology for accurate automated tracing of neurites
Frontiers in Neuroanatomy 8:37.
https://doi.org/10.3389/fnana.2014.00037
- PubMed
- Google Scholar
Software
1. Gala R
2. Lebrecht D
3. Sahlender DA
4. Jorstad A
5. Knott G
6. Holtmaat A
7. Stepanyants A
(2017) BoutonAnalyzer, version 531a792
GitHub.

https://github.com/neurogeometry/BoutonAnalyzer
1. Gray EG
(1959)
Axo-somatic and axo-dendritic synapses of the cerebral cortex: an electron microscope study

Journal of Anatomy 93:420–433.
- PubMed
- Google Scholar
1. Grillo FW
2. Song S
3. Teles-Grilo Ruivo LM
4. Huang L
5. Gao G
6. Knott GW
7. Maco B
8. Ferretti V
9. Thompson D
10. Little GE
11. De Paola
(2013) Increased axonal bouton dynamics in the aging mouse cortex
PNAS 110:E1514–E1523.
https://doi.org/10.1073/pnas.1218731110
- PubMed
- Google Scholar
1. Harris KM
2. Weinberg RJ
(2012) Ultrastructure of synapses in the mammalian brain
Cold Spring Harbor Perspectives in Biology 4:a005587.
https://doi.org/10.1101/cshperspect.a005587
- PubMed
- Google Scholar
Book
(2009)
The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed)

New York: Springer.
- Google Scholar
1. Holtmaat A
2. Bonhoeffer T
3. Chow DK
4. Chuckowree J
5. De Paola
6. Hofer SB
7. Hübener M
8. Keck T
9. Knott G
10. Lee WC
11. Mostany R
12. Mrsic-Flogel TD
13. Nedivi E
14. Portera-Cailliau C
15. Svoboda K
16. Trachtenberg JT
17. Wilbrecht L
(2009) Long-term, high-resolution imaging in the mouse neocortex through a chronic cranial window
Nature Protocols 4:1128–1144.
https://doi.org/10.1038/nprot.2009.89
- PubMed
- Google Scholar
1. Holtmaat A
2. Svoboda K
(2009) Experience-dependent structural synaptic plasticity in the mammalian brain
Nature Reviews Neuroscience 10:647–658.
https://doi.org/10.1038/nrn2699
- PubMed
- Google Scholar
1. Holtmaat A
2. Caroni P
(2016) Functional and structural underpinnings of neuronal assembly formation in learning
Nature Neuroscience 19:1553–1562.
https://doi.org/10.1038/nn.4418
- PubMed
- Google Scholar
(2016) Rule learning enhances structural plasticity of long-range axons in frontal cortex
Nature Communications 7:10785.
https://doi.org/10.1038/ncomms10785
- PubMed
- Google Scholar
1. Jorstad A
2. Nigro B
3. Cali C
4. Wawrzyniak M
5. Fua P
6. Knott G
(2015) NeuroMorph: a toolset for the morphometric analysis and visualization of 3D models derived from electron microscopy image stacks
Neuroinformatics 13:83–92.
https://doi.org/10.1007/s12021-014-9242-5
- PubMed
- Google Scholar
Software
1. Jorstad A
2. Knott G
(2017) NeuroMorph/NeuroMorph_CenterLines_CrossSections, version 1b3da6e
GitHub.

https://github.com/NeuroMorph-EPFL/NeuroMorph/tree/master/NeuroMorph_CenterLines_CrossSections
1. Keck T
2. Scheuss V
3. Jacobsen RI
4. Wierenga CJ
5. Eysel UT
6. Bonhoeffer T
7. Hübener M
(2011) Loss of sensory input causes rapid structural changes of inhibitory neurons in adult mouse visual cortex
Neuron 71:869–882.
https://doi.org/10.1016/j.neuron.2011.06.034
- PubMed
- Google Scholar
1. Maco B
2. Holtmaat A
3. Cantoni M
4. Kreshuk A
5. Straehle CN
6. Hamprecht FA
7. Knott GW
(2013) Correlative in vivo 2 photon and focused ion beam scanning electron microscopy of cortical neurons
PLoS One 8:e57405.
https://doi.org/10.1371/journal.pone.0057405
- PubMed
- Google Scholar
1. Maco B
2. Cantoni M
3. Holtmaat A
4. Kreshuk A
5. Hamprecht FA
6. Knott GW
(2014) Semiautomated correlative 3D electron microscopy of in vivo-imaged axons and dendrites
Nature Protocols 9:1354–1366.
https://doi.org/10.1038/nprot.2014.101
- PubMed
- Google Scholar
(2006) Remodeling of synaptic structure in sensory cortical areas in vivo
Journal of Neuroscience 26:3021–3029.
https://doi.org/10.1523/JNEUROSCI.4454-05.2006
- PubMed
- Google Scholar
1. Markram H
2. Muller E
3. Ramaswamy S
4. Reimann MW
5. Abdellah M
6. Sanchez CA
7. Ailamaki A
8. Alonso-Nanclares L
9. Antille N
10. Arsever S
11. Kahou GA
12. Berger TK
13. Bilgili A
14. Buncic N
15. Chalimourda A
16. Chindemi G
17. Courcol JD
18. Delalondre F
19. Delattre V
20. Druckmann S
21. Dumusc R
22. Dynes J
23. Eilemann S
24. Gal E
25. Gevaert ME
26. Ghobril JP
27. Gidon A
28. Graham JW
29. Gupta A
30. Haenel V
31. Hay E
32. Heinis T
33. Hernando JB
34. Hines M
35. Kanari L
36. Keller D
37. Kenyon J
38. Khazen G
39. Kim Y
40. King JG
41. Kisvarday Z
42. Kumbhar P
43. Lasserre S
44. Le Bé JV
45. Magalhães BR
46. Merchán-Pérez A
47. Meystre J
48. Morrice BR
49. Muller J
50. Muñoz-Céspedes A
51. Muralidhar S
52. Muthurasa K
53. Nachbaur D
54. Newton TH
55. Nolte M
56. Ovcharenko A
57. Palacios J
58. Pastor L
59. Perin R
60. Ranjan R
61. Riachi I
62. Rodríguez JR
63. Riquelme JL
64. Rössert C
65. Sfyrakis K
66. Shi Y
67. Shillcock JC
68. Silberberg G
69. Silva R
70. Tauheed F
71. Telefont M
72. Toledo-Rodriguez M
73. Tränkler T
74. Van Geit W
75. Díaz JV
76. Walker R
77. Wang Y
78. Zaninetta SM
79. DeFelipe J
80. Hill SL
81. Segev I
82. Schürmann F
(2015) Reconstruction and Simulation of Neocortical Microcircuitry
Cell 163:456–492.
https://doi.org/10.1016/j.cell.2015.09.029
- PubMed
- Google Scholar
1. Meyer HS
2. Wimmer VC
3. Hemberger M
4. Bruno RM
5. de Kock CP
6. Frick A
7. Sakmann B
8. Helmstaedter M
(2010) Cell type-specific thalamic innervation in a column of rat vibrissal cortex
Cerebral Cortex 20:2287–2303.
https://doi.org/10.1093/cercor/bhq069
- PubMed
- Google Scholar
(2013) Altered synaptic dynamics during normal brain aging
Journal of Neuroscience 33:4094–4104.
https://doi.org/10.1523/JNEUROSCI.4825-12.2013
- PubMed
- Google Scholar
1. Parekh R
2. Ascoli GA
(2013) Neuronal morphology goes digital: a research hub for cellular and system neuroscience
Neuron 77:1017–1038.
https://doi.org/10.1016/j.neuron.2013.03.008
- PubMed
- Google Scholar
(2003) ScanImage: flexible software for operating laser scanning microscopes
BioMedical Engineering OnLine 2:13.
https://doi.org/10.1186/1475-925X-2-13
- PubMed
- Google Scholar
1. Qiao Q
2. Ma L
3. Li W
4. Tsai JW
5. Yang G
6. Gan WB
(2016) Long-term stability of axonal boutons in the mouse barrel cortex
Developmental Neurobiology 76:252–261.
https://doi.org/10.1002/dneu.22311
- PubMed
- Google Scholar
1. Schindelin J
2. Arganda-Carreras I
3. Frise E
4. Kaynig V
5. Longair M
6. Pietzsch T
7. Preibisch S
8. Rueden C
9. Saalfeld S
10. Schmid B
11. Tinevez JY
12. White DJ
13. Hartenstein V
14. Eliceiri K
15. Tomancak P
16. Cardona A
(2012) Fiji: an open-source platform for biological-image analysis
Nature Methods 9:676–682.
https://doi.org/10.1038/nmeth.2019
- PubMed
- Google Scholar
1. Shepherd GM
2. Harris KM
(1998)
Three-dimensional structure and composition of CA3-->CA1 axons in rat hippocampal slices: implications for presynaptic connectivity and compartmentalization

Journal of Neuroscience 18:8300–8310.
- PubMed
- Google Scholar
1. Song S
2. Grillo FW
3. Xi J
4. Ferretti V
5. Gao G
6. De Paola
(2016) EPBscore: a Novel Method for Computer-Assisted Analysis of Axonal Structure and Dynamics
Neuroinformatics 14:121–127.
https://doi.org/10.1007/s12021-015-9274-5
- PubMed
- Google Scholar
(2002) Geometry and structural plasticity of synaptic connectivity
Neuron 34:275–288.
https://doi.org/10.1016/S0896-6273(02)00652-9
- PubMed
- Google Scholar
1. Stepanyants A
2. Chklovskii DB
(2005) Neurogeometry and potential synaptic connectivity
Trends in Neurosciences 28:387–394.
https://doi.org/10.1016/j.tins.2005.05.006
- PubMed
- Google Scholar
1. Stettler DD
2. Yamahachi H
3. Li W
4. Denk W
5. Gilbert CD
(2006) Axons and synaptic boutons are highly dynamic in adult visual cortex
Neuron 49:877–887.
https://doi.org/10.1016/j.neuron.2006.02.018
- PubMed
- Google Scholar
1. Trachtenberg JT
2. Chen BE
3. Knott GW
4. Feng G
5. Sanes JR
6. Welker E
7. Svoboda K
(2002) Long-term in vivo imaging of experience-dependent synaptic plasticity in adult cortex
Nature 420:788–794.
https://doi.org/10.1038/nature01273
- PubMed
- Google Scholar
1. Van Gehuchten A
(1904)
Boutons terminaux et reseau pericellulaire

Nevraxe 8:81–116.
- Google Scholar
1. Yang Y
2. Liu DQ
3. Huang W
4. Deng J
5. Sun Y
6. Zuo Y
7. Poo MM
(2016) Selective synaptic remodeling of amygdalocortical connections associated with fear memory
Nature Neuroscience 19:1348–1355.
https://doi.org/10.1038/nn.4370
- PubMed
- Google Scholar

Decision letter

Eve Marder

Reviewing Editor; Brandeis University, United States

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your article "Computer assisted detection of axonal bouton structural plasticity in in vivo time-lapse images" for consideration by eLife. Your article has been reviewed by three peer reviewers, and the evaluation has been overseen by Eve Marder as the Senior Editor and Reviewing Editor. The following individuals involved in review of your submission have agreed to reveal their identity: Sen Song (Reviewer #1); Albert Cardona (Reviewer #2). A further reviewer remains anonymous.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

The authors proposed new algorithms to analyze in vivo two-photon time-lapse images for axonal bouton structural plasticity and validated the method against EM reconstructions of the same tissue. The manuscript reports on a new method for quantifying synaptic boutons in light-microscopy images of fluorescently labeled axons, and validates the method and parameter choices by using correlative light-electron microscopy, providing the nanometer-scale reconstruction of axons and synaptic surfaces of the micrometer-scale light-microscopy images. The method models sources of variability, both controllable and non-controllable, while also acknowledging and including the inherent ambiguity of synaptic boutons in predicting the presence of a synaptic surface (not all boutons house synapses or, as the author's put it, postsynaptic densities). The normalization approach is appropriate and accurate, and its structure reveals the careful, neuroanatomy-based reasoning that led to its design. The method applies to both small varicosities and varying imaging conditions, including low-intensity and low-contrast conditions, and reports a precision and recall good enough that, together with the modeling of variability and the ability to track varicosities over time on the same axons, essentially sets the stage for fully-automated estimation of synaptic weights from light-microscopy images of brain tissue for chronic studies.

Essential revisions:

1) One of the issues that arose during the review is that some of your previously published methods are inaccessible without paying exorbitant fees to other publishers. Consequently, please include all of the methods you used in detail here, so that this paper stands alone and exists in the OPEN ACCESS world with all of its methods. eLife does not restrict the space that can be used for methods, so it will be a service to the community to have the methods here. Among specific issues raised by the reviewers:

a) There is an insufficiently detailed EM fixation and counterstaining protocol: no concentrations given for aldehydes, osmium, uranyl acetate, and no specifications on the individual steps.

b) More detail on the trace optimization method.

c) No open source code repository is reported, which would be critical to distributing the software to facilitate the application of this novel method and provide commit hashes for reference when reporting the use of the method, towards ensuring reproducibility of results. Attaching the source code to the paper is an old practice from when public source code repositories were rare or hard to setup, and while the practice ensures archiving of the source code, it is not conducive to further corrections, extensions or modifications. Which source version control repository hosts the code, and what hash / commit number corresponds to the attached code zip file? This is critical for eLife publication!

2) Please address the issue of whether the laplacian of gaussian filter for detection of boutons introduces biases in estimating bouton intensities. Figure 4 addresses some of those issues, but the profile intensities there are after several further steps of processing. This issue need to be explored in a bit more depth by perhaps comparing with some other methods. Address how the parameters were chosen for the LOG filter.

3) One reviewer says, "The detection of putative boutons based on the Backward-Stepwise Subset Selection method is also novel. I think the fitting of foreground peaks using a variable size gaussian filter is a very good idea. But I am less convinced of fitting the background peaks also with Gaussian functions. There is no a priori reason why the background is also peaky. Have the authors explored other functions for fitting the background. What is the physical intuition of the background peaks?"

4) For the shaft intensity, why did you choose the positions where the boutons were present for measurement? It seems more intuitive to measure from areas which are devoid of boutons. The current method seems more like an average bouton intensity. Normalizing the image by this kind of quantity suffers from one drawback, which is if a large fraction of boutons are gained or lost, this might lead to a bias.

5) Fitting the bouton gain and loss functions using a probabilistic function is a very good idea. But it is not very clear how this could benefit final biological measurements and interpretation. Is it useful for taking/getting more meaningful interpretation for different amounts of measurement noises? Some discussion of this would be useful.

6) The correlation with EM looks quite good, but is it better than previous methods? Some comparison would be useful.

Optional: One reviewer felt that one potential way to increase the impact is to demonstrate its robustness for data previously published by other labs. Other reviewers did not feel this was necessary, but we wanted you to think about this.

https://doi.org/10.7554/eLife.29315.017

Author response

Essential revisions:

1) One of the issues that arose during the review is that some of your previously published methods are inaccessible without paying exorbitant fees to other publishers. Consequently, please include all of the methods you used in detail here, so that this paper stands alone and exists in the OPEN ACCESS world with all of its methods. eLife does not restrict the space that can be used for methods, so it will be a service to the community to have the methods here. Among specific issues raised by the reviewers:

a) There is an insufficiently detailed EM fixation and counterstaining protocol: no concentrations given for aldehydes, osmium, uranyl acetate, and no specifications on the individual steps.

b) More detail on the trace optimization method.

c) No open source code repository is reported, which would be critical to distributing the software to facilitate the application of this novel method and provide commit hashes for reference when reporting the use of the method, towards ensuring reproducibility of results. Attaching the source code to the paper is an old practice from when public source code repositories were rare or hard to setup, and while the practice ensures archiving of the source code, it is not conducive to further corrections, extensions or modifications. Which source version control repository hosts the code, and what hash / commit number corresponds to the attached code zip file? This is critical for eLife publication!

We have expanded the Materials and methods section to include additional details related to EM methods and trace optimization. The source code of BoutonAnalyzer is now hosted on GitHub, and the version tagged v1.0 (commit number 531a792) is used in conjunction with the manuscript.

2) Please address the issue of whether the laplacian of gaussian filter for detection of boutons introduces biases in estimating bouton intensities. Figure 4 addresses some of those issues, but the profile intensities there are after several further steps of processing. This issue need to be explored in a bit more depth by perhaps comparing with some other methods. Address how the parameters were chosen for the LOG filter.

Axon intensity profiles are produced in two steps, (1) sliding the LoG_xy filter along the trace and (2) normalizing the result with the shaft intensity. In this heuristic procedure, normalization was included to remove bias due to axon specific calibers and fluorophore expression levels. CLEM analysis shows that bouton weights resulting from this procedure are well correlated with bouton volumes, and therefore, we have no reason to think that the LoG_xy filter biases the results. It is difficult to be more conclusive here, because the size of the CLEM dataset is relatively small.

Nevertheless, we explored this issue in some detail and now provide comparisons with other plausible bouton detection strategies in our manuscript. We added Figure 4—figure supplement 1 showing intensity profiles obtained without filtering (raw voxel intensities along the trace), and produced with mean, Gaussian, and median filters of different but fixed sizes. This figure shows that in the absence of filtering, profiles appear jagged, which hinders bouton detection. At the other extreme, large filters suppress small boutons and merge closely positioned boutons. By tuning sizes of the considered filters we were able to obtain profiles that appear similar to those of multi-scale LoG_xy, although with higher baselines. Still, we prefer LoG_xy because its negative surround produces near-zero baselines, which simplifies bouton detection. In addition, the multi-scale feature of this filter eliminates the need for size tuning.

We also examined the combined effect of filtering and normalization on bouton measurement by comparing the amplitudes of profile peaks to corresponding bouton volumes. Figure 4—figure supplement 1E shows that the overall procedure described in the manuscript leads to the highest correlation as compared to the best of the considered alternatives.

We would like to emphasize that we did not attempt to find the best procedure to fit the CLEM dataset. Some other combination of filter type, normalization, and parameters may perform marginally better, but this would likely be a case of over-fitting the data. Instead, our procedure was designed based on theoretical considerations, and the parameters were chosen based on observed bouton sizes. These points are now mentioned in the last paragraph of the Results subsection “Validation of LM-based bouton detection methodology with EM”.

3) One reviewer says, "The detection of putative boutons based on the Backward-Stepwise Subset Selection method is also novel. I think the fitting of foreground peaks using a variable size gaussian filter is a very good idea. But I am less convinced of fitting the background peaks also with Gaussian functions. There is no a priori reason why the background is also peaky. Have the authors explored other functions for fitting the background. What is the physical intuition of the background peaks?"

Axon background intensity defined in the manuscript is the intensity an axon intensity profile would have in the absence of boutons. If bouton density were sufficiently low, background intensity could be deduced from inter-bouton portions on the axon. However, for high bouton densities, which is often the case for cortical axons, background intensity has to be disentangled from bouton contributions. We did this with a two-step fitting procedure described in the manuscript. To fit the background, we used multiple, relatively wide Gaussian peaks (σ_k^b ≥ 20 μm, Equation 2). This was done to account for the possibility of variations in background intensity over relatively large distances along the axon (>> 1 μm or bouton size). Such variations in intensity may result from changes in axon caliber or changes in density of fluorescent molecules. Gaussian peaks were used for convenience, but any other slowly varying function would work as well. We would like to emphasize that the resulting background, which is a sum of multiple overlapping Gaussians, varies very smoothly and excludes intensity of putative boutons as shown in Figure 2C (red line). We now emphasize these points in the subsection “LM-based bouton detection and measurement of structural changes”.

4) For the shaft intensity, why did you choose the positions where the boutons were present for measurement? It seems more intuitive to measure from areas which are devoid of boutons. The current method seems more like an average bouton intensity. Normalizing the image by this kind of quantity suffers from one drawback, which is if a large fraction of boutons are gained or lost, this might lead to a bias.

Our method was designed to produce robust results, regardless of bouton density. In particular, when density of boutons is high, e.g. Figure 2, identifying areas devoid of boutons can be next to impossible. Therefore, we infer shaft intensity by using a fitting procedure which disentangles it from bouton contributions. Specifically, axon intensity profiles are fitted simultaneously with foreground and background peak functions, and only the background peak functions are used to determine the shaft intensity (red line in Figure 2C). The resulting shaft intensity is independent of bouton density, and, thus, it is expected to be insensitive to changes in density arising from bouton addition or elimination. We now clarify this point in the subsection “LM-based bouton detection and measurement of structural changes”.

5) Fitting the bouton gain and loss functions using a probabilistic function is a very good idea. But it is not very clear how this could benefit final biological measurements and interpretation. Is it useful for taking/getting more meaningful interpretation for different amounts of measurement noises? Some discussion of this would be useful.

When the measured bouton weight is well above/below w_threshold, it may be said with confidence that an LM bouton is present/absent. In such cases, deterministic definition of a bouton is sufficient, and it is in agreement with Equation 10. In practice, because the distribution of bouton weights is unimodal (see Figure 2—figure supplement 2B), a large fraction of weights will lie within the range of uncertainty of w_threshold, regardless of its value. Such ambiguous boutons could be discarded, which may bias biological interpretation. Alternatively, they could be treated probabilistically as described in the manuscript, which is our preferred method. We think that this method may offer distinct benefits for biological interpretation. One could consider the following specific examples of biological measurements where a probabilistic approach is essential. (1) Estimate of expected number of LM boutons. Here, since bouton weight distribution is non-uniform (monotonically decreasing), one cannot simply count the number of weights above w_threshold to estimate the expected number of LM boutons, even for a large sample size. This count would result in an underestimate, as many more measured sub-threshold weights may have a true weight > w_threshold than the other way around. Thus, it is essential to add LM bouton probabilities defined by Equation 10. (2) The same argument holds for calculations of the expected numbers of added, eliminated, potentiated, and depressed boutons. (3) Most bouton structures are stable and do not change substantially over days-to-weeks. Therefore, changes in weight often lie within the range of measurement uncertainty and can only be described probabilistically according to Equation 11. More importantly, probabilistic description is required for calculation of error-bars and establishing significance of experimental measurements. This is absolutely essential for correct biological interpretation of results. These points are now mentioned in the last paragraph of the Discussion.

6) The correlation with EM looks quite good, but is it better than previous methods? Some comparison would be useful.

We are aware of only one publicly available software tool for bouton detection and measurement, EPBscore (Song et al., 2016), which we cite in our manuscript. This software generates an axon intensity profile based on a combination of fixed-size Gaussian and median filters, and subsequently normalizes it by its median. It is designed to work well on isolated axons. However, when multiple axons in close proximity cross paths, which is the case in our CLEM dataset, EPBscore does not provide a utility to segment individual axons or to obtain accurate traces of axons in 3D. Thus, unfortunately, we were not able to successfully use EPBscore here due to a relatively high density of labeled axons in our dataset (see e.g. Figure 1).

There are several other publications related to bouton detection and measurement. Some of these studies use local shaft intensity for normalization, but this can only be done for low bouton density axons. Other studies use complex sequences of thresholds to determine normalization, which is unlikely to generalize on different types of images. There are also studies that normalize by the mean or median axon intensity. These normalizations are reasonable for low bouton density axons, but can otherwise bias the results. Absence of publicly available tools and/or source codes precluded direct comparisons of these studies with our method.

Instead, we incorporated several of the above strategies into our bouton detection framework and now directly compare them to the method described in this study (see Figure 4—figure supplement 1 and related discussion in response to Essential revision 2).

Optional: One reviewer felt that one potential way to increase the impact is to demonstrate its robustness for data previously published by other labs. Other reviewers did not feel this was necessary, but we wanted you to think about this.

We would like to test the software on other CLEM datasets, but we are not aware of any datasets that are publicly available. Based on our knowledge of the literature, such data are extremely rare and usually include small numbers of reconstructed en passant boutons. For example, one of the largest CLEM datasets we know (Grillo et al., PNAS 2013), contains only 9 en passant boutons. If the reviewers know of available CLEM data, we would be happy to perform the analyses and include the results in the manuscript.

https://doi.org/10.7554/eLife.29315.018

Article and author information

Author details

Rohan Gala

Department of Physics and Center for Interdisciplinary Research on Complex Systems, Northeastern University, Boston, United States

Contribution
Conceptualization, Software, Formal analysis, Validation, Methodology, Writing—original draft, Writing—review and editing

Contributed equally with
Daniel Lebrecht

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-1872-0957
Daniel Lebrecht
1. Department of Basic Neurosciences, Faculty of Medicine, University of Geneva, Geneva, Switzerland
2. Lemanic Neuroscience Doctoral School, Switzerland
Contribution
Conceptualization, Resources, Validation, Investigation, Methodology, Writing—review and editing

Contributed equally with
Rohan Gala

Competing interests
No competing interests declared
Daniela A Sahlender

Biological Electron Microscopy Facility, Centre of Electron Microscopy, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland

Contribution
Resources, Validation, Investigation, Writing—review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-0510-9529
Anne Jorstad

Biological Electron Microscopy Facility, Centre of Electron Microscopy, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland

Contribution
Resources, Software, Validation, Investigation, Writing—review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6438-1979
Graham Knott

Biological Electron Microscopy Facility, Centre of Electron Microscopy, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland

Contribution
Resources, Investigation, Software, Supervision, Funding acquisition, Validation, Methodology, Project administration, Writing—review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-2956-9052
Anthony Holtmaat

Department of Basic Neurosciences, Faculty of Medicine, University of Geneva, Geneva, Switzerland

Contribution
Conceptualization, Resources, Supervision, Funding acquisition, Validation, Methodology, Writing—original draft, Project administration, Writing—review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-7577-0769
Armen Stepanyants

Department of Physics and Center for Interdisciplinary Research on Complex Systems, Northeastern University, Boston, United States

Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Validation, Methodology, Writing—original draft, Project administration, Writing—review and editing

For correspondence
a.stepanyants@neu.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-9387-2320

Funding

National Institutes of Health (R01 NS091421)

Armen Stepanyants

Air Force Office of Scientific Research (FA9550-15-1-0398)

Armen Stepanyants

Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung (331003A_153448)

Anthony Holtmaat

Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung (CRSII3-154453)

Graham Knott
Anthony Holtmaat

Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung (51NF40_158776)

Anthony Holtmaat

International Foundation for Research in Paraplegia (Chair Alain Rossier)

Anthony Holtmaat

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We are grateful to Jerome Blanc, Raeann Dalton, Rammy Dang, and Chi Zhang for their help in tracing neurons and annotating boutons. This work was supported by the NIH grant R01 NS091421 and AFOSR grant FA9550-15-1-0398 to AS, Swiss National Science Foundation (SNF) grants 331003A_153448 and 51NF40_158776 (National Centre for Competence in Research, SYNAPSY), and the International Foundation for Research on Paraplegia (chair Alain Rossier) to AH, and SNF grant CRSII3-154453 to AH and GK.

Ethics

Animal experimentation: All experiments were performed according to the guidelines of the Swiss Federal Act on Animal Protection and Swiss Animal Protection Ordinance. The ethics committee of the University of Geneva and the Cantonal Veterinary Office of Geneva, Switzerland (approval code GE/61/17) approved all experiments.

Reviewing Editor

Eve Marder, Brandeis University, United States

Publication history

Received: June 6, 2017
Accepted: October 22, 2017
Accepted Manuscript published: October 23, 2017 (version 1)
Version of Record published: November 7, 2017 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.