Figures and data in Stochastic resonance mediates the state-dependent effect of periodic stimulation on cortical alpha oscillations

Figures
Tables
Additional files

7 figures, 1 table and 1 additional file

Figures

Figure 1

Download asset Open asset

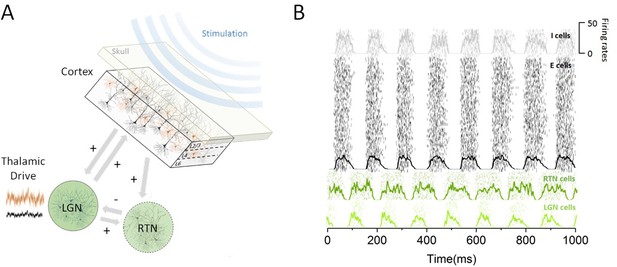
Thalamo-cortical circuit schematic and resting state activity.

(A) Our computational model of the thalamo-cortical system is composed of both cortical (excitatory and inhibitory) and sub-cortical (lateral geniculate nucleus [LGN] and reticular [RTN]) populations. Sensory input, whose intensity scales with state, is assumed to arrive at the thalamus to then influence the dynamics of the whole circuit. Non-invasive periodic stimulation is applied only to cortical neurons. (B) In the resting state, both cortical and sub-cortical neurons are maintained in a deeply synchronous regime, displaying phase-locked firing rate oscillations in the alpha band (8 Hz). The spiking response of both cortical and thalamic populations is plotted for a single trial. Overlays represent the mean firing rate across neurons.

https://doi.org/10.7554/eLife.32054.002

Figure 2

Download asset Open asset

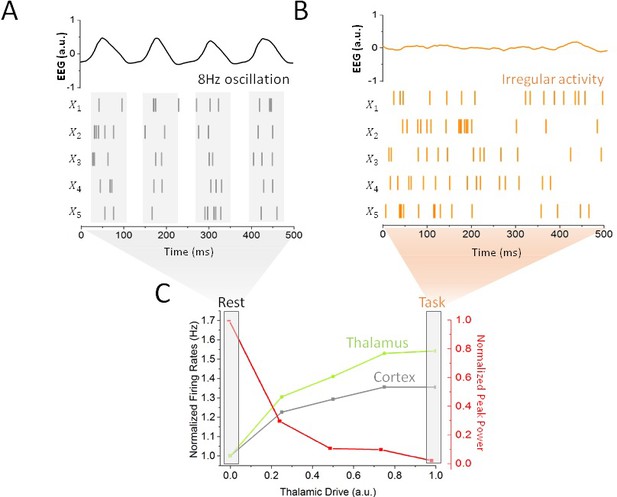
Impact of thalamic drive on firing rates and alpha power without stimulation.

(A) Sample spiking activity of five randomly selected excitatory cortical cells in the resting state, which is defined as a regime of minimal thalamic drive ( $D_{L G N} = 1 x 10^{- 4}$ ). The firing activity of those neurons is highly correlated, and synchronized to the phase of simulated EEG alpha oscillations (top). (B) Activity of the same cortical neurons in the task state, where thalamic drive is high ( $D_{L G N} = 1$ ). The spiking activity is now irregular and asynchronous, leading to a flat EEG activity where alpha oscillations have been suppressed. (C) Effect of gradual increase in thalamic drive on alpha power and mean firing rates for both cortical (grey) and sub-cortical (green) neurons.

https://doi.org/10.7554/eLife.32054.003

Figure 3

Download asset Open asset

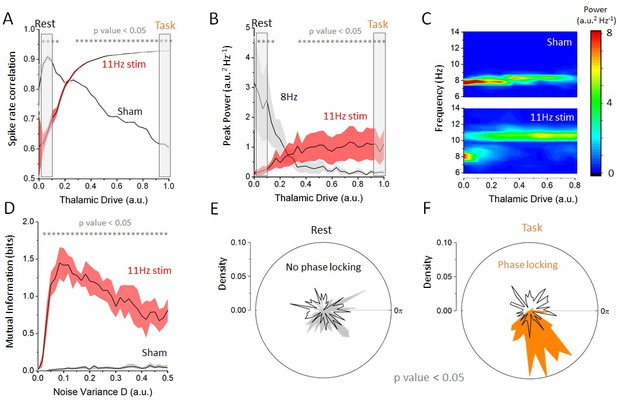
Effect of increasing thalamic drive on network dynamics with stimulation.

(A) Firing-rate correlations of cortical excitatory neurons (average pairwise correlation between firing rates) as a function of thalamic drive with 11 Hz stimulation and sham (no stimulation). Without stimulation (sham), correlations in the network decrease as endogenous oscillations are suppressed. By contrast, with 11 Hz stimulation, correlations increase monotonically with thalamic input as the cells become entrained by the stimulation. (B) Peak power at the endogenous alpha frequency ( $ω_{o}$ =8 Hz) and at the stimulation frequency ( $ω_{s t i m}$ =11 Hz) as a function of increasing thalamic drive. The power of the endogenous oscillations is gradually suppressed, whereas the opposite occurs at the stimulation frequency, suggesting a transition between oscillatory regimes. (C) Full-power spectral density distribution as a function of thalamic drive. Without stimulation, increase in thalamic drive destabilizes endogenous alpha oscillations and power is gradually suppressed. In presence of stimulation, the destabilization of endogenous oscillations is more abrupt and is replaced by spectral power at the stimulation frequency. Stimulation parameters for (A), (B) and (C) were $S =$ 0.15, $ω_{s t i m}$ =11 Hz. (D) Mutual information between stimulation and network response as a function of increasing noise throughout the network, both with and without stimulation. When stimulation of weak amplitude (here $S =$ 0.10) is applied, and the mutual information peaks at some intermediate value of noise, indicating that stochastic resonance is involved. (E) Phase distribution of firing-rate responses across trials at 11 Hz in the rest state ( $D_{L G N} = 1 x 10^{- 5}$ ). In each trial, the stimulation was applied at a random phase. This is why the phase distribution is uniform over all angles (black line). The phase difference between the stimulation and the network response is also uniform, indicating that the network dynamics are not phase locked to the stimulus (i.e. there is no entrainment). (F) By contrast, in the task state ( $D_{L G N} = 1 x 10^{- 5}$ ), cortical firing rates are phase locked to the stimulation, and the distribution shows a strong peak at the preferred phase (orange area). Here, $S = 0.1$ and $ω_{s t i m}$ = 11 Hz.

https://doi.org/10.7554/eLife.32054.004

Figure 4

Download asset Open asset

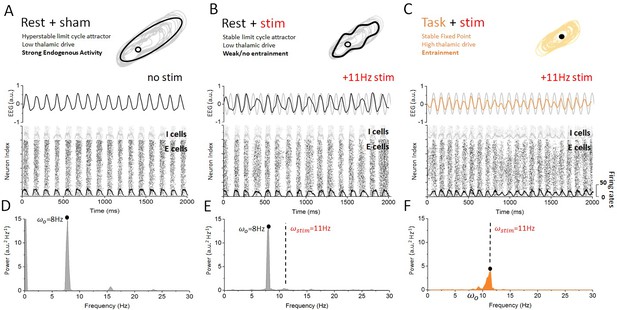
Dynamics of cortical neurons in the rest and task states with and without stimulation.

(A) In the absence of stimulation, the resting state is characterized with strong synchronous alpha oscillations, leading to stable attractor dynamics. These oscillations correspond to a stable limit cycle surrounding an unstable fixed point. Both excitatory and inhibitory neurons display firing-rate modulations (black and gray overlays) at the endogenous frequency. (B) When stimulation is applied in the rest state, the interaction between correlated neural activity and stimulation-induced fluctuations in membrane voltage results in weak entrainment. Despite the presence of periodic stimulation impacting all cortical neurons equally, the dynamics of the simulated EEG are predominantly characterized by endogenous oscillations (top). The spiking activity of both excitatory and inhibitory neurons remains locked to endogenous cycles, where stimulation has little to no impact on network activity (bottom). (C) By contrast, endogenous oscillations are suppressed in the task state, where the dynamics now evolve around a fixed point. Simulated EEG activity is fully entrained to the stimulation (top), and so are cortical neurons whose spiking is phased locked to the stimulation frequency. (C) The power spectral density distribution of the EEG response in the rest state. The spectrum is largely dominated by endogenous oscillations ( $ω_{o} =$ 8 Hz) and only weak contribution can be observed at the stimulation frequency ( $ω_{s t i m} =$ 11 Hz), indicating that network oscillations are not entrained by the stimulation. (D) The power spectral density distribution of the EEG response in the task state. Here, by contrast, the power at the endogenous frequency has been almost fully suppressed and a clear peak can be seen at the stimulation frequency. This implies that network oscillatory activity is fully determined by the stimulation. Stimulation parameters here are $S =$ 0.15, $ω_{s t i m}$ = 11 Hz.

https://doi.org/10.7554/eLife.32054.005

Figure 5

Download asset Open asset

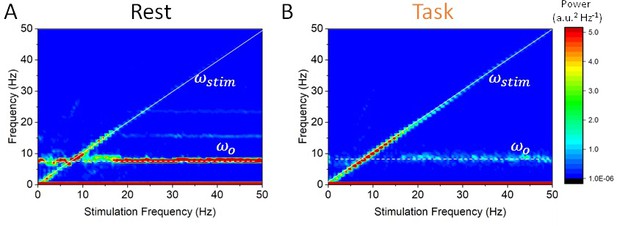
State-dependent responses to periodic stimulation with variable frequency.

(A) Power in the rest state is concentrated at the endogenous frequency (horizontal dashed line at 8 Hz) while the stimulation frequency $ω_{s t i m}$ is increased from 0 to 50 Hz. The peak power found at the stimulation frequency (dashed line along the diagonal) is small unless $ω_{o} \approx ω_{s t i m}$ , that is, when the stimulation frequency is close to the peak alpha frequency. (B) In the task state, power is instead concentrated at the stimulation frequency across the range of values visited (along the diagonal). By contrast, power at the endogenous oscillation is much smaller. Note that the power at the stimulation frequency scales with the distance with respect to the alpha peak at 8 Hz. Stimulation parameters here are $S =$ 0.15 while $ω_{s t i m}$ was varied from 0 to 50 Hz.

https://doi.org/10.7554/eLife.32054.006

Figure 6

Download asset Open asset

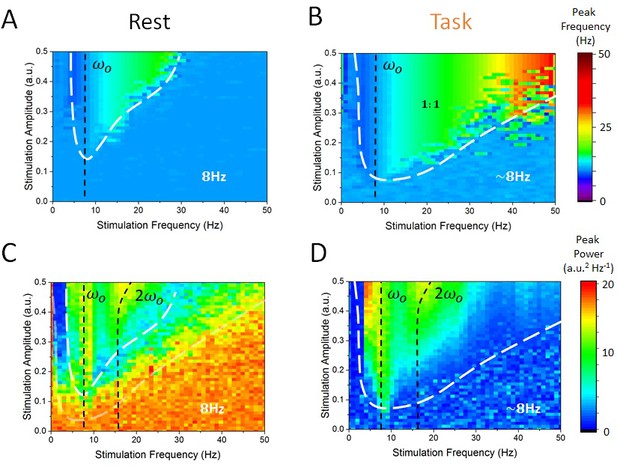
State-dependent Arnold tongues as a function of stimulation amplitude and frequency.

By systematically varying the stimulation amplitude ( $S$ ) and frequency ( $ω_{s t i m}$ ) and identifying the associated peak frequency (i.e. frequency where maximal power can be found) and peak power (i..e power at the peak frequency) in each case, we can delimit regions in parameter space where cortical dynamics are either governed by endogenous alpha oscillations or locked to the stimulation. (A) In the rest state, the vast majority of stimulation parameter space is characterized by an absence of entrainment. The peak frequency of cortical EEG activity remains at 8 Hz. However, as stimulation amplitude is increased for stimulation frequency near 8 Hz, entrainment occurs. However, this triangular region — called the Arnold tongue — remains narrow. (B) In the task state, the Arnold tongue increases significantly, and occupies most of the range of stimulation parameters considered — entrainment is thus more prevalent in the task state. (C) Peak power in the rest state for varying stimulation parameters. (D) Same as in (C) for the task state. Stimulation amplitude was varied within [0, 0.5] and its frequency within [0, 50 Hz].

https://doi.org/10.7554/eLife.32054.007

Figure 7

Download asset Open asset

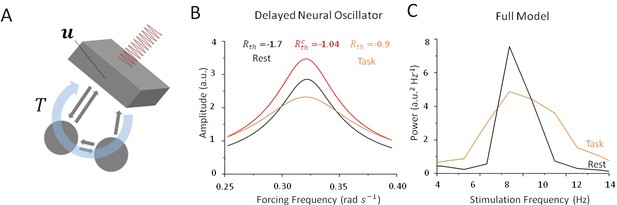
Stochastic resonance in a noisy and delayed neural oscillator.

(A) We investigated the dynamics of a conceptual delayed feedback model in the presence of periodic forcing (i.e. stimulation) as a proxy for the thalamo-cortical circuit subjected to additive noise. The mean activity $u$ experiences delayed feedback with delay $T$ , additive noise and periodic forcing. (B) Amplitude of entrained solution both above and below the Hopf bifurcation threshold. Below the bifurcation (black line), the linear gain $| R_{t h} |$ remains high because noise intensity is small. Solutions have a high amplitude only near the intrinsic critical frequency. Above the bifurcation (orange line), the linear gain $| R_{t h} |$ becomes smaller under the effect of noise. As a consequence, the amplitude of all non-resonant solutions increases, while the amplitude of resonant solution decreases. (C) Peak power at $ω_{s t i m}$ in the rest (black) and task (orange) states as stimulation frequency varies in the vicinity of $ω_{o}$ . Although resulting from a more complex model, the effect remains qualitatively similar to the simplified case in (B).

https://doi.org/10.7554/eLife.32054.008

Tables

Table 1

Model parameter efinitions and Values.

https://doi.org/10.7554/eLife.32054.009

Symbol	Definition	Value
$Ω$	Network spatial extent	1
$N_{e}$	Number of excitatory cells	800
$N_{i}$	Number of inhibitory cells	200
$N_{t h}$	Number of thalamic cells	200
$N_{r t n}$	Number of reticular cells	200
$β$	Neural response function gain	150
$h$	Firing rate threshold	0.1
$f_{o}$	Maximal firing rate	0.2
$τ_{m}$	Membrane time constant	1
$α_{e}$	Membrane rate constant — excitatory cortical cells	0.9
$α_{i}$	Membrane rate constant — inhibitory cortical cells	1.3
$α_{t h}$	Membrane rate constant — thalamic neurons	0.5
$α_{r t n}$	Membrane rate constant — reticular cells	0.5
$a$	Neural adaptation rate constant	0.01
$b$	Neural adaptation gain	0.3
$I_{e}$	Constant current bias	0
$I_{i}$	Constant current bias	−0.3
$I_{t h}$	Constant current bias	−0.3
$I_{r t n}$	Constant current bias	−0.3
$τ_{t h}$	Thalamo-cortical delay	45 ms
$τ_{r t n}$	Reticular-thalamic delay	10 ms
c	Conduction velocity	0.35 m/s
$ρ$	Connection probability	0.2
$w_{e - > e}^{o}$	Synaptic connection strength	20.4
$w_{e - > i}^{o}$	Synaptic connection strength	30.6
$w_{i - > e}^{o}$	Synaptic connection strength	−30.6
$w_{i - > i}^{o}$	Synaptic connection strength	20.4
$w_{e - > l g n}^{o}$	Synaptic connection strength	34
$w_{e - > r t n}^{o}$	Synaptic connection strength	34
$w_{l g n - > e}^{o}$	Synaptic connection strength	85
$w_{l g n - > i}^{o}$	Synaptic connection strength	85
$w_{l g n - > r t n}^{o}$	Synaptic connection strength	34
$w_{r t n - > l g n}^{o}$	Synaptic connection strength	−34
$σ_{e - > e}^{2}$	Synaptic connection range	0.01
$σ_{e - > i}^{2}$	Synaptic connection range	0.01
$σ_{i - > e}^{2}$	Synaptic connection range	0.25
$σ_{i - > i}^{2}$	Synaptic connection range	0.25
$σ_{e - > t h}^{2}$	Synaptic connection range	0.01
$σ_{e - > r t n}^{2}$	Synaptic connection range	0.01
$σ_{t h - > e}^{2}$	Synaptic connection range	0.25
$σ_{t h - > i}^{2}$	Synaptic connection range	0.25
$σ_{t h - > r t n}^{2}$	Synaptic connection range	0.25
$σ_{r t n - > t h}^{2}$	Synaptic connection range	0.25
dt	Integration time step	0.1