1. Cell Biology

An optimized method for 3D fluorescence co-localization applied to human kinetochore protein architecture

  1. Aussie Suzuki  Is a corresponding author
  2. Sarah K Long
  3. Edward D Salmon
  1. University of North Carolina at Chapel Hill, United States
https://doi.org/10.7554/eLife.32418
Share this article
Cite this article
  1. Aussie Suzuki
  2. Sarah K Long
  3. Edward D Salmon
(2018)
An optimized method for 3D fluorescence co-localization applied to human kinetochore protein architecture
eLife 7:e32418.
https://doi.org/10.7554/eLife.32418
  2. Download BibTeX
  3. Download .RIS

Abstract

Two-color fluorescence co-localization in 3D (three-dimension) has the potential to achieve accurate measurements at the nanometer length scale. Here, we optimized a 3D fluorescence co-localization method that uses mean values for chromatic aberration correction to yield the mean separation with ~10 nm accuracy between green and red fluorescently labeled protein epitopes within single human kinetochores. Accuracy depended critically on achieving small standard deviations in fluorescence centroid determination, chromatic aberration across the measurement field, and coverslip thickness. Computer simulations showed that large standard deviations in these parameters significantly increase 3D measurements from their true values. Our 3D results show that at metaphase, the protein linkage between CENP-A within the inner kinetochore and the microtubule-binding domain of the Ndc80 complex within the outer kinetochore is on average ~90 nm. The Ndc80 complex appears fully extended at metaphase and exhibits the same subunit structure in vivo as found in vitro by crystallography.

https://doi.org/10.7554/eLife.32418.001

Introduction

Confocal light microscopy (LM) is widely used for understanding protein localization, architecture, and functions in cells, but the maximum resolution without any image processing is still only ~200 nm in the x-y image plane and ~400 nm along the z-axis. The scale of many protein complexes is smaller than the diffraction limit of LM. In order to deduce the function of protein complexes, it is critical to develop a method to determine the three-dimensional (3D) locations of proteins within a complex in their native environment.

Kinetochores are protein assemblies at the periphery of centromeric chromatin that have vital functions for achieving accurate chromosome segregation during mitosis and meiosis. A modified histone H3, CENP-A, within nucleosomes at centromeric chromatin marks the site of kinetochore assembly. CENP-A recruits ~25 different kinds of core-structural proteins including Constitutive Centromere Associated Protein Network (CCAN) proteins and outer kinetochore proteins called the KMN network (Knl1, Mis12 complex, and Ndc80 complex) (Cheeseman et al., 2006; McKinley and Cheeseman, 2016; Musacchio and Desai, 2017; Pesenti et al., 2016; Takeuchi and Fukagawa, 2012). Two important linkers in human kinetochores are CENP-C and CENP-T because they connect between centromeric chromatin and the KMN network proteins (Huis In 't Veld et al., 2016; Klare et al., 2015; Musacchio and Desai, 2017; Nishino et al., 2013; Nishino et al., 2012; Screpanti et al., 2011; Suzuki et al., 2015; Suzuki et al., 2014). The highly conserved Ndc80 complex (Hec1(Ndc80), Nuf2, Spc24, Spc25) is one of the best structurally characterized kinetochore proteins, and it has a major role in kinetochore microtubule (kMT) attachment (Ciferri et al., 2008; Musacchio and Desai, 2017).

We previously reported a nm-scale map of how human kinetochore proteins are organized on average along the inner to outer kinetochore axis at metaphase, obtained using the ‘Delta’ two-color fluorescence co-localization method (Wan et al., 2009). The Delta method provided local chromatic aberration (CA) correction in the x-y image plane by measurements along the K-K axis between pairs of sister kinetochores. More recently, Fuller and Straight (2012) developed a 3D method (termed CICADA [Co-localization and In-situ Correction of Aberration for Distance Analysis]) to measure the mean separation of red and green fluorescent centroids at individual kinetochores while locally correcting for CA in the x, y, and z directions using a third color (Fuller and Straight, 2012). Their method yielded an identical value to what was obtained by the Delta method (Fuller and Straight, 2012; Suzuki et al., 2014; Wan et al., 2009). In contrast, a recent report by Smith et al., 2016 used a 3D measurement method to obtain mean separation values for protein domains within kinetochores that were significantly greater than our Delta values and the 3D value obtained by the CICADA method (Fuller and Straight, 2012; Smith et al., 2016; Suzuki et al., 2014; Wan et al., 2009). This group questioned the accuracy and significance of the Delta values because they were ‘1D measurements and neglected z-axis information’.

In this paper, we have tested the above conclusion by optimizing a 2D and 3D fluorescence co-localization method to obtain the mean separation between the centroids of green and red foci with ~10 nm accuracy (Figure 1). The method depends on correcting CA based on mean values from a fluorescent standard, a method commonly used for fluorescence co-localization, but not previously optimized and rigorously analyzed for sources of error, as performed here. Computer simulations were used to understand how well the measurement method works and to find how accuracy is limited in our method. This study revealed major sources of error produced by standard deviations (SDs) in fluorescent centroid determination, CA correction, and coverslip thickness, as well as addressing several issues concerning fixation methods. We found that our 3D measurements applied to human kinetochores were similar to the Delta measurements and much shorter than those reported by Smith et al., 2016. Their larger measurements may be explained by much larger SDs in centroid determination and CA correction than typical of our experiments. We also used the known structure of the Ndc80 complex as a ‘Molecular Ruler’ to verify the accuracy of our measurement method, and to determine its subunit structure and conformation within the kinetochore.

Figure 1
Download asset Open asset
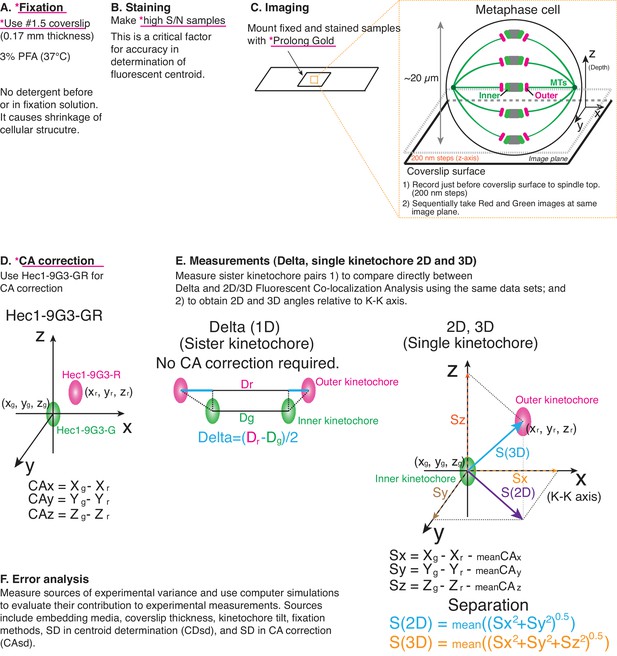
Principle of procedure used in this study.

(A) Fixation: 3% PFA in PHEM buffer without any detergent was used as standard fixation in this study (Details in Text and Methods). (B) Staining: Fixed samples were immunofluorescently labeled with antibodies to enhance S/N. Samples were usually mounted with Prolong Gold. (C) Imaging was performed by spinning disk confocal microscopy (See Materials and methods for details). (D) For CA correction, Hec1-9G3 monoclonal antibody was labeled by green and red tagged secondary antibodies (Hec1-9G3-GR). (E) Measurements: X, Y, Z coordinates of the centroids of green and red kinetochore fluorescence were determined by 3D Gaussian fitting. Details of equations for separation measurements are in Text, Figures, and Methods. (F) Error analysis: computer simulations were used for error analysis of the method. The sources of potential errors in separation measurements were highlighted in pink underline with *.

https://doi.org/10.7554/eLife.32418.002
Figure 1—source data 1

Pipeline for obtaining mean 3D separation measurements with nm-scale accuracy.

Critical factors were: (1) prepare bright high signal to noise samples to reduce standard deviation (SD) of centroid determination; (2) use mounting media like ProLong Gold to suppress z-axis spherical aberration; (3) use 0.17 mm thick coverslips for all measurements including CA measurement; (4) align imaging system and image using only a small region within the center of camera to suppress SD of CA; and (5) use warmed PFA fixation without pre-extraction or detergent in fixation solution.

https://doi.org/10.7554/eLife.32418.003

Results

Principles of the method

Sample preparation

HeLa cells were grown on #1.5 coverslips, the design value for the microscope objective, to prevent Z-axis CA (chromatic aberration) (Figure 1A). Cells were fixed with paraformaldehyde (PFA) without pre-extraction or supplement of detergent in the PFA solution, and stained with primary antibodies using a protocol from previous studies (Figure 1A) (Suzuki et al., 2015; Suzuki et al., 2014; Suzuki et al., 2011). The concentration of green and red secondary antibodies was adjusted to give nearly equal fluorescence intensity (Figure 1B). Integrated kinetochore fluorescence above background (>100,000 photon counts per kinetochore) was important to minimize the SD of centroid determination (CDsd) close to 5 nm (Thompson et al., 2002). Labeled samples were typically mounted with ProLong Gold mounting media. For the cellular CA correction standard, a monoclonal antibody (9G3) was used to label Hec1 (hsNdc80) protein at a site just inside of its MT binding CH domain, and this antibody was double labeled with green and red fluorescence by secondary antibodies (called Hec1-9G3-GR).

Imaging

Imaging was performed using a confocal light microscope with a high NA objective lens (100x/1.4 NA) and a camera with small pixel size (64 nm, less than 1/3 resolution limit) (Figure 1C). Metaphase cells were positioned in the central field of view of the camera. Images were recorded at 200 nm intervals along the z-axis beginning just before the coverslip surface and extending to the top of the spindle to measure equal numbers of kinetochores below and above the middle of the spindle.

Image analysis

We selected sister kinetochores for measurement not only for Delta values (Figure 1D–E), but also to obtain the direction of the sister-sister kinetochore axis (K-K). For each kinetochore, we obtained the x, y, z coordinates for the centroids of green (Xg, Yg, Zg) and red (Xr, Yr, Zr) using 3D Gaussian fitting methods (Wan et al., 2009). The Sx, Sy, and Sz coordinates of the separation vector S between green and red foci were calculated from Sx = Xg-Xr-meanCAx (CAmx), Sy = Yg-Yr-meanCAy (CAmy), and Sz = Zg-Zr-meanCAz (CAmz) (Figure 1E), where the mean values of CAx, CAy, and CAz were obtained from kinetochores labeled with Hec1-9G3-GR within our measurement volume (Figure 1D). ‘Raw’ values for the mean separation vector lengths in 2D and 3D were calculated for each pair of green-red kinetochore labels as S(2D) = mean ((Sx2 + Sy2)0.5) and S(3D) = mean ((Sx2 + Sy2 + Sz2)0.5) from measurements of 200 to 400 kinetochores obtained from 5 to 20 different cells (Figure 1E). The mean of these ‘raw’ separation values (S(2D), and S(3D)) were over-estimates (Churchman et al., 2006; Churchman et al., 2005). In order to obtain more accurate mean separation values, a maximum likelihood method was applied to the raw separation data (called ML2D and ML3D) (Churchman et al., 2006; Churchman et al., 2005).

Error analysis

Potential errors from different embedding media, the wrong coverslip thickness, kinetochore tilt, and different fixation methods were examined experimentally (Listed in Figure 1—source data 1). A computer simulation of the measurement method was used to evaluate the significance of these errors, as well as errors produced by the SDs in centroid determination (CDsd) and CA (CAsd) over the field of measurement (Figure 1F).

Chromatic aberration (CA) measurements from a cellular standard

CA within our measurement was determined from CAx = Xg-Xr, CAy = Yg-Yr, and CAz = Zg-Zr measured for Hec1-9G3-GR labeled kinetochores of metaphase cells (Figures 1D and 2). The mean values of CAx, CAy, and CAz plus their standard deviations (SDs) are listed in Table 1 for several different preparations. Note the mean values for CAx, CAy, and CAz were each very similar between different preparations. We included one preparation where the embedding solution was PBS. PBS has a refractive index near water, 1.33, and far from the refractive index of the coverslip (~1.52). The mean CAx, CAy, and CAz values were similar to those using the ProLong Gold embedding medium (Table 1). The major difference was a much larger SD for CAz compared to ProLong Gold (48 nm vs ~18 nm, Table 1). This occurs because the lower refractive index induces spherical aberration that increases with z-axis depth from the coverslip surface (Figure 2—figure supplement 1). We also tested one sample with glutaraldehyde (GA) fixation and embedding with ProLong Gold. The mean CA values were nearly identical to the results obtained from PFA fixation (Table 1).

Figure 2 with 3 supplements see all
Download asset Open asset
CA (Chromatic aberration) measurements using Hec1-9G3-GR.

Schematic model of Hec1-9G3-GR. Hec1-9G3 antibody was labeled by secondary antibodies with Rhodamine Red-X and Alexa 488 (left). Representative Hec1-9G3-GR images in samples fixed by PFA or GA mounted with Prolong Gold or PBS.

https://doi.org/10.7554/eLife.32418.004
Table 1
Mean and SD values of CAx, CAy, CAz for different sample preparations.
https://doi.org/10.7554/eLife.32418.008
FixationMMGreenRedCAx (nm)CAy (nm)CAz (nm)N
Use for correctionPFAPL9G39G313.1 ± 9.115.8 ± 7.53.5 ± 17.6166
PFAPL9G39G314.7 ± 11.413.2 ± 12.11.5 ± 17.0256
PFAPL9G39G315.7 ± 12.515.6 ± 8.2−4.8 ± 20.2206
Use for correctionPFAPBS9G39G313.2 ± 10.718.7 ± 10.4−2.7 ± 47.5168
Use for correctionGAPL9G39G319.2 ± 10.316.0 ± 9.0−6.8 ± 18.8170

A small measurement region in the center of the camera detector (~300×200 pixels) was used for the entire analysis in this study (Figure 2—figure supplement 2A–B). In the measurement region, there was a gradient for CAx in the x direction (~30 nm/ 280 pixels (19 µm)), but not in the y or z directions. There was a gradient for CAy in the y direction (~21 nm/180 pixels (11.5 µm)), but not in the x or z directions. There was no noticeable gradient for CAz in either the x, y, or z directions compared to the SD (Figure 2—figure supplement 3). These gradients in CA had no more effect on measurement accuracy than randomly distributed CA values with the same mean and SD (see computer simulations below).

Validation of our 2D and 3D co-localization method for known separations within the kinetochore

We initially measured the 2D and 3D separations between an antibody to CENP-T (CENP-T (M), Gascoigne et al., 2011) and Hec1-9G3 because previous studies reported values of Delta and 3D mean separations (by the CICADA method) using these same antibodies (Fuller and Straight, 2012; Suzuki et al., 2014; Wan et al., 2009). The reported 1D and 3D values for CENP-T (M) and Hec1-9G3 were ~60 and~62 nm respectively. Our mean separation ±SD between CENP-T (M) and Hec1-9G3 for Delta = 60 ± 7.5 nm, S(2D)=63 ± 11.2 nm, ML2D = 62 ± 11.3 nm, S(3D)=69 ± 12.3 nm, and ML3D = 66 ± 12.5 nm (Figure 3A–B), almost identical to the previous studies (Fuller and Straight, 2012; Suzuki et al., 2014; Wan et al., 2009).

Figure 3
Download asset Open asset
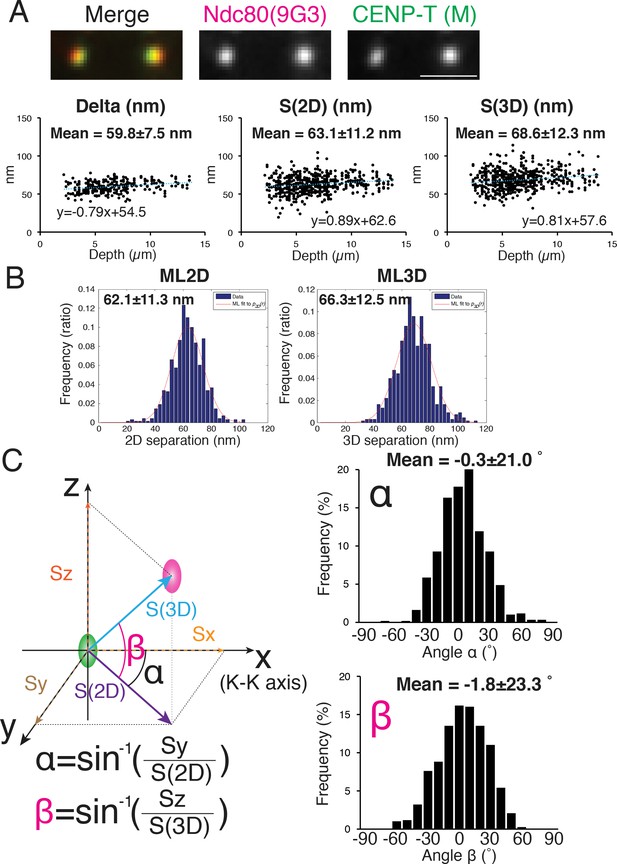
Mean Delta, 2D, and 3D separations between Hec1-9G3 and CENP-T (M).

(A) Representative immunofluorescent (IF) images (top) and plots of Depth verses Delta, S(2D) and S(3D) for the separation between CENP-T(M) and Hec1-9G3 (bottom). (B) Histograms of maximum likelihood fit used to calculate ML2D and ML3D. (C) Orientation of the S(3D) separation vector relative to the sister K-K axis (x-axis in this diagram). Angle α is the rotation of the S(2D) vector component in the x-y plane away from the K-K (x-axis) and angle β is the rotation of the S(3D) vector away from the x-y plane and toward the z-axis (schematic on left). Histograms of α and β values (Right). n > 600 individual kinetochores. All values were mean ±SD. Note, CENP-T(M) is a polyclonal antibody against whole CENP-T protein, and its epitope is not precisely known (Gascoigne et al., 2011).

https://doi.org/10.7554/eLife.32418.009

The orientation of the separation vector at each kinetochore was also calculated relative to the K-K axis. For CENP-T(M) to Hec1-9G3, the mean vector angle to the K-K axis in the X-Y plane, angle α = −0.3 ± 20.1 degrees, while the mean vector angle relative to the Z-axis (angle β) was −1.8 ± 23.3 degrees (Figure 3C). A significant fraction of the SD in these angles may be due to errors from CDsd and CAsd (see computer simulations below).

To further test the accuracy of our 2D/3D co-localization method, we examined the mean separation of different domains within the Ndc80 complex. We chose the Ndc80 complex as a molecular ruler, since its protein structure is well known. The Ndc80 complex contains a dimer of Ndc80/Nuf2 and a dimer of Spc24/Spc25 (Cheeseman et al., 2006; Ciferri et al., 2008; Musacchio and Desai, 2017). Most of the length of the Ndc80 complex is alpha helical coiled-coil, and its contour length is 55 ~ 60 nm, as measured in vitro by electron microscopy and crystallography (Ciferri et al., 2008; Huis In 't Veld et al., 2016; Valverde et al., 2016; Wei et al., 2005). To reveal the cellular Ndc80 complex structure, we developed HeLa cells stably expressing EGFP-Ndc80, Ndc80-EGFP, EGFP-Nuf2, Nuf2-EGFP, EGFP-Spc24, Spc24-EGFP, EGFP-Spc25, or Spc25-EGFP (Figure 4A). Figure 4B and Figure 4—source data 1 show the separation values relative to Hec1-9G3 to different ends of the Ndc80, Nuf2, Spc24, and Spc25 proteins, tagged in each case with EGFP. For example, the mean separation measurements between Spc25-EGFP and Hec1-9G3 were Delta = 49 ± 5 nm, S(2D)=52 ± 10 nm, S(3D)=55 ± 10 nm, ML2D = 51 ± 10 nm, and ML3D = 53 ± 10 nm. The Ndc80 complex is likely extended along kMTs since the Delta and ML3D values for the length of the Ndc80 complex are nearly identical. Also, overall, our Delta, 2D, and 3D mean separation measurements yielded a close fit to a Ndc80 complex structure that was determined in vitro (Ciferri et al., 2008; Valverde et al., 2016). As expected, the C-terminus of Spc24 is located a few nm inside of the C-terminus of Spc25, and Spc24 is longer than Spc25 (Figure 4—figure supplement 1) (Valverde et al., 2016). The CH-domain of Nuf2 is located a few nm inside of the N-terminal CH domain of Ndc80, and Ndc80 is longer than Nuf2 (Figure 4—figure supplement 1) (Ciferri et al., 2008; Valverde et al., 2016). Unexpectedly, in vivo, the C-terminus of Ndc80 locates much closer to the globular domains of Spc24/Spc25 (Figure 4B). This difference might be caused by structural restrictions on the position of the EGFP tag, which was tethered to the protein end by a nine amino acid linker.

Figure 4 with 1 supplement see all
Download asset Open asset
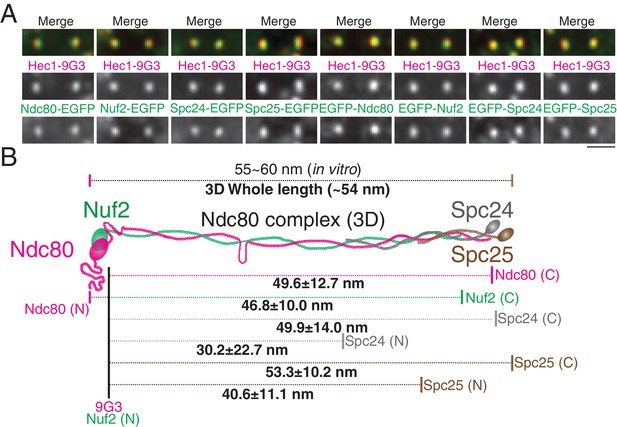
2D/3D co-localization measurements of a structural standard, the extended Ndc80 complex.

(A) Representative immunofluorescent images of Hec1-9G3 and EGFP fused to different protein domains along the Ndc80 complex (See Text and Materials and methods). (B) Schematic summary of the ML3D Ndc80 complex measurements at metaphase. All values were mean ±SD. n > 200 kinetochores for each measurement. Detail values are listed in Figure 4—figure supplement 1.

https://doi.org/10.7554/eLife.32418.010
Figure 4—source data 1

The list for Ndc80 complex measurements.

List of mean values of Delta, S(2D), S(3D), ML2D, ML3D between EGFP-Ndc80, Ndc80-EGFP, EGFP-Nuf2, Nuf2-EGFP, EGFP-Spc24, Spc24-EGFP, EGFP-Spc25, or Spc25-EGFP and Hec1-9G3. All values listed are mean ±S.D.

https://doi.org/10.7554/eLife.32418.012

Sister kinetochore pairs were used for the majority of measurements in this study to directly compare separations obtained by Delta and 2D/3D fluorescent co-localization methods using the same data sets. To test if selection of sister pairs influenced our measurements, we measured 120 kinetochores selected randomly in a single metaphase cell. This produced a mean separation value nearly identical to the mean value for single kinetochore measurements of sister pairs obtained from six metaphase cells (Table 2).

Table 2
Comparison of measurements for kinetochores that were part of sister pairs and kinetochores selected at random from a single metaphase cell.
https://doi.org/10.7554/eLife.32418.013
MethodsGreenRedDelta (nm)S(2D) (nm)S(3D) (nm)ML2D (nm)ML3D (nm)n
Sister pairSpc25-EGFP9G349.4 ± 4.651.5 ± 9.655.2 ± 10.050.6 ± 9.753.3 ± 10.2280 (140 pairs) from 6 cells
RandomSpc25-EGFP9G3N.A.50.8 ± 6.755.3 ± 7.750.3 ± 6.754.2 ± 7.8120 from single cell

The mean human kinetochore protein architecture at metaphase measured by the Delta method and our 3D method are similar

Figure 5 shows how the centroids of protein labels are separated on average along the inner-outer kinetochore axis based on our 2D/Delta measurements (Top) and 3D measurements (bottom). All of our 2D and Delta values are nearly identical (usually less than 3 nm difference). In general, our 3D measurements were only ~5 nm larger than the Delta or 2D values (Figure 5 and the Figure 5—source data 1). Unlike the 3D kinetochore protein architecture proposed by (Smith et al., 2016), our data showed no ~70 nm gap between CCAN protein domains and the Ndc80 complex. The inner kinetochore proteins are much closer to the outer kinetochore, corresponding to the previous studies using Delta measurements (Suzuki et al., 2014). For example, our 3D mean separation between CENP-A and Hec1-9G3 is ~90 nm, which is nearly identical to values obtained by Delta (~84 nm) and ML2D (~85 nm). In Figure 5, the Ndc80 complex and protein linkage to the inner kinetochore are shown aligned with the axis of kMTs because the ML3D mean separation values are only slightly greater than their corresponding Delta values, and the Delta value is a projection of the ML3D value along the K-K axis.

Figure 5
Download asset Open asset
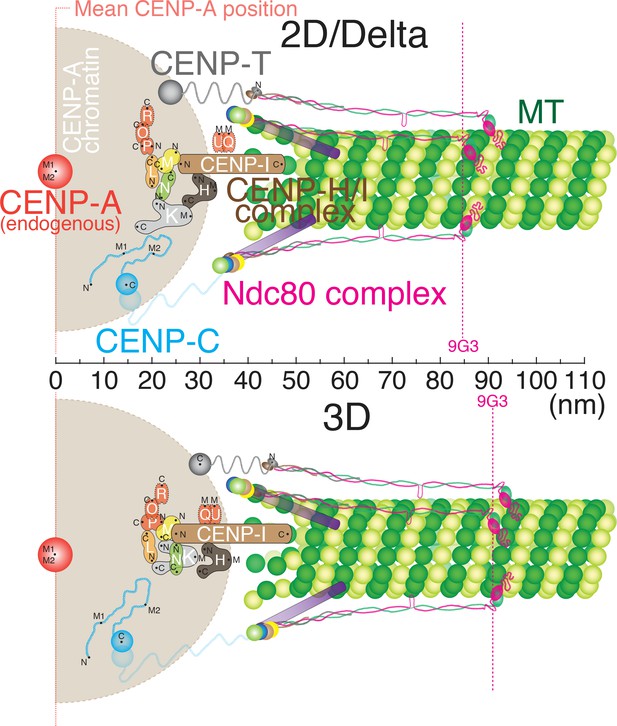
Schematic core-kinetochore drawing measured by 2D/Delta or 3D co-localization method.

Schematic picture of the mean positions of protein labels within the core kinetochore protein architecture measured using ML2D/Delta (top) and ML3D (bottom) methods. N or C are the mean positions of N-terminal or C-terminal EGFP fusions or specific antibodies. M indicates the mean position measured using polyclonal antibodies whose epitope(s) are not precisely known.

https://doi.org/10.7554/eLife.32418.014
Figure 5—source data 1

List for core-kinetochore protein measurements.

List of mean values of Delta, S(2D), S(3D), ML2D, ML3D, Z-offset, and zML3D (Z-offset subtracted) for core kinetochore proteins. The differences between ML3D and ML2D (ML3D-ML2D), ML3D and zML3D (ML3D-zML3D) are also listed. All values listed are mean ±S.D.

https://doi.org/10.7554/eLife.32418.015
Figure 5—source data 2

List of primary antibodies.

List of antibodies used in this study with source and references.

https://doi.org/10.7554/eLife.32418.016

Coverslip thickness both greater and less than 0.17 mm produces z-axis chromatic aberration (Z-offset) independent of focal depth

Normally the value of Z-offset (mean Sz) for each coverslip-slide preparation was within ±25 nm of zero (Figure 5—source data 1). However, occasionally, significantly large positive or negative values occurred, which made the 3D measurement much larger than for small Z-offsets. The largest Z-offset occurred for one sample stained for CENP-T(M) and 9G3,~80 nm (Table 3A), which increased the S(3D) from 65 to 103 nm (Table 3A,). If this large Z-offset was subtracted from the Sz data, the mean zS3D (S(3D) with subtracted Z-offset) value became close to the value with near zero Z-offset,~65 nm (Table 3A). This comparison indicated that the higher Z-offset was independent of the actual mean separation between green and red labels. This comparison also indicated that there was something about specimen preparation causing variation in z-axis CA.

Table 3
(A) List of Delta, S(2D), S(3D), Z-offset, and zS(3D) (Z-offset subtracted) for the mean separation between CENP-T(M) and Hec1(9G3) in samples with or without large Z-offset.

(B) List of Delta, S(2D), S(3D), Z-offset, and zS(3D) in samples with #1, #1.5, and #2 coverslips. The value zS(3D) was calculated from the S(3D) data after subtraction of the mean Z-offset in the middle of the spindle from the Sz values. All values were mean ±SD.

https://doi.org/10.7554/eLife.32418.017
AGreenRedDelta nm)S(2D)(nm)S(3D) (nm)Z-offset (nm)zS(3D) (nm)
Example 1CENP-T (M)9 G359.5 ± 6.360.8 ± 8.8102.4 ± 26.779.7 ± 32.968.9 ± 10.2
Example 2CENP-T (M)9 G357.3 ± 7.360.1 ± 11.764.8 ± 11.36.9 ± 23.264.5 ± 10.8
BThicknessGreenRedDelta nm)S(2D)(nm)S(3D) (nm)Z-offset (nm)zS(3D) (nm)
Experiment 1#1CENP-T (M)9 G360.4 ± 6.963.5 ± 12.475.2 ± 17.6−28.6 ± 31.170.4 ± 14.2
Experiment 2#1CENP-T (M)9 G359.2 ± 10.062.6 ± 11.772.6 ± 16.3−18.3 ± 33.970.6 ± 14.6
Experiment 1#1.5CENP-T (M)9 G357.3 ± 7.360.1 ± 11.664.8. ± 11.36.9 ± 23.264.5 ± 10.8
Experiment 2#1.5CENP-T (M)9 G357.0 ± 7.160.6 ± 11.164.0 ± 11.66.0 ± 20.063.8 ± 11.2
Experiment 1#2CENP-T (M)9 G359.6 ± 7.762.1 ± 11.982.1 ± 27.246.4 ± 36.469.6 ± 21.9
Experiment 2#2CENP-T (M)9 G359.8 ± 7.462.5 ± 10.974.2 ± 16.228.7 ± 30.269.4 ± 10.8

To explore possible optical factors, we used a mathematical analysis reported previously (Gibson and Lanni, 1992). This analysis calculates, relative to the design values for the objective, changes in optical path for light coming from a fluorescent point as a function of the refractive index and thickness of the specimen media, the coverslip thickness, and immersion oil, as well as wavelength. It showed that the amount of z-axis CA is highly sensitive to changes in the thickness of the coverslip. We tested this possibility by using different thickness of coverslips. We did most of our experiments reported in this paper using # 1.5 coverslips. We measured their thickness with a micrometer, and the mean value was 0.17 mm with a range of 0.16 to 0.19 (Figure 6, n > 100). For #1 coverslips, the mean was 0.15 mm and for #2 coverslips it was 0.22 mm (Figure 6). The mean Sz (Z-offset) for CENP-T(M) to Hec1-9G3 showed ~±10 nm for #1.5 coverslips, −29 to −19 nm for #1 coverslips, and 29 to 46 nm for # 2 (Table 3B). The plot in Figure 6—figure supplement 1 illustrates the sensitivity of Z-offset to coverslip thickness. A steep slope is seen when measured Z-offset values in Table 3B are plotted as a function of the mean thickness we measured for #1, #1.5 and #2 coverslips. Based on these experimental results, we suspect that unusually large Z-offset values (>25 nm) measured in our experiments (Figure 5—source data 1) were largely produced by coverslip thicknesses much thinner or thicker than 0.17 mm.

Figure 6 with 2 supplements see all
Download asset Open asset
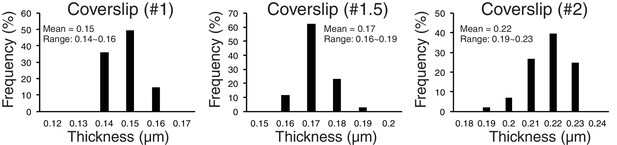
Accuracy of separation measurements depends critically on mean z-axis CA (Z-offset) produced by coverslip thickness variations from standard value.

Measured variability of coverslip thickness within #1, #1.5, and #2 coverslips.

https://doi.org/10.7554/eLife.32418.018

In our study, we were careful to include similar numbers of kinetochores above and below the spindle equator. This is because kinetochores and their kMTs become tilted progressively with their radial distance away from the spindle axis (Figure 6—figure supplement 2A) (Smith et al., 2016;Wan et al., 2009). Both the inner and outer domains of metaphase kinetochores typically have their faces perpendicular to their kMTs (Wan et al., 2009). If kinetochores are only measured on the bottom half of the spindle, the mean value of Sz will not be zero because the upward kinetochore tilt in the lower half spindle is not canceled by the downward tilt from kinetochores in the upper half-spindle (Figure 6—figure supplement 2A–B). This kinetochore tilt had no effect on measured 3D mean separation since values from only kinetochores in the upper half of the spindle yielded similar results as from kinetochores in the lower half of the spindle (data not shown). Unlike 3D separation, the mean tilt angle β (but not angle α) was sensitive to unequal numbers of kinetochores above and below the spindle equator. The mean angle β is near zero in the middle of the spindle and reaches mean values of about 20–25 degrees at the bottom and top of the spindle (Figure 6—figure supplement 2C–D).

PFA fixation does not cause shrinkage, but pre-extraction or detergent in PFA solution causes shrinkage of cellular structure

A recent study raised the issue that PFA fixation induced shrinkages compared to GA fixation (Magidson et al., 2016). GA has two aldehyde radicals and provides more robust fixation compared to PFA fixation. Because of this reason, GA fixation is usually used for electron microscopy. On the other hand, GA fixation exhibits strong auto fluorescence, and induces significantly less reactivity between cellular antigen and antibodies compared to PFA fixation. For immunofluorescence, a non-ionic detergent, such as Triton-X 100 or NP40, is often used to improve antibody penetration into the cell before, with, or after fixation. It is uncertain how these pre-permeabilization processes affect cellular architecture. For example, Magidson et al. (2016) concluded PFA fixation causes shrinkage. However, they actually supplemented 1% Triton-X 100 in their PFA fixation solution. Our standard method was primary fixation by PFA without detergent (Method one in Table 4), a method significantly different than the PFA fixation method used by (Magidson et al., 2016).

Table 4
Summary of fixation methods used in Figure 7.

Detailed protocols for the different fixation methods used in Figure 7. Method 1 is the protocol used in this study.

https://doi.org/10.7554/eLife.32418.021
MethodPre-fixationPre-perme-
abilization		FixationQuenchingPost-perme-
abilization		Primary
antibody		Secondery
anitbody		References (use
for nm-resolution analysis)
Method 13% PFA in
PHEM (37°C)		0.5% NP4037°C for 90 min37°C for 90 minSuzuki et al., 2011
;Suzuki et al., 2014
 ;Tauchman et al., 2015; this study
Method 23% PFA in
PHEM (37°C)		0.5% triton in
PHEM (37°C)		3% PFA in
PHEM (37°C)		0.5% NP4037°C for 90 min37°C for 90 minWan et al. (2009);
Varma et al., 2013
Method 31% triton in
PHEM (37°C)		3% PFA in
PHEM (37°C)		0.5% NP4037°C for 90 min37°C for 90 min
Method 41% GA in
PHEM (37°C)		NaBH40.5% NP4037°C for 90 min37°C for 90 min
Method 51%GA w 1% triton
in PHEM (37°C)		NaBH40.5% NP4037°C for 90 min37°C for 90 minMagidson et al. (2016)
Method 61% triton in
PHEM (37°C)		1% GA in
PHEM (37°C)		NaBH40.5% NP4037°C for 90 min37°C for 90 min
Method 71% triton in
PHEM (37°C)		1% GA w 3% PFA
in PHEM (37°C)		NaBH40.5% NP4037°C for 90 min37°C for 90 min
Method 8MeOH (−20°C)0.5% NP4037°C for 90 min37°C for 90 min
Method 93%PFA w 1% triton
in PHEM (37°C)		0.5% NP4037°C for 90 min37°C for 90 minMagidson et al. (2016)

To test the effect of fixation and detergent for antibody reaction and separation measurements, we tested nine different fixation methods (Table 4, and Materials and methods). We used CENP-T (M) and Hec1-9G3 antibodies for this comparison (Figure 7A). These antibodies were the exact same antibodies used in Figure 3 in this study, and in previous reports (Fuller and Straight, 2012; Magidson et al., 2016; Suzuki et al., 2014; Wan et al., 2009). We first compared CENP-T(M) and Hec1-9G3 signal levels at kinetochores in the different methods (Figure 7B). Interestingly, both CENP-T(M) and Hec1-9G3 signal levels in GA fixation samples (Methods 4–7) were significantly reduced by ~35% to 60% compared to PFA fixation (Method 1), PFA with detergent fixation (by 20–30%), or MeOH fixation (~20%) (Figure 7B). However, local background levels (surrounding area of kinetochore) were not significantly different between all fixation methods, indicating that GA fixation significantly reduced the signal to noise ratio (S/N) compared to PFA or MeOH fixation (Figure 7B).

Figure 7
Download asset Open asset
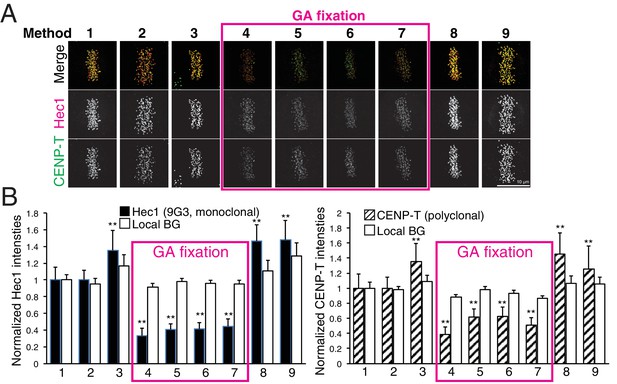
Comparison of various fixation methods for signal intensity and mean fluorescence co-localization analysis.

(A) Representative immunofluorescent images stained by CENP-T(M) and Hec1-9G3 antibodies using the fixation protocols listed in Table 4. (B) The plots of normalized signal intensity of Hec1-9G3 (left) and CENP-T (right) at kinetochores using the fixation protocols listed in Table 4. The signal intensities were normalized for the mean values of PFA fixation (~20,000 integrated fluorescence counts above local background for Method 1). All values were mean ±SD. n > 200 individual kinetochores for each experiment. **p<0.05 (t-test).

https://doi.org/10.7554/eLife.32418.022

Next, we measured mean separation between CENP-T(M) and Hec1-9G3. Surprisingly, we could not find any significant differences between PFA fixation (Methods 1–2) and GA fixation (Methods 4–7). However, we observed significant shrinkage when samples were fixed by Methods 3, 8, and 9 (Table 5). Interestingly, we could not see any shrinkage when we fixed by GA with Triton X-100, Triton X-100 treatment before GA or GA/PFA (Methods 5–7). Although there are no differences between PFA and GA fixation for the separation between CENP-T(M) and Hec1-9G3, we found that pre-extraction by Triton X-100 or PFA fixation with Triton X-100 induced significant shrinkage compared to GA with Triton X-100. This result is consistent with the report of Magidson et al. (2016). However, our standard PFA fixation method (Method 1) did not produce any shrinkage.

Table 5
The list of measured values for Delta, ML2D, ML3D, dDelta, dML2D, and dML3D using protocols in Table 4.

The dDelta, dML2D, dML3D were differences from Method 1 (PFA fixation). All values were mean ±SD. n > 200 individual kinetochores for each experiment.

https://doi.org/10.7554/eLife.32418.023
Red-Green = mean ± S.D. nm
Delta (nm)ML2D (nm)ML3D (nm)dDelta (nm)dML2D (nm)dML3D (nm)
Method 157.2 ± 7.359.1 ± 11.662.6 ± 11.5000.0
Method 256.8 ± 6.058.6 ± 8.861.3 ± 8.6−0.4−0.5−1.3
Method 350.1 ± 7.152.8 ± 8.556.4 ± 8.2−7.1−6.3−6.2
Method 458.7 ± 9.161.5 ± 12.463.1 ± 22.91.52.40.5
Method 555.2 ± 8.956.9 ± 11.761.3 ± 15.5-2−2.2−1.3
Method 657.2 ± 9.060.0 ± 12.963.5 ± 21.600.90.9
Method 754.0 ± 10.057.2 ± 12.157.7 ± 12.2−3.2−1.9−4.9
Method 846.4 ± 5.348.3 ± 7.752.0 ± 7.7−10.8−10.8−10.6
Method 951.8 ± 7.453.8 ± 9.756.7 ± 10.0−5.4−5.3−5.9

Computer simulations for understanding the method and its limitations

The method using mean values of CA to correct chromatic aberration is widely used, but the limitations of this method are not well established. We evaluated the method by computer simulations. Critical factors are SDs of centroid determination (CDsd) and CA (CAsd). In our simulations, kinetochores were located at 10 pixel intervals in both the X and Y axis directions for the typical image region of 0–280 pixels in the X- direction and 0 to 190 pixels in the Y-direction (Figure 8). At each kinetochore position (p), the separation vector extended from the origin to a length S in the x direction. The green (Xgp, Ygp, Zgp) values at the origin had a mean of zero plus a CDsd determined by sampling CDsd times a normalized random number for the x, y, and z directions (Figure 8). The red (Xrp, Yrp, Zrp) values included S in the x-direction and Z-offset in the Z direction. They also included a value for the CA at each kinetochore position, CAp, plus CDsd for each direction (Figure 8). Two methods were used to generate the CAp values. In the first, for each x, y, and z direction, CAp was calculated from the measured mean CA plus the CAsd times a normalized random number. In the second, CAp for the x and y directions were calculated from least square fits to the CA cellular data because of the 30 nm and 20 nm decrease respectively across the measurement field (Figure 2—figure supplement 3). However, this second procedure gave identical results as the first method outlined in Figure 8, which is the CA correction method we used experimentally. Mean and SD values for S(2D), S(3D), ML2D, ML3D, angle α, and angle β were calculated using the same equations as we did in analysis of cellular data (Figures 1E and 3C).

Figure 8
Download asset Open asset
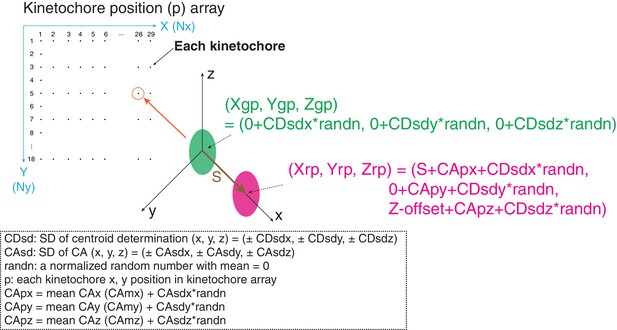
Diagram of simulation model.

We used a 290 × 180 pixel region (x and y) and kinetochores at positions (p) separated by 10 pixels in each direction. All simulated values S(2D), S(3D), angle α, and angle β were averaged from 29 × 18 = 551 kinetochores. The maximum likelihood fit was applied to the raw simulated S(2D) and S(3D) values in the same way as for the experimental analysis in this study.

https://doi.org/10.7554/eLife.32418.024

To obtain an estimate of the error contributed from the CDsd, we used results from Delta analysis which in principle have local CA correction. For example, the Delta value measured for CENP-T(M) to Hec1-9G3 is 60 ± 7.5 nm. In the simulation, we made the CAsd = zero, and asked how much CDsd is needed to make the measured Delta SD =±7.5 for S = 60 nm. The result was CDsd (x, y, z) = (±4,±4,±8) (Table 6A). Because resolution in the z direction is half that in the x and y directions, we set CDsd of z = 2 * CDsd of x or y. Simulations that include the CDsd, but exclude CAsd, yielded mean values for ML3D and ML3D nearly identical to the input 60 nm value (Table 6A). This result indicates that the SD in our centroid measurement is very small and only slightly enhances the 3D measurements from the true value.

Table 6
Computer simulations to determine measurement SD and to test the accuracy of using mean CA for CA correction.

(A) Comparison of ~60 nm experimental results to simulated results for a fixed S value of 60 nm, the estimated CDsd for our measurements, and with or without CAsd. (B) Simulated S(3D), and ML3D values for different input S values with fixed angles (0˚), CDsd (x, y, z) = (±4, ±4, ±8) and CAsd (x, y, z) = (±9.1, ±7.5, ±17.6). All simulated values were mean ±SD.

https://doi.org/10.7554/eLife.32418.025
ADelta (nm)S(2D) (nm)S(3D) (nm)ML2D (nm)ML3D (nm)α (°)β (°)
ExperimentCENP-T(M)-Hec1-9G360 ± 7.563.1 ± 1168.6 ± 12.362.1 ± 11.366.3 ± 12.3−0.3 ± 21−1.8 ± 23
Simulation (S = 60 nm)SDc (x, y,z) = (±4, ±4, ±8)
No CAsd60.4 ± 5.761.5 ± 5.860.4 ± 5.761.5 ± 5.80.1 ± 5.40 ± 10.7
CAsd (x, y, z) = (±9.1, ±7.5, ±17.6)N/A60.7 ± 10.964.5 ± 11.359.7 ± 1162.3 ± 11.5−0.2 ± 9.4−0.1 ± 19.4
Binput valuessimulation results
S ± 0 nmα (±0˚)β (±0˚)α˚β˚S(3D) (nm)ML3D (nm)
0000.3 ± 51.21.8 ± 51.822 ± 10.50 ± 14.1
1000−2.4 ± 44.8−3.2 ± 48.824.6 ± 10.90 ± 15.5
15001.1 ± 36−0.6 ± 43.526.5 ± 11.10 ± 16.6
20000.9 ± 30.9−2.4 ± 40.329.5 ± 11.420.7 ± 13.8
40000.8 ± 14.8−0.3 ± 27.247 ± 12.343.1 ± 12.9
60000.1 ± 9.1−0.5 ± 19.363.9 ± 11.461.8 ± 11.5
8000−0.1 ± 6.61 ± 14.383.1 ± 11.281.6 ± 11.3
100000.2 ± 5.50.3 ± 11.4102.9 ± 11.1101.7 ± 11.1

The measured CAsd (x, y, z) = (±9.1, ±7.5, ±17.6 nm) are only about twice those for centroid determination, and make only a slightly larger contribution to errors in measured S(2D), S(3D), ML2D, ML3D, angle α, and angle β (Table 6A). For S = 60 nm, the mean of S(2D) and S(3D) are increased by a CDsd and CAsd to 61 and 65 nm, but this 1–5 nm error is mostly corrected by application of maximum likelihood fit to yield ML2D = 60 ± 11 nm and ML3D = 62.3 ± 12 nm (Table 6A). This result shows that our method of subtracting the mean values of CA combined with maximum likelihood data analysis can yield accurate mean 3D values for separation vector length.

To see how the CDsd and CAsd of our measurement method affect the SDs in the angles α and β, we entered into the simulation constant values for S between zero and 100 nm (Table 6B). The SD in the angles α and β are largest for small separations (Table 6B). For example, they were 9 and 19 degrees (S = 60 nm) or 6 and 11 degrees (S = 100 nm). These results indicate that our CDsd and CAsd caused about half to two-thirds of the SD measured in cells for separations of 60 nm (SDs of angles α and β were 21 and 23 degrees, respectively; CENP-T-Hec1-9G3 in Figure 3C) or 90 nm (SDs of angles α and β were 16 and 22 degrees, respectively; CENP-A-Hec1-9G3 in Figure 6—figure supplement 2C–D). These simulations also showed that our SDs inhibit maximum likelihood fit below S = ~18 nm (Table 6B). These simulation results indicate that much of our measured SD in the cell is not caused by variability between different kinetochores, but by the SDs in centroid measurement and CA correction.

Discussion

There are several key factors that influence the accuracy of the 3D fluorescence co-localization method we used for determining mean separation distances (all factors we identified are listed in Figure 1—source data 1). High S/N and bright specimens are needed for small CDsd. The measurement field should be restricted in area to keep the CAsd small. The correct coverslip thickness should be used to prevent Z-offset. These procedures are important because computer simulations show that mean 2D/3D separations and SDs in angles (α and β) all increase from their true values as a power function of the magnitudes of CDsd, CAsd, and Z-offset (Figure 9A–C). In addition, the use of the maximum likelihood method corrects the overestimate of mean separations obtained from S(2D) and S(3D) (Churchman et al., 2005).

Figure 9 with 1 supplement see all
Download asset Open asset
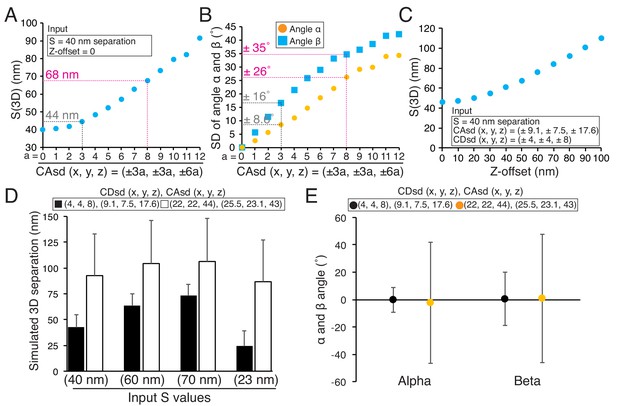
Origins of error in mean separation measurements and comparison of our results to previous reports.

(A) Plots of simulated S(3D) for 40 nm separation with increasing values of CAsd (SD of CA) where the mean CA values were held constant at our measured values of 13.1, 15.8, and 3.5 nm respectively. Grey dashed line is nearly identical to the CAsd for our measurements and the red dashed line is nearly identical to the CAsd for the Smith et al., 2016 measurements. (B) Plots of SD of simulated angle α and β for 60 nm separation using the same condition in (A). (C) Plots of simulated S(3D) for S = 40 nm separation for increasing values of Z-offset and the CAsd reported by Smith et al. (2016). (D) The simulated 3D separation using our SDs (black bars) or in Smith et al. (2016) (white bars). The true separations (S values) are 40, 60, 70, and 23 nm from left to right, which correspond to the mean values from Delta analysis in Table 7. (E) The simulated mean angle α and β with ±SD for the conditions in (E). Note, the input mean angle α and β were zero, and S = 60 nm.

https://doi.org/10.7554/eLife.32418.026
Figure 9—source data 1

Estimation of SD for centroid determination (CDsd).

Computer simulations were used with zero CAsd to estimate CDsd (x, y, z) from the SD of Delta measurements (local CA correction) in our study (top) or Smith et al., 2016 (bottom).

https://doi.org/10.7554/eLife.32418.028
Figure 9—source data 2

Estimation of kinetochore-kinetochore variability (Ksd) in our measurements.

The table of experimental or simulated results using fixed S value (60 nm), CDsd ((x, y, z) = (±4, ±4, ±8)), and CAsd ((x, y, z) = (±9.1, ±7.5, ±17.6)) with kinetochore-to-kinetochore variability (Ksd = ±0, ±5, ±10, or ±15 nm).

https://doi.org/10.7554/eLife.32418.029

Z-offset is a major source of error only if it is not produced by the specimen. As a general rule, we do not recommend subtracting Z-offset from Sz data since there could be a specimen contribution. When using our method, we recommend repeating the specimen measurement with a 0.17 mm coverslip if Z-offset is larger than ±25 nm to make sure there is not an unknown specimen contribution. Computer simulations of the measurement method showed that only absolute values of Z-offset >30 nm make 3D mean separation measurements significantly larger (Figure 9C). Also, our method produces nearly identical results from multiple samples. Figure 5—source data 1 has measurements between CENP-A and Hec1-9G3 from four different coverslip preparations. Their Z-offsets varied between −17 and 4.4 nm, while their ML3D mean values varied between 86 and 93 nm.

Smith et al., 2016 reported that the mean 3D separation between endogenous CENP-A and the C-terminus of Ndc80 was 81.7 ± 0.7 nm SEM (n = 3302, SD =±40 nm), about 42 nm larger than our measured value of 40 nm ± ~ 10 nm (SD) (Table 7). Table 7 also provides three more examples showing differences of 24 nm to 60 nm between their and our mean 3D separation measurements. Since Smith et al., 2016 used mean CA values for CA correction as we did in this study, we investigated the possibility that significantly higher CDsd and CAsd compared to our values might be responsible for their larger 3D separation values. We estimated the CDsd from the SD of their Delta measurements for CENP-A to Spc24, which was ~35 nm, compared to our value of 6 nm (Figure 9—source data 1) (Smith et al., 2016; Suzuki et al., 2014). This analysis yielded values for CDsd about five times larger than ours (22 nm, 22 nm, and 44 nm compared to 4 nm, 4 nm and 8 nm in the x, y and z directions) (Figure 9—source data 1). Such high CDsd values could explain why their Delta measurements are significantly larger than ours (Figure 9—source data 1). Their reported CAsd was also significantly larger than ours (26 nm, 23 nm and 43 nm compared to 9 nm, 7.5 nm and 18 nm in the x, y and z directions) (Smith et al., 2016). Results of simulations in Figure 9D using the values we estimated for their CDsd and their reported CAsd produce results nearly identical to their mean separation measurements, and show how the differences in the SDs between their and our measurements could be responsible for their much larger values. In addition, the higher levels for CDsd and CAsd are likely responsible for the very large SDs they measured for the angles α and β compared to ours (Figure 9E). In our measurements, large values of Z-offset were rare (Figure 5—source data 1); we have no information to judge how much other sources of error like Z-offset, contributed to the Smith et al. (2016) measurements.

Table 7
List of four examples of Delta and 3D mean separation measurements with ±SD from this study and Smith et al., 2016.
https://doi.org/10.7554/eLife.32418.030
Delta (Mean ± SD nm)3D separation (Mean ± SD nm)
1Smith et al., 2016EGFP-CENP-ANdc80(C-term)58 ± 35 (n = 1002,±1.1 (SE))98 ± 58 (n = 4291,±0.9 (SE))
Smith et al., 2016endogeous CENP-ANdc80(C-term)N/A84 ± 40 (n = 3302,±0.7 (SE))
This studyendogeous CENP-ACENP-T (N-term)40 ± 6 (n = 110)46 ± 12 (n = 220)
2Smith et al., 2016endogenous CENP-CNdc80 (N-term)N/A103 ± 74 (n = 7476,±0.8 (SE))
This studyendogenous CENP-CHec1-9G358 ± 5 (n = 62)67 ± 8 (n = 124)
3Smith et al., 2016EGFP-CENP-CNdc80 (N-term)N/A101 ± 76 (n = 1769,±1.8 (SE))
This studyEGFP-CENP-CHec1-9G369 ± 9 (n = 102)77 ± 15 (n = 124)
4Smith et al., 2016EGFP-CENP-ONdc80(C-term)N/A81 ± 52 (n = 1881,±1.2 (SE))
This studyEGFP-CENP-ONdc80(C-term)23 ± 11 (n = 97)*21 ± 16 (n = 194)*

  1. *These values were caliculated by (EGFP-CENP-O - Hec1-9G3) minus (Ndc80-EGFP - Hec1-9G3).

Human kinetochores are built from multiple copies of core-kinetochore proteins (Suzuki et al., 2015). A previous study has shown that the accuracy of separation measurements is sensitive to the spatial staggering of the labeled molecules along the kinetochore inner to outer axis only for stagger greater than 200 nm, which has the possibility of producing two fluorescent peaks instead of a single peak if staggering is not random (Joglekar et al., 2009). All kinetochores labeled by specific antibodies or EGFP in our study exhibited a Gaussian distribution with a single peak. This indicates that our centroid measurements correspond to the mean position of the fluorescently labeled protein epitopes within human kinetochores.

Magidson et al. (2016) questioned whether the mean separation measurements averaged from multiple kinetochores (typically 200–400 kinetochores from 5 to 20 cells in our study) hide variation in the position of proteins relative to each other between different kinetochores (Magidson et al., 2016). We tried to address this question in several ways. First, we found that mean measurements of individual kinetochores (not sister pairs) within a single cell yielded the identical value at metaphase as the mean obtained from kinetochores (sister pairs) within six different cells (Table 2). Thus, variations between cells or selected kinetochore measurements like in the Delta analysis is not an issue. Second, as expected for the Gaussian distribution measured for separation values (e.g. Figure 3B), we found that only 10–15 kinetochores were needed to be averaged to achieve the mean and SD typical of >150 kinetochores (Figure 9—figure supplement 1). Third, the SD of our 2D/3D measurements are small, typically less than 12 nm, and a significant part of this SD must be from the CDsd and CAsd (Table 6A and see above discussion) and not from differences between kinetochores. To see this more clearly, we used the same simulations as in Figures 8–9 but with mean kinetochore-to-kinetochore variability (Ksd = ±0, ±5, ±10, or ±15 nm) (Figure 9—source data 2). Simulation results showed that Ksd of about ±5 nm or less plus measurement CDsd and CAsd yielded the experimental mean SD value of 12.5 nm (Figure 9—source data 2). These results imply that the vast majority of kinetochores at metaphase have a similar protein architecture.

We found that our PFA fixation does not shrink kinetochore structure and produces exactly the same Delta, 2D, and 3D mean separation values obtained by the GA fixation. A major problem with GA fixation is that it interferes with antibody labeling, preventing immunofluorescence with many antibodies, and reduced fluorescence for others like those used in Figure 7. In addition, our data indicate that primary GA fixation may not be suitable for analysis of molecular distribution by immuno-electron microscopy because of poor recognition by antibodies. For immuno-electron microscopy, GA fixation should be used as the post-fixation solution, but only after the antibody reaction has been performed.

This study provides an optimized 3D fluorescence co-localization method with error analysis. It can achieve ~10 nm accuracy for mean separations larger than 18 nm. Our mean 3D fluorescence co-localization measurements for human kinetochore protein architecture are close to the mean values obtained using local correction of CA (Wan et al., 2009; Fuller and Straight, 2012) and successfully predict the known structural lengths of the Ndc80 complex components (Ciferri et al., 2008; Valverde et al., 2016; Musacchio and Desai, 2017). This optimized 3D co-localization method is a useful tool for broad research fields that need to determine mean protein architecture with nm-accuracy.

Materials and methods

Cell culture

Request a detailed protocol

HeLa cells were cultured in Dulbecco’s modified Eagle’s medium (Gibco) supplemented with 10% fetal bovine serum (Sigma), 100 U/ml penicillin and 100 mg/ml streptomycin at 37 ˚C in a humidified atmosphere with 5% CO2 (Suzuki et al., 2015). siRNA resistance EGFP-Ndc80, Ndc80-EGFP, EGFP-Nuf2, Nuf2-EGFP, EGFP-Spc24, Spc24-EGFP, EGFP-Spc25, and Spc25-EGFP constructs were linearized by restriction enzymes, and then purified plasmids were transfected using Effectene regents (Qiagen) according to the manufacturer’s instruction. The transfected cells were selected by Geneticin (Invitrogen) 48 hr after transfection. We collected more than 20 individual positive colonies from each transfection, then we tested expression levels of EGFP-tagged proteins by immunofluorescence. We selected cell lines expressing EGFP-fusion protein at a similar level to the endogenous protein, as measured by immunofluorescence stained kinetochores using Spc24 and Hec1-9G3 antibodies. Other EGFP strains were described in a previous study (Suzuki et al., 2015; Suzuki et al., 2014). All cells were monoclonal cell lines. RNAi experiments were conducted using LipofectamineRNAi MAX (Invitrogen) according to the manufacturer’s instructions. siRNA was performed with 100 nM of siRNA duplex and siRNA sequences of CENP-T, CENP-C, Ndc80, and Nuf2 were described previously (DeLuca et al., 2002; Suzuki et al., 2015). Sequences for Spc24 (GGUCGACGAGGACACGACA), Spc25 (CUGCAAAUAUCCAGGAUCU), and Nuf2 (GAAGUCAUGUAUCCACAUU) were used. The efficiency for depletion of CENP-T, CENP-C, and Hec1 was greater than 95% by kinetochore immunofluorescence and western blot (Suzuki et al., 2015). The efficiency for Nuf2, Spc24, and Spc25 was 90, 80, and 70%, respectively, by kinetochore immunofluorescence using Hec1-9G3 antibodies. (We could not obtain antibodies that specifically recognized Nuf2, Spc24, or Spc25.) Although we used siRNA for endogenous proteins when we used cell lines expressing an EGFP tagged protein, there was no significant difference for Delta, 2D, and 3D separation measurements in Ndc80-EGFP stable cells with or without siRNA for Ndc80.

Sample preparation

Request a detailed protocol

Cells were grown on acid washed #1.5 coverslips (~0.17 mm thick, Corning). For Figure 5 experiments, cells were also grown on acid washed #1 or #2 coverslips (Corning). For samples embedded by PBS, cells were grown on 35 mm glass bottom dish with #1.5 coverslip (MatTek). Cells were fixed by pre-warmed 3% PFA (freshly made from paraformaldehyde powder (Sigma)) at 37°C in PHEM buffer (120 mM Pipes, 50 mM HEPES, 20 mM EGTA, 4 mM magnesium acetate, pH7.0) for 10–15 min for all experiments except for those in Figure 7. For Figure 7 experiments, we fixed cells following nine different kinds of fixation (details in Table 4). Method 1: cells were fixed by 3% PFA in PHEM buffer for 10–15 min. Method 2: cells were fixed by 3% PFA in PHEM for 1 min, then cells were incubated in 0.5% triton in PHEM buffer, and cells were re-fixed by 3% PFA in PHEM buffer for an additional 10–15 min. Method 3: cells were incubated in 1% triton in PHEM for 1 min before fixation, then cells were fixed by 3% PFA in PHEM for 10–15 min. Method 4: cells were fixed by 1% GA (Glutaraldehyde, Sigma) in PHEM buffer for 10–15 min. Method 5: cells were fixed by 1% GA with 1% triton in PHEM buffer for 10–15 min. Method 6–7: cells were incubated in 1% triton before fixation, then cells were fixed by 1% GA (Method 6) or 1% GA with 3% PFA (Method 7) in PHEM buffer for 10–15 min. Method 8: cells were fixed by cold MeOH for 15 min at −20 ˚C. Method 9: cells were fixed by 3% PFA with 0.5% triton in PHEM buffer. Method 1 was used in the following studies (Suzuki et al., 2014; Suzuki et al., 2011; Tauchman et al., 2015; Wan et al., 2009), and this study). Methods 5 and 9 were used in Magidson et al. (2016). All fixation, except for Method 8, was performed at 37 ˚C. For samples fixed by GA (Method 4–7), after fixation, samples were incubated in NaBH4 (Sigma) for quenching to reduce autofluorecence. Fixed samples were permeabilized by 0.5% NP40 (Roche) in PHEM buffer, and incubated in 0.5% BSA (Sigma) or BGS (Boiled Goat Serum) or BDS (Boiled Donkey Serum) for 30 min at room temperature. Then, samples were incubated for 1.5 hr at 37°C with primary antibodies. Primary antibodies used in this study are listed in Figure 5—source data 2. CENP-A, CENP-T, and CENP-I antibodies were a gift from Drs. Aaron Straight, Iain Cheeseman, and Song-Tao Liu (Carroll et al., 2009; Gascoigne et al., 2011; Liu et al., 2003). After primary antibody incubation, samples were incubated for an additional 1.5 hr at 37°C with secondary antibodies. Secondary antibodies were conjugated with Alexa488 or Rhodamine Red-X (Jackson ImmunoResearch). After DNA staining by DAPI, samples were mounted using Prolong Gold Aintifade (Molecular Probe) or PBS. For samples mounted with Prolong Gold, we usually waited >1 week for the refractive index to increase to near 1.46.

Imaging

Request a detailed protocol

For image acquisition, 3D stacks of 70–90 frame pairs of red and green fluorescent images were obtained sequentially at 200 nm steps along the z axis through the cell using MetaMorph 7.8 software (Molecular Devices) and a high-resolution Nikon Ti inverted microscope equipped with an Orca AG cooled CCD camera with gain set to zero (Hamamatsu) and an 100X/1.4NA (PlanApo) DIC oil immersion objective (Nikon). Stage movement was controlled by MS2000-500 (ASI) with piezo-stage for z-axis stepping (Suzuki et al., 2015; Suzuki et al., 2014). The image magnification yielded a 64 nm pixel size. Solid state laser (Andor) illuminations at 488 and 568 nm were projected through Borealis (Andor) for uniform illumination of a spinning disk confocal head (Yokogawa CSU-10; Perkin Elmer). Raw 12 bit images without any image processing were used for all Delta, 2D, 3D separation analysis and signal intensity analysis.

Intensity analysis

Request a detailed protocol

Integrated fluorescence intensity (minus local back ground (BG)) measurements were obtained for kinetochores as described previously (Suzuki et al., 2015). A 10 × 10 pixel region was centered on a fluorescent kinetochore to obtain integrated fluorescence, whereas a 14 × 14 pixel region centered on the 10 × 10 pixel region was used to obtain surrounding BG intensity. Measured values were calculated by: Fi (integrated fluorescence intensity minus BG)=integrated intensity for 10 × 10 region – (integrated intensity for the 14 × 14 – integrated intensity for 10 × 10) x pixel area of the 10 × 10/(pixel area of the 14 × 14 region – pixel area of a 10 × 10 region). Measurements were made with Metamorph 7.7 software (Molecular Devices) using Region Measurements (Suzuki et al., 2015). For Figure 7, the local kinetochore background signals were measured by (integrated intensity for the 14 × 14 – integrated intensity for 10 × 10) x pixel area of the 10 × 10/(pixel area of the 14 × 14 region – pixel area of a 10 × 10 region). At least two independent replicates of measurements were performed.

Chromatic aberration (CA) calibration

Request a detailed protocol

To calibrate CA of our confocal microscope, we prepared samples with kinetochores stained by Hec1-9G3 primary antibodies and green (Alexa 488) and red (Rhodamine Red-X) labeled secondary antibodies. In addition, we also prepared coverslips with 100 nm or 500 nm TetraSpeck beads (Invitrogen) using a method described previously (Churchman and Spudich, 2012), except for using Prolong Gold as embedding media. X, Y, and Z coordinates of Green and Red fluorophores were determined by a 3D Gaussian fitting function in MatLab (MathWorks) (Wan et al., 2009). Details of CA correction methods are described in Text. Red and green fluorescent beads bound to the inner surface of a coverslip and embedded in Prolong Gold gave similar mean and SD values for CAx, CAy, CAz measured using Hec1-9G3-GR (Data not shown). At least two independent replicates of measurements were performed.

Delta method

Request a detailed protocol

For each kinetochore, 3D centroid positions were first measured for each fluorescent color by a 3D Gaussian fitting function. For each sister kinetochore pair, the centroids of one color were projected to the axis defined by the centroids of the other color, and the average separation of the projected distance between the signals of different colors for that pair (Wan et al., 2009). At least two independent replicates of Delta measurements were performed.

2D and 3D separation measurements

Request a detailed protocol

For each single kinetochore, X, Y, Z coordinates for 2D or 3D centroid positions were measured for each fluorescent color by using a 3D Gaussian fitting function and saved in an Excel file. The values of X, Y, Z coordinates were copied into another Excel file named ‘2D 3D separation’. The 2D 3D separation file had all equations and calculated S(2D) and S(3D) using the equations described in Text and Figure 1. We applied Maximum likelihood fit (Churchman et al., 2006) for raw 2D or raw 3D values termed ML2D and ML3D when the separation was larger than 18 nm (See Text). The Matlab program called ML2D and ML3D read the raw 2D and raw 3D values in the Excel file and applied maximum likelihood fit to produce ML2D and ML3D. Then, the final ML2D and ML3D values with SD were copied from Matlab to the 2D 3D separation Excel file. The 2D 3D separation Excel file also provided the values of angle α and β (detail in Text). Note, because angles α and β were the angles relative to K-K axis, it required placing the x, y, z coordinates of sister kinetochore pairs in order. Then, the values were reorganized based on their x coordinate values within sister kinetochore pair in the Excel file. To obtain angle α and β values and also to directly compare the separation values by using Delta, 2D and 3D methods with same data sets, we usually measured sister kinetochore pairs in this study. However, the values for S(2D), S(3D), ML2D, and ML3D do not require sister kinetochore pairs. The programs used in this study can be obtained in the supplementary materials (Source code 2–3). At least two independent replicates of 2D and 3D separation measurements were performed.

Statistical analysis

Request a detailed protocol

Statistical significance was determined using two tailed unpaired student’s t-test for comparison between two independent groups. For significance, **p<0.05 was considered statistically significant. The Delta, 2D, 3D separation and signal intensity experiments were replicated at least two independent experiments.

Computational simulations

Request a detailed protocol

The computational simulation used for Figures 8 and 9 was described in the text, Figure 8, and in the MatLab computer simulation files (Source code 1–3). The simulation code is available as a supplementary material.

References

Decision letter

  1. Andrea Musacchio
    Reviewing Editor; Max Planck Institute of Molecular Physiology, Germany

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

[Editors’ note: a previous version of this study was rejected after peer review, but the authors submitted for reconsideration. The first decision letter after peer review is shown below.]

Thank you for submitting your work entitled "Protein Architecture of the Human Kinetochore/Microtubule Interphase at Metaphase from 3-D Fluorescence Co-Localization" for consideration by eLife. Your article has been reviewed by three peer reviewers, one of whom, Andrea Musacchio (Reviewer #1), is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Vivek Malhotra as Senior.

Our decision has been reached after consultation between the reviewers. Based on these discussions and the individual reviews below, we regret to inform you that your work will not be considered further for publication in eLife.

As you will see, all three reviewers recognise the considerable merit of your work. They also recognise that previous work leading to the development of the "δ" concept in the Salmon laboratory has been transformative for the kinetochore field. Finally, the reviewers appreciate that the work presented here confirms the general usefulness of the method, and is therefore timely, also in consideration of the recent work from the Khodjakov and McAinsh laboratories, part of which published in eLife, which questioned some aspects of the work.

All this said, however, the three reviewers and the Reviewing Editor share the view that the current form of the manuscript lacks the clarity required to be accepted by the community as a generally useful technical resource. All three reviewers advocate an almost complete re-writing of the manuscript. As we realise that this will require considerable time and effort, we feel forced to return the manuscript to you and leave you an opportunity to decide on further moves. We will be happy to consider a revised form of the manuscript that fully meets the indications provided by the reviewers. This, however, will have to be considered a new submission.

Reviewer #1:

In this manuscript, the authors revisit and extend a method for 3D fluorescence co-localization that they originally developed with the goal of measuring distances between various proteins in the kinetochore. In short, the method allows assigning three-dimensional coordinates to the centroids of the fluorescence distributions of selected proteins (or antibodies that bind to them), and, after appropriate corrections, determining their mean distance. The layered distribution of proteins makes this approach particularly suited to the study of kinetochores. However, two recent papers (Smith et al., 2016; Magidson et al., 2016) have questioned, on different grounds, the conclusions of the authors' previous work, and solicited this response.

The Smith et al. paper applied a conceptually similar approach to the one originally proposed by the authors, but extended the analysis to three dimensions, finding co-localization distances that were significantly larger than those originally described by the authors. The Magidson et al. paper, on the other hand, questioned the foundation of the approach, in particular because it found, through an electron microscopy analysis, that the surface of kinetochores undergoes shrinking and becomes uneven under the fixation conditions originally used by the authors. Here, the authors appear to respond convincingly to both these previous papers. Their broad and thoughtful analysis identified all potential sources of errors in their methodology (the variance in fluorescence centroid determination, the variance of the mean chromatic aberration used for correction, and the thickness of the coverslip), and demonstrates that it is possible to obtain largely consistent distance measurements in one, two, and three dimensions provided that these sources of error are adequately addressed. Furthermore, the authors demonstrate that their approach provides estimates of distances that are largely independent of the specific fixation procedure.

Overall, the study provides further support to the usefulness of a method that has already contributed quite decisively to our understanding of kinetochore organization. Although the study is largely confirmatory for what regards kinetochore architecture (addressing which was not the main purpose of the manuscript), confirmation of the method's robustness has the potential to provide the community with a tool that can contribute to resolve crucial questions in kinetochore biology, in particular for what concerns the effects of force in kinetochore architecture.

On a less positive tone, as written the paper is a true heavy weight, and I rather strongly feel that the authors have to work very seriously to streamline their descriptions, simplify the figures, and shorten the text to make the paper more accessible. For instance, the mathematical analysis currently in Figure 3 could be summarized and presented in a separate box. Each figure comes with approximately 15 panels, and it would be preferable to present most of these data in form of a table in the main text and as plots in Supplementary. Also, the authors may want to harmonize font size throughout their figures, as the figures look very heterogeneous.

Reviewer #2:

Summary of the work and its relation to previous publications:

This paper presents exhaustive measurements of nanoscale distances between components within the kinetochores of human tissue-culture cells (HeLa cells). It is one of a series of studies, beginning with ground-breaking work from the Salmon lab (Wan et al., 2009), aimed at mapping the arrangement of kinetochore components, i.e. "the protein architecture of the kinetochore", in human cells fixed at metaphase of the cell cycle. The overall approach is to label by immunofluorescence two different kinetochore components with markers of two different colors, and then to measure the "intra-kinetochore distance" between the centroids of the two partially overlapping spots with sub-wavelength accuracy, from optical micrographs. The method is beautifully simple in principle. However, it is challenging in practice for technical reasons. There are limitations inherent to multi-color optical microscopy, such as the inevitable misregistration between images recorded in different color channels, and the statistical uncertainty in localization of any sub-wavelength object of finite brightness. There are also limitations due to prep-to-prep, cell-to-cell, and kinetochore-to-kinetochore variability. Nevertheless, sub-wavelength optical mapping of intra-kinetochore distances has provided very important information about how kinetochore components are arranged in cells, on average, and has had a major impact on how mitosis researchers view the kinetochore. A key concept has emerged, that changes in certain intra-kinetochore distances ('intra-kinetochore stretch') might provide the molecular basis for selective silencing of checkpoint signals and stabilization of microtubule attachments when sister kinetochores are properly bioriented.

This new paper is a response to recent publications from other groups that raised questions about the interpretation of sub-wavelength kinetochore maps (Magidson et al., 2016 and Smith, McAinsh and Burroughs, 2016). In earlier work, intra-kinetochore distances were measured as projections along a line, drawn between two sister kinetochores in the horizontal (x-y) plane, and then averaged to give a single value, called "Δ", for both sister kinetochores. The Δ method corrects locally for color mis-registration, because chromatic shifts will be opposite for kinetochores facing in exactly opposite (anti-parallel) directions. However, the Δ method ignores the possibility that two sister kinetochores might have different architectures or non-anti-parallel orientations. The studies of Magidson et al. and Smith et al. suggest that there can be significant tilting or swiveling of the outer portions of a kinetochore relative to the line connecting it to its sister, especially after treatment with microtubule poisons such as taxol or nocodazole. Magidson et al. also used correlative light and electron microscopy to show that individual kinetochores can become distorted, and that deviations from the canonical trilaminar plate morphology might correlate with high Δ values. Both Magidson et al. and Smith et al. suggest intra-kinetochore distances should be measured in two or three dimensions (2D or 3D), to account for tilting/swiveling, and both warn that projection onto the (1D) line connecting sisters, and averaging over the sisters, as in the Δ method, could underestimate distances and lead to misleading conclusions about the effects of microtubule drugs. Magidson et al. further show that different fixation methods (e.g., glutaraldehyde versus formaldehyde) can change the measured distances. Overall, these papers suggest exercising caution when interpreting Δ measurements.

In response, the new paper by Suzuki et al. presents an enormous amount of data. Control experiments with two colors labeling the same epitope are used to estimate chromatic shifts in 2D and 3D, for two different types of fixation and two different mounting media. Intra-kinetochore distances from the 9G3 epitope on Ndc80 to many other epitopes, on Cenp-T, Nuf2, Spc24, Spc25, and Cenp-A, are mapped using three different analysis methods, including the 1D Δ method, 2D, and fully 3D methods. Besides raw mean intra-kinetochore distances (+/- standard deviations), maximum likelihood methods are also applied in 2D and 3D, to account for the non-gaussian distributions expected whenever distances between two imperfectly localized objects are measured. The 9G3-to-Cenp-T distance is also mapped repeatedly for nine different fixation/permabilization protocols. Simulations were performed to assess how uncertainties in spot localization and in chromatic shifts influence the estimates of intra-kinetochore distance and tilt angles when using the various (2D and 3D) analysis methods. It is suggested that the true amount of kinetochore tilting is negligible, on the basis that a large fraction of the variability in measured tilt angles can be explained by uncertainties in localization and chromatic shift. The possibility of kinetochore-to-kinetochore variability in the measured distances is likewise discounted, again on the basis that much of the apparent variability can be explained by uncertainties in localization and chromatic shift. The possibility of cell-to-cell variability is discounted on the basis that the mean intra-kinetochore distance (between 9G3 and Spc25-EGFP) for a set of 120 individual kinetochores within a single cell is indistinguishable from that of 140 sister pairs in several cells. The overall conclusions are that kinetochore architecture is quite uniform, sisters are very nearly anti-parallel, and previous suggestions to the contrary were flawed because localization uncertainty was not adequately taken into account.

General assessment:

While the shear amount of data here is impressive, it unfortunately is not presented in an accessible way. Without a much clearer presentation, I do not feel the manuscript in its current form can serve as a useful technical resource. In many instances, it is extremely difficult to understand what is being plotted, and what are the primary important messages that the authors wish to draw from each piece of data. Some interesting and potentially valuable technical concepts are considered, such as the likelihood that variation in coverslip thickness causes large chromatic shifts in the z-direction, and the possibility that kinetochore tilting seen by other groups could be an artifact due to the inherent uncertainty in localizing dim fluorescence spots. However, it is extremely difficult to discern whether either of these potentially interesting points can be supported by the data. In my view, this paper is not ready for publication. Below I have listed specific comments which I hope can help the authors improve their presentation.

Substantive concerns:

Results section: "Because other Δ measurements had smaller SDs, we settled on values of Sxsd=Sysd = 4 and Szsd = 8, since there could have been some unexpected CA contribution to Δ variance from unknown local changes in refractive index." This seems arbitrary. The sentences just prior to this one suggested that larger values were needed to explain the data. Why go through the trouble to estimate carefully what is needed to explain the data, only to then impose an ad hoc reduction?

Results section: "The simulation data also shows that the combination of variances in centroid measurement and CA correction can account for a large fraction of the variance in tilt angles[…]This suggests that the majority of proteins linking the inner to outer kinetochore are aligned along the kMT axis." This is one of the key conclusions of the paper but it is not well supported. A thorough analysis would state explicitly how much of the variability is explained by the uncertainties in localization and chromatic shift, and also how much real kinetochore tilting would be consistent with the data.

Results section: "after depletion of the endogenous protein by RNAi" How effective was the depletion?

Results section: "This result indicates that most of the Z-offset in the original Sz data is not produced by unequal numbers of kinetochores from above and below the spindle axis, but likely from somewhat thinner coverslips than the standard 0.17 mm thickness (Figure 7C)." This potentially interesting point is not rigorously supported without a demonstration that coverslips of known thickness but deviating from the standard 0.17 mm produce predictable changes in Z-offset. It seems that it would be a straightforward experiment to measure coverslips thicknesses and then prepare and analyze cells on those coverslips that happen to deviate from the standard.

Discussion section: "[…]we found that measurements of individual kinetochores (not sister pairs) within a single cell yielded the identical value at metaphase as the mean obtained from kinetochores within several cells. Thus, variations between cells or selected kinetochore measurements like Δ analysis is not an issue." This is overstated. The data in Figure 4E show only that mean values for populations of hundreds of kinetochores are consistent. But they say nothing about kinetochore-to-kinetochore variability. And "several cells" is unclear. How many cells? If the number is very small then the data cannot strongly support the conclusion that cell-to-cell variability is negligible.

The widespread, inconsistent, and redundant use of variables in this paper is extremely confusing. Figure 3 alone introduces at least 25 different variables: X1p, Y1p, Z1p, Sxsd, Sysd, Szsd, CAxp, CAyp, CAzp, CAxsd, CAysd, CAzsd, randn, Sxp, Syp, Szp, Sxyp, Sxyzp, CAxe, CAxs, CAye, CAys, CAze, CAzs. Sometimes two different variables seem to denote the same quantities, for example in Figure 1C, where both CAx and Xg – Xr are used, whereas in Figure 1—figure supplement 1, only Xg – Xr is used. Conversely, two different calculations are sometimes represented by the same variable, such as S(3D), which does not include the correction for chromatic shift in Figure 1, but does include the correction in later figures. When the variables x and y are used in the equations for regression lines, they are often contradictory with respect to the plotted quantities, such as in Figure 1—figure supplement 1, where the regression variable x sometimes denotes Y (y-axis position in pixels) and the regression variable y sometimes denotes Xg-Xr (chromatic shift along x-axis in nanometers). When used sparingly and consistently, variables can make difficult mathematical concepts easier to follow. But here the use of variables seems to obfuscate things. It might help to adopt vector notation, to allow more compact expressions that capture the important conceptual relationships without explicitly showing all three cardinal directions.

The paper includes a huge number of scatterplots (I count ~59) and histograms (~32). Most of the scatterplots lack clear trends with respect to changes in the x-, y-, or z-position. In general, these plots seem to provide lots of clutter without adding much insight.

Reviewer #3:

This manuscript addresses a significant challenge: how to appropriately localize kinetochore components to measure distances between them. Different distance measurement methods have been used, and have at times led to different results. To move forward on solid ground, discrepancies must be reconciled, understood and explained. This is what this works attempts to do: it systematically and carefully explores the effect of different parameters (centroid determination, chromatic aberration correction, coverslip thickness and fixation method) on measured distances. The authors also provide a helpful computational framework for exploring how the variance in some of these parameters affects distance measurements. Importantly, the manuscript presents a 'molecular ruler' for checking the accuracy of 1D, 2D and 3D localization of kinetochore components by using the Ndc80 complex as a standard. Pending some changes outlined below, this work can become a significant contribution as a tool and resource, not just to those interested in kinetochores but to those interested in a broad array of cellular macromolecular assemblies.

Major concerns:

The paper as written is challenging to read and needs significant changes to both the text and figures to become an accessible – and used – resource.

1) While it is clear that the authors achieve more accurate centroid localization than previous works, the text does not clearly synthesize which practices together made this possible, and what experimental and analysis pipeline people should use to achieve such accuracy (what's good enough, and what isn't?). As one example to help guide changes, Figure 7 illustrates how Sz varies with imaging depth and kinetochore tilt, but the text describing this figure does not explain how this data relates to the rest of the work nor makes a concrete suggestion about best practices. Making a clear connection between the data and actionable outcomes is critical for this work to be a useful tool, and will help create a constructive, positive tone towards improving future measurements. On this note, it would be helpful to integrate in a single new figure the final suggested pipeline for obtaining accurate 3D measurements – unless the authors have a better idea for how to do that.

2) The figures are unnecessarily complicated and often very hard to read. The authors should take the time to think about which figures are essential for the main text and which are not, and should take the time to make their figures clear enough to stand alone. Figures should be significantly simplified. As examples, Figure 1D could be moved to the supplement and Figures 5 and 6 could be moved or condensed. (In addition, it is critical that plots in all figures have clearly labeled axes in readable font sizes, and there must be no confusion about what is measured).

[Editors’ note: what now follows is the decision letter after the authors submitted for further consideration.]

Thank you for resubmitting your work entitled "An Optimized Method for 3D Fluorescence Co-Localization Applied to Human Kinetochore Protein Architecture" for further consideration at eLife. Your revised article has been favorably evaluated by Andrea Musacchio (Senior editor) and two reviewers.

This new version of the manuscript is greatly improved and we thank you for the effort you put into your resubmission. There are however some remaining issues that you might elect to address in a final version of the manuscript before acceptance, as outlined below. I have retained the reviewers' comments without editing them, as both reviewers feel that you should feel free to decide whether to incorporate change or not. I would be grateful if you could consider these points carefully, especially the major comments expressed by Reviewer 2.

Reviewer #1:

This is a resubmission of a previously reviewed manuscript. This manuscript addresses a significant challenge: how to appropriately localize kinetochore components to measure distances between them. Different distance measurement methods have been used, and have at times led to different results. To move forward on solid ground, discrepancies must be reconciled, understood and explained. This is what this works does, using both experiment and computation. The new manuscript largely addresses my two previous major concerns: it now synthesizes what experimental and analysis pipeline people should be used to achieve optimal accuracy, and presents simplified/clearer figures and text. This work is now a significant contribution as a tool and resource, not just to those interested in kinetochores but to those interested in a broad array of cellular macromolecular assemblies.

Reviewer #2:

This paper is very significantly improved. I commend the authors for their very careful reworking. I think the result is a paper that can serve as a very important resource, not only to the community of scientists interested in kinetochore architecture, but also more broadly, to microscopists studying the architectures of other large molecular assemblies inside cells. I hope the following relatively minor comments will help the authors further improve their manuscript in preparation for publication. In particular, I feel the impact of the paper could be boosted by a more quantitative analysis of the amount of true, kinetochore-to-kinetochore variability that would be compatible with the measurements, as explained in the last two comments below.

Results section: "Unexpectedly, in vivo, the C-terminus of Ndc80 locates much closer to the globular domains of Spc24/Spc25 (Figure 4B). This difference might be caused by structural restrictions on the position of the EGFP tag, which was tethered to the protein end by a 9 amino acid linker." A structure for the tetramerization domain within the Ndc80 complex is available (Valverde, Ingram and Harrison, 2016). Can the apparent arrangement in vivo of the C-termini of Ndc80 and Nuf2 and the N-termini of Spc24 and Spc25 be reconciled with this published structure? Or does one need to further invoke "restrictions" on the epitopes/antibodies to reconcile these different views of the Ndc80 complex? More generally, the published structures for the Ndc80 complex can provide predictions for the distances between many of the antibody pairs used in this study. Why not include a comprehensive, graphical comparison of predicted versus measured distances? If the correlation is good, then such a comparison would provide very compelling additional support for the accuracy of the fluorescence colocalization technique. It would also help clarify what is the in vivo structure of the Ndc80 complex.

Discussion section: "Note that their higher SDc values explains why their Δ measurements are significantly larger than ours (Figure 9—figure supplement 1)." This statement seems a bit overstated to me considering that the authors can only estimate the SDc values of their competitor's work – they do not know the SDc values from that work with 100% certainty. In my view, it would be more correct, and would not undercut the impact of the present paper at all, to qualify the sentence very slightly as follows: "Such high SDc values could explain[…]" or "Such high SDc values probably explain[…]"

Discussion section; "A previous study has shown that the accuracy of separation measurements is sensitive to the spatial staggering of the labeled molecules along the kinetochore inner to outer axis only for stagger greater than 150 nm, which produces two fluorescent peaks instead of a single peak (Joglekar et al., 2009)." This statement seems over-simplified to me, and potentially confusing. The production of two peaks is not a general consequence of staggering of the labeled molecules. It occurred in a highly idealized simulation in the cited paper, where the simulated positions of six red spots were shifted by fixed distances in the x-direction relative to a corresponding set of six green spots. More random staggered arrangements could retain a single fluorescent peak, but with a larger width compared to a case without staggering.

Discussion section: "Second, the SD of our 2D/3D measurements are small, typically less than 10 nm, and a significant part of this SD must be from the SDc and CAsd (see above discussion) and not from differences between kinetochores." This is interesting, but it only weakly supports the "uniform architecture" hypothesis. A key question is, how much true, kinetochore-to-kinetochore variability in distance is compatible with the measured SDs? Based on the data and analyses presented in this paper, it should be possible to make a quantitative statement about how wide the underlying distribution of true distances is likely to be. The purely qualitative statement, that the architecture is "very" uniform, seems a bit hollow.

Discussion section: "Surprisingly, only 10~15 kinetochores needed to be averaged to achieve the mean and SD typical of > 150 kinetochores (Figure 9—figure supplement 2)." This observation merely indicates that 10 to 15 kinetochores are sufficient to estimate the mean and width of the distribution. It does not by itself indicate anything about the width, i.e. about the level of kinetochore-to-kinetochore variability.

https://doi.org/10.7554/eLife.32418.036

Author response

[Editors’ note: the author responses to the first round of peer review follow.]

All this said, however, the three reviewers and the Reviewing Editor share the view that the current form of the manuscript lacks the clarity required to be accepted by the community as a generally useful technical resource. All three reviewers advocate an almost complete re-writing of the manuscript. As we realise that this will require considerable time and effort, we feel forced to return the manuscript to you and leave you an opportunity to decide on further moves. We will be happy to consider a revised form of the manuscript that fully meets the indications provided by the reviewers. This, however, will have to be considered a new submission.

We appreciate that all reviewers found our study important and with considerable merit. We also thank the reviewers for their constructive comments and suggestions. As requested by the reviewers and the editor, both the text and figures have been reorganized and edited to “improve clarity of the manuscript to the level required by the community as a general useful technical resource.”

Significant modifications in the revised manuscript to improve clarity are as follows:

1) Addition of a “Principles of the Method” section to the beginning of the Results with a corresponding Figure containing schematic and numerical information of the analytical method to provide the requested “pipeline for obtaining accurate 3D measurements”, and Figure 1—source data 1 providing details of each step and potential error sources.

2) Re-organization of all figures to put key findings in the main Figures and supporting data in corresponding Figure supplement in a logical way to comply with their presentation in eLife.

3) Unified the names of variables used in both the experimental data analysis and the computer simulation of the method to make the fundamental principles clearer for the reader to follow.

4) Provided new data in the Materials and methods to address the question from the reviewers about missing data: the efficiency of endogenous protein depletion by siRNA for the EGFP labeled protein components of the Ndc80 complex.

5) Made modifications or additions to the text in response to the specific reviewer’s concerns as listed below.

Reviewer #1:

[…]

On a less positive tone, as written the paper is a true heavy weight, and I rather strongly feel that the authors have to work very seriously to streamline their descriptions, simplify the figures, and shorten the text to make the paper more accessible. For instance, the mathematical analysis currently in Figure 3 could be summarized and presented in a separate box. Each figure comes with approximately 15 panels, and it would be preferable to present most of these data in form of a table in the main text and as plots in Supplementary. Also, the authors may want to harmonize font size throughout their figures, as the figures look very heterogeneous.

We addressed this issue as summarized in “Significant modifications in the revised manuscript to improve clarity”.

Reviewer #2:

[…]

General assessment:

While the shear amount of data here is impressive, it unfortunately is not presented in an accessible way. Without a much clearer presentation, I do not feel the manuscript in its current form can serve as a useful technical resource. In many instances, it is extremely difficult to understand what is being plotted, and what are the primary important messages that the authors wish to draw from each piece of data. Some interesting and potentially valuable technical concepts are considered, such as the likelihood that variation in coverslip thickness causes large chromatic shifts in the z-direction, and the possibility that kinetochore tilting seen by other groups could be an artifact due to the inherent uncertainty in localizing dim fluorescence spots. However, it is extremely difficult to discern whether either of these potentially interesting points can be supported by the data. In my view, this paper is not ready for publication. Below I have listed specific comments which I hope can help the authors improve their presentation.

We addressed the general “clarity” issue as summarized in “Significant modifications in revised manuscript to improve clarity”.

Substantive concerns:

Results section: "Because other Δ measurements had smaller SDs, we settled on values of Sxsd=Sysd = 4 and Szsd = 8, since there could have been some unexpected CA contribution to Δ variance from unknown local changes in refractive index." This seems arbitrary. The sentences just prior to this one suggested that larger values were needed to explain the data. Why go through the trouble to estimate carefully what is needed to explain the data, only to then impose an ad hoc reduction?

To clarify this issue, we edited the relevant paragraph in the results to read (Note Ssd is now named SDc for variance in centroid determination):

“To obtain an estimate of the error contributed from the SDc, we used results from Δ analysis which in principle have local CA correction. […] This result indicates that the variance in our centroid measurement is very small and only slightly enhances the 3D measurements from the true value.”

Results section: "The simulation data also shows that the combination of variances in centroid measurement and CA correction can account for a large fraction of the variance in tilt angles[…]This suggests that the majority of proteins linking the inner to outer kinetochore are aligned along the kMT axis." This is one of the key conclusions of the paper but it is not well supported. A thorough analysis would state explicitly how much of the variability is explained by the uncertainties in localization and chromatic shift, and also how much real kinetochore tilting would be consistent with the data.

We deleted this conclusion from the simulation section of the revised manuscript and inserted the following sentence at the end of the section of the Results entitled: “The Mean Human Kinetochore Protein Architecture at Metaphase Measured by the Δ Method and Our 3D Method are Similar.” to read:

“In Figure 5, the Ndc80 complex and protein linkage to the inner kinetochore are shown aligned with the axis of kMTs because the ML3D mean separation values are only slightly greater than their corresponding Δ values and the Δ value is a projection of the ML3D value along the K-K axis.”

In addition, we have added the potential errors in angle measurements in the result section of kinetochore tilt and simulation in revised manuscript to read:

“Unlike 3D separation, the mean tilt angle β was sensitive to unequal numbers of kinetochores above and below the spindle equator. The mean angle β is near zero in the middle of the spindle and reaches mean values of about 20-25 degrees at the bottom and top of the spindle (Figure 6 —figure supplement 2C).”

and

“To see how the SDc and CAsd of our measurement method effect the variances in the angles α and β, we entered into the simulation constant values for S between zero and 100 nm (Figure 8B). The variance in the angles α and β are largest for small separations (Figure 8B). Our SDc and CAsd caused about half to two-thirds of the variance measured in cells for separations of 60 nm (CENP-T-Hec1-9G3 in Figure 3C) or 90 nm (CENP-A-Hec1-9G3 in Figure 6—figure supplement 2).”

Results section: "after depletion of the endogenous protein by RNAi" How effective was the depletion?

We have added the efficiency of protein depletion in Materials and methods of the revised manuscript. The new sentences read:

“siRNA was performed with 100 nM of siRNA duplex and siRNA sequences of CENP-T, CENP-C, Ndc80, and Nuf2 were described previously (DeLuca et al., 2002; Suzuki et al., 2015). […]Although we performed siRNA for endogenous proteins when we used cell lines expressing EGFP tagged protein, there was no significant differences for Δ, 2D, and 3D separation measurements in Ndc80-EGFP stable cells with or without siRNA for Ndc80.”

Results section: "This result indicates that most of the Z-offset in the original Sz data is not produced by unequal numbers of kinetochores from above and below the spindle axis, but likely from somewhat thinner coverslips than the standard 0.17 mm thickness (Figure 7C)." This potentially interesting point is not rigorously supported without a demonstration that coverslips of known thickness but deviating from the standard 0.17 mm produce predictable changes in Z-offset. It seems that it would be a straightforward experiment to measure coverslips thicknesses and then prepare and analyze cells on those coverslips that happen to deviate from the standard.

To address this issue, we added a new Graph and the following sentence:

“The plot in Figure 6—figure supplement 1 illustrates the sensitivity of Z-offset to coverslip thickness. A steep slope is seen when measured Z-offset values in Figure 6C are plotted as a function of the mean thickness we measured for #1, #1.5 and #2 coverslips.”

Discussion section: "[…]we found that measurements of individual kinetochores (not sister pairs) within a single cell yielded the identical value at metaphase as the mean obtained from kinetochores within several cells. Thus, variations between cells or selected kinetochore measurements like Δ analysis is not an issue." This is overstated. The data in Figure 4E show only that mean values for populations of hundreds of kinetochores are consistent. But they say nothing about kinetochore-to-kinetochore variability. And "several cells" is unclear. How many cells? If the number is very small then the data cannot strongly support the conclusion that cell-to-cell variability is negligible.

The above sentence was miss-worded. The corrected sentences read:

“Sister kinetochore pairs were used for majority of measurements in this study to directly compare separations obtained by Δ and 2D/3D fluorescent co-localization methods using the same data sets. To test if selection of sister pairs influenced our measurements, we measured 120 kinetochores selected randomly in a single cell. This produced a mean separation value nearly identical to the mean value for single kinetochore measurements of sister pairs obtained from 6 metaphase cells (Figure 4C).”

The widespread, inconsistent, and redundant use of variables in this paper is extremely confusing. Figure 3 alone introduces at least 25 different variables: X1p, Y1p, Z1p, Sxsd, Sysd, Szsd, CAxp, CAyp, CAzp, CAxsd, CAysd, CAzsd, randn, Sxp, Syp, Szp, Sxyp, Sxyzp, CAxe, CAxs, CAye, CAys, CAze, CAzs. Sometimes two different variables seem to denote the same quantities, for example in Figure 1C, where both CAx and Xg – Xr are used, whereas in Figure 1—figure supplement 1, only Xg – Xr is used. Conversely, two different calculations are sometimes represented by the same variable, such as S(3D), which does not include the correction for chromatic shift in Figure 1, but does include the correction in later figures. When the variables x and y are used in the equations for regression lines, they are often contradictory with respect to the plotted quantities, such as in Figure 1—figure supplement 1, where the regression variable x sometimes denotes Y (y-axis position in pixels) and the regression variable y sometimes denotes Xg-Xr (chromatic shift along x-axis in nanometers). When used sparingly and consistently, variables can make difficult mathematical concepts easier to follow. But here the use of variables seems to obfuscate things. It might help to adopt vector notation, to allow more compact expressions that capture the important conceptual relationships without explicitly showing all three cardinal directions.

We significantly unified variable names between those used for experimental analysis and those used in the computer simulations.

The paper includes a huge number of scatterplots (I count ~59) and histograms (~32). Most of the scatterplots lack clear trends with respect to changes in the x-, y-, or z-position. In general, these plots seem to provide lots of clutter without adding much insight.

We have significantly modified Figure construction to put key data in the major figures and supporting data in Supplemental Figures using the eLife format.

Reviewer #3:

Major concerns:

The paper as written is challenging to read and needs significant changes to both the text and figures to become an accessible and used resource.

1) While it is clear that the authors achieve more accurate centroid localization than previous works, the text does not clearly synthesize which practices together made this possible, and what experimental and analysis pipeline people should use to achieve such accuracy (what's good enough, and what isn't?). As one example to help guide changes, Figure 7 illustrates how Sz varies with imaging depth and kinetochore tilt, but the text describing this figure does not explain how this data relates to the rest of the work nor makes a concrete suggestion about best practices. Making a clear connection between the data and actionable outcomes is critical for this work to be a useful tool, and will help create a constructive, positive tone towards improving future measurements. On this note, it would be helpful to integrate in a single new figure the final suggested pipeline for obtaining accurate 3D measurements – unless the authors have a better idea for how to do that.

We have significantly modified the manuscript and figures to address these concerns as outlined in the first page in “Significant modifications in revised manuscript to improve clarity.”

2) The figures are unnecessarily complicated and often very hard to read. The authors should take the time to think about which figures are essential for the main text and which are not, and should take the time to make their figures clear enough to stand alone. Figures should be significantly simplified. As examples, Figure 1D could be moved to the supplement and Figures 5 and 6 could be moved or condensed. (In addition, it is critical that plots in all figures have clearly labeled axes in readable font sizes, and there must be no confusion about what is measured).

Again, we have significantly modified the manuscript and figures to address these concerns as outlined in the first page in “Significant modifications in revised manuscript to improve clarity.”

[Editors' note: the author responses to the re-review follow.]

Reviewer #2:

This paper is very significantly improved. I commend the authors for their very careful reworking. I think the result is a paper that can serve as a very important resource, not only to the community of scientists interested in kinetochore architecture, but also more broadly, to microscopists studying the architectures of other large molecular assemblies inside cells. I hope the following relatively minor comments will help the authors further improve their manuscript in preparation for publication. In particular, I feel the impact of the paper could be boosted by a more quantitative analysis of the amount of true, kinetochore-to-kinetochore variability that would be compatible with the measurements, as explained in the last two comments below.

Results section: "Unexpectedly, in vivo, the C-terminus of Ndc80 locates much closer to the globular domains of Spc24/Spc25 (Figure 4B). This difference might be caused by structural restrictions on the position of the EGFP tag, which was tethered to the protein end by a 9 amino acid linker." A structure for the tetramerization domain within the Ndc80 complex is available (Valverde et al., 2016). Can the apparent arrangement in vivo of the C-termini of Ndc80 and Nuf2 and the N-termini of Spc24 and Spc25 be reconciled with this published structure? Or does one need to further invoke "restrictions" on the epitopes/antibodies to reconcile these different views of the Ndc80 complex? More generally, the published structures for the Ndc80 complex can provide predictions for the distances between many of the antibody pairs used in this study. Why not include a comprehensive, graphical comparison of predicted versus measured distances? If the correlation is good, then such a comparison would provide very compelling additional support for the accuracy of the fluorescence colocalization technique. It would also help clarify what is the in vivo structure of the Ndc80 complex.

We have added a detailed comparison between our measurements and previous studies in vitro (Huis In 't Veld et al., 2016; Valverde et al., 2016; Wei et al., 2005) in Figure 4—figure supplement 1.

Discussion section: "Note that their higher SDc values explains why their Δ measurements are significantly larger than ours (Figure 9—figure supplement 1)." This statement seems a bit overstated to me considering that the authors can only estimate the SDc values of their competitor's work – they do not know the SDc values from that work with 100% certainty. In my view, it would be more correct, and would not undercut the impact of the present paper at all, to qualify the sentence very slightly as follows: "Such high SDc values could explain[…]" or "Such high SDc values probably explain[…]"

Thank you for an important suggestion. We have modified this and subsequent sentences to read;

“Such high CDsd values could explain why their Δ measurements are significantly larger than ours (Figure 9—source data 1). […]In our measurements, large values of Zoffset were rare (Figure 5—source data 1); we have no information to judge how much other sources of error like Z-offset, contributed to the Smith, McAinsh and Burroughs, 2016 measurements.”

Discussion section; "A previous study has shown that the accuracy of separation measurements is sensitive to the spatial staggering of the labeled molecules along the kinetochore inner to outer axis only for stagger greater than 150 nm, which produces two fluorescent peaks instead of a single peak (Joglekar et al., 2009)." This statement seems over-simplified to me, and potentially confusing. The production of two peaks is not a general consequence of staggering of the labeled molecules. It occurred in a highly idealized simulation in the cited paper, where the simulated positions of six red spots were shifted by fixed distances in the x-direction relative to a corresponding set of six green spots. More random staggered arrangements could retain a single fluorescent peak, but with a larger width compared to a case without staggering.

Our writing was not clear. This paragraph now reads:

“Human kinetochores are built from multiple copies of core-kinetochore proteins (Suzuki et al., 2016). […] This indicates that our centroid measurements correspond to the mean position of the fluorescently labeled protein epitopes within human kinetochores.”

Discussion section: "Second, the SD of our 2D/3D measurements are small, typically less than 10 nm, and a significant part of this SD must be from the SDc and CAsd (see above discussion) and not from differences between kinetochores." This is interesting, but it only weakly supports the "uniform architecture" hypothesis. A key question is, how much true, kinetochore-to-kinetochore variability in distance is compatible with the measured SDs? Based on the data and analyses presented in this paper, it should be possible to make a quantitative statement about how wide the underlying distribution of true distances is likely to be. The purely qualitative statement, that the architecture is "very" uniform, seems a bit hollow.

Discussion section: "Surprisingly, only 10~15 kinetochores needed to be averaged to achieve the mean and SD typical of > 150 kinetochores (Figure 9—figure supplement 2)." This observation merely indicates that 10 to 15 kinetochores are sufficient to estimate the mean and width of the distribution. It does not by itself indicate anything about the width, i.e. about the level of kinetochore-to-kinetochore variability.

We asked how much kinetochore-to-kinetochore variability can be involved in our experimental measurements using simulations in Figure 9—source data 2. Based on these results, we have modified sentences to read: “Second, as expected for the Gaussian distribution measured for separation values (e.g. Figure 3B), we found that only 10~15 kinetochores were needed to be averaged to achieve the mean and SD typical of > 150 kinetochores (Figure 9—figure supplement 1). Third, the SD of our 2D/3D measurements are small, typically less than 12 nm, and a significant part of this SD must be from the CDsd and CAsd (Table 6A and see above discussion) and not from differences between kinetochores. To see this more clearly, we used the same simulations in Figures 8–9 with mean kinetochore-to-kinetochore variability (Ksd = ± 0, ± 5, ± 10, or ± 15 nm) (Figure 9—source data 2). Simulation results showed that Ksd of about ± 5 nm or less plus measurement CDsd and CAsd yielded the experimental mean SD value of 12.5 nm (Figure 9—source data 2). These results imply that the vast majority of kinetochores at metaphase have a similar protein architecture”

https://doi.org/10.7554/eLife.32418.037

Article and author information

Author details

  1. Aussie Suzuki

    Department of Biology, University of North Carolina at Chapel Hill, Chapel Hill, United States
    Contribution
    Conceptualization, Resources, Data curation, Software, Formal analysis, Funding acquisition, Investigation, Visualization, Methodology, Writing—original draft, Writing—review and editing
    For correspondence
    suzukia@email.unc.edu
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-7390-5116

  2. Sarah K Long

    Department of Biology, University of North Carolina at Chapel Hill, Chapel Hill, United States
    Contribution
    Data curation
    Competing interests
    No competing interests declared

  3. Edward D Salmon

    Department of Biology, University of North Carolina at Chapel Hill, Chapel Hill, United States
    Contribution
    Conceptualization, Resources, Software, Supervision, Writing—original draft, Project administration, Writing—review and editing
    Competing interests
    No competing interests declared

Funding

National Institutes of Health (R01GM24364)

  • Edward Salmon

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Dr. Frederick Lanni for providing axial intensities of point spread functions based on his paper (Gibson and Lanni, 1992). We also thank Dr. Kerry Bloom and Josh Lawrimore for critical reading of the manuscript. This work was supported by R01GM24364 (EDS) from National Institute of Health.

Reviewing Editor

  1. Andrea Musacchio, Max Planck Institute of Molecular Physiology, Germany

Publication history

  1. Received: September 30, 2017
  2. Accepted: December 22, 2017
  3. Version of Record published: January 11, 2018 (version 1)
  4. Version of Record updated: January 12, 2018 (version 2)

Copyright

© 2018, Suzuki et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 1,993
    Page views
  • 309
    Downloads
  • 14
    Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Aussie Suzuki
  2. Sarah K Long
  3. Edward D Salmon
(2018)
An optimized method for 3D fluorescence co-localization applied to human kinetochore protein architecture
eLife 7:e32418.
https://doi.org/10.7554/eLife.32418

Categories and tags

Research organism

Further reading

    1. Cell Biology

    Insights into cargo sorting by SNX32 and its role in neurite outgrowth

    Jini Sugatha, Amulya Priya ... Sunando Datta
    Research Article Updated

    Sorting nexins (SNX) are a family of proteins containing the Phox homology domain, which shows a preferential endo-membrane association and regulates cargo sorting processes. Here, we established that SNX32, an SNX-BAR (Bin/Amphiphysin/Rvs) sub-family member associates with SNX4 via its BAR domain and the residues A226, Q259, E256, R366 of SNX32, and Y258, S448 of SNX4 that lie at the interface of these two SNX proteins mediate this association. SNX32, via its PX domain, interacts with the transferrin receptor (TfR) and Cation-Independent Mannose-6-Phosphate Receptor (CIMPR), and the conserved F131 in its PX domain is important in stabilizing these interactions. Silencing of SNX32 leads to a defect in intracellular trafficking of TfR and CIMPR. Further, using SILAC-based differential proteomics of the wild-type and the mutant SNX32, impaired in cargo binding, we identified Basigin (BSG), an immunoglobulin superfamily member, as a potential interactor of SNX32 in SHSY5Y cells. We then demonstrated that SNX32 binds to BSG through its PX domain and facilitates its trafficking to the cell surface. In neuroglial cell lines, silencing of SNX32 leads to defects in neuronal differentiation. Moreover, abrogation in lactate transport in the SNX32-depleted cells led us to propose that SNX32 may contribute to maintaining the neuroglial coordination via its role in BSG trafficking and the associated monocarboxylate transporter activity. Taken together, our study showed that SNX32 mediates the trafficking of specific cargo molecules along distinct pathways.

    1. Cell Biology
    2. Stem Cells and Regenerative Medicine

    Atf3 defines a population of pulmonary endothelial cells essential for lung regeneration

    Terren K Niethamer, Lillian I Levin ... Edward E Morrisey
    Research Article

    Following acute injury, the capillary vascular bed in the lung must be repaired to reestablish gas exchange with the external environment. Little is known about the transcriptional and signaling factors that drive pulmonary endothelial cell (EC) proliferation and subsequent regeneration of pulmonary capillaries, as well as their response to stress. Here, we show that the transcription factor Atf3 is essential for the regenerative response of the mouse pulmonary endothelium after influenza infection. Atf3 expression defines a subpopulation of capillary ECs enriched in genes involved in endothelial development, differentiation, and migration. During lung alveolar regeneration, this EC population expands and increases the expression of genes involved in angiogenesis, blood vessel development, and cellular response to stress. Importantly, endothelial cell-specific loss of Atf3 results in defective alveolar regeneration, in part through increased apoptosis and decreased proliferation in the endothelium. This leads to the general loss of alveolar endothelium and persistent morphological changes to the alveolar niche, including an emphysema-like phenotype with enlarged alveolar airspaces lined with regions that lack vascular investment. Taken together, these data implicate Atf3 as an essential component of the vascular response to acute lung injury that is required for successful lung alveolar regeneration.

    1. Cell Biology
    2. Microbiology and Infectious Disease

    Profiling the bloodstream form and procyclic form Trypanosoma brucei cell cycle using single-cell transcriptomics

    Emma M Briggs, Catarina A Marques ... Keith R Matthews
    Research Article Updated

    African trypanosomes proliferate as bloodstream forms (BSFs) and procyclic forms in the mammal and tsetse fly midgut, respectively. This allows them to colonise the host environment upon infection and ensure life cycle progression. Yet, understanding of the mechanisms that regulate and drive the cell replication cycle of these forms is limited. Using single-cell transcriptomics on unsynchronised cell populations, we have obtained high resolution cell cycle regulated (CCR) transcriptomes of both procyclic and slender BSF Trypanosoma brucei without prior cell sorting or synchronisation. Additionally, we describe an efficient freeze–thawing protocol that allows single-cell transcriptomic analysis of cryopreserved T. brucei. Computational reconstruction of the cell cycle using periodic pseudotime inference allowed the dynamic expression patterns of cycling genes to be profiled for both life cycle forms. Comparative analyses identify a core cycling transcriptome highly conserved between forms, as well as several genes where transcript levels dynamics are form specific. Comparing transcript expression patterns with protein abundance revealed that the majority of genes with periodic cycling transcript and protein levels exhibit a relative delay between peak transcript and protein expression. This work reveals novel detail of the CCR transcriptomes of both forms, which are available for further interrogation via an interactive webtool.